在交通流量随机波动较大的交叉口，感应控制的策略能够有效提升绿灯利用率，增加交叉口的通行效率^[1]. 经典的感应控制是利用检测器获取交叉口各个进口道车流的信息，通过改变相位顺序和时长进行实时信号控制的方法^[2]. 学者对感应控制策略的研究较为广泛，相关研究主要集中在控制参数的优化^[3]和相位方案的设计^[4]方面，形成了以交叉口排队车辆数最小或停车延误时长最小为优化目标的各种研究方法.

感应控制参数的优化能够有效提升控制方法的效率. 提出者利用每个阶段的实时排队数据和交通流到达特性^[5]，采用模糊控制^[6]、随机模型^[7]、拉格朗日解析法^[8]动态优化最小和最大绿灯时间，以及单位绿灯延长时间^[9]. 面对多变的交叉口车流环境，分开研究单个参数优化来提升感应控制性能的效果有限，罗小芹等^[10-11]对多个参数进行组合研究. 罗小芹等^[10]采用交通强度指标来确定各相位的初始绿灯时间、最大绿灯时间在混合交通状态下的具体取值，徐洪锋等^[11]在单点全感应控制中采用正交试验方法筛选对交叉口车均延误有重要影响的优化参数组合. 对于感应控制相位方案的设计，刘家瑞^[12]从控制参数和相位控制逻辑2个角度优化感应控制；卢凯等^[13]建立交叉口相位时间多轮分配模型，设计相位设置与信号配时的同步优化方法；王力等^[14]采用交通波理论对剩余排队进行分析量化可控状态，以可控状态为判断条件建立交叉口信号切换控制模型. 利用深度Q学习（deep Q-network，DQN）算法^[15]对交叉口的信号控制优化有一定效果，但是强化学习算法的信号控制应用研究绝大多数集中于交通状态^[16]，忽略了不同流量下其他信号控制参数的取值对动作选取和算法效率的影响.

虽然在进行感应控制策略和深度强化学习算法交叉口应用研究时，学者们考虑到了多变的交通流特征，但是感应控制的关键参数组合的优化方式较为单一，对控制参数取值影响深度强化学习算法的思考较少. 本研究以降低交叉口车辆平均延误为目标，通过设计正交试验筛选感应控制下对交叉口性能具有重要影响的参数组合，确定参数组合的最优取值；设计对比实验验证感应控制参数组合和最佳取值的有效性；将最优参数组合应用在DQN算法中，进一步优化感应信号的控制.

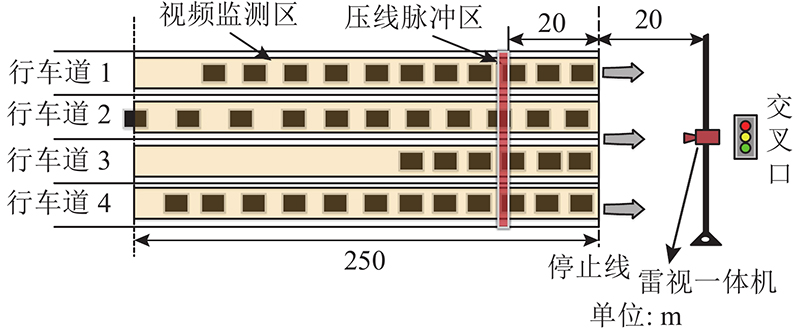
多目标视频跟踪雷达（以下简称雷视一体机）可用于路段车道全天候的监控和相关数据记录分析，它能够对交通信号周期内车流量、平均车速、平均车头时距、平均车道空间占有率、排队长度、排队延误等进行监测和统计. 如图1所示，雷视一体机设置在路口场景中距离停止线20 m处，监测的道路范围为0~250 m. 设置0.5~2.0 m的压线脉冲区，车辆经过该区时计入流量统计，同时检测速度、车头时距信息. 本研究基于雷视一体机的工作机制提出改进的感应控制方法. 视频监测各个进口车道的排队长度，在某个相位绿灯时长内，获得通行权的是没有冲突的车道组合，因此可以利用视频检测区内车道组合平均排队长度来衡量该相位时间内的排队情况：

(1) $ {O_k} = \frac{{{O_{1,k}}+{O_{2,k}}+ \cdots +{O_{n,k}}}}{n} . $

式中：k为相位数，n为某相位内获得通行权的车道数，O_n,k为第k相位内获得通行权的第n条车道的排队长度，O_k为第k相位内获得通行权的车道组合平均排队长度. 在具体的交叉口，可以通过设置合适长度的视频监测区来获取车道组合平均排队长度. 当某一相位获得通行权车道组合的平均排队长度达到最大值时，将其作为感应控制策略中相位改变的阈值. 为了确保黄灯启亮时刻临近停止线且处于中高速运行状态的车辆能够在黄灯结束前通过停止线，将压线脉冲区设置在靠近停车线20 m的入口道内侧，监测是否有临近交叉口的车辆.

改进的感应控制逻辑如图2所示，其中T_min为最小绿灯时长，L_max为车道组合平均排队长度的最大值. 在绿灯启亮时，获得通行权的车道排队车辆开始消散. 本相位最小绿灯时长结束时，系统将判断下一相位即将获得通行权的车道组合排队是否超过L_max，如果超过L_max，则绿灯转入下一项位；如果未超过L_max，则继续判断本相位的压线脉冲区是否被触发，此时根据各条车道的车流量情况设置单位绿灯延长时间和相位切换机制. 为了提升感应控制方案面对不同交通流量的适用性，采用优先排队、优先延误和固定顺序3种相位切换机制. 当本相位的最大绿灯时长结束，且各相位均未达到各自最大排队长度的阈值时：1）优先排队相位切换机制根据各相位车辆的实时平均排队长度进行排序，优先切换到当前时刻车辆平均排队长度最大的相位；2）优先延误切换机制根据各相位车辆实时停车延误时长进行排序，优先切换到当前时刻车辆停车延误时长最大的相位；3）固定顺序切换机制按照固定配时的顺序依次切换相位.

1）交叉口各进口道在距停止线100 m内无岔路存在、无非机动车混行，避免不确定因素使得排队长度误差过大；交叉口能够满足雷视一体机对车道信息的采集条件. 2）交叉口交通各方向流量不均衡，且随机变化较大，交叉口各进口道长度尽可能不超过雷视一体机监测的最长距离.

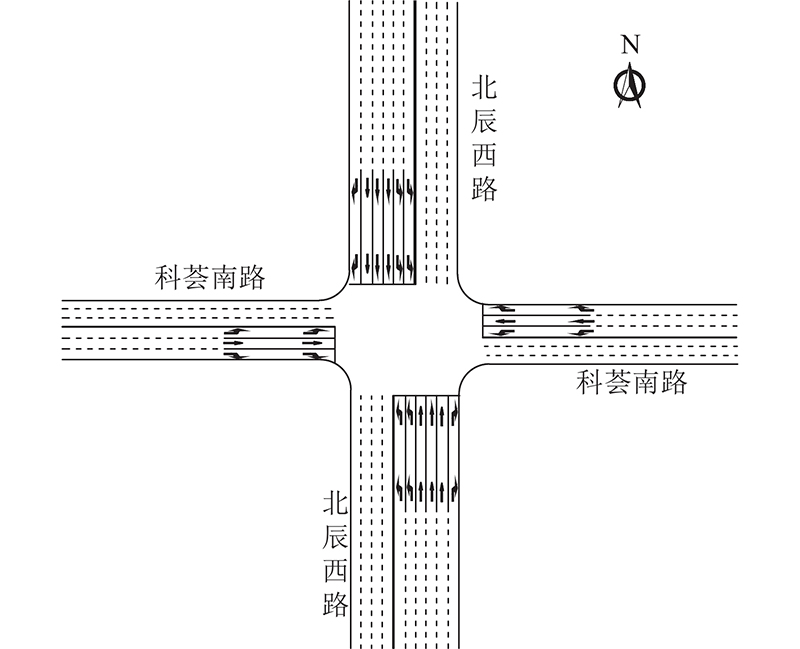
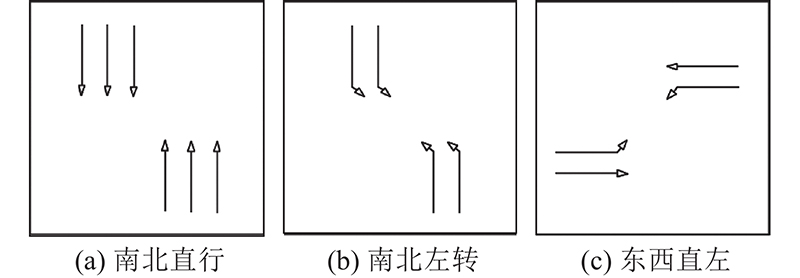
通过SUMO（simulation of urban mobility）仿真软件建立北辰西路与科荟南路交叉口的道路空间，如图3所示. 该交叉口位于北京市朝阳区，南、北进口方向均为6条进口道，东、西进口方向均3条进口道，所有进口道均无岔路、机非无混行. 车道宽度均为3.5 m，道路限制车速为60 km/h，东、南、西、北4个方向的进口道长度分别为135、222、205、235 m，均在雷视一体机能够监测范围内. 如图4所示，该交叉口的固定相位方案采用南北直行、南北左转、东西直左3种相位方案. 各相位在不同时间段的固定配时方案如表1所示，其中T_NS为南北直行相位绿灯时长，T_NSL为南北左转相位绿灯时长，T_EW为东西直左相位绿灯时长，T为信号周期时长. 各相位在绿灯结束后均有4 s黄灯时长和2 s全红时长.

在2022年4月统计的北辰西路与科荟南路各进口道车流量数据中选取单日7:00—21:00的每个小时交通流量，将进入交叉口的车流量按大小划分为低流量（低于2 000 pcu/h）、中等流量（2 000~3000 pcu/h）、高流量（超过3000 pcu/h）3组. 交通流量组的具体划分结果如表2所示, 其中Q_NS为南北直行相位车流量，Q_NSL为南北左转相位车流量，Q_EW为东西直左相位车流量，Q为交叉口总的车流量. 由表可知，交通流量随机变化较大，适合采用感应控制策略.

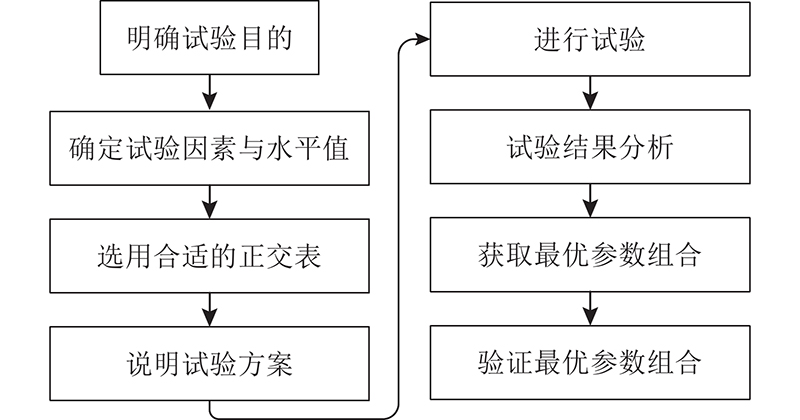
影响交叉口感应控制策略控制效率的因素较多，全面试验的规模很大，往往因试验条件的限制而难于实施. 正交设计可以从多因素试验的全部水平组合中挑选部分有代表性的水平组合进行试验，通过分析这部分试验结果了解全面试验的情况，找出最优水平组合. 本研究中将设计正交试验来筛选对感应控制性能有影响的各个参数（以下简称影响参数），具体的试验流程如图5所示.

1）相位顺序. 相位切换的顺序对感应控制的效率影响很大. 在传统的半感应控制和全感应控制的交叉口应用中，相位的切换时机由绿灯时长和检测器检测情况确定，切换顺序一般按照固定配时顺序进行周期内各相位循环切换. 由于雷视一体机能够获取交叉口各进口道排队长度和行车延误信息，在切换相位时，除了固定顺序切换机制以外，还增加了优先排队、优先延误2种相位切换机制，从而在不同车流量条件下增加了相位切换顺序的灵活性和准确性.

2）单位绿灯延长时间. 单位绿灯延长时间是压线脉冲区存在连续机动车通行需求的判定标准，也定义了某一相位所允许的车辆间最大时距. 该参数取值过大会导致绿灯时间浪费，取值过小则无法满足车辆通过. 试验选取交叉口的压线脉冲区采集到平均车头时距为3.25 s，结合85%的车头时距的分布区间为2~4 s，确定适宜的单位绿灯延长时间为2~4 s.

3）最小绿灯时长. 最小绿灯时长要保证停在检测器与停车线之间的全部车辆经过加速启动后都能够顺利通过交叉口，同时最小绿灯时长还要保证换相时行人能够安全过街^[17]. 除了平均车头时距为3.25 s外，该参数还包括4 s的启动反应时间：

(2) $ {T_{\min }} = {{{\rm{Integer}}}}\left[4+t\left({d}/{l}\right)\right] . $

式中：T_min为最小绿灯时长；t为车头时距分布区间，取t=2~4 s；d为停止线与压线脉冲区的间距；l为排队车辆的车头间距，取l=6 m；Integer为取整运算，取不小于且最接近与目标值的整数. 试验选取交叉口适宜的最小绿灯时长为11~18 s.

4）最大绿灯时长增量. 最大绿灯时长增量为在最小绿灯时长基础上延长的绿灯时长部分. 试验选取交叉口交通流量在各个时间段有明显的变化，为了满足不同时间段的交通需求，最大绿灯时长增量以实际道路所用固定方案的各相位绿灯时长为依据，因此取南北直行、南北左转、东西直左的最大绿灯时长增量分别为50~70、10~20、20~40 s.

正交试验因素的数目是由感应控制参数数目和交叉口相位决定的，其中相位顺序、单位绿延时、最小绿灯时长、最大绿灯时长增量为4个感应控制参数. 交叉口是三相位，因此最大绿灯时长增量分为3个相位各自的最大绿灯时长增量，优化后正交试验的6个因素如下：相位顺序、单位绿灯延长时间T_ext、最小绿灯时长T_min、南北直行最大绿灯时长增量T_max-NS、南北左转最大绿灯时长增量T_max-NSL、东西直左最大绿灯时长增量T_max-EW. 为了使各因素值更具代表性，在它们各自的适宜取值范围内均匀选取3个水平，得到各影响参数的正交水平表如表3所示. 构建L₁₈(3⁶)的正交试验表，即本研究的正交试验方案共18个，每个方案都是各个因素的不同水平值组合.

车均延误是指各进口道车辆因交叉口红灯停车造成延误时长的平均值，是感应控制交叉口性能的常用评价指标. 车均延误越低，交叉口的整体通行效率越高，驾驶员通过交叉口或干道系统时的通行体验越好. 本研究将降低交叉口车均延误作为感应控制策略优化的主要目的，即正交试验的试验指标为交叉口车均延误. 利用3种交通流量组内的不同时间段交通流量进行正交试验，在14个时间段交通流量下，进行18回合仿真试验，共得到252个试验结果. 如表4所示为每个时间段交通流量下进行18回合仿真试验得到平均交叉口车均延误T_avg.

方差分析法的目的是找到具有显著影响的因素. 若各号试验处理都只有1个观测值，即各流量下的交叉口车辆平均延误，则称之为单个观测值正交试验. 利用单变量一般线性模型进行数值分析，将交叉口车均延误作为分析的因变量，将6个影响参数作为固定因子进行主体间效应检验. 1）计算每个因素的离差平方和S_j，判断试验指标的分散或集中程度. 2）通过自由度和均方的计算获取F统计量，取显著性水平为0.05，筛选出对交叉口车辆平均延误具有显著影响的因素：

(3) $ {S _j} = \frac{1} {n} {{\displaystyle\sum\limits_{m = 1}^n { {{K_{jm}}^2} } }} - \frac {1} {h} {{{{\left( {\displaystyle\sum\limits_{i = 1}^h {{y_i}} } \right)}^2}}} \text{，} $

(4) $ S = \displaystyle\sum\limits_{i = 1}^h { {{y_i}^2} } - \frac {1} {h} {{{{\left( {\displaystyle\sum\limits_{i = 1}^h {{y_i}} } \right)}^2}}} \text{，} $

(5) $ {S _{\text{e}}} = S - \sum\limits_{j = 1}^6 {{S _j}} . $

式中：S_j为第j个因素的离差平方和；K_jm为第j个因素下第m水平所对应的试验指标和；y_i为第i回合试验的试验指标；n为水平数，n=3；h为试验回合数，h=18；S为总平方和；S_e为误差平方和.

(6) $ {\text{d}}{{\text{f}}_{\text{t}}} = h - 1 \text{，} $

(7) $ {\text{d}}{{\text{f}}_j} = n - 1 \text{，} $

(8) $ {\text{d}}{{\text{f}}_{\text{e}}} = {\text{d}}{{\text{f}}_{\text{t}}}- \sum\limits_{j = 1}^6 {{\text{d}}{{\text{f}}_j}} . $

式中：df_t为总自由度；df_j为第j个因素的自由度；df_e为误差项自由度. 计算得到df_t=17，6个因素的自由度均为2，误差项自由度为5.

(9) $ {\text{M}}{{\text{S}}_j} = \frac{{{S_j}}}{{{\text{d}}{{\text{f}}_j}}} \text{，} $

(10) $ {\text{M}}{{\text{S}}_{\text{e}}} = \frac{{{S_{\text{e}}}}}{{{\text{d}}{{\text{f}}_{\text{e}}}}} \text{，} $

(11) $ {F_j} = \frac{{{\text{M}}{{\text{S}}_j}}}{{{\text{M}}{{\text{S}}_{\text{e}}}}} . $

式中：MS_j为第j个因素的均方，MS_e为误差项的均方，F_j为第j个因素的F统计量. 此F统计量服从第一自由度为df_j，第二自由度为df_e的F分布. 3）在0.05的显著性水平下对F统计量进行检验，若某一因素的显著性水平小于0.05，则该因素代表的影响参数对交叉口车辆平均延误具有显著影响；反之，则影响不显著. 如表5所示为3个流量组不同时间段下各个影响参数显著性水平均值，其中P_ph为相位顺序的显著性水平均值，P_ext为单位绿灯延长时间的显著性水平均值，P_min为最小绿灯时长的显著性水平均值，P_max-NS为南北直行最大绿灯时长增量的显著性水平均值，P_max-NSL为南北左转最大绿灯时长增量的显著性水平均值，P_max-EW为东西直左最大绿灯时长增量的显著性水平均值.

在正交试验中，某一因素的极差值越大，说明该因素数值在试验范围内变化时，试验指标数值的变化越大. 因此各个影响参数对试验指标的影响从大到小的排序，就是将各个影响参数极差值从大到小的排序.

(12) $ {k_{jm}} = \frac{{{K_{jm}}}}{n}\text{，} $

(13) $ {R_j} = \max {k_j} - \min {k_j}. $

式中：k_jm为K_jm的平均值，若忽略试验误差，则同一因素k_jm的差异由此因素所处的水平不同造成，可以反映出此因素水平值的改变对试验指标的影响. 本试验设定试验指标越小越好，因此k_jm越小，相应的水平值更优，也因此可以由k_jm的大小判断第j因素的优水平和各因素的优水平组合，即最优参数组合. R_j为第j个因素的极差，即第j个因素各水平下k指标值的最大值与最大值之差. R_j反映第j列因素在水平变动时试验指标的变动幅度. R_j越大，说明该因素对试验指标的影响越大，该因素对应的影响参数也就越重要. 如图6所示为通过极差分析得到的各个交通流量组下各个影响参数的平均极差值R_avg. 针对每个交通流量组正交试验得到的平均交叉口车均延误值进行直观分析. 取各影响参数在每一水平下的极差阈值为3 s，筛选出对交叉口车均延误具有显著影响的影响参数.

如表6所示为方差分析和极差分析之后获得的各影响参数对平均交叉口车均延误影响的显著性表示. 表中，Y表示显著，N表示不显著. 可以看出，在北辰西路与科荟南路交叉口，3个流量组中的相位顺序均是重要影响参数；在低流量组中，单位绿灯延长时间和南北直行最大绿灯时长增量为重要影响参数；在中等流量组中，单位绿灯延长时间和最小绿灯时长为重要影响参数；在高流量组中，最小绿灯时长、东西直左最大绿灯时长增量成为重要影响参数. 在极差分析中通过k_jm的大小判断第j个影响参数的最优水平. 即每个影响参数下选取最小的k_jm值，其对应的水平值取为最优水平值. 最终得到不同交通流量组中能够使得平均交叉口车均延误达到最小值的最优参数组合，结果如表7所示.

为了验证获得的感应控制参数组合以及最优取值的有效性，设置对比实验. 使用最优参数组合的感应控制策略（以下简称最优感应控制）、未使用最优参数组合的感应控制策略（以下简称普通感应控制）以及固定配时策略，在每种交通流量组内的各时间段车流量下，分别进行14回合的仿真实验. 普通感应控制须体现不同影响参数组合的普遍性，因此将正交试验中除了最优参数组合以外的其他参数组合的试验均称为普通感应控制试验，每个时间段车流量下正交试验得到的平均交叉口车均延误作为普通感应控制下获得的结果，对比最优感应控制和固定配时策略下的平均交叉口车均延误值.

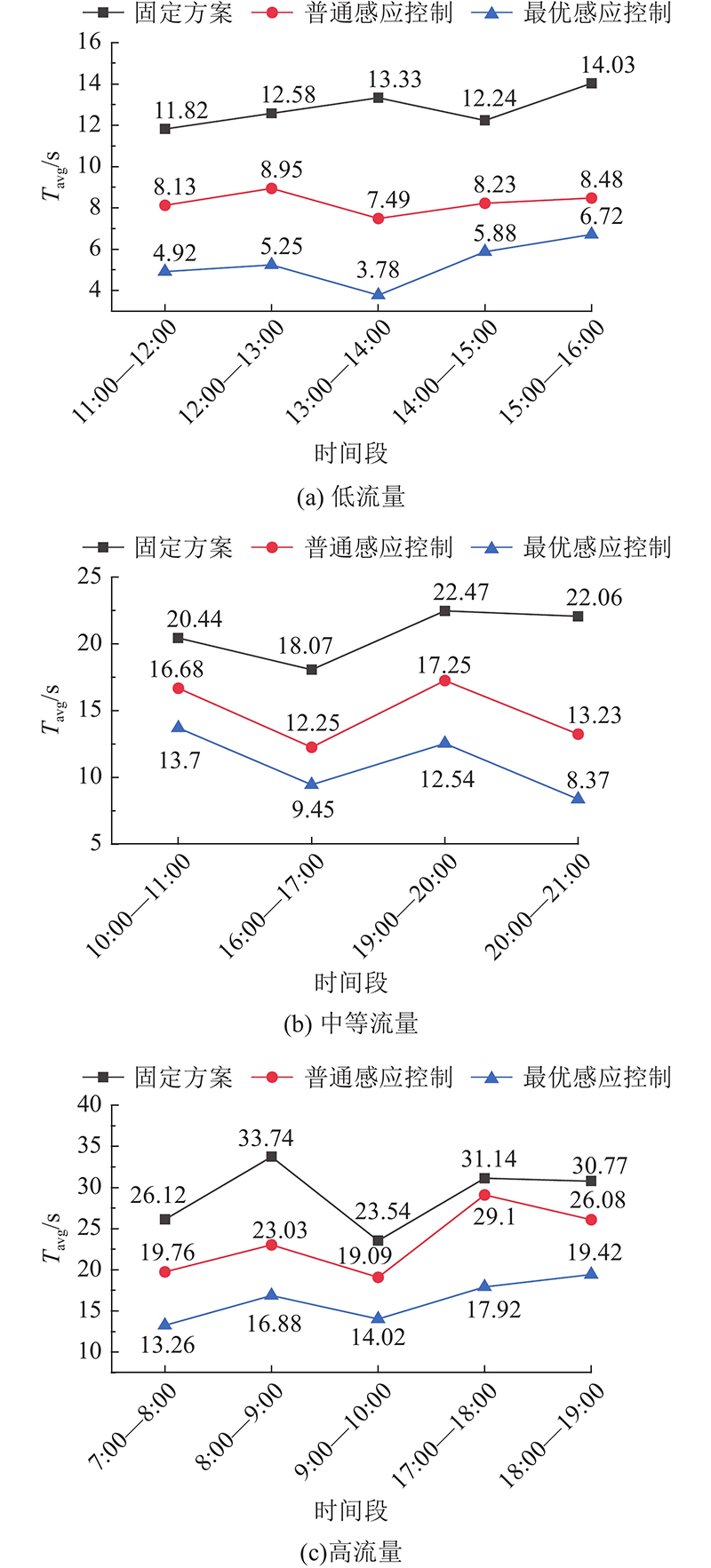
如图7所示，对比3种交通流量下不同控制策略的平均交叉口车均延误T_avg可知，当将交叉口的车均延误的平均值作为评价指标时，感应控制策略明显优于固定配时策略. 无论交通流量大小如何，在正交试验获得的最优感应控制策略下产生的平均交叉口车均延误，均小于普通感应控制策略和固定配时策略下产生的平均交叉口车均延误. 分析结果证实了本研究采用正交试验获取相关参数最佳取值的有效性.

DQN算法能够实现与交叉口环境交互，是优化感应控制策略的智能控制算法^[18]，包含强化学习（reinforcement learning）的Q学习过程和深度神经网络训练过程. 该算法将交叉口的车流状态作为输入，利用假定控制动作来模拟效果，不断训练得到深度神经网络，通过隐式建模控制动作选取来不断寻求最佳信号控制策略^[19-20].

状态空间的选取由正交试验获得的最优参数组合决定. 低流量下状态空间为每个相位对应车道的排队长度. 组成的状态空间数组为S_n={L₁，L₂，···，L_n，G_i，G_t}. 其中L_n为在第n个相位所对应的排队长度，G_i为当前绿灯相位的编号（1 ≤ G_i ≤ n），G_t为当前绿灯相位已持续时间. 中等流量下状态空间为每个相位对应的车道的车均延误. 对于采用n个相位的交通信号控制系统，组成的状态空间数组为S_n={Y₁，Y₂，···，Y_n，G_i，G_t}. 其中Y_n为在第n个相位所对应的车均延误. 高流量下最优的相位切换顺序为固定顺序，因此不作验证.

为了减少信号控制智能体的复杂性，将动作空间选取为相位方案，根据交叉口相位数量决定动作空间为A={相位1，相位2，相位3}，智能体会从在每个决策点中选择1种相位方案，如果选择的动作和当前绿灯相位方案相同，则执行当前绿灯相位，否则需要先执行黄灯相位和全红相位，根据正交试验得到的最优参数组合中对应的相位切换顺序设置相位切换优先级. 除此之外，感应控制的其他参数均由正交试验筛选得到最优参数组合决定.

选择单回合内交叉口的累计车均延误作为奖励值. 在仿真实验中，由仿真历史数据设置交叉口最大累计车均延误值Y_max，当累计车均延误大于Y_max时，终止本次仿真，直接开始下次仿真. 当累计车均延误小于Y_max时，其值越大，奖励值越小；其值越小，奖励值越大.

(14) $ {r}_{t}=\frac{{Y}_{{\max}}-{Y}_{t}}{{Y}_{{\max}}}=\frac{{Y}_{{\max}}-({Y}_{t1}+{Y}_{t2}+\cdots +{Y}_{tn})}{{L}_{{\max}}} . $

式中：r_t为第t步奖励值，Y_t为t时刻仿真记录的交叉口累计车均延误.

基于正交试验结果，将DQN算法分别应用于最优感应控制策略和普通感应控制策略上，验证最优参数组合是否能够提升算法运行效率. 算法的状态输入和动作空间保持一致，前者的控制参数对应为最优参数组合；后者的控制参数为正交试验中除最优参数组合以外的其他参数组合，进行逐个试验后取平均值. 算法训练回合N=200，每回合仿真时长为500 s，设置DQN算法的学习率为0.1，奖励折扣因子为0.9，神经网络更新频率为500步/次.

如图8所示为2种交通流量组的各时间段训练回合的平均累计车均延误T_sum. 因为固定配时方案的相位顺序和各灯色时长均不变，所以每回合内的累计车均延误均为常数. 对比固定方案和应用DQN算法的普通感应控制、最优感应控制的方法，可以看出，前期DQN算法对交叉口状态感知较弱，选择动作的随机性较大，因此出现远大于固定方案的累计车均延误值. 随着训练次数增加，普通感应控制和最优感应控制的学习效率均有提升，收敛到低于固定配时方案的累计车均延误值.

如表8所示为各控制策略的效果对比，其中v为收敛速度，即累计车均延误收敛到小于固定配时方案常数值所用的训练回合数；T_SUM为算法结果收敛到低于固定配时方案的常数值以后，每回合的平均累计车均延误值. 在低、中等流量下，最优感应控制在收敛速度上比普通感应控制分别提升了48.14%、38.89%；在平均累计车均延误上减少了8.45%、7.09%.

（1）不同的车流量条件下，感应控制的各个影响参数取值对控制性能的影响程度不同. 在实际的交叉口中，应注意相位切换顺序的影响始终显著. 在低、中等车流量（交叉口总流量小于3000 pcu/h）时，分别采用优先排队、优先延误的切换方式；在高流量（交叉口总流量大于3000 pcu/h）下，虽然采用感应控制的策略并使用感应控制参数，但也选用了固定顺序的相位最优切换方式，在保留感应控制对交叉口的感知能力的同时在一定程度上限制了信号相位“变动频繁”. 实验结果表明，按照固定顺序切换相位适用于高流量条件的交叉口环境.

（2）通过正交试验的方法将各个影响参数组合进行仿真实验分析的方法减少了试验次数，能够较快地得到各个参数对感应控制影响的显著性，也能够较为准确地获取最优参数组合. 在感应信号控制中，将最优参数组合加入DQN算法中，加快了算法的收敛速度，降低了交叉口车均延误.

（3）尽管本研究有一定的现实意义，但试验场景要求须符合感应控制的条件. 本研究存在不足之处：未考虑不满足条件的交叉口适用情况，未考虑感应控制参数的交互作用. 这些将在后续研究中改进.