随着人口快速增长与城市化进程的加快，我国的水资源供需矛盾日益严重，用水量的飞速增长和水资源的极度缺乏使得水资源规划和优化配置愈发重要^[1-3]. 城市短期供水量预测的预测步长为每小时或每天，以运营成本最低为目标满足城市用户的水资源需求，是水务公司实现城市内部配水系统优化调度和日常管理的重要依据^[4]. 如何提高日供水量预测的精度与泛用性已逐渐成为城市水资源规划的重难点问题.

随着计算机技术的飞速发展，为了推动短期供水量预测方法的改良提升，集成学习算法与深度学习算法被引入供水预测领域. Brentan等^[5]提出改进的支持向量回归方法，并进行短期水资源需求预测，消除了固定回归结构在响应新的输出时间序列时固有的偏差. 物联网集成的基于长短时记忆（long short term memory，LSTM）神经网络的配水网络相比于采用整合移动平均自回归方法（ARIMA）的配水网络，将运输过程中的损失和对消费者的水质量的损失降到更低^[6]. 通过插值和外推2种情景，Shuang等^[7]在传统统计模型和机器学习模型中寻找最合适的预测模型，结果表明相比于线性回归法、Lasso回归与岭回归法、AdaBoost法，梯度推进决策树方法的预测性能最佳. Guo等^[8]建立门限递归单元网络(GRUN)需水预测模型，该模型性能明显优于人工神经网络和季节性差分自回归滑动平均模型. Xenochristou等^[9]使用随机森林模型预测英国居民的日需水量，并运用可解释的机器学习技术量化预测因素对用水量的影响，此方法结合了机器学习模型的高精度和统计方法的可解释性. Huang等^[10]将BP神经网络集合到AdaBoost算法中，有效提高了需水预测的准确性与稳定性.

日供水量预测方法主要有单一深度学习方法、单一集成学习方法、耦合数据前处理方法与深度学习方法的方法等，这些方法的预测精度、稳定性与泛化性能均较差. 此外，耦合集成学习算法与深度学习算法的方法的研究不多. 为了扩展短期供水预测的应用，本研究以义乌市为研究区域，运用自相关系数法与网格搜索法的结合方法进行数据特征选择，采用拉依达准则对日供水数据进行预处理，提出AdaBoost集成学习算法改进的LSTM神经网络的组合短期供水预测方法，并与随机森林（random forest, RF）、AdaBoost（adaptive boosting）与LSTM神经网络3种短期供水预测方法进行比较，验证改良短期供水预测方法的适用性与准确性.

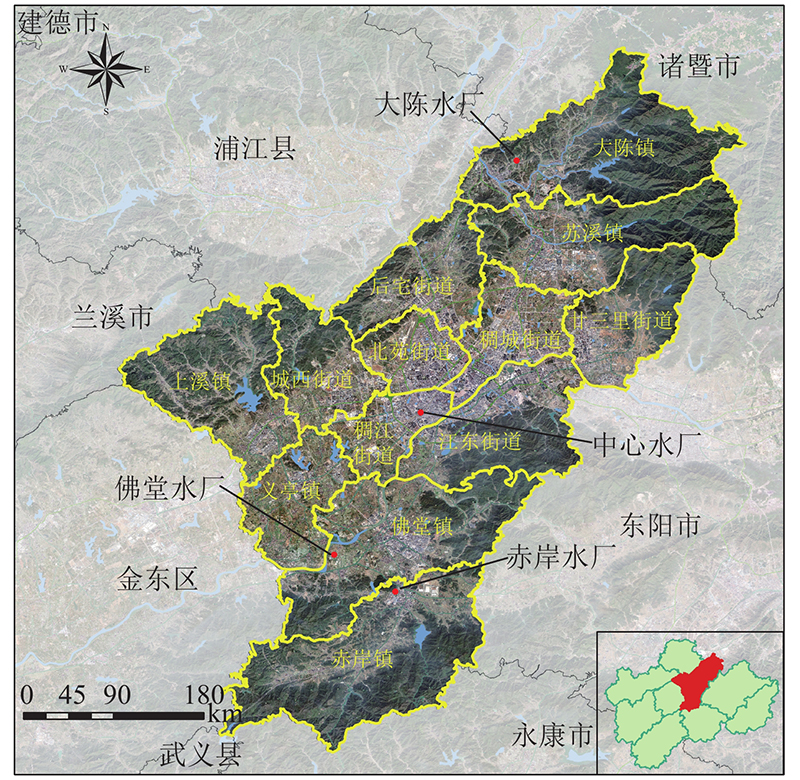
义乌市地处浙中盆地，属亚热带季风气候，温和湿润，四季分明. 尽管地处南方丰水地区，受独特的地理位置和空间条件限制，义乌市仍是重度缺水地区^[11]，水资源总量仅占浙江省总量的0.86%，人均水资源量仅为410 $ {\mathrm{m}}^{3} $，相当于浙江省平均水平的1/4^[12]，全国平均水平的1/5^[13]，水资源供需矛盾突出，水资源已成为制约义乌市区域经济社会发展的主要瓶颈之一^[14]. 如图1所示，本研究采用义乌市内佛堂水厂、中心水厂、大陈水厂、赤岸水厂的日供水量资料. 佛堂水厂和中心水厂的数据采集时间为2015年1月1日至2021年3月1日，共2 251 d；大陈水厂的为2015年12月1日至2021年3月1日，共1 917 d；赤岸水厂日的为2017年4月1日至2021年3月1日，共1 430 d.

RF基于决策树，是自助投票(Bagging)集成算法的代表算法. Breiman^[15]结合Bagging集成学习理论与随机子空间理论^[16]提出RF. 它利用Bootstrap即自助法进行随机重采样，通过节点随机分裂形成多棵决策树，再将决策树汇集成随机森林. RF方法结构简单，有极强的鲁棒性和良好的准确性，能够以随机属性选择的方式防止训练模型过拟合.

AdaBoost是Freund^[17]在Boosting算法上改进的、拥有自适应增强能力的集成学习算法. 依据加权方法，AdaBoost组合同一训练集上训练能力较差的多个弱学习器，构成训练能力极强的强学习器. AdaBoost可以有效避免过拟合，能够作为算法框架优化其他算法，应用极为灵活.

LSTM神经网络是循环神经网络（RNN)的改良型. 门控结构由遗忘门、输入门和输出门组成，控制着信息的取舍、输入、更新、输出，因此LSTM神经网络具备长时间的记忆功能，可以有效地解决RNN在训练时产生的梯度爆炸和梯度消失问题，极大增强了RNN的准确度^[18-20].

遗忘门的公式为

(1) $ {{\boldsymbol{f}}_{{t}}} = \sigma ({{\boldsymbol{W}}_{\text{f}}}\;{{\boldsymbol{h}}_{({{t}} - 1)}}+{{\boldsymbol{U}}_{\text{f}}}\;{x_{{t}}}+{{\boldsymbol{b}}_{\text{f}}}\;). $

输入门的公式为

(2) $ {{\boldsymbol{i}}_{{t}}} = \sigma ({{\boldsymbol{W}}_{\text{i}}}\;{{\boldsymbol{h}}_{({{t}} - 1)}}+{{\boldsymbol{U}}_{{{\rm{i}}}}}\;{{\boldsymbol{x}}_{{t}}}+{{\boldsymbol{b}}_{\text{i}}}\;), $

(3) $ \widetilde {{{\boldsymbol{C}}_{{t}}}} = \tanh \;({{\boldsymbol{W}}_{\text{c}}}\;{{\boldsymbol{h}}_{({{t}} - 1)}}+{{\boldsymbol{U}}_{\text{c}}}\;{{\boldsymbol{x}}_{{t}}}+{{\boldsymbol{b}}_{\text{c}}}), $

(4) $ {{\boldsymbol{C}}_{{t}}} = {{\boldsymbol{C}}_{({{t}} - 1)}} \odot {{\boldsymbol{f}}_{{t}}}+{{\boldsymbol{i}}_{{t}}} \odot \widetilde {{{\boldsymbol{C}}_{{t}}}}. $

输出门的公式为

(5) $ {{\boldsymbol{o}}_{{t}}} = \sigma ({{\boldsymbol{W}}_{\text{o}}}\;{{\boldsymbol{h}}_{({{t}} - 1)}}+{{\boldsymbol{U}}_{{{\rm{o}}}}}\;{x_{{t}}}+{{\boldsymbol{b}}_{\text{o}}})， $

(6) $ {{\boldsymbol{h}}_{{t}}} = {{\boldsymbol{o}}_{{t}}} \odot \tanh \;({{\boldsymbol{C}}_{{t}}}). $

式中： $\odot $为矩阵元素积，W_c为单位状态到输入的权值矩阵，W_f、W_i、W_o分别为从遗忘、输入、输出门到输入的权值矩阵，U_c为单位状态到隐藏层的权值矩阵，U_f、U_i、U_o分别为从遗忘、输入、输出门到隐藏层的权值矩阵，b_c为单位状态的偏向量，b_f、b_i、b_o分别为遗忘、输入、输出门的偏置向量， $ \mathrm{\sigma } $为sigmoid激活函数，tanh为双曲正切激活函数.

基于集成学习改进的LSTM方法（以下简称改进LSTM）以集成学习的方式增强LSTM神经网络方法的预测精度与鲁棒性，通过AdaBoost集成学习算法串行训练多个LSTM弱预测器，并在训练过程中不断调整样本与弱预测器权重，再将弱预测器进行加权组合生成强预测器，输出最终的预测结果. 改进LSTM融合了AdaBoost深度挖掘算法潜力与LSTM处理时间序列问题的优势，解决了多层LSTM参数选择复杂的难题，改善了AdaBoost对异常值敏感的缺陷.

改进LSTM的构造流程如下.

1）赋予每个样本数据相同的权重：

(7) $ {D}_{{n}}=1/{M};\;\;\;\;n=1,2, \cdots ,{M}. $

式中：D_n为第n个样本数据的权重，M为样本数据总数量.

2）设定网络超参数，并设定LSTM弱预测器总数为N_n，采用LSTM神经网络训练样本.

3）对第 $ n $个LSTM弱预测器，计算该弱预测器在训练集上的最大误差为

(8) $ {E_{{n}}} = \max \left| {{y_{{i}}} - {G_{{n}}}({x_{{i}}})} \right|. $

式中：y_i为弱预测器在训练集上的预测值，G_n(x_i)为训练集的观测值.

4）计算每个样本的相对误差为

(9) $ {e_{{{n,i}}}} = \frac{{{{({y_{{i}}} - {G_{{n}}}({x_{{i}}}))}^2}}}{{E_{{n}}^2}}. $

式中：e_n,i为第n个弱预测器的第i个样本数据的相对误差.

5）得到第 $ n $个LSTM弱预测器的误差率为

(10) $ {e_{{n}}} = \sum\limits_{i = 1}^{{M}} {{w_{{{n,i}}}}{e_{{{n,i}}}}} . $

式中：e_n为第n个若预测器的误差率，w_n,i为第n个弱预测器的第i个样本数据的权重.

6）获得第 $ n $个LSTM弱预测器的权重系数为

(11) $ {\alpha _{{n}}} = \frac{{{e_{{n}}}}}{{1 - {e_{{n}}}}}. $

7）对第 $ n+1 $个弱学习器进行权重更新：

(12) $ {w _{{{n+1,i}}}} = \frac{{{w _{{{n,i}}}}}}{{{Z_{{n}}}}}\alpha _{{n}}^{1 - {e_{{{n,i}}}}}. $

其中规范化因子为

(13) $ {Z_{{n}}} = \sum\limits_{i = 1}^{{M}} {{w _{{{n,i}}}}\alpha _{{n}}^{1 - {e_{{{n,i}}}}}} . $

8）采用取中位数的结合方法，将多个弱学习器融合为强学习器：

(14) $ f(x) = \sum\limits_{i = 1}^{{N_{{n}}}} {\left(\ln \frac{1}{{{\alpha _{{n}}}}}\right)g(x)} . $

式中： $ g\left(x\right) $为 $ {\alpha _{{n}}}{G_{{n}}}(x) $的中位数.

选择平均绝对误差MAE，均方根误差RMSE和纳什效率系数NSE为评估预测方法性能的代表性指标，计算式分别为

(15) $ {\text{MAE}} = \frac{1}{{{M}}} \times \sum\limits_{i = 1}^{{M}} {\left| {{Q_{({\text{p,}}i)}} - {Q_{({\text{t,}}i)}}} \right|}, $

(16) $ {\text{RMSE}} = \sqrt {\frac{1}{{{M}}} \times \sum\limits_{i = 1}^{{M}} {{{({Q_{{{({\rm{p}},i)}}}} - {Q_{{{({\rm{t}},i)}}}})}^2}} } , $

(17) $ {\text{NSE}} = 1 - \frac{{\displaystyle\sum {{{({Q_{{{({\rm{p}},i)}}}} - {Q_{{{({\rm{t}},i)}}}})}^2}} }}{{\displaystyle\sum {{{({Q_{{{({\rm{p}},i)}}}} - {\overline{Q}_0} )}^2}} }}. $

式中：M为总时间步长数， $ {Q}_{\mathrm{p},{i}} $为i时刻供水量预测数据， $ {Q}_{\mathrm{t},{i}} $为i时刻供水量观测数据， ${\overline{Q}_{0}}$为供水量预测数据的平均值. NSE∈(−∞, 1]，当NSE=1时，表示方法结果完美拟合实测值. RMSE、MAE∈[0, ＋∞)，RMSE、MAE的数值越大，表示预测值与观测值偏差越大；当RMSE、MAE = 0时，方法拟合效果最好.

供水数据一般持续时间长，并会受检测设施、人为因素或极端天气影响而产生异常值，导致供水数据的准确性降低，因此在使用供水数据进行训练分析前，须筛选和剔除异常值. 本研究采用拉依达准则进行异常值筛选与替换. 拉依达准则假定数据为正态分布，利用数据的均值 $ \;{\mu } $和标准差 $ \mathrm{\sigma } $来估计基本分布；数值分布在( $\; {\mu }-3\mathrm{\sigma },\;\mathrm{\mu }+3\mathrm{\sigma } $)的概率为0.997 4，因此认为 $ {x}_{i} $的取值几乎全部集中在( $ \;{\mu }-3\mathrm{\sigma },\; \mathrm{\mu }+3\mathrm{\sigma } $)，超出这个区间的可能性不到0.3%. 依据拉依达准则，处于( $ \;{\mu }-3\mathrm{\sigma },\;\mathrm{\mu }+3\mathrm{\sigma } $)的供水量数据视为正常值，否则为异常值. 异常值处理原则：如果 ${x}_{{i}} \geqslant \mathrm{\mu }+3\mathrm{\sigma }，$则 $ {x}_{{i}}=\mathrm{\mu }+3\mathrm{\sigma } $；如果 $ {x}_{{i}} < \mathrm{\mu }-3\mathrm{\sigma } $，则 $ {x}_{{i}}=\mathrm{\mu }-3\mathrm{\sigma } $.

本研究选取的是水厂4~6 a的日供水数据，数据量较大，若直接输入至神经网络进行训练，预测效果较差. 为此，将采用拉依达准则筛选后的供水量数据进行归一化处理，这样既加快了训练收敛速度，又提高了预测精度. 将供水量数据归一化至[0, 1.0]，数据归一化 $ \widehat{x} $与反归一化 $ x $计算式分别为

(18) $ \widehat x = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}， $

(19) $ x = \widehat x({x_{\max }} - {x_{\min }})+{x_{\min }}. $

式中： $ {x}_{\mathrm{m}\mathrm{i}\mathrm{n}} $、 $ {x}_{\mathrm{m}\mathrm{a}\mathrm{x}} $分别为训练样本中的输入样本最小值、最大值.

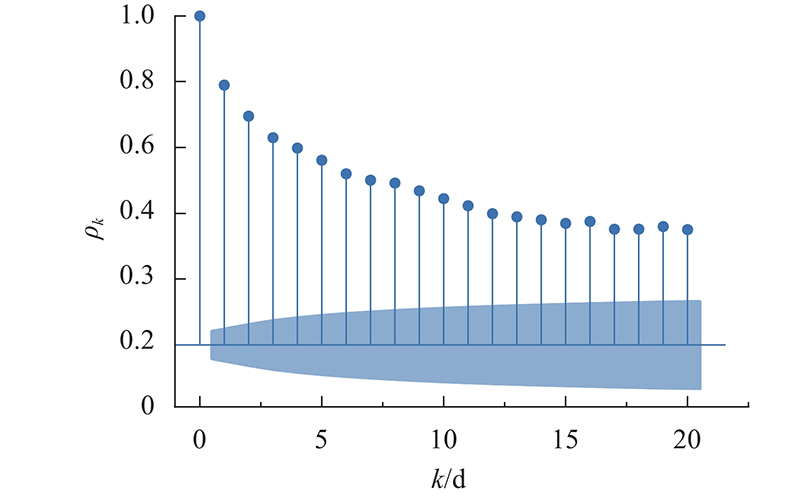
在日供水量预测领域中，数据输入变量往往使用2种主要特征：历史供水量与气象因素（如温度、湿度与降雨）. 特征选取得越多不代表方法性能越好，与供水量相关系数较低的特征变量（如温度）往往会影响深度学习方法的训练与学习，从而影响方法性能. 因此，本研究选择历史供水量作为唯一输入. 在选择供水量作为唯一输入的前提下，须重构水需求数据以更好表示样本数据间的关系，而不同时期的用水需求间存在时间相关性^[10]. 以义乌市中心水厂为例，采用自相关系数法与网格搜索法确认数据输入的格式. 自相关系数法的计算式为

(20) $ {\rho _{_{k}}} = \dfrac{{\dfrac{1}{{{N_{\text{d}}} - k}}\displaystyle\sum\limits_{t = k+1}^{{N_{\text{d}}}} {({x_{{t}}} - \overline x )({x_{{{{{t}} {\text{-}} {{k}}}}}} - \overline x )} }}{{\dfrac{1}{{{N_{\text{d}}}}}\displaystyle\sum\limits_{t = 1}^{{N_{\text{d}}}} {{{({x_{{t}}} - \overline x )}^2}} }}. $

式中：N_d为总日期，k为延迟期天数，x_t为第t天的供水量， $ \overline{x} $为供水量平均值. 式（20）表示经过某些阶数滞后形成的供水序列间存在某种程度的相关性. 如图2所示，灰色区域代表95%的置信区间，由图可知，延迟期不超过20 d，数据间的相关性依旧很强，因此结合试算法继续探究合适的输入天数. 网格搜索法适用于规模很小的超参数优化，最初被应用于支持向量机的参数优化，本质为穷举法. 本研究以步长为1 d在[2,10] d选择合适的时长，结果如表1所示. 当输入时长T_d=7 d时，LSTM方法获得最好的性能，NSE为最大值（0.927），因此本研究确定输入天数为7 d.

RF方法可供调节的参数较少，参数择优一般是调节决策树个数N_RF和决策树深度D_RF. 以中心水厂为例，本研究依据网格搜索法确定RF方法的最佳决策树N_RF=70，如表2所示；决策树的最大深度D_RF=4，如表3所示.

影响AdaBoost方法精度的参数主要有基学习器类型、基学习器的最大个数、基学习器的权重缩减系数，其中对方法精度起主要作用为基学习器的个数N_AB. 当N_AB=1时，AdaBoost方法无法使用；当N_AB较小时，方法易欠拟合；当N_AB较大时，易过拟合并导致严重的计算负担. 以中心水厂为例，本研究依据网格搜索法确定AdaBoost方法的最佳基学习器数量为30，如表4所示.

为了方便方法性能比较，LSTM神经网络方法中的神经网络超参数设置与改进LSTM中弱预测器LSTM方法保持一致.

以前7 d的供水数据作为方法数据输入，以当天的供水数据作为方法输出结果，故输入节点为7个，输出节点为1个. 该方法以单层LSTM作为弱预测器，避免选取多层参数的烦琐，因此选取神经网络隐藏层层数为1层，神经网络隐藏层内神经元个数由网格搜索法确定为128个，神经网络训练期间将均方误差MSE作为损失误差，采用Adam优化算法训练LSTM方法. 学习率根据文献[21]、[22]及方法默认值设定为0.001. 迭代次数依据LSTM训练日志设定为100. 本研究由网格搜索法设定批量大小N_BS=32，如表5所示. 为了避免方法过拟合，使用正则化方法，dropout=0.2，训练集与测试集的划分比例为8∶2.

AdaBoost算法参数须设置的参数主要为用于构建强预测器的LSTM方法个数. 以赤岸水厂为例，使用网格搜索法对弱预测器个数N∈[2,10]的方法性能进行评估. 为了消除深度学习模型训练的随机性误差，运行5次改进LSTM，再以NSE平均值选择最佳的弱预测器个数. 不同弱预测器个数的预测方法平均NSE如表6所示，最终确定本方法选用的最佳弱预测器个数为2.

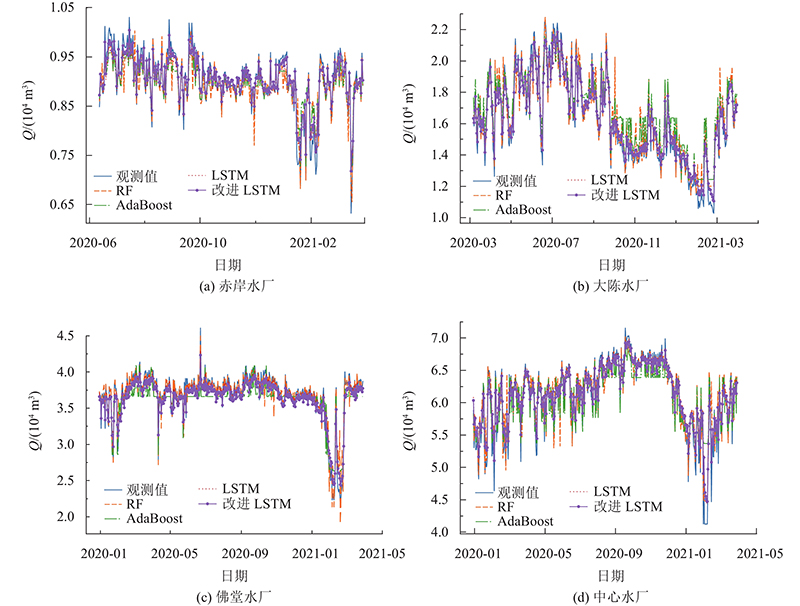
选用4个水厂的日供水量数据建立4种基于集成学习、深度学习的日供水量预测方法，并对比方法的性能. 集成学习与深度学习每次运行会产生不同的预测结果，为了更合理地评估方法性能，对每个方法都运行5次取平均值. 如图3所示为各方法的预测结果曲线，其中Q为日供水量. 可以看出，RF方法、AdaBoost方法的预测值均与实际数值的变化趋势拟合度较其他2种方法的低，部分时间跨度以线性变化形式反映供水曲线的变化，局部时间范围的预测值甚至维持不变，对峰值的拟合也无法达到令人满意的效果，且均为负偏差. LSTM神经网络方法对变化趋势与峰值的拟合效果均较好，可以有效捕捉供水量极值点的信息，其曲线趋势基本与实测曲线相合，但仍有较大偏差. 改进LSTM对变化趋势与峰值的拟合效果比LSTM方法的更好，原因是引入AdaBoost算法使得改进LSTM对未被预测精确的样本的学习能力更强. 如表7所示为各方法的性能对比. 由表可知，改进LSTM的日供水量预测性能显著优于其他传统集成学习与深度学习方法的. 原因是改进LSTM将LSTM方法对复杂非线性时序数据的优秀处理能力与AdaBoost方法对大误差数据的强学习能力结合. 改进LSTM的优越性通过最高的NSE、最低的MAE与RMSE来验证. 在经由AdaBoost集成算法改进后，LSTM方法的精度有了较大的提升. 以赤岸水厂为例，NSE由0.900提升至0.929，性能提升了3.2%，MAE由158.3 $ {\mathrm{m}}^{3}/\mathrm{d} $降至118.4 $ {\mathrm{m}}^{3}/\mathrm{d} $，性能提升了25.2%，RMSE由196.1 $ {\mathrm{m}}^{3}/\mathrm{d} $降低至165.2 $ {\mathrm{m}}^{3}/\mathrm{d} $，性能提升了15.8%. 综上所述，无论是在方法的预测性能方面，还是方法的稳定性方面，改进LSTM均优于3种基准方法.

将基于AdaBoost集成学习算法改进的LSTM神经网络方法与3种基准方法（RF方法、AdaBoost方法、LSTM方法）进行对比. RF方法过分追求训练集上的预测性能，导致测试集上的精度下降，易出现过拟合现象. AdaBoost方法在训练过程中会偏向预测困难的样本，易受异常值干扰. LSTM方法虽然对时序数据有较好的处理能力，但仍有精度限制. 改进LSTM结合LSTM方法对复杂非线性时序数据的优秀处理能力与AdaBoost方法对大误差数据的强学习能力，方法的性能获得极大提升. 将改进LSTM应用于义乌市的4个水厂，方法预测性能、对供水曲线变化趋势与峰值的拟合效果在4个方法中皆为最优，证明改进LSTM具有较好的泛化能力和稳定的预测性能. 本研究仍存在诸多不足： 1）直接采用历史供水数据进行分析，未提取供水数据的趋势和残差特性，未考虑供水数据的非平稳性；2）对比基准方法选择较少，仅选用集成学习与深度学习的代表方法，未构建传统供水预测方法（如多元线性回归法或灰色预测法）进行性能比较. 下一步研究将考虑采用时间序列分解方法，并搭建更多基准模型用于性能比较.