(3) $ {\boldsymbol{\beta}} ({u_i},{v_i},{t_i}) = {({{\boldsymbol{x}}_i^{\rm{T}}}{\boldsymbol{w}}({u_i},{v_i},{t_i}){\boldsymbol{x}})^{ - 1}}{{\boldsymbol{x}}_i^{\rm{T}}}{\boldsymbol{w}}({u_i},{v_i},{t_i})\hat {{\boldsymbol{y}} }. $
式中: $ {y_i} $ $ i $ $ {u_i}、{v_i}、{t_i} $ $ i $ $ \;{\beta _0}({u_i},{v_i},{t_i}) $ $ i $ $ {x_{ik}} $ $ i $ $ k $ $ K $ $ \;{\beta _k}({u_i},{v_i},{t_i}) $ $ {{\boldsymbol{x}}_{ik}} $ $ {\varepsilon _i} $ $ i $ T 和()−1 分别为转置和逆运算; $ {\boldsymbol{\beta}} ({u_i},{v_i},{t_i})$ x i $ {\boldsymbol{x}}_i $ $ i $ $ \hat {\boldsymbol{y}} $ $ {\boldsymbol{w}}({u_i},{v_i},{t_i}) $ $ {w_{i1}},{w_{i2}},\cdots ,{w_{in}} $ ) 为对角矩阵, $ n $ $ {w_{ij}} $ $ i $ $ {u_i},{v_i},{t_i} $ ) 处基于和测量点 $ j $ $ {w_{ij}} $
[1]
BARBOUR N, ZHANG Y, MANNERING F A statistical analysis of bike sharing usage and its potential as an auto-trip substitute
[J]. Journal of Transport and Health , 2019 , 12 : 253 - 262
DOI:10.1016/j.jth.2019.02.004
[本文引用: 1]
[2]
DU Y C, DENG F W, LIAO F X A model framework for discovering the spatio-temporal usage patterns of public free-floating bike-sharing system
[J]. Transportation Research Part C: Emerging Technologies , 2019 , 103 : 39 - 55
DOI:10.1016/j.trc.2019.04.006
[本文引用: 1]
[3]
GU T Q, KIM I, CURRIE G Measuring immediate impacts of a new mass transit system on an existing bike-share system in China
[J]. Transportation Research Part A: Policy and Practice , 2019 , 124 : 20 - 39
DOI:10.1016/j.tra.2019.03.003
[本文引用: 1]
[4]
SHEN Y, ZHANG X H, ZHAO J H Understanding the usage of dockless bike sharing in Singapore
[J]. International Journal of Sustainable Transportation , 2018 , 12 (9 ): 686 - 700
DOI:10.1080/15568318.2018.1429696
[本文引用: 1]
[5]
SHELAT S, HUISMAN R, VAN OORT N Analysing the trip and user characteristics of the combined bicycle and transit mode
[J]. Research in Transportation Economics , 2018 , 69 : 68 - 76
DOI:10.1016/j.retrec.2018.07.017
[本文引用: 1]
[6]
HUA M Z, CHEN X W, ZHENG S J, et al Estimating the parking demand of free-floating bike sharing: a journey-data-based study of Nanjing, China
[J]. Journal of Cleaner Production , 2020 , 244 : 118764
DOI:10.1016/j.jclepro.2019.118764
[本文引用: 1]
[7]
艾媒咨询. 2017年共享单车夏季市场专题报告 [EB/OL]. (2017-06-16). https://www.iimedia.cn/c400/59210.html.
[本文引用: 1]
[8]
万敏. 基于数据的共享单车需求预测和调度研究 [D]. 南京: 南京大学, 2020.
[本文引用: 1]
WAN Min. Research on forecasting and scheduling of shared bicycle demand based on data [D]. Nanjing: Nanjing University, 2020.
[本文引用: 1]
[9]
XU Y, CHEN D C, ZHANG X H, et al Unravel the landscape and pulses of cycling activities from a dockless bike-sharing system
[J]. Computers, Environment and Urban Systems , 2019 , 75 : 184 - 203
DOI:10.1016/j.compenvurbsys.2019.02.002
[本文引用: 1]
[11]
GAO K, YANG Y, LI A Y, et al Spatial heterogeneity in distance decay of using bike sharing: an empirical large-scale analysis in Shanghai
[J]. Transportation Research Part D: Transport and Environment , 2021 , 94 : 102814
DOI:10.1016/j.trd.2021.102814
[本文引用: 4]
[13]
WANG X Z, LINDSEY G, SCHONER J E, et al Modeling bike share station activity: effects of nearby businesses and jobs on trips to and from stations
[J]. Journal of Urban Planning and Development , 2015 , 142 (1 ): 04015001
[本文引用: 1]
[14]
曹小曙, 罗依 中国大陆城市建成环境与共享单车配置的关系
[J]. 中山大学学报:自然科学版 , 2020 , 59 (1 ): 77 - 85
[本文引用: 1]
CAO Xiao-shu, LUO Yi Relationship between built environment and bikeshare allocation in the mainland of China
[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni , 2020 , 59 (1 ): 77 - 85
[本文引用: 1]
[15]
LI A Y, ZHAO P X, HUANG Y Z, et al An empirical analysis of dockless bike-sharing utilization and its explanatory factors: case study from Shanghai, China
[J]. Journal of Transport Geography , 2020 , 88 : 102828
DOI:10.1016/j.jtrangeo.2020.102828
[本文引用: 3]
[16]
MA X W, JI Y J, YUAN Y F, et al A comparison in travel patterns and determinants of user demand between docked and dockless bike-sharing systems using multi-sourced data
[J]. Transportation Research Part A: Policy and Practice , 2020 , 139 : 148 - 173
DOI:10.1016/j.tra.2020.06.022
[本文引用: 1]
[17]
HUANG B, WU B, BARRY M Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices
[J]. International Journal of Geographical Information Science , 2010 , 24 (3 ): 383 - 401
DOI:10.1080/13658810802672469
[本文引用: 2]
[18]
WU C, REN F, HU W, et al Multiscale geographically and temporally weighted regression: exploring the spatiotemporal determinants of housing prices
[J]. International Journal of Geographical Information Science , 2019 , 33 (3 ): 489 - 511
DOI:10.1080/13658816.2018.1545158
[本文引用: 2]
[19]
上海统计局. 《2018年上海市国民经济和社会发展统计公报》[EB/OL]. (2019-03-01). http://tjj.sh.gov.cn/tjgb/20191115/0014-1003219.html?ivk_sa=1024320u.
[本文引用: 1]
[20]
XING Y Y, WANG K, LU J J Exploring travel patterns and trip purposes of dockless bike-sharing by analyzing massive bike-sharing data in Shanghai, China
[J]. Journal of Transport Geography , 2020 , 87 : 102787
DOI:10.1016/j.jtrangeo.2020.102787
[本文引用: 1]
[21]
CRANEY T A, SURLES J G Model-dependent variance inflation factor cutoff values
[J]. Quality Engineering , 2002 , 14 (3 ): 391 - 403
DOI:10.1081/QEN-120001878
[本文引用: 1]
[22]
马新卫, 季彦婕, 金雪, 等 租赁自行车用户出行特征及方式的影响因素分析
[J]. 浙江大学学报: 工学版 , 2020 , 54 (6 ): 1202 - 1209
[本文引用: 1]
MA Xin-wei, JI Yan-jie, JIN Xue, et al Analysis on travel characteristics of bike-sharing users andinfluence factors on way to travel
[J]. Journal of Zhejiang University: Engineering Science , 2020 , 54 (6 ): 1202 - 1209
[本文引用: 1]
[23]
FOTHERINGHAM A S, YANG W B, KANG W Multiscale geographically weighted regression (MGWR)
[J]. Annals of the American Association of Geographers , 2017 , 107 (6 ): 1247 - 1265
DOI:10.1080/24694452.2017.1352480
[本文引用: 1]
[24]
YU K, PARK B U, MAMMEN E Smooth backfitting in generalized additive models
[J]. The Annals of Statistics , 2008 , 36 (1 ): 228 - 260
[本文引用: 1]
[25]
GAO K, YANG Y, LI A Y, et al Quantifying economic benefits from free-floating bike-sharing systems: a trip-level inference approach and city-scale analysis
[J]. Transportation Research Part A: Policy and Practice , 2021 , 144 : 89 - 103
DOI:10.1016/j.tra.2020.12.009
[本文引用: 1]
[27]
FOTHERINGHAM A S, CRESPO R, YAO J Geographical and temporal weighted regression (GTWR)
[J]. Geographical Analysis , 2015 , 47 (4 ): 431 - 452
DOI:10.1111/gean.12071
[本文引用: 1]
[28]
MA X L, ZHANG J Y, DING C, et al A geographically and temporally weighted regression model to explore the spatiotemporal influence of built environment on transit ridership
[J]. Computers, Environment and Urban Systems , 2018 , 70 : 113 - 124
DOI:10.1016/j.compenvurbsys.2018.03.001
[本文引用: 1]
[29]
YANG H T, ZHANG Y B, ZHONG L Z, et al Exploring spatial variation of bike sharing trip production andattraction: a study based on Chicago’s Divvy system
[J]. Applied Geography , 2020 , 115 : 102130
DOI:10.1016/j.apgeog.2019.102130
[本文引用: 1]
[30]
HAMPSHIRE R C, MARLA L. An analysis of bike sharing usage: explaining trip generation and attraction from observed demand [C]// 91st Annual Meeting of the Transportation Research Board . Washington, DC: TRB, 2012: 12-2099.
[本文引用: 1]
[32]
ZHANG Y, THOMAS T, BRUSSEL M, et al Exploring the impact of built environment factors on the use of publicbikes at bike stations: case study in Zhongshan, China
[J]. Journal of Transport Geography , 2017 , 58 : 59 - 70
DOI:10.1016/j.jtrangeo.2016.11.014
[本文引用: 1]
[33]
TAN X Y, ZHU X L, LI Q, et al Tidal phenomenon of the dockless bike-sharing system and its causes: the case of Beijing
[J]. International Journal of Sustainable Transportation , 2022 , 16 (4 ): 287 - 300
DOI:10.1080/15568318.2020.1871129
[本文引用: 1]
[34]
高楹, 宋辞, 郭思慧, 等 接驳地铁站的共享单车源汇时空特征及其影响因素
[J]. 地球信息科学学报 , 2021 , 23 (1 ): 155 - 170
DOI:10.12082/dqxxkx.2021.200351
[本文引用: 1]
GAO Ying, SONG Ci, GUO Si-hui, et al Spatial-temporal characteristics and influencing factors of source and sink of dockless sharing bicycles connected to subway stations
[J]. Journal of Geo-Information Science , 2021 , 23 (1 ): 155 - 170
DOI:10.12082/dqxxkx.2021.200351
[本文引用: 1]
A statistical analysis of bike sharing usage and its potential as an auto-trip substitute
1
2019
... 为了实现城市可持续发展的战略目标,国家积极倡导低碳出行,推动共享经济的发展. 公共自行车作为一种环保、主动的交通方式在减少交通碳排放和缓解道路拥堵方面被证明是有效的[1 ] . 自2016年以来,新型无桩式共享单车系统在中国、荷兰和新加坡等国家经历了飞跃式的增长[2 ] . 截止到2018年2月,中国共享单车系统中部署的单车数量已增至2300万辆[3 ] . 相比于传统定桩式共享单车,无桩共享单车不受车桩的限制,便捷的使用方式给用户的最后一公里出行提供了一个更好的选择[4 -5 ] . ...
A model framework for discovering the spatio-temporal usage patterns of public free-floating bike-sharing system
1
2019
... 为了实现城市可持续发展的战略目标,国家积极倡导低碳出行,推动共享经济的发展. 公共自行车作为一种环保、主动的交通方式在减少交通碳排放和缓解道路拥堵方面被证明是有效的[1 ] . 自2016年以来,新型无桩式共享单车系统在中国、荷兰和新加坡等国家经历了飞跃式的增长[2 ] . 截止到2018年2月,中国共享单车系统中部署的单车数量已增至2300万辆[3 ] . 相比于传统定桩式共享单车,无桩共享单车不受车桩的限制,便捷的使用方式给用户的最后一公里出行提供了一个更好的选择[4 -5 ] . ...
Measuring immediate impacts of a new mass transit system on an existing bike-share system in China
1
2019
... 为了实现城市可持续发展的战略目标,国家积极倡导低碳出行,推动共享经济的发展. 公共自行车作为一种环保、主动的交通方式在减少交通碳排放和缓解道路拥堵方面被证明是有效的[1 ] . 自2016年以来,新型无桩式共享单车系统在中国、荷兰和新加坡等国家经历了飞跃式的增长[2 ] . 截止到2018年2月,中国共享单车系统中部署的单车数量已增至2300万辆[3 ] . 相比于传统定桩式共享单车,无桩共享单车不受车桩的限制,便捷的使用方式给用户的最后一公里出行提供了一个更好的选择[4 -5 ] . ...
Understanding the usage of dockless bike sharing in Singapore
1
2018
... 为了实现城市可持续发展的战略目标,国家积极倡导低碳出行,推动共享经济的发展. 公共自行车作为一种环保、主动的交通方式在减少交通碳排放和缓解道路拥堵方面被证明是有效的[1 ] . 自2016年以来,新型无桩式共享单车系统在中国、荷兰和新加坡等国家经历了飞跃式的增长[2 ] . 截止到2018年2月,中国共享单车系统中部署的单车数量已增至2300万辆[3 ] . 相比于传统定桩式共享单车,无桩共享单车不受车桩的限制,便捷的使用方式给用户的最后一公里出行提供了一个更好的选择[4 -5 ] . ...
Analysing the trip and user characteristics of the combined bicycle and transit mode
1
2018
... 为了实现城市可持续发展的战略目标,国家积极倡导低碳出行,推动共享经济的发展. 公共自行车作为一种环保、主动的交通方式在减少交通碳排放和缓解道路拥堵方面被证明是有效的[1 ] . 自2016年以来,新型无桩式共享单车系统在中国、荷兰和新加坡等国家经历了飞跃式的增长[2 ] . 截止到2018年2月,中国共享单车系统中部署的单车数量已增至2300万辆[3 ] . 相比于传统定桩式共享单车,无桩共享单车不受车桩的限制,便捷的使用方式给用户的最后一公里出行提供了一个更好的选择[4 -5 ] . ...
Estimating the parking demand of free-floating bike sharing: a journey-data-based study of Nanjing, China
1
2020
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
1
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
1
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
1
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
Unravel the landscape and pulses of cycling activities from a dockless bike-sharing system
1
2019
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
Electric fence planning for dockless bike-sharing services
1
2019
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
Spatial heterogeneity in distance decay of using bike sharing: an empirical large-scale analysis in Shanghai
4
2021
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
... 基于现有文献分析[11 -12 ] ,重点分析建成环境和区域社会经济属性对共享单车出行的影响. 调查的建成环境特征包括人口密度、道路属性、土地利用和服务设施密度、公共交通可达性和区位条件,数据来源于Openstreetmap提供的路网数据、人口普查获得的密度数据和百度地图爬取的兴趣点(point of interest,POI)数据. 社会经济属性包括研究区域房价和GDP数据,数据来源于资源环境科学与数据中心( https://www.resdc.cn/ )和上海市链家网( https://sh.lianjia.com/ ). 摩拜单车数据采用的是wgs84坐标系,将上述数据统一成wgs84坐标进行统计. 为了不影响后续模型的结果,利用方差膨胀因子[21 ] 对变量的多重共线性进行检验,表达式如下: ...
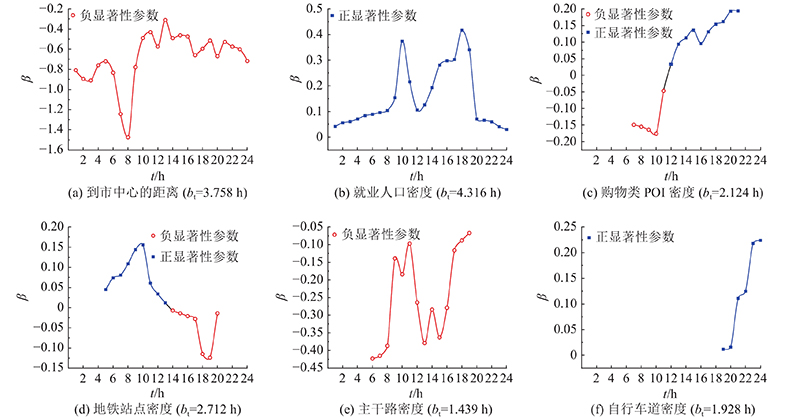
... 由图8 (b)可知,就业人口密度对停车需求具有促进作用,并且呈现出双峰特征,反映了共享单车主要用于工作日居民的日常通勤. 图8 (f)结果显示自行车道密度在19:00—24:00对停车需求也具有显著的促进作用,这种促进作用随着夜间的来临变得越发明显,可能是因为夜间照明条件有限,考虑到出行的安全性人们会选择自行车道集中分布的地方行驶和停放共享单车. 尽管Gao等[11 ] 指出自行车专用道与共享单车出行无显著关联,但其未从时间维度考虑这种影响关系的变化. ...
... 除了单一的时间影响关系之外,部分变量的估计参数在时间维度存在正负异质现象. 由图8 (c)可知,购物类POI密度的估计参数在7:00—21:00具有显著性,并且在上午为负值,在下午为正值,这在一定程度上反映了该地居民以共享单车为主的非机动化购物出行主要集中在下午,且在19:00—21:00达到最大. 相比于Gao等[11 ] 认为商场会吸引更多的骑行用户,本研究基于局部时间关系的分析揭示了这种影响关系的时间异质特征. 此外,图8 (d)显示地铁站点密度对于共享单车停车需求在4:00—20:00的影响显著,但影响关系存在时间差异,早高峰时段表现为正向影响,这表明地铁站点密集的地方共享单车停车需求较大. 然而,晚高峰则表现为负向影响,这种不一致的现象可能由于上午通勤到站人流量大,导致大量单车流入,而下午通勤时地铁站周边单车的流出率较高,抑制了停车需求的增加,这与Tan等[33 ] 、高楹等[34 ] 揭示的地铁站周边共享单车潮汐现象显著的结论相近,但本研究在考虑时间尺度后可以进一步精细化地揭示这类潮汐特征的时间变化. ...
共享单车出行的建成环境影响机制: 以上海市为例
3
2020
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
... 基于现有文献分析[11 -12 ] ,重点分析建成环境和区域社会经济属性对共享单车出行的影响. 调查的建成环境特征包括人口密度、道路属性、土地利用和服务设施密度、公共交通可达性和区位条件,数据来源于Openstreetmap提供的路网数据、人口普查获得的密度数据和百度地图爬取的兴趣点(point of interest,POI)数据. 社会经济属性包括研究区域房价和GDP数据,数据来源于资源环境科学与数据中心( https://www.resdc.cn/ )和上海市链家网( https://sh.lianjia.com/ ). 摩拜单车数据采用的是wgs84坐标系,将上述数据统一成wgs84坐标进行统计. 为了不影响后续模型的结果,利用方差膨胀因子[21 ] 对变量的多重共线性进行检验,表达式如下: ...
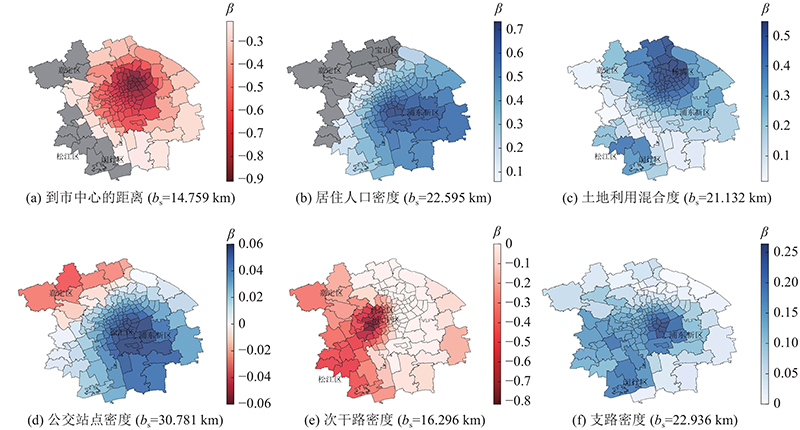
... 如图7 (b)所示为居住人口密度与停车需求的空间关系. 可以看出,居住人口密度在浦东新区及以东地区对停车需求的正向影响显著,这与此前研究认为高密度人口居住区会吸引更多的骑行用户的结论一致[30 -31 ] . 然而,MGTWR模型基于居住人口密度的微观空间作用尺度进一步揭示了这种影响机制在嘉定、宝山地区并不显著,可能是由于这部分区域中居住区距离地铁站较远,共享单车无法满足长距离出行需求,较多依赖公交接驳地铁. 图7 (c)显示土地利用混合度与共享单车停车需求整体上呈正相关,说明多样化的土地利用在一定程度上会吸引较多的骑行用户,这与Zhang等[32 ] 研究发现多样化的土地利用对共享单车出行吸引量具有促进作用的结论相符. 然而,估计参数的局部空间变化显著,对北部的杨浦和西南部的松江、闵行区等地的正向影响强烈,而对于西部的嘉定和东部的浦东地区影响相对较小,这与严亚磊等[12 ] 在街道尺度揭示的土地利用混合度与共享单车出行无显著关联等结论存在差异. 杨浦、松江和闵行等地汇集了众多高校,学生群体往往倾向于选择低碳环保的交通方式来完成多样化的出行目的. 相比之下,嘉定和浦东外围区域公共服务设施匮乏,交通条件不便,长距离出行增加了对机动车辆的依赖. 因此相较于全局分析结果而言,局部空间关系的探究可以更好地解释停车需求的变化. 由图7 (f)可知,支路密度对共享单车的停车需求也具有显著的正向影响,这种影响在中部的浦东新区和西南一侧的闵行地区最为明显. 闵行区和浦东新区地铁周边支线发达,并且居住着较多熟悉路网的本地居民,他们会倾向于选择共享单车通过便捷的支路来往返地铁站,因此停车需求与支路密度相关性更强. ...
共享单车出行的建成环境影响机制: 以上海市为例
3
2020
... 城市空间内共享单车规模的扩大和停车需求时空分布的显著差异给城市交通管理带来了巨大挑战[6 ] . 根据《2017年共享单车夏季市场专题报告》[7 ] ,42.0%的调查者认为乱停车问题比较严重,26.8%的调查者认为乱停车问题非常严重. 究其原因,主要是城市功能区的停车设施容量和位置与实际停车需求的潜在不匹配. 因此,开展共享单车规划研究对于城市的基础设施布局和单车分配调度具有重要意义. 近年来,国内外学者聚焦于共享单车的使用需求预测[8 ] 、时空出行模式分析[9 ] 和服务设施规划[10 ] 等,这些研究大多关注共享单车的使用需求、周转率、骑行时间与建成环境及区域社会经济属性之间的关联[11 -12 ] ,对共享单车停车问题的分析仍然有限. 鉴于此,须进一步探究共享单车停车需求的影响因素及其关系强度以完善相应的研究. ...
... 基于现有文献分析[11 -12 ] ,重点分析建成环境和区域社会经济属性对共享单车出行的影响. 调查的建成环境特征包括人口密度、道路属性、土地利用和服务设施密度、公共交通可达性和区位条件,数据来源于Openstreetmap提供的路网数据、人口普查获得的密度数据和百度地图爬取的兴趣点(point of interest,POI)数据. 社会经济属性包括研究区域房价和GDP数据,数据来源于资源环境科学与数据中心( https://www.resdc.cn/ )和上海市链家网( https://sh.lianjia.com/ ). 摩拜单车数据采用的是wgs84坐标系,将上述数据统一成wgs84坐标进行统计. 为了不影响后续模型的结果,利用方差膨胀因子[21 ] 对变量的多重共线性进行检验,表达式如下: ...
... 如图7 (b)所示为居住人口密度与停车需求的空间关系. 可以看出,居住人口密度在浦东新区及以东地区对停车需求的正向影响显著,这与此前研究认为高密度人口居住区会吸引更多的骑行用户的结论一致[30 -31 ] . 然而,MGTWR模型基于居住人口密度的微观空间作用尺度进一步揭示了这种影响机制在嘉定、宝山地区并不显著,可能是由于这部分区域中居住区距离地铁站较远,共享单车无法满足长距离出行需求,较多依赖公交接驳地铁. 图7 (c)显示土地利用混合度与共享单车停车需求整体上呈正相关,说明多样化的土地利用在一定程度上会吸引较多的骑行用户,这与Zhang等[32 ] 研究发现多样化的土地利用对共享单车出行吸引量具有促进作用的结论相符. 然而,估计参数的局部空间变化显著,对北部的杨浦和西南部的松江、闵行区等地的正向影响强烈,而对于西部的嘉定和东部的浦东地区影响相对较小,这与严亚磊等[12 ] 在街道尺度揭示的土地利用混合度与共享单车出行无显著关联等结论存在差异. 杨浦、松江和闵行等地汇集了众多高校,学生群体往往倾向于选择低碳环保的交通方式来完成多样化的出行目的. 相比之下,嘉定和浦东外围区域公共服务设施匮乏,交通条件不便,长距离出行增加了对机动车辆的依赖. 因此相较于全局分析结果而言,局部空间关系的探究可以更好地解释停车需求的变化. 由图7 (f)可知,支路密度对共享单车的停车需求也具有显著的正向影响,这种影响在中部的浦东新区和西南一侧的闵行地区最为明显. 闵行区和浦东新区地铁周边支线发达,并且居住着较多熟悉路网的本地居民,他们会倾向于选择共享单车通过便捷的支路来往返地铁站,因此停车需求与支路密度相关性更强. ...
Modeling bike share station activity: effects of nearby businesses and jobs on trips to and from stations
1
2015
... 在共享单车影响因素分析及其时空关系建模研究中,普通最小二乘回归(ordinary leastsquares regression,OLS)常用于探究建成环境与单车使用间的关系[13 ] . 然而,OLS模型未考虑建成环境与共享单车需求间的空间异质关系,因此一些学者利用地理加权回归(geographically weighted regression,GWR)模型来解决此类问题,例如曹小曙等[14 ] 利用GWR模型探究建成环境对中国大陆不同城市共享单车配置的空间异质影响,并证明了GWR模型的性能显著优于OLS回归模型. Li等[15 ] 探究建成环境对上海市共享单车利用模式的影响,同样发现GWR模型的解释力比OLS模型更高. 在GWR模型被广泛应用的同时,针对共享单车需求的时间非平稳性,Ma等[16 ] 利用时空地理加权回归(geographically and temporally weighted regression,GTWR)模型[17 ] 研究了南京市建成环境和社会经济属性在时空维度上对定桩和无桩共享单车使用的影响,证明同时考虑时间和空间非平稳性的GTWR模型相比于OLS和GWR具有更强的解释力. ...
中国大陆城市建成环境与共享单车配置的关系
1
2020
... 在共享单车影响因素分析及其时空关系建模研究中,普通最小二乘回归(ordinary leastsquares regression,OLS)常用于探究建成环境与单车使用间的关系[13 ] . 然而,OLS模型未考虑建成环境与共享单车需求间的空间异质关系,因此一些学者利用地理加权回归(geographically weighted regression,GWR)模型来解决此类问题,例如曹小曙等[14 ] 利用GWR模型探究建成环境对中国大陆不同城市共享单车配置的空间异质影响,并证明了GWR模型的性能显著优于OLS回归模型. Li等[15 ] 探究建成环境对上海市共享单车利用模式的影响,同样发现GWR模型的解释力比OLS模型更高. 在GWR模型被广泛应用的同时,针对共享单车需求的时间非平稳性,Ma等[16 ] 利用时空地理加权回归(geographically and temporally weighted regression,GTWR)模型[17 ] 研究了南京市建成环境和社会经济属性在时空维度上对定桩和无桩共享单车使用的影响,证明同时考虑时间和空间非平稳性的GTWR模型相比于OLS和GWR具有更强的解释力. ...
中国大陆城市建成环境与共享单车配置的关系
1
2020
... 在共享单车影响因素分析及其时空关系建模研究中,普通最小二乘回归(ordinary leastsquares regression,OLS)常用于探究建成环境与单车使用间的关系[13 ] . 然而,OLS模型未考虑建成环境与共享单车需求间的空间异质关系,因此一些学者利用地理加权回归(geographically weighted regression,GWR)模型来解决此类问题,例如曹小曙等[14 ] 利用GWR模型探究建成环境对中国大陆不同城市共享单车配置的空间异质影响,并证明了GWR模型的性能显著优于OLS回归模型. Li等[15 ] 探究建成环境对上海市共享单车利用模式的影响,同样发现GWR模型的解释力比OLS模型更高. 在GWR模型被广泛应用的同时,针对共享单车需求的时间非平稳性,Ma等[16 ] 利用时空地理加权回归(geographically and temporally weighted regression,GTWR)模型[17 ] 研究了南京市建成环境和社会经济属性在时空维度上对定桩和无桩共享单车使用的影响,证明同时考虑时间和空间非平稳性的GTWR模型相比于OLS和GWR具有更强的解释力. ...
An empirical analysis of dockless bike-sharing utilization and its explanatory factors: case study from Shanghai, China
3
2020
... 在共享单车影响因素分析及其时空关系建模研究中,普通最小二乘回归(ordinary leastsquares regression,OLS)常用于探究建成环境与单车使用间的关系[13 ] . 然而,OLS模型未考虑建成环境与共享单车需求间的空间异质关系,因此一些学者利用地理加权回归(geographically weighted regression,GWR)模型来解决此类问题,例如曹小曙等[14 ] 利用GWR模型探究建成环境对中国大陆不同城市共享单车配置的空间异质影响,并证明了GWR模型的性能显著优于OLS回归模型. Li等[15 ] 探究建成环境对上海市共享单车利用模式的影响,同样发现GWR模型的解释力比OLS模型更高. 在GWR模型被广泛应用的同时,针对共享单车需求的时间非平稳性,Ma等[16 ] 利用时空地理加权回归(geographically and temporally weighted regression,GTWR)模型[17 ] 研究了南京市建成环境和社会经济属性在时空维度上对定桩和无桩共享单车使用的影响,证明同时考虑时间和空间非平稳性的GTWR模型相比于OLS和GWR具有更强的解释力. ...
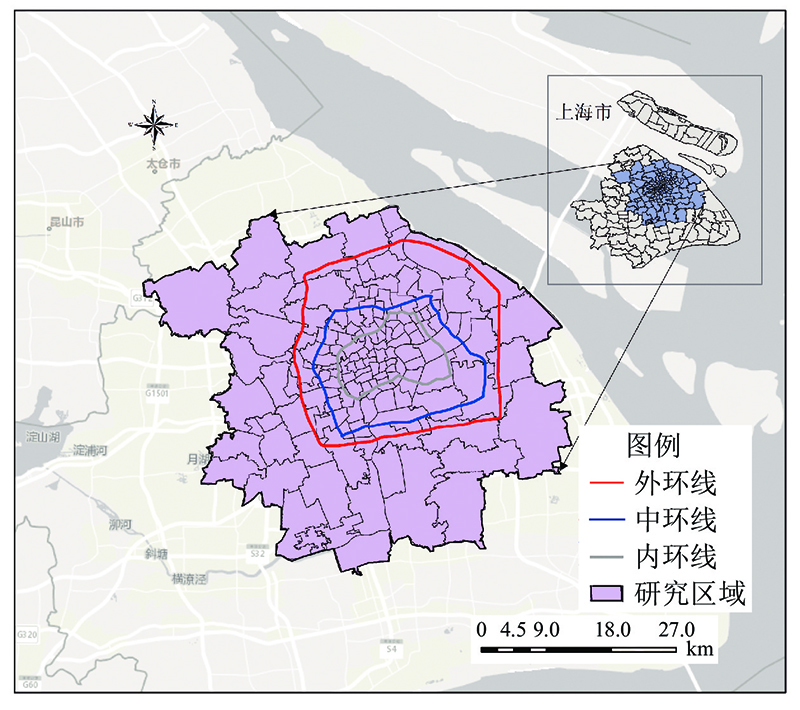
... 为了保证数据具有代表性,选择共享单车集中分布的范围作为研究区域,如图1 所示. 图中,黑色边界线以内为研究区域,面积约为1868.877 km2 ,涵盖了浦东新区、黄浦区、嘉定区、宝山区、徐汇区、普陀区、杨浦区、松江区、虹口区、长宁区、闵行区、静安区12个主要行政区. 本研究主要目的为通过街道和镇层面的异质差异来为城市规划管理提供理论支持,同时便于对人口与社会经济属性的统计,根据以往研究[15 ] 对上海市共享单车需求分析中研究单元的划分方法,将研究区域按照2010 年上海市第6次人口普查( https://tjj.sh.gov.cn/tjgb/20110502/0014-218818.html )的基本单位划分为136个研究单元,包含主要的镇和街道. ...
... 除了单一的空间影响关系之外,图7 (d)显示了公交站点密度与共享单车停车需求在空间上存在相反的关系,在徐汇和浦西地区呈正相关,这一发现表明共享单车在公交地铁发达的地区往往相互补充,以应对居民出行的最后一公里问题[15 ] . 然而,在西部嘉定郊区却呈负相关,这意味着公交站点对共享单车的停车需求具有抑制作用. 这部分区域地铁站点稀少,较多的公交站设置了在了地铁站、居住区和停车场附近,在连接地铁出行时与共享单车往往表现为竞争关系. ...
A comparison in travel patterns and determinants of user demand between docked and dockless bike-sharing systems using multi-sourced data
1
2020
... 在共享单车影响因素分析及其时空关系建模研究中,普通最小二乘回归(ordinary leastsquares regression,OLS)常用于探究建成环境与单车使用间的关系[13 ] . 然而,OLS模型未考虑建成环境与共享单车需求间的空间异质关系,因此一些学者利用地理加权回归(geographically weighted regression,GWR)模型来解决此类问题,例如曹小曙等[14 ] 利用GWR模型探究建成环境对中国大陆不同城市共享单车配置的空间异质影响,并证明了GWR模型的性能显著优于OLS回归模型. Li等[15 ] 探究建成环境对上海市共享单车利用模式的影响,同样发现GWR模型的解释力比OLS模型更高. 在GWR模型被广泛应用的同时,针对共享单车需求的时间非平稳性,Ma等[16 ] 利用时空地理加权回归(geographically and temporally weighted regression,GTWR)模型[17 ] 研究了南京市建成环境和社会经济属性在时空维度上对定桩和无桩共享单车使用的影响,证明同时考虑时间和空间非平稳性的GTWR模型相比于OLS和GWR具有更强的解释力. ...
Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices
2
2010
... 在共享单车影响因素分析及其时空关系建模研究中,普通最小二乘回归(ordinary leastsquares regression,OLS)常用于探究建成环境与单车使用间的关系[13 ] . 然而,OLS模型未考虑建成环境与共享单车需求间的空间异质关系,因此一些学者利用地理加权回归(geographically weighted regression,GWR)模型来解决此类问题,例如曹小曙等[14 ] 利用GWR模型探究建成环境对中国大陆不同城市共享单车配置的空间异质影响,并证明了GWR模型的性能显著优于OLS回归模型. Li等[15 ] 探究建成环境对上海市共享单车利用模式的影响,同样发现GWR模型的解释力比OLS模型更高. 在GWR模型被广泛应用的同时,针对共享单车需求的时间非平稳性,Ma等[16 ] 利用时空地理加权回归(geographically and temporally weighted regression,GTWR)模型[17 ] 研究了南京市建成环境和社会经济属性在时空维度上对定桩和无桩共享单车使用的影响,证明同时考虑时间和空间非平稳性的GTWR模型相比于OLS和GWR具有更强的解释力. ...
... 在定义MGTWR模型之前须引入GTWR模型的理论方法,有助于深入理解时空建模的过程. GTWR模型采用局部时空回归,并利用时间和空间域中附近的样本点来对局部观测点的回归系数进行校准[17 ] . GTWR模型的回归方程表达式和回归参数的校准方程分别如下: ...
Multiscale geographically and temporally weighted regression: exploring the spatiotemporal determinants of housing prices
2
2019
... 上述研究表明,GWR、GTWR相比于OLS模型能更好地解释多维因素对共享单车需求的异质影响,但仍存在一定的局限性. 首先,GTWR模型使用单一的平均带宽来计算变量的作用范围,忽视了不同变量作用的时空尺度差异,这可能会夸大或低估这种时空效应的变化,因此多尺度时空地理加权回归(multiscale geographically and temporally weighted regression,MGTWR)模型被提出以解决房价建模中变量作用尺度不一致的问题[18 ] . 然而,共享单车需求影响因素的时空作用尺度仍有待进一步探索. 其次,GWR、GTWR、MGTWR在构建局部空间权重矩阵时采用欧氏距离(Euclidean distance,ED),在面对复杂的地理空间环境特征时无法很好地表征区域之间的邻里关系,并且用欧氏距离来衡量骑行者的出行距离可能会导致结果产生一定的误差. ...
... MGTWR模型是一种广义加法模型,后退拟合算法常常被用于校准广义加法模型,因为该算法可以循环遍历加法模型的各个项,并使用适当的平滑器更新每一项,从而实现对每一个未知项的校准[24 ] . 因此,利用后退拟合算法来迭代更新寻找每个变量的最优带宽. 具体过程如下. 首先,根据 $ \hat {\boldsymbol{\varepsilon}} +{{\boldsymbol{f}}_1} $ $ {{\boldsymbol{x}}_1} $ $ {{\boldsymbol{x}}_1} $ $ {{\boldsymbol{f}}_1} $ $ \hat {\boldsymbol{\varepsilon}} $ . 将上述过程继续至下一个变量,直至所有解释变量的最优时空带宽、加法项、误差项均被更新. 上述为第1轮迭代,第2轮将使用第1轮更新后的加法项和误差项重复前一轮的过程,直至达到收敛准则时停止更新. 收敛准则为经典的残差平方和变化比例( $ {\text{SO}}{{\text{C}}_{{\rm{RSS}}}} $ ) ,使用 $ {{{\rm{SOC}}} _{{\rm{RSS}}}} \leqslant {10^{ - 5}} $ [18 ] ,具体公式如下: ...
1
... 本研究利用摩拜单车公司提供的2018年上海市DLBS交易数据进行分析. 摩拜单车是当时中国最大的共享单车公司,上海也是中国最大的都市之一. 2018年年底上海市人口达到2424万,2018年上海市GDP总量为32680亿元,占国内总量的6.6%[19 ] . 上海作为全球最大的共享单车城市之一,截止到2017年3月,共享单车投入量为45万辆,注册的单车用户达到450万[20 ] . 研究所用的数据记录了2018年8月26—9月8日时间跨度2周的64 万辆无桩共享单车的订单数据,有效订单量超3500 万,每天0:00—24:00的平均记录约为250 万,数据字段信息包括单车ID、记录时间、锁车状态(0开锁,1关锁)、位置信息(经纬度). ...
Exploring travel patterns and trip purposes of dockless bike-sharing by analyzing massive bike-sharing data in Shanghai, China
1
2020
... 本研究利用摩拜单车公司提供的2018年上海市DLBS交易数据进行分析. 摩拜单车是当时中国最大的共享单车公司,上海也是中国最大的都市之一. 2018年年底上海市人口达到2424万,2018年上海市GDP总量为32680亿元,占国内总量的6.6%[19 ] . 上海作为全球最大的共享单车城市之一,截止到2017年3月,共享单车投入量为45万辆,注册的单车用户达到450万[20 ] . 研究所用的数据记录了2018年8月26—9月8日时间跨度2周的64 万辆无桩共享单车的订单数据,有效订单量超3500 万,每天0:00—24:00的平均记录约为250 万,数据字段信息包括单车ID、记录时间、锁车状态(0开锁,1关锁)、位置信息(经纬度). ...
Model-dependent variance inflation factor cutoff values
1
2002
... 基于现有文献分析[11 -12 ] ,重点分析建成环境和区域社会经济属性对共享单车出行的影响. 调查的建成环境特征包括人口密度、道路属性、土地利用和服务设施密度、公共交通可达性和区位条件,数据来源于Openstreetmap提供的路网数据、人口普查获得的密度数据和百度地图爬取的兴趣点(point of interest,POI)数据. 社会经济属性包括研究区域房价和GDP数据,数据来源于资源环境科学与数据中心( https://www.resdc.cn/ )和上海市链家网( https://sh.lianjia.com/ ). 摩拜单车数据采用的是wgs84坐标系,将上述数据统一成wgs84坐标进行统计. 为了不影响后续模型的结果,利用方差膨胀因子[21 ] 对变量的多重共线性进行检验,表达式如下: ...
租赁自行车用户出行特征及方式的影响因素分析
1
2020
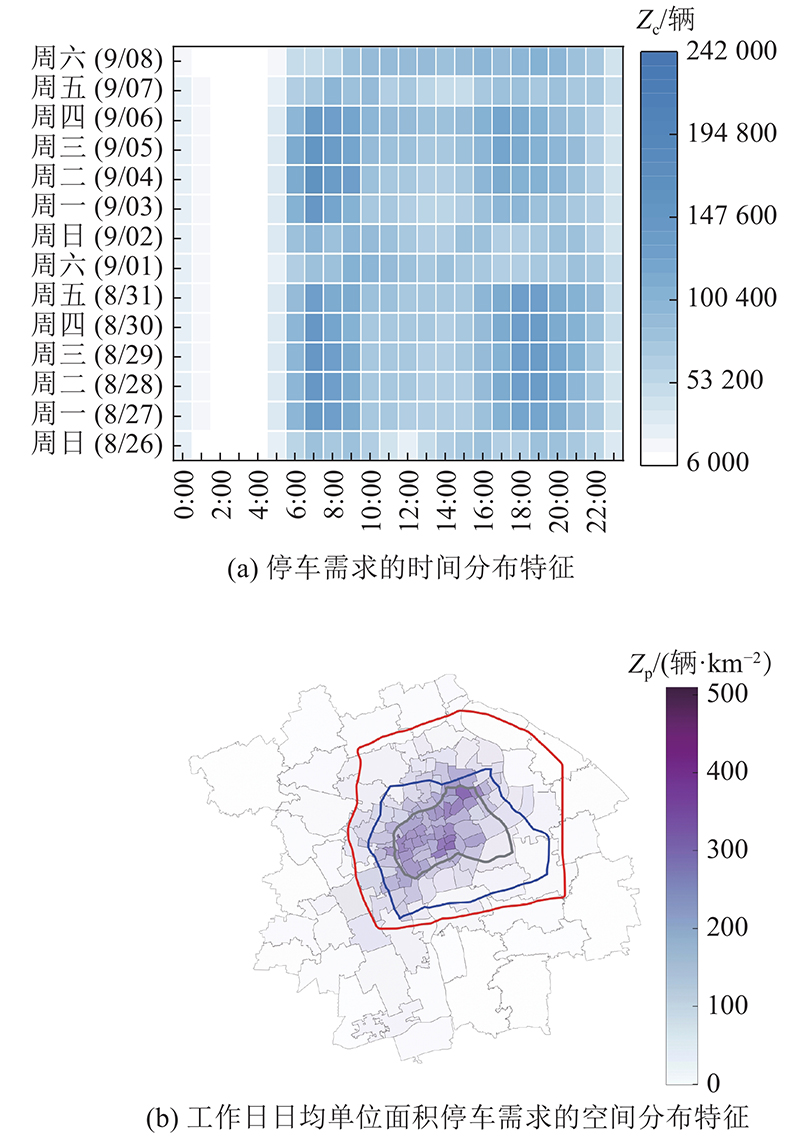
... 统计研究区域内14 d的共享单车的小时停车数和研究区域内每平方千米日均停车数,绘制停车需求的时空分布图,如图4 (a)、(b)所示. 图中, $ {Z_{\rm{c}}} $ $ {Z_{\rm{p}} } $ 图4 (a)可知,共享单车的停车需求呈现双峰特征,早晨7:00—9:00和傍晚17:00—19:00停车需求明显增加,这种现象在工作日的10 d中较为显著,表明共享单车在上海市居民通勤时受到广泛使用,这与马新卫等[22 ] 基于南京市共享单车的研究发现一致. 对于非工作日而言,由于居民出行目的的多样化,停车需求的变化趋势相对平稳. 由图4 (b)可知,外环线以内共享单车平均单位面积停车需求整体较高,向城市中心呈径向递增的趋势,主要是因为中心城区楼宇林立、商业和交通发达,居住人口高度集中,容易造成公共交通站点、购物商场及商务住宅等设施建筑周边共享单车呈潮汐式分布. 分析表明共享单车的停车需求呈现时空不平衡的现象,因此了解城市多维因素引起共享单车停车需求时空变化的潜在机制至关重要. 由于4 d非工作日均为雨天并且周末出行目的随机多变,本研究将天气状况良好的工作日日均单位面积的小时停车数作为模型的因变量. ...
租赁自行车用户出行特征及方式的影响因素分析
1
2020
... 统计研究区域内14 d的共享单车的小时停车数和研究区域内每平方千米日均停车数,绘制停车需求的时空分布图,如图4 (a)、(b)所示. 图中, $ {Z_{\rm{c}}} $ $ {Z_{\rm{p}} } $ 图4 (a)可知,共享单车的停车需求呈现双峰特征,早晨7:00—9:00和傍晚17:00—19:00停车需求明显增加,这种现象在工作日的10 d中较为显著,表明共享单车在上海市居民通勤时受到广泛使用,这与马新卫等[22 ] 基于南京市共享单车的研究发现一致. 对于非工作日而言,由于居民出行目的的多样化,停车需求的变化趋势相对平稳. 由图4 (b)可知,外环线以内共享单车平均单位面积停车需求整体较高,向城市中心呈径向递增的趋势,主要是因为中心城区楼宇林立、商业和交通发达,居住人口高度集中,容易造成公共交通站点、购物商场及商务住宅等设施建筑周边共享单车呈潮汐式分布. 分析表明共享单车的停车需求呈现时空不平衡的现象,因此了解城市多维因素引起共享单车停车需求时空变化的潜在机制至关重要. 由于4 d非工作日均为雨天并且周末出行目的随机多变,本研究将天气状况良好的工作日日均单位面积的小时停车数作为模型的因变量. ...
Multiscale geographically weighted regression (MGWR)
1
2017
... 式中: $ d_{ij}^{{\rm{st}}} $ $ i $ $ j $ $ d_{ij}^{{\rm{st}}} $ $\left[ {{\lambda {{(d_{ij}^{{\rm{s}}})}^2}+u{{(d_{ij}^{\rm{t}})}^2}}} \right]^{1/2}$ $d_{ij}^{{\rm{s}}}$ $ d_{ij}^{\rm{t}} $ $ \lambda $ $ u $ $ {b_{{\rm{st}}}} $ [23 ] . ...
Smooth backfitting in generalized additive models
1
2008
... MGTWR模型是一种广义加法模型,后退拟合算法常常被用于校准广义加法模型,因为该算法可以循环遍历加法模型的各个项,并使用适当的平滑器更新每一项,从而实现对每一个未知项的校准[24 ] . 因此,利用后退拟合算法来迭代更新寻找每个变量的最优带宽. 具体过程如下. 首先,根据 $ \hat {\boldsymbol{\varepsilon}} +{{\boldsymbol{f}}_1} $ $ {{\boldsymbol{x}}_1} $ $ {{\boldsymbol{x}}_1} $ $ {{\boldsymbol{f}}_1} $ $ \hat {\boldsymbol{\varepsilon}} $ . 将上述过程继续至下一个变量,直至所有解释变量的最优时空带宽、加法项、误差项均被更新. 上述为第1轮迭代,第2轮将使用第1轮更新后的加法项和误差项重复前一轮的过程,直至达到收敛准则时停止更新. 收敛准则为经典的残差平方和变化比例( $ {\text{SO}}{{\text{C}}_{{\rm{RSS}}}} $ ) ,使用 $ {{{\rm{SOC}}} _{{\rm{RSS}}}} \leqslant {10^{ - 5}} $ [18 ] ,具体公式如下: ...
Quantifying economic benefits from free-floating bike-sharing systems: a trip-level inference approach and city-scale analysis
1
2021
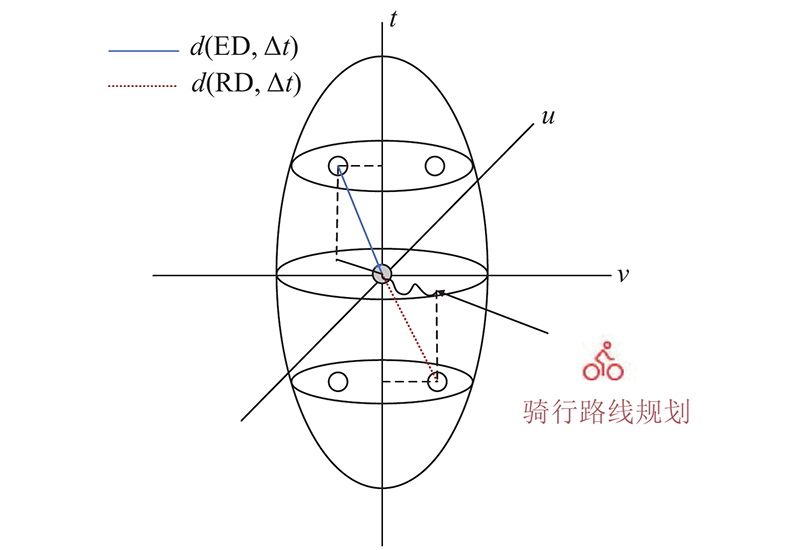
... 为了比较不同距离约束下模型的性能,须对式(4)的 $ d_{ij}^{{\rm{s}}} $ [25 -26 ] ,本研究调用百度地图API实现骑行路径规划,构造各个子区中心点之间的起讫点矩阵,输入经纬度坐标,将wgs84坐标转换成百度经纬度坐标bd09ll,构造请求的url(骑行路线规划服务网址 http://api.map.baidu.com/routematrix/v2/riding?output=json ),之后用requests向服务器发送请求,最终得到样本点间的最佳骑行距离,以重新计算空间距离权重,并构建以骑行距离为约束的多尺度时空地理加权回归(RD-MGTWR)模型,改进前、后时空距离图解如图5 所示. 图中, $ t $ $ u $ $ v $ $\Delta t $ d 为时空距离,ED为欧氏距离,RD为骑行距离. ...
Ride-sourcing compared to its public-transit alternative using big trip data
1
2021
... 为了比较不同距离约束下模型的性能,须对式(4)的 $ d_{ij}^{{\rm{s}}} $ [25 -26 ] ,本研究调用百度地图API实现骑行路径规划,构造各个子区中心点之间的起讫点矩阵,输入经纬度坐标,将wgs84坐标转换成百度经纬度坐标bd09ll,构造请求的url(骑行路线规划服务网址 http://api.map.baidu.com/routematrix/v2/riding?output=json ),之后用requests向服务器发送请求,最终得到样本点间的最佳骑行距离,以重新计算空间距离权重,并构建以骑行距离为约束的多尺度时空地理加权回归(RD-MGTWR)模型,改进前、后时空距离图解如图5 所示. 图中, $ t $ $ u $ $ v $ $\Delta t $ d 为时空距离,ED为欧氏距离,RD为骑行距离. ...
Geographical and temporal weighted regression (GTWR)
1
2015
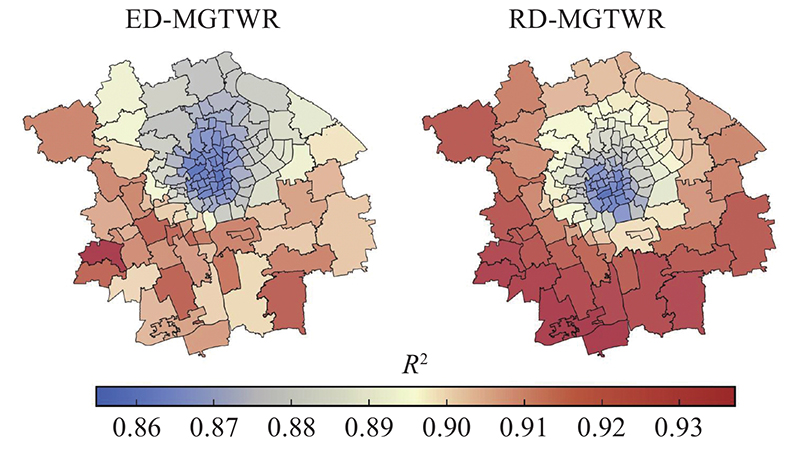
... 上述对4种局部模型进行了对比,但各变量的影响是否具有异质性仍然未知. 因此,基于现有研究对变量时空非平稳性的检验方法[27 -28 ] ,通过比较局部最优模型RD-MGTWR回归系数的四分位数差(上四分位数-下四分位数)和全局模型OLS两倍标准误差(2SE)的大小来做进一步判断,若前者大于后者表明解释变量的影响具有时空非平稳性. 如表3 所示,所有变量的估计参数均具有不同程度的变化,可以看出局部模型RD-MGTWR模型可以更好地刻画影响因素与停车需求之间的时空异质关系. 最后,将所有变量归一化处理,以允许解释变量的带宽和回归系数具有可比性. ...
A geographically and temporally weighted regression model to explore the spatiotemporal influence of built environment on transit ridership
1
2018
... 上述对4种局部模型进行了对比,但各变量的影响是否具有异质性仍然未知. 因此,基于现有研究对变量时空非平稳性的检验方法[27 -28 ] ,通过比较局部最优模型RD-MGTWR回归系数的四分位数差(上四分位数-下四分位数)和全局模型OLS两倍标准误差(2SE)的大小来做进一步判断,若前者大于后者表明解释变量的影响具有时空非平稳性. 如表3 所示,所有变量的估计参数均具有不同程度的变化,可以看出局部模型RD-MGTWR模型可以更好地刻画影响因素与停车需求之间的时空异质关系. 最后,将所有变量归一化处理,以允许解释变量的带宽和回归系数具有可比性. ...
Exploring spatial variation of bike sharing trip production andattraction: a study based on Chicago’s Divvy system
1
2020
... 由图7 (a)可知,到市中心的距离与共享单车的停车需求呈负相关,表明越靠近市中心共享单车停车需求表现出增加的趋势,这种负相关关系在中部地区的徐家汇街道、陆家嘴街道和南京西路街道等中央商务区最为明显,这与Yang等[29 ] 基于平均尺度的GWR模型分析得出靠近市中心会增加共享自行车的出行吸引力的结论相近. 然而,MGTWR模型得到的较小的空间带宽反映了空间关系差异化显著,主要表现为在西部和西南部的嘉定、松江、闵行等地区无显著关联,可能是因为这些区域位于上海市郊区,较少的单车投放和有限的地铁站点导致共享单车接驳需求减少. 可以推断,共享单车停车需求的集聚现象在市区比郊区更为明显. 图7 (e)显示次干路密度对共享单车停车需求也具有显著负向影响. 可能原因是次干路主要承担主干路与各分区的交通集散,支持私家车、网约车和公共汽车等机动车辆的运行,这些道路没有设计专用的自行车道导致对骑行用户的吸引减弱. 从估计参数的空间分布来看,普陀和长宁以西地区的负向影响高于东部的浦东新区,这在一定程度上反映了东西两侧路网结构的差异. ...
1
... 如图7 (b)所示为居住人口密度与停车需求的空间关系. 可以看出,居住人口密度在浦东新区及以东地区对停车需求的正向影响显著,这与此前研究认为高密度人口居住区会吸引更多的骑行用户的结论一致[30 -31 ] . 然而,MGTWR模型基于居住人口密度的微观空间作用尺度进一步揭示了这种影响机制在嘉定、宝山地区并不显著,可能是由于这部分区域中居住区距离地铁站较远,共享单车无法满足长距离出行需求,较多依赖公交接驳地铁. 图7 (c)显示土地利用混合度与共享单车停车需求整体上呈正相关,说明多样化的土地利用在一定程度上会吸引较多的骑行用户,这与Zhang等[32 ] 研究发现多样化的土地利用对共享单车出行吸引量具有促进作用的结论相符. 然而,估计参数的局部空间变化显著,对北部的杨浦和西南部的松江、闵行区等地的正向影响强烈,而对于西部的嘉定和东部的浦东地区影响相对较小,这与严亚磊等[12 ] 在街道尺度揭示的土地利用混合度与共享单车出行无显著关联等结论存在差异. 杨浦、松江和闵行等地汇集了众多高校,学生群体往往倾向于选择低碳环保的交通方式来完成多样化的出行目的. 相比之下,嘉定和浦东外围区域公共服务设施匮乏,交通条件不便,长距离出行增加了对机动车辆的依赖. 因此相较于全局分析结果而言,局部空间关系的探究可以更好地解释停车需求的变化. 由图7 (f)可知,支路密度对共享单车的停车需求也具有显著的正向影响,这种影响在中部的浦东新区和西南一侧的闵行地区最为明显. 闵行区和浦东新区地铁周边支线发达,并且居住着较多熟悉路网的本地居民,他们会倾向于选择共享单车通过便捷的支路来往返地铁站,因此停车需求与支路密度相关性更强. ...
老城区共享单车出行特征及影响因素研究: 以广州为例
1
2019
... 如图7 (b)所示为居住人口密度与停车需求的空间关系. 可以看出,居住人口密度在浦东新区及以东地区对停车需求的正向影响显著,这与此前研究认为高密度人口居住区会吸引更多的骑行用户的结论一致[30 -31 ] . 然而,MGTWR模型基于居住人口密度的微观空间作用尺度进一步揭示了这种影响机制在嘉定、宝山地区并不显著,可能是由于这部分区域中居住区距离地铁站较远,共享单车无法满足长距离出行需求,较多依赖公交接驳地铁. 图7 (c)显示土地利用混合度与共享单车停车需求整体上呈正相关,说明多样化的土地利用在一定程度上会吸引较多的骑行用户,这与Zhang等[32 ] 研究发现多样化的土地利用对共享单车出行吸引量具有促进作用的结论相符. 然而,估计参数的局部空间变化显著,对北部的杨浦和西南部的松江、闵行区等地的正向影响强烈,而对于西部的嘉定和东部的浦东地区影响相对较小,这与严亚磊等[12 ] 在街道尺度揭示的土地利用混合度与共享单车出行无显著关联等结论存在差异. 杨浦、松江和闵行等地汇集了众多高校,学生群体往往倾向于选择低碳环保的交通方式来完成多样化的出行目的. 相比之下,嘉定和浦东外围区域公共服务设施匮乏,交通条件不便,长距离出行增加了对机动车辆的依赖. 因此相较于全局分析结果而言,局部空间关系的探究可以更好地解释停车需求的变化. 由图7 (f)可知,支路密度对共享单车的停车需求也具有显著的正向影响,这种影响在中部的浦东新区和西南一侧的闵行地区最为明显. 闵行区和浦东新区地铁周边支线发达,并且居住着较多熟悉路网的本地居民,他们会倾向于选择共享单车通过便捷的支路来往返地铁站,因此停车需求与支路密度相关性更强. ...
老城区共享单车出行特征及影响因素研究: 以广州为例
1
2019
... 如图7 (b)所示为居住人口密度与停车需求的空间关系. 可以看出,居住人口密度在浦东新区及以东地区对停车需求的正向影响显著,这与此前研究认为高密度人口居住区会吸引更多的骑行用户的结论一致[30 -31 ] . 然而,MGTWR模型基于居住人口密度的微观空间作用尺度进一步揭示了这种影响机制在嘉定、宝山地区并不显著,可能是由于这部分区域中居住区距离地铁站较远,共享单车无法满足长距离出行需求,较多依赖公交接驳地铁. 图7 (c)显示土地利用混合度与共享单车停车需求整体上呈正相关,说明多样化的土地利用在一定程度上会吸引较多的骑行用户,这与Zhang等[32 ] 研究发现多样化的土地利用对共享单车出行吸引量具有促进作用的结论相符. 然而,估计参数的局部空间变化显著,对北部的杨浦和西南部的松江、闵行区等地的正向影响强烈,而对于西部的嘉定和东部的浦东地区影响相对较小,这与严亚磊等[12 ] 在街道尺度揭示的土地利用混合度与共享单车出行无显著关联等结论存在差异. 杨浦、松江和闵行等地汇集了众多高校,学生群体往往倾向于选择低碳环保的交通方式来完成多样化的出行目的. 相比之下,嘉定和浦东外围区域公共服务设施匮乏,交通条件不便,长距离出行增加了对机动车辆的依赖. 因此相较于全局分析结果而言,局部空间关系的探究可以更好地解释停车需求的变化. 由图7 (f)可知,支路密度对共享单车的停车需求也具有显著的正向影响,这种影响在中部的浦东新区和西南一侧的闵行地区最为明显. 闵行区和浦东新区地铁周边支线发达,并且居住着较多熟悉路网的本地居民,他们会倾向于选择共享单车通过便捷的支路来往返地铁站,因此停车需求与支路密度相关性更强. ...
Exploring the impact of built environment factors on the use of publicbikes at bike stations: case study in Zhongshan, China
1
2017
... 如图7 (b)所示为居住人口密度与停车需求的空间关系. 可以看出,居住人口密度在浦东新区及以东地区对停车需求的正向影响显著,这与此前研究认为高密度人口居住区会吸引更多的骑行用户的结论一致[30 -31 ] . 然而,MGTWR模型基于居住人口密度的微观空间作用尺度进一步揭示了这种影响机制在嘉定、宝山地区并不显著,可能是由于这部分区域中居住区距离地铁站较远,共享单车无法满足长距离出行需求,较多依赖公交接驳地铁. 图7 (c)显示土地利用混合度与共享单车停车需求整体上呈正相关,说明多样化的土地利用在一定程度上会吸引较多的骑行用户,这与Zhang等[32 ] 研究发现多样化的土地利用对共享单车出行吸引量具有促进作用的结论相符. 然而,估计参数的局部空间变化显著,对北部的杨浦和西南部的松江、闵行区等地的正向影响强烈,而对于西部的嘉定和东部的浦东地区影响相对较小,这与严亚磊等[12 ] 在街道尺度揭示的土地利用混合度与共享单车出行无显著关联等结论存在差异. 杨浦、松江和闵行等地汇集了众多高校,学生群体往往倾向于选择低碳环保的交通方式来完成多样化的出行目的. 相比之下,嘉定和浦东外围区域公共服务设施匮乏,交通条件不便,长距离出行增加了对机动车辆的依赖. 因此相较于全局分析结果而言,局部空间关系的探究可以更好地解释停车需求的变化. 由图7 (f)可知,支路密度对共享单车的停车需求也具有显著的正向影响,这种影响在中部的浦东新区和西南一侧的闵行地区最为明显. 闵行区和浦东新区地铁周边支线发达,并且居住着较多熟悉路网的本地居民,他们会倾向于选择共享单车通过便捷的支路来往返地铁站,因此停车需求与支路密度相关性更强. ...
Tidal phenomenon of the dockless bike-sharing system and its causes: the case of Beijing
1
2022
... 除了单一的时间影响关系之外,部分变量的估计参数在时间维度存在正负异质现象. 由图8 (c)可知,购物类POI密度的估计参数在7:00—21:00具有显著性,并且在上午为负值,在下午为正值,这在一定程度上反映了该地居民以共享单车为主的非机动化购物出行主要集中在下午,且在19:00—21:00达到最大. 相比于Gao等[11 ] 认为商场会吸引更多的骑行用户,本研究基于局部时间关系的分析揭示了这种影响关系的时间异质特征. 此外,图8 (d)显示地铁站点密度对于共享单车停车需求在4:00—20:00的影响显著,但影响关系存在时间差异,早高峰时段表现为正向影响,这表明地铁站点密集的地方共享单车停车需求较大. 然而,晚高峰则表现为负向影响,这种不一致的现象可能由于上午通勤到站人流量大,导致大量单车流入,而下午通勤时地铁站周边单车的流出率较高,抑制了停车需求的增加,这与Tan等[33 ] 、高楹等[34 ] 揭示的地铁站周边共享单车潮汐现象显著的结论相近,但本研究在考虑时间尺度后可以进一步精细化地揭示这类潮汐特征的时间变化. ...
接驳地铁站的共享单车源汇时空特征及其影响因素
1
2021
... 除了单一的时间影响关系之外,部分变量的估计参数在时间维度存在正负异质现象. 由图8 (c)可知,购物类POI密度的估计参数在7:00—21:00具有显著性,并且在上午为负值,在下午为正值,这在一定程度上反映了该地居民以共享单车为主的非机动化购物出行主要集中在下午,且在19:00—21:00达到最大. 相比于Gao等[11 ] 认为商场会吸引更多的骑行用户,本研究基于局部时间关系的分析揭示了这种影响关系的时间异质特征. 此外,图8 (d)显示地铁站点密度对于共享单车停车需求在4:00—20:00的影响显著,但影响关系存在时间差异,早高峰时段表现为正向影响,这表明地铁站点密集的地方共享单车停车需求较大. 然而,晚高峰则表现为负向影响,这种不一致的现象可能由于上午通勤到站人流量大,导致大量单车流入,而下午通勤时地铁站周边单车的流出率较高,抑制了停车需求的增加,这与Tan等[33 ] 、高楹等[34 ] 揭示的地铁站周边共享单车潮汐现象显著的结论相近,但本研究在考虑时间尺度后可以进一步精细化地揭示这类潮汐特征的时间变化. ...
接驳地铁站的共享单车源汇时空特征及其影响因素
1
2021
... 除了单一的时间影响关系之外,部分变量的估计参数在时间维度存在正负异质现象. 由图8 (c)可知,购物类POI密度的估计参数在7:00—21:00具有显著性,并且在上午为负值,在下午为正值,这在一定程度上反映了该地居民以共享单车为主的非机动化购物出行主要集中在下午,且在19:00—21:00达到最大. 相比于Gao等[11 ] 认为商场会吸引更多的骑行用户,本研究基于局部时间关系的分析揭示了这种影响关系的时间异质特征. 此外,图8 (d)显示地铁站点密度对于共享单车停车需求在4:00—20:00的影响显著,但影响关系存在时间差异,早高峰时段表现为正向影响,这表明地铁站点密集的地方共享单车停车需求较大. 然而,晚高峰则表现为负向影响,这种不一致的现象可能由于上午通勤到站人流量大,导致大量单车流入,而下午通勤时地铁站周边单车的流出率较高,抑制了停车需求的增加,这与Tan等[33 ] 、高楹等[34 ] 揭示的地铁站周边共享单车潮汐现象显著的结论相近,但本研究在考虑时间尺度后可以进一步精细化地揭示这类潮汐特征的时间变化. ...