浙江大学学报(工学版)

浙江大学学报(工学版), 2023, 57(1): 71-80 doi: 10.3785/j.issn.1008-973X.2023.01.008

土木工程

地铁车辆段上盖建筑道砟垫减振机理与效果

曹志刚,, 王思崎, 许逸飞, 白晓东, 袁宗浩, 马夏飞

1. 浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058

2. 浙江工业大学 岩土工程研究所，浙江 杭州 310023

3. 杭州市东胜置业有限公司，浙江 杭州 310020

Vibration mitigation mechanism and effect of ballast mats for over-track buildings on metro depot

CAO Zhi-gang,, WANG Si-qi, XU Yi-fei, BAI Xiao-dong, YUAN Zong-hao, MA Xia-fei

1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China

2. Institute of Geotechnical Engineering, Zhejiang University of Technology, Hangzhou 310023, China

3. Hangzhou Dongsheng Real Estate Limited Company, Hangzhou 310020, China

收稿日期: 2022-01-28  

基金资助: 国家自然科学基金资助项目(51778571, 51978611)；浙江省杰出青年基金资助项目(LR21E080004)

Received: 2022-01-28  

Fund supported: 国家自然科学基金资助项目(51778571,51978611)；浙江省杰出青年基金资助项目(LR21E080004)

作者简介 About authors

曹志刚（1983—），男，教授，从事土动力学的研究.orcid.org/0000-0002-1295-9353.E-mail：caozhigang2011@zju.edu.cn , E-mail：caozhigang2011@zju.edu.cn

摘要

为了分析道砟垫对上盖建筑的减振效果，对杭州市某地铁车辆段咽喉区、试车线碎石道床（含道砟垫）轨道和上盖建筑振动响应进行现场测试. 考虑桩与土体的相互作用，建立列车-轨道-土体-桩-上盖建筑三维全耦合动力学模型，揭示了车辆段列车引起上盖建筑振动传播的规律以及道砟垫对上盖建筑减振的机理，分析不同车速下道砟垫刚度对减振效果的影响. 结果发现，上盖建筑底层振动主频为40~80 Hz，高频成分随着层高衰减明显；建筑顶层振动主频为20~40 Hz，低频成分随着层高有增大的趋势. 道砟垫对上盖建筑的减振效果随着频率的增大呈整体改善的趋势，40 Hz以上的频段，结构最大插入损失可达7~12 dB. 车速越高，道砟垫刚度越小，道砟垫对上盖建筑的减振效果越好. 综合考虑道砟垫压缩量和减振效果，建议道砟垫刚度取值为0.012~0.024 N/mm3.

关键词： 地铁车辆段 ; 道砟垫 ; 上盖建筑物 ; 减振效果

Abstract

The vibration responses of track structures in the throat area and test line (with ballast mats) and those of over-track buildings at Hangzhou metro depot were tested in order to analyze the vibration mitigation effect of ballast mats on over-track buildings. A three-dimensional fully-coupled dynamic model of train-track-soil-pile-building was established by considering the interaction between pile and soil. The model revealed the vibration propagation laws of over-track buildings caused by train in the metro deport and the mitigation mechanism of ballast mats on over-track buildings. The influence of stiffness of ballast mats on vibration mitigation effect under different train speeds was analyzed. Results showed that the main frequency range of ground floor vibration was 40-80 Hz, and the high frequency component obviously attenuated with story height. The main frequency range of the vibration of the top floor of the building was 20-40 Hz, and the low frequency component tended to increase with the height of the building. Ballast mats had a good vibration mitigation effect on the over-track building with the increase of frequency. The maximum insertion loss of structures reached 7-12 dB in the frequency band above 40 Hz. The higher speed of the train, the smaller stiffness of ballast mats, the better the vibration mitigation effect of the ballast mats on over-track buildings would be. Compression deformation and vibration mitigation effect were considered. It was recommended that the stiffness range of ballast mats was 0.012-0.024 N/mm3.

Keywords： metro depot ; ballast mat ; over-track building ; isolation effectiveness

PDF (3481KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

曹志刚, 王思崎, 许逸飞, 白晓东, 袁宗浩, 马夏飞. 地铁车辆段上盖建筑道砟垫减振机理与效果. 浙江大学学报(工学版)[J], 2023, 57(1): 71-80 doi:10.3785/j.issn.1008-973X.2023.01.008

CAO Zhi-gang, WANG Si-qi, XU Yi-fei, BAI Xiao-dong, YUAN Zong-hao, MA Xia-fei. Vibration mitigation mechanism and effect of ballast mats for over-track buildings on metro depot. Journal of Zhejiang University(Engineering Science)[J], 2023, 57(1): 71-80 doi:10.3785/j.issn.1008-973X.2023.01.008

为了充分利用城市土地资源，以公共交通为导向的城市地铁上盖物业模式应运而生. 地铁轮轨诱发的振动以弹性波形式传递至上盖物业，影响上层居民的身心健康和生活质量，成为制约地铁车辆段上盖物业发展的重要因素之一. 有必要在设计阶段对车致结构振动进行评估，研究有效的减隔振措施，以保证上部结构的正常使用.

现阶段初步预测和分析轨道交通对邻近建筑的振动响应，依赖经验模型和结构振动预测分析[1-2]. Connolly等[3-4]基于欧洲轨道交通系统测试数据，提供了快速预测高铁沿线一层结构噪声和振动的经验模型. 为了预测不同楼层的振动响应，美国交通部联邦铁路管理局（FRA）[5]和联邦运输管理局（FTA）[6]发表了用来预测铁路运行对周围建筑物不同楼层影响的经验模型. Lurcock等[7-8]指出，FTA经验模型和实测数据之间存在显著差异. Kuo等[9]通过实测和分离式的数值混合预测模型，证明了FTA经验模型在土-建筑耦合损失因子上的局限性. 为了扩大经验方法的适用性，Auersch[10]基于传递函数，利用弹簧黏滞阻尼器对Winkler地基模型进行改进. 针对振动传递过程的不确定性[11]，上述模型经过大量简化，均未考虑建筑在空间的有限长度和非一致激励特性的影响.

Lópes等[12]认为进一步预测和分析建筑内部振动需要基于模态叠加的三维（3D）模型来实现. 为了简化计算，López-Mendoza等[13]在频域内用2.5D FEM-PML完美匹配层，对土与隧道衬砌进行耦合振动分析，将地表振动作为振源输入到建筑3D FEM中，开展结构振动响应分析. Di等[14-15]的仿真结果与Cao等[16-17]的振动测试得出的结论不同，差异可以归因于板-柱和桩-土的阻抗比不同. 不考虑建筑与地基尤其是桩-土相互作用，将地表振动响应输入建筑柱底或通过共节点的方式进行耦合分析，对大体量桩基支撑特殊布置形式的车辆段上盖振动预测已不再适用. 另外，工程中的隔振措施通常设置在振源[18-20]、传播路径[21-22]和结构底部[23-24]，地铁车辆段振源减振措施对上盖建筑的减振机理缺乏系统研究，道砟垫的减振效果尚未明确.

本文基于杭州市某地铁车辆段现场测试，提出考虑桩-土相互作用的列车-轨道-土体-上盖建筑3D全耦合振动分析模型. 探究上盖建筑的振动传播机理及特性，分析道砟垫对上盖建筑的减振效果.

1. 现场测试

1.1. 测试概况

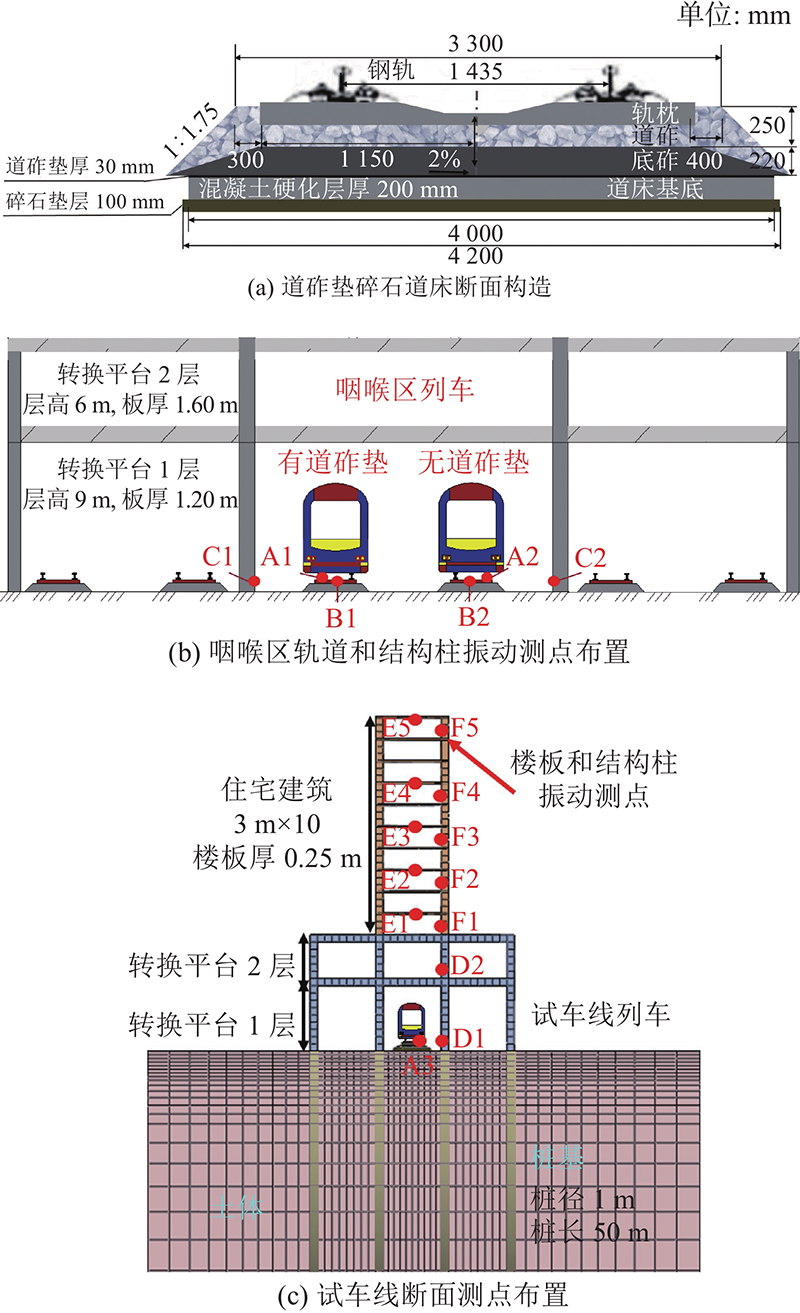
为了分析振源减振措施对上盖建筑的减振效果，对车辆段咽喉区以及试车线（有道砟垫）碎石道床的轨道结构及上盖建筑的振动响应进行现场测试. 地铁车辆段首层为咽喉区和试车线振动敏感区域，9 m板上的转换平台用作汽车停车场和商业区，15 m板上开发了10层商品住宅. 分别选取咽喉区有/无道砟垫轨道的钢轨、轨枕和结构柱进行测点布置，考察点设为A1/2、B1/2和C1/2. 试车线正上方转换平台1层和2层结构柱，分别布置测点D1和D2. 住宅建筑测点位于1层、3层、5层、7层和10层边柱及楼板中心，分别用F1~F5和E1~E5表示. 测试工况及测点布置如表1和图1所示.

表 1   测点布置

Tab.1  Arrangement of test point

工况 测点布置
咽喉区（有道砟垫） 钢轨A1 轨枕B1 柱C1
咽喉区（无道砟垫） 钢轨A2 轨枕B2 柱C2
试车线（有道砟垫） 钢轨A3 转换平台柱D1 转换平台柱D2
住宅建筑 1层F1/E1 3层F2/E2 5层F3/E3 7层F4/E4 10层F5/E5

新窗口打开| 下载CSV


图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   测试工况及测点布置

Fig.1   Test section and measuring-point arrangement


如图2所示为测试现场及设备，建筑结构采用中国地震局研发的941B型拾振仪进行测试，灵敏度为0.3 V·s2/m，分辨率为5×10−6 m/s2，最大量程为20 m/s2. 轨道结构采用扬州科动IEPE型KD1005LC加速度传感器进行测试，灵敏度为50 mV·s2/m，频率为1~8 000 Hz，最大量程为100 m/s2. 利用东方所INV3062V数据采集仪进行同步采集，轨道结构和建筑结构的采样频率分别设为2 000 Hz和512 Hz.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   现场测试及测试设备

Fig.2   Field test and equipment


现场测试车辆段内仅运行一列6节编组的AH型地铁，总长为117 m. 咽喉区铺设50 kg/m的钢轨，列车运行速度为5~15 km/h；试车线铺设60 kg/m的无缝钢轨，列车最大设计时速为80 km/h，夜间最大行车速度为60 km/h，现场测试最大行车速度为40 km/h. 对测点的三向振动加速度进行采集，列车往返12次，测试时间不小于1 h.

1.2. 测试结果及分析

根据《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》(JGJ/T 170-2009)[25]对振动加速度进行1/3倍频程分析，加速度级VL定义为

$ {\rm{VL}} = 20{\text{lg}}\left( {\frac{{{a_{{\text{rms}}}}}}{{{a_0}}}} \right) .$
(1)

式中：a0为基准加速度，取为10−6 m/s2；arms为1/3倍频程中心频率振动加速度的有效值，利用Coinv DASP软件进行全时域分步分析，重叠系数为126/127.

如表2所示为不同区域碎石道床钢轨和轨枕的振动响应. 表中，v为车速，w为挠度，VLmax为最大加速度级. 与普通无道砟垫碎石道床相比，咽喉区铺设道砟垫钢轨的振动加速度级可以减小6~8 dB，轨枕的振动加速度有放大趋势，但总体上未超过1 dB. 道砟垫使得钢轨和轨枕的挠度增大6.0~7.0倍. 结果表明，v越高，轨道和轨枕的振动越大，w越小.

表 2   钢轨和轨枕的振动响应

Tab.2  Vibration response of rails and sleepers

轨道结构类型 测点 v/(km·h−1) w/mm VLmax /dB
水平 竖直
有道砟垫
（咽喉区） 		A1 5 0.859 84.35 89.61
A1 10 0.638 86.13 91.27
A1 15 0.470 87.85 94.39
B1 5 0.298 83.02 87.26
B1 10 0.187 84.36 88.15
B1 15 0.153 85.12 88.47
无道砟垫
（咽喉区） 		A2 5 0.120 91.61 97.57
A2 10 0.103 92.01 98.53
A2 15 0.076 93.46 100.64
B2 5 0.047 82.59 87.22
B2 10 0.381 83.56 88.17
B2 15 0.024 84.20 88.39
有道砟垫
（试车线） 		A3 20 0.413 81.88 87.45
A3 30 0.231 82.01 90.26
A3 40 0.180 82.07 91.39

新窗口打开| 下载CSV


为了掌握测试结构的主要动力特性，基于随机子空间法和模态分析方法，估算得到结构前2阶水平、扭转和竖直振动频率分别为1.99~5.16 Hz，5.77~12.50 Hz和33.69~48.77 Hz. 当荷载激励接近该频段时，上盖建筑和结构构件易产生共振.

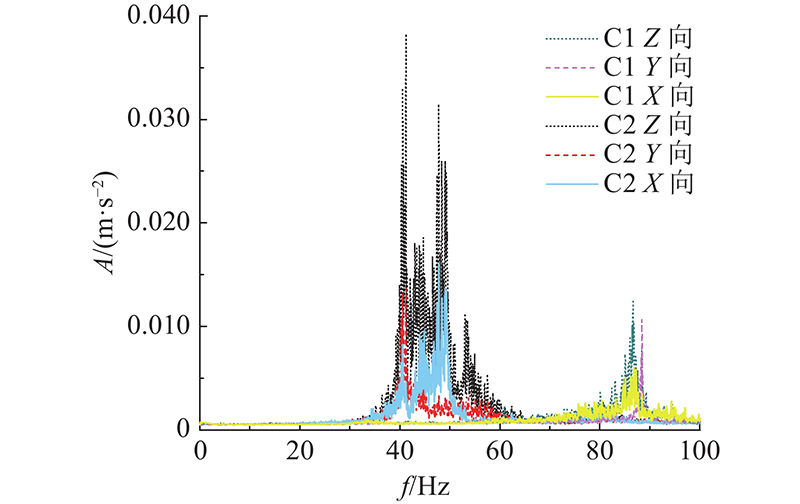
表3和图3给出当车速为5 km/h时，咽喉区碎石道床有、无道砟垫上盖建筑结构柱C1和C2的三向振动加速度幅值、主频和频谱. 表中，A为加速度幅值，fA为主频，f为频率.

表 3   结构柱C1和C2振动的对比

Tab.3  Vibration comparison of structure column C1 and C2

测点 A/(m·s−2) fA /Hz
Z向 Y向 X向
C1 0.332 0.231 0.159 85~90
C2 0.647 0.270 0.224 40~60

新窗口打开| 下载CSV


图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   结构柱C1和C2的频谱图

Fig.3   Spectrum of columns C1 and C2


在咽喉区轨道铺设道砟垫后，上盖平台结构柱的振动明显减小，Z向振动减幅可达48.69%. Y向振动加速度幅值A的衰减率约为X向的2倍. 道砟垫使得fA由40~60 Hz提升为85~90 Hz，避开了结构共振频段，降低了上盖建筑的振动水平.

表4和图4给出当试车线车速为40 km/h时，有道砟垫碎石道床上盖建筑D1~D2和F1~F5的三向振动最大加速度级、振动加速度幅值和峰值频率分布.

表 4   试车线上部结构振动的实测值

Tab.4  Measured value of superstructure vibration on test line

测点 A/ (m·s−2) fA /Hz
Z向 Y向 X向
D1 0.596 0.370 0.278 40~80
D2 0.091 0.076 0.077 40~80
F1 0.087 0.075 0.073 40~63
F2 0.082 0.070 0.065 0~20、31.5~50
F3 0.075 0.072 0.067 0~20、31.5~50
F4 0.072 0.064 0.068 0~10、20~40
F5 0.070 0.065 0.070 0~10、20~40

新窗口打开| 下载CSV


图 4

新窗口打开| 下载原图ZIP| 生成PPT

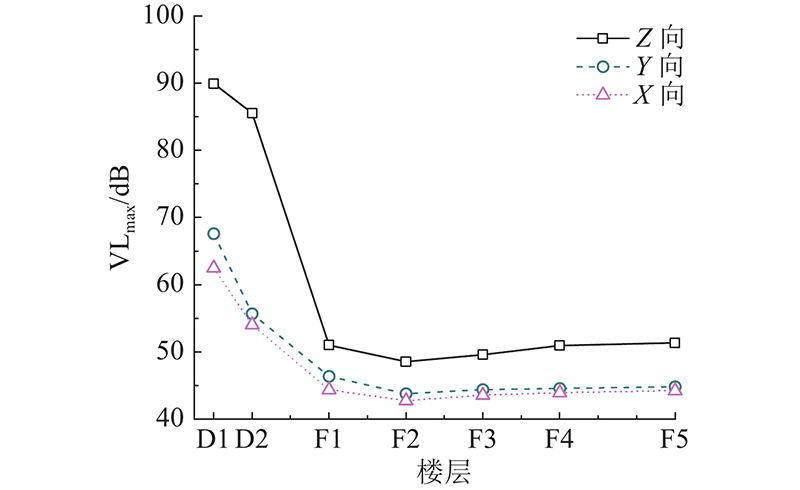
图 4   试车线上部结构的振动传播规律

Fig.4   Vibration propagation law of superstructures on test line


从表4可知，试车线上盖建筑结构的振动响应主频小于80 Hz. 住宅建筑结构柱F1~F5 Z向和Y向振动加速度峰值随着楼层的增大而减小，X向振动随着层高先减小后缓慢增大，无明显的线性关系. 由于顶层鞭梢效应和局部共振，上盖结构顶部及中间楼层出现振动放大的现象.

从图4可知，试车线上盖建筑振动以竖向为主. 竖向振动加速度级经转换平台迅速由85~90 dB衰减至50 dB左右，随后沿层高先减小后缓慢增大. 上盖建筑振动传递至3层，相对于1层的衰减率为5.63%，传递至10层，较3层放大了5.77%.

2. 数值模拟

2.1. 列车-轨道耦合动力模型

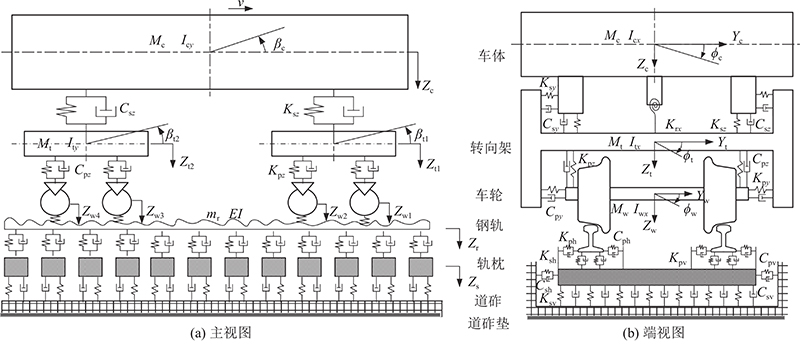
考虑轮轨几何不平顺的激励机制及地铁、钢轨、扣件、轨枕、道砟和道砟垫的相互作用，基于Cai等[26]提出的车-轨耦合动力学理论，建立列车-轨道动力相互作用模型，如图5所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   列车-轨道空间耦合动力学模型

Fig.5   Train-track spatial coupling dynamics model


AH型列车的每节车厢包括1个车体、2个转向架(i = 1、2)和4个轮对(j = 1~4)，每个部件包含5个自由度(横向 $ {Y_{\text{c}}} $、 $ {Y_{{\text{t}}i}} $、 $ {Y_{{\text{w}}j}} $；垂直 $ {Z_{\text{c}}} $、 $ {Z_{{\text{t}}i}} $、 $ {Z_{{\text{w}}j}} $；滚动 $ {\phi _{\text{c}}} $、 $ {\phi _{{\text{t}}i}} $、 $ {\phi _{{\text{w}}j}} $；摇动 $ {\psi _{\text{c}}} $、 $ {\psi _{{\text{t}}i}} $、 $ {\psi _{{\text{w}}j}} $和点头 $\; {\beta _{\text{c}}} $、 $ \;{\beta _{{\text{t}}i}} $、 $ \;{\beta _{{\text{w}}j}} $)，每节车厢的自由度为35. 车体与转向架之间为二系悬挂，转向架与轮对为一系悬挂，车辆动力学参数如表5所示.

表 5   车辆的动力学参数

Tab.5  Dynamic parameters of metro train

参数 数值
车体质量 48800 kg
单车尺寸(长×宽×高) 19.52 m×3.08 m×3.8 m
转向架轴距 2500 mm
车辆定距 15600 mm
车体转动惯量 1875000 kg∙m2
转向架质量 7358 kg
转向架转动惯量 5070 kg∙m2
轮对质量 1780 kg
一系悬挂刚度 5.1 kN/mm
一系悬挂阻尼系数 13 kN∙s/m
二系悬挂刚度 0.828 kN/mm
二系悬挂阻尼系数 30 kN∙s/m
轴重 ≤15 t

新窗口打开| 下载CSV


车辆的运动方程可以用二阶时域微分方程的矩阵形式表示为

$ {{\boldsymbol{M}}_{\text{C}}}{{\boldsymbol{\ddot q}}_{\text{C}}}+{{\boldsymbol{C}}_{\text{C}}}{{\boldsymbol{\dot q}}_{\text{C}}}+{{\boldsymbol{K}}_{\text{C}}}{{\boldsymbol{q}}_{\text{C}}} = {{\boldsymbol{F}}_{{\text{rail}}/{\text{wheel}}}}+{{\boldsymbol{F}}_{{\text{EXT}}}}. $
(2)

式中： $ {{\boldsymbol{q}}_{\text{C}}} $、 $ {{\boldsymbol{\dot q}}_{\text{C}}} $和 $ {{\boldsymbol{\ddot q}}_{\text{C}}} $分别为车辆的位移、速度和加速度矢量； $ {{\boldsymbol{M}}_{\text{C}}} $、 $ {{\boldsymbol{C}}_{\text{C}}} $和 $ {{\boldsymbol{K}}_{\text{C}}} $分别为质量矩阵、随速度变化的阻尼系数矩阵和随位移变化的刚度矩阵； $ {{\boldsymbol{F}}_{{\text{EXT}}}} $为曲线轨迹载荷矢量获得的附加外力，包括重力和向心力；轮轨接触力 $ {{\boldsymbol{F}}_{{\text{rail}}/{\text{wheel}}}} $由非线性赫兹(Hertzian)接触关系定义：

$ \left|{{\boldsymbol{F}}_{{\text{rail}}/{\text{wheel}}}} \right|= \left\{ {\begin{array}{*{20}{c}} {{{\left[\dfrac{1}{G}({{{Z}}_{\text{w}}} - {{{Z}}_{\text{r}}} - h)\right]}^{{1}/{2}}}},&{{{{Z}}_{\text{w}}} - {{{Z}}_{\text{r}}} - h \geqslant 0} ;\\ 0,&{{{{Z}}_{\text{w}}} - {{{Z}}_{\text{r}}} - h < 0} . \end{array}} \right. $
(3)

$ G = 3.86{R^{ - 0.115}} \times {10^{ - 8}}\;({\rm{m}}/{{\rm{N}}^{{2}/{3}}}). $
(4)

其中， $ {{{Z}}_{\text{w}}} $和 $ {{{Z}}_{\text{r}}} $分别为轮对和钢轨在轮轨接触点的垂直位移，h为垂直轨道不规则性的幅度，R为车轮的半径. G是与车轮和铁轨几何形状以及材料属性相关的参数.

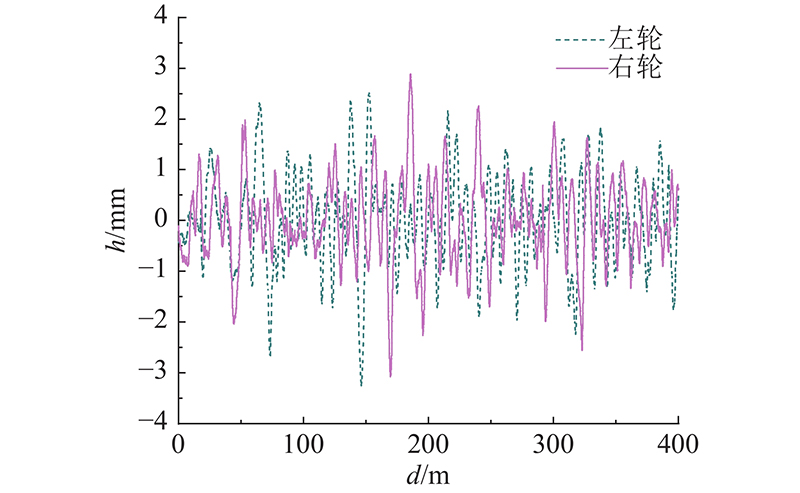
钢轨包含垂直、横向和扭转运动，用有限长度的Euler梁进行模拟. 轨枕是垂直方向上由钢弹簧支撑的弹性板，在水平面上视作可横向和旋转运动的刚体. 在数值分析中，车轮半径R为0.457 5 m，轨道垂直轮廓的数值样本取5号线一期工程五常地铁车辆段II标段钢轨静态不平顺谱（见图6）. 图中，d为轨道长度.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   钢轨的静态不平顺谱

Fig.6   Static irregularity spectrum of rail


将轨道结构视为3层质量-弹簧-阻尼器系统，弹性和阻尼特性分别由等效刚度和阻尼系数表征，引入相邻道砟的剪切刚度kw和阻尼系数cw，动态响应在时域中可以表示为

$ {{\boldsymbol{M}}_{\text{T}}}{{\boldsymbol{\ddot q}}_{\text{T}}}+{{\boldsymbol{C}}_{\text{T}}}{{\boldsymbol{\dot q}}_{\text{T}}}+{{\boldsymbol{K}}_{\text{T}}}{{\boldsymbol{q}}_{\text{T}}} = {{\boldsymbol{F}}_{\text{T}}}({{\boldsymbol{q}}_{\text{R}}},{{\boldsymbol{\dot q}}_{\text{R}}},{{\boldsymbol{q}}_{\text{T}}},{{\boldsymbol{\dot q}}_{\text{T}}}). $
(5)

式中： ${\boldsymbol{q}}_{\rm{R}}$、 ${\dot {\boldsymbol{q}}}_{\rm{R}}$分别为钢轨的广义位移和速度向量； $ {{\boldsymbol{q}}_{\text{T}}} $、 $ {{\boldsymbol{\dot q}}_{\text{T}}} $和 $ {{\boldsymbol{\ddot q}}_{\text{T}}} $分别为道砟轨道结构的广义位移、速度和加速度向量； $ {{\boldsymbol{M}}_{\text{T}}} $、 $ {{\boldsymbol{C}}_{\text{T}}} $和 $ {{\boldsymbol{K}}_{\text{T}}} $分别为轨道系统的广义质量、阻尼系数和刚度矩阵； $ {{\boldsymbol{F}}_{\text{T}}} $为轨道系统受到的广义荷载向量，由轮轨相互作用乘以钢轨的各阶振型函数组成.

轨道结构的动力学参数如表6所示. 道砟垫视为在道床质量-弹簧阻尼系统中插入弹性元件，运动微分方程为

表 6   轨道结构的动力学参数

Tab.6  Dynamic parameters of track structures

参数 数值
钢轨截面积 7.745×10−3 m2
钢轨单位质量 60.64 kg/m
钢轨截面惯性矩 3.217×10−5 m4
钢轨弹性垫阻尼系数 7.5×104 N∙s/m
轨枕间距 0.6 m
轨枕质量 251 kg
道砟密度 1750 kg/m3
道砟阻尼系数 5.88×104 N∙s/m
道砟剪切刚度 7.8×107 N/m
道砟弹性模量 0.8×108 Pa
道砟剪切阻尼系数 8.0×104 N∙s/m
地基弹性模量 9.0×107 Pa/m
地基阻尼系数 3.115×104 N∙s/m
道砟垫刚度 1.2×10−5~4.8×10−5 Pa

新窗口打开| 下载CSV


$ {m_{\text{V}}}{{\ddot {\boldsymbol z}}_{\text{V}}}(t)+{c_{\text{V}}}{\dot{\boldsymbol{ z}}_{\text{V}}}(t)+{k_{\rm{V}}}{{\boldsymbol{z}}_{\text{V}}}(t) = - {\boldsymbol{B}}{{\boldsymbol{P}}_{{0}}}(t) .$
(6)

式中： ${\boldsymbol{z}}_{\rm{v}}(t) $、 ${\dot {\boldsymbol{z}}}_{\rm{v}}(t) $、 ${\ddot {\boldsymbol{z}}}_{\rm{v}}(t) $分别为道砟垫的竖向广义位移、速度和加速度向量； $ {{\boldsymbol{P}}_{{0}}}(t) $为外荷载；B为单元矩阵； $ {m_{\text{V}}} $、 $ {c_{\text{V}}} $和 $ {k_{\rm{V}}} $分别为质量、阻尼系数和弹簧刚度.

当轮轨动力作用力为简谐力时，可得

$ {\ddot{\boldsymbol{ z}}_{\text{V}}}(t)+2\xi {\omega _{\text{n}}}{\dot{\boldsymbol{ z}}_{\text{V}}}(t)+{\omega _{\text{n}}^2}{\boldsymbol{z}}_{\text{V}}(t) = \frac{{ - {\boldsymbol{B}}{{\boldsymbol{P}}_{{0}}}(t)}}{m_{\rm{V}}}, $
(7)

$ {{\boldsymbol{z}}}_{\text{V}}(t)=\dfrac{{{\boldsymbol{P}}}_{0}/k}{\sqrt{\left(1-\dfrac{{\omega }^{2}}{{\omega }_{\text{n}}^{2}}\right)^{2}}+{\left(2\xi \dfrac{\omega }{{\omega }_{\text{n}}}\right)}^{2}}\mathrm{sin}\;(\omega t+{\phi }_{2}) .$
(8)

式中： $ \omega $为外激励频率； $ {\omega _{\text{n}}} $为系统固有频率， $ {\omega _{\text{n}}}{\text{ = }} \sqrt {k_{\rm{V}}/m_{\rm{V}}} $； $ {f_0} $为系统固有频率， $ {f_0} = \omega_{\rm{n}} /({\text{2}}{\text{π}})$； $ \xi $为阻尼比， $ \xi {\text{ = }}c_{\rm{V}}/(2m_{\rm{V}}{\omega _{\text{n}}}) $.

振动系统之间的力，通过弹性元件传给基础，由弹簧和阻尼两部分提供，大小分别为kz0和cVz0ω（其中z0为竖向变形），相位差为90°. 传给基础的力可以表达为

$ \begin{split} \left|{{\boldsymbol{P}}_{\rm{T}}}\right| =& \sqrt {{{(k{z_0})}^2}+{{(c_{\rm{V}}{z_0}\omega )}^2}} =\\ &\left|{{\boldsymbol{P}}_{{0}}}\right|\sqrt {\dfrac{{1+{{\left(2\xi \dfrac{\omega }{{{\omega _{\text{n}}}}}\right)}^2}}}{{{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{\text{n}}^2}}\right)}^2}+{{\left(2\xi \dfrac{\omega }{{{\omega _{\text{n}}}}}\right)}^2}}}} . \end{split}$
(9)

根据Zhai等[27]提出的简单快速显式积分法求解系统动力学方程，计算得到单车轮轨力.

2.2. 轨道-土体-桩基-建筑物有限元模型

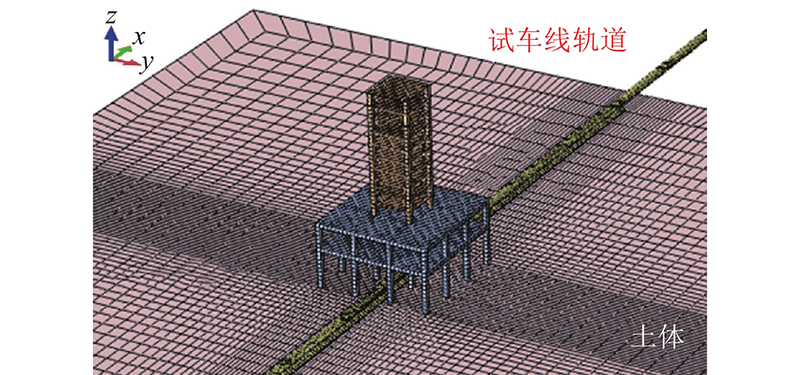
采用ABAQUS/Explicit有限元软件，建立轨道-土体-上盖建筑物3D有限元模型，如图7所示. 住宅建筑：3 m×10层，楼板厚0.25 m. 转换平台：2层高6 m，板厚1.60 m；1层高9 m，板厚1.20 m.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   轨道-土体-桩-建筑物3D有限元模型

Fig.7   3D finite element model of track-soil-pile-building


轨道结构和土体界面通过变形协调条件进行耦合，桩-土[28-29]相互作用通过非共结点的离散弹簧-阻尼连接器进行模拟. 上盖建筑梁柱截面尺寸分别为0.5 m×0.5 m和1.0 m×1.0 m，梁、板、柱和桩钢筋混凝土材料的弹性模量为30 GPa，密度为2 500 kg/m3，建筑结构的阻尼比为0.02. 楼板采用8节点壳单元S8R5，梁、柱和桩为实体单元C3D8.

根据地质钻探资料，将土体简化为5层，地层参数如表7所示. 表中，Hi为厚度，ρ为密度，E为弹性模量，μ为泊松比. 忽略孔隙率和含水量，地铁引起的周围环境结构振动应变小于10−4，按照弹性介质计算，土体采用3D实体单元C3D8进行模拟，尺寸小于最小剪切波长的1/6，边界为无限元边界.

表 7   地层参数

Tab.7  Parameters of soil layer

土层 Hi/m ρ/(kg·m−3) E/MPa μ $\xi $
人工填土 4 1.98 117 0.31 0.03
淤泥质土 2 1.53 78.3 0.30 0.03
细砂 14 1.86 220 0.32 0.03
中粗砂 20 1.96 280 0.23 0.03
含砂粉质 60 1.88 150.8 0.31 0.03

新窗口打开| 下载CSV


轨道结构参数见表8，将连续焊接的无缝钢轨简化为Euler梁. 弹条Ⅲ型分开式扣件用三向线性弹簧-阻尼单元模拟，垂向刚度和横向刚度分别为120和40 kN/mm，垂向阻尼系数和横向阻尼系数均为60 kN·s/m. 轨枕、道床和基础均采用实体单元模拟，采用连续支承三向弹簧-阻尼单元模拟道砟垫满铺形式.

表 8   结构模型的参数

Tab.8  Parameters of structural model

模型结构 E/MPa μ ρ/(kg·m−3)
钢轨 210000 0.25 7850
轨枕 30000 0.20 2400
道砟 130 0.35 1800
底碴 300 0.35 2200
混凝土水硬层 315000 0.30 2500

新窗口打开| 下载CSV


2.3. 3D全耦合模型和模型验证

将MATLAB中建立的列车-轨道动力学模型，进行微分方程求解，得到轮轨动态接触力随距离和时间变化的响应. 利用FORTRAN编写的VDLOAD移动荷载子程序，把计算得到的24个动态轮轨力作为输入载荷，作用在ABAQUS 3D有限元的钢轨上，动力模拟的时间步长为5×10−4 s. 采用隐式积分法求解移动荷载作用下的有限元模型，得到地铁列车运行引起的建筑结构的动力响应.

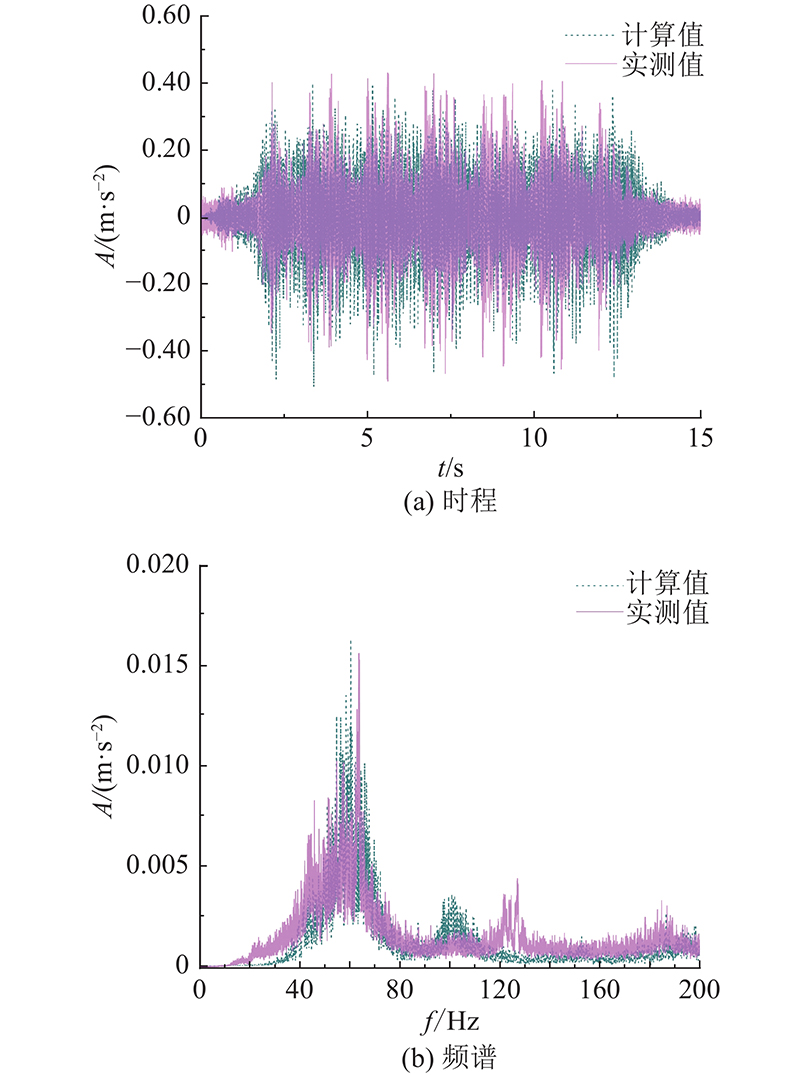
为了验证数值模型，当试车线车速为40 km/h，道砟垫刚度为0.024 N/mm3时，将结构柱T1计算的振动响应与现场测试数据进行对比，如图8所示.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   结构柱D1振动的时频验证

Fig.8   Time-frequency verification of column D1 vibration


如图8(a)所示，在时域中，计算得到的加速度在波形和整体趋势上与实测值接近，列车引起结构柱振动的持续时间约为12 s，两者均出现24个典型的振动加速度峰值，说明模型能够很好地反映列车经过的过程. 如图8(b)所示，在频域中，计算的加速度谱在总体趋势、频率分布及峰值频率上与实测值接近，振动主频均为0~80 Hz，峰值频率约为63 Hz，振幅和某些频率的差异可以归因于有限元模型中建筑结构的简化，与现场局部区域略有不同.

总体而言，振动变化趋势与实测值吻合较好，能够模拟列车引起上盖结构的振动，误差小于5%，验证了所建立的列车-轨道-土体-桩-上盖建筑全耦合动力学模型的正确性.

3. 减振分析

3.1. 时域分析

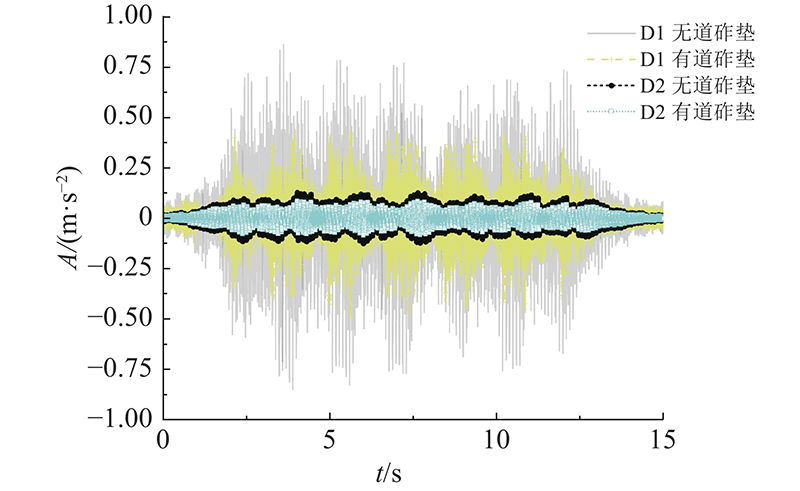
当列车时速为40 km/h时，试车线碎石道床有、无道砟垫转换平台结构柱D1和D2的垂向振动加速度时程如图9所示.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   结构柱D1和D2的加速度时程曲线

Fig.9   Acceleration time-history curve of column D1 and D2


从时域可以发现，在采用道砟垫减振前，结构柱D1和D2垂向加速度峰值分别为0.861 m/s2和0.127 m/s2；在铺设道砟垫后，峰值减幅分别为41.09%和32.50%. 有道砟垫碎石道床上盖转换平台结构的振动加速度峰值明显减小，一层结构的减振效果优于二层结构，说明铺设道砟垫能够发挥很好的减振效果，对近源结构的减振效果更佳.

3.2. 1/3倍频程

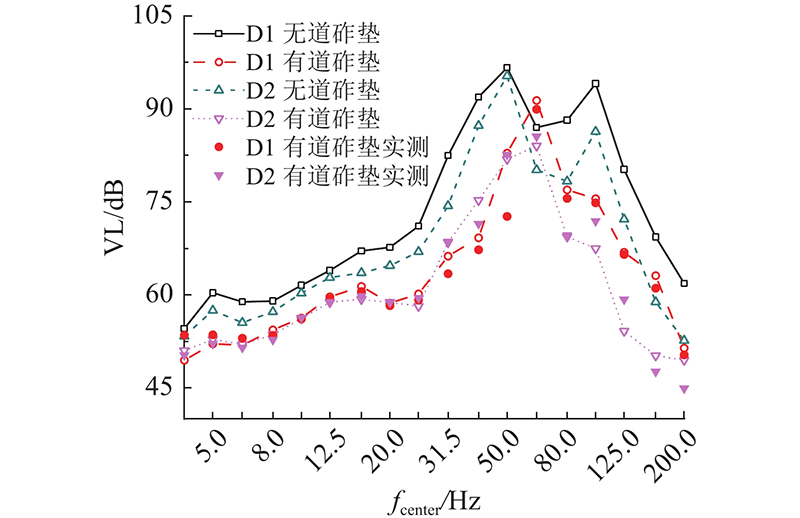
对计算得到的振动加速度时程进行傅里叶变换，获得1/3倍频程中心频率振动加速度级. 在轨道结构有、无道砟垫的情况下，上盖转换平台结构柱D1和D2垂向振动加速度频域特性如图10所示. 图中，fcenter为1/3倍频程中心频率.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   结构柱D1和D2的振动加速度级

Fig.10   Vibration acceleration level of column D1 and D2


从频域可以发现，转换平台结构柱D1和D2的振动频域主要分布在31.5~125 Hz频段，峰值出现在50~100 Hz，加速度级为44~97 dB. 在采用道砟垫后，结构柱D1和D2的振动主频由50 Hz提升到63 Hz，并在63 Hz处出现振动放大. 上盖平台结构柱D1和D2的最大插入损失分别为9.85 dB和18.87 dB，分别位于80 Hz和100 Hz处. 整体而言，道砟垫对上盖平台的减振效果明显.

3.3. 插入损失

在同一测点，非减振工况和减振工况在4~200 Hz频段内，1/3倍频程上各个频带中心频率点的振动加速度级之差为分频插入损失：

$ {L_{{\text{A-insert}}}} = {L_{{\text{A\_n}}}} - {L_{{\text{A\_v}}}} . $
(10)

式中：LA_n为非减振工况下的振动加速度级，LA_v为减振工况下的振动加速度级.

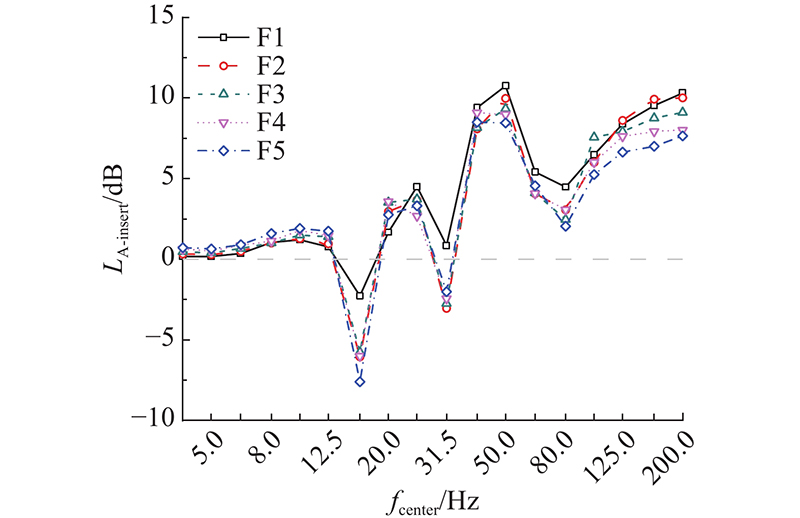
当列车速度为40 km/h时，车辆段上盖建筑结构柱F1~F5的分频插入损失如图11所示.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   结构柱F1~F5的插入损失

Fig.11   Insertion loss of structural column F1~F5


在采用道砟垫后，结构柱F1~F5在5、16和31.5 Hz处出现振动放大，与结构构件的固有频率和建筑模态相关. 在4~12.5 Hz频段内，楼层越高，插入损失越大，总体均未超过2 dB. 道砟垫在31.5 Hz以上的频段，减振效果显著，尤其是在50 Hz处，插入损失可以达到8.45~10.76 dB，说明该频率与未使用道砟垫时结构出现的共振频率接近. 80 Hz以上的插入损失为5~10 dB，说明道砟垫阻隔了列车振动的高频能量.

3.4. 列车速度的影响

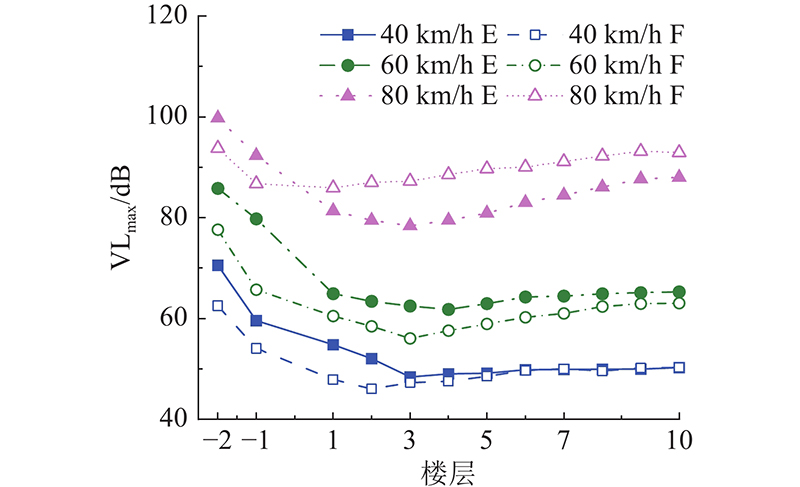
图12给出列车以不同时速运行时，无道砟垫轨道上盖结构竖向振动随楼层的变化规律.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   不同速度下上盖结构的振动传播规律

Fig.12   Vibration propagation law of superstructures at different velocities


从图12可以看出，车速增大，结构竖向振动加速度级显著增大. 当车速由40 km/h增加至80 km/h时，住宅建筑结构柱的竖向振动加速度级大于楼板，1层、3层和10层的最大动力响应分别增加了31.13、38.87和42.65 dB. 速度不同，结构最大振动响应出现的位置和楼层不同. 上盖建筑振动响应总体上随层高的递增先迅速衰减，后缓慢增大，呈波动变化.

如图13所示为列车以不同时速运行时，碎石道床有、无道砟垫对上盖建筑楼板最大振动加速度级的影响. 图中，限值采用JGJ/T 170-2009城市轨道交通沿线1类建筑物室内振动限值[25].

图 13

新窗口打开| 下载原图ZIP| 生成PPT

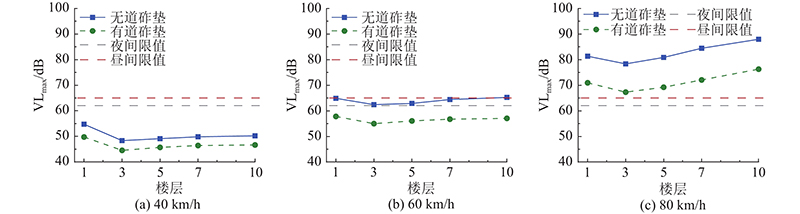
图 13   不同速度下的楼板E1~E5振动响应

Fig.13   Vibration response of roof E1~E5 building at different speed


从图13可知，上盖住宅建筑各层振动响应随车速的增加而增大. 当车速为60 km/h时，无道砟垫碎石道床上盖住宅建筑会超过夜间限值. 当车速分别为40、60和80 km/h时，道砟垫的减振效果分别可达3.83、7.44和11.43 dB，楼板振动响应最大值出现的位置与车速密切相关. 车速越高，道砟垫对上盖建筑的减振效果越明显.

3.5. 道砟垫刚度

在工程中，道砟垫刚度通常用基础模量表示. 为了探究道砟垫刚度对上盖建筑振动响应的影响，分别取0.012、0.024、0.036和0.048 N/mm3作为道砟垫的刚度进行参数分析，与普通无道砟垫轨道进行对比.

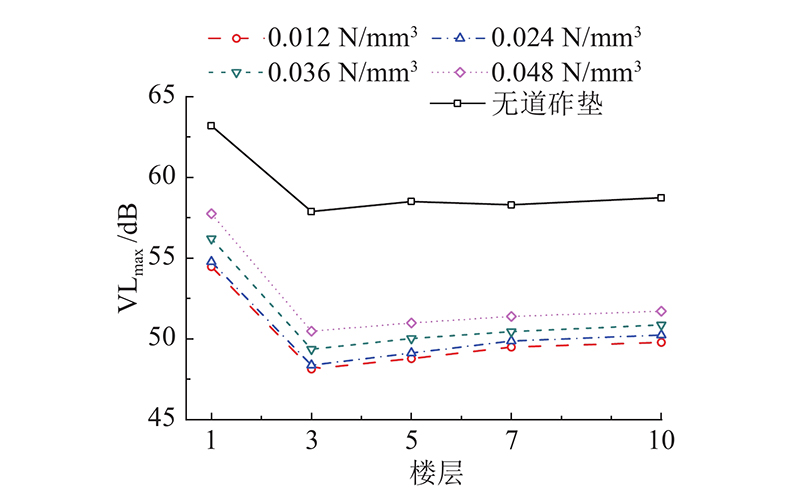
如图14所示为上盖建筑楼板E1~E5的振动响应，道砟垫刚度越小，加速度级越小. 当车速为40 km/h时，道砟垫刚度为0.012~0.048 N/mm3，刚度每减小0.012 N/mm3，最大速度级减幅分别为2.68%、2.56%和0.55%，刚度越小，道砟垫对上盖建筑楼板减振更有利. 在满足轨道变形要求的前提下，建议道砟垫刚度的取值为0.012~0.024 N/mm3.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   不同刚度道砟垫下楼板E1~E5的最大加速度级

Fig.14   Maximum acceleration level of floor slab E1~E5 under different modulus of ballast mats


4. 结　论

（1）上盖建筑底层振动主频为40~80 Hz，高频成分随层高衰减明显. 上盖建筑顶层振动主频为20~40 Hz，低频成分随层高有增大趋势.

（2）道砟垫对上盖建筑的减振效果随着频率的增加呈整体改善趋势，但在轨道固有频率处振动呈放大现象. 在40 Hz以上的频段，道砟垫的减振效果可达7~12 dB；随着建筑层高的增大，道砟垫的减振效果减弱.

（3）车速越高，道砟垫刚度越低，上盖建筑的减振效果越好. 综合考虑道砟垫压缩量和减振效果，建议道砟垫刚度取值为0.012~0.024 N/mm3.

参考文献

COLAÇO A, COSTA P A, AMADO-MENDES P, et al

Prediction of vibrations and reradiated noise due to railway traffic: a comprehensive hybrid model based on a finite element method and of fundamental solutions approach

[J]. Journal of Vibration and Acoustics, 2017, 139 (6): 061009

DOI:10.1115/1.4036929      [本文引用: 1]

YANG Y B, GE P, LI Q, et al

2.5D vibration of railway-side buildings mitigated by open or infilled trenches considering rail irregularity

[J]. Soil Dynamics and Earthquake Engineering, 2018, 106 (3): 204- 214

[本文引用: 1]

CONNOLLY D P, COSTA P A, KOUROUSSIS G, et al

Large scale international testing of railway ground vibrations across Europe

[J]. Soil Dynamics and Earthquake Engineering, 2015, 71 (39): 1- 12

[本文引用: 1]

PANEIRO G, DURÃO F O, SILVA M C E, et al

Prediction of ground vibration amplitudes due to urban railway traffic using quantitative and qualitative field data

[J]. Transportation Research Part D: Transport and Environment, 2015, 40 (OCTa): 1- 13

[本文引用: 1]

High-speed ground transportation noise and vibration impact assessment [S]. Washington, DC: Federal Railroad Administration, 2012.

[本文引用: 1]

QUAGLIATA A, AHEARN M, BOEKER E, et al. Transit noise and vibration impact assessment manual, technical report [S]. Washington, DC: Federal Transit Administration, 2018: 121–165.

[本文引用: 1]

LURCOCK D E J, THOMPSON D J, BEWES O G, et al

Groundborne railway noise and vibration in buildings: results of a structural and acoustic parametric study

[J]. Notes on Numerical Fluid Mechanics and Multidisciplinary, 2018, 139: 193- 204

[本文引用: 1]

SADEGHI J, ESMAEILI M H, AKBARI M

Reliability of FTA general vibration assessment model in prediction of subway induced ground borne vibrations

[J]. Soil Dynamics and Earthquake Engineering, 2019, 117: 300- 311

DOI:10.1016/j.soildyn.2018.11.002      [本文引用: 1]

KUO K A, PAPADOPOULOS M, LOMBAERT G, et al

The coupling loss of a building subject to railway induced vibrations: numerical modelling and experimental measurements

[J]. Journal of Sound and Vibration, 2019, 442: 459- 481

DOI:10.1016/j.jsv.2018.10.048      [本文引用: 1]

AUERSCH L

Simple and fast prediction of train-induced track forces, ground and building vibrations

[J]. Railway Engineering Science, 2020, 28 (3): 232- 250

DOI:10.1007/s40534-020-00218-7      [本文引用: 1]

马蒙, 刘维宁, 刘卫丰

列车引起环境振动预测方法与不确定性研究进展

[J]. 交通运输工程学报, 2020, 20 (3): 1- 16

[本文引用: 1]

MA Meng, LIU Wei-ning, LIU Wei-feng

Research progresses of prediction method and uncertainty of train-induced environmental vibration

[J]. Journal of Traffic and Transportation Engineering, 2020, 20 (3): 1- 16

[本文引用: 1]

LÓPES P, COSTA P A, CALÇADA R, et al

Influence of soil stiffness on vibrations inside buildings due to railway traffic: numerical study

[J]. Computers and Geotechnics, 2014, 61 (3): 277- 291

DOI:10.1016/j.compgeo.2014.06.005      [本文引用: 1]

LÓPEZ-MENDOZA D, CONNOLLY D P, ROMERO A, et al

A transfer function method to predict building vibration and its application to railway defects

[J]. Construction and Building Materials, 2020, 232: 117217

DOI:10.1016/j.conbuildmat.2019.117217      [本文引用: 1]

DI G, XIE Z, GUO J

Predict the influence of environmental vibration from high-speed railway on over-track buildings

[J]. Sustainability, 2021, 13 (6): 3218

DOI:10.3390/su13063218      [本文引用: 1]

SANAYEI M, ANISH K P, MOORE J A, et al

Measurement and prediction of train-induced vibrations in a full-scale building

[J]. Engineering Structure, 2014, 77: 119- 128

DOI:10.1016/j.engstruct.2014.07.033      [本文引用: 1]

CAO Z, GUO T, ZHANG Z

Vibration measurement in a metro depot with trains running in the top story

[J]. Journal of Vibroengineering, 2017, 19 (1): 502- 519

DOI:10.21595/jve.2016.17304      [本文引用: 1]

TAO Z, WANG Y, SANAYEI M, et al

Experimental study of train-induced vibration in over-track buildings in a metro depot

[J]. Engineering Structures, 2019, 198: 109473

DOI:10.1016/j.engstruct.2019.109473      [本文引用: 1]

ZOU C, WANG Y, MOORE J A, et al

Train-induced field vibration measurements of ground and over-track buildings

[J]. Science of the Total Environment, 2017, 575: 1339- 1351

DOI:10.1016/j.scitotenv.2016.09.216      [本文引用: 1]

COSTA P A, CALÇADA R, CARDOSO A S

Ballast mats for the reduction of railway traffic vibrations. numerical study

[J]. Soil Dynamics and Earthquake Engineering, 2012, 42: 137- 150

DOI:10.1016/j.soildyn.2012.06.014     

王一干, 刘鹏辉, 李腾, 等

车辆段轨道减振措施对上盖建筑减振降噪效果试验研究

[J]. 振动与冲击, 2020, 39 (21): 284- 291

DOI:10.13465/j.cnki.jvs.2020.21.038      [本文引用: 1]

WANG Yi-gan, LIU Peng-hui, LI Teng, et al

Tests for effect of track vibration reduction measures in a depot on vibration and noise reduction of a superstructure

[J]. Journal of Vibration and Shock, 2020, 39 (21): 284- 291

DOI:10.13465/j.cnki.jvs.2020.21.038      [本文引用: 1]

CAO Z G, CAI Y Q, SUN H L, et al

Dynamic responses of a poroelastic half-space from moving trains caused by vertical track irregularities

[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35 (7): 761- 786

DOI:10.1002/nag.919      [本文引用: 1]

CAO Z G, CAI Y Q, JIN H

Mitigation of ground vibration generated by high-speed trains on saturated poroelastic ground with under-sleeper pads

[J]. Journal of Transportation Engineering, 2014, 140 (1): 12- 22

DOI:10.1061/(ASCE)TE.1943-5436.0000610      [本文引用: 1]

谢伟平, 王政印, 孙亮明

地铁车辆段新型隔振支座的减振效果研究

[J]. 振动与冲击, 2018, 37 (10): 63- 70

DOI:10.13465/j.cnki.jvs.2018.10.010      [本文引用: 1]

XIE Wei-ping, WANG Zheng-yin, SUN Liang-ming

Vibration reduction effect of a new isolation bearing for a metro depot

[J]. Journal of Vibration and Shock, 2018, 37 (10): 63- 70

DOI:10.13465/j.cnki.jvs.2018.10.010      [本文引用: 1]

YANG J, ZHU S, ZHAI W, et al

Prediction and mitigation of train-induced vibrations of large-scale building constructed on subway tunnel

[J]. Science of the Total Environment, 2019, 668: 485- 499

DOI:10.1016/j.scitotenv.2019.02.397      [本文引用: 1]

城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准: JGJ/T 170-2009 [S]. 北京: 中国建筑工业出版社, 2009.

[本文引用: 2]

CAI C B, HE Q L, ZHU S Y, et al

, Dynamic interaction of suspension-type monorail vehicle and bridge: numerical simulation and experiment

[J]. Mechanical Systems and Signal Processing, 2019, 118: 388- 407

DOI:10.1016/j.ymssp.2018.08.062      [本文引用: 1]

ZHAI W M, XIA H, CAI C B, et al

High-speed train-track-bridge dynamic interactions part I: theoretical model and numerical simulation

[J]. International Journal of Rail Transportation, 2013, 1 (1/2): 3- 24

DOI:10.1080/23248378.2013.791498      [本文引用: 1]

PAPADOPOULOS M, FRANÇOIS S, DEGRANDE G, et al

The influence of uncertain local subsoil conditions on the response of buildings to ground vibration

[J]. Journal of Sound Vibration, 2018, 418 (4): 200- 220

[本文引用: 1]

COLAÇO A, COSTA P A, CASTANHEIRA-PINTO A, et al

Experimental validation of a simplified soil-structure interaction approach for the prediction of vibrations in buildings due to railway traffic

[J]. Soil Dynamics and Earthquake Engineering, 2021, 141 (1): 106499

[本文引用: 1]

/

〈 〉