无线电信号的调制识别是通信信号参数估计、信号解调、频谱感知的基础,在认知无线电、频谱监测、战场信号截获等应用领域中发挥重要的作用. 通常调制识别方法大体上可以分为2种[1]:基于最大似然判决的方法和基于特征提取的分类识别方法. 似然比判决的方法是贝叶斯理论最优算法,但是需要关于信号的均值、方差先验信息,算法复杂度相对较高. 相比而言,基于特征提取的识别方法选取最能体现调制信号的差异特征来实现分类. 当前提取的特征主要是时频域参数、高阶累积量、循环谱、小波变换、语谱图和信息熵等[2-4]. Ali等[5]对信号幅度包络进行傅里叶变换,构建4个特征参数,用于识别3类高阶幅度相位调制(amplitude phase shift keying, APSK). Xie等[6]利用5个高阶累积量特征参数对6类低阶调制进行识别,分析频率抖动和多径因素对识别结果的影响. Wang等[7]在对相移键控(phase shift keying, PSK)和正交幅度调制(quadrature amplitude modulation, QAM)多类调制识别时,级联使用星座图的特征来提升对QAM调制的识别性能. 李润东等[8]引入低秩表示算法,对信号的循环谱特征进行降噪处理后,对7种调制进行识别,取得较高的识别准确率.
近年来,深度学习在目标检测、语音识别、人脸识别等众多领域取得了突出的成就[9-12],因此有学者尝试利用深度学习的方法来提升对调制信号的识别性能. Huang等[13]通过改进损失函数训练网络,学习5种调制的最大差异特征. Teng等[14]将IQ信号的幅度和相位转换为统计分布图特征,利用轻量级的卷积神经网络对4种调制信号进行识别. Huynh-The等[15]利用卷积神经网络(convolution neural network, CNN)对24种调制信号进行分类识别,当信噪比为20 dB时,平均识别率达到93.59%. O'shea等[16]利用残差网络对调制信号的波形数据进行学习,取得了较好的识别性能.
上述的方法在针对特定调制方式识别时,有较好的识别结果,但均采取单一特征用于识别分类,建模时未考虑信号采样定时偏差的影响. 针对这些问题,在相关算法的启发下,本文利用深度学习的方法对常见的7种幅相类调制进行识别. 提取信号的相位星座图和矢量轨迹图2个联合特征,利用轻量级的残差网络对联合特征进行分层学习和融合识别. 仿真实验表明,在星座图特征识别的基础上融合相位矢量轨迹特征,提升了系统的识别性能.
1. 算法原理
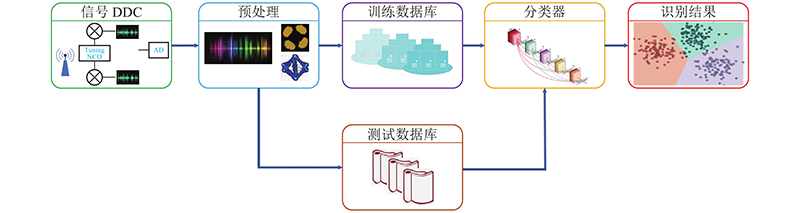
调制是无线通信系统中的一个基本环节,将待发送的低频信号搬移到高频后进行传输,用来提升系统的通信容量和可靠性. 在非协作通信的信号接收端,通常需要对信号进行参数估计和处理后,进行调制方式的识别. 本文调制识别的系统流程如图1所示.
图 1
1.1. 信号原理
对常见的幅相类调制信号进行识别,信道为高斯信道,假设信号的载波频率误差可以被理想估计. 接收信号
式中:
对于MPSK调制信号,可以表示为
式中:
对于方形星座的MQAM调制信号,可以表示为
式中:
对于MAPSK类信号,星座是由分布在不同半径的同心环上的点组成,可以表示为
式中:
1.2. 信号特征
信号星座图是将接收信号的最佳采样点映射到复平面上,形成二维分布的散点图. 信号相位矢量图是在复平面上,通过渐进变化的连续轨迹来描述基带成型后的信号波形. 在每条路径上都显示出信号的幅度变化和相位状态跳转关系信息. 在数字通信系统中,用于描述信号矢量图的数据量是过采样倍数的星座图的数据量,且矢量图含有调制信号的连续变化的相位信息. 通常来说,不同的调制信号有不同的星座图和矢量图,信噪比为15 dB时的信号特征如图2所示.
图 2
图 2 信噪比为 15 dB时各调制的星座图、矢量图
Fig.2 Modulation constellation diagram and vector diagram when SNR is 15 dB
2. 基于深度学习的调制识别
2.1. 融合学习网络
图 3
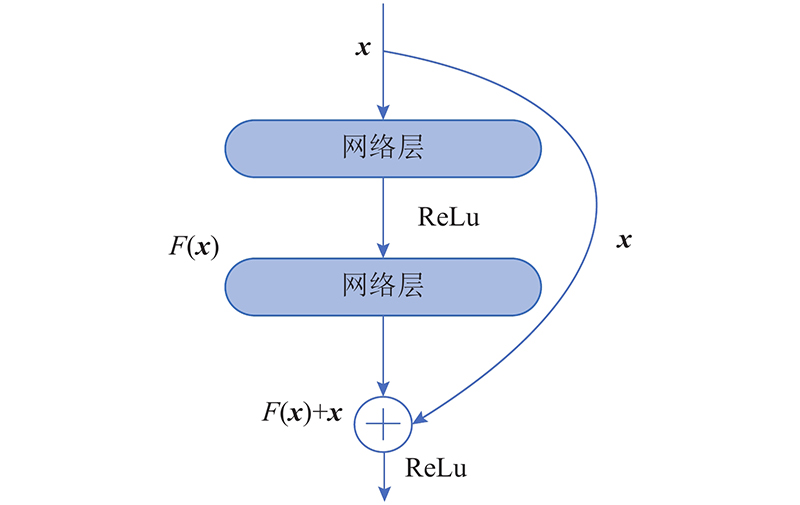
残差单元通过跳接路径将上层的输入与本层的输出相加,使得网络不再直接学习当前输入的特征,而是学习输入和输出之间的残差特征,简化了网络的训练问题. 在残差模块中,极端情况下,若残差项为0,则该网络相当于进行了一次恒等映射,将信息直接传递到下层网络. 在实际中,残差单元通常可以学习其他新的特征,因此在训练更深的网络时,残差网络的性能不会下降. 残差单元输出[19]可以表示为
式中:
图 4
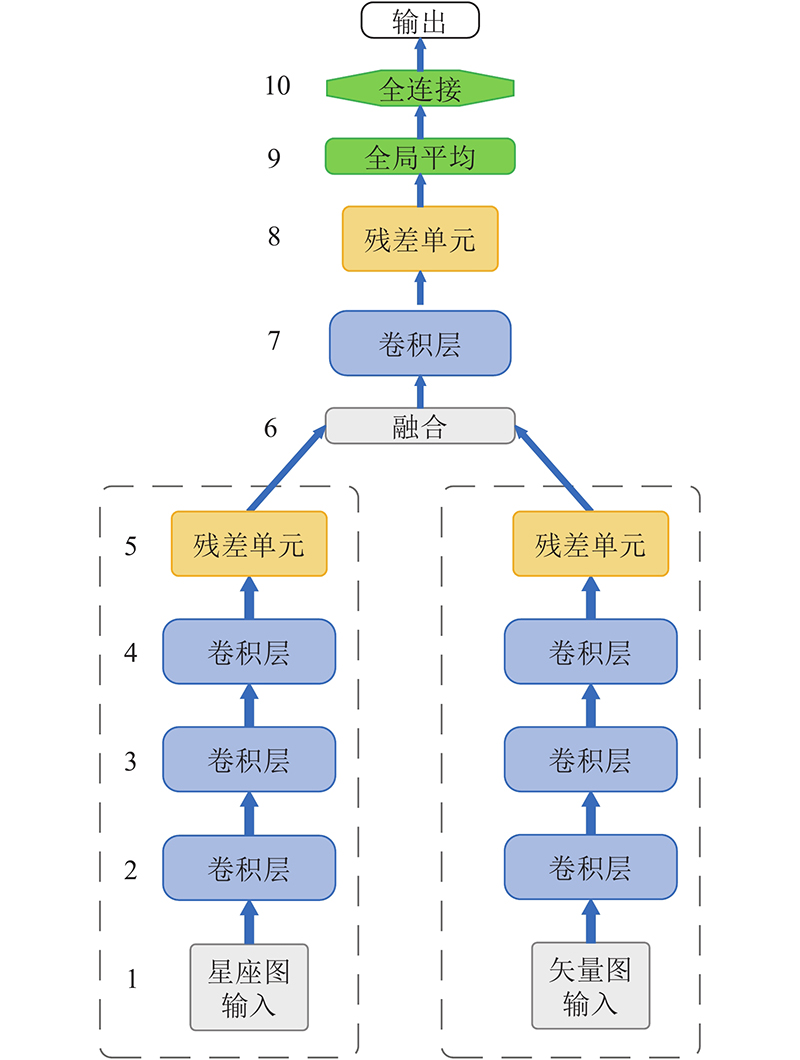
表 1 网络结构的细节
Tab.1
| 序号 | 组件 | 尺寸维度 | 描述 |
| 1 2 3 4 5 6 7 8 9 10 | 输入 卷积层 卷积层 卷积层 残差单元 融合 卷积层 残差单元 全局平均 全连接 | 3×224×224 32×112×112 32×112×112 32×112×112 32×112×112 64×112×112 128×56×56 256×28×28 256 7 | 星座图和矢量图输入 32×Conv(3,3), Stride=2 32×Conv(3,3), Stride=1 32×Conv(3,3), Stride=1 Channel=32, Stride=1 Concat 128×Conv(3,3), Stride=2 Channel =256, Stride=2 Average pooling 输出 |
相比于常见的CNN,基于联合特征输入的识别网络没有池化层,降采样过程是通过设置卷积核的步长完成的. 该网络前期由2个相同的支路同步对星座图和矢量图特征进行浅层学习,随后开展深度融合学习和识别分类. 融合方法是在网络中将2个并行支路的浅层网络学习到的特征在通道维度进行拼接和联合,组成新的特征矢量,作为下层网络的输入. 该网络的第1阶段是浅层特征提取阶段,通过3组卷积层学习输入特征图像的纹理、线条及局部信息. 其中第1个卷积模块的滑动步长设置为2,目的是对输入数据进行降采样处理,减少网络的计算量. 为了防止随着网络深度增加出现梯度消失的情况,在卷积层后使用基本的残差单元,将上层学习到的特征继续传导至下层卷积网络. 第2阶段是融合学习阶段,利用卷积层和残差单元对融合后的特征进行深度学习,以实现不同调制信号的差异性学习. 第3阶段是识别分类阶段,对网络学习到的特征全局压缩展平后,连接到全连接层,采用Softmax进行分类输出. 当对网络性能进行优化时,为了减少模型的过拟合,通过
2.2. 识别步骤
对幅相类调制信号进行识别的方法的主要步骤如下.
1)对接收信号进行匹配滤波,利用根升余弦滤波器对信号进行解卷处理,能够获得最大信噪比输出的信号.
2)信号采样过程中可能有定时偏差,须进行误差估计和处理. 定时估计算法采用非数据辅助的方式[20],定时偏差可以表示为
式中:
3)对网络参数进行初始化,利用产生的样本数据进行迭代训练和更新网络参数,不断学习样本数据的特征.
4)在训练完成后,选择最优模型,输入测试样本,对目标集合中的调制信号进行识别,获得系统的测试性能指标.
3. 实验仿真与分析
实验仿真数据利用Matlab 2020a软件来模拟产生. 信号成型时,滤波器的滚降系数工程上通常设为0.35;基带信号生成时,随机引入定时偏差,假设一次仿真过程的定时偏差一致;信号的过采样倍数为16. 针对每种调制信号,随机生成800个信号源符号数据,在信噪比为0~10 dB的条件下,各产生2 000个样本数据. 在对数据集划分时,训练、验证和测试数据的比例设置为0.70、0.15和0.15. 系统采用识别率
式中:
利用上述产生的样本数据对基于联合特征的网络进行训练,神经网络的超参数设置如表2所示.
表 2 神经网络的超参数
Tab.2
| 名称 | 含义 | 数值 |
| Learning rate Batch size Epoch Optimizer Weight decay Momentum | 学习率 块包含的数据样本 最大迭代训练轮次 优化器 权重衰减 动量因子 | 0.001 64 300 SGD 0.001 0.9 |
3.1. 系统性能及对比
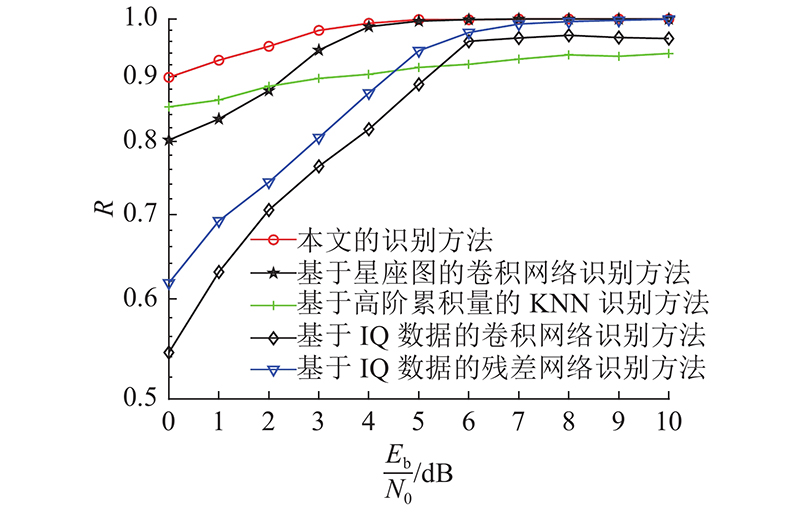
图 5
从上述结果综合来看,提出方法的识别性能表现更优. 当信噪比高于2 dB时,对目标集合内7种调制方式的平均识别率可达95.14%;当信噪比高于5 dB时,基于深度学习的4种方法的识别性能均优于基于高阶累积量的KNN方法,表现出深度学习具有强大的学习能力. 本文方法的识别性能较基于高阶累积量的KNN识别方法有优势.当信噪比高于5 dB时,基于高阶累积量的KNN识别方法的识别性能增益不明显,最高的识别率不超过94%. 这是由于部分调制信号的高阶累积量理论值比较接近,统计值受噪声的影响有一定的波动,影响了识别性能. 与基于星座图的卷积网络识别方法相比,本文方法在低信噪比下的识别性能有一定的增益,最大增益达到9.71%,这是由于本文方法融合了星座图和矢量图2种特征. 与基于IQ数据的2种识别方法相比,本文方法的性能增益明显,最大有35.48%的增益. 当信噪比低于6 dB时,基于IQ数据的2种识别方法的性能出现较大恶化. 这是由于基于IQ数据的识别方法直接对调制信号的时域波形数据进行学习,但在低噪比下学到的特征不够明显.
对不同调制方式下的识别性能进行分析,部分信噪比下的识别结果如表3所示. 可以看出,在各方法的识别性能中,高阶APSK 和QAM调制的平均识别性能低于低阶PSK调制的平均识别性能,如BPSK调制在低信噪比时,能够达到100%. 分析高阶MQAM(M = 16、64)调制的识别结果可知,本文方法的表现最优,较基于星座图的卷积网络识别的方法提升了24%和51.67%. 分析本文高阶调制的识别性能可知,QAM调制的识别率比APSK调制高,当信噪比为0 dB时,平均识别率提升了28.67%. 主要是由于QAM调制的联合特征在视觉分布上呈现方形的特点明显区分于APSK和PSK调制特征呈现的圆形特点.
表 3 部分信噪比下的调制识别率
Tab.3
| 调制方式 | 本文的方法 | 基于星座图的卷积 网络识别方法 | 基于高阶累积量的 KNN识别方法 | 基于IQ数据的卷积 网络识别方法 | 基于IQ数据的残差 网络识别方法 | ||||||||||||||
| 0 dB | 5 dB | 10 dB | 0 dB | 5 dB | 10 dB | 0 dB | 5 dB | 10 dB | 0 dB | 5 dB | 10 dB | 0 dB | 5 dB | 10 dB | |||||
| BPSK | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 99.85 | 100 | 100 | ||||
| QPSK | 98.33 | 100 | 100 | 98.33 | 100 | 100 | 100 | 100 | 100 | 44.25 | 100 | 100 | 81.80 | 100 | 100 | ||||
| 8PSK | 99.00 | 100 | 100 | 98.33 | 100 | 100 | 100 | 100 | 100 | 48.40 | 100 | 100 | 71.00 | 99.95 | 100 | ||||
| 16APSK | 77.67 | 100 | 100 | 77.67 | 100 | 100 | 68.50 | 75.83 | 82.33 | 35.60 | 83.40 | 99.95 | 47.05 | 97.65 | 100 | ||||
| 32APSK | 59.67 | 99.67 | 100 | 68.00 | 99.67 | 100 | 62.83 | 81.50 | 83.50 | 65.35 | 89.05 | 86.95 | 51.60 | 89.10 | 100 | ||||
| 16QAM | 100 | 100 | 100 | 76.00 | 100 | 100 | 84.17 | 90.50 | 95.33 | 17.65 | 60.85 | 100 | 38.90 | 86.05 | 100 | ||||
| 64QAM | 94.67 | 99.67 | 100 | 43.00 | 97.67 | 100 | 80.83 | 93.00 | 96.17 | 69.70 | 88.05 | 88.60 | 42.35 | 87.90 | 99.85 | ||||
| 平均识别率 | 89.90 | 99.90 | 100 | 80.19 | 99.62 | 100 | 85.19 | 91.55 | 93.90 | 54.42 | 88.76 | 96.50 | 61.79 | 94.38 | 99.98 | ||||
3.2. 参数分析
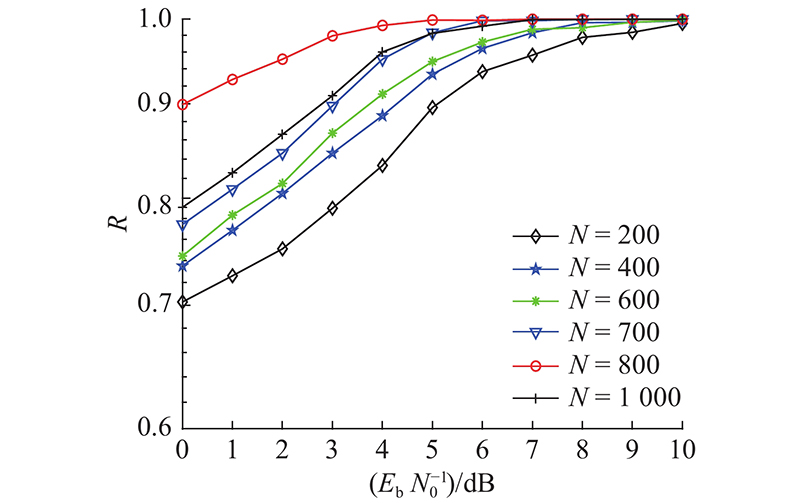
3.2.1. 调制符号数量的影响
在生成训练数据集时,信号符号长度影响数据量的大小,决定所提取的特征图片中像素块的疏密程度,对信号的识别结果产生影响. 设置符号数
图 6
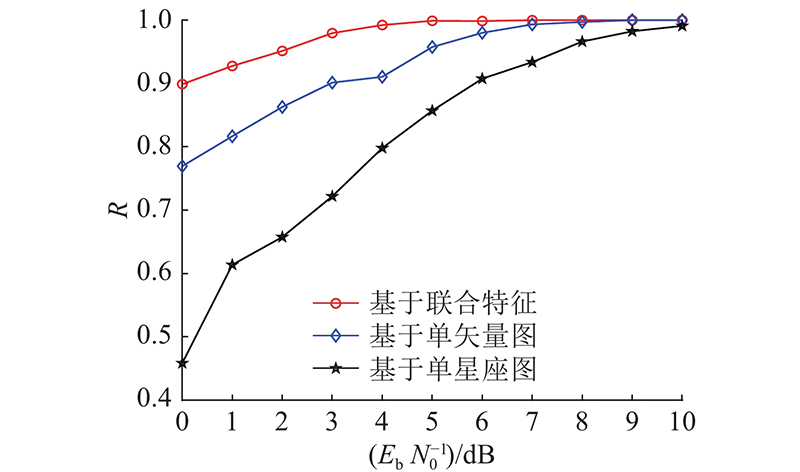
3.2.2. 联合特征的增益
图 7
图 7 基于单特征输入的卷积神经网络(星座图、矢量图)
Fig.7 CNN based on single feature input (constellation diagram and vector diagram)
图 8
从上述结果来看,联合特征的识别效果优于单星座图和单矢量图特征的识别效果,表明在星座图特征的基础上,融合相位矢量轨迹特征更能够反映不同调制间的差异性,增强了调制类别的特征属性.在基于单矢量图和单星座图的性能对比时,发现基于单矢量图的识别效果更好,这是由于矢量图同时携带了信号的相位轨迹和跳转信息.
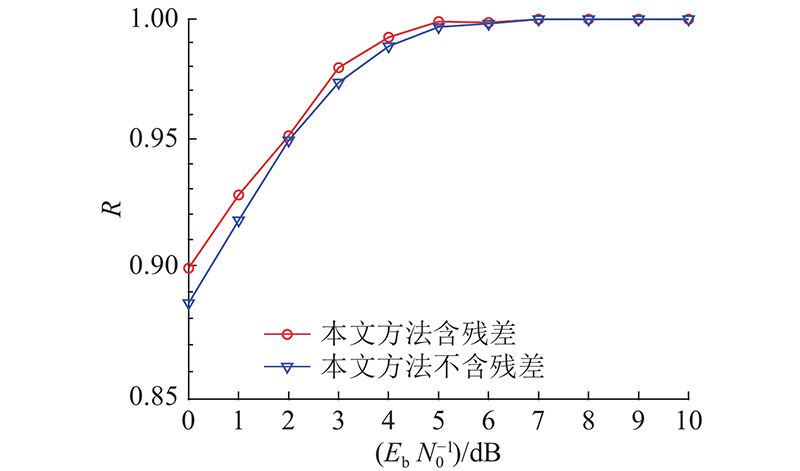
3.2.3. 残差模块的优势
为了分析网络中的残差模块对识别性能的影响,在基于联合特征输入的识别网络中去掉基本残差单元中的跳接模块,网络的其他结构和超参数保持不变,识别性能的结果如图9所示. 可以看出,当信噪比低于6 dB时,含残差的网络提升了系统的平均识别性能;当信噪比为0 dB时,性能提升了1.33%. 这是由于引入残差单元使得网络去学习残差特征,在一定程度上可以简化训练的难度,保证性能不会下降.
图 9
3.3. 扩展性测试
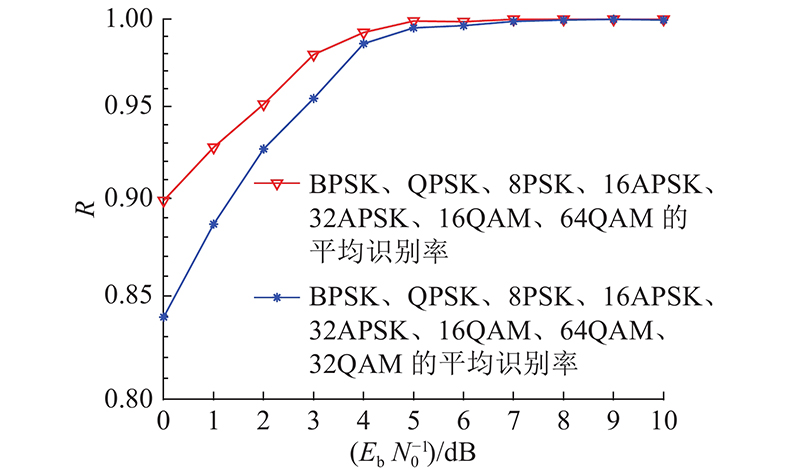
利用基于联合特征的识别方法提高了调制识别性能,增加1种新的调制方式32QAM,开展鲁棒性和可扩展性的测试. 在模型其他结构不变的情况下,只修改最后全连接层输出层的神经元数量. 在前期模型训练的基础上进行参数微调和适应性训练,识别性能的结果如图10所示.
图 10
从上述结果可以看出,在低信噪比下,增加32QAM调制后的识别结果最大仅出现了6%的性能下滑,但是经过适应训练后,性能随着信噪比稳步提升. 当信噪比高于5 dB时,扩展后的性能可以达到很高的识别率,表明提出的方法具有一定的鲁棒性和可扩展能力.
3.4. 复杂性分析
数据仿真及样本测试在主机CPU为Intel(R) Core(TM) i5-9400 CPU×6的环境下开展. 神经网络的训练在服务器CPU为Intel(R) Xeon(R) Gold 6248R CPU×96,GPU为GTX3080,内存为256 GB DDR4的环境下开展,深度学习开发框架为PyTorch版本1.7.1,Cuda加速库版本11.0. 在相同条件下,各方法的复杂度如表4所示. 表中,
表 4 不同算法的复杂度
Tab.4
| 识别方法 | | | |
| 本文的方法 基于星座图的卷积网络识别 基于高阶累积量的KNN识别 基于IQ数据的卷积网络识别 基于IQ数据的残差网络识别 | 0.758 0.168 0.0011 0.0023 0.0025 | 372.4 239.33 22.668 34.8 49.56 | 1070791 5967175 — 2748255 103337 |
从表4可以看出,本文方法的样本生成和训练时间的复杂度均高于其他4种方法. 这是由于本文方法需要生成和融合2种图特征,复杂度较高. 基于高阶累积量的KNN识别方法的样本生成时间和训练时间低于本文方法和其他3种对比的识别方法. 在网络模型的参数量上,本文方法的参数量少于基于星座图的卷积网络识别方法和基于IQ数据的卷积网络识别方法的参数量,占比为17.9%和38.9%. 综合来看,本文方法在使用联合特征后,增加了时间复杂度,但提升了系统的总体识别性能.
4. 结 语
本文研究基于联合特征和深度学习的调制识别方法. 考虑调制信号采样过程中存在定时偏差,对接收信号进行处理,将波形数据转化为2个图特征,利用轻量级残差网络对特征进行深度融合和识别分类. 仿真结果表明,采用基于星座图的相位矢量轨迹识别方法,增强了调制类别的特征属性,提高了识别性能. 考虑在非合作通信中,对接收的信号进行盲处理时,可能有较大的载波频偏残余,影响提取的特征及识别结果. 如何在载频估计不理想的情况下进行调制识别,是后续的研究方向.
参考文献
Survey of automatic modulation classification techniques: classical approaches and new trends
[J].DOI:10.1049/iet-com:20050176 [本文引用: 1]
Machine learning based automatic modulation recognition for wireless communications: a comprehensive survey
[J].
基于信息熵和GA-ELM的调制识别算法
[J].DOI:10.3969/j.issn.1001-506X.2020.01.30
Modulation recognition algorithm based on information entropy and GA-ELM
[J].DOI:10.3969/j.issn.1001-506X.2020.01.30
Spectrum analysis and convolutional neural network for automatic modulation recognition
[J].DOI:10.1109/LWC.2019.2900247 [本文引用: 1]
Automatic modulation recognition of DVB-S2X standard-specific with an APSK-based neural network classifier
[J].
Deep learning in digital modulation recognition using high order cumulants
[J].DOI:10.1109/ACCESS.2019.2916833 [本文引用: 1]
Data-driven deep learning for automatic modulation recognition in cognitive radios
[J].DOI:10.1109/TVT.2019.2900460 [本文引用: 1]
基于稀疏滤波神经网络的智能调制识别
[J].DOI:10.3969/j.issn.1001-0548.2019.02.001 [本文引用: 1]
Intelligent modulation recognition based on sparse filtering neural network
[J].DOI:10.3969/j.issn.1001-0548.2019.02.001 [本文引用: 1]
Deep learning: methods and applications
[J].
Learning pose-aware models for pose-invariant face recognition in the wild
[J].
Fusing MFCC and LPC features using 1D triplet CNN for speaker recognition in severely degraded audio signals
[J].
Deep imbalanced learning for face recognition and attribute prediction
[J].DOI:10.1109/TPAMI.2019.2914680 [本文引用: 1]
Automatic modulation classification using contrastive fully convolutional network
[J].DOI:10.1109/LWC.2019.2904956 [本文引用: 1]
Accumulated polar feature-based deep learning for efficient and lightweight automatic modulation classification with channel compensation mechanism
[J].DOI:10.1109/TVT.2020.3041843 [本文引用: 1]
Mcnet: an efficient CNN architecture for robust automatic modulation classification
[J].
Over-the-air deep learning based radio signal classification
[J].DOI:10.1109/JSTSP.2018.2797022 [本文引用: 1]
64-APSK constellation and mapping optimization for satellite broadcasting using genetic algorithms
[J].
Feedforward Ml-based timing estimation with PSK signals
[J].DOI:10.1109/4234.585803 [本文引用: 1]
Interpolation in digital modems. II. implementation and performance
[J].DOI:10.1109/26.231921 [本文引用: 1]
Modulation classification based on signal constellation diagrams and deep learning
[J].DOI:10.1109/TNNLS.2018.2850703 [本文引用: 1]
Automatic modulation classification using combination of genetic programming and KNN
[J].