液压机械臂采用集中式驱动方式,多执行器运动节流损失大,能量优化尤为重要[1]. 液压机械臂的能量优化包括降低液压系统能耗[2]和减少运动所需能量. 现有研究大多围绕前者展开. 针对后者,可利用液压机械臂多关节具备的冗余特性(即末端处于同一位置,而机械臂位姿并不相同),在相同末端轨迹时降低负载能耗[3]. 现有冗余分解方法针对电驱动的工业机器人设计,使其末端在沿预设轨迹运动的同时实现额外目标[4-7]. Peng等[8]设计的时间−能量−脉动优化的轨迹规划方法,采用非支配邻域免疫遗传算法优化机械臂的多个目标函数,得到各关节运动参数最优的规划曲线. 徐帷等[9]采用强化学习方法实现目标跟踪及避障的自主路径规划. 为了最小化机械臂的能量消耗,Yokose[10]提出结合辐射法与遗传算法的最优冗余分解方法. Yin等[11]提出基于机器学习的机器人轨迹规划方法以逼近能量消耗最优的轨迹. Ferrentino等[12]从拓扑角度研究基于运动可行性、平滑性指标的冗余分解,提出基于状态空间离散化的动态寻优冗余分解. 为了避免机械臂与障碍物间的交集,Gong等[13]在多解空间中寻找子空间,得到避免超过关节极限的冗余分解. Hoang等[14-15]采用梯度投影法实现加速度层面冗余分解,降低静态扭矩,使得扭矩产生的局部加速度减小. 梯度投影法计算量较小,已被广泛用于降低冗余机械臂的能耗[4,14].
液压机械臂采用集中式驱动方式,多个关节由液压泵供油,其能耗特性与分布式独立控制的电驱动机械臂存在显著差异,直接应用传统冗余分解方法难以获得液压机械臂的能量最优解. 考虑液压驱动特性,Beiner等[16]提出在梯度投影法基础上,以缸速范数最小作为优化准则,获得了良好的节能特性. 缸速范数最小是求解缸速的平方和最小,而非直接描述液压系统能耗的流量、压力目标,导致其能耗最小解存在随位姿时变的偏差,且难以通过计算补偿. Nurmi等[17-18]以液压系统能耗为优化准则,基于动态规划算法求解到了全局能量消耗最少的冗余分解. 但是,动态规划优化计算时间长(三自由度求解耗时30 min),易陷入“维数灾难”问题,不适用于实时在线运动规划. 最小缸速范数法求解结果虽为次优解,但相较梯度投影法优化效果更好,且具备动态规划算法欠缺的高计算效率. 最小缸速范数法的核心是雅可比矩阵变换. Chan等[19-20]指出加权雅可比矩阵可以调整机械臂冗余自运动,实现特定的目标优化. 刘志忠等[21]提出的可变加权矩阵法,简化了雅可比矩阵,提高了优化效率. 这些加权矩阵权值优化方法仅针对电驱动机械臂,优化目标为各向同性位姿、操作度最大[22],未涉及能量优化.
本研究提出基于流量最小的冗余分解方法. 基于冗余液压机械臂的运动学模型,推导得到缸速范数最小的冗余分解; 在缸速范数最小的基础条件下,采用优化加权矩阵权重的方法,进一步调整液压缸缸速分配关系,搜索直接决定液压机械臂能耗的系统流量最小值;在不同末端轨迹下开展试验验证.
1. 冗余液压机械臂模型
冗余液压机械臂在末端位置相同的情况下有不同的自运动流形,使得机械臂冗余分解的耗能存在优化空间. 不同于工程机械,液压机械臂对运动精度控制和响应特性要求极高,一般采用恒压伺服系统驱动. 本研究以系统的流量消耗来评价液压机械臂能耗,设定液压机械臂末端执行器的运动轨迹,并将轨迹离散化以便进行算法优化.
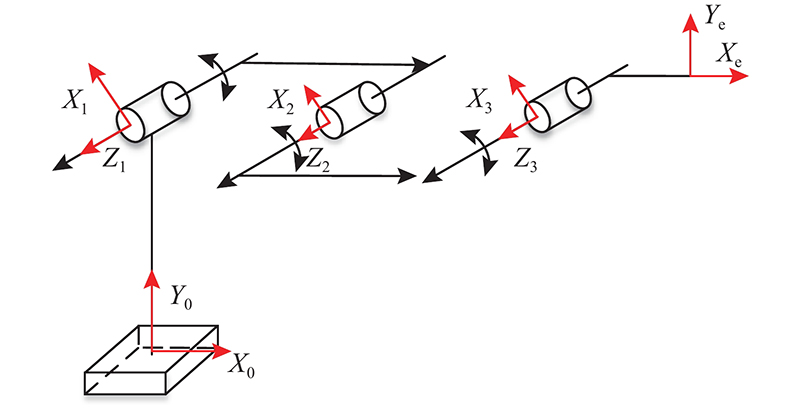
确定机械臂连杆i到连杆
式中:
式中:
机械臂末端速度和关节角度的运动学关系表达式为
式中:
把由雅可比矩阵解算得到的关节角度空间转换到驱动空间的液压缸缸速
式中:v为机械臂各关节液压缸缸速矢量,
式中:i为关节序号,
式中:
2. 最小流量优化
冗余液压机械臂运动所需的流量由各个关节的运动决定,为了减小机械臂运动过程中的流量消耗,由液压机械臂的正运动学方程推导出液压缸缸速和机械臂末端速度的关系. 在缸速最小范数的基础上引入加权矩阵,通过动态优化加权矩阵权值,使机械臂瞬时流量不断减小,实现能耗最少的冗余分解目标.
对于冗余液压机械臂能量优化问题,利用液压缸驱动空间确定液压缸缸速和机械臂末端速度的关系,表达式为
为了使冗余液压机械臂液压缸速度范数最小,构造目标函数L,使用拉格朗日乘数法求解关于L的多元函数最小值.
对速度范数
得到液压缸缸速v为
把式(17)代入式(13)有
由式(18)求解
由驱动空间液压缸缸速到末端执行器位置空间的伪逆矩阵为
将目标轨迹离散化成为N点,设定每两步的时间间隔为dt. 关节角度由液压缸缸速和前一步的角位移联合确定,计算式为
引入加权矩阵W(一般为对角矩阵),并给出加权矩阵的指数形式,求解液压缸缸速的伪逆矩阵为
加权矩阵的权值一般不随关节位姿变化,但是随着机械臂在运动时位姿变化,不同加权矩阵可以改变运动所需流量. 因此,动态调整加权矩阵权值,可以使机械臂在末端轨迹不变的情况下降低系统所需流量. 每个关节的角度q在第k时刻的表达式为
式中:
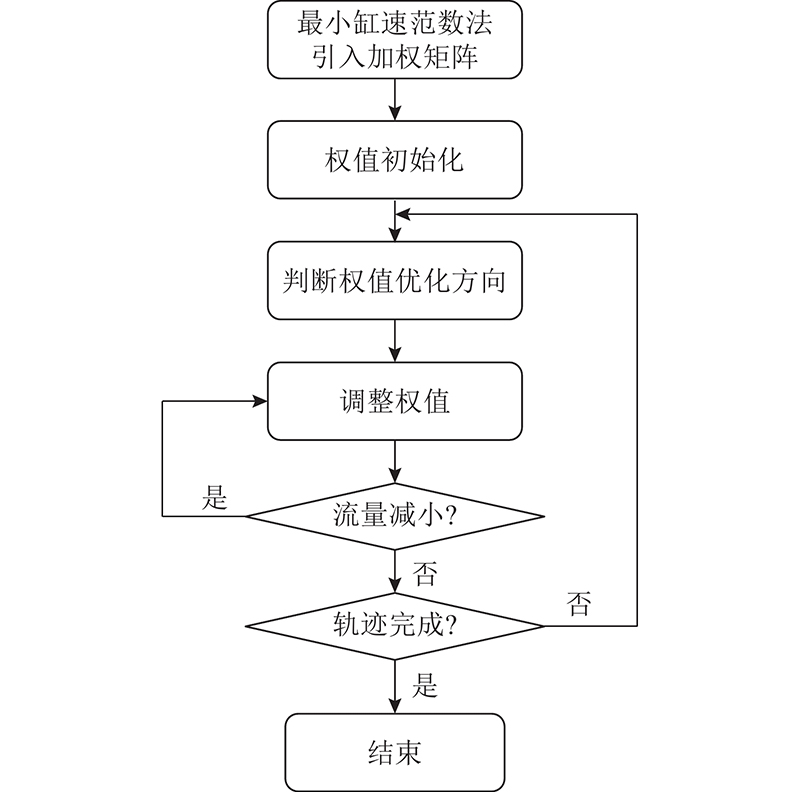
图 1
式中:N为末端轨迹的离散个数,
图 2
算法1 最小流量冗余分解
for i=1 to m do
set w_1k=1+dx
calculate Qp_1k
if Qp_1k< Qp_01
symbol_1k=1
else
symbol_1k=1
end if
w_1k=w_1k+symbol*dx
calculate Qp_1k(i+1)
if
Qp_1k(i+1)>= Qp_1k(i+1)
w_1k(i+1)= w_1k(i)
end if
end for
W=diag[w_1k(end),w_2k(end) ,w_3k(end)]
Calculate
end for
3. 算例验证
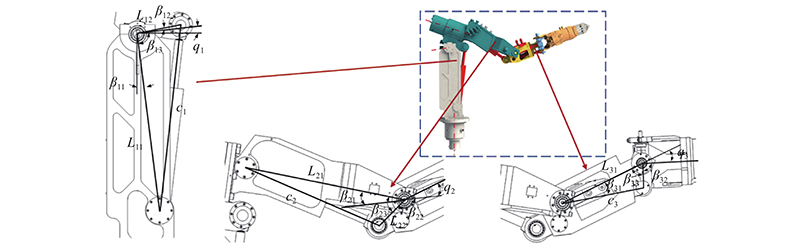
三关节液压机械臂在平面运动时已具有冗余特性,且更多关节机械臂的能量优化方法相比于三关节冗余机械臂仅增加了矩阵维度,因而平面三自由度冗余机械臂的能量优化结论可以扩展到更多关节的冗余液压机械臂. 以如图3所示的平面三关节液压机械臂为例研究能耗优化算法.
图 3
图 3 冗余液压机械臂算例的机构示意图
Fig.3 Schematic diagram of mechanism of redundant hydraulic robotic arm study
如图4所示,机械臂1、2、3关节为液压缸驱动关节转动,液压缸长度与关节角度用三角形的几何关系表示. 关节角度和液压缸长度的关系表达式为
图 4
图 4 液压机械臂各关节几何关系
Fig.4 Geometric relationship of each joint on hydraulic manipulator
式中:
式中:
以关节3初始角度为变量,由机械臂末端初始位置和关节3初始角度得到各关节的初始逆运动学解析解,以求得的解析解为基础,分别使用最小流量优化法(minimum flow method, MF)、最小缸速范数法(minimum acutator velocity norm, MAVN)、梯度投影法(gradient projection method, GP)对三角形轨迹和椭圆轨迹进行优化.
式中:
式中:
表 1 液压机械臂算例的结构参数
Tab.1
| i | L/m | d/mm | | |
| 1 | 0.875 | 63 | 7.16 | 5.10 |
| 2 | 0.360 | 63 | 18.30 | 161.14 |
| 3 | 0.740 | 45 | 9.69 | 90 |
图 5
图 6
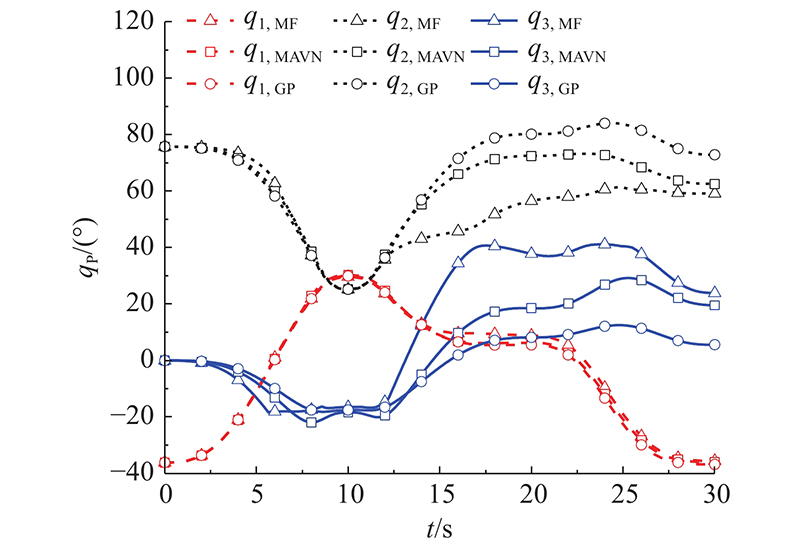
图 6 三角形轨迹下不同冗余分解方法的规划角度对比
Fig.6 Comparisons of planned joint angles among different redundancy resolution methods under triangle trajectory
图 7
图 8
图 8 椭圆轨迹下不同冗余分解方法的规划角度对比
Fig.8 Comparisons of planned joint angles among different redundancy resolution methods under elliptic trajectory
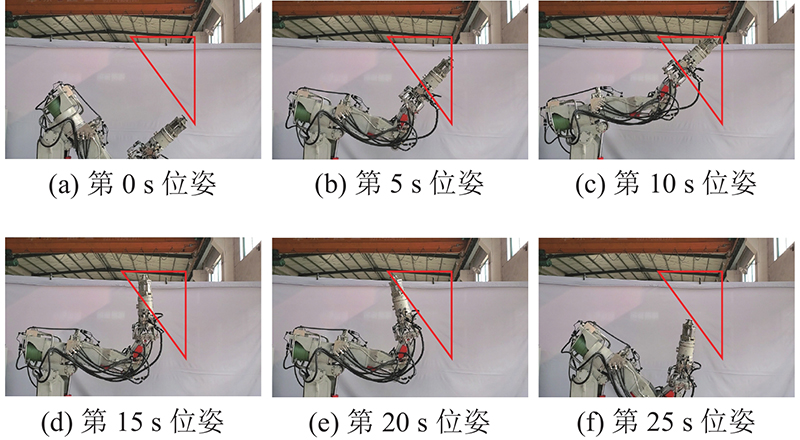
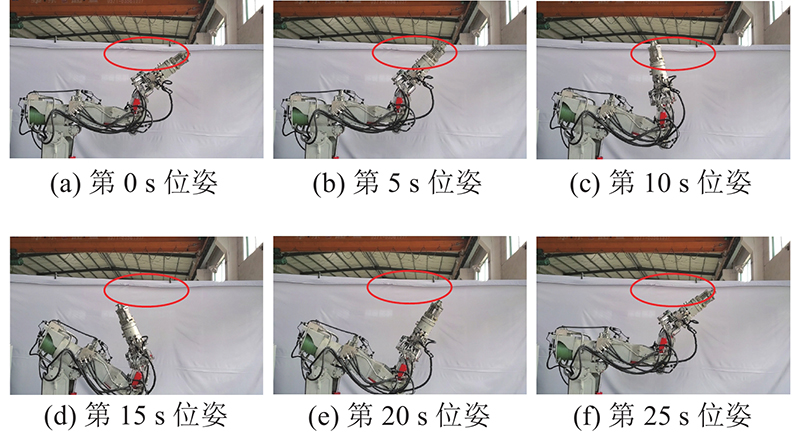
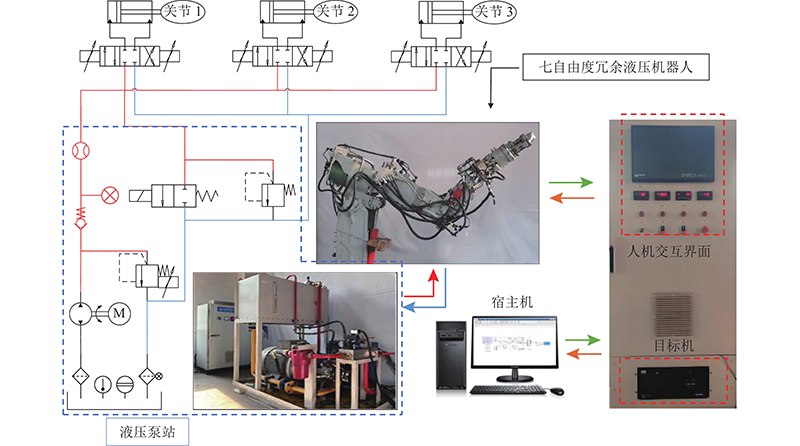
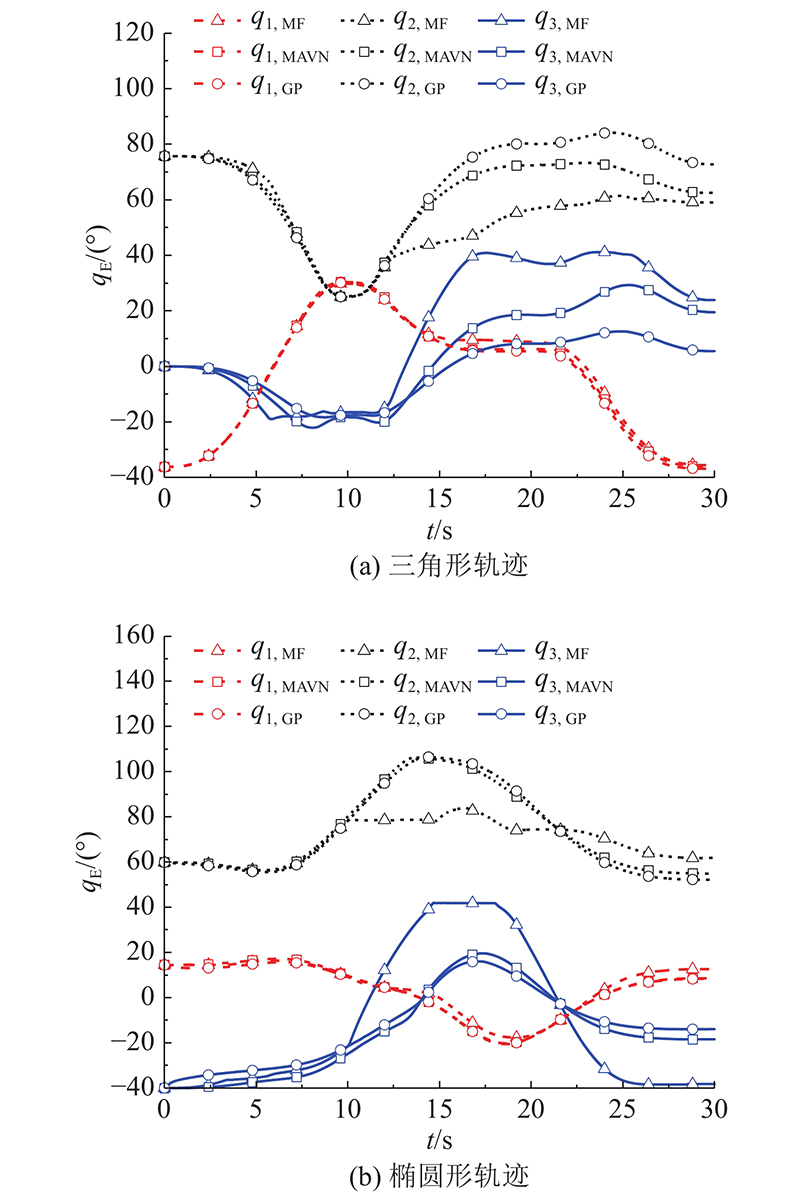
3)试验验证. 用于验证本研究所提算法的液压机械臂试验平台如图9所示. 液压系统由液压动力源、液压缸、液压滑环、伺服阀组成. 液压动力源的最大流量由变排量泵决定,系统压力由比例溢流阀调定. 流量计安装在机械臂高压进油口,实时检测液压机械臂的系统流量. 计算机控制系统采用Matlab/Simulink XPC-Target实时控制系统,以宿主机和目标机主从双机模式工作. 控制系统通过总线系统—采集卡—目标机—宿主机获得压力传感器、流量传感器、角度编码器的压力、流量、角度等反馈信息,并将计算控制信号输出至伺服阀,实现液压机械臂的高精度轨迹跟踪控制. 设计的三角轨迹和椭圆轨迹运行耗时30 s. 如图10为编码器测量的实际关节角位移。图中,qE为试验角度。如图11所示,将实际角位移代入冗余液压机械臂运动学正解,得到笛卡尔坐标系下执行器末端轨迹,在XOY平面内绘制出实际轨迹图. 可以看出,3种方法的液压机械臂均准确跟踪了规划的关节角度,其末端也完全沿着预设轨迹运动.
图 9
图 9 冗余液压机械臂试验台及其控制系统
Fig.9 Developed test rig of redundant hydraulic manipulator and its control system
图 10
图 10 不同轨迹下不同冗余分解方法的关节角度试验对比
Fig.10 Comparisons of tested joint angles among different redundancy resolution methods under different trajectories
图 11
图 11 不同轨迹下不同冗余分解方法的末端轨迹对比
Fig.11 Comparisons of end-effector trajectories among different redundancy resolution methods under different trajectories
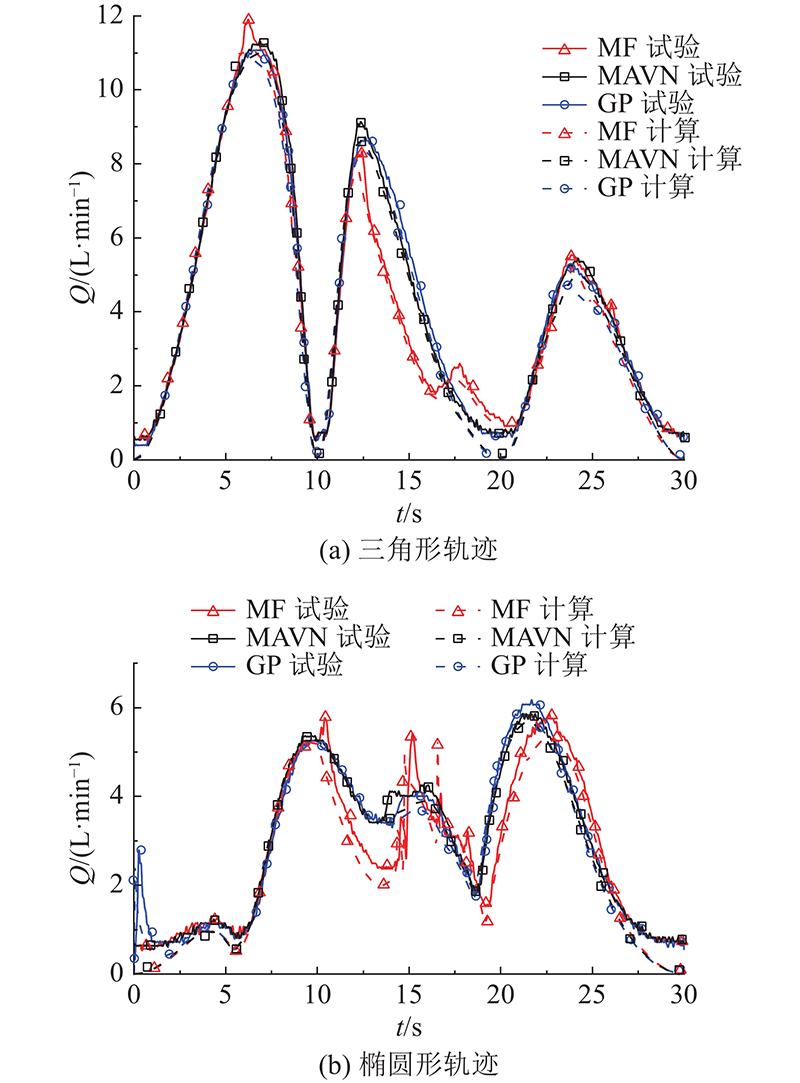
采集3种方法的系统流量数据如图12所示. 不同位姿下,液压缸伸出/缩进位移、臂杆末端的位置变化等均不同,本研究所提流量优化方法针对机械臂在运动中时变的位姿寻找流量耗费最少的解. 在试验模型中,关节3的液压缸活塞面积小于2. 经最小流量法优化后,关节2的运动幅度小于最小缸速范数法和梯度投影法的求解结果,关节3的运动幅度大于最小缸速范数法和梯度投影法求解结果. 说明流量优化方法在任意轨迹下均具备降低液压机械臂运动所需流量的能力. 对于三角形轨迹,当关节3运动到其极限位置时(t=16 s),由于关节3不能越过该极限位置,此时关节2开始运动完成设定轨迹,关节1的运动需要更多的流量,导致最小流量优化法的流量短暂高于最小缸速范数法和梯度投影法.
图 12
图 12 不同轨迹下不同冗余分解方法的系统流量对比
Fig.12 Comparisons of system flows among different redundancy resolution methods under different trajectories
在不考虑压力损失和流量泄漏的恒压系统中,系统能耗计算式为
式中:t1、t2分别为开始时间和结束时间,p为系统压力,
表 2 不同轨迹理论计算与试验验证能耗对比
Tab.2
| 算法 | Ec,t | Ec,e | |||
| 理论 | 试验 | 理论 | 试验 | ||
| MF | 10.17 | 11.39 | 15.76 | 16.84 | |
| MAVN | 11.17 | 12.00 | 16.65 | 17.74 | |
| GP | 11.21 | 12.04 | 16.68 | 17.78 | |
| 平均节能 | 7.2% | 5.1% | 7.4% | 5.3% | |
4. 结 语
梯度投影法和最小缸速范数法分别通过降低关节角速度范数和液压缸缸速范数来减少能耗,并未以直接考虑液压系统层面的流量作为优化目标. 本研究提出最小流量优化算法,通过动态调整加权矩阵权重降低预设轨迹每步的能耗,在不影响机械臂末端运动轨迹的条件下,降低了关节运动的流量需求,减少了系统的能耗. 液压机械臂的试验结果表明,采用本研究所提基于最小流量的冗余分解方法,相比于现有最小缸速范数法和梯度投影法,三角形和椭圆形轨迹下平均节能分别为5.1%、5.3%,节能效果更优. 本研究以恒压伺服系统为对象,下一步计划在负载敏感等压力/流量均变化的系统开展研究,以将所提方法拓展至更多的应用场合.
参考文献
Valve-based compensation for controllability improvement of the energy-saving electrohydraulic flow matching system
[J].DOI:10.1631/jzus.A1600346 [本文引用: 1]
非对称泵控装载机动臂特性研究
[J].DOI:10.3901/JME.2021.12.258 [本文引用: 1]
Research on the characteristics of wheel loader boom driven by the asymmetric pump controlled system
[J].DOI:10.3901/JME.2021.12.258 [本文引用: 1]
Real-time anti-saturation flow optimization algorithm of the redundant hydraulic manipulator
[J].DOI:10.3390/act10010011 [本文引用: 1]
A weighted gradient projection method for inverse kinematics of redundant manipulators considering multiple performance criteria
[J].
针对关节限位优化的7自由度机械臂逆运动学解法
[J].
Inverse kinematic optimization for 7-DoF serial manipulators with joint limits optimization
[J].
多节双八面体变几何桁架臂逆运动学解析算法
[J].
Analytical inverse kinematics algorithm for double-octahedral variable geometry truss manipulators
[J].
Trajectory optimization of pickup manipulator in obstacle environment based on improved artificial potential field method
[J].DOI:10.3390/app10030935 [本文引用: 1]
Trajectory optimization of an electro-hydraulic robot
[J].DOI:10.1007/s12206-020-0919-4 [本文引用: 1]
基于Sarsa(λ)强化学习的空间机械臂路径规划研究
[J].DOI:10.3873/j.issn.1000-1328.2019.04.008 [本文引用: 1]
Analysis of space manipulator route planning based on Sarsa(λ) reinforcement learning
[J].DOI:10.3873/j.issn.1000-1328.2019.04.008 [本文引用: 1]
Energy-saving trajectory planning for robots using the genetic algorithm with assistant chromosomes
[J].
A machine learning based energy efficient trajectory planning approach for industrial robots
[J].DOI:10.1016/j.procir.2019.03.074 [本文引用: 1]
On the optimal resolution of inverse kinematics for redundant manipulators using a topological analysis
[J].
Analytical inverse kinematics and self-motion application for 7-DOF redundant manipulator
[J].DOI:10.1109/ACCESS.2019.2895741 [本文引用: 1]
A new torque minimization method for heavy-duty redundant manipulators used in nuclear decommissioning tasks
[J].DOI:10.1007/s11370-021-00369-4 [本文引用: 2]
Globally optimal inverse kinematics method for a redundant robot manipulator with linear and nonlinear constraints
[J].DOI:10.3390/robotics9030061 [本文引用: 1]
An improved pseudoinverse solution for redundant hydraulic manipulators
[J].
Global energy-optimised redundancy resolution in hydraulic manipulators using dynamic programming
[J].DOI:10.1016/j.autcon.2016.09.006 [本文引用: 1]
Global energy efficiency improvement of redundant hydraulic manipulator with dynamic programming
[J].DOI:10.1016/j.enconman.2020.113762 [本文引用: 1]
A weighted least-norm solution based scheme for avoiding joint limits for redundant manipulators
[J].DOI:10.1109/70.370511 [本文引用: 1]
基于可变加权矩阵的机器人雅可比矩阵规范化
[J].DOI:10.3901/JME.2014.23.029 [本文引用: 1]
Jacobian matrix normalization based on variable weighting matrix
[J].DOI:10.3901/JME.2014.23.029 [本文引用: 1]
基于可操作度评价的冗余机器人逆解求解方法
[J].
Method of inverse kinematics solution for a redundant manipulator based on manipulability
[J].