RMAL-II平衡与排序联合决策问题始于Rubinovitz等 [ 5] 提出的机器人装配线平衡问题,被Gao 等 [ 6] 定义为第I类机器人装配线平衡问题,后Gao 等 [ 6] 又界定了第II类机器人装配线平衡问题,即将装配任务、机器人分配给指定数量的工作站,达到最小节拍. 该问题被Yoosefelahi 等 [ 7- 9] 认同. Zhang等 [ 10- 11] 有效解决了第II类机器人U型装配线平衡问题中装配任务与机器人的分配问题,引起更多学者对第II类机器人装配线平衡问题的关注. Zhang等 [ 12] 未对机器人作业与非作业状态计算机器人能耗提出明确的节能策略,也未考虑混流产品切换准备作业的问题. 一方面,上述研究对装配线优化问题缺乏多产品混流装配情境的探索;另一方面,考虑到混流产品切换作业,平衡与排序联合决策是充分且必要的.
关于生产过程能耗的研究,Nilakantan等 [ 13] 通过设备单位时间碳排量和工作时间的乘积,量化碳足迹;周炳海等 [ 14] 采用设备功率和工作时间乘积测度机器人能耗;Nilakantan等 [ 15] 发现机器人装配线的能耗目标与效率目标非严格正相关;Zhang等 [ 16] 指出设备闲置状态下的能耗不可忽略;Mouzon等 [ 17] 研究发现在机器空闲期间将其关闭能够节约13%的能源. 生产实践已尝试主动管理装配线空闲期间能耗. 例如产品能效管理创新技术PROFIenergy能在长暂停期实现节能,还能在短的甚至极短的暂停期实现节能. 智能上电与断电让设备寿命更长且故障更少 [ 18] . 本研究立足PROFIenergy能效管理理念,提出采用关停策略精细管控RMAL-II闲置期间的能耗.
本研究详细划分机器人的状态,测度机器人在不同状态下的能源消耗. 考虑机器人关停策略与产品切换准备作业,兼顾作业、能源效率,构建RMAL-II平衡与排序联合决策双目标优化模型,并设计改进的NSGA-II求解. 通过算例分析,揭示关停策略和产品切换准备作业对RMAL-II系统的具体影响.
1. 建模基础
1.1. 问题描述
考虑能源消耗的RMAL-II平衡与排序联合决策问题描述如下. 在混流生产遵循最小生产单元(minimal production set, MPS)循环排序方法的前提下,为了兼顾系统效率和能源消耗这2个优化目标,综合考虑产品切换与机器人关停策略这2个核心影响因素,通过同时决策工序分配、机器人分配、MPS产品投产顺序,实现在单个MPS周期内最大工作站工作时间、机器人能源消耗的最小化.
1.2. 机器人的工作状态及能耗组成
在RMAL-II的实践中,机器人运作状态有以下5种. 1)作业状态:机器人执行产品装配作业过程. 状态1)的能耗功率最高. 2)产品切换准备作业状态:装配线上前后装配的2个产品种类发生变化时,机器人进行夹具、作业工具、参数或其他的调整作业. 状态2)会产生能耗. 3)关机状态:机器人未接通电源,不能进行任何操作. 状态3)不产生能耗. 4)开、关机动作:机器人接通、断开电源. 一般情况下,完成状态4)需要花费时间并产生能耗. 5)待机状态:机器人保持电源接通但未执行操作,随时可以进行装配作业. 状态5)会产生待机能耗.
将机器人的状态3)、状态4)、状态5)统称为闲置状态,此状态下可能会产生能耗. 在MPS内,将各装配作业之间的闲置时间称为单元内闲置时间;1个工作站从开始做MPS中第1个装配作业到做完最后1个装配作业,并完成下一次作业的准备工作,所经历的时间记作该工作站的工作时间. 按照混流装配线的生产平稳性要求,每个MPS中,各工作站总时间须保持一致,这意味着当某个工作站的实际工作时间小于最大工作时间时,存在闲置时间,等待下个MPS开始,本研究称之为单元间闲置时间.
1.3. 机器人关停策略
客观上,机器人闲置时间不能完全避免,为了减少机器人在闲置时间产生的能耗,常通过合理资源配置和任务调度消减闲置时间. 本研究在此基础上,采取机器人关停策略,即当机器人待机能耗大于开关机能耗时,将其关闭以进一步减少能耗. 当机器人处于待机状态时,待机功率记为
机器人开关机产生的能耗为
当
事实上,机器人开关机并非瞬间完成. 当关停策略触发时,有
2. 整数规划模型建立
2.1. 模型前提和假设
1)所有产品的工序及优先关系可以通过综合装配顺序图展现,如果产品没有综合装配顺序图中的某个工序,表示为该产品该工序的作业时间为0.
2)同道工序在不同机器人上的装配时间可能不同,在满足工序之间的优先关系的条件下,每个工序只能分配给任意1个工作站.
3)每个机器人能但只能被分配给任意1个工作站.
4)每个工作站只能有1台机器人,且假定工作站的数量与机器人的数量相同.
5)产品在某个工作站的所有工序完成后,立刻被转移到缓冲区或下个工作站,并假定缓冲区容量无限,产品移动时间可以忽略.
6)不考虑工作站和机器人的故障或维修,且工作站和机器人工作过程不中断.
7)同时间工作站只能执行1个产品的1道工序.
8)仅当机器人前后装配2种不同产品时,消耗时间和能源执行产品切换准备作业.
9)每个MPS内均包含最后1个产品到下个MPS第1个产品之间的产品切换准备作业,即在1个MPS开始时,机器人已经开机且无切换准备作业.
10)机器人作业和待机状态的能耗通过作业功率与待机功率测算,设定产品转换能耗和开关机能耗为已知.
2.2. 符号与说明
决策变量. 当综合装配顺序图中工序
指标.
参数.  在机器人
在机器人
变量.  个产品在第
个产品在第  个产品生产结束到下个产品装配作业开始之间的闲置时间;
个产品生产结束到下个产品装配作业开始之间的闲置时间;
2.3. 模型的建立
2.3.1. 目标函数
设最小化最大工作站工作时间为
2.3.2. RMAL-II平衡约束
以Gao等 [ 6] 针对单一产品所建立的第II类机器人装配线平衡模型为基础,依托MPS综合装配图构建RMAL-II平衡约束,包括工序加工顺序和分配约束、机器人分配约束、MPS产品的总装配时间约束等,表达式分别为
式(4)表示综合装配图中的工序加工顺序约束,式(5)表示综合装配图中的每个工序只能分配给1个工作站,式(6)表示每个工作站只能配置1个机器人,式(7)表示每个机器人只能分配给1个工作站,式(8)表示产品
2.3.3. RMAL-II排序约束
Li等 [ 20] 认为一旦机器人分配和工序分配约束明确,混流装配线排序问题就转变为置换流水车间调度问题. 本研究依据置换流水车间调度问题属性及其模型原理,建立RMAL-II排序约束如下.
式(9)、(10)分别表示MPS中产品和投产顺序的关系约束;式(11)表示MPS产品投产顺序中第
2.3.4. 关停策略触发条件
为了揭示关停策略对RMAL-II平衡和排序联合决策的影响,建立机器人关停策略触发条件如下.
式(17)表示1个MPS周期内各工作站最大工作时间. 式(18)表示1个MPS周期内的闲置时间. 当
2.3.5. 能源消耗的测度
给出1个MPS循环周期内,机器人在闲置过程、作业过程及整个MPS内总能耗测度方程如下.
式(20)表示
3. 改进的NSGA-II算法设计
3.1. 算法流程
结合研究问题的特征,基于经典的NSGA-II算法,设计改进的NSGA-II,求解RMAL-II平衡与排序联合决策问题. 本研究算法特点:设计多层编码方式表示决策问题的复杂解,并根据编码方式设计交叉和变异操作,引入邻域搜索机制扩大算法搜索能力,避免陷入局部最优,以提高算法性能.
3.2. 编码解码方式
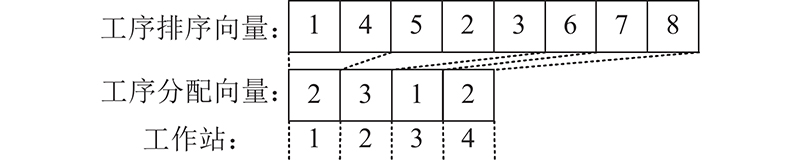
工序分配指将综合装配顺序图中的每道工序分配给每个工作站. 本研究采用工序排序向量和工序分配向量来共同实现工序分配,根据如 图1所示的综合装配顺序图生成的2个向量如 图2所示. 工序排序向量须满足综合装配顺序图中的工序先后顺序关系,为了保证初始产生可行的工序分配向量,初始化步骤如下. 1)根据综合装配顺序图生成优先关系矩阵(precedence relationship matrix,PRM),其为
图 1
图 2
图 2 工序排序向量、分配向量和工作站的关系
Fig.2 Relationship of process vector, allocation vector and workstation
机器人分配指每个工作站配置唯一工作的机器人. 本研究采用
MPS产品投产顺序指MPS周期内的所有产品投产顺序. 本研究采用MPS周期内产品的排序表示投产顺序,通过生成随机排序序列实现MPS产品投产顺序向量的初始化.
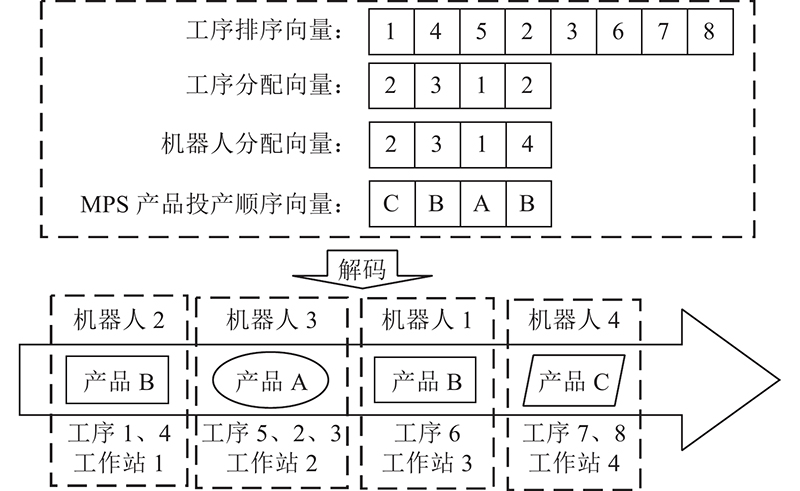
综上所述,本研究采用工序排序向量、工序分配向量共同表示工序分配方案,机器人分配向量表示机器人分配方案,MPS产品投产顺序向量表示产品投产顺序的方案,4个向量共同表征联合决策问题的解,编码向量与解码结果如 图3所示.
图 3
3.3. 交叉操作
图 4
图 5
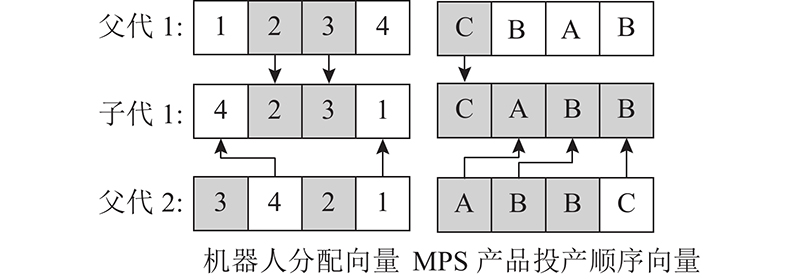
图 5 基于OX的机器人分配、MPS产品投产顺序向量交叉
Fig.5 Crossover of robot allocation vector, product sequence vector in MPS based on OX
3.4. 变异操作
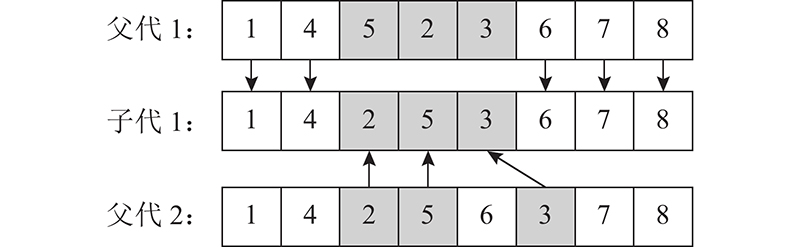
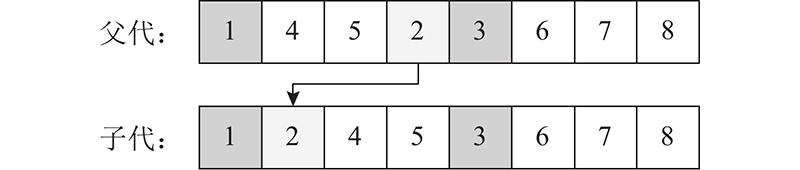
工序排序向量具有优先关系的限制,为了避免交叉操作产生不可行解,进行如 图6所示的变异操作:在随机选取工序的紧前工序和紧后工序之间随机移动,产生新的个体. 通过随机交换2个分量,实现工序分配、机器人分配和MPS产品投产顺序向量的变异.
图 6
3.5. 邻域搜索
设计邻域搜索增强算法的全局搜索能力,以维持种群基因的多样性.
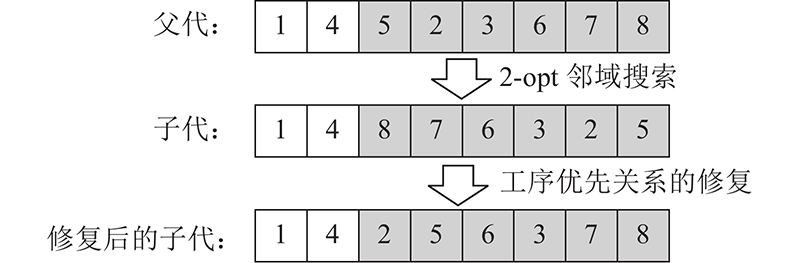
采用两分量优化(2-opt)对工序排序向量进行邻域搜索,即通过随机选择1个位置,反转该位置分量到最后1个分量, 如 图7所示. 该方法会使某些工序违背综合装配图中的工序优先关系,产生非可行解,为此采用以下修补步骤. 1)记工序总数为
图 7
将装配作业时间最长的工作站在工序分配向量中对应的值减少1,最短的加1,实现对于工序分配向量的邻域搜索. 机器人分配和MPS产品投产顺序向量通过随机选取并与相邻前1个分量交换,实现邻域搜索.
4. 算例分析
本研究算法程序在Matlab R2021a编写,运行环境为Intel(R) Core (TM) i5-8250U CPU @ 1.60 GHz 1.80 GHz.
4.1. 基准算例生成
表 1 基准算例数据表(部分)
Tab.1
| | | | | |
| 1 | 19 | 3 | 3 | 1,1,1 |
| 2 | 19 | 3 | 3 | 3,2,1 |
| 3 | 19 | 3 | 4 | 1,1,1 |
| 4 | 19 | 3 | 4 | 3,2,1 |
| 5 | 61 | 4 | 5 | 1,1,1,1 |
| 6 | 61 | 4 | 5 | 1,3,4,5 |
| 7 | 61 | 4 | 7 | 1,1,1,1 |
| 8 | 61 | 4 | 7 | 1,3,4,5 |
| 9 | 61 | 4 | 10 | 1,1,1,1 |
| 10 | 61 | 4 | 10 | 1,3,4,5 |
| 11 | 111 | 5 | 9 | 1,1,1,1,1 |
| 12 | 111 | 5 | 9 | 1,2,4,5,8 |
| 13 | 111 | 5 | 9 | 5,3,2,1,1 |
| 14 | 111 | 5 | 9 | 1,4,8,3,1 |
| 15 | 111 | 5 | 13 | 1,1,1,1,1 |
| 16 | 111 | 5 | 13 | 1,2,4,5,8 |
| 17 | 111 | 5 | 13 | 5,3,2,1,1 |
| 18 | 111 | 5 | 13 | 1,4,8,3,1 |
| 19 | 111 | 5 | 15 | 1,1,1,1,1 |
| 20 | 111 | 5 | 15 | 1,2,4,5,8 |
产品工序在不同机器人上的作业时间在[0.8 t, 1.2 t]随机生成, t为标准算例工序作业时间. 机器人能源消耗水平参照文献[ 12],机器人工作功率在[2.0, 5.0]随机生成,待机功率为工作功率的10%. 为了便于观测和比较,将大规模(
在RMAL-II平衡和排序问题中要考虑产品切换和机器人关停策略,为此假定:不同的2个产品切换准备时间在[1.0, 2.0]随机生成,产品切换的单位时间能耗在[2.0, 3.0]随机生成. 鉴于混流装配线相继生产2种相同产品时,不需要产品切换准备作业,视同种产品之间切换所需的时间和能耗为0. 机器人开关机能耗在[4.0, 6.0]随机生成.
4.2. 模型和算法的验证
4.2.1. 算法参数设置
采用Taguchi试验 [ 24] 设计NSGA-Ⅱ参数. 采用算例20,细分4个参数和4个因素水平,选用正交表
式中: n( n=10)为每个参数组合下重复运行的次数,
表 2 响应变量均值和显著性等级排序
Tab.2
| 水平 | | | | |
| 1 | 0.04 | 0.45 | 0.22 | 1.09 |
| 2 | 0.49 | 0.74 | 0.69 | 0.65 |
| 3 | 0.20 | 0.80 | 0.78 | 0.25 |
| 4 | 1.76 | 0.51 | 0.80 | 0.51 |
| | 1.72 | 0.36 | 0.58 | 0.85 |
| | 1.00 | 4.00 | 3.00 | 2.00 |
4.2.2. 算法有效性验证
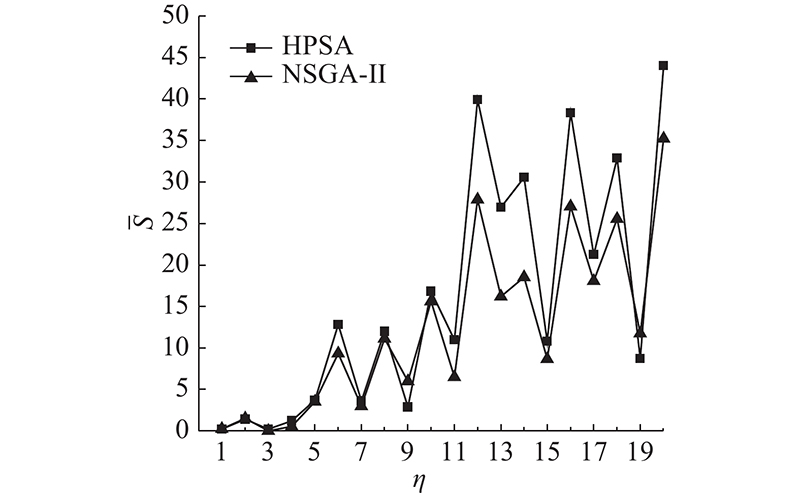
从算法的搜索能力、解的收敛性、解的分布性、算法时间复杂度4个方面,分别以非支配解的数量
表 3 基准算例下NSGA-II、HPSA性能指标均值
Tab.3
| | | | | | |||||||
| HPSA | NSGA-II | (HPSA, NSGA-II) | (NSGA-II, HPSA) | HPSA | NSGA-II | HPSA | NSGA-II | ||||
| 1 | 13.50 | 13.20 | 0.46 | 0.37 | 0.25 | 0.27 | 46.29 | 19.09 | |||
| 2 | 7.40 | 3.70 | 0.56 | 0.29 | 1.41 | 1.53 | 53.09 | 26.87 | |||
| 3 | 3.20 | 2.90 | 0.63 | 0.19 | 0.24 | 0.03 | 42.51 | 26.23 | |||
| 4 | 14.80 | 13.70 | 0.51 | 0.30 | 1.24 | 0.56 | 42.32 | 27.56 | |||
| 5 | 11.20 | 15.80 | 0.23 | 0.42 | 3.72 | 3.54 | 90.45 | 48.91 | |||
| 6 | 45.00 | 55.80 | 0.17 | 0.59 | 12.85 | 9.35 | 89.65 | 47.45 | |||
| 7 | 35.30 | 54.40 | 0.21 | 0.56 | 3.62 | 2.99 | 98.87 | 47.19 | |||
| 8 | 31.80 | 61.40 | 0.13 | 0.65 | 12.01 | 11.15 | 99.74 | 48.34 | |||
| 9 | 15.60 | 15.10 | 0.28 | 0.44 | 2.90 | 5.99 | 118.65 | 57.62 | |||
| 10 | 23.80 | 29.00 | 0.20 | 0.45 | 16.84 | 15.62 | 119.83 | 56.50 | |||
| 11 | 32.90 | 50.40 | 0.21 | 0.58 | 10.99 | 6.51 | 205.42 | 119.77 | |||
| 12 | 31.70 | 63.90 | 0.10 | 0.55 | 39.93 | 27.88 | 186.05 | 123.80 | |||
| 13 | 39.10 | 76.10 | 0.13 | 0.63 | 26.95 | 16.22 | 183.14 | 120.85 | |||
| 14 | 34.50 | 79.50 | 0.12 | 0.57 | 30.55 | 18.55 | 184.47 | 122.53 | |||
| 15 | 22.40 | 21.60 | 0.24 | 0.34 | 10.79 | 8.69 | 196.36 | 130.17 | |||
| 16 | 24.80 | 42.60 | 0.15 | 0.58 | 38.35 | 27.07 | 202.19 | 130.60 | |||
| 17 | 27.20 | 34.80 | 0.07 | 0.67 | 21.25 | 18.09 | 199.51 | 127.65 | |||
| 18 | 25.60 | 53.50 | 0.15 | 0.65 | 32.87 | 25.56 | 202.00 | 129.96 | |||
| 19 | 18.70 | 22.30 | 0.16 | 0.43 | 8.75 | 11.78 | 202.06 | 132.87 | |||
| 20 | 21.50 | 42.50 | 0.25 | 0.45 | 44.03 | 35.24 | 211.06 | 133.63 | |||
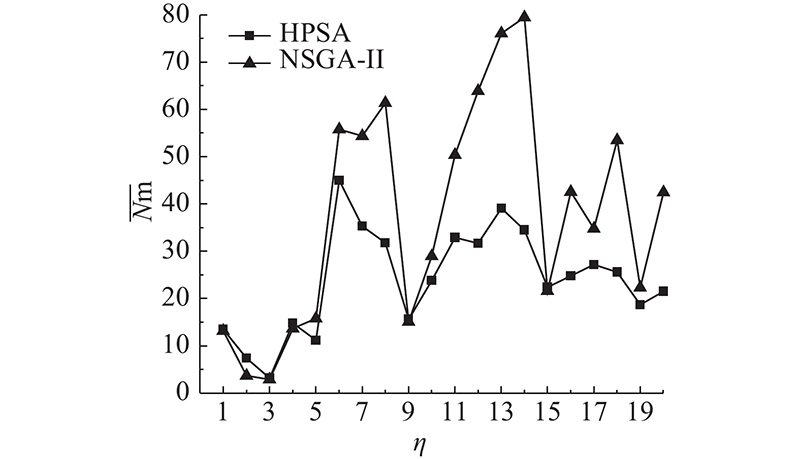
算法求得的非支配解数量越多,为决策者提供的选择方案越丰富,算法则更具优势. 如 图8所示为不同算例下NSGA-II、HPSA的
图 8
图 8 基准算例下算法求得的平均非支配解数量
Fig.8 Average number of non-dominated solutions of algorithms under benchmark data
图 9
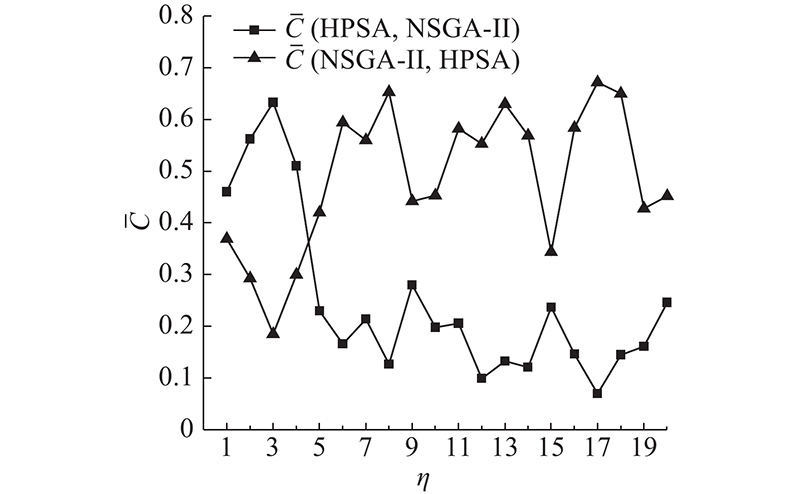
图 9 基准算例下算法的平均覆盖率
Fig.9 Average coverage rate of algorithms under benchmark data
图 10
图 11
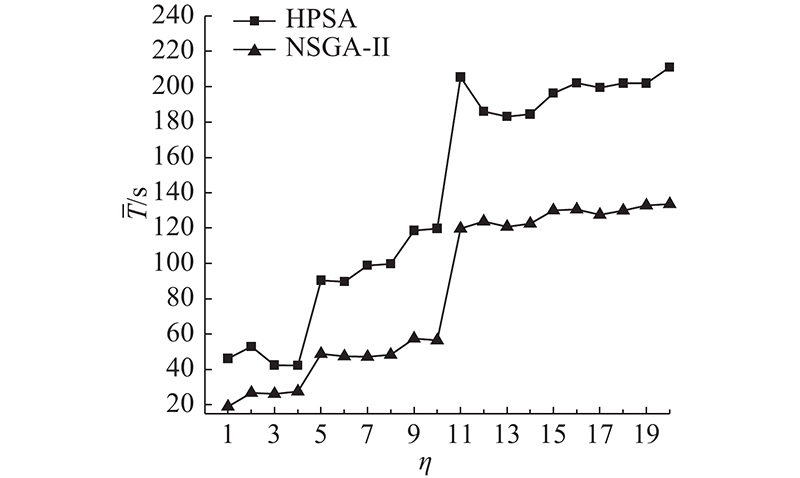
图 11 基准算例下算法的平均运行时间
Fig.11 Average run time of algorithms under benchmark data
综上所述,除在小规模算例下HPSA收敛性优于NSGA-II、搜索能力和分布性相近外;在小、中、大规模算例下,NSGA-II的搜索能力、解的收敛性、解的分布性、算法时间复杂度均优于HPSA. 因此,整体而言NSGA-II优于HPSA,NSGA-II具有一定的有效性.
4.2.3. 关停策略对RMAL-II平衡与排序联合决策的影响分析
以能耗节约率
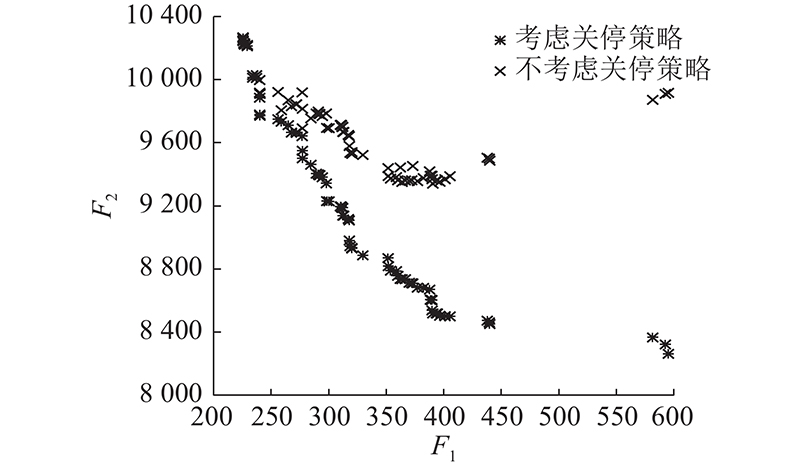
算例20 Pareto解的分布对比结果如 图12所示. 可知,关停策略均能够达成能源消耗节约目标. 不考虑关停策略时,得到的Pareto近似解已经不在Pareto前沿上,此时既不能实现节约能耗目标,也不能保障很好的生产效率. 考虑关停策略后,得到的Pareto前沿解增多,在一定程度上扩大了非支配解的解域,为决策者提供了更多选择方案,以根据自身的决策偏好选择最合适的解.
图 12
图 12 有无关停策略的Pareto解的分布
Fig.12 Distribution of Pareto solution with and without shutdown strategy
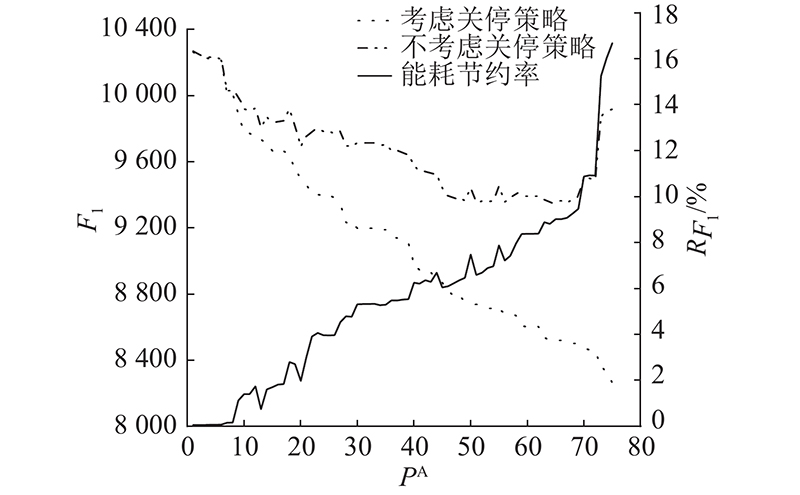
如 图13所示,当Pareto解的 F 1较小,即解对应的装配线平衡性较好时,
图 13
图 13 有无关停策略的能耗节约率对比
Fig.13 Comparison of energy saving rate with and without shutdown strategy
4.2.4. 产品切换对RMAL-II平衡与排序联合决策的影响分析
基于算例2,对比无产品切换的方案1和有产品切换的方案2,分析产品种类切换对混流装配线时间效率、能源消耗的影响程度. 对比结果如 表4所示. 表中,
表 4 有无产品切换的能效优化对比
Tab.4
| P A | 方案1 | 方案2 | | |||||
| F 1 | F 2 | F 1 | F 2 | F 1 | F 2 | |||
| 1 | 20.30 | 141.53 | 16.68 | 131.67 | 17.83 | 6.97 | ||
| 2 | — | — | 16.72 | 131.61 | 17.63 | 7.01 | ||
| 3 | — | — | 16.90 | 131.38 | 16.74 | 7.17 | ||
| 4 | — | — | 16.92 | 130.81 | 16.64 | 7.57 | ||
| 5 | — | — | 17.05 | 130.22 | 16.00 | 7.99 | ||
| 平均值 | 20.30 | 141.53 | 16.86 | 131.14 | 16.97 | 7.34 | ||
5. 结 论
(1)本研究考虑能源消耗的RMAL-II平衡与排序联合决策问题,根据生产运作流程,界定了工业机器人5种工作状态,量化了不同状态下的机器人能源消耗,解决了工作状态变化时机器人能源消耗的测量标准;同时,提出关停策略主动管理能耗,实现了规划节能和运行节能的同步考量,为构造理论模型提供了基础.
(2)兼顾生产制造效率和低能耗双目标,构建了RMAL-II平衡与排序联合决策多目标优化模型,补充完善了平衡约束、排序约束、关停策略约束和能源消耗约束,将产品切换准备作业时间体现在2个相邻产品装配时间关系约束中. 通过算法对比和基准算例分析表明,设计改进的NSGA-II求解在大、中、小算例规模下均具有一定的有效性.
(3)通过对关停策略和产品切换准备对RMAL-II平衡和排序联合决策的影响分析有如下发现. 关停策略在一定程度上能够带来能耗的节约. 能耗节约的程度与装配线系统的平衡性负相关,即随着平衡性变差,闲置时间逐渐增加,关停策略带来的效益愈加明显. 在RMAL-II平衡与排序问题中考虑切换准备作业对能效优化是有效和必要的. 在本研究使用的算例下,最大工作时间 F 1平均降低16.97%,机器人能源消耗 F 2平均降低7.34%. 可见,考虑切换准备作业的影响,能够降低最大工作时间和机器人能源消耗.
(4)本研究验证分析基于标准算例,未来将尝试采用企业真实运行数据. 同时,工业机器人节能技术创新空间较少,本研究限于机器人关停策略对生产制造能效目标的影响分析,未来计划探索工业互联网环境下基于PROFIenergy技术的其他节能模式对机器人混流装配优化问题的贡献.
参考文献
A genetic algorithm for robotic assembly line balancing
[J].DOI:10.1016/j.ejor.2004.07.030 [本文引用: 1]
Minimizing energy consumption and cycle time in two-sided robotic assembly line systems using restarted simulated annealing algorithm
[J].DOI:10.1016/j.jclepro.2016.06.131 [本文引用: 1]
An efficient approach for type II robotic assembly line balancing problems
[J].DOI:10.1016/j.cie.2008.09.027 [本文引用: 3]
Type II robotic assembly line balancing problem: an evolution strategies algorithm
[J].DOI:10.1016/j.jmsy.2011.10.002 [本文引用: 1]
Analysis of the type II robotic mixed-model assembly line balancing problem
[J].DOI:10.1080/0305215X.2016.1230208
Multi-objective metaheuristics for solving a type II robotic mixed-model assembly line balancing problem
[J].DOI:10.1080/21681015.2015.1126656 [本文引用: 2]
Modelling and optimization of energy-efficient U-shaped robotic assembly line balancing problems
[J].
Mathematical model and grey wolf optimization for low-carbon and low-noise U-shaped robotic assembly line balancing problem
[J].DOI:10.1016/j.jclepro.2019.01.030 [本文引用: 2]
Balancing and sequencing problem of mixed-model U-shaped robotic assembly line: mathematical model and dragonfly algorithm based approach
[J].DOI:10.1016/j.asoc.2020.106739 [本文引用: 3]
Multi-objective cooperative co-evolutionary algorithm for minimizing carbon footprint and maximizing line efficiency in robotic assembly line systems
[J].DOI:10.1016/j.jclepro.2017.04.032 [本文引用: 1]
考虑能效的多机器人协同装配线平衡方法
[J].
Multi-robot cooperative assembly line balancing method based on energy efficiency
[J].
An investigation on minimizing cycle time and total energy consumption in robotic assembly line systems
[J].DOI:10.1016/j.jclepro.2014.11.041 [本文引用: 1]
A multi-objective cellular genetic algorithm for energy-oriented balancing and sequencing problem of mixed-model assembly line
[J].DOI:10.1016/j.jclepro.2019.118845 [本文引用: 3]
A framework to minimize total energy consumption and total tardiness on a single machine
[J].DOI:10.1080/19397030802257236 [本文引用: 1]
基于PROFINET的节能技术PROFIenergy——节能技术新趋势
[J].DOI:10.3969/j.issn.1672-5611.2010.06.011 [本文引用: 1]
Energy-saving technology PROFIenergy based on PROFINET new trend of energy-saving technology
[J].DOI:10.3969/j.issn.1672-5611.2010.06.011 [本文引用: 1]
Mathematical model and metaheuristics for simultaneous balancing and sequencing of a robotic mixed-model assembly line
[J].DOI:10.1080/0305215X.2017.1351963 [本文引用: 1]
Genetic algorithm for assembly line balancing
[J].
Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach
[J].DOI:10.1109/4235.797969 [本文引用: 1]