(4) $ \begin{split} {A}_{i}\left({\boldsymbol{u}}\right)=&\Delta {Z}_{i-1}\left(\boldsymbol{u},{\boldsymbol{\xi }}_{i-1}^{i}\right)+{\tilde{A}}_{i-1}\left(w\left(\boldsymbol{u},{\boldsymbol{\xi }}_{i-1}^{i}\right)\right)\approx \\ &\Delta {Z}_{i-1}\left(\boldsymbol{u},{\boldsymbol{\xi }}_{i-1}^{i}\right)+\sum _{k=1}^{i-1}\mathrm{\Delta }{Z}_{k}\left(w\left(\boldsymbol{u},{\boldsymbol{\xi }}_{k+1}^{i-1}\right),{\boldsymbol{\xi }}_{k}^{k+1}\right).\end{split} $
[1]
FISCHLER M A, BOLLES R C Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography
[J]. Communications of the ACM , 1981 , 24 (6 ): 381 - 395
DOI:10.1145/358669.358692
[本文引用: 1]
[2]
TRIGGS B, MCLAUCHLAN P F, HARTLEY R I, et al. Bundle adjustment: a modern synthesis [M]// TRIGGS B, ZISSERMAN A, SZELISKI R. Vision algorithms: theory and practice . [S. l.]: Springer, 1999: 298-372.
[本文引用: 1]
[3]
高成强, 张云洲, 王晓哲, 等 面向室内动态环境的半直接法RGB-D SLAM算法
[J]. 机器人 , 2019 , 41 (3 ): 372 - 383
[本文引用: 3]
GAO Cheng-qiang, ZHANG Yun-zhou, WANG Xiao-zhe, et al Semi-direct RGB-D SLAM algorithm for dynamic indoor environments
[J]. Robot , 2019 , 41 (3 ): 372 - 383
[本文引用: 3]
[4]
SUN Y, LIU M, MENG M Q H Improving RGB-D SLAM in dynamic environments: a motion removal approach
[J]. Robotics and Autonomous Systems , 2017 , 89 : 110 - 122
DOI:10.1016/j.robot.2016.11.012
[本文引用: 1]
[5]
魏彤, 李绪 动态环境下基于动态区域剔除的双目视觉SLAM算法
[J]. 机器人 , 2020 , 42 (3 ): 336 - 345
[本文引用: 1]
WEI Tong, LI Xu Binocular vision SLAM algorithm based on dynamic region elimination in dynamic environment
[J]. Robot , 2020 , 42 (3 ): 336 - 345
[本文引用: 1]
[6]
ZHONG F, WANG S, ZHANG Z, et al. Detect-SLAM: making object detection and SLAM mutually beneficial [C]// 2018 IEEE Winter Conference on Applications of Computer Vision. Lake Tahoe: IEEE, 2018: 1001-1010.
[本文引用: 4]
[7]
BESCOS B, FACIL J M, CIVERA J, et al DynaSLAM: tracking, mapping, and inpainting in dynamic scenes
[J]. IEEE Robotics and Automation Letters , 2018 , 3 (4 ): 4076 - 4083
DOI:10.1109/LRA.2018.2860039
[8]
YU C, LIU Z, LIU X, et al. DS-SLAM: a semantic visual SLAM towards dynamic environments [C]// 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems . Madrid: IEEE, 2018: 1168-1174.
[本文引用: 3]
[9]
YUAN X, CHEN S. SaD-SLAM: a visual SLAM based on semantic and depth information [C]// 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems . Las Vegas: IEEE, 2020: 4930-4935.
[本文引用: 1]
[10]
ZHANG T, ZHANG H, NAKAMURA Y, et al. FlowFusion: dynamic dense RGB-D SLAM based on optical flow [C]// 2020 IEEE International Conference on Robotics and Automation . Paris: IEEE, 2020: 7322-7328.
[本文引用: 1]
[11]
艾青林, 刘刚江, 徐巧宁 动态环境下基于改进几何与运动约束的机器人RGB-D SLAM算法
[J]. 机器人 , 2021 , 43 (2 ): 167 - 176
[本文引用: 5]
AI Qing-lin, LIU Gang-jiang, XU Qiao-ning An RGB-D SLAM algorithm for robot based on the improved geometric and motion constraints in dynamic environment
[J]. Robot , 2021 , 43 (2 ): 167 - 176
[本文引用: 5]
[12]
DAI W, ZHANG Y, LI P, et al RGB-D SLAM in dynamic environments using point correlations
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2020 , 44 (1 ): 373 - 389
[本文引用: 3]
[13]
LI S, LEE D RGB-D SLAM in dynamic environments using static point weighting
[J]. IEEE Robotics and Automation Letters , 2017 , 2 (4 ): 2263 - 2270
DOI:10.1109/LRA.2017.2724759
[本文引用: 5]
[14]
KIM H, KIM P, KIM H J. Moving object detection for visual odometry in a dynamic environment based on occlusion accumulation [C]// 2020 IEEE International Conference on Robotics and Automation . Paris: IEEE, 2020: 8658-8664.
[本文引用: 8]
[15]
MUR-ARTAL R, TARDOS J D ORB-SLAM2: an open-source SLAM system for monocular, stereo, and RGB-D cameras
[J]. IEEE Transactions on Robotics , 2017 , 33 (5 ): 1255 - 1262
DOI:10.1109/TRO.2017.2705103
[本文引用: 1]
[16]
胡泽周 Kinect深度传感器深度误差分析和修正方法的研究
[J]. 测绘通报 , 2019 , (Suppl.2 ): 239 - 241
[本文引用: 1]
HU Ze-zhou Research on depth error analysis and correction method of Kinect depth sensor
[J]. Bulletin of Surveying and Mapping , 2019 , (Suppl.2 ): 239 - 241
[本文引用: 1]
[17]
KERL C, STURM J, CREMERS D. Dense visual SLAM for RGB-D cameras [C]// 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems . Tokyo: IEEE, 2014: 2100-2106.
[本文引用: 1]
[18]
KUMMERLE R, GRISETTI G, STRASDAT H, et al. g2 o: a general framework for graph optimization [C]// 2011 IEEE International Conference on Robotics and Automation . Shanghai: IEEE, 2011: 3607-3013.
[本文引用: 1]
[19]
STURM J, ENGELHARD N, ENDRES F, et al. A benchmark for the evaluation of RGB-D SLAM systems [C]// 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems . Vilamoura-Algarve: IEEE, 2012: 573-580.
[本文引用: 3]
Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography
1
1981
... 视觉同步定位与建图(simultaneous localization and mapping,SLAM)作为智能机器人的底层技术之一被广泛关注.传统视觉SLAM系统无法区分动静态像素点,错误利用动态像素点将导致估计的相机位姿与真实位姿产生较大偏差. 当动态像素点较少时,系统可利用随机抽样一致性 [ 1 ] 、光束平差法 [ 2 ] 减小动态点的干扰;当动态像素点占图像中大部分区域时,上述方法失效. ...
1
... 视觉同步定位与建图(simultaneous localization and mapping,SLAM)作为智能机器人的底层技术之一被广泛关注.传统视觉SLAM系统无法区分动静态像素点,错误利用动态像素点将导致估计的相机位姿与真实位姿产生较大偏差. 当动态像素点较少时,系统可利用随机抽样一致性 [ 1 ] 、光束平差法 [ 2 ] 减小动态点的干扰;当动态像素点占图像中大部分区域时,上述方法失效. ...
面向室内动态环境的半直接法RGB-D SLAM算法
3
2019
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
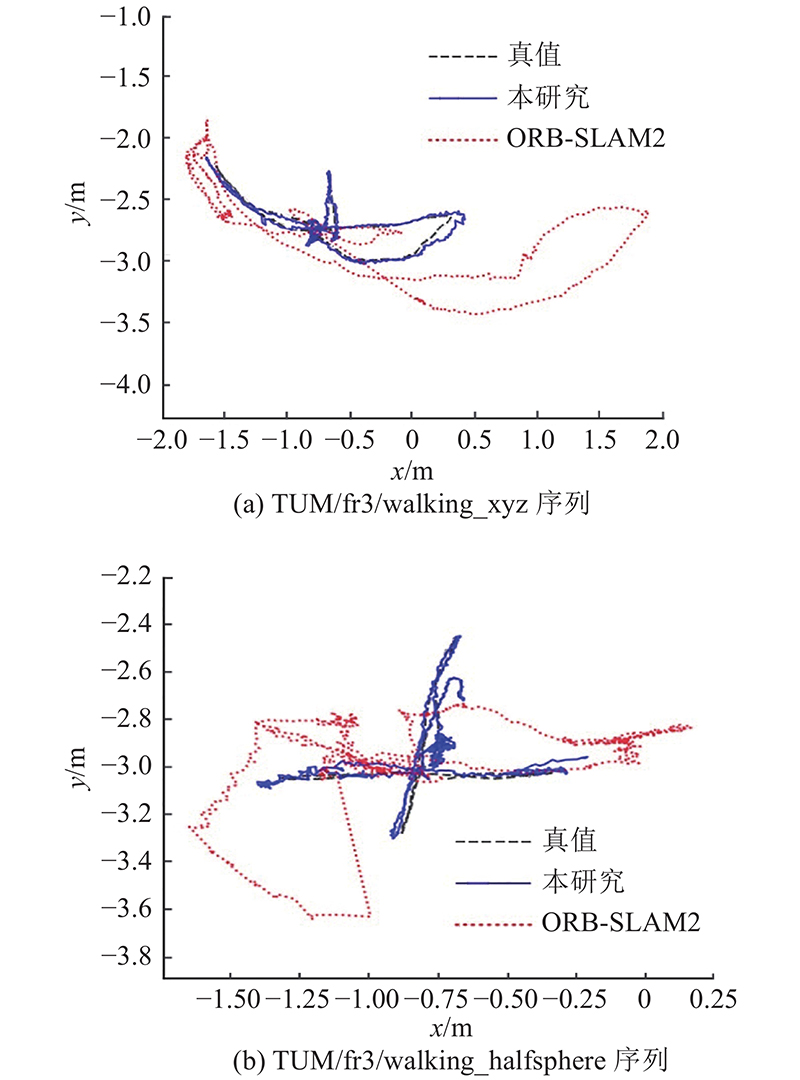
... 如 表3 所示,对本研究算法与先进的动态SLAM算法进行ATE对比. 表中,半直接法 [ 3 ] 为基于双单高斯模型动态检测的SLAM算法,Static-weight [ 13 ] 为基于深度边缘点静态概率的SLAM方法,Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 为基于深度学习动态检测的SLAM方法,改进几何与运动约束 [ 11 ] 、DSLAM [ 12 ] 利用运动一致性检测动态特征点. 除本研究算法外,表中结果均来自相关参考文献. 可知,带运动检测的SLAM算法都能适应动态场景问题,在低动态环境数据集“sitting”中,针对动态场景设计的各个算法都能有较好的轨迹估计结果. 在高度动态环境序列“walking_static”中,相机运动较小,RGB图像序列清晰,因此表中的对比方法在该序列中都能较好运行,得到的绝对轨迹误差相对较小. 在高度动态环境序列“walking_xyz”、“walking_halfsphere”和“walking_rpy”中,相机运动过快,图像运动模糊,导致特征点匹配困难,并且动态物体经常占据画面主要区域,使表中的算法出现较大的误差. 在“walking_rpy”序列中,半直接法甚至因图像运动模糊而造成跟踪失败,用“X”表示. 在“walking_xyz”序列中,由于动态目标比较完整,基于深度学习动态检测的Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... Comparison of ATE(RMSE) among different methods on TUM RGB-D datasets
m Tab.3 TUM_fr3序列 ATE 半直接法 [ 3 ] Detect-SLAM [ 6 ] DS-SLAM [ 8 ] 改进几何与运动约束 [ 11 ] DSLAM [ 12 ] Static-weight [ 13 ] 本研究 sitting_static — — 0.006 4 0.044 6 0.009 6 — 0.006 9 sitting_xyz 0.011 3 0.020 1 — 0.018 6 0.009 1 0.039 7 0.010 5 sitting_halfsphere 0.062 0 0.023 1 — 0.027 1 0.023 5 0.043 2 0.017 0 sitting_rpy — — — 0.038 5 0.022 5 — 0.026 1 walking_static 0.008 0 — 0.008 1 0.013 1 0.010 8 0.026 1 0.012 7 walking_xyz 0.037 1 0.024 1 0.024 7 0.035 4 0.087 4 0.060 1 0.054 4 walking_halfsphere 0.040 9 0.051 4 0.030 3 0.028 5 0.035 4 0.048 9 0.047 4 walking_rpy X 0.295 9 0.444 2 0.096 6 0.160 8 0.179 1 0.033 1 平均 X 0.082 9 0.102 7 0.037 8 0.044 9 0.066 2 0.026 0
3.5. 系统时间效率评估 如 表4 所示,为了衡量本研究算法的时间效率,分别测试低度动态“sitting_static”序列和高度动态“walking_static” 序列进行测试,对比本研究算法与ORB-SLAM2处理每帧图像的平均耗时 t ave . 可见,本研究算法的跟踪整体耗时较ORB-SLAM2更长,主要原因是动静态分割算法为稠密运算,耗费较多时间,导致实时性较差. 综合整体性能考虑,虽然本研究算方法的实时性表现较差,但在动态场景中的定位精度和鲁棒性较ORB-SLAM2更强. ...
面向室内动态环境的半直接法RGB-D SLAM算法
3
2019
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
... 如 表3 所示,对本研究算法与先进的动态SLAM算法进行ATE对比. 表中,半直接法 [ 3 ] 为基于双单高斯模型动态检测的SLAM算法,Static-weight [ 13 ] 为基于深度边缘点静态概率的SLAM方法,Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 为基于深度学习动态检测的SLAM方法,改进几何与运动约束 [ 11 ] 、DSLAM [ 12 ] 利用运动一致性检测动态特征点. 除本研究算法外,表中结果均来自相关参考文献. 可知,带运动检测的SLAM算法都能适应动态场景问题,在低动态环境数据集“sitting”中,针对动态场景设计的各个算法都能有较好的轨迹估计结果. 在高度动态环境序列“walking_static”中,相机运动较小,RGB图像序列清晰,因此表中的对比方法在该序列中都能较好运行,得到的绝对轨迹误差相对较小. 在高度动态环境序列“walking_xyz”、“walking_halfsphere”和“walking_rpy”中,相机运动过快,图像运动模糊,导致特征点匹配困难,并且动态物体经常占据画面主要区域,使表中的算法出现较大的误差. 在“walking_rpy”序列中,半直接法甚至因图像运动模糊而造成跟踪失败,用“X”表示. 在“walking_xyz”序列中,由于动态目标比较完整,基于深度学习动态检测的Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... Comparison of ATE(RMSE) among different methods on TUM RGB-D datasets
m Tab.3 TUM_fr3序列 ATE 半直接法 [ 3 ] Detect-SLAM [ 6 ] DS-SLAM [ 8 ] 改进几何与运动约束 [ 11 ] DSLAM [ 12 ] Static-weight [ 13 ] 本研究 sitting_static — — 0.006 4 0.044 6 0.009 6 — 0.006 9 sitting_xyz 0.011 3 0.020 1 — 0.018 6 0.009 1 0.039 7 0.010 5 sitting_halfsphere 0.062 0 0.023 1 — 0.027 1 0.023 5 0.043 2 0.017 0 sitting_rpy — — — 0.038 5 0.022 5 — 0.026 1 walking_static 0.008 0 — 0.008 1 0.013 1 0.010 8 0.026 1 0.012 7 walking_xyz 0.037 1 0.024 1 0.024 7 0.035 4 0.087 4 0.060 1 0.054 4 walking_halfsphere 0.040 9 0.051 4 0.030 3 0.028 5 0.035 4 0.048 9 0.047 4 walking_rpy X 0.295 9 0.444 2 0.096 6 0.160 8 0.179 1 0.033 1 平均 X 0.082 9 0.102 7 0.037 8 0.044 9 0.066 2 0.026 0
3.5. 系统时间效率评估 如 表4 所示,为了衡量本研究算法的时间效率,分别测试低度动态“sitting_static”序列和高度动态“walking_static” 序列进行测试,对比本研究算法与ORB-SLAM2处理每帧图像的平均耗时 t ave . 可见,本研究算法的跟踪整体耗时较ORB-SLAM2更长,主要原因是动静态分割算法为稠密运算,耗费较多时间,导致实时性较差. 综合整体性能考虑,虽然本研究算方法的实时性表现较差,但在动态场景中的定位精度和鲁棒性较ORB-SLAM2更强. ...
Improving RGB-D SLAM in dynamic environments: a motion removal approach
1
2017
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
动态环境下基于动态区域剔除的双目视觉SLAM算法
1
2020
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
动态环境下基于动态区域剔除的双目视觉SLAM算法
1
2020
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
4
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
... 如 表3 所示,对本研究算法与先进的动态SLAM算法进行ATE对比. 表中,半直接法 [ 3 ] 为基于双单高斯模型动态检测的SLAM算法,Static-weight [ 13 ] 为基于深度边缘点静态概率的SLAM方法,Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 为基于深度学习动态检测的SLAM方法,改进几何与运动约束 [ 11 ] 、DSLAM [ 12 ] 利用运动一致性检测动态特征点. 除本研究算法外,表中结果均来自相关参考文献. 可知,带运动检测的SLAM算法都能适应动态场景问题,在低动态环境数据集“sitting”中,针对动态场景设计的各个算法都能有较好的轨迹估计结果. 在高度动态环境序列“walking_static”中,相机运动较小,RGB图像序列清晰,因此表中的对比方法在该序列中都能较好运行,得到的绝对轨迹误差相对较小. 在高度动态环境序列“walking_xyz”、“walking_halfsphere”和“walking_rpy”中,相机运动过快,图像运动模糊,导致特征点匹配困难,并且动态物体经常占据画面主要区域,使表中的算法出现较大的误差. 在“walking_rpy”序列中,半直接法甚至因图像运动模糊而造成跟踪失败,用“X”表示. 在“walking_xyz”序列中,由于动态目标比较完整,基于深度学习动态检测的Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... Comparison of ATE(RMSE) among different methods on TUM RGB-D datasets
m Tab.3 TUM_fr3序列 ATE 半直接法 [ 3 ] Detect-SLAM [ 6 ] DS-SLAM [ 8 ] 改进几何与运动约束 [ 11 ] DSLAM [ 12 ] Static-weight [ 13 ] 本研究 sitting_static — — 0.006 4 0.044 6 0.009 6 — 0.006 9 sitting_xyz 0.011 3 0.020 1 — 0.018 6 0.009 1 0.039 7 0.010 5 sitting_halfsphere 0.062 0 0.023 1 — 0.027 1 0.023 5 0.043 2 0.017 0 sitting_rpy — — — 0.038 5 0.022 5 — 0.026 1 walking_static 0.008 0 — 0.008 1 0.013 1 0.010 8 0.026 1 0.012 7 walking_xyz 0.037 1 0.024 1 0.024 7 0.035 4 0.087 4 0.060 1 0.054 4 walking_halfsphere 0.040 9 0.051 4 0.030 3 0.028 5 0.035 4 0.048 9 0.047 4 walking_rpy X 0.295 9 0.444 2 0.096 6 0.160 8 0.179 1 0.033 1 平均 X 0.082 9 0.102 7 0.037 8 0.044 9 0.066 2 0.026 0
3.5. 系统时间效率评估 如 表4 所示,为了衡量本研究算法的时间效率,分别测试低度动态“sitting_static”序列和高度动态“walking_static” 序列进行测试,对比本研究算法与ORB-SLAM2处理每帧图像的平均耗时 t ave . 可见,本研究算法的跟踪整体耗时较ORB-SLAM2更长,主要原因是动静态分割算法为稠密运算,耗费较多时间,导致实时性较差. 综合整体性能考虑,虽然本研究算方法的实时性表现较差,但在动态场景中的定位精度和鲁棒性较ORB-SLAM2更强. ...
DynaSLAM: tracking, mapping, and inpainting in dynamic scenes
0
2018
3
... 如 表3 所示,对本研究算法与先进的动态SLAM算法进行ATE对比. 表中,半直接法 [ 3 ] 为基于双单高斯模型动态检测的SLAM算法,Static-weight [ 13 ] 为基于深度边缘点静态概率的SLAM方法,Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 为基于深度学习动态检测的SLAM方法,改进几何与运动约束 [ 11 ] 、DSLAM [ 12 ] 利用运动一致性检测动态特征点. 除本研究算法外,表中结果均来自相关参考文献. 可知,带运动检测的SLAM算法都能适应动态场景问题,在低动态环境数据集“sitting”中,针对动态场景设计的各个算法都能有较好的轨迹估计结果. 在高度动态环境序列“walking_static”中,相机运动较小,RGB图像序列清晰,因此表中的对比方法在该序列中都能较好运行,得到的绝对轨迹误差相对较小. 在高度动态环境序列“walking_xyz”、“walking_halfsphere”和“walking_rpy”中,相机运动过快,图像运动模糊,导致特征点匹配困难,并且动态物体经常占据画面主要区域,使表中的算法出现较大的误差. 在“walking_rpy”序列中,半直接法甚至因图像运动模糊而造成跟踪失败,用“X”表示. 在“walking_xyz”序列中,由于动态目标比较完整,基于深度学习动态检测的Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... Comparison of ATE(RMSE) among different methods on TUM RGB-D datasets
m Tab.3 TUM_fr3序列 ATE 半直接法 [ 3 ] Detect-SLAM [ 6 ] DS-SLAM [ 8 ] 改进几何与运动约束 [ 11 ] DSLAM [ 12 ] Static-weight [ 13 ] 本研究 sitting_static — — 0.006 4 0.044 6 0.009 6 — 0.006 9 sitting_xyz 0.011 3 0.020 1 — 0.018 6 0.009 1 0.039 7 0.010 5 sitting_halfsphere 0.062 0 0.023 1 — 0.027 1 0.023 5 0.043 2 0.017 0 sitting_rpy — — — 0.038 5 0.022 5 — 0.026 1 walking_static 0.008 0 — 0.008 1 0.013 1 0.010 8 0.026 1 0.012 7 walking_xyz 0.037 1 0.024 1 0.024 7 0.035 4 0.087 4 0.060 1 0.054 4 walking_halfsphere 0.040 9 0.051 4 0.030 3 0.028 5 0.035 4 0.048 9 0.047 4 walking_rpy X 0.295 9 0.444 2 0.096 6 0.160 8 0.179 1 0.033 1 平均 X 0.082 9 0.102 7 0.037 8 0.044 9 0.066 2 0.026 0
3.5. 系统时间效率评估 如 表4 所示,为了衡量本研究算法的时间效率,分别测试低度动态“sitting_static”序列和高度动态“walking_static” 序列进行测试,对比本研究算法与ORB-SLAM2处理每帧图像的平均耗时 t ave . 可见,本研究算法的跟踪整体耗时较ORB-SLAM2更长,主要原因是动静态分割算法为稠密运算,耗费较多时间,导致实时性较差. 综合整体性能考虑,虽然本研究算方法的实时性表现较差,但在动态场景中的定位精度和鲁棒性较ORB-SLAM2更强. ...
1
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
1
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
动态环境下基于改进几何与运动约束的机器人RGB-D SLAM算法
5
2021
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
... 如 表3 所示,对本研究算法与先进的动态SLAM算法进行ATE对比. 表中,半直接法 [ 3 ] 为基于双单高斯模型动态检测的SLAM算法,Static-weight [ 13 ] 为基于深度边缘点静态概率的SLAM方法,Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 为基于深度学习动态检测的SLAM方法,改进几何与运动约束 [ 11 ] 、DSLAM [ 12 ] 利用运动一致性检测动态特征点. 除本研究算法外,表中结果均来自相关参考文献. 可知,带运动检测的SLAM算法都能适应动态场景问题,在低动态环境数据集“sitting”中,针对动态场景设计的各个算法都能有较好的轨迹估计结果. 在高度动态环境序列“walking_static”中,相机运动较小,RGB图像序列清晰,因此表中的对比方法在该序列中都能较好运行,得到的绝对轨迹误差相对较小. 在高度动态环境序列“walking_xyz”、“walking_halfsphere”和“walking_rpy”中,相机运动过快,图像运动模糊,导致特征点匹配困难,并且动态物体经常占据画面主要区域,使表中的算法出现较大的误差. 在“walking_rpy”序列中,半直接法甚至因图像运动模糊而造成跟踪失败,用“X”表示. 在“walking_xyz”序列中,由于动态目标比较完整,基于深度学习动态检测的Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... Comparison of ATE(RMSE) among different methods on TUM RGB-D datasets
m Tab.3 TUM_fr3序列 ATE 半直接法 [ 3 ] Detect-SLAM [ 6 ] DS-SLAM [ 8 ] 改进几何与运动约束 [ 11 ] DSLAM [ 12 ] Static-weight [ 13 ] 本研究 sitting_static — — 0.006 4 0.044 6 0.009 6 — 0.006 9 sitting_xyz 0.011 3 0.020 1 — 0.018 6 0.009 1 0.039 7 0.010 5 sitting_halfsphere 0.062 0 0.023 1 — 0.027 1 0.023 5 0.043 2 0.017 0 sitting_rpy — — — 0.038 5 0.022 5 — 0.026 1 walking_static 0.008 0 — 0.008 1 0.013 1 0.010 8 0.026 1 0.012 7 walking_xyz 0.037 1 0.024 1 0.024 7 0.035 4 0.087 4 0.060 1 0.054 4 walking_halfsphere 0.040 9 0.051 4 0.030 3 0.028 5 0.035 4 0.048 9 0.047 4 walking_rpy X 0.295 9 0.444 2 0.096 6 0.160 8 0.179 1 0.033 1 平均 X 0.082 9 0.102 7 0.037 8 0.044 9 0.066 2 0.026 0
3.5. 系统时间效率评估 如 表4 所示,为了衡量本研究算法的时间效率,分别测试低度动态“sitting_static”序列和高度动态“walking_static” 序列进行测试,对比本研究算法与ORB-SLAM2处理每帧图像的平均耗时 t ave . 可见,本研究算法的跟踪整体耗时较ORB-SLAM2更长,主要原因是动静态分割算法为稠密运算,耗费较多时间,导致实时性较差. 综合整体性能考虑,虽然本研究算方法的实时性表现较差,但在动态场景中的定位精度和鲁棒性较ORB-SLAM2更强. ...
动态环境下基于改进几何与运动约束的机器人RGB-D SLAM算法
5
2021
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
... 如 表3 所示,对本研究算法与先进的动态SLAM算法进行ATE对比. 表中,半直接法 [ 3 ] 为基于双单高斯模型动态检测的SLAM算法,Static-weight [ 13 ] 为基于深度边缘点静态概率的SLAM方法,Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 为基于深度学习动态检测的SLAM方法,改进几何与运动约束 [ 11 ] 、DSLAM [ 12 ] 利用运动一致性检测动态特征点. 除本研究算法外,表中结果均来自相关参考文献. 可知,带运动检测的SLAM算法都能适应动态场景问题,在低动态环境数据集“sitting”中,针对动态场景设计的各个算法都能有较好的轨迹估计结果. 在高度动态环境序列“walking_static”中,相机运动较小,RGB图像序列清晰,因此表中的对比方法在该序列中都能较好运行,得到的绝对轨迹误差相对较小. 在高度动态环境序列“walking_xyz”、“walking_halfsphere”和“walking_rpy”中,相机运动过快,图像运动模糊,导致特征点匹配困难,并且动态物体经常占据画面主要区域,使表中的算法出现较大的误差. 在“walking_rpy”序列中,半直接法甚至因图像运动模糊而造成跟踪失败,用“X”表示. 在“walking_xyz”序列中,由于动态目标比较完整,基于深度学习动态检测的Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... Comparison of ATE(RMSE) among different methods on TUM RGB-D datasets
m Tab.3 TUM_fr3序列 ATE 半直接法 [ 3 ] Detect-SLAM [ 6 ] DS-SLAM [ 8 ] 改进几何与运动约束 [ 11 ] DSLAM [ 12 ] Static-weight [ 13 ] 本研究 sitting_static — — 0.006 4 0.044 6 0.009 6 — 0.006 9 sitting_xyz 0.011 3 0.020 1 — 0.018 6 0.009 1 0.039 7 0.010 5 sitting_halfsphere 0.062 0 0.023 1 — 0.027 1 0.023 5 0.043 2 0.017 0 sitting_rpy — — — 0.038 5 0.022 5 — 0.026 1 walking_static 0.008 0 — 0.008 1 0.013 1 0.010 8 0.026 1 0.012 7 walking_xyz 0.037 1 0.024 1 0.024 7 0.035 4 0.087 4 0.060 1 0.054 4 walking_halfsphere 0.040 9 0.051 4 0.030 3 0.028 5 0.035 4 0.048 9 0.047 4 walking_rpy X 0.295 9 0.444 2 0.096 6 0.160 8 0.179 1 0.033 1 平均 X 0.082 9 0.102 7 0.037 8 0.044 9 0.066 2 0.026 0
3.5. 系统时间效率评估 如 表4 所示,为了衡量本研究算法的时间效率,分别测试低度动态“sitting_static”序列和高度动态“walking_static” 序列进行测试,对比本研究算法与ORB-SLAM2处理每帧图像的平均耗时 t ave . 可见,本研究算法的跟踪整体耗时较ORB-SLAM2更长,主要原因是动静态分割算法为稠密运算,耗费较多时间,导致实时性较差. 综合整体性能考虑,虽然本研究算方法的实时性表现较差,但在动态场景中的定位精度和鲁棒性较ORB-SLAM2更强. ...
RGB-D SLAM in dynamic environments using point correlations
3
2020
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
... 如 表3 所示,对本研究算法与先进的动态SLAM算法进行ATE对比. 表中,半直接法 [ 3 ] 为基于双单高斯模型动态检测的SLAM算法,Static-weight [ 13 ] 为基于深度边缘点静态概率的SLAM方法,Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 为基于深度学习动态检测的SLAM方法,改进几何与运动约束 [ 11 ] 、DSLAM [ 12 ] 利用运动一致性检测动态特征点. 除本研究算法外,表中结果均来自相关参考文献. 可知,带运动检测的SLAM算法都能适应动态场景问题,在低动态环境数据集“sitting”中,针对动态场景设计的各个算法都能有较好的轨迹估计结果. 在高度动态环境序列“walking_static”中,相机运动较小,RGB图像序列清晰,因此表中的对比方法在该序列中都能较好运行,得到的绝对轨迹误差相对较小. 在高度动态环境序列“walking_xyz”、“walking_halfsphere”和“walking_rpy”中,相机运动过快,图像运动模糊,导致特征点匹配困难,并且动态物体经常占据画面主要区域,使表中的算法出现较大的误差. 在“walking_rpy”序列中,半直接法甚至因图像运动模糊而造成跟踪失败,用“X”表示. 在“walking_xyz”序列中,由于动态目标比较完整,基于深度学习动态检测的Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... Comparison of ATE(RMSE) among different methods on TUM RGB-D datasets
m Tab.3 TUM_fr3序列 ATE 半直接法 [ 3 ] Detect-SLAM [ 6 ] DS-SLAM [ 8 ] 改进几何与运动约束 [ 11 ] DSLAM [ 12 ] Static-weight [ 13 ] 本研究 sitting_static — — 0.006 4 0.044 6 0.009 6 — 0.006 9 sitting_xyz 0.011 3 0.020 1 — 0.018 6 0.009 1 0.039 7 0.010 5 sitting_halfsphere 0.062 0 0.023 1 — 0.027 1 0.023 5 0.043 2 0.017 0 sitting_rpy — — — 0.038 5 0.022 5 — 0.026 1 walking_static 0.008 0 — 0.008 1 0.013 1 0.010 8 0.026 1 0.012 7 walking_xyz 0.037 1 0.024 1 0.024 7 0.035 4 0.087 4 0.060 1 0.054 4 walking_halfsphere 0.040 9 0.051 4 0.030 3 0.028 5 0.035 4 0.048 9 0.047 4 walking_rpy X 0.295 9 0.444 2 0.096 6 0.160 8 0.179 1 0.033 1 平均 X 0.082 9 0.102 7 0.037 8 0.044 9 0.066 2 0.026 0
3.5. 系统时间效率评估 如 表4 所示,为了衡量本研究算法的时间效率,分别测试低度动态“sitting_static”序列和高度动态“walking_static” 序列进行测试,对比本研究算法与ORB-SLAM2处理每帧图像的平均耗时 t ave . 可见,本研究算法的跟踪整体耗时较ORB-SLAM2更长,主要原因是动静态分割算法为稠密运算,耗费较多时间,导致实时性较差. 综合整体性能考虑,虽然本研究算方法的实时性表现较差,但在动态场景中的定位精度和鲁棒性较ORB-SLAM2更强. ...
RGB-D SLAM in dynamic environments using static point weighting
5
2017
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
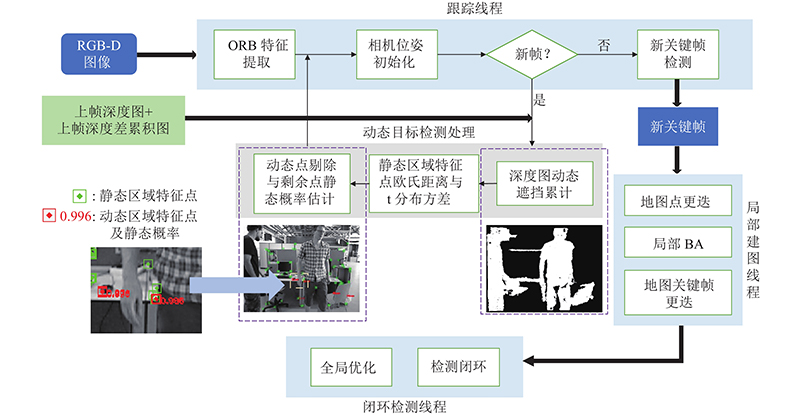
... 本研究基于ORB-SLAM2开源算法 [ 15 ] ,利用重投影深度差累积图 [ 14 ] 分割场景动静态区域.类似于深度边缘点静态概率方法 [ 13 ] ,计算动态区域特征点与匹配地图点的欧氏距离,以此对特征点进行剔除和静态概率估计.将静态区域特征点和动态区域特征点以不同权重加入位姿优化. ...
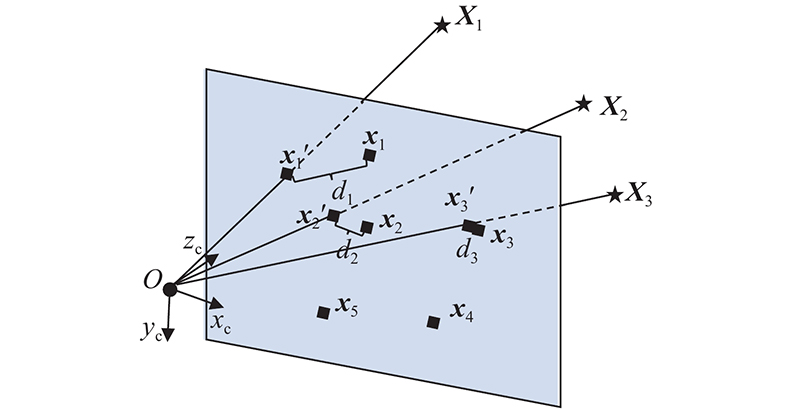
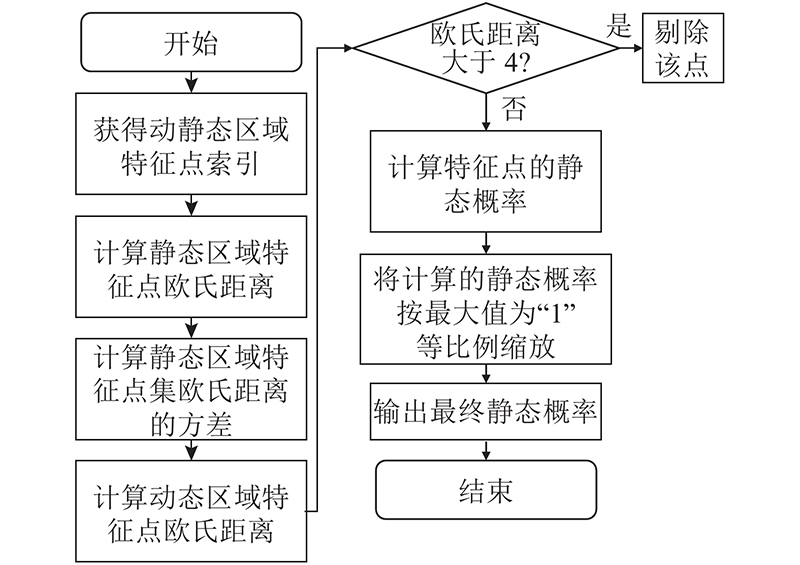
... 式中: $ {d}_{i} $ [ 17 ] . 不同于文献[ 13 ]的方法中点云的欧氏距离,本研究通过PnP(perspective-n-point)计算匹配点对的欧氏距离,估计动态区域特征点的静态概率: ...
... 如 表3 所示,对本研究算法与先进的动态SLAM算法进行ATE对比. 表中,半直接法 [ 3 ] 为基于双单高斯模型动态检测的SLAM算法,Static-weight [ 13 ] 为基于深度边缘点静态概率的SLAM方法,Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 为基于深度学习动态检测的SLAM方法,改进几何与运动约束 [ 11 ] 、DSLAM [ 12 ] 利用运动一致性检测动态特征点. 除本研究算法外,表中结果均来自相关参考文献. 可知,带运动检测的SLAM算法都能适应动态场景问题,在低动态环境数据集“sitting”中,针对动态场景设计的各个算法都能有较好的轨迹估计结果. 在高度动态环境序列“walking_static”中,相机运动较小,RGB图像序列清晰,因此表中的对比方法在该序列中都能较好运行,得到的绝对轨迹误差相对较小. 在高度动态环境序列“walking_xyz”、“walking_halfsphere”和“walking_rpy”中,相机运动过快,图像运动模糊,导致特征点匹配困难,并且动态物体经常占据画面主要区域,使表中的算法出现较大的误差. 在“walking_rpy”序列中,半直接法甚至因图像运动模糊而造成跟踪失败,用“X”表示. 在“walking_xyz”序列中,由于动态目标比较完整,基于深度学习动态检测的Detect-SLAM [ 6 ] 、DS-SLAM [ 8 ] 都能够准确分割动态目标,得到的绝对轨迹误差较低. 在“walking_halfsphere”序列中,动态目标经常占据图像大量区域,改进几何与运动约束方法 [ 11 ] 可以通过跟踪动态物体计算相机位姿,获得较低的绝对轨迹误差. 在“walking_rpy”序列中,场景中的物体离相机较远,图像的深度梯度变化明显,动静态区域分割结果较准. 得益于特征点静态概率估计算法,保留了足够静态特征点用于位姿估计,使得本研究算法的定位精度优于其他方法,较次最优方法的位姿精度提升65.7%. 虽然有时由于特征点匹配不足导致跟踪丢失,但算法在地图中保留静态点,也能迅速重定位并继续跟踪,整体鲁棒性较好. 本研究算法的鲁棒性较好,在表中的定位结果都比较准确,相比于对比算法中定位精度最高的改进几何与运动约束方法 [ 11 ] ,本研究算法的整体ATE精度提升31.2%,提升效果比较明显. ...
... Comparison of ATE(RMSE) among different methods on TUM RGB-D datasets
m Tab.3 TUM_fr3序列 ATE 半直接法 [ 3 ] Detect-SLAM [ 6 ] DS-SLAM [ 8 ] 改进几何与运动约束 [ 11 ] DSLAM [ 12 ] Static-weight [ 13 ] 本研究 sitting_static — — 0.006 4 0.044 6 0.009 6 — 0.006 9 sitting_xyz 0.011 3 0.020 1 — 0.018 6 0.009 1 0.039 7 0.010 5 sitting_halfsphere 0.062 0 0.023 1 — 0.027 1 0.023 5 0.043 2 0.017 0 sitting_rpy — — — 0.038 5 0.022 5 — 0.026 1 walking_static 0.008 0 — 0.008 1 0.013 1 0.010 8 0.026 1 0.012 7 walking_xyz 0.037 1 0.024 1 0.024 7 0.035 4 0.087 4 0.060 1 0.054 4 walking_halfsphere 0.040 9 0.051 4 0.030 3 0.028 5 0.035 4 0.048 9 0.047 4 walking_rpy X 0.295 9 0.444 2 0.096 6 0.160 8 0.179 1 0.033 1 平均 X 0.082 9 0.102 7 0.037 8 0.044 9 0.066 2 0.026 0
3.5. 系统时间效率评估 如 表4 所示,为了衡量本研究算法的时间效率,分别测试低度动态“sitting_static”序列和高度动态“walking_static” 序列进行测试,对比本研究算法与ORB-SLAM2处理每帧图像的平均耗时 t ave . 可见,本研究算法的跟踪整体耗时较ORB-SLAM2更长,主要原因是动静态分割算法为稠密运算,耗费较多时间,导致实时性较差. 综合整体性能考虑,虽然本研究算方法的实时性表现较差,但在动态场景中的定位精度和鲁棒性较ORB-SLAM2更强. ...
8
... 根据对动态区域的处理方式不同,动态场景下的SLAM算法主要分为2类. 1)对图像进行动静态区域分割,仅利用静态区域信息进行定位估计. 高成强等 [ 3 ] 构建基于图像块灰度值的双单高斯模型,根据方差变化分割动态目标. Sun等 [ 4 ] 利用帧间的像素强度差检测动态目标像素点,通过矢量量化深度图分割动态目标. 魏彤等 [ 5 ] 利用光流法和极线方程检测动态点,并通过超像素分割方法分割前景场景的动态目标. 上述方法基于图像几何算法分割动静态区域,分割结果不够准确,影响SLAM系统定位的准确性. 与传统图像几何方法检测动态目标相比,深度神经网络检测的动态目标更完整,SLAM系统的定位精度更高 [ 6 - 9 ] . 但深度神经网络只能检测特定动态目标,具有局限性,并且可能错误检测静止目标,导致静态特征点过少,降低SLAM系统定位的准确性. 2)考虑特征对相机位姿估计的影响,动静态建模分析图像特征. Zhang等 [ 10 ] 将图像强度和深度残差结合,通过最小化聚类的平均残差计算3D地图点簇的静态概率. 该方法涉及稠密光流计算,计算量较大,受光照影响较大. 艾青林等 [ 11 ] 利用几何和运动约束,将特征点分为多种状态,以不同权重进行相机位姿估计. 该方法静态点几何约束的阈值设置容易将微小运动识别为静态,使相机位姿估计不够准确. Dai等 [ 12 ] 提出基于点运动相关性的分割方法,将动态目标与静态场景分离,利用静态连通点及其关联边求解相机位姿. 该方法需要动态目标满足运动一致性假设,对非刚体动态目标的检测效果较差.使用RGB-D传感的导航任务,稠密的深度信息包含环境结构信息,不易受环境光照影响,有利于完整识别动态目标. Li等 [ 13 ] 提出基于关键帧深度边缘点的动态SLAM算法,利用迭代最近点算法计算当前帧地图点与目标地图点的欧氏距离,估计地图点的静态概率,减少动态地图点对位姿估计的影响. 该方法仅利用深度边缘点进行位姿估计,受深度传感器误差影响较大,位姿估计精度较低. Kim等 [ 14 ] 对相邻帧的深度差进行累积建模检测动态目标,剔除动态目标后利用DVO算法估计位姿. 该方法利用初步估计的位姿进行深度重投影,在相机快速运动和深度复杂场景中的动静态分割结果不准确,直接剔除动态目标信息将导致SLAM系统的精度和鲁棒性较差. ...
... 本研究基于ORB-SLAM2开源算法 [ 15 ] ,利用重投影深度差累积图 [ 14 ] 分割场景动静态区域.类似于深度边缘点静态概率方法 [ 13 ] ,计算动态区域特征点与匹配地图点的欧氏距离,以此对特征点进行剔除和静态概率估计.将静态区域特征点和动态区域特征点以不同权重加入位姿优化. ...
... 深度相机采集的场景深度具有丰富信息且不受光照影响,能够帮助检测动态目标. 本研究利用重投影深度累积图 [ 14 ] 对图像进行动静态分割:补全深度图缺失部分,计算相邻帧的深度差值,进行累积建模,预测图像中新场景的深度差累积值,并根据整体累积图分割图像的动静态区域. ...
... 利用深度累积图方法可以分割出图像中的动静态区域. 在完成动静态分割的基础上,文献[ 14 ]利用DVO算法进行位姿估计. 由于特征点法更加鲁棒,适用性更广,本研究将上述动静态区域分割方法与ORB-SLAM2结合. ...
... 选用LARR RGB-D动态数据集 [ 14 ] 和TUM RGB-D动态数据集 [ 19 ] 进行测试实验. LARR动态场景数据集按相机运动状态分为2类:“dynamic”序列中相机自运动、“static”序列中相机静止. 该数据集中的动态目标为board、man、constructed building,分别代表大尺寸纹理板、行人、建筑物模型,这些目标都占据场景的主要部分,为高度动态环境. ...
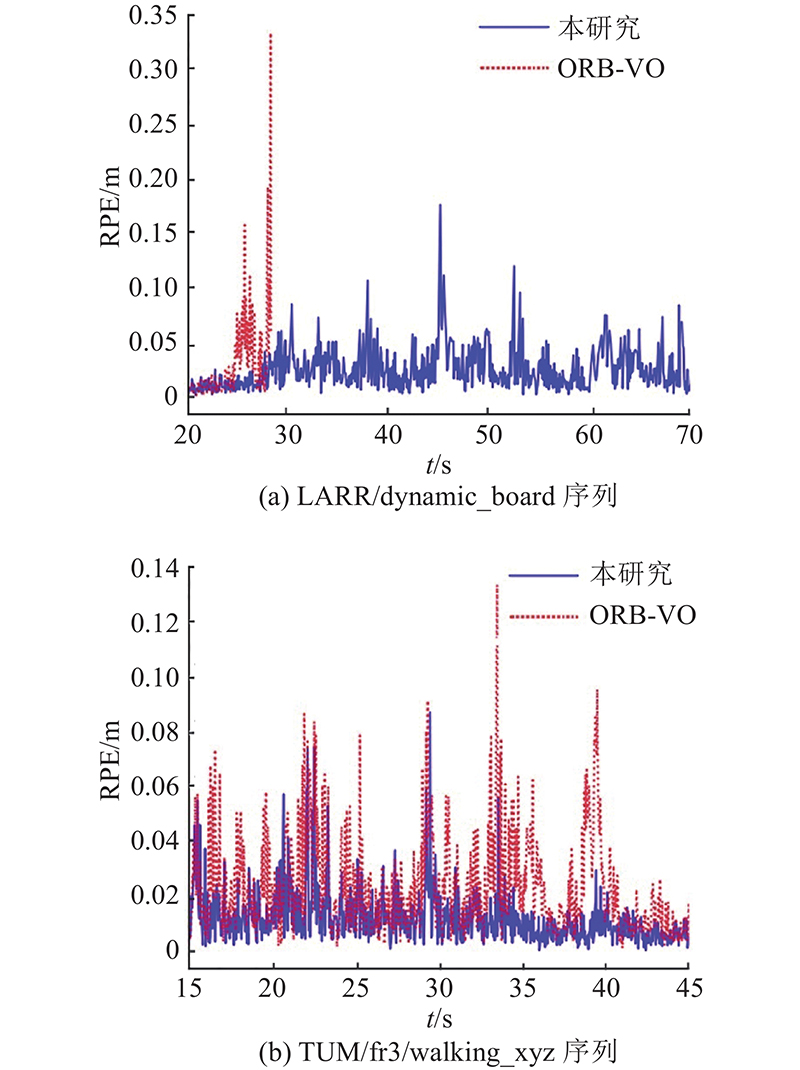
... 为了比较本研究算法相较于参考方法的定位精度提升效果,使用相对位姿误差(relative pose error,RPE) [ 19 ] 评估各自方法视觉里程计的定位精度. 利用LARR和TUM fr3数据集对基于深度遮挡累积动态点剔除的DVO [ 14 ] (eDVO)、ORB-SLAM2的视觉里程计(ORB-VO)、基于深度累积图动态点剔除的ORB-VO(eORB-VO)以及本研究特征点静态概率估计的视觉里程计进行对比实验. ...
... Comparison of RPE(RMSE) among different methods on LARR and TUM RGB-D datasets
Tab.1 序列 $R_{\rm{t}}$ −1 ) $R_{\rm{r}}$ −1 ) eDVO [ 14 ] ORB-VO eORB-VO 本研究 eDVO [ 14 ] ORB-VO eORB-VO 本研究 static_board 0.292 0.034 0.022 0.024 4.839 0.018 0.009 0.010 static_construct 0.153 0.033 0.003 0.003 3.821 0.017 0.001 0.001 dynamic_board 0.111 X 0.027 0.028 1.939 X 0.031 0.031 dynamic_man1 0.157 0.039 0.025 0.023 4.108 0.053 0.053 0.053 fr3/sitting_xyz 0.073 0.008 0.010 0.009 1.860 0.008 0.008 0.008 fr3/walking_static 0.217 0.016 0.013 0.012 0.197 0.008 0.006 0.006 fr3/walking_xyz 0.259 0.028 0.020 0.015 4.069 0.016 0.012 0.010
与eORB-VO相比,为了避免错误剔除特征点,本研究算法估计了动态区域特征点的静态概率. 在场景简单的LARR数据集中,动静态区域分割准确,直接剔除动态区域特征点有利于位姿估计,因此本研究算法较eORB-VO,平移RPE精度降低1.3%,旋转RPE精度降低1.1%. 在场景复杂的TUM/fr3数据集中,动静态区域分割不准确,本研究算法有效避免了错误剔除静态特征点,较动态点剔除方法,平移RPE精度提升16.3%,旋转RPE精度提升7.7%. 可见,本研究算法的鲁棒性更好. ...
... [
14 ]
ORB-VO eORB-VO 本研究 static_board 0.292 0.034 0.022 0.024 4.839 0.018 0.009 0.010 static_construct 0.153 0.033 0.003 0.003 3.821 0.017 0.001 0.001 dynamic_board 0.111 X 0.027 0.028 1.939 X 0.031 0.031 dynamic_man1 0.157 0.039 0.025 0.023 4.108 0.053 0.053 0.053 fr3/sitting_xyz 0.073 0.008 0.010 0.009 1.860 0.008 0.008 0.008 fr3/walking_static 0.217 0.016 0.013 0.012 0.197 0.008 0.006 0.006 fr3/walking_xyz 0.259 0.028 0.020 0.015 4.069 0.016 0.012 0.010 与eORB-VO相比,为了避免错误剔除特征点,本研究算法估计了动态区域特征点的静态概率. 在场景简单的LARR数据集中,动静态区域分割准确,直接剔除动态区域特征点有利于位姿估计,因此本研究算法较eORB-VO,平移RPE精度降低1.3%,旋转RPE精度降低1.1%. 在场景复杂的TUM/fr3数据集中,动静态区域分割不准确,本研究算法有效避免了错误剔除静态特征点,较动态点剔除方法,平移RPE精度提升16.3%,旋转RPE精度提升7.7%. 可见,本研究算法的鲁棒性更好. ...
ORB-SLAM2: an open-source SLAM system for monocular, stereo, and RGB-D cameras
1
2017
... 本研究基于ORB-SLAM2开源算法 [ 15 ] ,利用重投影深度差累积图 [ 14 ] 分割场景动静态区域.类似于深度边缘点静态概率方法 [ 13 ] ,计算动态区域特征点与匹配地图点的欧氏距离,以此对特征点进行剔除和静态概率估计.将静态区域特征点和动态区域特征点以不同权重加入位姿优化. ...
Kinect深度传感器深度误差分析和修正方法的研究
1
2019
... 式中: $ A_i ({\boldsymbol{u}}) $ i 帧的深度差累积图, $ {A}_{1}\left(\boldsymbol{u}\right) $ $ \boldsymbol{u} $ $(\forall \boldsymbol{u}\in \boldsymbol{\varOmega } )\; {A}_{1}\left(\boldsymbol{u}\right)=0,$ $ \boldsymbol{\varOmega } $ ${\tilde{A}}_{i-1}{({\boldsymbol{u}})}$ ${A}_{i-1}{{(\boldsymbol{u})}}$ $ k $ $ \boldsymbol{u} $ [ 16 ] . 为了避免深度测量误差累积影响深度遮挡结果,设置误差阈值 ...
Kinect深度传感器深度误差分析和修正方法的研究
1
2019
... 式中: $ A_i ({\boldsymbol{u}}) $ i 帧的深度差累积图, $ {A}_{1}\left(\boldsymbol{u}\right) $ $ \boldsymbol{u} $ $(\forall \boldsymbol{u}\in \boldsymbol{\varOmega } )\; {A}_{1}\left(\boldsymbol{u}\right)=0,$ $ \boldsymbol{\varOmega } $ ${\tilde{A}}_{i-1}{({\boldsymbol{u}})}$ ${A}_{i-1}{{(\boldsymbol{u})}}$ $ k $ $ \boldsymbol{u} $ [ 16 ] . 为了避免深度测量误差累积影响深度遮挡结果,设置误差阈值 ...
1
... 式中: $ {d}_{i} $ [ 17 ] . 不同于文献[ 13 ]的方法中点云的欧氏距离,本研究通过PnP(perspective-n-point)计算匹配点对的欧氏距离,估计动态区域特征点的静态概率: ...
1
... 式中: $ {w}_{i} $ [ 18 ] . ...
3
... 选用LARR RGB-D动态数据集 [ 14 ] 和TUM RGB-D动态数据集 [ 19 ] 进行测试实验. LARR动态场景数据集按相机运动状态分为2类:“dynamic”序列中相机自运动、“static”序列中相机静止. 该数据集中的动态目标为board、man、constructed building,分别代表大尺寸纹理板、行人、建筑物模型,这些目标都占据场景的主要部分,为高度动态环境. ...
... 为了比较本研究算法相较于参考方法的定位精度提升效果,使用相对位姿误差(relative pose error,RPE) [ 19 ] 评估各自方法视觉里程计的定位精度. 利用LARR和TUM fr3数据集对基于深度遮挡累积动态点剔除的DVO [ 14 ] (eDVO)、ORB-SLAM2的视觉里程计(ORB-VO)、基于深度累积图动态点剔除的ORB-VO(eORB-VO)以及本研究特征点静态概率估计的视觉里程计进行对比实验. ...
... 使用相机估计轨迹和真实轨迹间的绝对轨迹误差(absolute trajectory error,ATE) [ 19 ] ,评估视觉SLAM系统的性能. 为了探究本研究算法较经典ORB-SLAM2方法和ORB-SLAM2框架下剔除动态点方法(eORB-SLAM2)的定位效果的提升情况,如 表2 所示为各个方法在LARR和TUM fr3数据集中的ATE均方根值的对比结果. 可见,在低动态场景序列 “sitting”中,ORB-SLAM2算法利用光束法平差,将少量动态点判断为外点,得到较准确的运动轨迹. 但在LARR数据集和“walking”序列等高动态场景中,ORB-SLAM2受到动态目标影响,得到运动轨迹的ATE较大. 相比于ORB-SLAM2算法,本研究算法加入动态分割和特征点静态概率估计,显著提高算法在动态环境下的定位精度,整体绝对轨迹精度提升96.1%,精度提升效果明显. 在场景深度复杂的图像序列“fr3/walking”和“fr3/sitting”中,动态分割容易出现误检,直接剔除动态区域特征点导致定位精度较差. 本研究算法估计动态区域特征点静态概率,避免剔除静态特征点,提高了本研究算法的定位精度,较动态点剔除方法绝对轨迹精度提升74.4%,可见本研究算法更鲁棒. ...