改进的机器学习方式被应用于识别多类别、信号区分度低的任务,如改进随机森林(random forest, RF)[12]、改进支持向量机(support vector machine, SVM)[13]. 这些分类器不但极大依赖数据集的样本特征,而且学习速度较慢,难以应用于花键偏角CS的识别. 极限学习机(extreme learning machine, ELM)是单隐层前馈神经网络(single-hidden layer feedforward neural networks,SLFNs)学习算法,其网络结构包括输入层、隐藏层和输出层[14]. 虽然ELM具有网络结构简单、学习速度快的优点,但是其分类精度依赖自身参数. 研究者利用不同的启发式优化算法优化ELM的输入权重和隐藏层偏置以提高其分类精度,如粒子群算法(particle swarm optimization, PSO)[15]、遗传算法(genetic algorithm, GA)[16]、鲸鱼优化算法(whale optimization algorithm, WOA)[17]等. WOA的参数寻优能力优于PSO、GA[18],但是和其他启发式优化算法一样,WOA存在收敛速度慢、容易陷入局部最优的问题,从而影响偏角识别的精度和速度. 本研究提出基于参数优化的机器人偏角感知识别方法. 采用混合鲸鱼优化算法(hybrid WOA,HWOA)优化的ELM(WOA-ELM),识别多类别、信号区分度小的偏角CS. 引入混沌映射策略[19],及改进的对立学习策略,优化ELM的初始参数种群. 引入偏角经验库的概念和SVDD算法,实现偏角的在线感知. 通过偏角经验库的更新,使HWOA-ELM获得识别新偏角CS的能力.
1. 相关算法
1.1. 支持向量数据描述算法
花键轴孔装配过程中不同偏角的力/力矩信号存在差别,可以将力传感器采集力/力矩信号作为花键装配偏角的CS,表示为
式中:
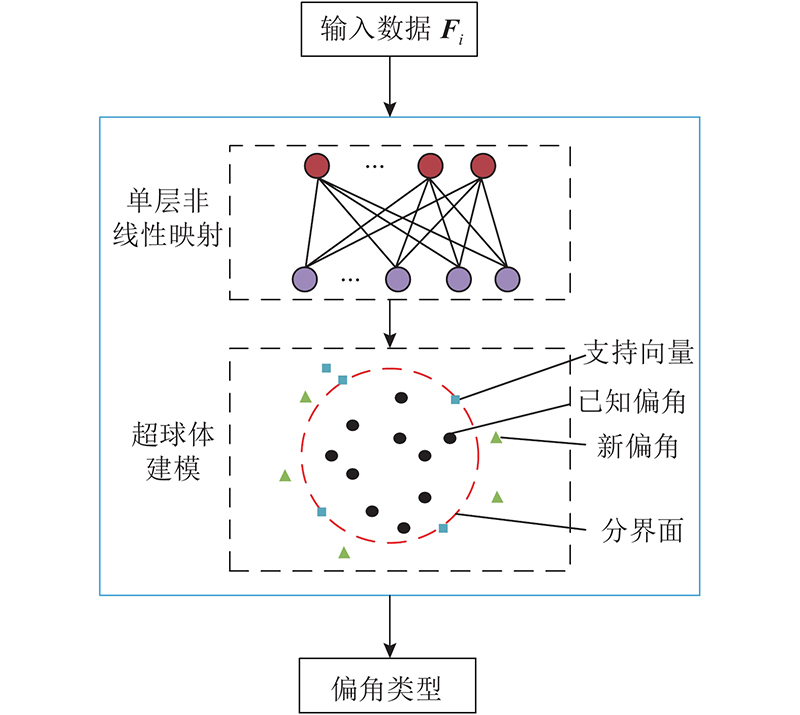
如图1所示,SVDD是单分类算法,其基本框架包括:单层非线性映射和超球体建模. SVDD将已知的非线性数据映射到高维特征空间,构建半径最小的超球体包围所有训练样本. 通过超球体可以判断,如果未定义偏角对应的信号距超球体球心的距离小于半径,则属于已知偏角;反之,则属于新偏角.
图 1
给定已知偏角的CS数据集
其中R为超球体半径,o为超球体中心,
式中:
式中:
1.2. 极限学习机
ELM是单隐层前馈神经网络算法,包含输入层、隐藏层和输出层. 采集I个已知偏角样本信号和对应标签
式中:
式中:P为隐藏层输出矩阵;
原始ELM的泛化性较差,须对ELM进行正则化优化以提高分类器的泛化性. 正则化ELM的误差公式和目标矩阵分别为
式中:C为正则化因子.
ELM的输入权重矩阵
1.3. 混合鲸鱼优化算法
1.3.1. 鲸鱼优化算法
WOA是由鲸鱼捕食行为而启发的优化算法,包括3个阶段:包围捕食、泡网攻击和猎物搜索.
在包围捕食阶段,WOA假定当前搜索到的参数个体
式中:t为当前迭代次数;
泡网攻击阶段包含收缩包围机制和螺旋更新机制,设定概率
式中:h为螺旋线形状参数,
猎物搜索阶段的
式中:
WOA的数学模型的表达式为
式中:
WOA在更新最佳参数时容易陷入局部最优,并且收敛速度较慢,需要进一步改进以增强其参数寻优的能力.
1.3.2. 初始参数种群优化策略
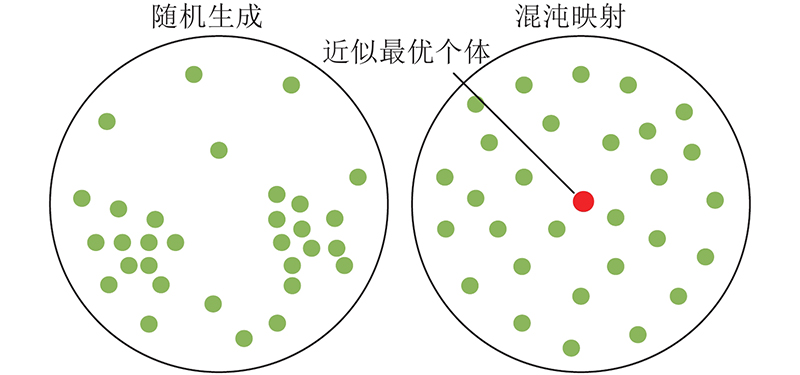
针对WOA容易陷入局部最优而导致收敛精度低的问题,引入混沌映射策略. 如图2所示,混沌映射能生成具有一定遍历性和普适性的初始参数种群,因此更容易产生具有近似最优的个体.
图 2
经过混沌映射策略优化后的初始参数个体定义为
式中:k为初始化参数个体的标号,
为了解决WOA收敛速度慢的问题,引入对立的学习策略[20]进一步优化初始参数种群. 对立的学习策略根据参数阈值:1)产生与初始参数种群个体数量一致的对立参数个体,2)利用适应度函数
为了避免对立的学习策略导致初始参数种群向对立种群过度迁移,引入小波变异方法[21]对适应度值低于平均适应度的参数个体执行适当的变异,增加ELM参数种群的丰富度,扩大WOA的全局搜索范围. 经过小波变异的参数个体为
式中:ϑ为变异因子,受迭代次数影响.
混合鲸鱼优化算法的具体步骤如下.
1)给定初始参数种群数量s和阈值
2)通过式(15)获得对立参数种群个体
3)根据适应度值选择最优的一半,形成新的参数初始种群.
4)计算平均适应度
5)将优化后的参数种群重新导入WOA,迭代后获得最佳参数个体.
2. 花键装配偏角感知识别方法
本研究提出的偏角感知识别方法由2个部分组成. 1)在离线状态下,利用机器人调整末端偏角以获得不同的花键轴线偏角,并进行装配实验,通过六维力传感器采集不同装配过程中的六维力信号,作为已知偏角的CS. 通过HWOA-ELM识别已知偏角的CS并建立X、Y轴偏角经验库. 2)在在线状态下,通过SVDD感知新采集的偏角,若属于已知偏角,则利用HWOA-ELM识别该偏角具体CS;若属于新偏角,则将该偏角CS作为新类加入偏角经验库,并更新HWOA-ELM,以便二次装配时能成功识别该偏角CS.
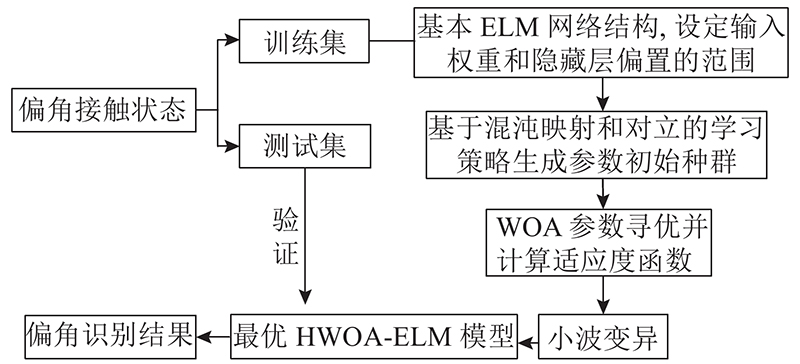
HWOA-ELM偏角识别流程如图3所示. 1)对采集的力信号进行滤波处理,将花键偏角的六维力信号按K折交叉验证法分成训练集和测试集;2)设定ELM的参数阈值,利用HWOA进行参数寻优以获得最优HWOA-ELM分类模型;3)通过测试集验证HWOA-ELM分类器的识别能力,得到偏角CS的识别结果.
图 3
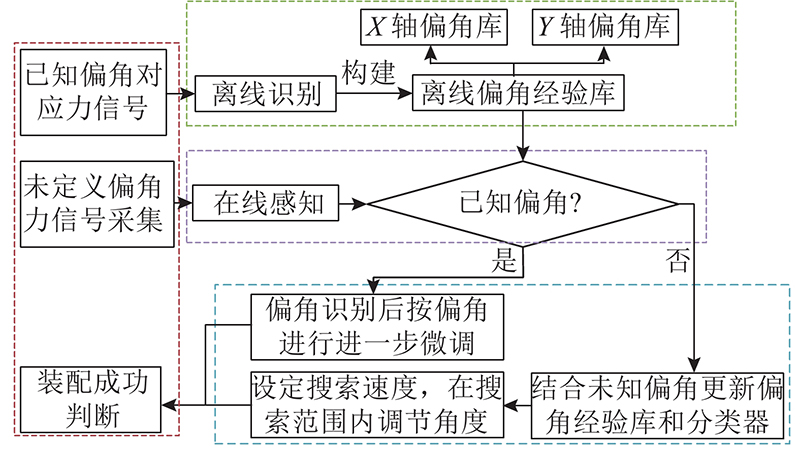
如图4所示,基于HWOA-ELM和SVDD算法的花键装配偏角感知识别方法流程包括4个模块:装配过程、偏角离线识别、偏角在线感知、装配动作反馈. 1)装配过程模块:利用六维力传感器采集多组花键装配时不同装配偏角的力信号,并能根据花键插入深度判断花键是否装配成功. 2)偏角离线识别模块:将采集到的偏角信号导入HWOA-ELM分类器中,识别已知偏角的CS;根据已知偏角CS构建在离线状态下X、Y轴的偏角经验库. 3)偏角在线感知模块:将已知偏角的CS经过数据降维后,通过SVDD算法,构建X、Y轴偏角的2个超球体模型. 在新采集的偏角导入超球体模型后,实时感知是否属于已知偏角. 若属于已知偏角,则通过偏角离线识别模块识别该偏角CS;若属于新偏角,则将该偏角CS加入偏角经验库中,并更新HWOA-ELM分类器,利用装配动作反馈模块进行调整. 4)装配动作反馈模块:能根据偏角感知识别的情况进行花键姿态调整. 若识别为已知偏角,则根据偏角调整相应度数;若感知为新偏角,则设定偏角调整步长,在搜索范围内进行多次装配尝试并重新感知识别每次获得的装配偏角,直至花键装配成功.
图 4
图 4 花键装配偏角感知识别方法流程
Fig.4 Deflection angle perception and recognition method process in spline assembly
3. 实验结果与分析
3.1. 机器人装配系统
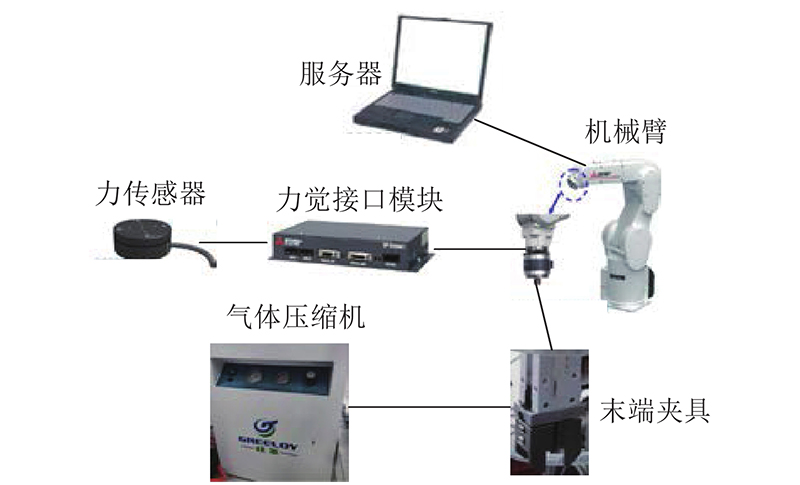
花键装配系统如图5所示,包括机器人本体、末端气动夹具、服务器和六维力传感器、气体压缩机等. 机器人本体为三菱RV-2F的六轴机械臂,其重复定位误差为
图 5
3.2. 花键装配偏角接触状态数据采集与处理
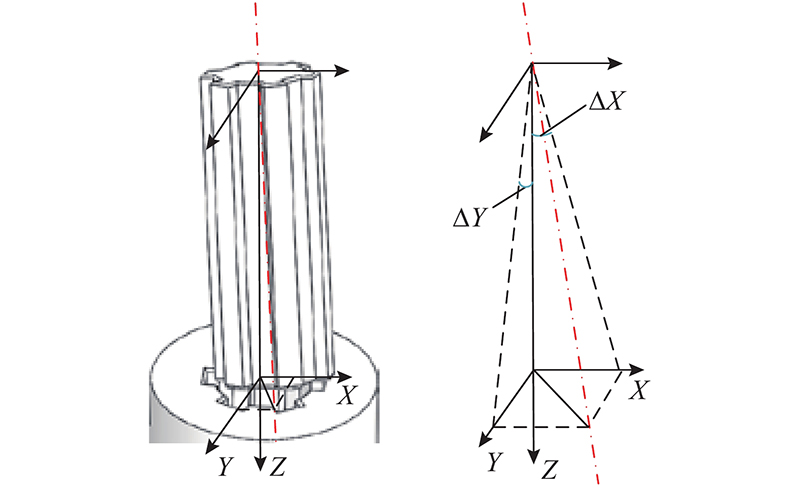
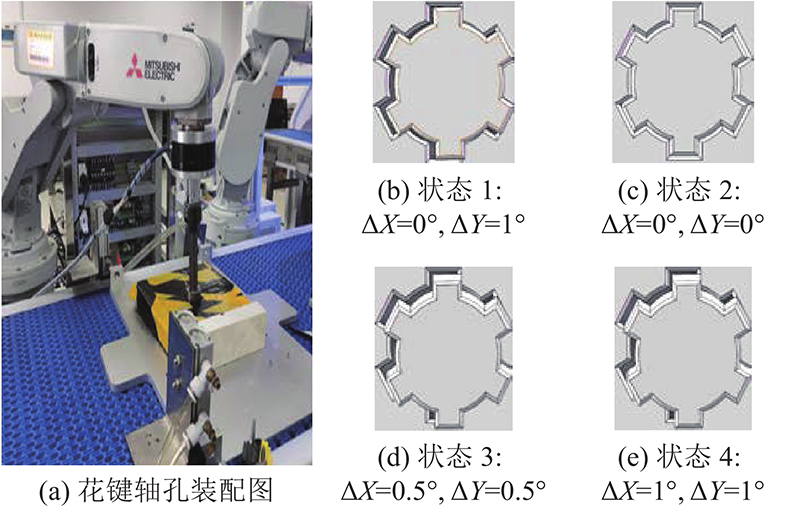
以六齿花键轴孔装配为例进行实验和分析. 在实际花键装配时,机器人末端夹持花键轴时容易产生偏差,导致花键装配的轴孔间的轴线无法重合,存在装配误差偏角,因此无法竖直装配. 此外,虽然机器人定位精度也会影响装配偏角,但对于夹持误差来说,机器人定位精度产生的影响可以忽略不计. 如图6所示,将装配过程中花键轴与花键套轴线间的误差偏角映射到XOZ和YOZ面上,获得X、Y轴上的偏角
图 6
图 7
图 7 花键轴孔装配与部分偏角接触状态俯视图
Fig.7 Spline shaft hole assembly and top view of partial assembly deflection angle contact state
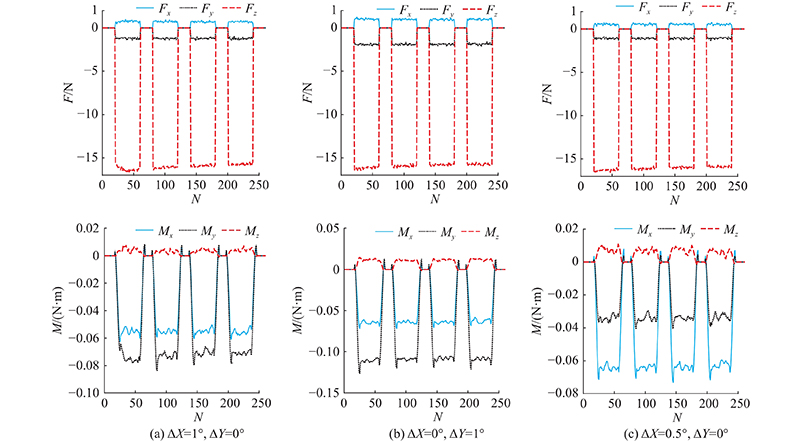
图 8
图 8 部分装配偏角接触状态对应六维力信号
Fig.8 Part of assembly deflection angle contact state corresponds to six-dimensional force signal
3.3. 基于HWOA-ELM的偏角离线识别性能验证
为了验证HWOA-ELM的离线识别性能,将HWOA-ELM、LWA-ELM、WOA-ELM、PSO-ELM、DE-ELM、ELM和HWOA-SVM对偏角CS的识别结果进行对比. 其中LWA为只使用混沌映射策略优化的WOA,PSO为粒子群优化算法,DE为差分进化算法. 设置所有启发式优化算法的迭代次数t=100,参数个体
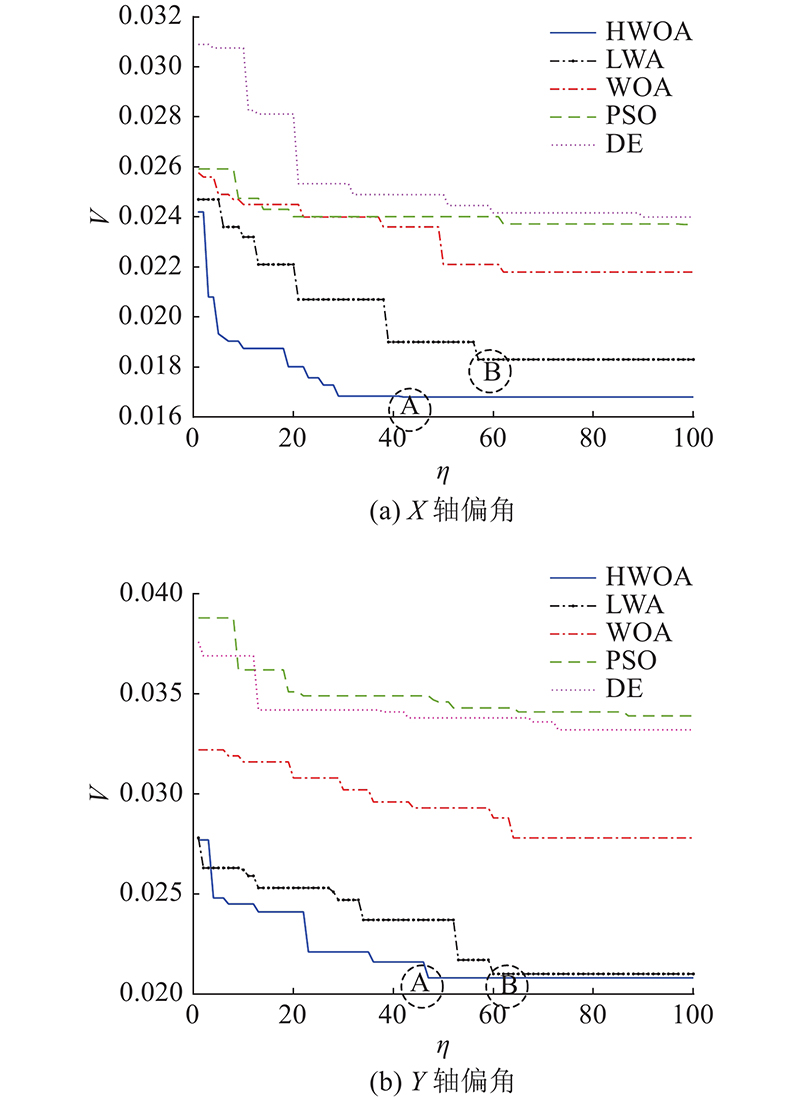
如图9所示为HWOA、LWA、WOA、PSO、DE的适应度迭代结果. 图中,V为适应度、η为迭代次数. 其中适应度函数设置为1−A,适应度V越小,表示其优化的分类器识别准确率A越高. 可知,HWOA的最佳适应度值低于其他几种优化算法,原因是混沌映射和小波变异策略生成了合理的初始参数种群,提高了算法的全局搜索能力,产生了更优的参数解. 对比图中区域A、B可知,HWOA相对于LWA的迭代速度更快,这得益于改进的对立学习策略减少了适应度值较低的参数个体,避免了算法的过度探索.
图 9
为了验证样本数据量对HWOA-ELM识别准确率的影响,设置每个偏角CS的数据量为50、100、150、200组并分别对应4个组别,导入HWOA-ELM中进行实验. 实验结果如表1所示,T0为训练HWOA-ELM的时长,综合考虑分类器识别准确率和分类器训练时长,将每个偏角CS的样本数据量定为100组并做后续实验.
表 1 不同样本数据量的分类器对比
Tab.1
| 组别 | A/% | T0/s | 组别 | A/% | T0/s | |
| 一 | 95.72 | 246.8 | 三 | 98.43 | 543.1 | |
| 二 | 98.24 | 356.4 | 四 | 98.56 | 1039.4 |
如表2所示为不同分类器10次运算的平均准确率A0、T为分类时间. 可知,HWOA-ELM对已知偏角CS的平均识别准确率优于其他分类器;从分类时间上看,经过参数优化的分类器分类时长均有一定程度的增加,原因是算法的混合会增加分类器的运算负担,而HWOA-ELM的分类速度优于其他被优化的分类器,可以满足花键装配作业的实时性要求;从算法的迭代次数上看,HWOA-ELM的平均迭代次数最低,说明该算法的收敛速度最快.
表 2 不同分类器性能对比
Tab.2
| 分类器 | A0/% | T/s | η | ||
| ELM,X轴 | 90.33 | 0.008 | — | ||
| ELM,Y轴 | 91.26 | 0.007 | — | ||
| DE-ELM,X轴 | 93.53 | 0.032 | 67.3 | ||
| DE-ELM,Y轴 | 94.61 | 0.047 | 77.2 | ||
| PSO-ELM,X轴 | 95.60 | 0.036 | 63.4 | ||
| PSO-ELM,Y轴 | 95.28 | 0.053 | 75.3 | ||
| WOA-ELM,X轴 | 95.82 | 0.026 | 61.3 | ||
| WOA-ELM,Y轴 | 96.22 | 0.038 | 66.8 | ||
| LWA-ELM,X轴 | 97.79 | 0.052 | 56.9 | ||
| LWA-ELM,Y轴 | 97.86 | 0.063 | 57.2 | ||
| HWOA-SVM,X轴 | 96.69 | 2.018 | 45.6 | ||
| HWOA-SVM,Y轴 | 95.43 | 2.322 | 46.7 | ||
| HWOA-ELM,X轴 | 98.32 | 0.016 | 43.5 | ||
| HWOA-ELM,Y轴 | 97.92 | 0.033 | 45.8 | ||
3.4. 基于SVDD算法的偏角在线感知性能验证
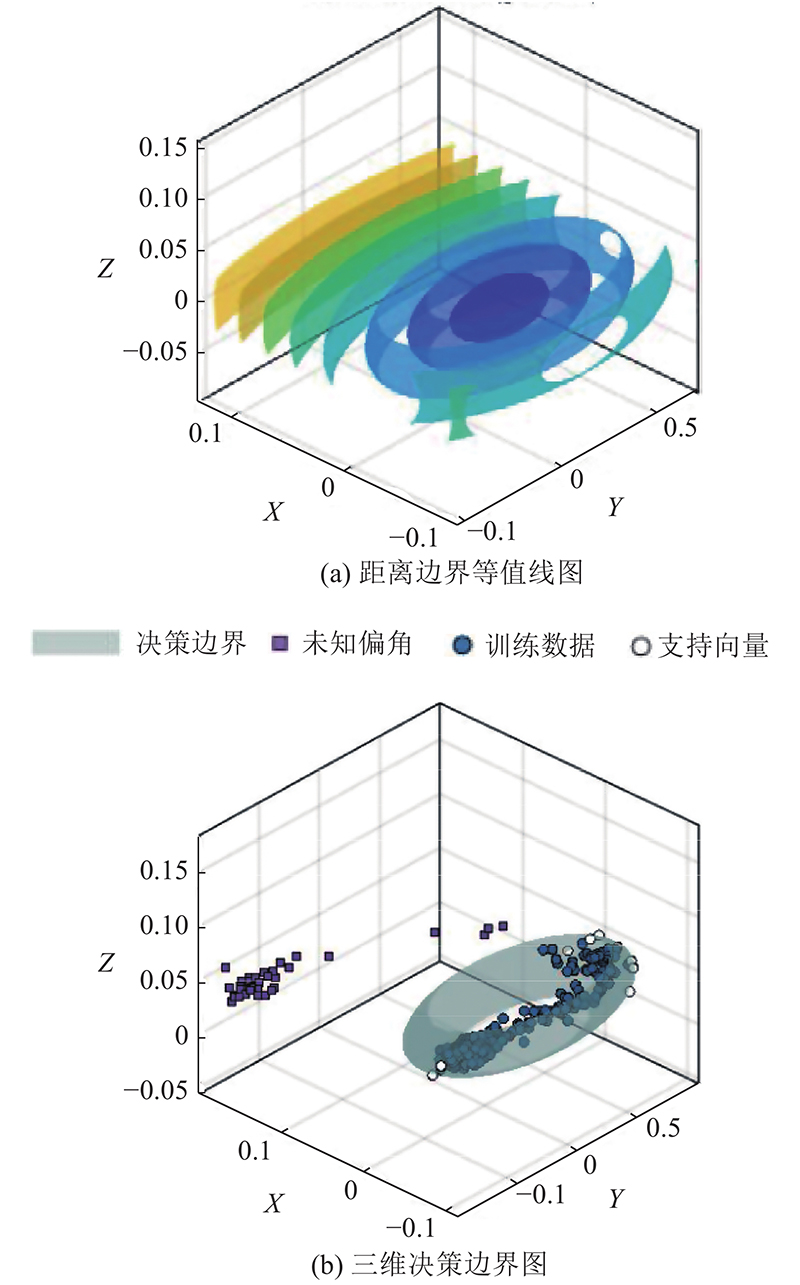
为了验证SVDD算法对偏角CS在线感知的效果,依次选取偏角经验库中4种已知偏角CS共400组CS信号作为SVDD算法的训练数据;将剩余的100组已知偏角CS信号视作未定义偏角,并作为测试数据;设定SVDD算法的核函数为高斯核函数,设置松弛因子
图 10
图 10 SVDD算法的在线偏角(X轴)感知结果
Fig.10 Online deflection (X-axis) perception results of SVDD algorithm
不同偏角CS的感知情况如表3所示. 可得,SVDD算法对偏角的感知成功率S超过98.8%. 此外,感知单一偏角CS的平均时长为0.013 s,能满足在线偏角感知的实时性要求. 当SVDD算法感知到未定义偏角为已知偏角时,须再通过分类器识别其具体的CS. SVDD算法结合ELM、LWA-ELM、HWOA-SVM、HWOA-ELME对已知偏角CS的识别准确率A分别为87.92%、96.82%、94.47%、98.12%. 可知,SVDD算法结合HWOA-ELM对已知偏角CS的识别准确率优于SVDD算法与其他的分类器结合的识别准确率,说明该算法能有效感知识别偏角.
表 3 未定义偏角感知情况
Tab.3
| 未定义偏角标签 | 样本判断结果 | S/% | |
| 已知 | 未知 | ||
| 0,X轴 | 402 | 98 | 99.6 |
| 0,Y轴 | 396 | 104 | 99.2 |
| 1,X轴 | 399 | 101 | 99.8 |
| 1,Y轴 | 394 | 106 | 98.8 |
| 2,X轴 | 400 | 100 | 100 |
| 2,Y轴 | 400 | 100 | 100 |
| 3,X轴 | 403 | 97 | 99.4 |
| 3,Y轴 | 403 | 97 | 99.4 |
| 4,X轴 | 396 | 104 | 99.2 |
| 4,Y轴 | 406 | 94 | 98.8 |
3.5. 花键柔性装配结果分析
花键装配的调整过程如图11所示. 花键轴孔首次接触时通过力传感器采集力信号,当采集一组花键装配偏角CS后,抬升至一定高度,通过服务器运行花键偏角感知识别方法对该偏角CS进行感知识别,分别获得X、Y轴对应偏角度数并指导机器人末端调整对应角度,实现花键的插入. 此外,由于装配的花键存在倒角,能有效降低微小偏角的影响,当轴线偏角<0.1°时,花键能完成装配.
图 11
花键装配实验须根据部分已知偏角CS和HWOA-ELM分类器构建离线偏角经验库;利用机器人执行装配动作,装配过程中新获得的力信号作为未定义偏角CS,并通过SVDD算法在线感知该偏角类型. 若感知结果为已知偏角,则通过HWOA-ELM识别出该偏角,机器人再根据对应偏角调整位姿,实现花键轴孔装配;若感知结果为新偏角,则先将新偏角CS加入偏角经验库中并更新HWOA-ELM,将机械臂复位,设定偏角调整步长为0.1°并重复装配至感知识别出该偏角CS,首次装配后再进行多次装配实验. 此外,若花键初始偏角过大,则在装配过程中会出现不满足的花键装配几何约束,导致对齿失败的问题。这种情况须重新调整花键装配的初始位置后再进行装配.
实验分为2组,第1组选取离线经验库中的已知偏角作为未定义偏角;第2组随机调整花键装配角度并将其作为未定义偏角. 每组实验的装配动作执行100次并计算实验的装配成功率. 第1组已知偏角的装配实验结果如下。未定义偏角标签0、1、2、3、4对应的装配成功率分别为98%、99%、100%、98%、99%. 由第1组实验结果可知,本研究所提方法能有效识别已知偏角并指导机器人执行花键装配动作. 第2组实验随机调整花键装配角度,首次装配的成功率为47%,后续的装配都是在前一次装配的基础上进行,装配次数为2、3、4、5对应的装配成功率分别为72%、88%、96%、98%. 在第2组实验中,首次装配由于未定义偏角并未存储于偏角经验库中,机器人根据偏角调整步长进行多次不确定性的姿态调整,导致装配成功率较低. 随着装配次数的增加,装配成功率逐渐提高,原因是在完成每次装配后,成功装配的新偏角CS会加入偏角经验库并更新HWOA-ELM,通过不断积累经验来识别上一次装配成功的偏角CS.
4. 结 语
提出基于参数优化的机器人花键装配偏角感知识别方法. 通过HWOA-ELM识别偏角接触状态并构建偏角经验库,结合SVDD算法实时更新偏角经验库和HWOA-ELM,感知识别花键装配偏角接触状态,指导机器人执行装配任务. 实验结果表明,相比于其他偏角识别方法,本研究所提方法通过HWOA-ELM结合SVDD算法,对已知偏角的识别准确率为98.12%,对未定义偏角感知的成功率超过98.8%,因此该方法对花键的装配具有一定的指导意义. 本研究所提方法对新偏角的识别取决于多次装配获得的经验,装配耗时较长且未定义偏角、偏角调整步长均为人为设立,因此方法具有一定的局限性. 实际装配过程中存在更多的未知偏角接触状态,当偏角初始值过大时,该方法须结合花键对齿策略进行进一步的调整. 在下一步的工作中,将深入探索偏角调整策略并增加样本数量和类别以确保该方法的可行性.
参考文献
基于齿轴压装的花键自动对齿方法
[J].DOI:10.3969/j.issn.1009-9492.2020.12.067 [本文引用: 1]
The method of spline automatic tooth alignment based on gear shaft press fitting
[J].DOI:10.3969/j.issn.1009-9492.2020.12.067 [本文引用: 1]
航空发动机套齿结构动态装配关系稳健性优化设计
[J].
Robustness optimization of dynamic assembly parameters for aero-engine spline structure
[J].
Assembly process monitoring algorithm using force data and deformation data
[J].DOI:10.1016/j.rcim.2018.09.008 [本文引用: 1]
Contact states recognition in robotic part mating based on support vector machines
[J].DOI:10.1007/s00170-011-3501-5 [本文引用: 1]
Information-level real-time AR instruction: a novel dynamic assembly guidance information representation assisting human cognition
[J].DOI:10.1007/s00170-020-05034-1 [本文引用: 1]
On the achievable rate of generalized spatial modulation using multiplexing under a Gaussian mixture model
[J].DOI:10.1109/TCOMM.2016.2515624 [本文引用: 1]
基于过程建模的机器人分阶引导装配方法
[J].
Robot phased guided assembly based on process modeling
[J].
基于机器人与视觉引导的星载设备智能装配方法
[J].DOI:10.3901/JME.2018.23.063 [本文引用: 1]
Intelligent robotic assembly method of spaceborne equlpment based on visual guidance
[J].DOI:10.3901/JME.2018.23.063 [本文引用: 1]
基于接触状态感知发育的机器人柔性装配方法
[J].
Flexible assembly method based on contact state perception development
[J].
基于随机森林算法的 Android 恶意行为识别与分类方法
[J].DOI:10.3785/j.issn.1008-973X.2019.10.019 [本文引用: 1]
Android malicious behavior recognition and classification method based on random forest algorithm
[J].DOI:10.3785/j.issn.1008-973X.2019.10.019 [本文引用: 1]
基于粒子群优化的SVM多分类的电动车价格预测研究
[J].
Study on electric vehicle price prediction based on PSO-SVM multi-classification method
[J].
Extreme learning machine: theory and applications
[J].DOI:10.1016/j.neucom.2005.12.126 [本文引用: 1]
基于GA-ELM的电压暂降源识别研究
[J].
Research on recognition of voltage sag source based on GA-ELM
[J].
Evolving support vector machines using whale optimization algorithm for spam profiles detection on online social networks in different lingual contexts
[J].DOI:10.1016/j.knosys.2018.04.025 [本文引用: 1]
Optimizing connection weights in neural networks using the whale optimization algorithm
[J].DOI:10.1007/s00500-016-2442-1 [本文引用: 1]
Improved whale optimization algorithm based on nonlinear adaptive weight and golden sine operator
[J].DOI:10.1109/ACCESS.2020.2989445 [本文引用: 1]
Parameter estimation of solar cells diode models by an improved opposition-based whale optimization algorithm
[J].DOI:10.1016/j.enconman.2018.05.062 [本文引用: 1]
具有高斯扰动的局部引导粒子群优化算法
[J].DOI:10.3969/j.issn.1007-130X.2016.06.018 [本文引用: 1]
A particle swarm optimization algorithm based on local guidance and Gauss perturbation
[J].DOI:10.3969/j.issn.1007-130X.2016.06.018 [本文引用: 1]