各大电商企业为吸引客户竞相开展促销活动,客户需求呈井喷状态. 这一现象致使物流业务量呈爆炸式增长,物流配送问题受到企业的高度重视[1]. 因众包物流可充分利用社会闲散资源、提高物流配送效率、缓解物流配送压力,其思想逐渐在物流配送领域得到应用. 如亚马逊的众包业务、人人快递、京东到家等皆是众包物流的典型代表[2-3]. 众包物流由于缺乏相应政策、参与门槛低、服务质量参差不齐,其发展受限[4]. 学术界从未停止研究众包物流. 刘春玲等[5]将众包应用于冷链,提出基于众包模式下单级冷链物流配送车辆路径优化模型,降低配送成本的同时提高了客户满意度. 在实际物流配送中,客户集中区域设置了中转站,大型车辆为中转站服务,小型车辆为客户服务[6-8],车辆均来自企业,完成配送任务后回到出发点,形成两级闭环车辆路径[9-11].
众包平台包括赞助者、参与者和众包平台[12],其中的参与者数量巨大,人员主要分布于城市. 对于众包物流的研究主要集中在“最后一公里”[13-14],在需求井喷下的两级众包配送研究较少. 曾正洋等[15-16]使用现有中转站,让第三方运输公司完成一级配送,此方案不能解决爆仓问题. Kafle等[17]将中转点及附近客户捆绑,使用众包资源完成中转点向周围的客户服务,卡车访问有客户捆绑的中转点、未与任何中转点捆绑的客户. Huang等[18]在Kafle等[17]的基础上,进一步考虑众包车辆的路径以更好的评估外包成本. 以上研究主要以卡车运输为主,众包资源为辅. 在需求井喷下的物流配送,主要问题是运力资源不足,因此研究应以众包资源为主. 两级车辆路径问题的常见求解算法有1)精确求解算法,如分支切割算法[19-20]、分支定价算法[21]、分支降低算法[22]等;2)近似求解算法,如模拟退火算法[23]、禁忌搜索算法[24-26]、大邻域搜索算法[27]、自适应邻域搜索算法[28-29]、遗传算法(genetic algorithm, GA)[30]等. 精确求解算法运算时间长,近似求解算法可以利用元启发式的全局搜索能力,求解时间短. 麻雀搜索算法属于新型群智优化算法,在搜索精度、收敛速度和稳定性方面具有很强的竞争力[31]. 本研究提出离散麻雀搜索算法(discrete sparrow search algorithm,DSSA),用于解决两级开闭混合式车辆路径问题.
本研究考虑现有中转站位置优劣及存储能力的限制,将众包引入两级车辆路径. 以路径成本与服务延时惩罚成本最小为优化目标,建立带时间窗的两级开闭混合式车辆路径规划数学模型. 针对模型特点提出离散麻雀搜索算法,以期为物流企业在众包模式下的物流配送提供有益的参考.
1. 问题描述与假设
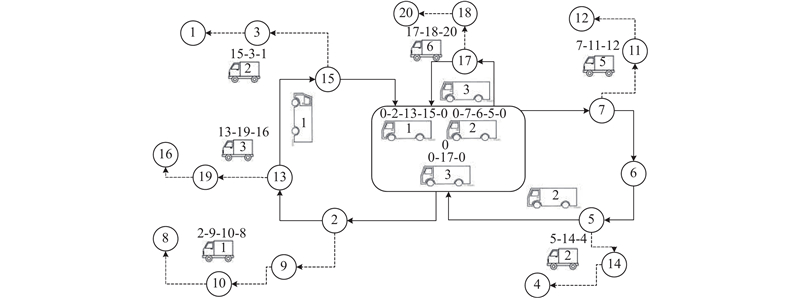
在本研究的两级开闭混合式车辆路径问题中,企业车辆完成一级配送任务后回到配送中心,形成闭环车辆路径;社会车辆从中转站出发完成二级配送任务后不必回到出发点,形成开环车辆路径. 在该配送系统中,决策者是一家物流公司,该公司拥有一批大型车辆(下称企业车辆)和有足够可供调度的社会车辆(下称众包车辆). 设置系统的目的是运用企业车辆和众包车辆将配送中心的货物交付给客户,并期望减少物流配送成本和提高客户满意度. 考虑中转站位置分布的优劣以及存储能力的限制,从客户群体中选择若干合适客户作为中转站. 采用企业车辆将货物从配送中心运输至城市内的中转站,众包车辆将货物从中转站运输至客户完成货物交付. 企业车辆与众包车辆构成的两级车辆配送路径如图1所示. 图中,实线为企业车辆路径,虚线为众包车辆路径,编号0的节点代表配送中心,编号1~20的节点代表客户,点2、5、6、7、13、15、17被选作为中转站.
图 1
上述两级车辆路径问题可看作是包含不同中转站、不同车辆、不同路径和不同服务对象的组合优化问题。将其拆分为3个逻辑子问题:1)根据客户分布确定中转站的最佳位置;2)根据中转站位置,确定企业车辆路径和各中转站的配送货物量;3)根据客户分布,确定社会车辆配送路径. 子问题相互影响、相互制约,分别求解或集成其中2个子问题都难以达到整体优化的效果. 因此考虑子问题相互影响与制约关系、车辆容量及客户对订单服务时间的要求,建立集成中转站选址约束和两级车辆路径优化的配送模型,达到全局优化效果. 根据两级车辆路径和中转站选址问题的特点,做出如下假设:1)同级别车辆型号一致;2)众包车辆与企业车辆充足;3)服务时间超出客户要求将产生惩罚成本;4)中转站总需求货物可拆分配送,客户需求不可拆分配送;5)众包车辆准时在中转站接受订单;6)企业车辆完成配送任务后必须回到配送中心,众包车辆完成配送任务后不必回到中转站.
2. 两级开闭混合式车辆路径优化模型
2.1. 符号说明
表 1 带时间窗的两级开闭混合式车辆路径规划数学模型参数
Tab.1
| 符号 | 参数 | 符号 | 参数 | |
| D | 仓库集合 | E | 企业车辆 e 集合 | |
| C | 需求点集合 | K | 众包车辆 k 集合 | |
| Q1 | 企业车辆最大载重 | qi | 需求点i的需求量 | |
| Q2 | 众包车辆最大载重 | qj | 需求点 j 的需求量 | |
| c1 | 企业车辆单位距离成本 | N | 中转站最大数量 | |
| c2 | 众包车辆单位距离成本 | M | 足够大的实数 | |
| c3 | 单位时间延时惩罚成本 | Tij | 车辆从 i到 j所需时间 | |
| dij | 节点 i到节点 j间的距离 | Ti | 需求点 i期望服务时间 |
表 2 带时间窗的两级开闭混合式车辆路径规划数学模型决策变量
Tab.2
| 符号 | 说明 | 符号 | 说明 | |
| fi、fj | 需求点i 、j被选作为中转站,fi、fj=1;否则,fi、fj=0 | Ue | e被使用, Ue=1;否则,Ue=0 | |
| zki | k经过中转站 j,zki=1;否则,zki=0 | | e访问中转站i后访问中转站 j, | |
| uk | k被使用,uk=1;否则,uk =0 | gie | e给中转站 j的货物量 | |
| ski | k经过需求点 j,ski=1;否则,ski=0 | lie | 消除企业车辆路径子回路的中间变量 | |
| | k访问需求点i后访问需求点 j, | hie | e到中转站的时间 | |
| Lik | 消除众包车辆路径子回路的中间变量 | F | 企业车辆到达中转站的最大时间 | |
| Sijk | 需求点i的货物由 k从中转站 j获取 | ti | 货物到达需求点 i的实际用时 | |
| yie、yje | e服务中转站 i、j,yie、 yje=1;否则,yie、yje=0 | Ri | 货物到达需求点 i的延迟时间 | |
| y0e | e服务配送中心 ,y0e=1;否则,y0e=0 | Vim | ti−Ti > 0, Vi1 =1;否则, Vi2=0,m∈{1, 2} | |
| Hik | k到达客户i所用时间 | uie | e到中转站 i的时间为企业车辆到达中转站的最大时间,uie =1;否则,uie =0 | |
| wj | 中转站 j的总货物需求量 |
2.2. 模型构建
根据问题描述与符号说明,以路径成本与服务延时惩罚成本最小为优化目标,建立带时间窗的两级开闭混合式车辆路径优化数学模型:
目标函数式(1)中第1项为企业车辆路径成本,第2项为众包车辆路径成本,第3项为服务延时惩罚成本;式(2)判断众包车辆是否经过中转站;式(3)限制最大中转站数量;式(4)表示众包车辆仅经过1个中转站;式(5)判断众包车辆是否经过的需求点;式(6)确保需求点仅由1辆众包车服务;式(7)确保众包车辆不会超载;式(8)、(9)限制众包车辆进出节点的次数;式(10)限制众包车辆路径出现子回路现象;式(11)~(13)线性化表示需求点的货物由众包车辆从中转站获取;式(14)求中转站货物总需求量;式(15)表示中转站被企业车辆至少服务一次;式(16)表示企业车辆必须经过配送中心;式(17)表示企业配送网络流量均衡约束;式(18)表示中转站需求被满足;式(19)表示企业车辆不超载;式(20)表示中转站被企业车辆服务后才能提供货物;式(21)表示企业车辆进入节点的次数取决于该节点是否被该车辆服务;式(22)表示企业车辆从节点出发的次数取决于该节点是否被该车辆服务;式(23)消除企业车辆路径子回路;式(24)~(27)线性化表示企业车辆到中转站的时间;式(28)~(31)线性化表示众包车辆到需求点的时间;式(32)~(34)线性化表示企业车辆到达中转站的最大时间;式(35)表示货物从配送中心运输至需求点总耗时;式(36)~(40)线性化表示货物到达需求点的延迟时间.
3. 算法设计
本研究的两级开闭混合式车辆路径问题属于组合优化问题,启发式算法在求解组合优化问题时,具有在短时间内求得满意解的能力. 麻雀搜索算法通过模拟麻雀觅食行为,根据适应度将种群划分为发现者和追随者,并从种群中随机选择一部分麻雀作为警戒者,不同个体类型执行不同操作来更新种群,以达到在迭代过程中个体能够自适应选择操作算子. 麻雀搜索算法提出者将该算法应用于求解连续问题,因此原有启发式算子在求解本研究的问题时不能被直接应用. 在这种情况下应根据两级开闭混合式车辆路径问题特点,设计新的自然数编码和启发式策略将麻雀搜索算法离散化.
3.1. 编码
本研究的两级开闭混合式车辆路径问题,要求在编码过程中融合中转站选址,并区分企业车辆路径和众包车辆路径来形成可行的配送方案. 为此,提出新的自然数编码方式表示可行的两级物流配送方案,以8个客户为例说明编码方式,如图2所示. 图中,配送方案由麻雀个体表示,三角形表示客户被选为中转站,先后顺序表示企业车辆路径;正方形内客户的先后顺序表示众包车辆路径;计算机不易区分三角形与正方形,设置圆内的数字表示中转站数量.
图 2
3.2. 解码
中转站总货物需求可能超过企业车辆容量Q1,因此要判断在企业车辆路径序列内各个中转站总需求是否超过企业车辆容量:
若超载,则针对超载部分先按照式(41)安排企业满载车辆配送,对剩余中转站依次安排到同一辆车,直至超出企业车辆容量,然后安排下一辆企业车辆的组合配送策略. 因为在众包车辆路径序列中,客户需求不超过车辆容量,所以按照依次安排客户到同一辆车,直至超出众包车辆容量Q2后安排下一辆众包车辆的组合配送策略. 为了降低成本、提高配送效率,在客户分配至众包车辆中未超载,且当该客户至车辆已服务的最后一个客户距离比至中转站的距离远时,将该客户安排到新的车辆中.
3.3. 编码初始解生成算法
为了提高算法求解效率,设计算法获得较优的初始解,其步骤如下. 1)随机产生中转站数量和集合. 2)选择距离配送中心最近中转站作为企业车辆的首个服务点,从距离企业车辆所服务的最后一个中转站最近w个未被安排的中转站中,随机选择1个作为车辆即将服务的中转站,若超出车辆载重能力,则启用新的车辆,直至所用中转站均被完成服务,完成企业车辆路径构造. 3)选择距离中转站最近客户作为众包车辆的首个服务点,从距离车辆最后一个客户点最近w个未被安排的客户点中,随机选择1个作为车辆即将服务的客户;若加入客户后超出车辆载重能力,则启用新的车辆,直至所有客户均被安排,完成众包车辆路径构造.
若步骤2)、3)中被安排的中转站或客户点数量小于w,则从剩余中转站或客户中随机选择1个作为车辆的下个服务点,且w越大,生成的初始种群多样性越好,但解的质量会相对下降.
3.4. 方向搜索
麻雀种群中的发现者负责为整个种群寻找食物并为所有的追随者提供觅食方向. 为此设计使发现者向更好位置移动的方向搜索策略. 该策略首先随机选择变换元素x0,再计算该元素向2个不同方向变换后的元素x1、x2.
式中:n为随机正整数,范围不超过个体中最大元素xmax;b、c分别用于判断x1、x2是否超出个体中最大或最小元素,若超出此范围,则为1,否则为0. 其次针对当前发现者分别交换x0与x1、x0与x2得到2个新个体,并计算该新个体的适应度. 最后保留原始个体和新个体中的优秀个体.
3.5. 追随操作
追随操作是模拟麻雀种群中的追随者追随发现者,并在发现者周围觅食的过程. 首先计算发现者i的被追随概率:
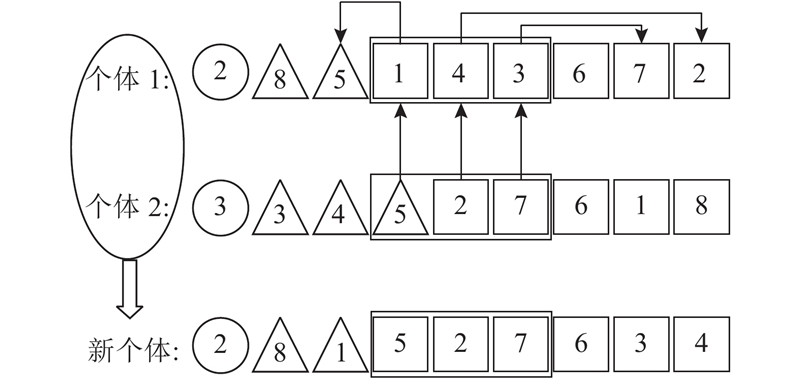
式中:fi为发现者的适应度,Sd为发现者集合. 再根据追随算子完成追随操作从追随算子原理为追随者中某段位置元素由发现者相应位置元素替换,学习发现者中较好的序列特征以达到优化效果. 为了消除追随者中重复元素,将被替换位置的元素与替换元素交换位置. 追随算子过程如图3所示.
图 3
3.6. 逃离操作
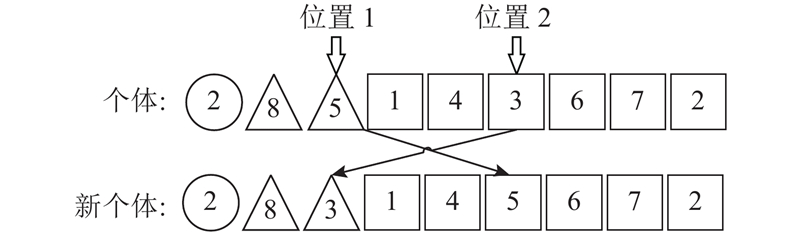
为了防止被捕食,麻雀种群中存在警戒者,它可能属于发现者,也可能属于追随者. 如图4所示,当警戒者发现危险时便会发出信号并逃离原地,逃离过程的操作是交换个体中2个随机位置的元素.
图 4
3.7. 算法流程
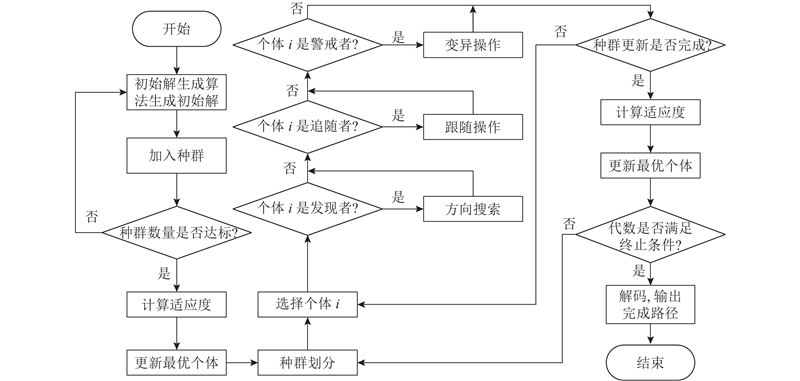
基于以上设计的离散启发式算子及麻雀搜索算法架构提出DSSA,算法步骤如下. 1)采用初始解生成算法获取较好的初始种群. 2)计算麻雀适应度和最优麻雀. 3)根据适应度将麻雀种群划分为发现者与追随者,适应度较好的个体作为发现者,适应度较差的个体作为追随者,并从种群中随机选择一部分个体选充当警戒者. 4)判断个体类型并执行相应的操作算子完成个体更新. 若个体属于发现者,则执行方向搜索;若个体属于追随者,则执行追随操作;若个体属于警戒者,则执行逃离操作. 5)计算更新后的种群适应度,并更新最优个体. 6)判断终止条件是否满足,满足输出最优解,否则返回步骤2)继续迭代. DSSA流程如图5所示.
图 5
4. 算法验证与配送模式分析
4.1. 算法验证
实验在配置为Intel(R) Core(TM) i5-7500 CPU 3.4GHz的计算机上进行,使用GUROBI、DSSA、GA分别求解2e-VRP标准算例中的Set2a数据,对比验证DSSA求解众包模式下的两级开闭混合式车辆路径问题的有效性. DSSA与GA实验程序在同一硬件环境下使用Python开发,2种算法的种群数均为100,最大迭代次数均为500. DSSA的发现者、警戒者均占种群数量的5%,GA的变异概率、交叉概率分别为10%、80%. 为了说明不同客户规模下DSSA的求解性能,首先在Set2a数据的基础上将客户规模扩充至31,扩充后的算例数据见表3. 表中,编号0代表配送中心,编号1至31代表客户. 其次从客户规模为13开始,每组增加2个客户,例如0~13为1个算例,0~15为1个算例,依次类推,间隔为2,直到取值为31,组成10个不同客户规模的算例. 最后对比不同方法求解上述算例,验证DSSA在不同客户规模下的求解性能. 算例中企业车辆容量设置为15000件,众包车辆容量设置为6000件.
表 3 客户规模扩充后的Set2a算例数据
Tab.3
| 编号 | X/km | Y/km | q | T/h | 编号 | X/km | Y/km | q | T/h | |
| 0 | 145 | 215 | 0 | 0 | 16 | 141 | 206 | 2 100 | 4 | |
| 1 | 151 | 264 | 1 100 | 3 | 17 | 147 | 193 | 1 000 | 4 | |
| 2 | 159 | 261 | 700 | 4 | 18 | 164 | 193 | 900 | 3 | |
| 3 | 130 | 254 | 800 | 6 | 19 | 129 | 189 | 2 500 | 6 | |
| 4 | 128 | 252 | 1 400 | 5 | 20 | 155 | 185 | 1 800 | 6 | |
| 5 | 163 | 247 | 2 100 | 4 | 21 | 139 | 182 | 700 | 5 | |
| 6 | 146 | 246 | 400 | 3 | 22 | 140 | 213 | 900 | 6 | |
| 7 | 161 | 242 | 800 | 4 | 23 | 160 | 180 | 1 000 | 5 | |
| 8 | 142 | 239 | 100 | 3 | 24 | 136 | 196 | 800 | 4 | |
| 9 | 163 | 236 | 500 | 6 | 25 | 143 | 208 | 400 | 3 | |
| 10 | 148 | 232 | 600 | 3 | 26 | 126 | 228 | 900 | 5 | |
| 11 | 128 | 231 | 1 200 | 5 | 27 | 150 | 190 | 600 | 6 | |
| 12 | 156 | 217 | 1 300 | 5 | 28 | 169 | 202 | 1 000 | 6 | |
| 13 | 129 | 214 | 1 300 | 6 | 29 | 119 | 178 | 300 | 4 | |
| 14 | 146 | 208 | 300 | 3 | 30 | 128 | 240 | 500 | 5 | |
| 15 | 164 | 208 | 900 | 3 | 31 | 113 | 192 | 600 | 6 |
设置2组模型参数,验证模型及算法的优化性能. 1)当企业车辆和众包车辆单位距离成本相同时,不考虑单位时间延时惩罚成本,即c1、c2=1,c3=0,表示优化过程中忽略服务延迟情况,等同于以路径最短为优化目标,其模型求解结果见表4. 2)当企业车辆和众包车辆单位距离成本相同时,单位时间延时惩罚成本为2时,即c1、c2=1,c3=2,表示优化过程中考虑服务延迟情况,其模型求解结果见表5. 表中,f0、V0分别为GUROBI求得的最优值、求解时间;f1、avg1、V1分别为GA求解10次的最优值、平均值、平均求解时间;f2、avg2、V2分别为DSSA求解10次的最优值、平均值、平均求解时间;GAP为数学规划方法求解过程中上界与下界差距的百分比;gap′为启发式方法求得最优解与数学规划方法求得精确解差距的百分比,gap′=((f1or f2)-f0)/f0. 经测试,客户规模小于21的算例在以路径最短为目标时,数学规划方法能在合理的时间内求得精确解,当客户规模超过23时,求解时间急剧增加;在考虑服务延迟情况下,数学规划方法求解时间均较长. 由此可知,随着客户规模及目标函数考虑因素增加,数学规划方法求解时间大幅增加. 为了兼顾求解效率,运用在GUROBI 9.0.1优化器中运算1 000 s时的精确解,给启发式算法(DSSA和GA)运行结果提供对比依据.
表 4 不同方法以路径最短为目标的优化结果
Tab.4
| 客户规模 | GUROBI | GA | DSSA | ||||||||||
| f0/元 | GAP/% | V0/s | f1/元 | avg1/元 | gap′/% | V1/s | f2/元 | avg2/元 | gap′/% | V2/s | |||
| 13 | 169.60 | 0.00 | 56 | 170.45 | 172.59 | 0.50 | 22 | 169.60 | 172.10 | 0.00 | 19 | ||
| 15 | 188.86 | 0.00 | 38 | 192.22 | 195.31 | 1.78 | 25 | 188.86 | 191.60 | 0.00 | 20 | ||
| 17 | 210.48 | 0.00 | 123 | 210.48 | 215.51 | 0.00 | 28 | 210.48 | 215.29 | 0.00 | 23 | ||
| 19 | 243.91 | 0.00 | 283 | 247.34 | 250.99 | 1.40 | 30 | 245.27 | 247.14 | 0.56 | 28 | ||
| 21 | 263.33 | 0.00 | 322 | 265.27 | 276.85 | 0.74 | 33 | 264.68 | 272.92 | 0.51 | 31 | ||
| 23 | 275.45 | 5.63 | 1000 | 274.50 | 283.27 | −0.34 | 34 | 273.14 | 282.57 | −0.84 | 33 | ||
| 25 | 283.49 | 9.09 | 1000 | 281.93 | 289.52 | −0.55 | 36 | 277.69 | 285.96 | −2.05 | 34 | ||
| 27 | 311.02 | 17.80 | 1000 | 288.00 | 302.56 | −7.40 | 37 | 287.84 | 297.51 | −7.45 | 35 | ||
| 29 | 366.64 | 26.80 | 1000 | 319.23 | 330.68 | −12.90 | 38 | 311.63 | 323.52 | −15.00 | 38 | ||
| 31 | 388.91 | 28.20 | 1000 | 341.27 | 359.50 | −12.20 | 41 | 340.84 | 356.60 | −12.40 | 40 | ||
| 平均值 | 270.17 | 8.75 | 582 | 259.07 | 267.68 | −2.90 | 32 | 257.00 | 264.52 | −3.67 | 30 | ||
表 5 不同方法考虑服务延迟的优化结果
Tab.5
| 客户规模 | GUROBI | GA | DSSA | ||||||||||
| f0/元 | GAP/% | V0/s | f1/元 | avg1/元 | gap′/% | V1/s | f2/元 | avg2/元 | gap′/% | V2/s | |||
| 13 | 188.54 | 518 | 0.00 | 191.11 | 194.71 | 1.36 | 23 | 191.11 | 191.11 | 1.36 | 20 | ||
| 15 | 209.64 | 1000 | 11.80 | 219.22 | 222.27 | 4.57 | 25 | 213.56 | 215.92 | 1.87 | 22 | ||
| 17 | 230.37 | 1000 | 10.30 | 230.37 | 234.03 | 0.00 | 28 | 230.37 | 232.60 | 0.00 | 26 | ||
| 19 | 265.45 | 818 | 0.00 | 269.06 | 276.32 | 1.36 | 31 | 265.45 | 271.54 | 0.00 | 28 | ||
| 21 | 292.29 | 1000 | 11.80 | 295.39 | 301.65 | 1.06 | 31 | 284.86 | 295.50 | −2.54 | 30 | ||
| 23 | 297.44 | 1000 | 13.70 | 309.60 | 317.50 | 4.09 | 34 | 301.90 | 310.73 | 1.50 | 32 | ||
| 25 | 303.85 | 1000 | 14.70 | 305.63 | 322.68 | 0.59 | 37 | 303.37 | 321.37 | −0.16 | 36 | ||
| 27 | 374.49 | 1000 | 31.40 | 312.15 | 328.75 | −16.60 | 39 | 311.73 | 326.97 | −16.8 | 37 | ||
| 29 | 350.51 | 1000 | 22.70 | 358.92 | 376.46 | 2.40 | 40 | 348.53 | 368.84 | −0.57 | 40 | ||
| 31 | 388.91 | 1000 | 28.20 | 393.46 | 408.65 | 1.17 | 45 | 379.93 | 394.84 | −2.31 | 44 | ||
| 平均值 | 290.15 | 934 | 14.46 | 288.49 | 298.30 | 0.00 | 33 | 283.08 | 292.94 | −1.77 | 32 | ||
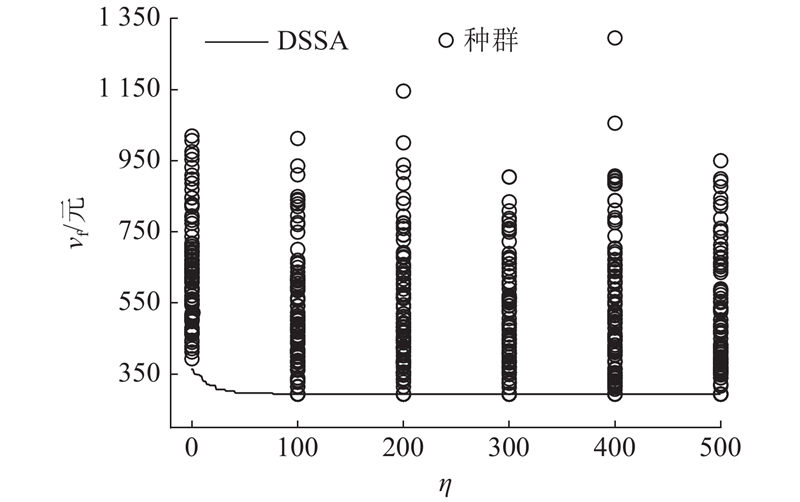
图 6
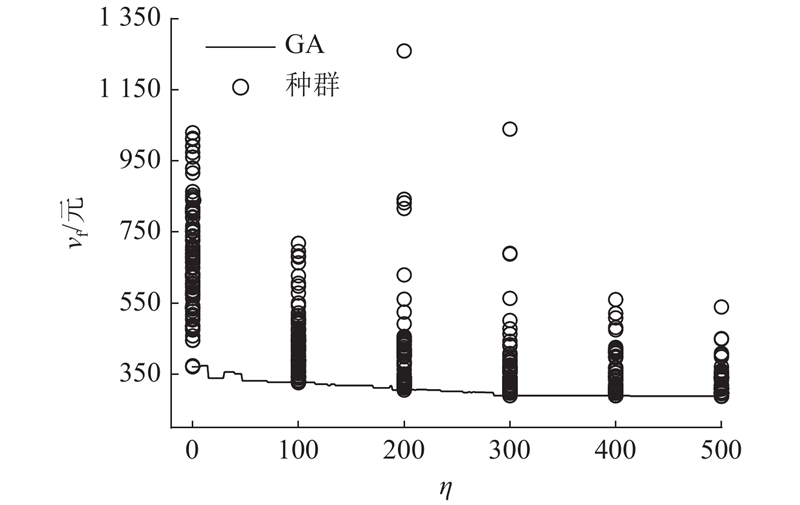
图 7
4.2. 配送模式分析
为了说明本研究所提物流配送策略具有提高需求井喷条件下物流配送效率的能力,以Set2a算例数据为例,使用DSSA分别求解在不同配送模式下各项成本和服务延迟的情况.
表 6 不同配送模式下离散麻雀搜索算法的优化结果
Tab.6
| c1/元 | c2/元 | c3 | 配送模式 | C1/元 | C2/元 | nDL | TL/h | TC/元 |
| 1 | 1 | 0 | 两级开闭混合 | 59.59 | 205.10 | 15 | 31.43 | 327.55 |
| 1 | 1 | 0 | 两级闭环 | 87.51 | 278.22 | 18 | 65.60 | 496.93 |
| 1 | 1 | 2 | 两级开闭混合 | 36.50 | 226.82 | 8 | 10.77 | 284.86 |
| 1 | 1 | 0 | 两级闭环 | 56.83 | 325.59 | 11 | 21.53 | 425.48 |
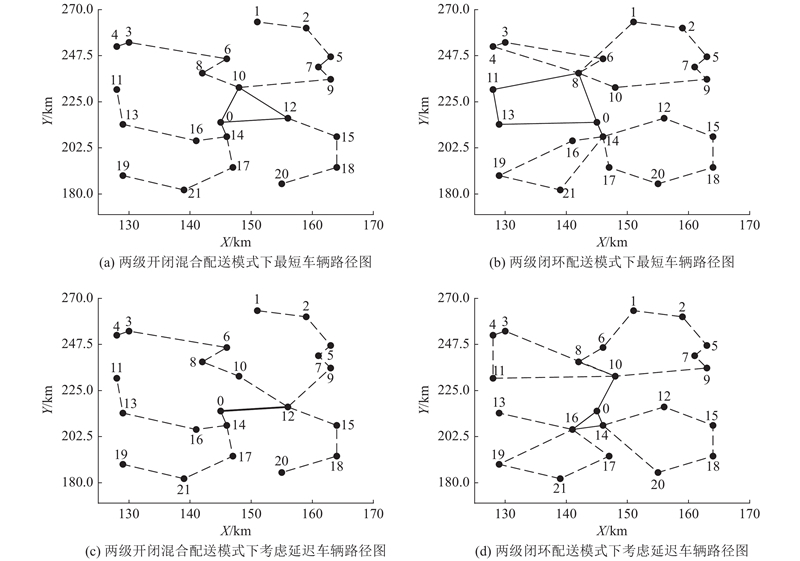
图 8
图 8 不同配送模式下离数麻雀搜索算法的车辆路径图
Fig.8 Vehicle route chart of discrete sparrow search algorithm under different distribution modes
表6中结果为10次计算中的最优值,在2组模型参数下,两级开闭混合式配送模式的总成本在相较于两级闭环配送模式分别减少34.09%、33.05%. 说明两级开闭混合式配送模式可有效降低配送成本. 通过分析车辆行驶路径可知,造成这种情况的原因主要有:1)两级开闭混合配送模式减少了车辆回到出发点的距离;2)在车辆足够的情况下,两级开闭混合式不会出现车辆即将服务的客户至车辆已服务的最后一个客户间的距离,大于该车辆即将服务客户至中转站间的距离. 由表6还可知,在同一模型参数下,两级开闭混合配送模式相较于两级闭环配送模式在延时客户数量和总延时时间上均有减少;在2种配送模式下,考虑服务延迟优化结果在延时客户数量和总延时时间上均有减少. 说明考虑服务延时优化以及采用两级开闭混合配送模式可有效提高客户满意度. 证明本研究所提优化算法和众包下的两级开闭混合配送策略,能够有效缓解需求井喷条件下的物流配送压力.
由图8 可知,针对同一批客户,采用不同配送模式和不同模型参数,车辆路径相差较大,充当中转站的客户也不相同,说明在不同客户群体以及配送模式下采用现有固定中转站方案并非最优. 可在需求井喷条件下适当分出一部分客户,采用两级众包物流模式配送,另一部分客户按照原有模式配送,以充分利用社会与企业资源.
4.3. 灵敏度分析
在实际物流配送中,不同车辆型号的单位行驶距离成本不同. 为了说明众包模式在不同单位距离成本下的优势,分析车辆行驶的单位距离成本对优化结果的影响,各单位距离成本下的优化结果见表7. 表中,C3为众包模式下得成本,C4为传统模式下的成本,P为成本节约成本占比. 可知众包配送模式成本均低于传统配送模式,平均节约成本32.57%. 说明使用众包模式在不同车辆单位距离成本下具有较大优势.
表 7 车辆单位距离成本对DSSA优化结果的影响
Tab.7
| c1 | c2 | c3 | C3 | C4 | P/% |
| 1.0 | 1.0 | 2.0 | 284.86 | 425.48 | 33.05 |
| 2.0 | 1.0 | 2.0 | 321.37 | 480.79 | 33.12 |
| 3.0 | 1.0 | 2.0 | 357.87 | 521.87 | 31.43 |
| 3.0 | 1.5 | 2.0 | 471.28 | 701.95 | 32.86 |
| 3.0 | 2.0 | 2.0 | 584.69 | 864.75 | 32.39 |
在实际物流配送中,不同型号的车辆装载能力不同,为了说明众包模式在不同车辆容量下的优势,分析车辆容量对优化结果的影响,不同车辆容量下的优化结果见表8. 可知众包配送模式成本均低于传统配送模式,平均节约成本32.64%. 说明使用众包模式在不同车辆容量下具有较大优势.
表 8 车辆容量对DSSA优化结果的影响
Tab.8
| Q1 | Q2 | C3 | C4 | P/% |
| 11 000 | 6 000 | 293.40 | 433.86 | 32.37 |
| 13 000 | 6 000 | 293.40 | 425.49 | 31.04 |
| 15 000 | 6 000 | 284.86 | 425.48 | 33.05 |
| 15 000 | 5 000 | 298.44 | 436.07 | 31.56 |
| 15 000 | 4 000 | 300.74 | 463.99 | 35.18 |
在实际物流配送中,当配送中心距离中转站较远时,为了降低物流配送成本,应尽可能使一级车辆访问更少的节点. 为此分析最大中转站数量对优化结果的影响,限制最大中转站数量后的优化结果见表9. 可知众包配送模式优于传统配送模式,平均节约成本32.19%. 说明众包模式在限制最大中转站数量后仍具有较大优势.
表 9 中转站数量对DSSA优化结果的影响
Tab.9
| N | C3 | C4 | P/% |
| 2 | 306.44 | 446.26 | 31.33 |
| 3 | 293.40 | 437.03 | 32.87 |
| 不限制 | 293.40 | 433.86 | 32.37 |
上述分析的车辆单位距离成本、车辆容量、最大中转站数量对优化结果的影响,表明众包配送模式优于传统的配送模式.
5. 结 论
(1)针对需求井喷条件下的物流运力不足和社会及企业资源利用效率不高的问题,提出具有最优中转站的两级众包物流配送策略,并构建混合整数规划模型.
(2)根据模型特点,设计了使用新编码方式和启发式策略的算法:DSSA. 使用DSSA、GA、GUROBI求解器计算随机生成的不同规模的算例,验证DSSA在求解质量和求解效率方面均优于GA. 通过分析DSSA与GA迭代过程图,进一步说明DSSA具有较好的种群多样性,收敛速度快的特点.
(3)通过算例计算在不同配送模式下的各项物流配送成本,说明本研究所提物流配送策略确能有效减少物流配送成本,提高物流配送效率以及客户满意度.
(4)本研究所提配送策略在一级配送网络中使用企业大型车辆,二级配送网络中使用众包车辆,且考虑现有中转站运力资源和所处位置优劣. 将所提配送策略应用在现有中转站不能及时处理的订单配送中,可有效减轻物流配送压力. 为了进一步结合实际物流配送情况和充分利用社会与企业资源,应考虑现有中转站的转运能力,因此合理分配订单至不同配送模式的组合配送策略将是今后的研究重点.
参考文献
基于客户分流策略的电商促销下车辆路径问题研究
[J].DOI:10.3969/j.issn.1000-386x.2019.05.006 [本文引用: 1]
Vehicle routing under E-commerce promotion based on customer segregation strategy
[J].DOI:10.3969/j.issn.1000-386x.2019.05.006 [本文引用: 1]
分享经济视阈下的众包物流信息服务平台模型构建
[J].
Constructing crowd-sourcing logistics information service platform model from the perspective of sharing econ-omy
[J].
Modeling the acceptability of crowdsourced goods deliveries: role of context and experience effects
[J].DOI:10.1016/j.tre.2017.06.007 [本文引用: 1]
众包物流的发展现状及前景分析
[J].
Analysis on the development status and prospect of crowdsourcing logistics
[J].
众包模式下冷链物流配送模型的仿真和优化分析
[J].
Simulation and optimization model of cold chain logistics delivery under crowdsourcing mode
[J].
基于场景动态度的两级配送路径问题
[J].
Two-echelon distribution routing problem based on scene dynamics degree
[J].
Models and methods for two-echelon location routing problem with time constraints in city logistics
[J].
基于Memetic算法的两级车辆路径优化
[J].DOI:10.11835/j.issn.1000-582X.2017.03.011 [本文引用: 1]
Two stage vehicle routing optimization based on Memetic algorithm
[J].DOI:10.11835/j.issn.1000-582X.2017.03.011 [本文引用: 1]
Matheuristic for a two-echelon capacitated vehicle routing problem with environmental considerations in city logistics service
[J].DOI:10.1016/j.trd.2017.09.018 [本文引用: 1]
Two-echelon vehicle routing problem with simultaneous pickup and delivery: mathematical model and heuristic approach
[J].
The two-echelon vehicle routing problem with covering options: city logistics with cargo bikes and parcel lockers
[J].DOI:10.1016/j.cor.2020.104919 [本文引用: 1]
Equilibrium decisions for an innovation crowdsourcing platform
[J].
城市物流中的开闭混合式两级车辆路径问题
[J].
Open-close mixed two-echelon vehicle routing problem in city logistics
[J].
The two-echelon open location routing problem: mathematical model and hybrid heuristic
[J].
Design and modeling of a crowdsource-enabled system for urban parcel relay and delivery
[J].DOI:10.1016/j.trb.2016.12.022 [本文引用: 2]
A decision model for last-mile delivery planning with crowdsourcing integration
[J].DOI:10.1016/j.cie.2019.06.059 [本文引用: 1]
A branch-and-cut algorithm for the two-echelon capacitated vehicle routing problem with grouping constraints
[J].DOI:10.1016/j.ejor.2017.10.017 [本文引用: 1]
A branch-and-price algorithm for the home health care scheduling and routing problem with stochastic service times and skill requirements
[J].DOI:10.1080/00207543.2015.1082041 [本文引用: 1]
Formulations and branch-and-cut algorithms for multivehicle production and inventory routing problems
[J].DOI:10.1287/ijoc.2013.0550 [本文引用: 1]
An improved branch-cut-and-price algorithm for the two-echelon capacitated vehicle routing problem
[J].DOI:10.1016/j.cor.2019.104833 [本文引用: 1]
基于并行模拟退火算法求解时间依赖型车辆路径问题
[J].
Solving time dependent vehicle routing problem based on parallel simulated annealing algorithm
[J].
A tabu search heuristic for periodic and multi-depot vehicle routing problems
[J].
基于改进禁忌搜索算法的车辆路径问题模型
[J].
A model of vehicle routing problem based on improved tabu search algorithm
[J].
Simulation-based optimisation approach for the stochastic two-echelon logistics problem
[J].
A large neighbourhood based heuristic for two-echelon routing problems
[J].DOI:10.1016/j.cor.2016.06.014 [本文引用: 1]
An adaptive large neighborhood search heuristic for two-echelon vehicle routing problems arising in city logistics
[J].DOI:10.1016/j.cor.2012.04.007 [本文引用: 1]
An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization
[J].DOI:10.1016/j.ejor.2016.03.040 [本文引用: 1]
A genetic-algorithm-based approach to the two-echelon capacitated vehicle routing problem with stochastic demands in logistics service
[J].DOI:10.1057/s41274-016-0170-7 [本文引用: 1]
A novel swarm intelligence optimization approach: sparrow search algorithm
[J].DOI:10.1080/21642583.2019.1708830 [本文引用: 1]