气体绝缘金属封闭开关(gas insulated switchgear, GIS)是变电站的主要电器设备之一,其发生器老化、机械损伤故障后应及时对GIS管道内部产生缺陷的地方进行检测. 受限于GIS管道的尺寸和复杂的内部结构,传统的内窥镜检测方法难以完成垂直管道和离观察口较远的管道深处的检测工作. 因此,有必要开发一种代替内窥镜完成GIS管道检测工作的管道机器人.
四足机器人的冗余特性使得其运动学及步态规划相对复杂. Bi等[14]为模块化机器人开发的运动学和动力学模块库具有较强的通用性. Gülhan等[15]提出基于遗传算法的运动学分析方法,在解算足式机器人的运动学问题上具有一定的创新性. 有研究倾向于对机器人的腿部进行运动学分析,忽视机身的运动学特性. Chen等[16]将四足机器人作为整体运动学链系统进行分析,把机身的运动学正解转化为关于关节变量的十六阶多项式方程. 有研究提出将机身和腿部视为串联机构的运动学解算方法[17-18],在一定程度上简化了解算难度. 实际上,多足爬壁机器人是串并混联机构,许多学者将多足机器人作为并联机构进行运动学研究[19-20]. Howard等[21]提出基于并联机构的步行机运动学模型,求解机器人的逆运动学问题. 合理的步态轨迹是足式机器人运动稳定的基础. 对角步态是多数四足机器人的常用的行走方式,具有较高的运动效率[22-23]. 对于爬壁机器人而言,首要考虑的应该是机器人的运动稳定性和安全性. 基于机器人运动学的运动控制及合理的步态轨迹是实现机器人平稳运动的基础.
本研究对自制负压吸附的GIS管道内壁检测四足爬壁机器人,进行机器人的腿部和机身运动学分析. 将机器人整体视为并联机构,采用改进的牛顿迭代法求解,通过自适应调节下山参数,保证迭代收敛的同时以最快的速度收敛,解决机身正运动学求解困难的问题. 分别对机器人沿管道轴向和圆周方向的运动进行步态规划,并提出运动过程零冲击的轨迹规划方法,解决机器人运动平稳性问题. 利用Adams对机器人进行运动仿真,并在机器人样机上进行水平管道和垂直管道的全方位爬壁实验.
1. 机器人机构与曲面适应性分析
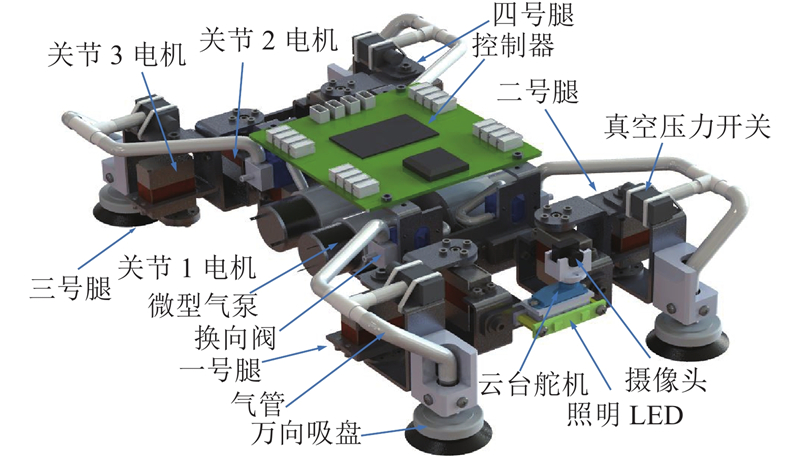
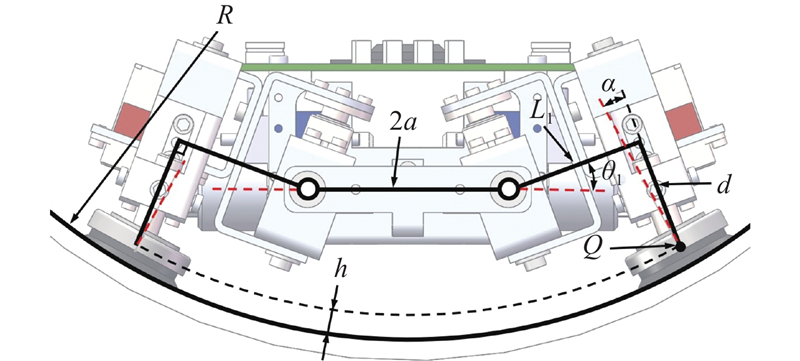
本研究设计的爬壁机器人结构如图1所示. 机器人本体由机身和4条腿组成. 4条腿呈对称分布结构连接在机身上,每条腿等效三自由度的串联操作臂,关节电机具有位置和速度的反馈. 其中关节1实现抬/放腿动作,关节2、3协调完成腿部的伸缩腿运动,腿部末端安装万向吸盘作为吸附足. 机器人机身上搭载控制器和微型气泵及换向阀,前端安装用于检测的摄像头. 当机器人四足支撑时,通过4条腿的协调运动带动机身的运动. 忽略吸盘的微量变形对机器人状态的影响,当机器人在管道内进行爬壁运动时,关节1的初始角度和万向吸盘的偏角直接决定机器人能够适应的壁面曲率,如图2所示. 图中,R为管道内壁半径,2a为机身宽度,a为关节1与机器人几何中心在机身宽度方向的垂直距离,L1、d分别为腿部相应的杆件长度,Q为万向吸盘的偏摆中心,h为万向吸盘偏转中心的高度,
图 1
图 2
令
与传统的负压吸附机器人相比,自适应的脚掌结构提高了机器人的运动能力,使其能适应不同曲率的曲面进行爬壁运动. 为了使机器人能够在不同的工作面,实现准确、平稳的爬壁运动,应对机器人腿部和机身的运动进行运动学分析并进行相应的步态轨迹规划.
2. 爬壁机器人的运动学分析
2.1. 腿部运动学分析
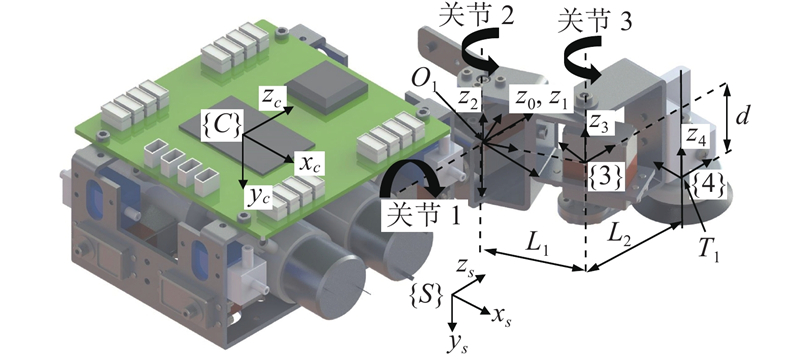
机器人的4条腿具有相同的运动特性,仅对机器人的一号腿进行运动学分析. 对于串联结构的腿部,根据D-H变化矩阵[25]的规则,对一号腿建立坐标系,如图3所示. 图中,关节轴1与关节轴2垂直相交于点
设腿部的3个关节变量为
表 1 机器人串联腿部结构的D-H参数
Tab.1
| | | | | |
| 1 | 0 | 0 | 0 | |
| 2 | 0 | 90° | 0 | |
| 3 | | 0 | 0 | |
| 4(末端) | | 0 | | 0 |
根据D-H方法和表1,可以得到末端坐标系{4}到坐标系{0}的齐次变化矩阵为
图 3
式中:
根据式(4),可以求得腿部的逆运动学解为
同理,可以求得其他3条腿的运动学解.
当机器人进行足端运动时,足端速度与各个关节的角速度之间的变化关系为
雅克比矩阵表达式为
通过建立运动学模型,分别得到腿部关节角度、角速度和足端位置、足端速度的对应关系,为后续的步态与轨迹规划做准备.
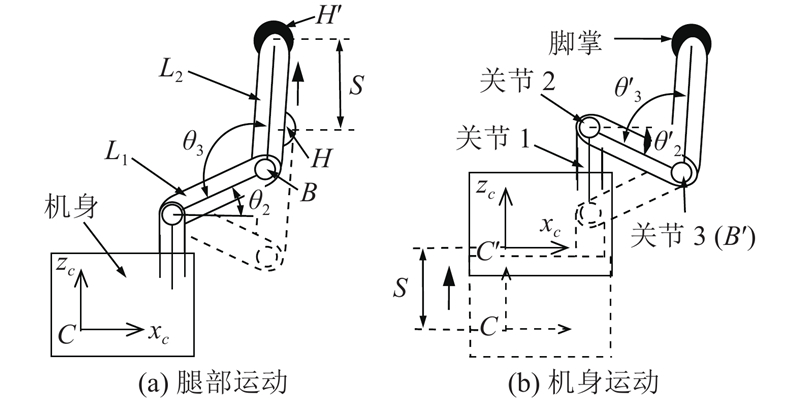
2.2. 机身运动学分析
机器人机身的运动由支撑足协同运动完成,可视为4支链的并联机构. 如图3所示,为了简化计算,将机身坐标系{C}固连在机身平面的几何中心,姿态与每条腿的坐标系{0}一致,原点C与4条腿坐标系{0}的原点共面. 工作空间坐标系{S}固定在机器人的爬行面,初始位置与坐标系{C}重合. 用X-Y-Z欧拉角表示坐标系{C}相对于坐标系{S}的旋转矩阵:
式中:α、β、γ为欧拉角参数.
2.2.1. 机身逆运动学求解
对于机身的逆运动学求解,可以独立计算各个支链,转化为腿部的逆运动学求解. 同样以一号腿为例,在建立的运动学模型中,存在如下关系
式中:
旋转矩阵
在机身的逆运动学中,
2.2.2. 机身正运动学求解
对于机身的正运动学求解,问题可以描述为已知各条支撑腿的关节变量
由式(10)同理可得
式中:
将式(13)分别与式(14)~(16)相减消去方程组中的
式中:k表示第k次迭代,原方程组是有6个冗余方程的超定方程组,其导数矩阵是奇异的,使用
传统的牛顿迭代算法[27]依赖初值
在原来的牛顿迭代法的基础上引入下山因子
牛顿下山法的关键是寻找满足式(20)且尽可能大的
3. 步态分析与足端轨迹规划
3.1. 步态分析
图 4
图 5
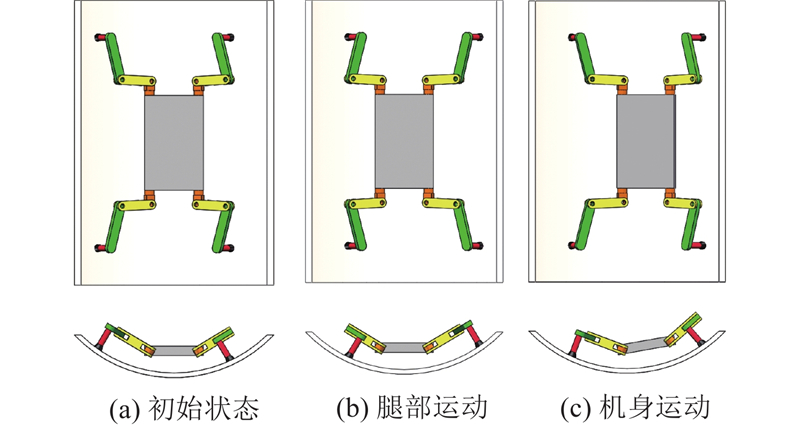
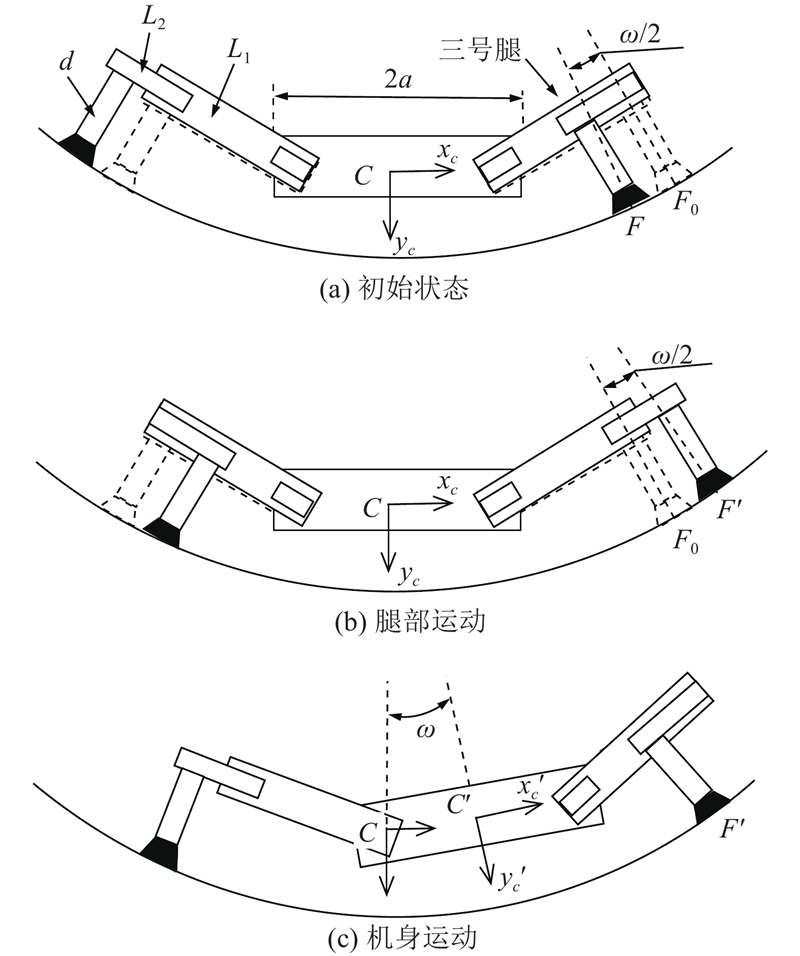
3.1.1. 轴向步态规划
图 6
以机身坐标系{C}为基准,对一号腿进行分析. 机器人以轴向步态沿
根据腿部运动学逆解式(5),求出机器人腿部运动时各个关节的变化,以此控制电机. 机身与其他3条腿的控制与此类似. 事实上,机身移动前后关节3的位置相同,根据几何关系,可以得到机器人执行轴向步态时腿部各关节变量的变化满足
3.1.2. 圆周步态规划
图 7
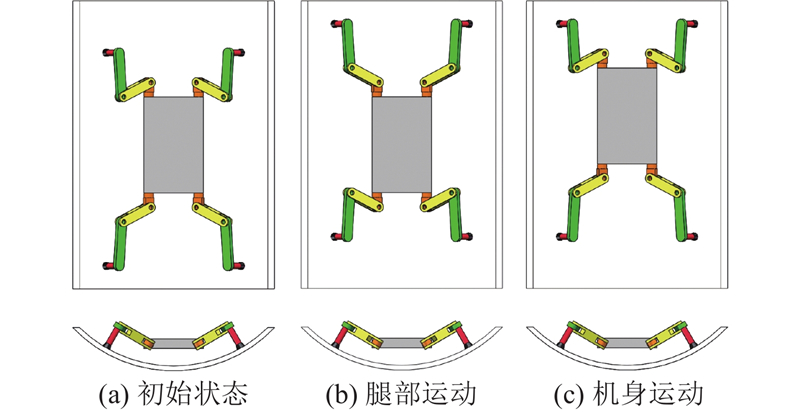
每1个圆周步态完成后的机器人状态即为下个步态周期的初始状态,如图7(a)~(c)所示的机器人状态一致. 以机身坐标系{C}为基准,对三号腿的运动进行分析,令图7中
3.2. 运动轨迹规划
3.2.1. 机器人平稳运动指标
机器人在爬行的过程中,其运动轨迹的优劣极大程度上影响着爬行运动的平稳性. 为了防止机器人在运动过程中出现较大的惯性力和打滑现象,保证爬行运动过程中的平稳性,建立机器人运动时应满足的约束指标如下:1)腿部或机身运动时,轨迹应圆滑连续、平稳协调,无明显的波动和摇晃; 2)腿部或机身运动时应保证零冲击,避免打滑现象,即实现运动开始和结束时各个方向的速度和加速度为零; 3)在运动过程中,各个关节角度必须在旋转角度范围内,关节角速度不能超过允许的极限值.
令机器人机身或足端的轨迹变化曲线为
式中:
对于所规划的运动轨迹,如果不满足关节角度限制条件
3.2.2. 足端轨迹规划
基于五阶方程提出运动过程零冲击的轨迹规划方法. 令机器人摆腿时,沿工作空间坐标系
为了保证腿部运动的零冲击,须分别满足轨迹、速度、加速度要求:
将式(28)代入轨迹曲线方程求解可以得到摆动腿足端沿
同理得摆动腿足端沿
3.2.3. 机身轨迹规划
机身的运动轨迹规划与足端类似,应满足运动过程平稳协调,无明显冲击,且要求始末时刻的速度和加速度为零.
令某时刻机身位姿为
机身的姿态轨迹曲线为
4. 运动仿真与样机实验
借助Adams对机器人进行运动仿真,并进行样机在真实管道内的全方位爬壁实验. 样机中的所有关节电机均使用型号为STS3032的总线舵机,最大角速度为62RPM即
表 2 机器人关节角度限制
Tab.2
| 编号 | | | |
| 一号腿 | | | |
| 二号腿 | | | |
| 三号腿 | | | |
| 四号腿 | | | |
4.1. 运动仿真
在Adams仿真中,建立的坐标系与图3一致,其中工作空间坐标系位于管道圆心处,规划机器人在
图 8
图 9
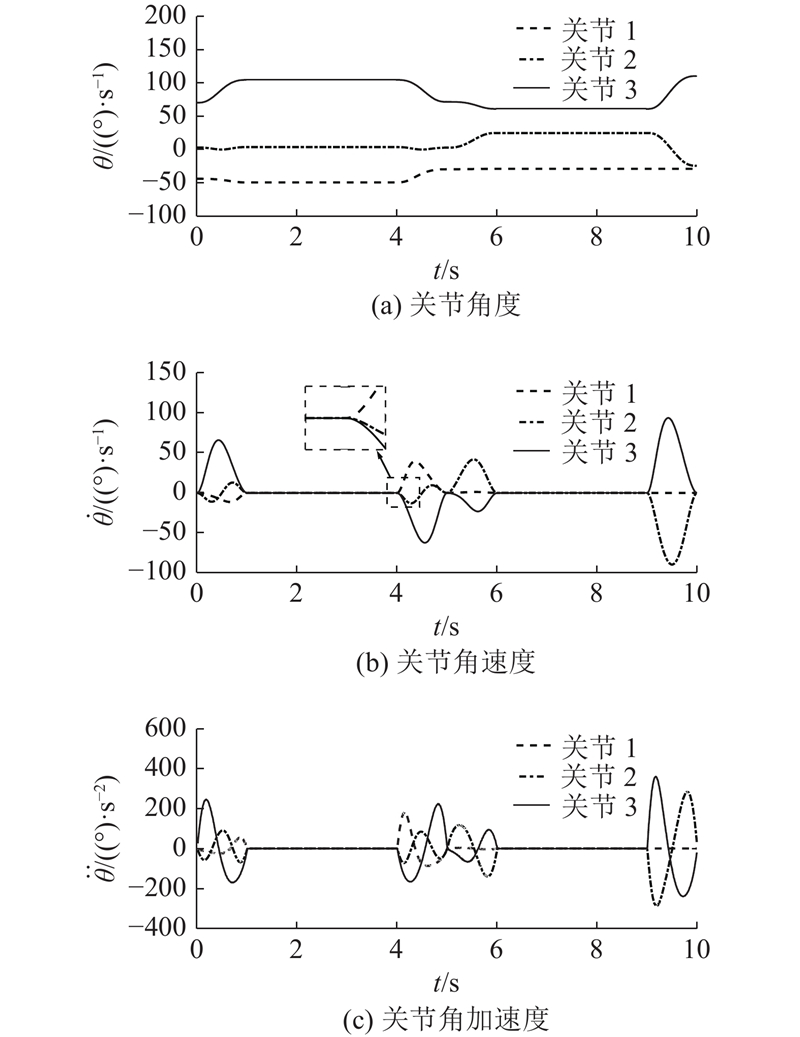
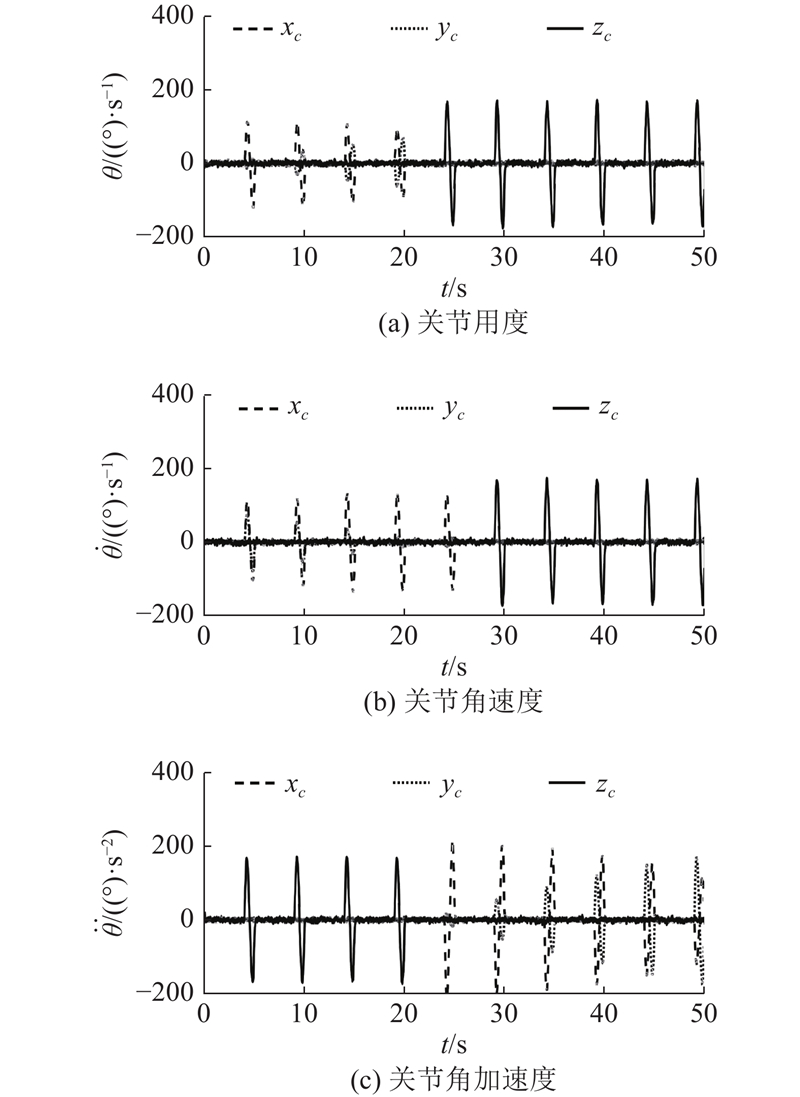
图 9 零冲击规划一号腿关节角度、角速度与角加速度
Fig.9 Joint angle, angular velocity and angular acceleration of leg one by zero impact planning
图 10
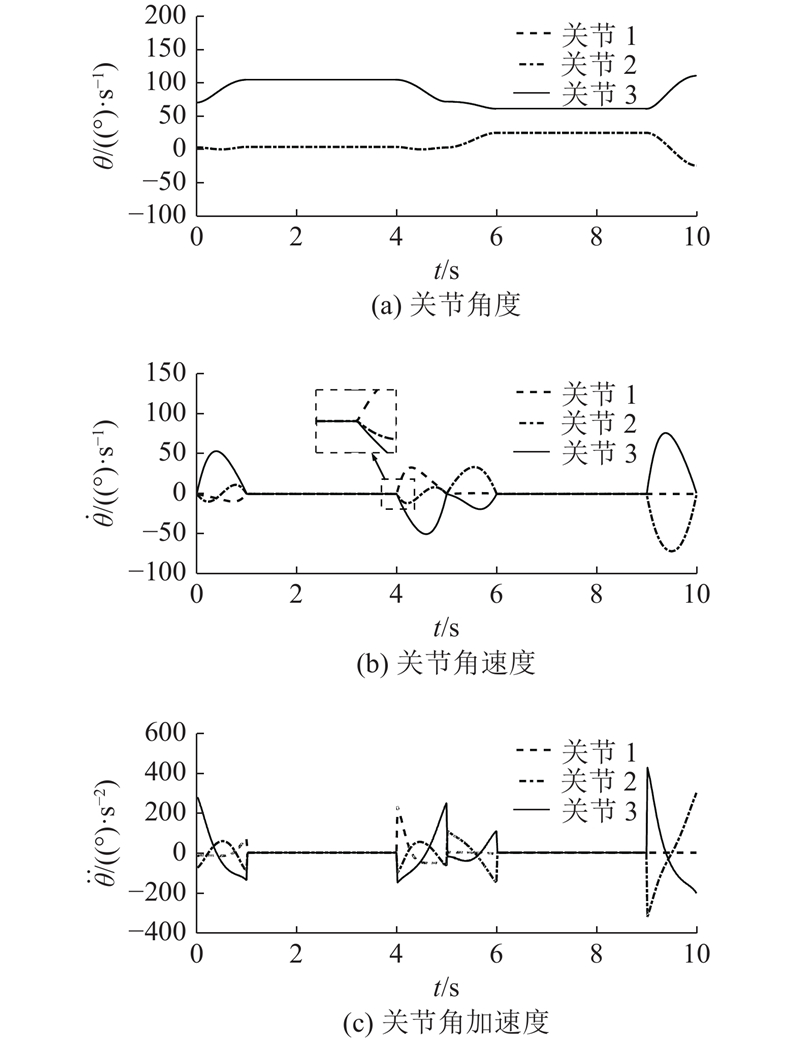
图 10 3次样条插值法一号腿关节角度、角速度与角加速度
Fig.10 Joint angle, angular velocity and angular acceleration of leg one by cubic spline interpolation
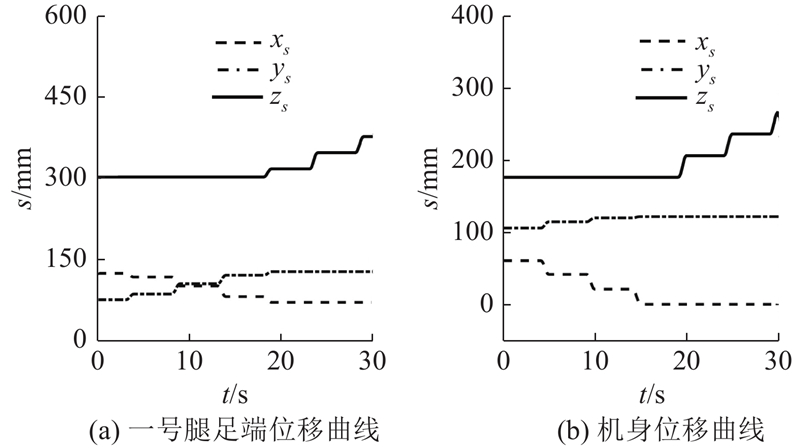
由图8可知,机身和足端沿各方向的运动轨迹与所规划的运动相符,且整个运动过程的轨迹曲线圆滑连续,平稳协调,无明显的波动和摇晃. 从图9可以看出,每个关节均满足式(26)中的关节角度约束和关节角速度约束条件. 角度、角速度和角加速度曲线随时间连续变化,电机转动平稳. 比较图9、10中2种轨迹规划方法的关节角速度和关节角加速度变化曲线,在零冲击轨迹规划方法下的关节角速度和角加速度曲线圆滑连续,不存在突变,且每个运动周期的始末时刻角速度和角加速度均为零,满足式(26)所述的机器人平稳运动的指标,说明机器人在运动过程中各关节不存在冲击现象,保证了机器人运动过程中的平稳性. 使用3次样条插值轨迹规划方法下的关节角速度,在执行腿部运动或机身运动的初始和结束阶段变化很快,角加速度曲线不连续,每个运动的始末时刻存在加速度突变,整个运动过程存在加大的惯性力和冲击现象.
4.2. 样机及实验
4.2.1. 控制系统设计
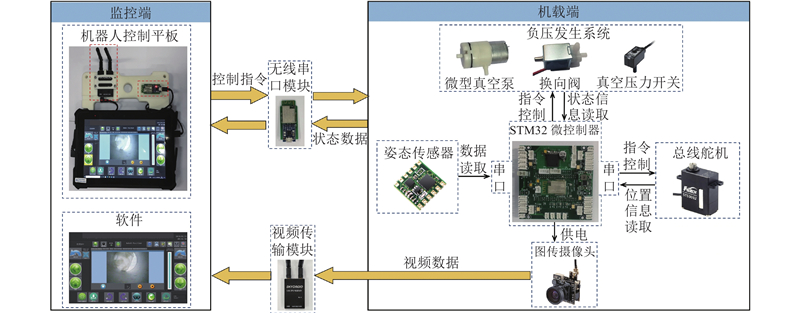
为了控制机器人在管道内进行爬壁运动,使用STM32系列单片机作为机器人机载端控制器,建立双层控制系统,如图11所示. 使用型号为STS3032的总线舵机作为机器人的关节电机,其内部集成微控制器和码盘,可通过串口通信实时反馈位置和速度信息. 机器人机身的几何中心装有型号为JY901的微型九轴姿态传感器,包括三轴加速度计、三轴陀螺仪和三轴数字罗盘,姿态传感器通过串口通信与机载端主控制器进行通信,并实时反馈机身的姿态和加速度信息. 由姿态传感器获取的机身加速度和姿态信息,以及12个关节电机的位置信息一起装包后,通过无线串口模块,反馈到监控端的控制平板上. 在机器人上安装图传摄像头,通过视频传输模块实现无线传输,将检测视频实时传输回监控端.
图 11
在监控端,使用Microsoft Visual 2018开发的控制平台软件,可以实现对机器人的运动控制和相应的信息采集. 操作者不仅可以控制机器人的运动,还可以观察管道和机器人的状态.
4.2.2. 管道爬壁实验
在运动仿真的基础上,进行机器人的管道爬壁实验,机器人样机的所有几何参数如前文所述. 设定机器人每个轴向步态的步幅
图 12
图 13
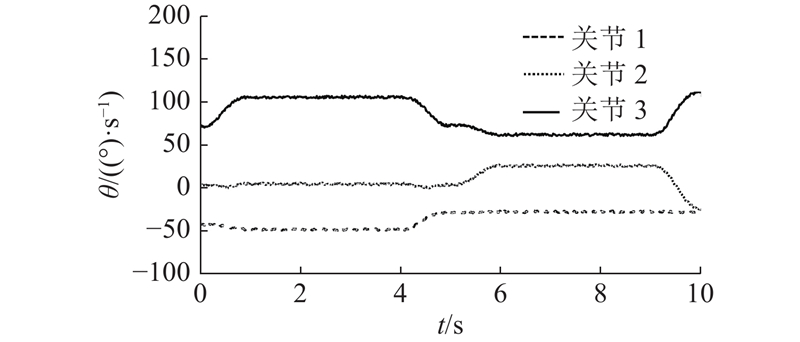
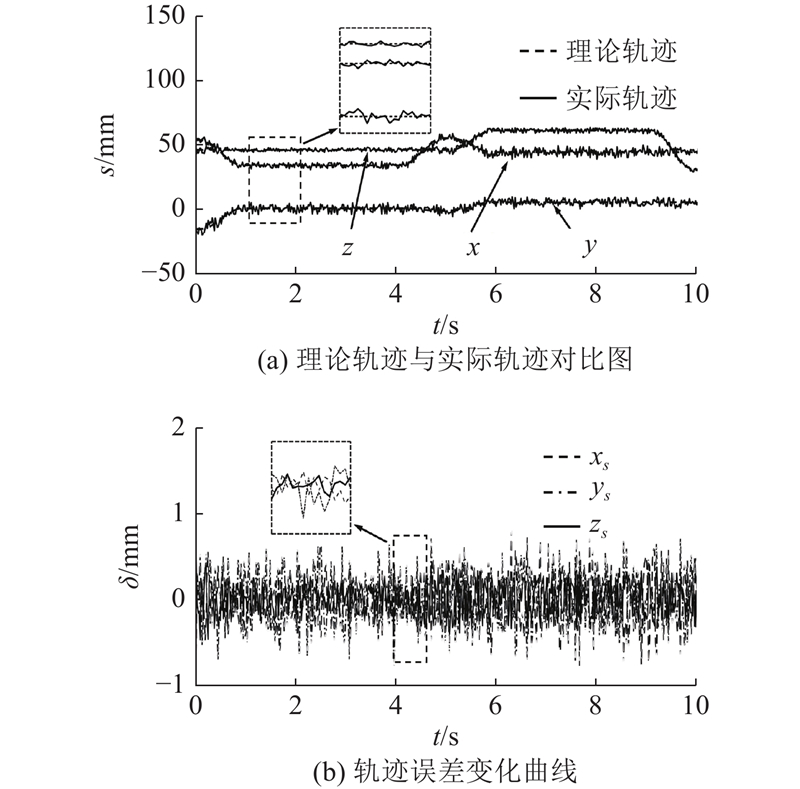
在实验过程中,通过无线串口实时采集机器人各个关节的实际关节角度,采样频率为50 Hz,同样取一号腿在圆周步态和轴向步态过渡阶段2个步态周期内连续10 s各关节的关节角度进行分析,变化曲线如图14所示. 以一号腿的基坐标系{0}为基准,根据图14所示的实际关节角度和腿部的正运动学解式(4),求解一号腿足端相对于基坐标系{0}的实际运动轨迹,并与所规划的理论轨迹进行误差分析,如图15所示. 图14所示的一号腿实际关节角度变化曲线与图9(a)所示运动仿真测量的一号腿关节角度曲线基本拟合,验证了机器人运动学求解的正确性,且每个关节均满足式(26)中的关节角度约束. 由图15可知,机器人在实际工作环境下的运动轨迹与理论轨迹大体一致,但也存在较小的误差. 其中,3个方向的最大误差分别为0.75、0.82、0.50 mm,平均误差分别为0.23、0.24、0.15 mm,各个方向的最大误差值均不超过1 mm,在允许的范围内. 实际轨迹与理论轨迹存在误差,主要是由关节电机的误差导致的:1)关节电机的分辨率为0.28°,输入和输出的误差会导致实际轨迹计算和运动的误差;2)爬壁机器人的结构上存在机械间隙和变形,在重力的作用下,也会导致电机的实际输出角度存在微量的误差.
图 14
图 15
为了考量机器人在管道内的运动平稳性和准确性,由姿态传感器实时测量机器人的机身加速度和姿态. 在水平管道实验中,取机器人在圆周爬壁运动和轴向运动过渡阶段一段时间内所测得的机身加速度和姿态数据,并使用卡尔曼滤波算法进行处理,结果如图16所示. 图中,ψ为机身姿态比那花值。前15 s内机器人执行圆周步态,并爬上管道顶端,如图13(c)所示,后15 s机器人在管道顶端执行轴向步态进行管道内的爬壁运动. 由图16(a)可知,机器人在执行圆周步态时,沿管道的轴向(
图 16
4.3. 现场应用
使用本研究所设计的管道爬壁机器人在变电站中,进行不同管径的水平管道和垂直管道的爬壁实验,如图17所示. 其中图17(a)为变电站现场的GIS管道布局,多以水平管道和垂直管道为主,尺寸为
图 17
在实验过程中,通过姿态传感器实时返回机器人机身的加速度,各取不同工况下10个步态周期的数据并使用卡尔曼滤波算法处理后,如图18所示. 在不同工况下,机器人机身的加速度曲线均不存在突变,且实现先加速后减速,说明机器人运动过程中不存在较大的惯性力,实现了在GIS管道里的平稳运动.
图 18
5. 结 论
(1)研制基于负压吸附的管道内壁四足爬壁机器人,可用于GIS管道内壁的全方位检测. 对机器人进行运动学分析,将机器人整体视为并联机构,采用改进的牛顿迭代法求解,通过自适应调节下山参数,保证迭代收敛的同时,以最快的速度收敛,解决机身正运动学求解困难的问题.
(2)分析机器人静态稳定爬行的轴向步态和圆周步态,提出运动过程零冲击的轨迹规划方法,保证机器人的运动平稳性.
(3)利用Adams对机器人进行运动仿真并进行机器人样机在水平管道和垂直管道以及变电站现场的GIS管道内的爬壁实验,机器人实现在不同工况下的全方位运动,过程平稳连续,无冲击现象,验证运动学模型的正确性和所规划步态的合理性.
(4)对于封闭GIS管道内部的检测,操作人员只能根据机器人回传的检测视频,判断该段管道是否存在故障,无法获取其具体方位. 未来计划开发机器人在管道内的定位系统,以准确定位故障位置.
参考文献
Differential-drive in-pipe robot for moving inside urban gas pipelines
[J].DOI:10.1109/TRO.2004.838000 [本文引用: 1]
An overview of shape memory alloy-coupled actuators and robots
[J].DOI:10.1089/soro.2016.0008 [本文引用: 1]
Development of in-pipe inspection robot
[J].DOI:10.1016/j.matpr.2018.06.406
Normal-force control for an in-pipe robot according to the inclination of pipelines
[J].
三轴差动式管道机器人机械自适应驱动技术
[J].DOI:10.3321/j.issn:0577-6686.2008.09.022
Mechanical self-adaptive drive technology of triaxial differential pipe-robot
[J].DOI:10.3321/j.issn:0577-6686.2008.09.022
Virtual prototyping, design and analysis of an in-pipe inspection mobile robot
[J].
轮式磁吸附超声检测爬壁机器人的设计与吸附稳定性分析
[J].DOI:10.11817/j.issn.1672-7207.2019.12.008
Design and adsorption stability analysis of wall climbing robot based on wheeled magnetic adsorption for ultrasonic detection
[J].DOI:10.11817/j.issn.1672-7207.2019.12.008
爬壁机器人磁吸附组件优化设计与试验研究
[J].DOI:10.3785/j.issn.1008-973X.2018.10.001
Optimization design and experimental research on magnetic components for wall-climbing robot
[J].DOI:10.3785/j.issn.1008-973X.2018.10.001
具有良好壁面过渡能力的新型爬壁机器人动力学建模与分析
[J].DOI:10.3969/j.issn.1001-3881.2018.23.001 [本文引用: 1]
Dynamic modeling and analysis of new climbing robot with good wall transition capability
[J].DOI:10.3969/j.issn.1001-3881.2018.23.001 [本文引用: 1]
Automated geneartion of the D–H parameters for configuration design of modular manipulators
[J].DOI:10.1016/j.rcim.2006.02.014 [本文引用: 1]
Kinematic arrangement optimization of a quadruped robot with genetic algorithms
[J].
Kinematic solution of a quadruped walking robot-posture analysis of TITAN-VIII
[J].DOI:10.1016/S1474-6670(17)56140-6 [本文引用: 1]
Kinematic analysis and experimental verification on the locomotion of gecko
[J].DOI:10.1016/S1672-6529(08)60121-3 [本文引用: 1]
Kinematic analysis of a walking machine
[J].
基于ADAMS的仿壁虎机器人步态规划及仿真
[J].DOI:10.3724/SP.J.1218.2010.00499 [本文引用: 1]
Gait planning and simulation of gecko inspired robot based on ADAMS
[J].DOI:10.3724/SP.J.1218.2010.00499 [本文引用: 1]
Gait planning based on kinematics for a quadruped gecko model with redundancy
[J].DOI:10.1016/j.robot.2009.11.009 [本文引用: 1]
A modular biped wall-climbing robot with high mobility and manipulating function
[J].DOI:10.1109/TMECH.2012.2213303 [本文引用: 1]
Introduction to robotics: mechanics and control
[J].DOI:10.1016/0924-0136(91)90096-W [本文引用: 1]
Closed-form forward kinematics solutions of a 4-DOF parallel robot
[J].DOI:10.1007/s12555-009-0520-1 [本文引用: 1]
Nonlinear programming: theories and algorithms of some unconstrained optimization methods (steepest descent and Newton's method)
[J].
A new algorithm for computing the inverse and generalized inverse of the scaled factor circulant matrix
[J].