[1]
GRAIMANN B, ALLISON B, PFURTSCHELLER G. Brain-computer interface: a gentle introduction [M]. The frontiers collection. Berlin, Heidelberg: Springer, 2009: 1-27.
[本文引用: 1]
[2]
ADAMS M, BEN-SALEM S, ISLAM Z, et al. Towards an SSVEP-BCI controlled smart home [C]// 2019 IEEE International Conference on Systems Man and Cybernetics (SMC) . Bari: IEEE, 2019: 2737-2742.
[本文引用: 1]
[3]
CHEN L, WANG Z P, HE F, et al. An online hybrid brain-computer interface combining multiple physiological signals for webpage browse [C]// 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society . Milan: IEEE, 2015: 1152-1155.
[本文引用: 1]
[4]
WONG C M, TANG Q, WAN F, et al. A multi-channel SSVEP-based BCI for computer games with analogue control [C]// Proceedings of the 2015 IEEE International Conference on Computational Intelligence and Virtual Environments for Measurement Systems and Application (CIVEMSA) . Shenzhen: IEEE, 2015: 1-6.
[本文引用: 1]
[5]
PFURTSCHELLER G, LOPES DA SILVA F H Event-related EEG/MEG synchronization and desynchronization: basic principles
[J]. Clinical Neurophysiology , 1999 , 110 (11 ): 1842 - 1857
DOI:10.1016/S1388-2457(99)00141-8
[本文引用: 1]
[7]
BAIG M Z, ASLAML N, SHUM H P H Filtering techniques for channel selection in motor imagery EEG applications: a survey
[J]. Artificial Intelligence Review , 2020 , 53 (3 ): 1207 - 1232
URL
[本文引用: 1]
[8]
霍首君, 郝琰, 石慧宇, 等 基于深度卷积网络的运动想象脑电信号模式识别
[J]. 计算机应用 , 2020 , 41 (4 ): 1042 - 1048
URL
[本文引用: 1]
HUO Shou-jun, HAO Yan, SHI Hui-yu, et al Pattern recognition of motor imagery EEG based on deep convolutional networks
[J]. Computer Applications , 2020 , 41 (4 ): 1042 - 1048
URL
[本文引用: 1]
[9]
CHATTERJEE R, BANDYOPADHYAY T, SANYAL D K, et al. Comparative analysis of feature extraction techniques in motor imagery EEG signal classification [C]// Proceedings of First International Conference on Smart System, Innovations and Computing. Smart Innovation, Systems and Technologies . Jaipur: Springer, 2018, 79: 73-83.
[本文引用: 1]
[10]
WANG Y J, GAO S K, GAO X R, et al. Common spatial pattern method for channel selection in motor imagery based brain-computer interface [C]// International Conference of the Engineering in Medicine and Biology Society . Shanghai: IEEE, 2005: 5392-5395.
[本文引用: 1]
[11]
ANG K K, CHINY C, ZHANG H H, et al. Filter bank common spatial pattern (FBCSP) in brain-computer interface [C]// Proceedings of the IEEE International Joint Conference on Neural Networks . Hong Kong: IEEE, 2008: 2391–2398.
[本文引用: 1]
[13]
TYAGI A, NEHRA V. Time frequency analysis of non-stationary motor imagery EEG signal [C]// 2017 International Conference on Computing and Communication Technologies for Smart Nation (IC3TSN) . Gurgaon: IEEE, 2017: 44-50.
[本文引用: 1]
[14]
LIU J, CHENG Y, ZHANG W. Deep learning EEG response representation for brain computer interface [C]// 34th Chinese Control Conference. Hangzhou: IEEE, 2015: 3518-3523.
[本文引用: 1]
[15]
KUMAR S, SHARMA A, MAMUN K, et al. A deep learning approach for motor imagery EEG signal classification [C]// 2016 3rd Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE) . Nadi: IEEE, 2016: 34-39.
[本文引用: 1]
[16]
LEE H K, CHOI Y. A convolutional neural networks scheme for classification of motor imagery EEG based on wavelet time-frequency image [C]// 2018 International Conference on Information Networking (ICOIN) . Chiang Mai: IEEE, 2018: 906-909.
[本文引用: 1]
[17]
ZHU X Y, LI P Y, LI C B, et al Separated channel convolutional neural network to realize the training free motor imagery BCI systems
[J]. Biomedical Signal Processing and Control , 2019 , 49 : 396 - 403
DOI:10.1016/j.bspc.2018.12.027
[本文引用: 1]
[18]
YANG T, PHUA K S, YU J H, et al. Image-based motor imagery EEG classification using convolutional neural network [C]// 2019 IEEE EMBS International Conference on Biomedical and Health Informatics (BHI) . Chicago: IEEE, 2019: 1-4.
[本文引用: 1]
[19]
LI Y, ZHANG X R, LEI M Y, et al A channel-projection mixed-scale convolutional neural network for motor imagery EEG decoding
[J]. IEEE Transaction on Neural Systems and Rehabilitation Engineering , 2019 , 27 (6 ): 1170 - 1180
DOI:10.1109/TNSRE.2019.2915621
[本文引用: 1]
[20]
WU H, NIU Y, LI F, et al A parallel multiscale filter bank convolutional neural networks for motor imagery EEG classification
[J]. Frontiers in Neuroscience , 2019 , 26 (13 ): 1275
URL
[本文引用: 1]
[21]
ROY S, MCCREADIE K, PRASAD G. Can a single model deep learning approach enhance classification accuracy of an EEG-based brain-computer interface? [C]// 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC) . Bari: IEEE, 2019: 1317-1321.
[本文引用: 1]
[22]
TANG X B, ZHAO J C, FU W L, et al. A novel classification algorithm for MI-EEG based on deep learning [C]// 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC) . Chongqing: IEEE, 2019: 606-611.
[23]
SHEN Y R, LU H T, JIA J. Classification of motor imagery EEG signal with deep learning models [C]// International Conference on Intelligent Science and Big Data Engineering . Dalian: Springer, 2017: 181-190.
[本文引用: 1]
[24]
LASHGARI E, LIANG D, MAOZ U Data augmentation for deep-learning-based electroencephalography
[J]. Journal of Neuroscience Methods , 2020 , 346 : 108885
DOI:10.1016/j.jneumeth.2020.108885
[本文引用: 1]
[25]
BASHIVAN P, RISH I, YEASIN M, et al. Learning representations from EEG with deep recurrent-convolutional neural networks [EB/OL]. (2015-11-19) [2020-12-28]. https://arxiv.org/abs/1511.06448v3.
[本文引用: 1]
[26]
CHANG L, DENG X M, ZHOU M Q, et al Convolutional neural networks in image understanding
[J]. Acta Automatica Sinica , 2016 , 42 (9 ): 1300 - 1312
URL
[本文引用: 1]
[27]
DING Y, ROBINSON N, ZENG Q H, et al. TSception: a deep learning framework for emotion detection using EEG [EB/OL]. (2020-04-02) [2020-12-28]. https://arxiv.org/abs/2004.02965.
[本文引用: 1]
[28]
王卫星, 孙守迁, 李超, 等 基于卷积神经网络的脑电信号上肢运动意图识别
[J]. 浙江大学学报:工学版 , 2017 , 51 (7 ): 1381 - 1389
URL
[本文引用: 1]
WANG Wei-xing, SUN Shou-qian, LI Chao, et al Recognition of upper limb motion intention of EEG signal based on convolutional neural network
[J]. Journal of Zhejiang University: Engineering Science , 2017 , 51 (7 ): 1381 - 1389
URL
[本文引用: 1]
[29]
TANGERMANN M, MÜLLER K R, AERTSEN A, et al Review of the BCI competition IV
[J]. Frontiers Neuroscience , 2012 , 6 : 55
URL
[本文引用: 1]
[30]
LI D L, WANG J H, XU J C, et al Densely feature fusion based on convolutional neural networks for motor imagery EEG classification
[J]. IEEE Access , 2019 , 7 : 132720 - 132730
DOI:10.1109/ACCESS.2019.2941867
[本文引用: 4]
[31]
DAI G, ZHOU J, HUANG J, et al HS-CNN: a CNN with hybrid convolutional scale for EEG motor imagery classification
[J]. Journal of Neural Engineering , 2020 , 17 (1 ): 016025
DOI:10.1088/1741-2552/ab405f
[本文引用: 2]
[32]
MAJIDOV I, WHANGBO T Efficient classification of motor imagery electroencephalography signal using deep learning methods
[J]. Sensors , 2019 , 19 (7 ): 1736 - 1749
DOI:10.3390/s19071736
[本文引用: 2]
[33]
ZHANG R, QUN Z, DOU L, et al A novel hybrid deep learning scheme for four-class motor imagery classification
[J]. Journal of Neural Engineering , 2019 , 16 (6 ): 1 - 11
URL
[本文引用: 4]
[34]
MA X G, WANG D S, LIU D H, et al DWT and CNN based multi-class motor imagery electroencephalographic signal recognition
[J]. Journal of Neural Engineering , 2020 , 17 (1 ): 016073
DOI:10.1088/1741-2552/ab6f15
[本文引用: 1]
[35]
GAUR P, PACHORI R B, WANG H, et al A multi-class EEG-based BCI classification using multivariate empirical mode decomposition based filtering and Riemannian Geometry
[J]. Expert Systems with Applications , 2018 , 95 : 201 - 211
DOI:10.1016/j.eswa.2017.11.007
[本文引用: 2]
[36]
XU J, ZHENG H, WANG J, et al Recognition of EEG signal motor imagery intention based on deep multi-view feature learning
[J]. Sensors , 2020 , 20 (12 ): 3496
DOI:10.3390/s20123496
[本文引用: 3]
[37]
XU M, YAO J, ZHANG Z, et al Learning EEG topographical representation for classification via convolutional neural network
[J]. Pattern Recognition , 2020 , 105 : 107390
DOI:10.1016/j.patcog.2020.107390
[本文引用: 3]
[38]
SAKHAVI S, GUAN C, YAN S Learning temporal information for brain-computer interface using convolutional neural networks
[J]. IEEE Transaction on Neural Networks and Learning Systems , 2018 , 29 (11 ): 5619 - 5629
DOI:10.1109/TNNLS.2018.2789927
[本文引用: 3]
[39]
ZHAO X, ZHANG H, ZHU G, et al A multi-branch 3D convolutional neural network for EEG-based motor imagery classification
[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering , 2019 , 27 (10 ): 2164 - 2177
DOI:10.1109/TNSRE.2019.2938295
[本文引用: 2]
[40]
ANG K K, CHIN Z Y, WANG C, et al Filter bank common spatial pattern algorithm on BCI Competition IV datasets 2a and 2b
[J]. Frontiers in Neuroscience , 2012 , 6 : 39
URL
[本文引用: 4]
[41]
COHEN J A coefficient of agreement for nominal scales
[J]. Educational and Psychological Measurement , 1960 , 20 (1 ): 37 - 46
DOI:10.1177/001316446002000104
[本文引用: 1]
1
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
1
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
1
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
1
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
Event-related EEG/MEG synchronization and desynchronization: basic principles
1
1999
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
脑机接口技术及其在神经科学中的应用
1
2021
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
脑机接口技术及其在神经科学中的应用
1
2021
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
Filtering techniques for channel selection in motor imagery EEG applications: a survey
1
2020
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
基于深度卷积网络的运动想象脑电信号模式识别
1
2020
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
基于深度卷积网络的运动想象脑电信号模式识别
1
2020
... 人类试图通过脑科学揭示和感知大脑活动和功能的内部机制,这是21世纪最具挑战性的研究领域之一. 脑机接口(brain-computer interface, BCI)系统架起了人与计算机之间直接进行交流的桥梁并促进了人脑活动的研究[1 ] . 基于脑电信号(electroencephalogram, EEG)的BCI具有便利性和安全性的优势,引起了人们的关注并得到了广泛的应用. BCI为人工智能的发展提供了更多的解决方案,如直接通过大脑意识实现智能家居的控制[2 ] 、网页浏览[3 ] 和娱乐游戏[4 ] 等. 运动想象(motor imagery, MI)是BCI广泛使用的范式之一,当人们想象肢体运动而不进行实际运动时,事件相关去同步和事件相关同步现象分别发生在对侧半球和同侧半球的感觉运动区域[5 ] . BCI在医学领域能够发挥重要作用,开发基于MI的BCI系统对中风以及其他患有严重运动障碍的病人具有重要意义[6 ] . 失去运动能力的病人经过运动想象训练后,可以通过想象肢体或者肌肉的运动完成对外部设备的控制,自主进行康复训练或完成其他操作,例如控制轮椅或假肢以改善生活质量[7 ] . BCI系统功能的实现主要包括脑电信号采集、信号预处理、特征提取与选择、分类以及将分类结果转化为控制指令[8 ] ,其中特征的提取、选择以及分类是当前研究的重点. 将患者的意图准确地转化为相应的控制指令须对采集的脑电信号高精度分类,因此提取合适的特征并选择适当的分类器实现准确分类是BCI持续发展面临的一个挑战. 由于非侵入性EEG采集设备收集到的EEG信噪比较低,并且个体之间的EEG信号存在差异,造成多类运动想象信号分析困难. 因此,有必要设计能够克服个体差异影响并提高多分类准确性的新方法. ...
1
... 为了高精度地识别MI模式,早期研究主要是根据经验进行特征提取以及利用机器学习完成分类. 小波变换、功率谱密度和频谱图等是常使用的时频特征提取方法[9 ] ,有助于探索EEG信号随时间变化的频率信息. 接着,学者们开始研究脑电信号中存在的空间相关性,其中最著名的算法是共空间模式(common spatial pattern, CSP)[10 ] ,它通过计算空间滤波器最大化2个类别之间的方差. 由于个体差异,CSP选择的带宽频率可能并不适合所有个体,于是提出滤波器组公共空间模式[11 ] ,将脑电信号分为多个子频带再分别进行CSP滤波提取特征. 在特征提取工作完成后,可以采用主流的机器学习模型如采用支持向量机[12 ] 或线性判别算法[13 ] 完成分类. ...
1
... 为了高精度地识别MI模式,早期研究主要是根据经验进行特征提取以及利用机器学习完成分类. 小波变换、功率谱密度和频谱图等是常使用的时频特征提取方法[9 ] ,有助于探索EEG信号随时间变化的频率信息. 接着,学者们开始研究脑电信号中存在的空间相关性,其中最著名的算法是共空间模式(common spatial pattern, CSP)[10 ] ,它通过计算空间滤波器最大化2个类别之间的方差. 由于个体差异,CSP选择的带宽频率可能并不适合所有个体,于是提出滤波器组公共空间模式[11 ] ,将脑电信号分为多个子频带再分别进行CSP滤波提取特征. 在特征提取工作完成后,可以采用主流的机器学习模型如采用支持向量机[12 ] 或线性判别算法[13 ] 完成分类. ...
1
... 为了高精度地识别MI模式,早期研究主要是根据经验进行特征提取以及利用机器学习完成分类. 小波变换、功率谱密度和频谱图等是常使用的时频特征提取方法[9 ] ,有助于探索EEG信号随时间变化的频率信息. 接着,学者们开始研究脑电信号中存在的空间相关性,其中最著名的算法是共空间模式(common spatial pattern, CSP)[10 ] ,它通过计算空间滤波器最大化2个类别之间的方差. 由于个体差异,CSP选择的带宽频率可能并不适合所有个体,于是提出滤波器组公共空间模式[11 ] ,将脑电信号分为多个子频带再分别进行CSP滤波提取特征. 在特征提取工作完成后,可以采用主流的机器学习模型如采用支持向量机[12 ] 或线性判别算法[13 ] 完成分类. ...
四类运动想象脑电信号特征提取与分类算法
1
2012
... 为了高精度地识别MI模式,早期研究主要是根据经验进行特征提取以及利用机器学习完成分类. 小波变换、功率谱密度和频谱图等是常使用的时频特征提取方法[9 ] ,有助于探索EEG信号随时间变化的频率信息. 接着,学者们开始研究脑电信号中存在的空间相关性,其中最著名的算法是共空间模式(common spatial pattern, CSP)[10 ] ,它通过计算空间滤波器最大化2个类别之间的方差. 由于个体差异,CSP选择的带宽频率可能并不适合所有个体,于是提出滤波器组公共空间模式[11 ] ,将脑电信号分为多个子频带再分别进行CSP滤波提取特征. 在特征提取工作完成后,可以采用主流的机器学习模型如采用支持向量机[12 ] 或线性判别算法[13 ] 完成分类. ...
四类运动想象脑电信号特征提取与分类算法
1
2012
... 为了高精度地识别MI模式,早期研究主要是根据经验进行特征提取以及利用机器学习完成分类. 小波变换、功率谱密度和频谱图等是常使用的时频特征提取方法[9 ] ,有助于探索EEG信号随时间变化的频率信息. 接着,学者们开始研究脑电信号中存在的空间相关性,其中最著名的算法是共空间模式(common spatial pattern, CSP)[10 ] ,它通过计算空间滤波器最大化2个类别之间的方差. 由于个体差异,CSP选择的带宽频率可能并不适合所有个体,于是提出滤波器组公共空间模式[11 ] ,将脑电信号分为多个子频带再分别进行CSP滤波提取特征. 在特征提取工作完成后,可以采用主流的机器学习模型如采用支持向量机[12 ] 或线性判别算法[13 ] 完成分类. ...
1
... 为了高精度地识别MI模式,早期研究主要是根据经验进行特征提取以及利用机器学习完成分类. 小波变换、功率谱密度和频谱图等是常使用的时频特征提取方法[9 ] ,有助于探索EEG信号随时间变化的频率信息. 接着,学者们开始研究脑电信号中存在的空间相关性,其中最著名的算法是共空间模式(common spatial pattern, CSP)[10 ] ,它通过计算空间滤波器最大化2个类别之间的方差. 由于个体差异,CSP选择的带宽频率可能并不适合所有个体,于是提出滤波器组公共空间模式[11 ] ,将脑电信号分为多个子频带再分别进行CSP滤波提取特征. 在特征提取工作完成后,可以采用主流的机器学习模型如采用支持向量机[12 ] 或线性判别算法[13 ] 完成分类. ...
1
... 深度学习是近年来受到广泛关注的机器学习方法,其经典模型神经网络被认为是一项极为重要的突破性技术. 具有深层结构的深度神经网络可以通过分层非线性映射来学习MI的更高级别的特征[14 ] ,被认为是提取脑电信号特征的有前途的工具. Kumar等[15 ] 采用广泛使用的CSP方法来提取基于方差的特征,然后将其放入深度神经网络中进行分类. Lee等[16 ] 利用连续小波变换获得MI中EEG信号的时频表示,它具有将频谱信息保持在信号时频域的能力. 考虑到CSP算法提取了空间关系但丢失了时频信息,Zhu等[17 ] 设计分离的通道卷积网络对CSP通道进行编码,保留了有助于区分的时变信息. ...
1
... 深度学习是近年来受到广泛关注的机器学习方法,其经典模型神经网络被认为是一项极为重要的突破性技术. 具有深层结构的深度神经网络可以通过分层非线性映射来学习MI的更高级别的特征[14 ] ,被认为是提取脑电信号特征的有前途的工具. Kumar等[15 ] 采用广泛使用的CSP方法来提取基于方差的特征,然后将其放入深度神经网络中进行分类. Lee等[16 ] 利用连续小波变换获得MI中EEG信号的时频表示,它具有将频谱信息保持在信号时频域的能力. 考虑到CSP算法提取了空间关系但丢失了时频信息,Zhu等[17 ] 设计分离的通道卷积网络对CSP通道进行编码,保留了有助于区分的时变信息. ...
1
... 深度学习是近年来受到广泛关注的机器学习方法,其经典模型神经网络被认为是一项极为重要的突破性技术. 具有深层结构的深度神经网络可以通过分层非线性映射来学习MI的更高级别的特征[14 ] ,被认为是提取脑电信号特征的有前途的工具. Kumar等[15 ] 采用广泛使用的CSP方法来提取基于方差的特征,然后将其放入深度神经网络中进行分类. Lee等[16 ] 利用连续小波变换获得MI中EEG信号的时频表示,它具有将频谱信息保持在信号时频域的能力. 考虑到CSP算法提取了空间关系但丢失了时频信息,Zhu等[17 ] 设计分离的通道卷积网络对CSP通道进行编码,保留了有助于区分的时变信息. ...
Separated channel convolutional neural network to realize the training free motor imagery BCI systems
1
2019
... 深度学习是近年来受到广泛关注的机器学习方法,其经典模型神经网络被认为是一项极为重要的突破性技术. 具有深层结构的深度神经网络可以通过分层非线性映射来学习MI的更高级别的特征[14 ] ,被认为是提取脑电信号特征的有前途的工具. Kumar等[15 ] 采用广泛使用的CSP方法来提取基于方差的特征,然后将其放入深度神经网络中进行分类. Lee等[16 ] 利用连续小波变换获得MI中EEG信号的时频表示,它具有将频谱信息保持在信号时频域的能力. 考虑到CSP算法提取了空间关系但丢失了时频信息,Zhu等[17 ] 设计分离的通道卷积网络对CSP通道进行编码,保留了有助于区分的时变信息. ...
1
... 上述深度学习方法取得了较好的效果,但特征提取工作仍须根据经验知识手动完成. 特征提取与分类工作分离的方法不能充分表征采集到信号的特征,且无法考虑到不同个体脑电信号之间的差异性,导致分类精度低、费时费力. 原始EEG信号中包含的多模态信息无法得到充分利用,以及神经网络从原始数据中学习抽象表达的能力无法得到证明. 利用深度学习基于原始数据进行端到端的学习则可以直接提取到信号中隐藏的特征进行分类. Yang等[18 ] 根据采集脑电时电极的3D位置将EEG信号映射为2D网格图像格式,并提出基于图像格式EEG信号的卷积神经网络(convolutional neural network, CNN). 利用2D和3D卷积核对左手和右手的运动进行分类的精度分别为68.38%±7.029%和65.94%±8.5%. 深度学习是受数据驱动的方法,Li等[19 ] 利用幅值干扰作为数据增强手段扩充数据集,并构造了通道投影混合尺度CNN来端到端解码EEG,该框架采用原始多通道EEG信号作为输入,提高了解码精度. Wu等[20 ] 提出并行的多尺度滤波器组CNN来进行MI分类,建立多尺度卷积用于时频特征提取,并将提取的输出特征连接到空间卷积层中,完成脑电信号多模态特征的融合. Roy等[21 -23 ] 探索了利用不同的融合模型自动完成对原始信号的多模态特征提取以及分类. ...
A channel-projection mixed-scale convolutional neural network for motor imagery EEG decoding
1
2019
... 上述深度学习方法取得了较好的效果,但特征提取工作仍须根据经验知识手动完成. 特征提取与分类工作分离的方法不能充分表征采集到信号的特征,且无法考虑到不同个体脑电信号之间的差异性,导致分类精度低、费时费力. 原始EEG信号中包含的多模态信息无法得到充分利用,以及神经网络从原始数据中学习抽象表达的能力无法得到证明. 利用深度学习基于原始数据进行端到端的学习则可以直接提取到信号中隐藏的特征进行分类. Yang等[18 ] 根据采集脑电时电极的3D位置将EEG信号映射为2D网格图像格式,并提出基于图像格式EEG信号的卷积神经网络(convolutional neural network, CNN). 利用2D和3D卷积核对左手和右手的运动进行分类的精度分别为68.38%±7.029%和65.94%±8.5%. 深度学习是受数据驱动的方法,Li等[19 ] 利用幅值干扰作为数据增强手段扩充数据集,并构造了通道投影混合尺度CNN来端到端解码EEG,该框架采用原始多通道EEG信号作为输入,提高了解码精度. Wu等[20 ] 提出并行的多尺度滤波器组CNN来进行MI分类,建立多尺度卷积用于时频特征提取,并将提取的输出特征连接到空间卷积层中,完成脑电信号多模态特征的融合. Roy等[21 -23 ] 探索了利用不同的融合模型自动完成对原始信号的多模态特征提取以及分类. ...
A parallel multiscale filter bank convolutional neural networks for motor imagery EEG classification
1
2019
... 上述深度学习方法取得了较好的效果,但特征提取工作仍须根据经验知识手动完成. 特征提取与分类工作分离的方法不能充分表征采集到信号的特征,且无法考虑到不同个体脑电信号之间的差异性,导致分类精度低、费时费力. 原始EEG信号中包含的多模态信息无法得到充分利用,以及神经网络从原始数据中学习抽象表达的能力无法得到证明. 利用深度学习基于原始数据进行端到端的学习则可以直接提取到信号中隐藏的特征进行分类. Yang等[18 ] 根据采集脑电时电极的3D位置将EEG信号映射为2D网格图像格式,并提出基于图像格式EEG信号的卷积神经网络(convolutional neural network, CNN). 利用2D和3D卷积核对左手和右手的运动进行分类的精度分别为68.38%±7.029%和65.94%±8.5%. 深度学习是受数据驱动的方法,Li等[19 ] 利用幅值干扰作为数据增强手段扩充数据集,并构造了通道投影混合尺度CNN来端到端解码EEG,该框架采用原始多通道EEG信号作为输入,提高了解码精度. Wu等[20 ] 提出并行的多尺度滤波器组CNN来进行MI分类,建立多尺度卷积用于时频特征提取,并将提取的输出特征连接到空间卷积层中,完成脑电信号多模态特征的融合. Roy等[21 -23 ] 探索了利用不同的融合模型自动完成对原始信号的多模态特征提取以及分类. ...
1
... 上述深度学习方法取得了较好的效果,但特征提取工作仍须根据经验知识手动完成. 特征提取与分类工作分离的方法不能充分表征采集到信号的特征,且无法考虑到不同个体脑电信号之间的差异性,导致分类精度低、费时费力. 原始EEG信号中包含的多模态信息无法得到充分利用,以及神经网络从原始数据中学习抽象表达的能力无法得到证明. 利用深度学习基于原始数据进行端到端的学习则可以直接提取到信号中隐藏的特征进行分类. Yang等[18 ] 根据采集脑电时电极的3D位置将EEG信号映射为2D网格图像格式,并提出基于图像格式EEG信号的卷积神经网络(convolutional neural network, CNN). 利用2D和3D卷积核对左手和右手的运动进行分类的精度分别为68.38%±7.029%和65.94%±8.5%. 深度学习是受数据驱动的方法,Li等[19 ] 利用幅值干扰作为数据增强手段扩充数据集,并构造了通道投影混合尺度CNN来端到端解码EEG,该框架采用原始多通道EEG信号作为输入,提高了解码精度. Wu等[20 ] 提出并行的多尺度滤波器组CNN来进行MI分类,建立多尺度卷积用于时频特征提取,并将提取的输出特征连接到空间卷积层中,完成脑电信号多模态特征的融合. Roy等[21 -23 ] 探索了利用不同的融合模型自动完成对原始信号的多模态特征提取以及分类. ...
1
... 上述深度学习方法取得了较好的效果,但特征提取工作仍须根据经验知识手动完成. 特征提取与分类工作分离的方法不能充分表征采集到信号的特征,且无法考虑到不同个体脑电信号之间的差异性,导致分类精度低、费时费力. 原始EEG信号中包含的多模态信息无法得到充分利用,以及神经网络从原始数据中学习抽象表达的能力无法得到证明. 利用深度学习基于原始数据进行端到端的学习则可以直接提取到信号中隐藏的特征进行分类. Yang等[18 ] 根据采集脑电时电极的3D位置将EEG信号映射为2D网格图像格式,并提出基于图像格式EEG信号的卷积神经网络(convolutional neural network, CNN). 利用2D和3D卷积核对左手和右手的运动进行分类的精度分别为68.38%±7.029%和65.94%±8.5%. 深度学习是受数据驱动的方法,Li等[19 ] 利用幅值干扰作为数据增强手段扩充数据集,并构造了通道投影混合尺度CNN来端到端解码EEG,该框架采用原始多通道EEG信号作为输入,提高了解码精度. Wu等[20 ] 提出并行的多尺度滤波器组CNN来进行MI分类,建立多尺度卷积用于时频特征提取,并将提取的输出特征连接到空间卷积层中,完成脑电信号多模态特征的融合. Roy等[21 -23 ] 探索了利用不同的融合模型自动完成对原始信号的多模态特征提取以及分类. ...
Data augmentation for deep-learning-based electroencephalography
1
2020
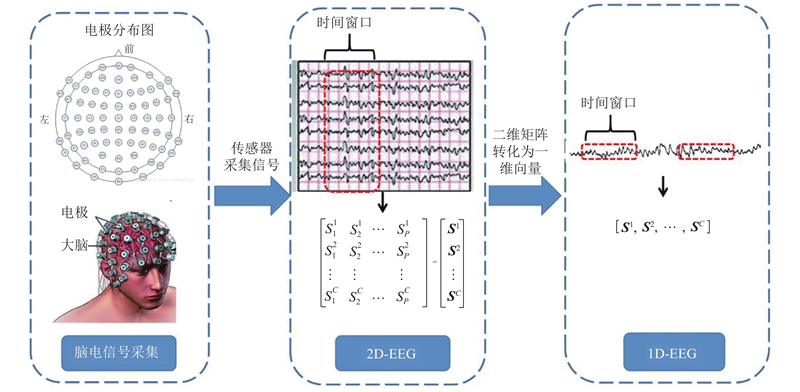
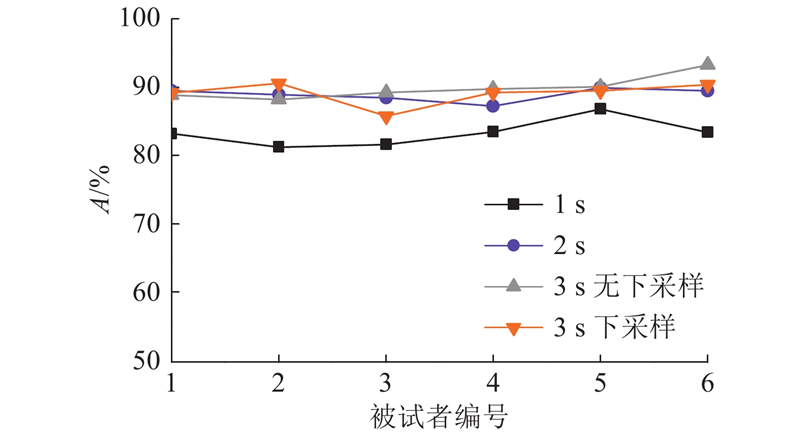
... 深度神经网络具有许多成功的应用案例,但是分类效果严重依赖数据量. 运动想象脑电信号采集实验程序复杂且规则严格,而且容易受到噪声的污染,因此难以获得足够的EEG信号用于神经网络模型的训练. 为了解决这个问题,许多研究已经提出了一些数据增强方法来额外增加数据样本[24 ] . 目前使用频率最高的数据增强方法是滑动窗口和添加噪声,文献[25 ]经过实验对比发现神经网络无法从额外添加的噪声中学习到和脑电活动有关的信息. 本研究根据脑电信号多通道采集的特点,将收集到的脑电信号样本根据通道进行重新排列,实现了输入从多通道到单通道的转换. 在无须利用其他手段增加数据集内容来扩充样本量的同时增加了神经网络的输入样本数量. ...
1
... 深度神经网络具有许多成功的应用案例,但是分类效果严重依赖数据量. 运动想象脑电信号采集实验程序复杂且规则严格,而且容易受到噪声的污染,因此难以获得足够的EEG信号用于神经网络模型的训练. 为了解决这个问题,许多研究已经提出了一些数据增强方法来额外增加数据样本[24 ] . 目前使用频率最高的数据增强方法是滑动窗口和添加噪声,文献[25 ]经过实验对比发现神经网络无法从额外添加的噪声中学习到和脑电活动有关的信息. 本研究根据脑电信号多通道采集的特点,将收集到的脑电信号样本根据通道进行重新排列,实现了输入从多通道到单通道的转换. 在无须利用其他手段增加数据集内容来扩充样本量的同时增加了神经网络的输入样本数量. ...
Convolutional neural networks in image understanding
1
2016
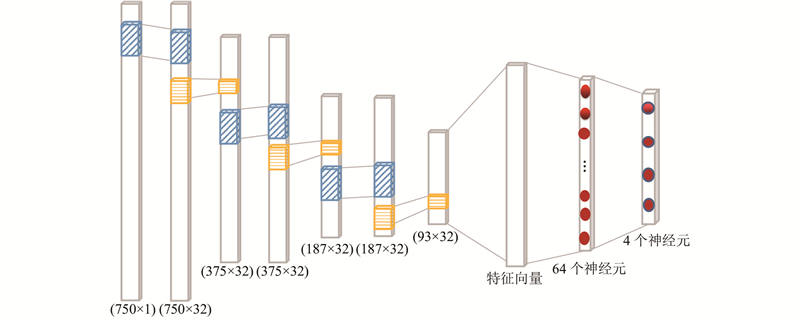
... 在足够的数据条件下,根据输入样本的特点选择合适的神经网络模型进行训练和学习也是分类中的关键工作. 本研究选择利用卷积神经网络对构造的EEG数据集进行分类. CNN是经典的前馈神经网络,在计算机视觉中得到广泛使用,并且取得了优异的表现[26 ] . CNN具有学习输入数据表示的能力,因此它被用于学习信号中的时频变化. 该网络结构主要包括卷积层、池化层以及全连接层. ...
1
... 利用卷积核对输入层进行滑动点乘运算完成卷积操作,可以获得浅层输出表示. 其中长卷积核适合学习长时间和低频的多样性表示,而短卷积核适合提取短时间和高频表示[27 ] . ...
基于卷积神经网络的脑电信号上肢运动意图识别
1
2017
... 3)全连接层. 在神经网络模型中,增加全连接层能够增强网络的非线性映射能力,并对网络规模进行限制[28 ] . 将卷积层提取到的局部特征合并在一起形成全局特征,然后利用具有4个神经元的全连接层输出最终的多分类任务. ...
基于卷积神经网络的脑电信号上肢运动意图识别
1
2017
... 3)全连接层. 在神经网络模型中,增加全连接层能够增强网络的非线性映射能力,并对网络规模进行限制[28 ] . 将卷积层提取到的局部特征合并在一起形成全局特征,然后利用具有4个神经元的全连接层输出最终的多分类任务. ...
Review of the BCI competition IV
1
2012
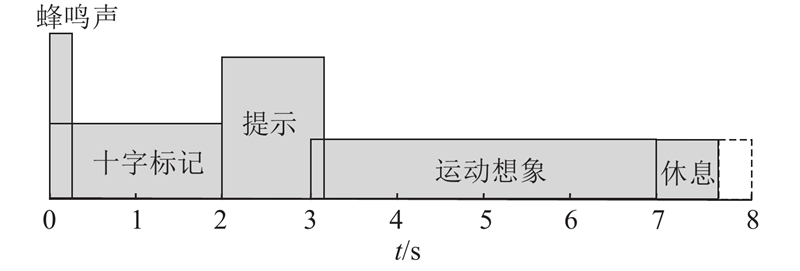
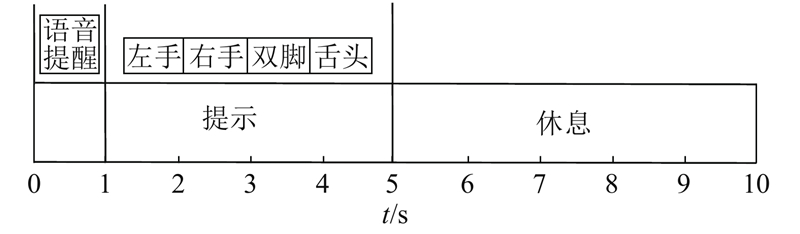
... 选择在BCI Competition IV 2a[29 ] 数据集(BCI IV 2a数据集)上将所提方法与前沿优秀算法进行对比. 该数据集在MI领域得到学者们的认可,并且已经在许多类似研究中使用. 该数据集使用国际10-20系统记录EEG信号,将25个电极放在头皮上采集脑电信号,其中包括3个用于状态判断但不参与算法训练和测试的EOG电极,将Fz设置为参考电极,采样率为250 Hz. 该数据集由9个健康受试者的运动想象EEG信号组成,共包含4种类型的运动:左手、右手、舌头和脚(分别对应类0、1、2、3). 数据集共包括9个被试者2轮实验的数据,被试者在每轮实验中进行6组实验,每组实验进行48次运动想象,共进行288次想象试验. 其中单次运动想象实验范式如图3 所示. 在试验开始时,出现了固定交叉在黑屏上,此外,还给出了简短的声音警告. 在2 s后,以箭头形式显示任务提示,出现在左、右、下或上(对应左手、右手、脚或舌头)并停留在屏幕上1.25 s,这促使受试者进行所需的运动成像任务. 数据集已经对采集的数据进行0.5~100.0 Hz之间的带通滤波器,以及50 Hz的陷波滤波消除工频干扰. 后续在此数据集上无须进行额外的数据预处理工作. ...
Densely feature fusion based on convolutional neural networks for motor imagery EEG classification
4
2019
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification accuracy between proposed method and comparative references
Tab.3 被试者 A /% 本研究方法 DFFN[30 ] HC-CNN[31 ] PSO-CNN[32 ] CNN-LSTM[33 ] SS-MEMDBF[35 ] RBM-SVM[36 ] ETRCNN[37 ] 1 99.14 85.40 90.07 93.30 98.82 91.49 86.61 85.88 2 99.49 69.30 80.28 84.59 98.64 60.56 61.26 75.41 3 99.68 90.29 97.08 91.68 96.92 94.16 87.27 91.32 4 99.01 71.07 89.66 84.55 96.50 76.72 75.20 83.45 5 99.61 65.41 97.04 86.54 92.75 58.52 64.55 72.11 6 98.86 69.45 87.04 76.92 91.84 68.52 65.91 91.72 7 98.58 88.18 92.14 94.03 95.07 78.67 83.78 85.71 8 99.82 86.46 98.51 93.20 95.25 97.01 89.91 91.32 9 98.98 93.54 92.31 92.24 99.23 93.85 92.08 93.23 平均值 99.24 79.90 91.57 85.56 96.13 79.94 78.51 85.57 均方差 0.3998 10.25 5.41 5.46 2.486 14.13 11.29 7.08
除了准确率,还计算了所提算法分类结果的Kappa值,并与其他算法进行对比. Kappa值主要用于一致性测试,可以用于测量分类准确性及消除随机分类的影响[41 ] . Kappa值为−1.0~1.0,数值越大表明算法分类性能越好. Kappa值表达式如下: ...
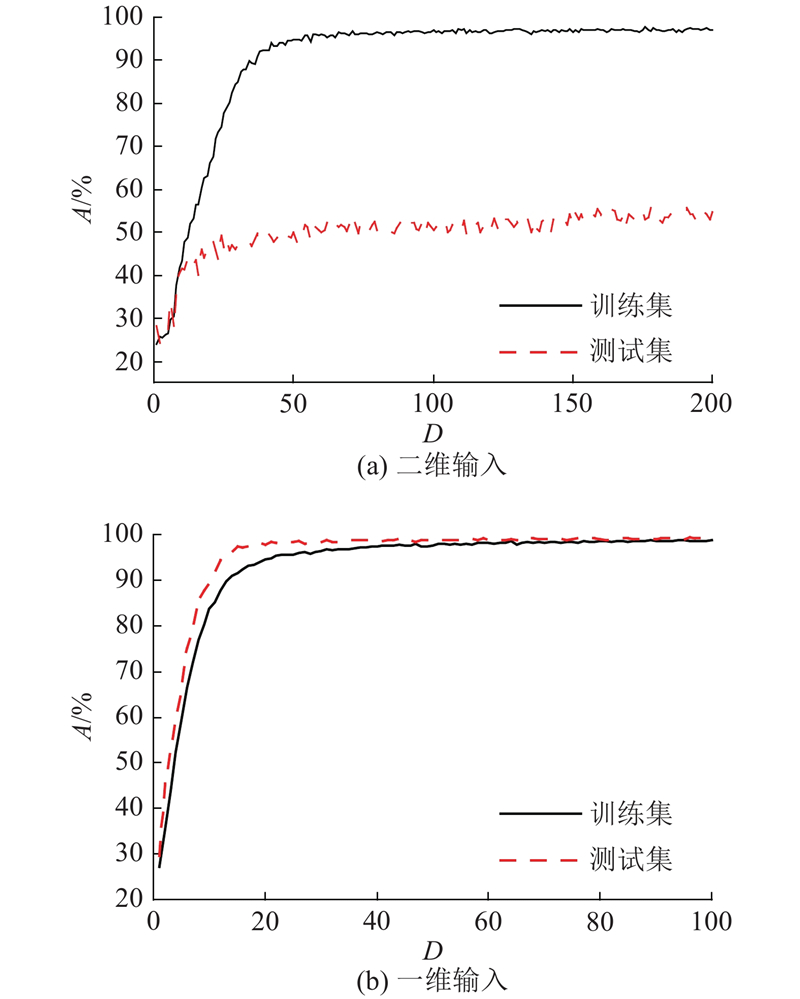
... 将本研究方法与其他最新方法在公共数据集进行了比较,如表3 、4 所示为不同算法[30 -40 ] 对BCI IV 2a数据集中9个被试者运动想象数据分类的准确率和Kappa值结果. 根据表中准确率平均值可知,整体上本研究方法分类得到的准确率和Kappa值优于对比算法,而且在9个被试者数据集上分别获得了最高结果. 值得一提的是,各被试者之间的分类表现没有明显差异. 说明本研究方法克服了个体脑电信号差异性的影响,能够自动学习到不同被试者4种想象状态下的独特的脑电信号活动模式. 本研究方法在所有对比算法中获得了最高的分类平均准确度和平均Kappa值,分别为99.24%和0.9898. 并获得最低的均方差,分别为0.3998和0.0053. 该结果表明本研究方法具有较好的鲁棒性和更好的分类性能. 由表3 、4 中均方差结果可以看出,本研究算法能够在模型无须进行参数调整的条件下,克服个体差异实现无差别分类,这有助于BCI应用的进展. 传统机器学习方法在用于运动想象脑电信号分类任务时,需要繁琐的特征提取和选择工作. 利用单一方法提取到的特征不足以表征运动想象信号模式,而多种方法结合提取多模态特征会造成获得的特征维度大、特征选择工作困难,这种方法依赖专业经验而且灵活度低,造成分类准确率低以及多个被试者分类结果差异明显. 对比文献中深度学习方法都选择利用CNN网络进行深层次的特征提取以及分类工作. 如DFFN中加入密集连接层有利于特征的融合,C2CM将二维卷积分解为在时间和空间维度上的分布一维卷积[38 ] ,CNN-LSTM则选择用混合网络分别提取空间信息以及时间相关信息[33 ] . 这些算法都获取了比传统机器学习算法更好的结果,但是仍然使用了人工设计的特征作为网络输入,神经网络从特征输入中再次学习到的信息有限. 3D-CNN提出了一种新的数据表示形式,将采集到的多通道脑电信号按照电极3D分布映射为图像,并设计多分支3D-CNN网络框架以充分利用脑电信号各维度特征. 但深度学习方法性能受数据驱动,需要充分的训练样本进行学习. 滑动窗口是进行数据增强的有效方法,相邻窗口之间大部分片段重叠,最终得到的样本信息丰富度较差. 与参考文献[30 -40 ] 相比,本研究利用深度学习基于原始信号进行端到端学习,并提出将多通道脑电信号串联放置形成一维序列信号的方法,该方法能够明显提升样本数量. 而且样本中富含与运动想象活动有关的信息,来自相同通道的样本来自不同时间,而来自相同时间段的样本来自不同通道. 本研究设计的1D-CNN网络框架更加适合接收原始一维序列信号作为输入,通过多次迭代训练学习脑电信号中不同运动想象模式. 与对比算法选择将二维卷积拆分为2个方向上的一维卷积不同,本研究设计的1D-CNN网络始终只在时间方向进行卷积操作. 多层网络结构能够随着网络的加深提取到更加抽象的特征. 该网络能够灵活地从不同被试者的原始信号中提取到与不同运动想象模式相关的信息,整体分类准确率以及被试者间方差都优于对比算法中的模型,而且1D卷积使得模型的计算量也较低. ...
... [30 -40 ]相比,本研究利用深度学习基于原始信号进行端到端学习,并提出将多通道脑电信号串联放置形成一维序列信号的方法,该方法能够明显提升样本数量. 而且样本中富含与运动想象活动有关的信息,来自相同通道的样本来自不同时间,而来自相同时间段的样本来自不同通道. 本研究设计的1D-CNN网络框架更加适合接收原始一维序列信号作为输入,通过多次迭代训练学习脑电信号中不同运动想象模式. 与对比算法选择将二维卷积拆分为2个方向上的一维卷积不同,本研究设计的1D-CNN网络始终只在时间方向进行卷积操作. 多层网络结构能够随着网络的加深提取到更加抽象的特征. 该网络能够灵活地从不同被试者的原始信号中提取到与不同运动想象模式相关的信息,整体分类准确率以及被试者间方差都优于对比算法中的模型,而且1D卷积使得模型的计算量也较低. ...
HS-CNN: a CNN with hybrid convolutional scale for EEG motor imagery classification
2
2020
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification accuracy between proposed method and comparative references
Tab.3 被试者 A /% 本研究方法 DFFN[30 ] HC-CNN[31 ] PSO-CNN[32 ] CNN-LSTM[33 ] SS-MEMDBF[35 ] RBM-SVM[36 ] ETRCNN[37 ] 1 99.14 85.40 90.07 93.30 98.82 91.49 86.61 85.88 2 99.49 69.30 80.28 84.59 98.64 60.56 61.26 75.41 3 99.68 90.29 97.08 91.68 96.92 94.16 87.27 91.32 4 99.01 71.07 89.66 84.55 96.50 76.72 75.20 83.45 5 99.61 65.41 97.04 86.54 92.75 58.52 64.55 72.11 6 98.86 69.45 87.04 76.92 91.84 68.52 65.91 91.72 7 98.58 88.18 92.14 94.03 95.07 78.67 83.78 85.71 8 99.82 86.46 98.51 93.20 95.25 97.01 89.91 91.32 9 98.98 93.54 92.31 92.24 99.23 93.85 92.08 93.23 平均值 99.24 79.90 91.57 85.56 96.13 79.94 78.51 85.57 均方差 0.3998 10.25 5.41 5.46 2.486 14.13 11.29 7.08
除了准确率,还计算了所提算法分类结果的Kappa值,并与其他算法进行对比. Kappa值主要用于一致性测试,可以用于测量分类准确性及消除随机分类的影响[41 ] . Kappa值为−1.0~1.0,数值越大表明算法分类性能越好. Kappa值表达式如下: ...
Efficient classification of motor imagery electroencephalography signal using deep learning methods
2
2019
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification accuracy between proposed method and comparative references
Tab.3 被试者 A /% 本研究方法 DFFN[30 ] HC-CNN[31 ] PSO-CNN[32 ] CNN-LSTM[33 ] SS-MEMDBF[35 ] RBM-SVM[36 ] ETRCNN[37 ] 1 99.14 85.40 90.07 93.30 98.82 91.49 86.61 85.88 2 99.49 69.30 80.28 84.59 98.64 60.56 61.26 75.41 3 99.68 90.29 97.08 91.68 96.92 94.16 87.27 91.32 4 99.01 71.07 89.66 84.55 96.50 76.72 75.20 83.45 5 99.61 65.41 97.04 86.54 92.75 58.52 64.55 72.11 6 98.86 69.45 87.04 76.92 91.84 68.52 65.91 91.72 7 98.58 88.18 92.14 94.03 95.07 78.67 83.78 85.71 8 99.82 86.46 98.51 93.20 95.25 97.01 89.91 91.32 9 98.98 93.54 92.31 92.24 99.23 93.85 92.08 93.23 平均值 99.24 79.90 91.57 85.56 96.13 79.94 78.51 85.57 均方差 0.3998 10.25 5.41 5.46 2.486 14.13 11.29 7.08
除了准确率,还计算了所提算法分类结果的Kappa值,并与其他算法进行对比. Kappa值主要用于一致性测试,可以用于测量分类准确性及消除随机分类的影响[41 ] . Kappa值为−1.0~1.0,数值越大表明算法分类性能越好. Kappa值表达式如下: ...
A novel hybrid deep learning scheme for four-class motor imagery classification
4
2019
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification accuracy between proposed method and comparative references
Tab.3 被试者 A /% 本研究方法 DFFN[30 ] HC-CNN[31 ] PSO-CNN[32 ] CNN-LSTM[33 ] SS-MEMDBF[35 ] RBM-SVM[36 ] ETRCNN[37 ] 1 99.14 85.40 90.07 93.30 98.82 91.49 86.61 85.88 2 99.49 69.30 80.28 84.59 98.64 60.56 61.26 75.41 3 99.68 90.29 97.08 91.68 96.92 94.16 87.27 91.32 4 99.01 71.07 89.66 84.55 96.50 76.72 75.20 83.45 5 99.61 65.41 97.04 86.54 92.75 58.52 64.55 72.11 6 98.86 69.45 87.04 76.92 91.84 68.52 65.91 91.72 7 98.58 88.18 92.14 94.03 95.07 78.67 83.78 85.71 8 99.82 86.46 98.51 93.20 95.25 97.01 89.91 91.32 9 98.98 93.54 92.31 92.24 99.23 93.85 92.08 93.23 平均值 99.24 79.90 91.57 85.56 96.13 79.94 78.51 85.57 均方差 0.3998 10.25 5.41 5.46 2.486 14.13 11.29 7.08
除了准确率,还计算了所提算法分类结果的Kappa值,并与其他算法进行对比. Kappa值主要用于一致性测试,可以用于测量分类准确性及消除随机分类的影响[41 ] . Kappa值为−1.0~1.0,数值越大表明算法分类性能越好. Kappa值表达式如下: ...
... Comparison of classification Kappa value between proposed method and comparative references
Tab.4 被试者 Kappa值 所提方法 CNN-LSTM[33 ] RBM-SVM[36 ] ETRCNN[37 ] C2CM[38 ] 3D-CNN[39 ] FBCSP[40 ] 1 0.9885 0.8500 0.8214 0.8420 0.8750 0.6990 0.6800 2 0.9933 0.5400 0.4838 0.6630 0.6528 0.4590 0.4200 3 0.9957 0.8700 0.7696 0.8770 0.9028 0.7880 0.7500 4 0.9863 0.7800 0.6664 0.7610 0.6667 0.5940 0.4800 5 0.9948 0.7700 0.5024 0.5710 0.6250 0.6470 0.4000 6 0.9848 0.6600 0.5301 0.8910 0.4549 0.5380 0.2700 7 0.9810 0.9500 0.7837 0.8090 0.8959 0.6530 0.7700 8 0.9976 0.8300 0.8655 0.8900 0.8333 0.7020 0.7600 9 0.9864 0.9000 0.8942 0.9070 0.7951 0.7130 0.6100 平均值 0.9898 0.7944 0.7019 0.8012 0.7446 0.6437 0.5711 均方差 0.0053 0.1197 0.1518 0.1097 0.1446 0.0942 0.1737
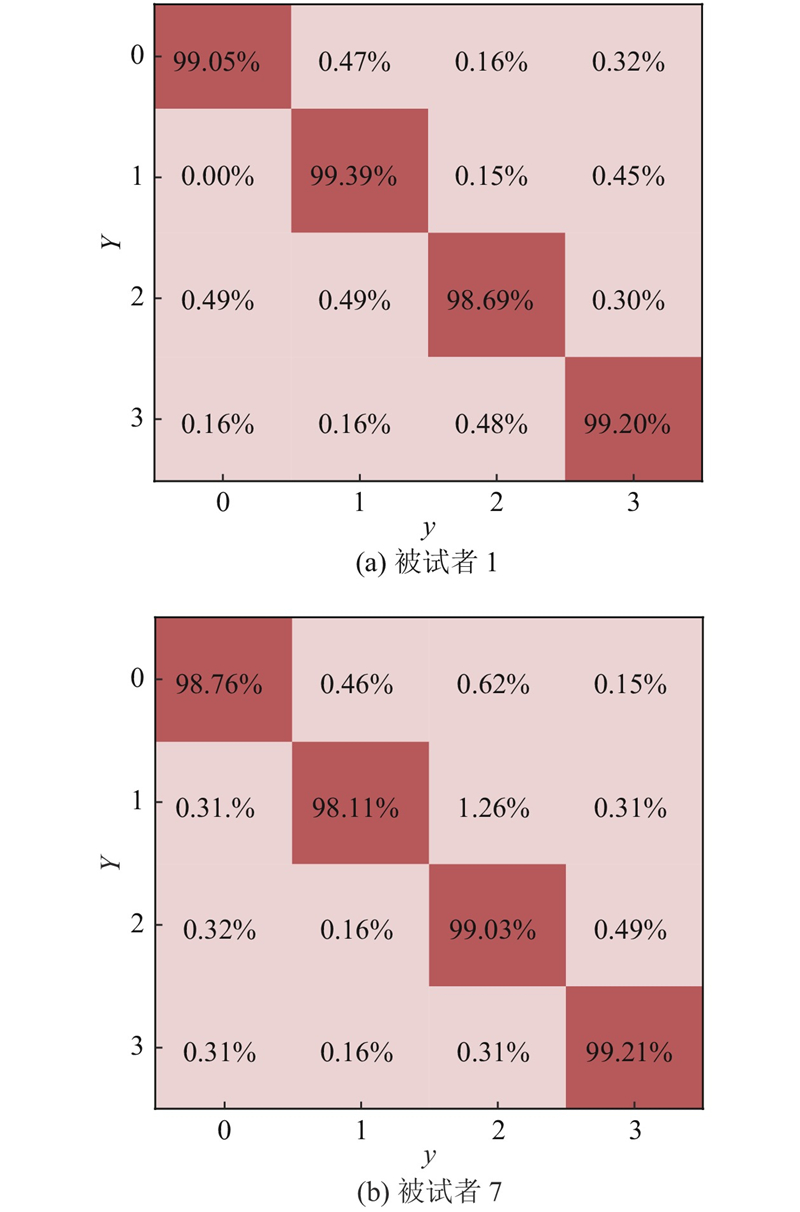
为了进一步探索所提算法对每个类别进行分类的能力,本研究对其他分类指标进行计算,包括分类的混淆矩阵、分类精度、召回率、F-score和接受者操作特性曲线(receiver operating characteristic curve, ROC). 被试者分类结果的混淆矩阵如图5 所示. 图中,y 为预测类别,Y 为真实类别. 混淆矩阵显示不同MI任务的分类结果,主对角线和非对角线分别表示每个类别的正确分类和错分到其他类别的概率. 4种类别的精度(precision, PR),召回率(recall, RE)和F-score如表5 所示. 精度、召回率、F-score表达式如下: ...
... 将本研究方法与其他最新方法在公共数据集进行了比较,如表3 、4 所示为不同算法[30 -40 ] 对BCI IV 2a数据集中9个被试者运动想象数据分类的准确率和Kappa值结果. 根据表中准确率平均值可知,整体上本研究方法分类得到的准确率和Kappa值优于对比算法,而且在9个被试者数据集上分别获得了最高结果. 值得一提的是,各被试者之间的分类表现没有明显差异. 说明本研究方法克服了个体脑电信号差异性的影响,能够自动学习到不同被试者4种想象状态下的独特的脑电信号活动模式. 本研究方法在所有对比算法中获得了最高的分类平均准确度和平均Kappa值,分别为99.24%和0.9898. 并获得最低的均方差,分别为0.3998和0.0053. 该结果表明本研究方法具有较好的鲁棒性和更好的分类性能. 由表3 、4 中均方差结果可以看出,本研究算法能够在模型无须进行参数调整的条件下,克服个体差异实现无差别分类,这有助于BCI应用的进展. 传统机器学习方法在用于运动想象脑电信号分类任务时,需要繁琐的特征提取和选择工作. 利用单一方法提取到的特征不足以表征运动想象信号模式,而多种方法结合提取多模态特征会造成获得的特征维度大、特征选择工作困难,这种方法依赖专业经验而且灵活度低,造成分类准确率低以及多个被试者分类结果差异明显. 对比文献中深度学习方法都选择利用CNN网络进行深层次的特征提取以及分类工作. 如DFFN中加入密集连接层有利于特征的融合,C2CM将二维卷积分解为在时间和空间维度上的分布一维卷积[38 ] ,CNN-LSTM则选择用混合网络分别提取空间信息以及时间相关信息[33 ] . 这些算法都获取了比传统机器学习算法更好的结果,但是仍然使用了人工设计的特征作为网络输入,神经网络从特征输入中再次学习到的信息有限. 3D-CNN提出了一种新的数据表示形式,将采集到的多通道脑电信号按照电极3D分布映射为图像,并设计多分支3D-CNN网络框架以充分利用脑电信号各维度特征. 但深度学习方法性能受数据驱动,需要充分的训练样本进行学习. 滑动窗口是进行数据增强的有效方法,相邻窗口之间大部分片段重叠,最终得到的样本信息丰富度较差. 与参考文献[30 -40 ] 相比,本研究利用深度学习基于原始信号进行端到端学习,并提出将多通道脑电信号串联放置形成一维序列信号的方法,该方法能够明显提升样本数量. 而且样本中富含与运动想象活动有关的信息,来自相同通道的样本来自不同时间,而来自相同时间段的样本来自不同通道. 本研究设计的1D-CNN网络框架更加适合接收原始一维序列信号作为输入,通过多次迭代训练学习脑电信号中不同运动想象模式. 与对比算法选择将二维卷积拆分为2个方向上的一维卷积不同,本研究设计的1D-CNN网络始终只在时间方向进行卷积操作. 多层网络结构能够随着网络的加深提取到更加抽象的特征. 该网络能够灵活地从不同被试者的原始信号中提取到与不同运动想象模式相关的信息,整体分类准确率以及被试者间方差都优于对比算法中的模型,而且1D卷积使得模型的计算量也较低. ...
DWT and CNN based multi-class motor imagery electroencephalographic signal recognition
1
2020
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
A multi-class EEG-based BCI classification using multivariate empirical mode decomposition based filtering and Riemannian Geometry
2
2018
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification accuracy between proposed method and comparative references
Tab.3 被试者 A /% 本研究方法 DFFN[30 ] HC-CNN[31 ] PSO-CNN[32 ] CNN-LSTM[33 ] SS-MEMDBF[35 ] RBM-SVM[36 ] ETRCNN[37 ] 1 99.14 85.40 90.07 93.30 98.82 91.49 86.61 85.88 2 99.49 69.30 80.28 84.59 98.64 60.56 61.26 75.41 3 99.68 90.29 97.08 91.68 96.92 94.16 87.27 91.32 4 99.01 71.07 89.66 84.55 96.50 76.72 75.20 83.45 5 99.61 65.41 97.04 86.54 92.75 58.52 64.55 72.11 6 98.86 69.45 87.04 76.92 91.84 68.52 65.91 91.72 7 98.58 88.18 92.14 94.03 95.07 78.67 83.78 85.71 8 99.82 86.46 98.51 93.20 95.25 97.01 89.91 91.32 9 98.98 93.54 92.31 92.24 99.23 93.85 92.08 93.23 平均值 99.24 79.90 91.57 85.56 96.13 79.94 78.51 85.57 均方差 0.3998 10.25 5.41 5.46 2.486 14.13 11.29 7.08
除了准确率,还计算了所提算法分类结果的Kappa值,并与其他算法进行对比. Kappa值主要用于一致性测试,可以用于测量分类准确性及消除随机分类的影响[41 ] . Kappa值为−1.0~1.0,数值越大表明算法分类性能越好. Kappa值表达式如下: ...
Recognition of EEG signal motor imagery intention based on deep multi-view feature learning
3
2020
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification accuracy between proposed method and comparative references
Tab.3 被试者 A /% 本研究方法 DFFN[30 ] HC-CNN[31 ] PSO-CNN[32 ] CNN-LSTM[33 ] SS-MEMDBF[35 ] RBM-SVM[36 ] ETRCNN[37 ] 1 99.14 85.40 90.07 93.30 98.82 91.49 86.61 85.88 2 99.49 69.30 80.28 84.59 98.64 60.56 61.26 75.41 3 99.68 90.29 97.08 91.68 96.92 94.16 87.27 91.32 4 99.01 71.07 89.66 84.55 96.50 76.72 75.20 83.45 5 99.61 65.41 97.04 86.54 92.75 58.52 64.55 72.11 6 98.86 69.45 87.04 76.92 91.84 68.52 65.91 91.72 7 98.58 88.18 92.14 94.03 95.07 78.67 83.78 85.71 8 99.82 86.46 98.51 93.20 95.25 97.01 89.91 91.32 9 98.98 93.54 92.31 92.24 99.23 93.85 92.08 93.23 平均值 99.24 79.90 91.57 85.56 96.13 79.94 78.51 85.57 均方差 0.3998 10.25 5.41 5.46 2.486 14.13 11.29 7.08
除了准确率,还计算了所提算法分类结果的Kappa值,并与其他算法进行对比. Kappa值主要用于一致性测试,可以用于测量分类准确性及消除随机分类的影响[41 ] . Kappa值为−1.0~1.0,数值越大表明算法分类性能越好. Kappa值表达式如下: ...
... Comparison of classification Kappa value between proposed method and comparative references
Tab.4 被试者 Kappa值 所提方法 CNN-LSTM[33 ] RBM-SVM[36 ] ETRCNN[37 ] C2CM[38 ] 3D-CNN[39 ] FBCSP[40 ] 1 0.9885 0.8500 0.8214 0.8420 0.8750 0.6990 0.6800 2 0.9933 0.5400 0.4838 0.6630 0.6528 0.4590 0.4200 3 0.9957 0.8700 0.7696 0.8770 0.9028 0.7880 0.7500 4 0.9863 0.7800 0.6664 0.7610 0.6667 0.5940 0.4800 5 0.9948 0.7700 0.5024 0.5710 0.6250 0.6470 0.4000 6 0.9848 0.6600 0.5301 0.8910 0.4549 0.5380 0.2700 7 0.9810 0.9500 0.7837 0.8090 0.8959 0.6530 0.7700 8 0.9976 0.8300 0.8655 0.8900 0.8333 0.7020 0.7600 9 0.9864 0.9000 0.8942 0.9070 0.7951 0.7130 0.6100 平均值 0.9898 0.7944 0.7019 0.8012 0.7446 0.6437 0.5711 均方差 0.0053 0.1197 0.1518 0.1097 0.1446 0.0942 0.1737
为了进一步探索所提算法对每个类别进行分类的能力,本研究对其他分类指标进行计算,包括分类的混淆矩阵、分类精度、召回率、F-score和接受者操作特性曲线(receiver operating characteristic curve, ROC). 被试者分类结果的混淆矩阵如图5 所示. 图中,y 为预测类别,Y 为真实类别. 混淆矩阵显示不同MI任务的分类结果,主对角线和非对角线分别表示每个类别的正确分类和错分到其他类别的概率. 4种类别的精度(precision, PR),召回率(recall, RE)和F-score如表5 所示. 精度、召回率、F-score表达式如下: ...
Learning EEG topographical representation for classification via convolutional neural network
3
2020
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification accuracy between proposed method and comparative references
Tab.3 被试者 A /% 本研究方法 DFFN[30 ] HC-CNN[31 ] PSO-CNN[32 ] CNN-LSTM[33 ] SS-MEMDBF[35 ] RBM-SVM[36 ] ETRCNN[37 ] 1 99.14 85.40 90.07 93.30 98.82 91.49 86.61 85.88 2 99.49 69.30 80.28 84.59 98.64 60.56 61.26 75.41 3 99.68 90.29 97.08 91.68 96.92 94.16 87.27 91.32 4 99.01 71.07 89.66 84.55 96.50 76.72 75.20 83.45 5 99.61 65.41 97.04 86.54 92.75 58.52 64.55 72.11 6 98.86 69.45 87.04 76.92 91.84 68.52 65.91 91.72 7 98.58 88.18 92.14 94.03 95.07 78.67 83.78 85.71 8 99.82 86.46 98.51 93.20 95.25 97.01 89.91 91.32 9 98.98 93.54 92.31 92.24 99.23 93.85 92.08 93.23 平均值 99.24 79.90 91.57 85.56 96.13 79.94 78.51 85.57 均方差 0.3998 10.25 5.41 5.46 2.486 14.13 11.29 7.08
除了准确率,还计算了所提算法分类结果的Kappa值,并与其他算法进行对比. Kappa值主要用于一致性测试,可以用于测量分类准确性及消除随机分类的影响[41 ] . Kappa值为−1.0~1.0,数值越大表明算法分类性能越好. Kappa值表达式如下: ...
... Comparison of classification Kappa value between proposed method and comparative references
Tab.4 被试者 Kappa值 所提方法 CNN-LSTM[33 ] RBM-SVM[36 ] ETRCNN[37 ] C2CM[38 ] 3D-CNN[39 ] FBCSP[40 ] 1 0.9885 0.8500 0.8214 0.8420 0.8750 0.6990 0.6800 2 0.9933 0.5400 0.4838 0.6630 0.6528 0.4590 0.4200 3 0.9957 0.8700 0.7696 0.8770 0.9028 0.7880 0.7500 4 0.9863 0.7800 0.6664 0.7610 0.6667 0.5940 0.4800 5 0.9948 0.7700 0.5024 0.5710 0.6250 0.6470 0.4000 6 0.9848 0.6600 0.5301 0.8910 0.4549 0.5380 0.2700 7 0.9810 0.9500 0.7837 0.8090 0.8959 0.6530 0.7700 8 0.9976 0.8300 0.8655 0.8900 0.8333 0.7020 0.7600 9 0.9864 0.9000 0.8942 0.9070 0.7951 0.7130 0.6100 平均值 0.9898 0.7944 0.7019 0.8012 0.7446 0.6437 0.5711 均方差 0.0053 0.1197 0.1518 0.1097 0.1446 0.0942 0.1737
为了进一步探索所提算法对每个类别进行分类的能力,本研究对其他分类指标进行计算,包括分类的混淆矩阵、分类精度、召回率、F-score和接受者操作特性曲线(receiver operating characteristic curve, ROC). 被试者分类结果的混淆矩阵如图5 所示. 图中,y 为预测类别,Y 为真实类别. 混淆矩阵显示不同MI任务的分类结果,主对角线和非对角线分别表示每个类别的正确分类和错分到其他类别的概率. 4种类别的精度(precision, PR),召回率(recall, RE)和F-score如表5 所示. 精度、召回率、F-score表达式如下: ...
Learning temporal information for brain-computer interface using convolutional neural networks
3
2018
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification Kappa value between proposed method and comparative references
Tab.4 被试者 Kappa值 所提方法 CNN-LSTM[33 ] RBM-SVM[36 ] ETRCNN[37 ] C2CM[38 ] 3D-CNN[39 ] FBCSP[40 ] 1 0.9885 0.8500 0.8214 0.8420 0.8750 0.6990 0.6800 2 0.9933 0.5400 0.4838 0.6630 0.6528 0.4590 0.4200 3 0.9957 0.8700 0.7696 0.8770 0.9028 0.7880 0.7500 4 0.9863 0.7800 0.6664 0.7610 0.6667 0.5940 0.4800 5 0.9948 0.7700 0.5024 0.5710 0.6250 0.6470 0.4000 6 0.9848 0.6600 0.5301 0.8910 0.4549 0.5380 0.2700 7 0.9810 0.9500 0.7837 0.8090 0.8959 0.6530 0.7700 8 0.9976 0.8300 0.8655 0.8900 0.8333 0.7020 0.7600 9 0.9864 0.9000 0.8942 0.9070 0.7951 0.7130 0.6100 平均值 0.9898 0.7944 0.7019 0.8012 0.7446 0.6437 0.5711 均方差 0.0053 0.1197 0.1518 0.1097 0.1446 0.0942 0.1737
为了进一步探索所提算法对每个类别进行分类的能力,本研究对其他分类指标进行计算,包括分类的混淆矩阵、分类精度、召回率、F-score和接受者操作特性曲线(receiver operating characteristic curve, ROC). 被试者分类结果的混淆矩阵如图5 所示. 图中,y 为预测类别,Y 为真实类别. 混淆矩阵显示不同MI任务的分类结果,主对角线和非对角线分别表示每个类别的正确分类和错分到其他类别的概率. 4种类别的精度(precision, PR),召回率(recall, RE)和F-score如表5 所示. 精度、召回率、F-score表达式如下: ...
... 将本研究方法与其他最新方法在公共数据集进行了比较,如表3 、4 所示为不同算法[30 -40 ] 对BCI IV 2a数据集中9个被试者运动想象数据分类的准确率和Kappa值结果. 根据表中准确率平均值可知,整体上本研究方法分类得到的准确率和Kappa值优于对比算法,而且在9个被试者数据集上分别获得了最高结果. 值得一提的是,各被试者之间的分类表现没有明显差异. 说明本研究方法克服了个体脑电信号差异性的影响,能够自动学习到不同被试者4种想象状态下的独特的脑电信号活动模式. 本研究方法在所有对比算法中获得了最高的分类平均准确度和平均Kappa值,分别为99.24%和0.9898. 并获得最低的均方差,分别为0.3998和0.0053. 该结果表明本研究方法具有较好的鲁棒性和更好的分类性能. 由表3 、4 中均方差结果可以看出,本研究算法能够在模型无须进行参数调整的条件下,克服个体差异实现无差别分类,这有助于BCI应用的进展. 传统机器学习方法在用于运动想象脑电信号分类任务时,需要繁琐的特征提取和选择工作. 利用单一方法提取到的特征不足以表征运动想象信号模式,而多种方法结合提取多模态特征会造成获得的特征维度大、特征选择工作困难,这种方法依赖专业经验而且灵活度低,造成分类准确率低以及多个被试者分类结果差异明显. 对比文献中深度学习方法都选择利用CNN网络进行深层次的特征提取以及分类工作. 如DFFN中加入密集连接层有利于特征的融合,C2CM将二维卷积分解为在时间和空间维度上的分布一维卷积[38 ] ,CNN-LSTM则选择用混合网络分别提取空间信息以及时间相关信息[33 ] . 这些算法都获取了比传统机器学习算法更好的结果,但是仍然使用了人工设计的特征作为网络输入,神经网络从特征输入中再次学习到的信息有限. 3D-CNN提出了一种新的数据表示形式,将采集到的多通道脑电信号按照电极3D分布映射为图像,并设计多分支3D-CNN网络框架以充分利用脑电信号各维度特征. 但深度学习方法性能受数据驱动,需要充分的训练样本进行学习. 滑动窗口是进行数据增强的有效方法,相邻窗口之间大部分片段重叠,最终得到的样本信息丰富度较差. 与参考文献[30 -40 ] 相比,本研究利用深度学习基于原始信号进行端到端学习,并提出将多通道脑电信号串联放置形成一维序列信号的方法,该方法能够明显提升样本数量. 而且样本中富含与运动想象活动有关的信息,来自相同通道的样本来自不同时间,而来自相同时间段的样本来自不同通道. 本研究设计的1D-CNN网络框架更加适合接收原始一维序列信号作为输入,通过多次迭代训练学习脑电信号中不同运动想象模式. 与对比算法选择将二维卷积拆分为2个方向上的一维卷积不同,本研究设计的1D-CNN网络始终只在时间方向进行卷积操作. 多层网络结构能够随着网络的加深提取到更加抽象的特征. 该网络能够灵活地从不同被试者的原始信号中提取到与不同运动想象模式相关的信息,整体分类准确率以及被试者间方差都优于对比算法中的模型,而且1D卷积使得模型的计算量也较低. ...
A multi-branch 3D convolutional neural network for EEG-based motor imagery classification
2
2019
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification Kappa value between proposed method and comparative references
Tab.4 被试者 Kappa值 所提方法 CNN-LSTM[33 ] RBM-SVM[36 ] ETRCNN[37 ] C2CM[38 ] 3D-CNN[39 ] FBCSP[40 ] 1 0.9885 0.8500 0.8214 0.8420 0.8750 0.6990 0.6800 2 0.9933 0.5400 0.4838 0.6630 0.6528 0.4590 0.4200 3 0.9957 0.8700 0.7696 0.8770 0.9028 0.7880 0.7500 4 0.9863 0.7800 0.6664 0.7610 0.6667 0.5940 0.4800 5 0.9948 0.7700 0.5024 0.5710 0.6250 0.6470 0.4000 6 0.9848 0.6600 0.5301 0.8910 0.4549 0.5380 0.2700 7 0.9810 0.9500 0.7837 0.8090 0.8959 0.6530 0.7700 8 0.9976 0.8300 0.8655 0.8900 0.8333 0.7020 0.7600 9 0.9864 0.9000 0.8942 0.9070 0.7951 0.7130 0.6100 平均值 0.9898 0.7944 0.7019 0.8012 0.7446 0.6437 0.5711 均方差 0.0053 0.1197 0.1518 0.1097 0.1446 0.0942 0.1737
为了进一步探索所提算法对每个类别进行分类的能力,本研究对其他分类指标进行计算,包括分类的混淆矩阵、分类精度、召回率、F-score和接受者操作特性曲线(receiver operating characteristic curve, ROC). 被试者分类结果的混淆矩阵如图5 所示. 图中,y 为预测类别,Y 为真实类别. 混淆矩阵显示不同MI任务的分类结果,主对角线和非对角线分别表示每个类别的正确分类和错分到其他类别的概率. 4种类别的精度(precision, PR),召回率(recall, RE)和F-score如表5 所示. 精度、召回率、F-score表达式如下: ...
Filter bank common spatial pattern algorithm on BCI Competition IV datasets 2a and 2b
4
2012
... Introduction of methods and models used in comparative references
Tab.2 对比方法 输入设计 分类器 网络特点 DFFN[30 ] CSP CNN 考虑相邻层和跨层特征之间的相关性,减少卷积运算过程中的信息丢失 HC-CNN[31 ] 相同标签样本进行分割后交换重组,然后按照频率带划分,同一频率带的不同片段进行交换重组 CNN 对不同频率带的脑电信号设计不同的卷积核尺度,利用一维卷积核在时间和空间维度进行卷积操作 PSO-CNN[32 ] 滤波后的信号输入到CSP滤波器,同时计算不同频率带的PSD,引入粒子群优化算法进行特征优化 CNN 只有1层卷积层,紧跟着2层全连接层 CNN-LSTM[33 ] FBCSP CNN+LSTM 混合网络提取多模态特征 DWT-CNN[34 ] 滑动窗口进行数据增强,计算最优频率带的PSD CNN 结构与VGGNet相似,3 × 3卷积核分解为4 × 1或者2 × 1 SS-MEMDBF[35 ] 多元经验模式分解(MEMD) 黎曼几何 − RBM-SVM[36 ] 分别提取时-频-空域特征,利用参数t分布随机邻居嵌入进行参数降维 SVM − ETRCNN[37 ] 脑电图地形表征能量 CNN 网络能够从结合了时频特征和脑功能连通性的输入特征中学习到多模态信息 C2CM[38 ] FBCSP CNN 分别在时间和空间维度进行卷积,但须针对不同的对象更改参数 3D-CNN[39 ] 根据电极的3D分布将脑电信号映射为2D图像表示 CNN 构造3路不同卷积核尺寸的卷积网络,最后将3路网络获取的特征融合 FBCSP[40 ] FBCSP SVM −
表 3 所提方法与对比文献的分类准确率对比 ...
... Comparison of classification Kappa value between proposed method and comparative references
Tab.4 被试者 Kappa值 所提方法 CNN-LSTM[33 ] RBM-SVM[36 ] ETRCNN[37 ] C2CM[38 ] 3D-CNN[39 ] FBCSP[40 ] 1 0.9885 0.8500 0.8214 0.8420 0.8750 0.6990 0.6800 2 0.9933 0.5400 0.4838 0.6630 0.6528 0.4590 0.4200 3 0.9957 0.8700 0.7696 0.8770 0.9028 0.7880 0.7500 4 0.9863 0.7800 0.6664 0.7610 0.6667 0.5940 0.4800 5 0.9948 0.7700 0.5024 0.5710 0.6250 0.6470 0.4000 6 0.9848 0.6600 0.5301 0.8910 0.4549 0.5380 0.2700 7 0.9810 0.9500 0.7837 0.8090 0.8959 0.6530 0.7700 8 0.9976 0.8300 0.8655 0.8900 0.8333 0.7020 0.7600 9 0.9864 0.9000 0.8942 0.9070 0.7951 0.7130 0.6100 平均值 0.9898 0.7944 0.7019 0.8012 0.7446 0.6437 0.5711 均方差 0.0053 0.1197 0.1518 0.1097 0.1446 0.0942 0.1737
为了进一步探索所提算法对每个类别进行分类的能力,本研究对其他分类指标进行计算,包括分类的混淆矩阵、分类精度、召回率、F-score和接受者操作特性曲线(receiver operating characteristic curve, ROC). 被试者分类结果的混淆矩阵如图5 所示. 图中,y 为预测类别,Y 为真实类别. 混淆矩阵显示不同MI任务的分类结果,主对角线和非对角线分别表示每个类别的正确分类和错分到其他类别的概率. 4种类别的精度(precision, PR),召回率(recall, RE)和F-score如表5 所示. 精度、召回率、F-score表达式如下: ...
... 将本研究方法与其他最新方法在公共数据集进行了比较,如表3 、4 所示为不同算法[30 -40 ] 对BCI IV 2a数据集中9个被试者运动想象数据分类的准确率和Kappa值结果. 根据表中准确率平均值可知,整体上本研究方法分类得到的准确率和Kappa值优于对比算法,而且在9个被试者数据集上分别获得了最高结果. 值得一提的是,各被试者之间的分类表现没有明显差异. 说明本研究方法克服了个体脑电信号差异性的影响,能够自动学习到不同被试者4种想象状态下的独特的脑电信号活动模式. 本研究方法在所有对比算法中获得了最高的分类平均准确度和平均Kappa值,分别为99.24%和0.9898. 并获得最低的均方差,分别为0.3998和0.0053. 该结果表明本研究方法具有较好的鲁棒性和更好的分类性能. 由表3 、4 中均方差结果可以看出,本研究算法能够在模型无须进行参数调整的条件下,克服个体差异实现无差别分类,这有助于BCI应用的进展. 传统机器学习方法在用于运动想象脑电信号分类任务时,需要繁琐的特征提取和选择工作. 利用单一方法提取到的特征不足以表征运动想象信号模式,而多种方法结合提取多模态特征会造成获得的特征维度大、特征选择工作困难,这种方法依赖专业经验而且灵活度低,造成分类准确率低以及多个被试者分类结果差异明显. 对比文献中深度学习方法都选择利用CNN网络进行深层次的特征提取以及分类工作. 如DFFN中加入密集连接层有利于特征的融合,C2CM将二维卷积分解为在时间和空间维度上的分布一维卷积[38 ] ,CNN-LSTM则选择用混合网络分别提取空间信息以及时间相关信息[33 ] . 这些算法都获取了比传统机器学习算法更好的结果,但是仍然使用了人工设计的特征作为网络输入,神经网络从特征输入中再次学习到的信息有限. 3D-CNN提出了一种新的数据表示形式,将采集到的多通道脑电信号按照电极3D分布映射为图像,并设计多分支3D-CNN网络框架以充分利用脑电信号各维度特征. 但深度学习方法性能受数据驱动,需要充分的训练样本进行学习. 滑动窗口是进行数据增强的有效方法,相邻窗口之间大部分片段重叠,最终得到的样本信息丰富度较差. 与参考文献[30 -40 ] 相比,本研究利用深度学习基于原始信号进行端到端学习,并提出将多通道脑电信号串联放置形成一维序列信号的方法,该方法能够明显提升样本数量. 而且样本中富含与运动想象活动有关的信息,来自相同通道的样本来自不同时间,而来自相同时间段的样本来自不同通道. 本研究设计的1D-CNN网络框架更加适合接收原始一维序列信号作为输入,通过多次迭代训练学习脑电信号中不同运动想象模式. 与对比算法选择将二维卷积拆分为2个方向上的一维卷积不同,本研究设计的1D-CNN网络始终只在时间方向进行卷积操作. 多层网络结构能够随着网络的加深提取到更加抽象的特征. 该网络能够灵活地从不同被试者的原始信号中提取到与不同运动想象模式相关的信息,整体分类准确率以及被试者间方差都优于对比算法中的模型,而且1D卷积使得模型的计算量也较低. ...
... -40 ]相比,本研究利用深度学习基于原始信号进行端到端学习,并提出将多通道脑电信号串联放置形成一维序列信号的方法,该方法能够明显提升样本数量. 而且样本中富含与运动想象活动有关的信息,来自相同通道的样本来自不同时间,而来自相同时间段的样本来自不同通道. 本研究设计的1D-CNN网络框架更加适合接收原始一维序列信号作为输入,通过多次迭代训练学习脑电信号中不同运动想象模式. 与对比算法选择将二维卷积拆分为2个方向上的一维卷积不同,本研究设计的1D-CNN网络始终只在时间方向进行卷积操作. 多层网络结构能够随着网络的加深提取到更加抽象的特征. 该网络能够灵活地从不同被试者的原始信号中提取到与不同运动想象模式相关的信息,整体分类准确率以及被试者间方差都优于对比算法中的模型,而且1D卷积使得模型的计算量也较低. ...
A coefficient of agreement for nominal scales
1
1960
... 除了准确率,还计算了所提算法分类结果的Kappa值,并与其他算法进行对比. Kappa值主要用于一致性测试,可以用于测量分类准确性及消除随机分类的影响[41 ] . Kappa值为−1.0~1.0,数值越大表明算法分类性能越好. Kappa值表达式如下: ...