车辆稳定性判据是稳定性控制系统的基础,决定了控制介入的时机[12]. 轮胎力法能够准确、及时地对车辆是否进入极限工况进行判定,因此常被用作基准判据来研究参考横摆角速度法、β-β'相平面法等判据的时效性[13]. 轮胎侧滑,尤其是后轮侧滑对安全行车的威胁较大,严重时可能造成碰撞、翻车等恶性交通事故. 目前,横摆角速度或质心侧偏角常用于无人驾驶车辆稳定性控制[7-9],通过轮胎侧偏角决策前轮转角的相关研究较少. 刘凯等[10-11]利用传统的模型预测控制(model predictive control, MPC)方法,将前、后轮侧偏角约束在稳定性包络线之内或附近,有效改善了高速无人驾驶车辆的行驶稳定性. 该研究未考虑车身侧偏对轨迹跟踪性能的影响,且该方法需要对模型精度、跟踪精度和实时性三者进行权衡,虽然滚动时域的方式使得MPC具有一定的鲁棒性,但未与min-max问题或H∞相结合,不足以处理模型不确定性和系统扰动. 自抗扰控制中的扩张状态观测器可以对系统参数不确定性、未建模动态及外界干扰进行实时观测和补偿,因此不依赖精确的数学模型,具有较强的鲁棒性[14-15].
为了同时提升高速无人驾驶车辆的轨迹跟踪性能和稳定性,本文对轨迹跟踪偏差进行修正,以车辆航向角偏差和侧向位移偏差趋于零为控制目标,利用前馈-反馈控制确保智能汽车保持良好的轨迹跟踪性能. 提出后轮侧偏角自抗扰控制方法,以提升无人驾驶车辆的行驶稳定性和控制器的鲁棒性. 通过对比仿真,验证了本文方法的有效性.
1. 车辆动力学模型
忽略悬架系统的作用和路面不平等的影响,基于平面运动的侧向、横摆二自由度车辆系统模型,设计控制器. 忽略转向系统和行驶系统的影响,以前轮转角和轮胎驱动、制动力矩作为车辆系统的输入.
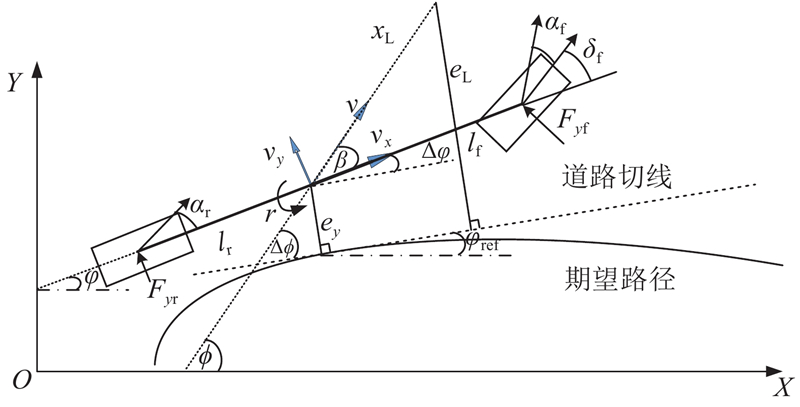
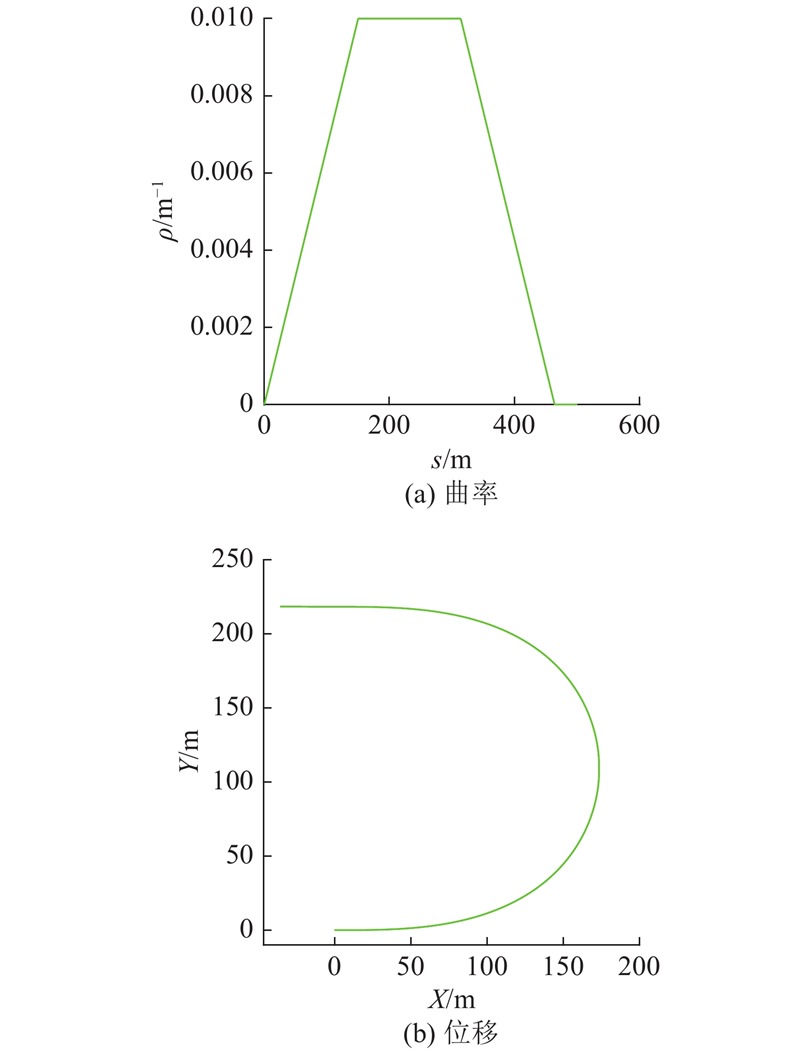
无人驾驶车辆的轨迹跟踪偏差模型和车辆系统模型如图1所示. 图中,OXY为大地坐标系,实线为期望路径,虚线为图示时刻车辆质心到期望路径最短距离对应的道路切线,φref为期望路径切线的航向角,φ为车辆横摆角,Δφ为车辆横摆角偏差,v为车辆质心速度,
图 1
基于δf和Δ
式中:m为车辆的质量,Iz为车辆横摆转动惯量,s为车辆沿期望路径的行驶距离,ρ为道路曲率.
轮胎模型采用魔术公式,轮胎侧向力可由下式计算[17]:
式中:μ为路面附着系数;Fz为轮胎垂向载荷;bi(i=1,···,8)为拟合系数,取值分别为b1=−22.1,b2=1011,b3=1078,b4=1.82,b5=0.208,b6=0,b7 = −0.354, b8 = 0.707.
引入等效侧偏刚度概念,轮胎模型可以表述为如下线性形式[8]:
式中:Fyf、Fyr分别为前、后轴轮胎侧向力,Cf、Cr分别为前、后轴轮胎的等效侧偏刚度, Cf0、Cr0为前轴和后轴轮胎侧偏角非常小时的标称侧偏刚度,ΔCf、ΔCr表示前、后轴轮胎侧偏刚度的不确定部分.
基于小角度假设可知,前、后轴轮胎侧偏角可由下式计算:
前、后轴轮胎侧偏角之间的关系可以表示为
式中:l为轴距.
2. 控制器设计
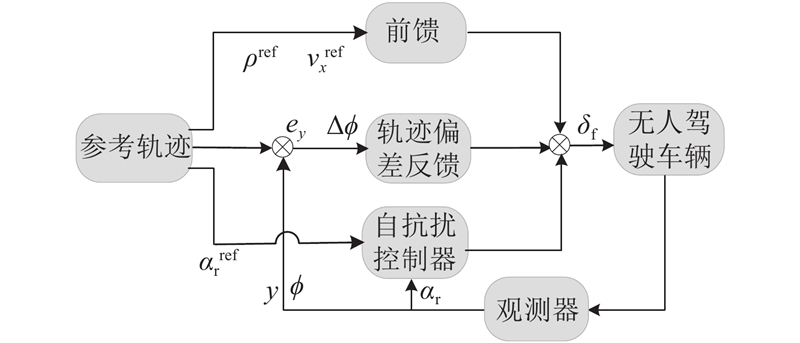
图 2
通过前馈、轨迹偏差反馈和后轮侧偏角自抗扰控制,改善高速无人驾驶车辆的轨迹跟踪性能和稳定性.
2.1. 前馈和轨迹偏差反馈
将稳态前轮转角作为前馈控制转角[5],稳态转向时,将Fyr = mρvx2,r = ρvx,
式中: Fyfr和Fyrr分别为稳态转向时前、后轴轮胎侧向力.
根据式(5),并联合式(3)、(6),可得前馈控制转角为
式中:
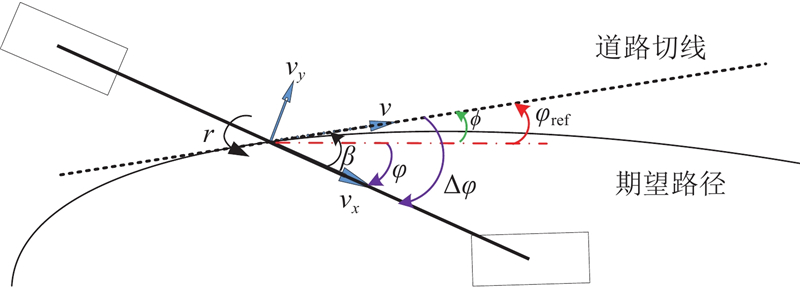
图 3
2.2. 后轮侧偏角自抗扰控制
2.2.1. 被控系统模型
对式(4)中的后轮侧偏角求导,分别代入式(1)、(5),可得
对式(5)求导,并联立式(1)、(3)可得
将式(9)中的αf用
对式(9)再求导,并将式(10)、(11)代入,化简可得
将式(12)前轮转角系数项Cf中的不确定部分ΔCf分离出来作为系统扰动,令
式中:
δf为车辆系统总的控制量,
其中δs为后轮侧偏角自抗扰控制得到的前轮转角.
将式(7)、(8)、(14)代入式(13),将前馈转角项、轨迹偏差反馈转角项作为系统扰动,可将系统(13)转化为控制系统(15):
式中:
其中w(t)为系统未建模动态和侧向风干扰等内、外界扰动,fw为系统已知干扰和未知干扰的总和.
2.2.2. 自抗扰控制器设计
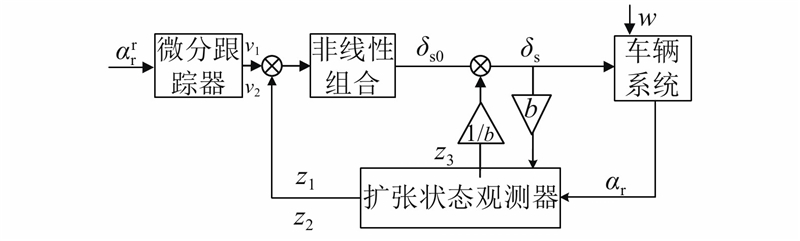
图 4
1)微分跟踪器. 微分跟踪器避免了由误差e提取de/dt,利用“快速控制最优综合函数”最快的跟踪微分信号,离散形式为
由式(16)求得的快速控制最优综合函数为
式中:h为积分仿真步长,本文取0.001 s;控制器设计参数r0为决定跟踪速度的速度因子,一般选取较大的值.
2)扩张状态观测器. 设计扩张状态观测器时,将总扰动fw作为扩张的状态变量,对系统总的未建模动态和未知扰动给予观测并补偿. 令状态观测器输出为z1、z2 和z3,分别为x1、x2和fw的观测值,则系统输出的观测误差为 e=z1−y = z1−x1. 观测器的状态方程为
式中:
3)非线性组合. 跟踪微分器输出和状态观测器输出之间的偏差为
利用fal函数具有的小误差产生大增益和大误差产生小增益的特性,设计非线性PD控制器:
式中:α3、α4为设计参数,一般选取为0 < α3< 1 <α4[14],可取α3=0.75, α4=1.5;kp和kd为设计参数,凭经验选取.
后轮侧偏角自抗扰控制的补偿转角δs可由下式求得:
经此变换相当于将不确定系统进行实时“动态线性化”,从而转化成积分器串联型系统:
3. 仿真验证
3.1. 不同控制器的效果对比
为了验证本文控制器作用下无人驾驶车辆的轨迹跟踪和稳定性控制效果,设计以下2组对比试验. 1)采用车辆横摆角偏差反馈和采用车辆航向角偏差反馈的对比试验,验证轨迹跟踪性能. 2)均采用车辆航向角偏差反馈,无后轮侧偏角控制和有后轮侧偏角控制的对比试验,验证车辆的行驶稳定性.
图 5
图 6
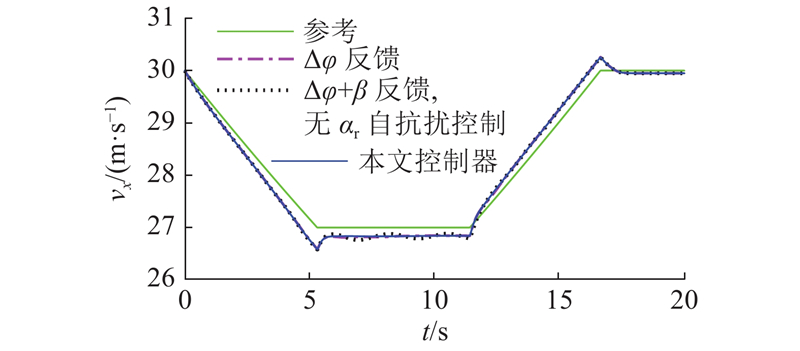
图 6 不同控制器的纵向速度跟踪结果
Fig.6 Velocity tracking simulation results of different controllers
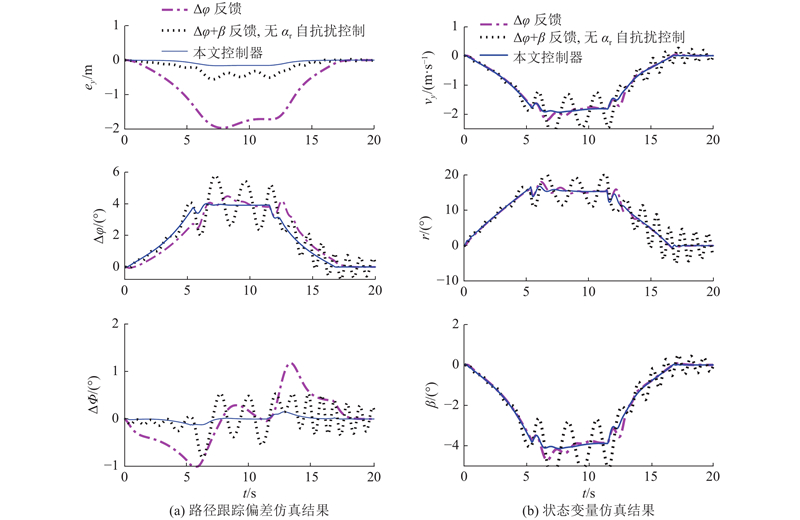
不同控制器作用下的路径跟踪仿真结果如图7所示. 可以看出,利用横摆角偏差进行反馈时,车辆侧向位移偏差和车辆航向角偏差最大. 利用车辆航向角偏差进行反馈但后轮侧偏角无控制时,侧向位移偏差大幅减小,但车辆的侧向速度、横摆角速度、质心侧偏角和路径跟踪偏差均出现震荡,车辆的行驶稳定性显著下降. 采用车辆航向角偏差反馈,并增加后轮侧偏角自抗扰控制(本文控制器)后,较后轮侧偏角无控制时的车辆侧向位移偏差和车辆航向角偏差都明显减小,侧向位移偏差峰值由0.55 m下降到0.16 m,且弯道内侧向速度、横摆角速度和质心侧偏角都比采用横摆角偏差反馈、采用车辆航向角偏差反馈但无后轮侧偏角控制时小,稳定性更好.
图 7
图 7 不同控制器的路径跟踪仿真结果
Fig.7 Trajectory tracking simulation results of different controllers
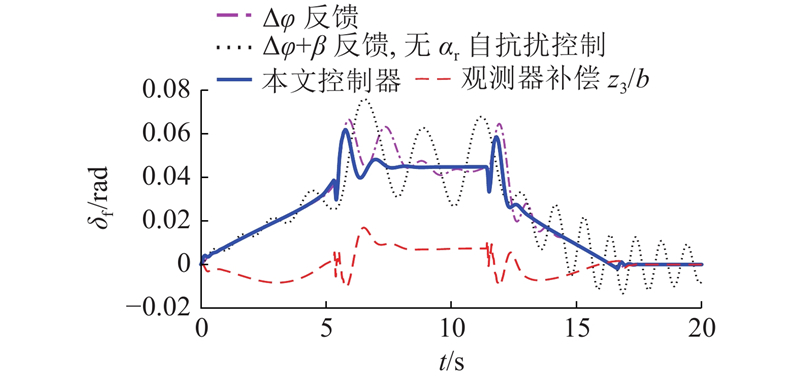
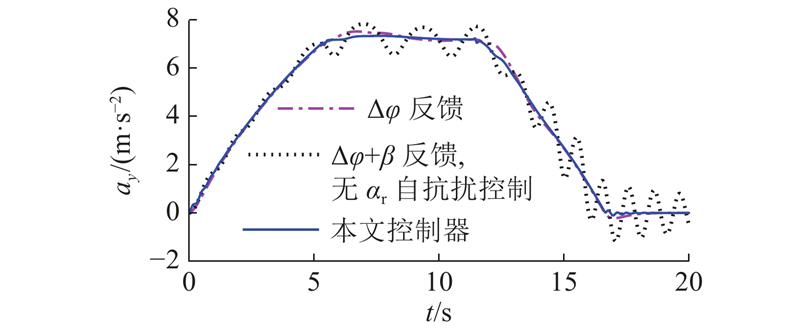
如图8所示为不同控制器和扩张状态观测器输出的前轮转角仿真结果. 本文控制器作用时扩张状态观测器可以估计系统总扰动并对前轮转角进行补偿,固定曲率弯道内前轮转角可以迅速收敛. 利用横摆角偏差进行反馈时,前轮转角幅值较大且存在小幅震荡;利用车辆航向角偏差进行反馈但无后轮侧偏角控制时,前轮转角幅值最大且存在明显震荡;本文控制作用时前轮转角幅值最小,基本无震荡. 车辆侧向加速度的仿真结果如图9所示,本文控制器作用下的车辆侧向加速度最平滑,峰值为7.29 m/s2,达到路面附着极限的82.6%. 综合上述分析可知,本文控制器考虑质心侧偏角并对后轮侧偏角进行控制后,无人驾驶车辆的轨迹跟踪性能和稳定性均得到了提升.
图 8
图 8 不同控制器的前轮转角仿真结果
Fig.8 Simulation results for front-wheel steering angle of different controllers
图 9
图 9 不同控制器的侧向加速度仿真结果
Fig.9 Simulation results for lateral acceleration of different controllers
3.2. 控制器对参数变化和干扰的鲁棒性
图 10
图 11
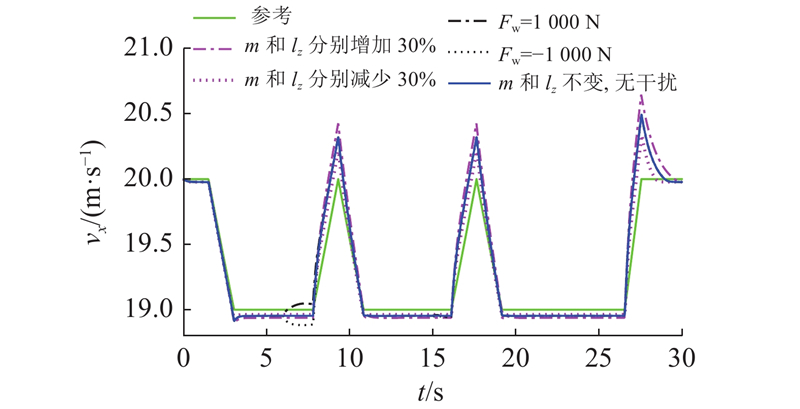
图 11 不同情况下的纵向速度跟踪结果
Fig.11 Velocity tracking simulation results in different situations
图 12
图 12 不同情况下的路径跟踪仿真结果
Fig.12 Trajectory tracking simulation results in different situations
图 13
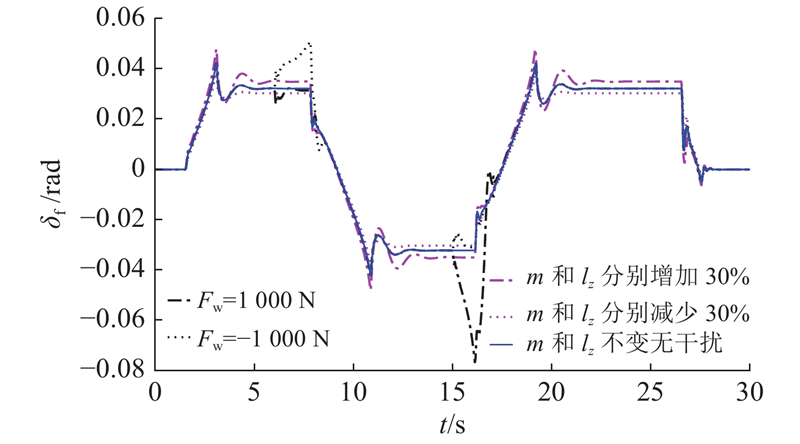
图 13 不同情况下前轮转角仿真结果
Fig.13 Simulation results for front-wheel steering angle in different situations
如图11所示为纵向速度跟踪结果,在本文控制器的作用下,当整车质量和横摆转动惯量变为原来的1.3倍、0.7倍或受到侧向风干扰时,曲率变化处纵向速度都有超调,但总体上均能够较好地跟随参考值.
如图12所示为车辆系统参数变化和受到侧向风干扰对应的不同情况下的路径跟踪仿真结果. 当整车质量和横摆转动惯量减少30%时,车辆跟踪期望轨迹的侧向偏差、横摆角偏差和质心侧偏角均减小. 当整车质量和横摆转动惯量增加30%时,车辆跟踪期望轨迹的侧向偏差、横摆角偏差和质心侧偏角均增大,其中侧向偏差峰值由0.03 m增加到0.08 m,质心侧偏角峰值增加0.6°,但是车辆仍能以较低的跟踪偏差稳定地跟踪期望路径行驶. 当车辆在2次出弯过程中受到阵风影响时,车辆的侧向位移跟踪偏差、航向角偏差、质心侧偏角均发生变化,其中侧向位移偏差约增大0.17 m,当风向和转弯方向相同时车辆的质心侧偏角约减小0.6°,当风向和转弯方向相反时车辆的质心侧偏角约增大1°. 总之,在本文控制器的作用下,车辆受到侧向阵风干扰时车辆的路径跟踪偏差小于0.2 m,质心侧偏角始终在稳定区域内,控制器对侧向风干扰的鲁棒性较好.
不同情况下控制器输出的前轮转角如图13所示,车辆质量和横摆转动惯量减少30%时控制器输出前轮转角基本不变;车辆质量和横摆转动惯量增加30%时,固定曲率弯道内前轮转角震荡幅值和范围稍有增加. 当车辆受到侧向风干扰时,由于扩张状态观测器可以对总扰动进行估计,对前轮转角进行补偿,使得车辆受到侧向风干扰时前轮转角发生大幅度变化,但能够在干扰消失后迅速收敛,车辆未发生失稳.
4. 结 论
(1)以修正的轨迹跟踪偏差和后轮侧偏角为控制目标,在现有的前馈-反馈控制基础上,提出后轮侧偏角自抗扰控制方法.
(2)设计扩张状态观测器,对系统的未建模动态和内外侧扰动进行实时估计和补偿,将不确定系统进行实时“动态线性化”.
(3)与采用横摆角偏差反馈控制、采用车辆航向角反馈但无后轮侧偏角控制2个控制器的对比仿真结果表明,设计的控制器可以保证无人驾驶车辆在高速行驶时具有更好的轨迹跟踪性能和稳定性.
(4)对控制器的鲁棒性进行仿真,结果表明,本文控制器能够适应不同的道路条件和比较复杂的道路曲率,对车辆系统参数变化和外界干扰具有较强的鲁棒性.
参考文献
智能时代的汽车控制
[J].
Automotive control in intelligent era
[J].
无人驾驶车辆的运动控制发展现状综述
[J].
Review on motion control of autonomous vehicles
[J].
Should the desired heading in path following of autonomous vehicles be the tangent direction of the desired path?
[J].
Design of a feedback-feedforward steering controller for accurate path tracking and stability at the limits of handling
[J].
车道保持预瞄控制及其稳态误差分析
[J].
Preview control for lane keeping and its steady-state error analysis
[J].
Autonomous vehicle control at the limits of handling
[J].DOI:10.1504/IJVAS.2012.051270 [本文引用: 4]
Robust path following control at driving/handling limits of an autonomous electric racecar
[J].DOI:10.1109/TVT.2019.2911862 [本文引用: 1]
基于线性矩阵不等式的智能车轨迹跟踪控制
[J].
Intelligent vehicle trajectory tracking control based on linear matrix inequality
[J].
高速无人驾驶车辆的操控稳定性研究
[J].
A research on handling stability of high-speed unmanned vehicles
[J].
智能汽车的路面附着极限横向轨迹跟踪控制
[J].DOI:10.3901/JME.2020.14.138 [本文引用: 2]
lateral trajectory following for automated vehicles at handling limits
[J].DOI:10.3901/JME.2020.14.138 [本文引用: 2]
考虑路面影响的车辆稳定性控制质心侧偏角动态边界控制
[J].DOI:10.3901/JME.2012.14.112 [本文引用: 1]
Research on side slip angle dynamic boundary control for vehicle stability control considering the impact of road surface
[J].DOI:10.3901/JME.2012.14.112 [本文引用: 1]
极限工况下车辆行驶的稳定性判据
[J].DOI:10.3901/JME.2015.10.103 [本文引用: 1]
Stability criterion for the vehicle under critical driving situation
[J].DOI:10.3901/JME.2015.10.103 [本文引用: 1]
从PID技术到"自抗扰控制"技术
[J].DOI:10.3969/j.issn.1671-7848.2002.03.003 [本文引用: 3]
From PID technology to auto disturbance rejection control technology
[J].DOI:10.3969/j.issn.1671-7848.2002.03.003 [本文引用: 3]
自抗扰控制思想探究
[J].DOI:10.7641/CTA.2013.31087 [本文引用: 1]
On the foundation of active disturbance rejection control
[J].DOI:10.7641/CTA.2013.31087 [本文引用: 1]
Modeling and control of the fuel injection system for rail pressure regulation in GDI engine
[J].DOI:10.1109/TMECH.2013.2285716 [本文引用: 1]
A variable structure extended Kalman filter for vehicle sideslip angle estimation on a low friction road
[J].DOI:10.1080/00423114.2013.877148 [本文引用: 2]
基于模糊逻辑的车辆侧偏角估计方法
[J].DOI:10.3321/j.issn:1000-680X.2005.04.010 [本文引用: 2]
Estimation of vehicle side slip angle based on fuzzy logic
[J].DOI:10.3321/j.issn:1000-680X.2005.04.010 [本文引用: 2]
Simultaneous estimation of tire side-slip angle and lateral tire force for vehicle lateral stability control
[J].DOI:10.1016/j.ymssp.2019.06.022 [本文引用: 1]
Robust vehicle yaw stability control by active front steering with active disturbance rejection controller
[J].DOI:10.1177/0959651818813515 [本文引用: 1]
Active steering and driving/ braking coupled control based on flatness theory and a novel reference calculation method
[J].DOI:10.1109/ACCESS.2019.2959941 [本文引用: 1]