搭载车联网技术的自动驾驶汽车称为网联自动车(connected and autonomous vehicle, CAV),由于其在安全、效率、环保等方面的潜在优势,吸引了许多国家政府、企业和学者的关注. 学术界已从多方面对自动驾驶进行了研究. 一些学者提出纯网联自动环境下交叉口无信号控制策略. Dresner等[1]提出自动交叉口管理策略(automatic intersection management,AIM),替代传统的交叉口信号控制. Hausknecht等[2]将AIM控制策略扩展到多个交叉口. Au等[3]进一步修改了AIM中的通行规则. Au等[4]在AIM中引入设定点算法,以更好地控制车辆的运行轨迹. 另一些学者开展了网联自动车运行轨迹优化、运行轨迹与信号配时协同优化等工作. Zhang等[5]将运行轨迹分解为车道保持和车道变换2个基本操作. Li等[6-8]开发了一套高效简约的方法,将整体车流划分成若干车队,对各车队进行纵向轨迹优化. Li等[9]采用滚动时域方法,对信号配时和车辆轨迹进行协同优化. Zhao等[10]采用滚动时域模型预测控制方法,对网联自动车和人工车辆混行交通流中的自动车轨迹进行优化. Yu等[11]构建混合整数线性规划模型来优化车辆轨迹和信号方案,且将换道行为纳入到模型中.
车道通行能力是交叉口渠化和信号配时所需的关键参数. 未来网联自动车进入路网与人工车辆大规模混行后,交叉口的时空资源需要重新配置. 针对该问题,晏松[18]以交叉口延误最小为目标,提出分步优化策略,训练决策树模型用于交叉口渠化设计,基于渠化设计优化信号控制方案. 本文建立统一的数学模型,协同优化车道渠化和信号配时方案. 构建网联自动车和人工车辆混行环境下的车道渠化约束集、流量分配约束集和信号配时约束集,以通行能力最大化为目标,建立混合整数线性规划模型. 以典型四车道十字交叉口为例,对该模型的可行性进行验证,分析网联自动车不同跟驰行为、网联自动车不同占比对交叉口时空资源配置结果的影响.
1. 网联自动车对通行能力的影响
在网联自动车和人工车辆混行的环境下,车道通行能力不再固定,随着网联自动车占比和最小车头时距变化. 采用Lazar等[15]构建的混行车流通行能力计算模型. 利用该模型能够分析网联自动车占比和最小车头时距对车道通行能力的影响,以反映混行流中不同车辆之间跟驰行为的变化.
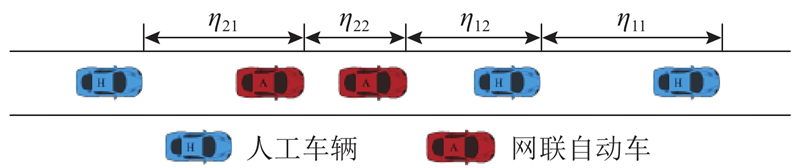
该模型认为混行车流中存在4种车头时距,如图1所示,
若网联自动车和人工车辆的最小跟驰时距不受前车类型的影响,
若网联自动车最小跟驰时距受前车类型的影响,人工车辆的最小跟驰时距不受前车类型的影响,且前车为人工车辆,2类车辆的最小跟驰时距相同,即
图 1
2. 混行交叉口时空资源优化模型
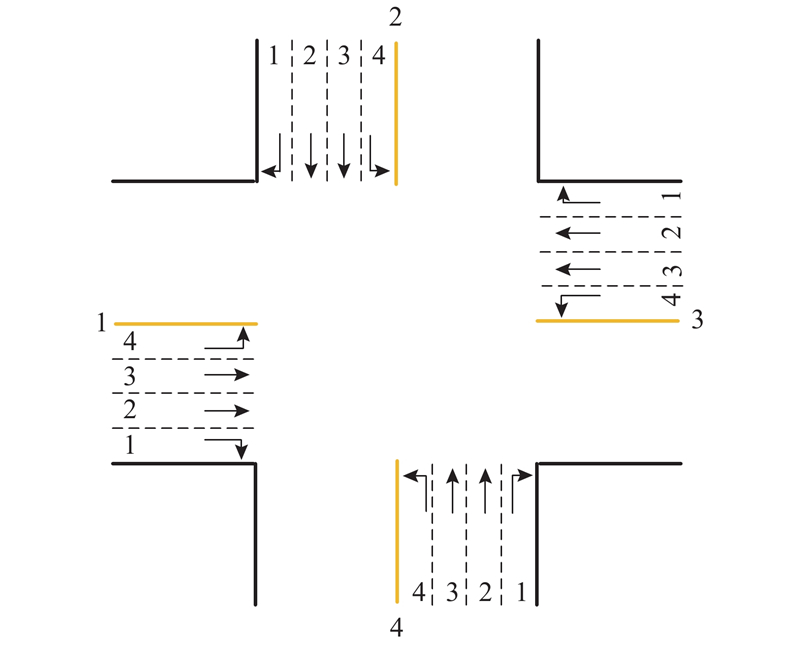
建立的交叉口时空资源优化模型属于基于车道的模型,有关该类模型的基础知识可以参阅文献[19~22]. 假设某信号交叉口有
图 2
2.1. 车道渠化约束
构建以下约束集,将交叉口车道资源分配给不同转向车流.
式中:
约束(1)保证至少有一股交通流通过车道
2.2. 流量分配约束
在分配完交叉口的车道资源后,各流向的交通流
式中:
约束(5)确保交通流
2.3. 信号配时约束
基于车道的信号配时约束构建如下.
式中:
约束(8)、(9)分别表示周期时长和流向
2.4. 目标函数
以交叉口通行能力最大化为目标. 假设所有转向交通流的需求按当前需求矩阵成比例增加,最大化单交叉口通行能力等价于最大化约束(7)中的公共乘子
假设
2.5. 混合整数线性规划模型
约束(6)和(16)中存在非线性项
辅助变量
混行交叉口时空资源配置优化问题可以整理为以下混合整数线性规划模型:
3. 典型交叉口算例
以典型四车道十字信号交叉口为例,验证模型的可行性,分析网联自动车占比和最小跟驰时距对混行环境下交叉口时空资源配置的影响. 未来,网联自动车与人工车辆混行后,具体驾驶行为(包括跟驰行为)存在不确定性,因此假设了2种情形,分别开展算例验证. 第1种情形中,网联自动车驾驶行为相对保守:只有当前车也为网联自动车时,前后两车可以协同运行,这时后车以较小的车头时距跟驰;当前车为人工车辆时,后车与前车无法协同,且前车未来运行意图未知,这时网联自动车采取较大的车头时距保守跟驰. 第2种情形中,网联自动车驾驶行为相对激进:不论前车为网联自动车还是人工车辆,网联自动车都采取较小的车头时距跟驰.
模型中的部分参数设置如下:信号最小和最大周期时长
表 1 算例中的交通需求
Tab.1
| i | Qi,j | |||
| j=1 | j=2 | j=3 | j=4 | |
| 1 | − | 400 | 700 | 300 |
| 2 | 600 | − | 200 | 600 |
| 3 | 600 | 200 | − | 400 |
| 4 | 400 | 800 | 300 | − |
3.1. 网联自动车跟驰受前车类型影响
假设网联自动车最小跟驰时距受前车类型的影响. 混行车流中4种车头时距设置为:
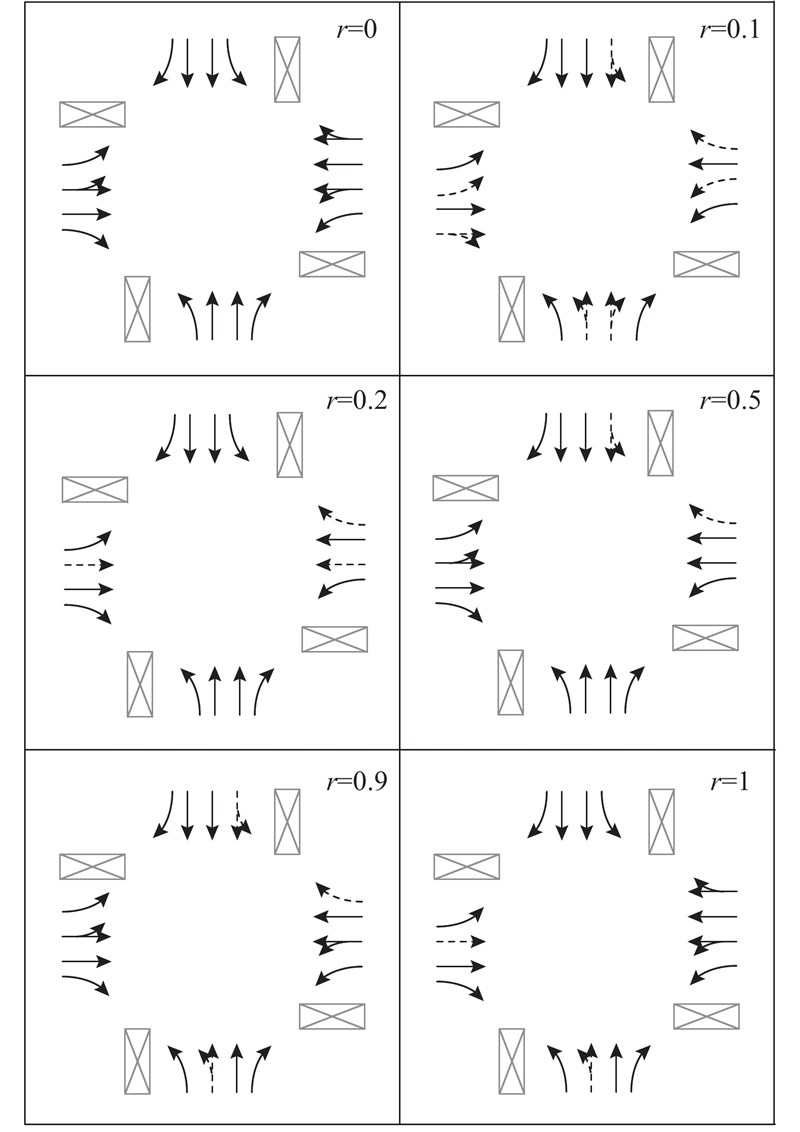
图 3
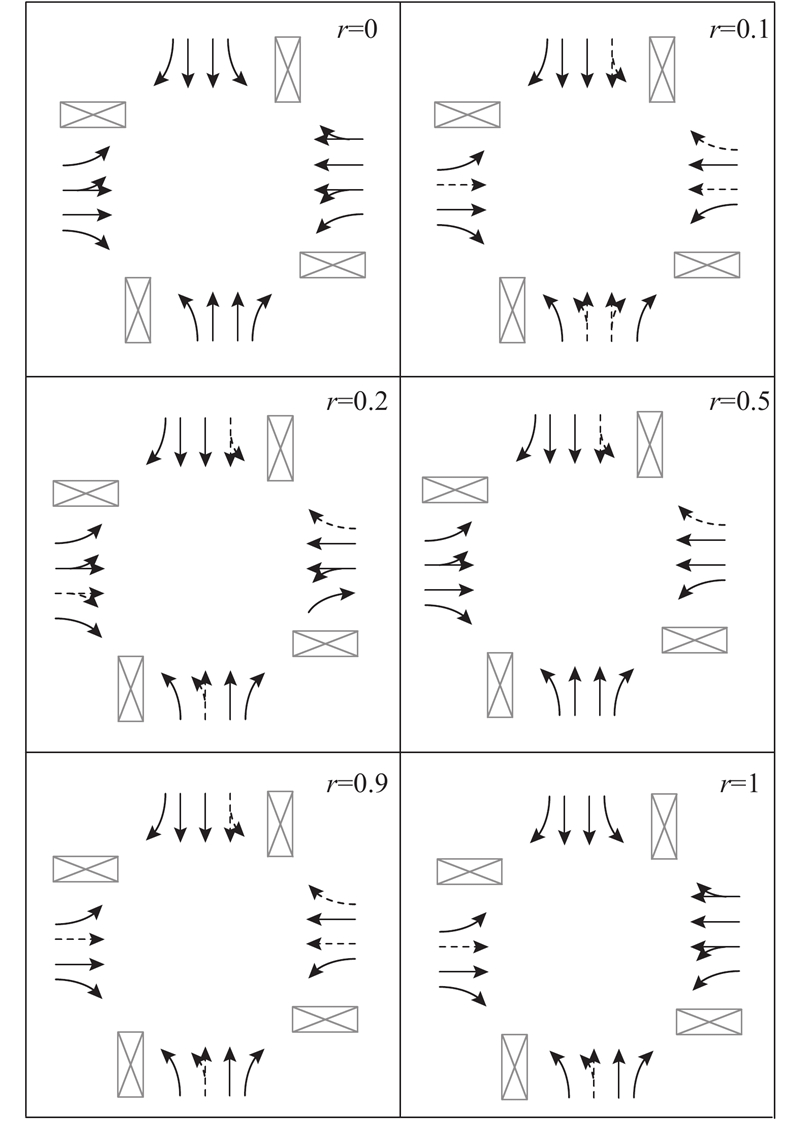
图 3 网联自动车跟驰受前车类型影响时的最优渠化方案
Fig.3 Optimal channelization schemes when headway of CAV is sensitive to vehicle type ahead
表 2 部分网联自动车占比下的最优信号方案
Tab.2
| | i=1, j=2 | i=1, j=3 | i=1, j=4 | i=2, j=1 | i=2, j=3 | i=2, j=4 | |||||||||||
| | | | | | | | | | | | | ||||||
| 0 | 0.706 | 0.200 | 0.706 | 0.200 | 0.000 | 0.456 | 0.225 | 0.500 | 0.483 | 0.100 | 0.506 | 0.150 | |||||
| 0.1 | 0.000 | 0.232 | 0.561 | 0.179 | 0.000 | 0.238 | 0.000 | 0.500 | 0.790 | 0.136 | 0.790 | 0.136 | |||||
| 0.2 | 0.000 | 0.214 | 0.000 | 0.214 | 0.000 | 0.214 | 0.000 | 0.500 | 0.781 | 0.136 | 0.781 | 0.136 | |||||
| 0.5 | 0.755 | 0.200 | 0.755 | 0.200 | 0.000 | 0.237 | 0.205 | 0.500 | 0.287 | 0.136 | 0.287 | 0.136 | |||||
| 0.9 | 0.000 | 0.232 | 0.019 | 0.179 | 0.000 | 0.238 | 0.000 | 0.500 | 0.552 | 0.136 | 0.552 | 0.136 | |||||
| 1 | 0.425 | 0.232 | 0.425 | 0.232 | 0.200 | 0.238 | 0.425 | 0.500 | 0.000 | 0.100 | 0.000 | 0.150 | |||||
| | i=3, j=1 | i=3, j=2 | i=3, j=4 | i=4, j=1 | i=4, j=2 | i=4, j=3 | |||||||||||
| | | | | | | | | | | | | ||||||
| 0 | 0.000 | 0.175 | 0.000 | 0.175 | 0.000 | 0.175 | 0.225 | 0.232 | 0.225 | 0.208 | 0.000 | 0.238 | |||||
| 0.1 | 0.561 | 0.179 | 0.561 | 0.150 | 0.000 | 0.232 | 0.282 | 0.229 | 0.282 | 0.229 | 0.282 | 0.229 | |||||
| 0.2 | 0.550 | 0.181 | 0.534 | 0.150 | 0.550 | 0.181 | 0.264 | 0.220 | 0.264 | 0.220 | 0.264 | 0.238 | |||||
| 0.5 | 0.005 | 0.150 | 0.000 | 0.150 | 0.005 | 0.232 | 0.473 | 0.232 | 0.473 | 0.208 | 0.005 | 0.237 | |||||
| 0.9 | 0.738 | 0.150 | 0.552 | 0.150 | 0.738 | 0.232 | 0.282 | 0.220 | 0.282 | 0.220 | 0.249 | 0.238 | |||||
| 1 | 0.200 | 0.175 | 0.200 | 0.175 | 0.200 | 0.175 | 0.706 | 0.220 | 0.706 | 0.220 | 0.000 | 0.375 | |||||
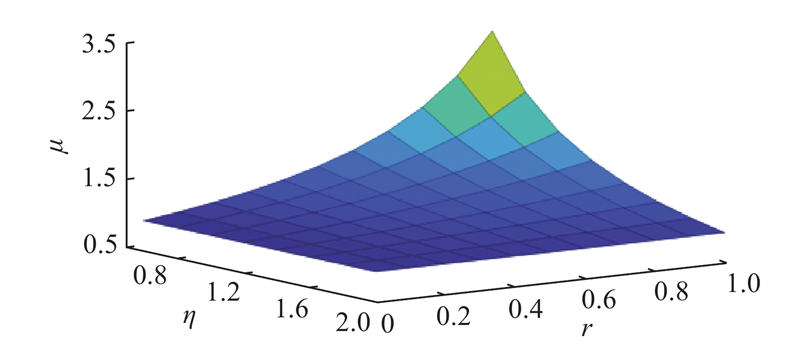
对网联自动车相关参数进行敏感性分析. 网联自动车占比
图 4
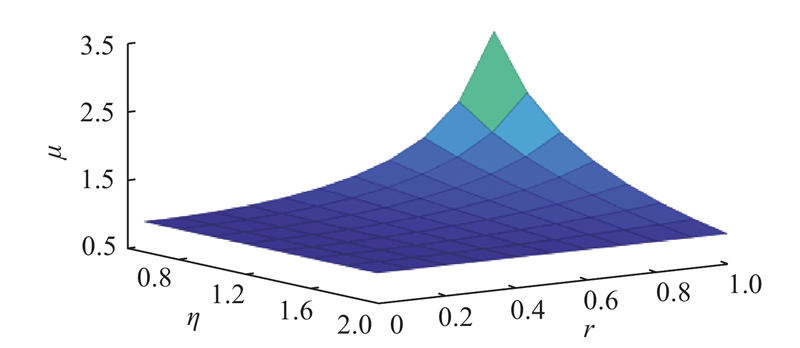
图 4 网联自动车跟驰受前车类型影响时的交叉口通行能力
Fig.4 Intersection capacity when headway of CAV is sensitive to vehicle type ahead
通行能力的增加一方面来源于网联自动车的加入对各车道通行能力的影响,另一方面来源于渠化方案和信号配时方案的改变. 以车头时距
3.2. 网联自动车跟驰不受前车类型影响
图 5
图 5 网联自动车跟驰不受前车类型影响时的部分最优渠化方案
Fig.5 Optimal channelization schemes when headway of CAV is indifferent to vehicle type ahead
图 6
图 6 网联自动车跟驰不受前车类型影响时的交叉口通行能力
Fig.6 Intersection capacity when headway of CAV is indifferent to vehicle type ahead
4. 结 语
当网联自动车与人工车辆在路段上混行时,车道通行能力受网联自动车占比和最小跟驰时距的影响,交叉口各进口车道的饱和度发生变化,传统人工驾驶环境下所确定的渠化方案和信号配时方案管控效能下降. 以交叉口通行能力最大化为目标,构建混合整数线性规划模型来分配混行车流环境下交叉口的时空资源,模型约束主要包括车道渠化、流量分配和信号配时相关约束.
以典型的四车道十字信号交叉口为例,分别优化网联自动车最小跟驰时距受前车类型影响和不受前车类型影响时交叉口的时空资源配置方案,优化结果验证了模型的可行性. 敏感性分析显示,当交通需求不变时,随着网联自动车占比和最小跟驰时距的改变,最优渠化方案和信号配时方案均发生变化. 网联自动车占比增大和最小跟驰时距减小,均有利于提高交叉口的通行能力,且当网联自动车跟驰时距不受前车类型的影响时,交叉口通行能力提高更多.
参考文献
A multiagent approach to autonomous intersection management
[J].
A piecewise trajectory optimization model for connected automated vehicles: exact optimization algorithm and queue propagation analysis
[J].DOI:10.1016/j.trb.2018.11.002 [本文引用: 1]
Parsimonious shooting heuristic for trajectory design of connected automated traffic part I: theoretical analysis with generalized time geography
[J].
Parsimonious shooting heuristic for trajectory design of connected automated traffic part II: computational issues and optimization
[J].DOI:10.1016/j.trb.2016.06.010 [本文引用: 1]
Signal control optimization for automated vehicles at isolated signalized intersections
[J].DOI:10.1016/j.trc.2014.10.001 [本文引用: 1]
A platoon based cooperative eco-driving model for mixed automated and human-driven vehicles at a signalized intersection
[J].DOI:10.1016/j.trc.2018.05.025 [本文引用: 1]
Integrated optimization of traffic signals and vehicle trajectories at isolated urban intersections
[J].DOI:10.1016/j.trb.2018.04.007 [本文引用: 1]
Adaptive cruise control design for active congestion avoidance
[J].DOI:10.1016/j.trc.2007.12.004 [本文引用: 1]
A multiclass cell transmission model for shared human and autonomous vehicle roads
[J].
Effects of autonomous vehicle ownership on trip, mode, and route choice
[J].DOI:10.3141/2493-04
Modeling connected and autonomous vehicles in heterogeneous traffic flow
[J].DOI:10.1016/j.physa.2017.08.015 [本文引用: 1]
A mixed traffic capacity analysis and lane management model for connected automated vehicles: a Markov chain method
[J].DOI:10.1016/j.trb.2017.09.022 [本文引用: 1]
Lane-based optimization of signal timings for isolated junctions
[J].DOI:10.1016/S0191-2615(01)00045-5 [本文引用: 1]
Optimal allocation of turns to lanes at an isolated signal-controlled junction
[J].
Integrated optimization of lane markings and timings for signalized roundabouts
[J].
Increasing the capacity of signalized intersections by allocating exit lanes to turning movements
[J].DOI:10.1002/atr.1457 [本文引用: 1]
Solving a discrete multimodal transportation network design problem
[J].DOI:10.1016/j.trc.2014.10.008 [本文引用: 1]
Pareto-improving congestion pricing on multimodal transportation networks
[J].DOI:10.1016/j.ejor.2010.10.016 [本文引用: 1]