软体机器人拥有连续变形机体结构,能实现多自由度的复杂运动,具有较好的运动能力和环境适应性. 多种驱动方式被应用于软体机器人,包括使用热能、电场和加压流体. 当软体机器人被加热到它们(固态)的相变温度时,形状记忆合金(shape memory alloys,SMAs)可以产生较大的收缩应力,但是有迟滞现象,而且周期较长[4].低成本的聚合物纤维如扭转的钓鱼线和缝纫线可以产生较大的力和较大的拉伸行程,但是能量转换效率较低[5]. 电活性聚合物(electroactive polymers,EAPs)分为离子型和介电型两大类[6-7],具有较高的能量转换效率、低重量和较大柔度等特性,但是须高电压或者密封包装,给实际应用带来了障碍. 利用电驱动水凝胶可以制造小尺度的可逆驱动的驱动器,但是它们的响应速度较慢[8-9]. 相变材料被用来制造具有高应变和高应力的电动驱动器,但是能量转换效率与SMAs接近,响应速度也较慢[10]. 流体驱动特别是气压驱动的驱动器方案简易,研制成本低,能量转换效率高,而且输出的驱动力和位移行程大,正成为最广泛使用的软体机器人驱动方式之一[11-12].
目前,软体机器人技术还较少被应用于空间捕获系统,本研究尝试发展气动软体捕获机器人技术. 相对刚性捕获机器人,软体机器人在捕获时受到的来自环境的反作用力大范围分布于软体组织表面,能够减小冲击破坏因而适合于存在碰撞的捕获任务[21-22]. 软体机器人由于其大变形能力,能够较好地捕获非合作目标. 本研究提出全软体空间捕获机器人方案,基于折纸理论设计气动自折叠机械臂,并研究其驱动特性和负载能力. 通过充气试验和数值分析研究气动自折叠机械臂在气压作用下的大变形过程,通过负载能力试验和仿真揭示气压、负载和变形之间的非线性关系,评估气动机械臂的轴拉和轴压负载能力,为全柔性空间捕获机器人的工程应用提供支撑.
1. 软体捕获机器人方案设计
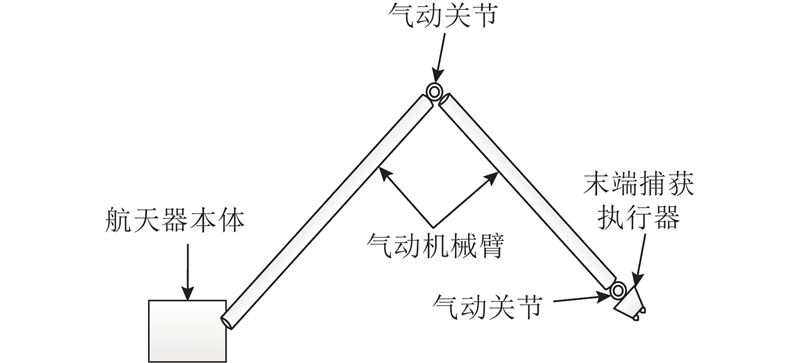
刚性机械臂捕获系统和柔性捕获系统的捕获机构结构复杂、体积尺寸大、质量大、系统控制方式复杂、发射成本高. 为了改善这些缺点,根据非合作目标柔性捕获的任务和功能需求,提出由线性软体驱动器和弯曲软体驱动器构成的全软体空间捕获机器人方案. 空间捕获机器人系统由航天器本体、2根气动自折叠机械臂、末端捕获执行器、气动关节、气源及控制器等组成,如图1所示. 与现有刚性和柔性捕获系统相比,全软体空间捕获机器人的任务空间更大、负载自重比较高、功耗和研制成本较低,并且可实现高速操作.
图 1
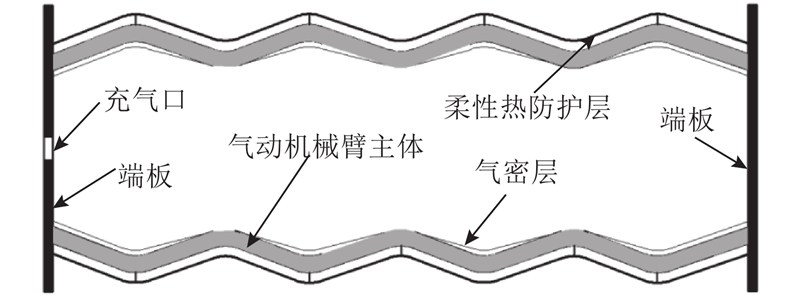
全软体空间捕获机器人的驱动装置主要有气动自折叠机械臂、气动关节及末端捕获执行器. 针对不同的捕获任务,末端捕获执行器须进行特殊设计. 空间捕获机器人在搭载发射时,可被折叠在较小的包装盒中,故要求气动自折叠机械臂具有较小的初始长度和较大的动作行程. 气动自折叠机械臂结构方案如图2所示,须能实现轴向大幅度收展. 气动机械臂主体拟采用超弹柔性材料制备,可在充气气压作用下发生可调控的大变形响应. 机械臂的展开驱动过程采用充气方式,自折叠过程通过超弹材料的弹性势能释放完成. 基于折纸理论,设计气动机械臂的结构方案,并基于3D打印技术制备机械臂主体. 为了适应空间热环境,在机械臂主体外壁包裹层合铝薄膜作为柔性热防护层,在内壁黏附kapton薄膜作为气密层. 如图2所示,柔性热防护层和气密层可间隔胶接于气动机械臂的折痕处,在2个连接点之间,柔性热防护层、气密层和机械臂主体脱离.
图 2
图 3
图 4
本研究重点关注气动自折叠机械臂的设计方法,包括材料/结构设计、驱动特性研究和负载能力评估. 由于柔性热防护层、气密层等对驱动特性和负载能力影响不大,后续只针对气动机械臂主体开展性能研究,暂未将柔性热防护层和气密层胶接在机械臂主体上. 关于机械臂的力学研究只和内外压差有关,因此太空的真空条件对机械臂驱动和承载性能的影响不大.
2. 气动自折叠机械臂结构
为了实现气动机械臂的高折叠率和自折叠驱动特性,基于hexagonal折纸样式设计气动自折叠机械臂的结构形态[23],通过折叠参数设计,获得满足折叠率要求的气动机械臂结构.另外,在结构方案设计过程中,须考虑后续3D打印工艺的可行性.
2.1. hexagonal折纸样式
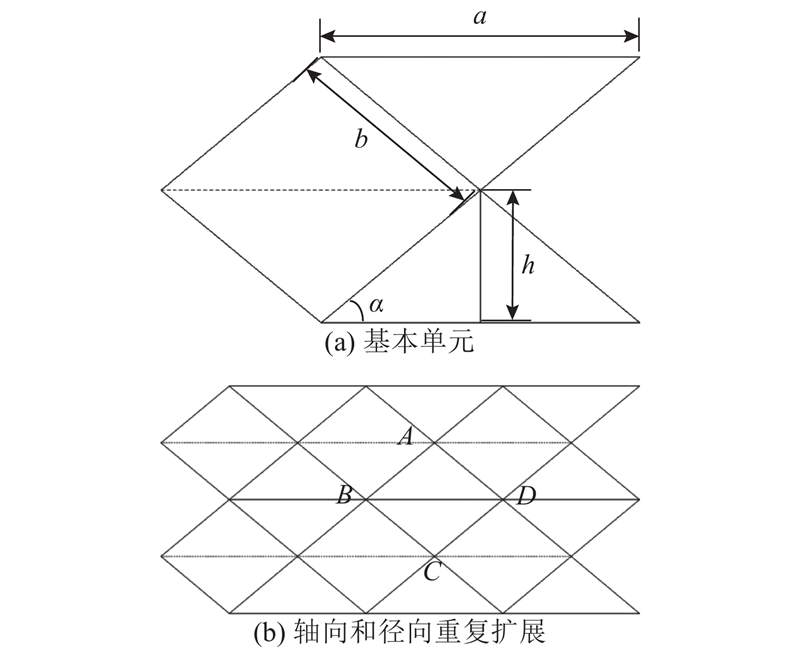
hexagonal折纸模型的基本单元为如图5(a)所示的2个等腰三角形,其斜边长b、高h可由边长a、底角α得到:
图 5
图 6
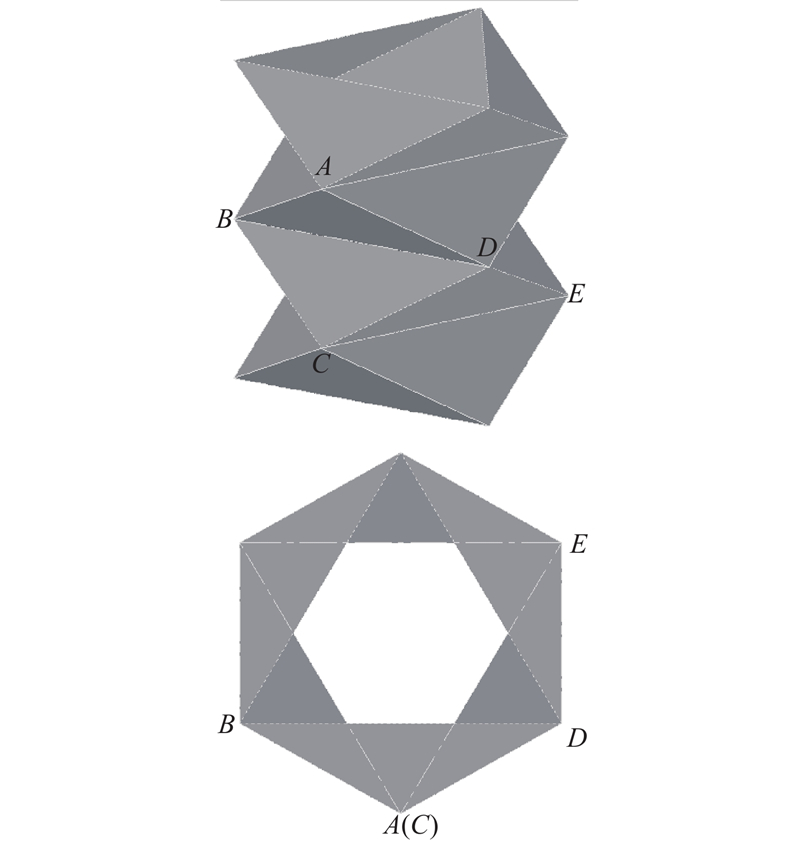
图 6 气动机械臂结构的初始结构构型
Fig.6 Initial structural configuration of pneumatic manipulators
取初始结构构型中的基本单元ABCD及相邻三角形CDE,如图7所示. 基于hexagonal折纸样式推导气动机械臂结构的折叠率和各几何设计参数之间的关系式.
图 7
图 7 气动机械臂结构基本单元间的几何关系
Fig.7 Geometric relationship between basic elements of pneumatic manipulators
过点A作
AF在水平面BDG中的投影为FG,故有
将式(2)和
式中:
在
故有
由
过点D作
式中:
从而有
最终有
气动机械臂初始构型中基本单元的高度为
采用hexagonal折纸样式,气动机械臂的轴向伸长率为
在气动机械臂的结构方案设计中,如果已知基本单元轴向层数M、径向截面边数N、基本单元底边长a及底角α,即可通过式(1)~(12)确定气动机械臂的初始结构构型及轴向伸长率.
2.2. 气动自折叠机械臂结构设计
根据hexagonal折纸样式,设计气动机械臂的初始结构构型. 气动自折叠机械臂基本单元的a=105 mm、
图 8
图 9
3. 气动机械臂驱动特性研究
3.1. 材料参数测试
为了获得气动机械臂硅橡胶材料的剪切模量,须设计试验件并完成单轴拉伸试验以测试其材料特性. 超弹材料单轴拉伸试验的试验件按照长宽比为15∶1设计,通过3D打印制备“骨头状”试验件,试验件的宽度为10 mm,厚度为2 mm,如图10所示.
图 10
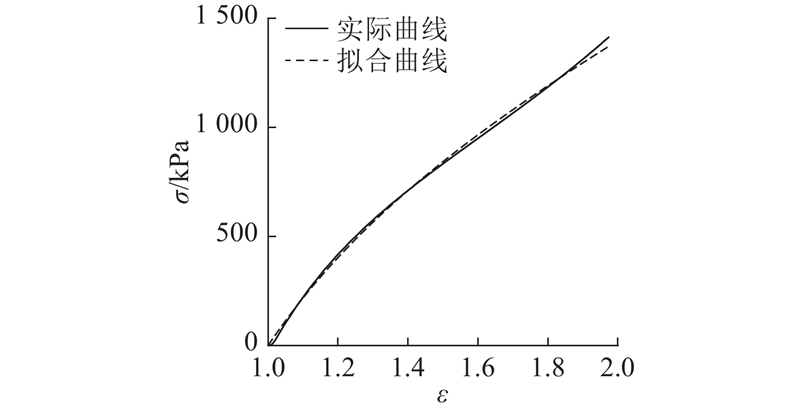
在HF-9002电脑式拉力试验机上进行试验件单轴拉伸试验,通过单轴拉伸试验获得试验件的应力
图 11
图 11 应力-伸长比试验与拟合结果对比
Fig.11 Comparison of simulation and test results of stress-elongation ratio test
3.2. 充气驱动试验
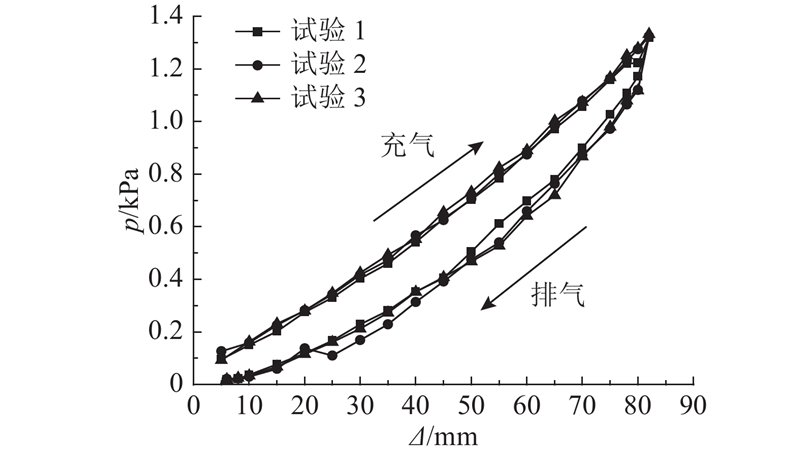
为了消除重力对气动机械臂驱动过程的影响,研制充气驱动试验装置. 将气动机械臂两端连接于亚克力板上,一端的亚克力板固定,充气管路布置在固定端,另一端亚克力板悬挂于一维展开的滑块下,如图12所示. 进行气动机械臂的充气驱动试验,打开充气阀开关对机械臂内腔进行充气,在气压作用下结构发生轴向伸长. 当自由端位移为80 mm时,打开排气阀开关进行排气,排气后结构弹性势能释放,从而实现自折叠收缩. 重复充气驱动和排气自折叠过程3次,实时监测气动机械臂中的气压和自由端的伸长量,得到气压p-伸长量Δ曲线,如图13所示. 由试验结果可以看出,在充气气压不断增大的过程中,气动机械臂沿轴向伸长,当自由端位移达到80 mm时,气压约为1.3 kPa. 在排气过程中,气压逐渐变小,气动机械臂自动折叠收缩,当气压卸载为零时,机械臂回到初始状态.
图 12
图 13
图 13 气动机械臂的气压-伸长量试验曲线
Fig.13 Pressure-elongation test curves of pneumatic manipulators
由测试结果可知,充气段的气压-伸长量曲线为非线性变化,随着气压增大,机械臂的伸长量不断变大,曲线斜率也不断变大. 表明随着内腔气压的增大,机械臂的结构刚度也变大. 当伸长量达到80 mm时,进入排气段,气压降低,机械臂自折叠收缩. 排气段的气压-伸长量曲线位于充气段曲线的下方,整个加卸载过程的滞回曲线明显.
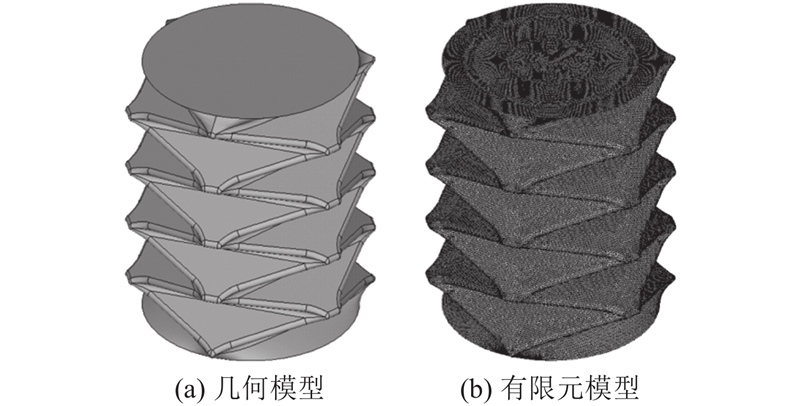
3.3. 充气驱动过程仿真
图 14
图 15
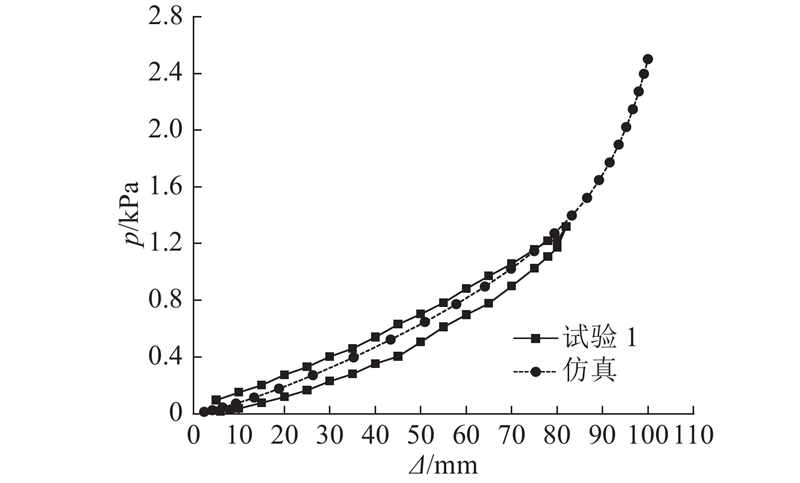
图 15 气动机械臂的气压-伸长量曲线对比
Fig.15 Comparison of pressure-elongation curves of pneumatic manipulators
通过仿真分析得到结构在1.3 kPa气压作用下的变形和应力分布等,如图16所示. 由结构变形分析结果可知,机械臂自由端能够发生80 mm的大幅轴向位移. 由应力结果可知,机械臂上的最大von Mises应力为0.43 MPa,主要分布在基本单元的折痕BD附近,最大应力小于硅橡胶的拉伸强度,满足结构强度要求. 对应地,机械臂上的最大应变点也分布在基本单元的折痕BD附近,数值为0.167. 当充气气压为2.5 kPa时,机械臂自由端轴向位移为100 mm. 此时结构刚度已经较大,继续增大充气气压,机械臂难以再伸长.
图 16
图 16 气动机械臂的结构变形和应力应变分布
Fig.16 Structural deformation and stress-strain distribution of pneumatic manipulators
4. 气动机械臂负载能力评估
空间捕获机器人在捕获空间目标物时,要求气动机械臂具有一定的负载能力. 软体机器人一般负载能力不大,因此有必要探究气动机械臂在有负载情况下的负载-充气气压-弹性变形之间的非线性关系,评估其在不同充气气压下的负载能力. 从试验和有限元仿真2个方面分析气动机械臂的负载能力.
4.1. 负载能力试验
为了揭示内腔气压对机械臂负载能力的影响规律,对不同设计气压时的气动机械臂进行轴向拉伸和压缩试验,如图17所示. 在试验中,将气动机械臂两端通过亚克力板固定在试验机上,向气动机械臂内腔充气,在达到设计气压后将力和位移传感器都归零,开始进行拉伸或者压缩试验. 在拉伸或者压缩过程中,一直保持机械臂的内腔气压为设计气压. 进行如表1所示的5组工况的拉压测试,设计气压p分别取0、482、964 Pa,拉伸试验中端部最大位移控制为80 mm,压缩试验中端部最大位移控制为40 mm. 每个试验工况分别进行2次试验,2次试验的重复性较好,得到气动机械臂在不同气压下的载荷位移曲线,如图18所示. 图中,F为气动机械臂负载.
表 1 气动机械臂负载能力试验工况
Tab.1
| 序号 | p/Pa | Δ/mm |
| 1 | 0 | 80(拉伸) |
| 2 | 482 | 80(拉伸) |
| 3 | 964 | 80(拉伸) |
| 4 | 482 | 40(压缩) |
| 5 | 964 | 40(压缩) |
图 17
图 17 气动机械臂的轴向拉伸/压缩试验
Fig.17 Axial tensile/compression test of pneumatic manipulators
图 18
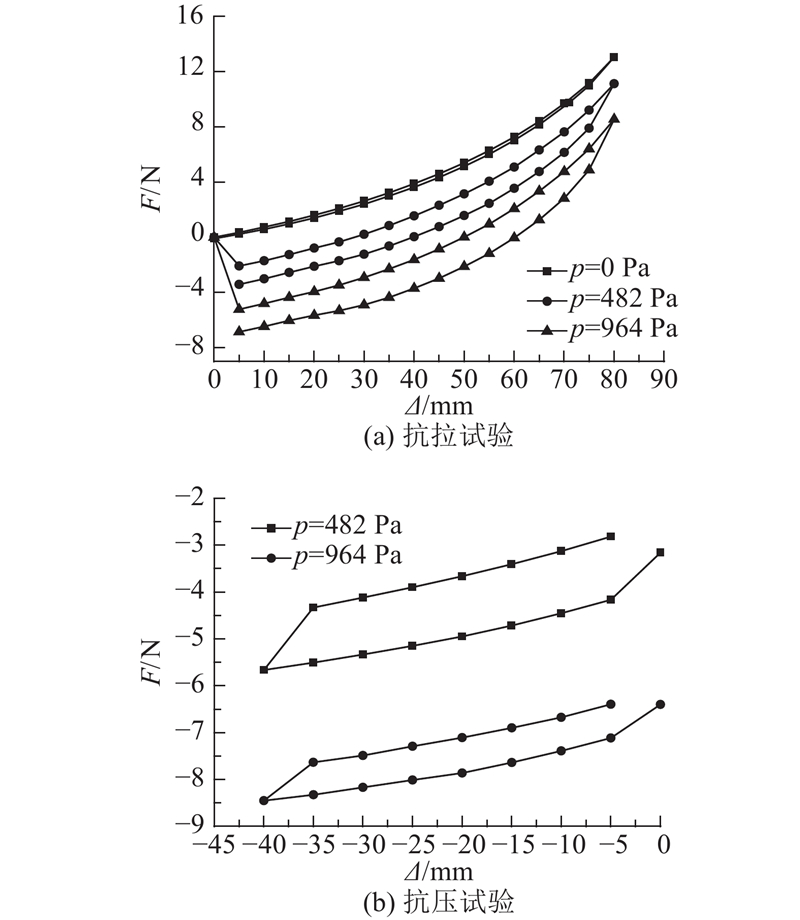
图 18 气动机械臂在不同气压下的载荷-位移曲线
Fig.18 Load-displacement curves of pneumatic manipulators in different pressures
在气动机械臂充气加载的起始阶段,由于气压的作用,负载为压力. 在抗拉试验中,随着位移的增大,负载不断变大,最终变为拉力. 力传感器测得的数值须减去初始时刻的压力,故图18(a)中所示482、964 Pa对应的初始负载为负值. 由图18(a)的抗拉试验结果可以看出,当机械臂内腔不充气(压差为零)时,在加载阶段,随着拉伸位移不断变大,载荷也不断变大,而且结构刚度越来越大,几何非线性明显. 当位移为80 mm时,载荷为13.04 N. 在卸载阶段,载荷-位移曲线基本沿加载段变化,相同位移对应的载荷比加载阶段小,滞回环不明显. 随着设计气压的不断变大,载荷-位移曲线沿着y轴整体下移. 当位移相同时,拉伸载荷随着设计气压的增大而减小,负载能力变小. 卸载段曲线在加载端曲线的下方,加载段和卸载段形成的滞回环面积变大. 当设计气压为482、964 Pa时,最大位移对应的载荷分别为11.11、8.54 N.
由图18(b)的抗压试验结果可知,当设计气压为482 Pa时,在加载阶段,随着压缩位移不断变大,载荷不断变大,结构刚度小幅变小;当位移为40 mm时,载荷为5.66 N. 在卸载时,载荷位移曲线基本沿y轴整体上移,相同位移对应的载荷比加载阶段小,结构刚度和加载阶段的刚度接近. 随着设计气压的变大,载荷-位移曲线沿y轴整体下移,在位移相同时载荷随设计气压的增大而增大,负载能力变大. 卸载段曲线在加载段曲线的上方,加载段和卸载段形成的滞回环面积变小. 当设计气压为964 Pa时,最大位移对应的载荷为8.45 N.
4.2. 负载能力仿真分析
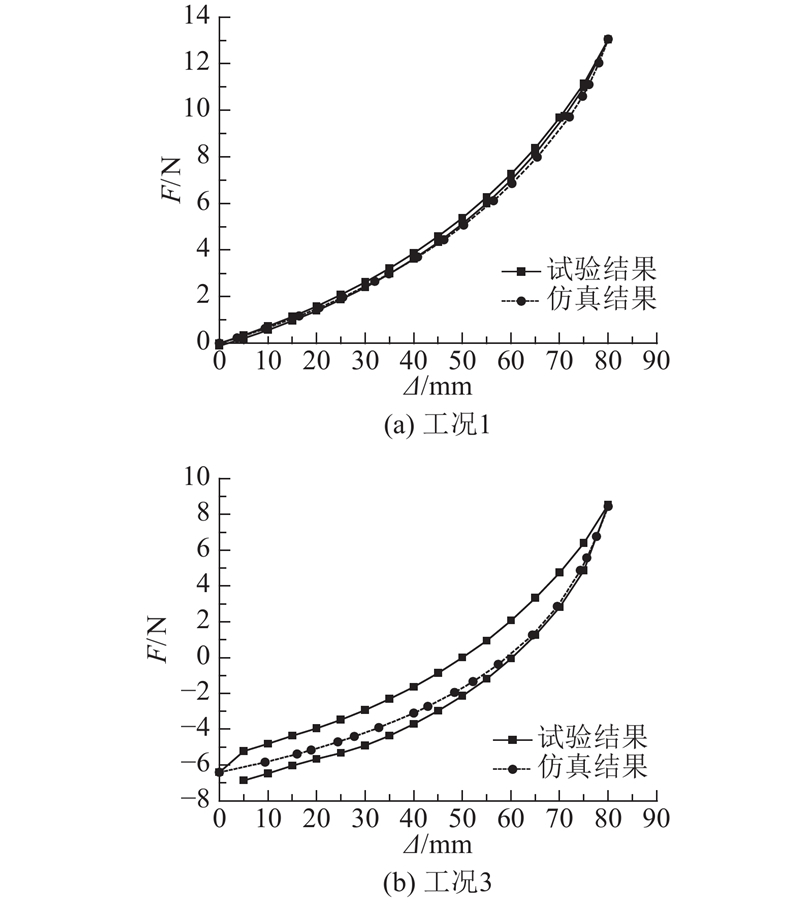
基于3.3节的气动机械臂有限元模型,进行负载能力仿真分析. 和前述的负载能力试验相同,分析5组工况下的拉伸、压缩性能. 其中,工况1、3仿真所得的载荷-位移曲线与试验结果的对比如图19所示.
图 19
图 19 不同工况下载荷位移仿真结果与试验结果的比较
Fig.19 Comparison of simulation and experimental results of load-displacement in different cases
5. 结 论
(1)由充气驱动试验可知,充气段和排气段的气压-伸长量曲线都呈非线性变化,随着气压增大,机械臂的伸长量不断变大,曲线斜率也不断变大,整个加卸载过程的滞回曲线明显. 基于非线性有限元的仿真分析验证了充气驱动的气压-伸长量曲线和结构强度. 研究表明该气动机械臂可以实现充气伸长、排气自主折叠收缩.
(2)在拉伸负载能力试验中,随着设计气压的不断变大,拉伸负载能力变小,滞回环变大. 当设计充气气压为0、482、964 Pa时,最大位移对应的拉伸载荷分别为13.04、11.11、8.54 N. 在抗压负载能力试验中,随着设计气压的变大,抗压负载能力变大,滞回环变小. 当设计充气气压为482、964 Pa时,最大位移对应的载荷分别为5.66、8.45 N.
(3)当机械臂不充气时机械臂负载能力的仿真结果和试验结果较接近,充气工况的仿真结果在试验结果的充气段和排气段之间,更接近排气段的曲线,从而验证了负载能力仿真模型的合理性.
考虑到制备工艺的难度,本研究设计的气动机械臂折叠率并不高,后续须进行折叠方案和结构拓扑优化设计以实现高折叠率. 在充气驱动和负载能力仿真模型中,可以采用更合适的硅橡胶弹塑性本构模型,还须考虑充气气体的可压缩性,以更精确地模拟气动机械臂的力学性能.
参考文献
Multibody dynamics driving GNC and system design in tethered nets for active debris removal
[J].DOI:10.1016/j.asr.2016.04.015 [本文引用: 1]
A review of shape memory alloy research, applications and opportunities
[J].DOI:10.1016/j.matdes.2013.11.084 [本文引用: 1]
Artificial muscles from fishing line and sewing thread
[J].DOI:10.1126/science.1246906 [本文引用: 1]
Ionic polymer-metal composites (IPMCS) as biomimetic sensors, actuators and artificial muscles-a review
[J].DOI:10.1088/0964-1726/7/6/001 [本文引用: 1]
Multilayer dielectric elastomers for fast, programmable actuation without prestretch
[J].DOI:10.1002/adma.201601842 [本文引用: 1]
Reversible patterning and actuation of hydrogels by electrically assisted ionoprinting
[J].
Hydrogel-based actuators: possibilities and limitations
[J].DOI:10.1016/j.mattod.2014.07.002 [本文引用: 1]
Soft material for soft actuators
[J].
Pneumatic torsional actuators for inflatable robots
[J].DOI:10.1115/1.4026629 [本文引用: 1]
Buckling pneumatic linear actuators inspired by muscle
[J].DOI:10.1002/admt.201600055 [本文引用: 1]
Origami-inspired active structures: a synthesis and review
[J].DOI:10.1088/0964-1726/23/9/094001 [本文引用: 1]
Using origami design principles to fold reprogrammable mechanical metamaterials
[J].DOI:10.1126/science.1252876 [本文引用: 1]
Research on the folding patterns and deployment dynamics of inflatable capsule structures
[J].
可展开薄膜结构折叠方式和展开过程研究
[J].
Fold methods and deployment analysis of deployable membrane structure
[J].
Review of inflatable booms for deployable space structures: packing and rigidization
[J].DOI:10.2514/1.A32598 [本文引用: 1]
Folding of a type of deployable origami structures
[J].DOI:10.1142/S021945541250054X [本文引用: 1]
Lower-order symmetric mechanism modes and bifurcation behavior of deployable bar structures with cyclic symmetry
[J].DOI:10.1016/j.ijsolstr.2017.05.008
An integrated geometric-graph-theoretic approach to representing origami structures and their corresponding truss frameworks
[J].DOI:10.1115/1.4042791 [本文引用: 1]
Pneumatically actuated soft robotic arm for adaptable grasping
[J].DOI:10.1007/s10338-018-0052-4 [本文引用: 1]
Development of a pneumatic soft actuator with pleated inflatable structures
[J].DOI:10.1080/01691864.2017.1345323 [本文引用: 1]