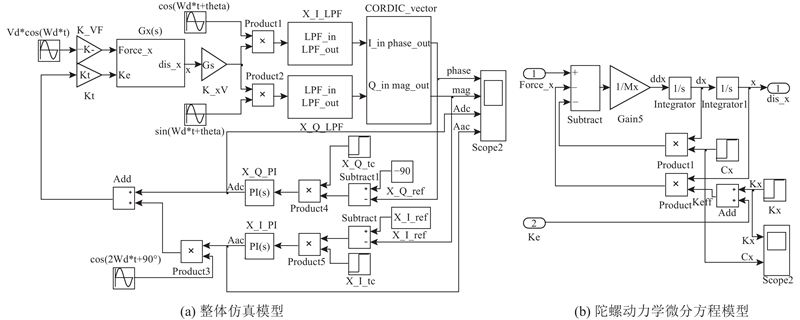
微机械陀螺的驱动模态控制方案通常采用基于锁相环和自动增益控制（PLL-AGC）环路：一方面，通过锁相环（phase-locked loop，PLL）将驱动振动位移和驱动信号的相位差锁定在−π/2，使得陀螺驱动信号跟踪陀螺驱动模态的谐振频率从而保持驱动模态工作在谐振频率处^[1-2]；另一方面，自动增益控制（automatic gain control，AGC）环路将陀螺驱动模态振动位移幅值锁定到参考幅值^[3]. 对于该控制方案，需要获得陀螺驱动振动的幅度信息和相位信息，并分别通过2个控制器实现对陀螺的驱动信号的幅度稳定和频率跟踪. 对于PLL-AGC闭环控制方案，陀螺驱动模态的谐振频率和品质因子仍然随环境温度波动，即陀螺驱动模态的动力学参数随温度缓变，使得陀螺输出不可避免地发生漂移.

为了克服陀螺谐振频率随温度漂移的影响，笔者所在课题组曾报道了一种基于三角形栅极电容的恒谐振频率驱动（constant resonant frequency drive，CRFD）方案，该方案通过实时调整陀螺本身的谐振频率实现恒定谐振频率驱动^[4]，报道中陀螺的幅度控制环路采用AGC控制方案，无法避免陀螺驱动模态品质因子随温度的漂移.

参量激励（parametric excitation，PE）是一种利用陀螺动力学方程中参数发生周期性振荡促使系统达到谐振状态的激励方案，微机械陀螺中可利用弹性系数周期变化实现参量激励^[5-8]. 参量激励可用来调整陀螺驱动品质因子从而调节振动幅度. 但目前微机械陀螺的参量激励主要基于变间距梳齿结构，其引入的静电刚度具有非线性项，参量激励时会加剧振动位移的非线性.

Gallacher等^[9-11]利用参量激励对品质因子的调节作用，实现驱动控制方案的幅度控制，但相位控制仍采用PLL，陀螺驱动模态谐振频率随温度的漂移依然无法避免.

三角形栅极电容是一种线性静电刚度调谐结构，其引入的静电刚度与振动位移无关. 本文首先介绍三角形栅极电容用于频率调谐和参量激励的工作原理，在此基础上提出基于三角形栅极电容的恒定谐振频率参量激励（constant resonant frequency parametric excitation，CRF-PE）驱动控制方案. 该方案通过三角形电容对陀螺驱动环路实时调谐，维持工作过程中陀螺驱动模态谐振频率恒定，并通过参量激励实时控制陀螺的驱动模态等效品质因子恒定.

如图1（a）所示为所用的栅结构微机械陀螺的示意图，外框质量块被限制沿着x轴振动，内框有x和y两个方向的自由度，内框沿y轴的振动能反映陀螺所敏感的角速度信号. 图1（b）给出了微机械陀螺可动质量块下方的固定电极图，包括矩形电极和三角形电极.

陀螺器件的加工过程可概括如下：在可动质量块背面刻蚀栅槽，如图1（b）所示，在玻璃上加工固定金属电极，包含矩形电极和三角形电极. 质量块背面栅条与玻璃衬底上的固定矩形电极形成差分电容检测结构，可动质量块的位移导致电容的交叠面积发生变化，一侧交叠面积变大，另一侧交叠面积变小，从而使得差分电容的电容量相应地发生改变，此电容变化量与可动质量块的位移成正比. 质量块的可动电极与玻璃衬底上的固定三角形电极形成如图1（c）所示的三角形栅极电容，即图1（b）中的陀螺调谐端，用来进行频率调谐和参量激励. 该变面积差分电容结构可以引入正弹性系数，称为三角形电容上调谐结构. 图1（d）显示的是微机械陀螺的照片.

对于如图1（c）中所示的三角形上调谐电容结构，其直角三角形固定电极与矩形可动电极的交叠部分为直角三角形. 根据文献[12]，差分调谐电压调谐效果是单边调谐电极的2倍，N对差分上调谐电极引入的弹性系数如下：

式中：a为三角形固定极板在x方向的长度，b为在y方向的交叠宽度，g为与可动极板在z方向形成的间距，k_e为静电弹性系数，N为差分上调谐电极数量，ε为真空介电常数，V_t为调谐电极上施加的调谐电压，K_T为表示静电弹性系数与调谐电压平方关系的调谐系数

图1（c）中陀螺三角形电极引入的静电弹性系数为正弹性系数，使陀螺驱动模态等效弹性系数增大，进而增大相应模态的谐振频率. 从式（1）可以看出，三角形上调谐电容结构引入的静电弹性系数与可动电极位移无关，而与直角三角形底长与高长的比值（b/a）成正比，与电极间距g成反比，并与调谐电压成平方正比关系. 将引入的静电弹性系数与调谐电压的平方关系系数用调谐系数K_T表示. 考虑引入的弹性系数后，微机械陀螺驱动模态为典型的弹簧-质量块-阻尼系统，遵循如下动力学方程：

式中：m为可动质量块的质量，c为阻尼系数，k为弹性系数，F₀为驱动力幅度，ω为工作频率.

参量激励是指在齐次系统中，某个参数发生周期性振荡促使系统达到谐振状态的激励方案，当被运用到微机械陀螺中时，发生周期性变化的参数一般是陀螺的弹性系数^[13]. 为了构建能满足参量激励条件的陀螺动力学微分方程，令调谐电压具有如下余弦开根号的形式：

式中：A_dc为调谐电压中的直流分量幅度，A_ac为调谐电压中的交流分量幅度，ω_d为驱动信号频率，φ_t为调谐电压中的交流分量相位. 那么，对应的微分方程改写为

根据文献[14]，当驱动模态频率满足式（5）的谐振条件时，参量激励后的幅度如式（6）所示.

式中： $E = {{{K_{\rm{T}}}{A_{{\rm{ac}}}}}/{\left( {2c{\omega _{{\rm{0eff}}}}} \right)}}$. 其中，ω_0eff为调谐后的等效谐振频率.

由式（6）可见，陀螺最终的谐振频率跟K_T和A_dc相关，K_T是和三角形栅极电容参数相关的物理量. 因此可以通过调节A_dc调节系统的弹性系数，系统弹性系数由未加电压时的k调节到施加电压后的k+K_TA_dc. 除了直流调谐作用之外，式（3）中的调谐电压同时引入了参量激励，其效果与参数A_ac和φ_t有关. 当调谐相位满足φ_t=π/2+2nπ，参量激励的效果为最显著的参量放大，固定φ_t=π/2后参量放大效果只与参数A_ac相关，且随着A_ac的增加，陀螺驱动模态等效品质因子增加，那么驱动模态振动位移幅度也随之增大，振动位移幅度与参数A_ac的关系如下：

若将无调谐（A_dc=A_ac=0）情况下的初始弹性系数记为k；直流调谐（A_dc>A_ac=0）情况下，等效弹性系数、等效谐振频率和品质因子记为k_eff、w_0eff和Q；经参量激励（A_dc>A_ac>0）后，品质因子得到放大，得到的等效品质因子记为Q_eff，则有

式中：ω₀为调谐前的自然谐振频率.

由式（7）和（8）可知，基于三角形栅极电容可以实现对陀螺驱动模态的直流调谐和参量激励，且由这种调谐结构引入的弹性系数与位移无关. 施加如式（3）所示的调谐电压后，当陀螺驱动模态的弹性系数k和品质因子Q受环境温度波动而发生改变时，可以分别通过A_dc和A_ac进行直流调谐和参量激励，保持驱动模态等效弹性系数和等效品质因子恒定不变，这是本文所提新型控制方案的基础. 据此设计新型的基于恒定谐振频率和参量激励的微机械陀螺驱动控制方案，通过闭环控制实现A_dc和A_ac的自动调节，最终使得陀螺驱动模态的谐振频率和等效品质因子在环境温度波动下都能保持恒定.

如图2（a）所示为传统锁相环和自动增益控制（PLL-AGC）方案的框图，通过锁相环（PLL）来使得陀螺始终驱动在其谐振频率上，同时通过自动增益控制（AGC）来保持驱动幅度恒定. 图中，G_x为陀螺器件的传递函数，ω₀为初始设定的驱动频率，F_x（t）为交流驱动力，A_ref为振动位移幅度参考值，θ_ref为振动位移相位参考值，2个比例-积分（proportional-integral，PI）控制器分别用于控制驱动振动位移相位和振动位移幅度，并反馈到驱动力的频率和幅度上. PLL-AGC环路的控制目标是使得振动位移相位和幅度分别控制在参考值，即陀螺驱动模态工作在谐振频率上且振动幅度保持恒定.

如图2（b）所示为恒谐振频率参量激励（CRF-PE）方案的框图，通过恒定谐振频率控制环路，使得陀螺的驱动谐振频率始终为固定频率，同时通过参量激励来保持驱动幅度恒定. 与传统PLL-AGC控制方案相比，新型CRF-PE控制方案也须对驱动振动位移进行相位和幅度的提取和控制. 不同的是，在新型CRF-PE控制方案中，驱动力的频率和幅度是不变的，发生改变的是调谐电压中的参数A_dc和A_ac，受到PI控制器的反馈调节，驱动力和调谐电压分别作用于如图1（b）所示的驱动电极和调谐电极上.

在传统PLL-AGC控制方案中，一方面，由于陀螺零偏输出的标度因子与工作频率成正比，工作频率的波动会造成标度因子的波动；另一方面，信号处理电路中存在相位对工作频率敏感的模块（如：滤波器），当相位漂移时会在驱动模态的PLL环路造成相位锁定误差^[15-16]，当检测模态的解调相位设为恒定值时，PLL环路的相位锁定误差会引起正交误差到零偏的耦合，同时会影响标度因数^[17]. 正交误差一方面来源于微机械加工工艺误差造成的弹性梁失配，另一方面由驱动力耦合中的正交成分引起，该耦合与驱动模态品质因子负相关^[18]，即驱动模态品质因子的波动会导致陀螺的零偏漂移.

当环境变化引起弹性系数和品质因子变化时，新型CRF-PE控制方案通过调节调谐电压的参数A_dc和A_ac保持驱动模态等效弹性系数和等效品质因子恒定，而传统PLL-AGC控制方案通过调节陀螺驱动力的频率和幅度，从而补偿掉弹性系数和品质因子变化对谐振状态和振动位移幅度的影响.

相比于传统PLL-AGC控制方案，新型CRF-PE控制方案具有以下几个优点：1）恒定谐振频率控制避免了信号处理电路中与陀螺工作频率相关的模块随频率变化引起的相位漂移. 2）参量激励使驱动模态的等效品质因子可以保持对初始品质因子的恒定放大，从而保证相同的驱动位移时降低驱动电压，减少驱动端和其他电极之间的电耦合. 3）当环境温度波动时，等效弹性系数和等效品质因子保持恒定，即陀螺在驱动模态具有恒定动力学参数，因此新型CRF-PE有望显著改善陀螺的温度性能.

平均化方法是一种能够等效分析同时包含快变化和慢变化的控制系统分析工具^[19]. 根据周期平均化方法可以分析新型CRF-PE控制方案中的2个参数A_dc、A_ac如何根据阻尼系数和弹性系数的变化进行调节，以及调节后驱动模态振动位移的幅度和相位的被控效果.

在ω_dt变化的一个周期内，图2（b）中的环路变量{a，θ，A_dc，A_ac，V_t}都可以近似地理解为常量，因此采用周期平均化方案来推导模态匹配算法的稳态解是合理的. 将图2（b）中低通滤波器（LPF）的作用用函数LPF{}表示，选取参量放大效应最明显的相位条件φ_t=π/2，系统控制方程为

驱动振动位移的稳态解依然为

对式（10）求时间t的一阶导数，得到的驱动振动速度为

假设 $\left| {\dot x} \right|\cos\; ({\omega _{\rm{d}}}t + {\varphi _x}) - \left| x \right|{\dot \varphi _x}\sin\; ({\omega _{\rm{d}}}t + {\varphi _x}) = 0$，则驱动振动速度可以重新写成：

对式（12）求时间t的一阶导数，得到的驱动振动加速度为

将驱动振动位移、速度和加速度公式（式（10）、（12）和（13））代入式（9）中的驱动模态运动方程，可得

将式（14）用矩阵形式表示，且左乘如下所示的非奇异矩阵：

所得新矩阵可拆成式（16）和（17）：

对式（15）和（16）进行积化和差后，在ω_dt变化的一个周期内对等式两边作积分运算，得到

最终得到控制系统的平均化方程组：

由式（20）可得，新型CRF-PE控制方案的闭环系统平衡点为

在新型CRF-PE控制方案中，被控制的2个对象依旧是检测到的振动位移的幅度和相位. 由式（21）可见，当驱动模态阻尼系数和弹性系数发生改变时，PI控制器对A_dc、A_ac进行调节，使得等效弹性系数和等效阻尼系数始终保持恒定，即陀螺驱动模态谐振频率和等效品质因子保持恒定.

如图3（a）所示，利用Matlab/Simulink仿真搭建新型CRF-PE控制方案的仿真模型，目的是进一步验证该方案可以在驱动模态的弹性系数和阻尼系数发生改变时调节参数A_dc、A_ac，从而保持等效弹性系数和等效品质因子不变. 仿真模型中包括驱动力产生、陀螺驱动模态、解调滤波、求幅度相位、PI控制器、调谐电压合成这5个模块，与图2（b）中的框图一一对应.

在仿真过程中需要模拟环境变化造成的驱动模态的弹性系数和阻尼系数的改变，因此陀螺的动力学微分方程采用带反馈环节的仿真模型，如图3（b）所示. 采用的仿真参数如表1所示. 表中，f₀为驱动模态本征谐振频率，Q₀为驱动模态本征品质因数，K_VF为驱动电压/驱动力转换系数，K_XV为振动位移/检测电压转换系数.

在仿真过程中，为了验证2个环路可以分别调节等效弹性系数和等效阻尼系数，在开环情况下，先改变弹性系数再进行相位路CRFD闭环，先改变阻尼系数再进行幅度路PE闭环. 具体的仿真过程如下.

1）t=0：驱动模态开环. 设定驱动信号频率为谐振频率，位移幅度逐渐起振到1.47×10⁻² μm，相位为−90°.

2）t=5 s：模拟环境变化造成的弹性系数波动. 驱动模态弹性系数从2 075.800 N/m变为2 076.026 N/m，对应的谐振频率从1 835.91 Hz变为1 836.01 Hz. 结果为驱动模态不再谐振，驱动位移开环幅度从1.47×10⁻² μm降到1.35×10⁻² μm，驱动位移开环相位从−90°变为−52.26°.

3）t=7 s：开始相位路的CRFD闭环，设置参考相位为−90°. 闭环后，相位路的PI控制器输出A_dc去调节等效弹性系数，最终等效弹性系数回到谐振时的2 076.026 N/m，意味着谐振频率通过调谐变回驱动信号频率，驱动模态回到谐振状态. 对振动位移的控制效果为位移相位被控制回参考相位(−90°)，对应的位移幅度变回1.47×10⁻² μm，与谐振时的数值一致.

4）t=10 s：模拟环境变化造成的阻尼系数波动. 驱动模态阻尼系数从2.25×10⁻⁵变为2.65×10⁻⁵，对应的品质因子从8 000变为6 792. 结果驱动位移开环幅度从1.47×10⁻² μm降到1.32×10⁻² μm.

5）t=12 s：开始幅度路的PE闭环，参考幅度为1.47×10⁻² μm. 闭环后，幅度路的PI控制器输出A_ac去调节等效品质因子，最终等效品质因子回到阻尼波动前的8 000. 对振动位移的控制效果为驱动位移闭环幅度从1.32×10⁻² μm被调节回1.47×10⁻² μm.

以上仿真过程对应的仿真结果如图4所示，其中，弹性系数k_x和阻尼系数c_x的变化在仿真模型图3（b）中设定，位移相位θ（t）、位移幅度a（t）、直流分量A_dc、交流分量幅度A_ac在仿真模型图3（a）中进行观察. 等效弹性系数k_eff和等效品质因子Q_eff根据式（8）进行计算.

对仿真结果总结如下，在恒频控制和参量激励控制环路闭环后，尽管驱动模态弹性系数和阻尼系数发生了改变，但是在闭环作用下直流分量A_dc和交流分量幅度A_ac分别调节了等效弹性系数k_eff和等效品质因子Q_eff，使其数值与改变前的弹性系数和阻尼系数相等. 仿真结果表明：CRF-PE控制方案能保持陀螺驱动等效弹性系数和等效品质因子恒定.

新型CRF-PE控制方案的实验平台如图5所示，包括硬件电路板、电脑、稳压源、示波器、矢量分析仪和转台.

首先，控制系统的幅度参考值A_ref和相位参考值θ_ref可通过扫频测试获得，A_ref=7×10⁵ bit，θ_ref=93°，相位参考值与仿真所设的−90°不相等是因为解调电路的滤波网络会引入相移. 在室温下应用CRF-PE控制方案，驱动位移的幅度和相位稳定性的1 h数据如图6所示，计算得到幅度变化的稳定性为2.724 6×10⁻⁵，相位变化的稳定性为0.001 74°（1σ）.

在CRF-PE控制方法中，幅度环路和相位环路2个PI控制器分别输出直流分量A_dc和交流分量幅度A_ac，以分别调节等效弹性系数和等效品质因子使其保持恒定. 图7给出了降温过程和室温2种情况下的直流分量A_dc和交流分量幅度A_ac的45 min数据. 降温过程即首先在温箱中设定控温60 °C，控温2 h后关闭温控，使陀螺系统自然降温，降温45 min后对应的温箱温度从60 °C降温到49 °C. 测试结果显示，在降温过程中，直流分量A_dc和交流分量幅度A_ac一直在自动调节，而在室温下，直流分量A_dc和交流分量幅度A_ac基本上稳定不变.

在室温下以10 Hz的采样频率分别采集传统PLL-AGC方案和CRF-PE控制方案的1 h零偏输出数据，利用Allan方差进行分析，得到分析曲线如图8所示. 图中，S_Allan为Allan方差，τ为Allan方差的积分时间. 在实验测试得到传统PLL-AGC控制方案的角度随机游走(angular random walk, ARW)为0.086°/ $\sqrt {\rm{h}} $，偏置不稳定性(bias instability, BI)为1.86°/h，而新型CRF-PE控制方案的角度随机游走为0.076°/ $ \sqrt {\rm{h}} $，偏置不稳定性为1.69°/h，可见新方案优于传统PLL-AGC方案.

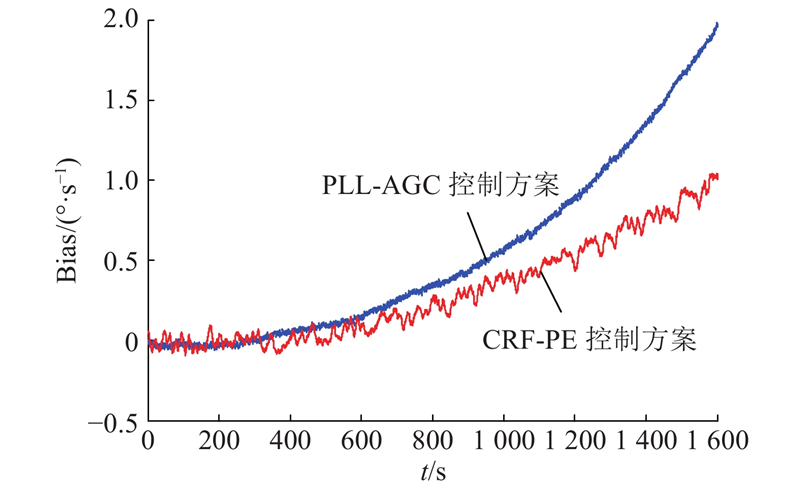
将传统PLL-AGC控制方案和CRF-PE控制方案分别应用到陀螺中，在温箱中设定控温为60 °C，控温2 h后关闭温控，使陀螺系统自然降温，降温1 600 s对应的温箱温度从60 °C降温到53 °C. 降温过程中，2种方案下的陀螺零偏（Bias）数据如图9所示，相比于传统PLL-AGC控制方案在此降温过程中的零偏漂移为2°/s，CRF-PE控制方案在1 600 s内的零偏漂移为1°/s，CRF-PE控制方案下陀螺漂移改善为PLL-AGC方案下的50%.

尽管CRF-PE控制方案下陀螺漂移相比PLL-AGC方案有了明显改善，改善幅度比预期较差，主要原因有以下几点：1）尽管驱动模态的谐振频率和等效品质因子控制为恒定值，但陀螺检测模态开环工作，温度引起的检测模态的动力学参数漂移仍然影响陀螺输出，对检测模态进行力平衡闭环可以进一步改善温度引起的零漂. 2）受限于器件加工时存在较大的硅玻璃键合对准误差，该栅陀螺驱动模态最大工作位移仅仅约为1 μm，在传统PLL-AGC方案测试中陀螺工作已达1 μm，因此所提CRF-PE方案参量放大倍数不能超过2倍，无法完全发挥出参量放大的优越性. 3）尽管新方案在谐振频率和品质因子波动的情况下可以进行调节使其恒定，陀螺零偏的温漂还受到其他因素的影响，如：位移/电容转换增益和检测电路增益.

本文所提的新型恒频参量激励（CRF-PE）控制方案，基于恒定谐振频率驱动和参量激励，与传统的锁相环和自动增益（PLL-AGC）控制方案相比，具有低驱动电压、低电耦合、高稳定性等优点.

通过实验测试得到新型CRF-PE控制方案的角度随机游走为0.076°/ $\sqrt {\rm{h}} $，偏置不稳定性为1.69°/h，优于传统PLL-AGC方案. 在降温过程中CRF-PE控制方案下的陀螺零偏漂移降到传统PLL-AGC方案下的50%.

所提新型CRF-PE控制方案有效改善了陀螺零偏的稳定性和温漂，但依然存在残留的温漂. 后续的研究可以从3个方面进行：1）对CRF-PE控制方案进行优化，通过对检测模态实现力平衡闭环，利用参量放大增加驱动模态的可动位移等方法，可以进一步改善CRF-PE控制方案下陀螺零偏的温漂；2）优化陀螺器件结构设计，提高三角形电极的调谐能力，即增大驱动模态的调谐系数K_T，可以提高新型CRF-PE控制方案的调节谐振频率和品质因子的能力，能使其适用于更广的工作温度范围；3）由于位移/电容转换增益和检测电路增益等依然会引起陀螺零偏发生温漂，可以将新型CRF-PE控制方案与自校准检测方案或者零偏补偿方案相结合，进一步改善零偏的温漂.