自动立库是众多设施和设备的集成系统,在现代仓储中发挥着重要作用,而堆垛机式自动立库因其具有高自动化、高效率等特点,大受市场欢迎. 从存储单元看,自动立库可分为托盘式自动立库和料箱式自动立库两类. 在库存持有单元(stock keeping unit, SKU)种类繁多、客户需求批量较小的行业,料箱式自动立库方兴未艾. 这是由于料箱式自动立库的堆垛机运行更快,噪音却更小[1].
传统自动立库的主要服务目标一般是更低的成本和更高的服务水平,即更快的响应速度和更准确的发货. 在以往的自动立库设计模型中,优化目标大多是成本或平均吞吐时间(单位时间内的吞吐量),很少考虑能耗,而且通常堆垛机的运动被简化为匀速运动.
由上述文献回顾可以发现,对自动立库作业效率的研究已经相对成熟,自动立库的设计往往以其为基础,但在能耗方面的研究有所不足,在自动立库设计中很少考虑能耗. 但是随着对能源节约和环境保护的日益重视,建设资源节约型仓库已经备受关注. 本文在设计自动立库存储区时,考虑堆垛机实际作业中存在的变速运动阶段,把降低设备能耗作为优化目标之一.
1. 料箱式自动立库设计中的多目标优化问题
1.1. 自动立库设计的顺序和内容
完成战略层面的设计后,一般已经明确客户的需求(最小吞吐量、最小货位数量等),确定了仓库的类型(包括使用哪些设备)和货载单元等. 在其后的战术层面,需要确定存储策略、存储区的大小、设施设备的选择(规格和数量)、布局和人员数量等. 在操作层面,需要决策人员的调度和任务的安排等.
本文提出的对料箱式自动立库存储区的设计属于战术层面,要决策的是存储区的大小及其设施设备的数量,并指导选择设备设施的规格.
1.2. 料箱式自动立库存储区的介绍
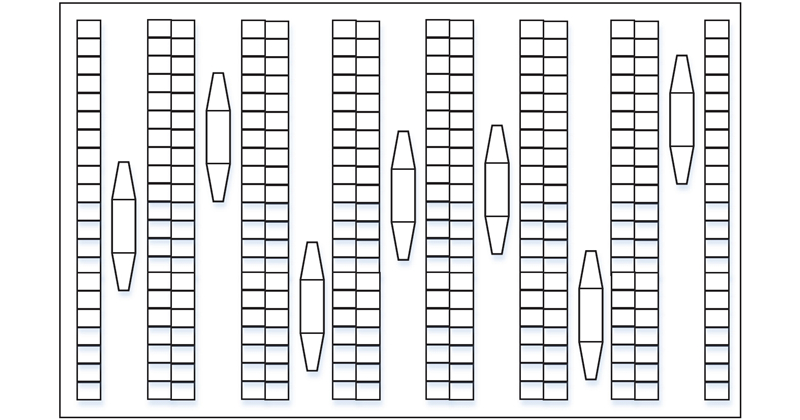
本研究的料箱式自动立库存储区的示意图(俯视图)如图1所示,1个堆垛机和1组货架交错,1个堆垛机可以服务于两侧的2个货架,出入库(input/output,I/O)位置位于每个货架的左下方.
图 1
1.3. 存储区设计中的多目标优化问题
由本文的多目标优化模型的决策变量可以确定存储区的大小和主要设备设施的选购(数量和规格,非具体型号).
2. 多目标优化模型的建立
2.1. 模型假设
为避免能耗、平均吞吐时间和成本的计算模型过于复杂,本文提出如下假设(部分假设是基于自动立库战略层的设计已经完成,是合理的).
1)堆垛机的运动被视作垂直方向和水平方向的运动相互独立,由水平方向和垂直方向2个引擎驱动.
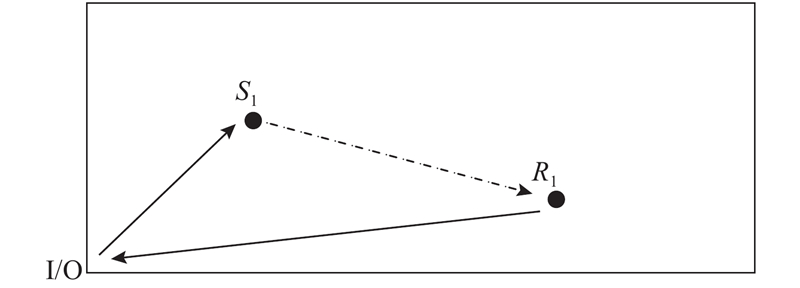
2)堆垛机的复合作业平均循环时间包括移动时间和装取货时间. 复合作业模式指堆垛机在一次作业中进行一次存货和一次取货作业. 复合作业过程如图2所示. 其中,S1为存货货位,R1为取货货位.
图 2
图 2 堆垛机的复合作业过程示意图
Fig.2 Diagram for dual-command cycle of storage and retrieval machine
3)每个货格的高度、长度和深度已由货箱(货载单元)大小确定.
4)堆垛机不是一直在匀速作业,而是由匀加速、匀速和匀减速过程构成.
5)货架的长度和高度足够堆垛机在水平方向和垂直方向运行到最大速度. 这一假设,既是建模的要求,也符合实际情况.
6)使用任意存储策略,任何货格被等概率存取货.
7)水平速度大于垂直方向的速度.
2.2. 能耗的计算模型
本文考虑的能耗是设备能耗,即堆垛机在作业过程中消耗的电能. 已有研究大多都假设设备始终处于匀速状态,设备运行中的能耗计算通常会被转化为对设备运行距离的计算. 本文的能耗计算考虑堆垛机的变速运动过程.
设备能耗可以由平均输出功率计算得到:
式中:E为设备能耗,P为均方根功率,η为能量传递效率,tyear为年作业时间,naisle为通道数量.
堆垛机的运动可以视作水平方向与垂直方向同时进行,堆垛机的平均输出功率可以用均方根功率描述:
式中:
堆垛机在加速、匀速和减速阶段的功率计算公式的更详细推导过程参见文献[24].
2.3. 平均吞吐时间的计算模型
平均循环时间指单台堆垛机单次作业的平均时间. 在复合作业模式下,堆垛机的平均循环时间的计算公式如下所示:
式中:TkDCC为复合命令下的平均循环时间,TkOT为堆垛机运行在I/O位置和货架某货格之间的平均时间,TkIT为堆垛机运行在货架2个货格之间的平均时间,T为堆垛机装卸货物总时间,k为取决于货架与堆垛机规格的参数[15].
平均吞吐时间是指,多个出库(或入库)命令下达以后,平均每个货物出库(或入库)所需要的总时间. 从自动立库系统的角度看,平均吞吐时间等于年作业时间与年吞吐量的比值:
式中:Tn为平均吞吐时间,λ为年吞吐量.
从堆垛机的角度看,平均吞吐时间等于单台堆垛机平均作业循环时间与堆垛机数量的比值:
Hwang等[15]提出了考虑加减速过程的堆垛机的平均循环时间计算模型,但该模型的表达式中存在大量的求导积分运算,这将严重影响求解模型时的运算速度,而且该研究只考虑了堆垛机的运行时间(TkOT和TkIT),没有考虑堆垛机装卸货物总时间T. 因此需要对原模型进一步化简和补充,化简思路如下.
1)将
2)将得到的多项式每一项都进行求导,然后乘以z,再积分. 因此,当
当z的幂次为0时,该项化简后不存在;在
3)根据函数的分段情况,将z的积分上、下限代入式(8),即可得到最终的化简式,消除所有的积分运算;再加上堆垛机装卸货物总时间T.
在复合作业模式下,堆垛机的平均循环时间的简化计算公式如下所示:
式中:
2.4. 成本的计算模型
在设计仓库时,应当考虑许多成本. 本文只考虑自动立库存储区初步设计中与存储区大小和设备设施选购相关的成本,主要是固定成本,包括以下部分:堆垛机的投资成本、货架的投资成本、土地租赁成本和能源消耗成本. 因此设计立体仓库的总成本:
式中:C为设计立体仓库的总成本,
2.5. 多目标优化模型的建立
根据上述物理模型,可以建立设计自动立库的多目标优化模型. 本文的优化目标是最小化能耗、平均吞吐时间和成本,决策变量是存储区的基本尺寸和堆垛机的运行参数. 基于假设3),存储区的基本尺寸由通道数量(堆垛机数量)、水平货格数量和垂直货格数量所决定. 因此需要分别将能耗模型、平均吞吐时间模型和成本模型,表示成目标函数关于决策变量的函数形式.
通过下式可以得到能耗关于决策变量的函数:
式中:vlmax为水平方向的最大速度,vhmax为垂直方向的最大速度,al为水平加速度和减速度的绝对值,ah为垂直加速度和减速度的绝对值.
只要使得
构建多目标优化函数:
式中:N为年最小吞吐量,M为最小货位数,lg为货格长度,hg为货格高度. li为第i个自变量的下界,ui为第i个自变量的上界. 在约束条件中:1代表吞吐量要求,2代表货位数量要求,3、4、5代表基于假设的要求,6代表变量的取值范围,7代表整数约束.
3. 算例实验
3.1. 基本参数的设置
表 1 多目标优化模型中常量的取值
Tab.1
| 参数 | 取值 | 单位 | 参数 | 取值 | 单位 | |
| ŋ | 0.9 | − | TIt | 15 | year | |
| tyear | 4 800 | h | C1 | 120 000 | ¥ | |
| m | 1 000 | kg | C2 | 20 | ¥ | |
| g | 9.8 | m/s2 | C3 | 400 | ¥ | |
| kr | 0.01 | − | C4 | 1.2 | ¥ | |
| kir | 1.15 | − | W | 2.2 | m | |
| lg | 0.5 | m | M | 20 000 | − | |
| hg | 0.5 | m | N | 8 000 | − | |
| T | 10 | s | − | − | − |
表 2 多目标优化模型中决策变量的取值范围
Tab.2
| 变量 | x1 | x2 | x3 | x4/ (m·s−1) | x5/ (m·s−1) | x6/ (m·s−2) | x7/ (m·s−2) |
| 对应参数 | naisle | n1 | nh | | al | | ah |
| 取值下限 | 1 | 10 | 4 | 1 | 1 | 1 | 1 |
| 取值上限 | 30 | 160 | 40 | 6.5 | 6.5 | 3.5 | 3.5 |
3.2. 使用遗传算法结合权重法的求解
通过权重法“化多为少”,把多目标优化问题转换为单目标优化问题,是一种常见多目标规划(multi objective programming, MOP)的解法,也是一种基本的解法. 核心的步骤有2个部分:一是无量纲化,消除各个目标在单位数量级的差异;二是赋予权重,使得每个目标被赋予合适的重要性. 因此,通过对能耗、平均吞吐时间和成本的目标函数进行无量纲化并赋予权重,可以将多目标优化问题转化为如下形式的特殊单目标优化(为行文方便,下文仍以多目标优化代称)问题:
式中:
将权重修改为0、1.0、0,可得到以为优化目标时各优化目标的取值. 将权重修改为0、1.0、0,可得到以C为优化目标时各优化目标的取值. 将多目标优化下E、Tn、C的取值,分别与单目标最优化下E、Tn和C的取值进行对比,如表3所示. 表中,括号中数值为各目标的优化百分比,即多目标优化下和单目标优化下优化目标的差值与单目标优化下的优化目标之比.
表 3 单目标优化和多目标优化的结果比较
Tab.3
| 优化结果比较 | E | Tn | C |
| | 202 960 | 3.464 | 5 928 484 |
| (−58.38%) | (74.02%) | (−128.88%) | |
| | 1 931 153 | 0.338 | 48 345 948 |
| (83.35%) | (−166.27%) | (71.93%) | |
| | 202 960 | 3.464 | 5 928 484 |
| (22.45%) | (−0.11%) | (−11.36%) | |
| 多目标优化 | 321 450 | 0.900 | 13 569 000 |
可以发现,多目标优化结果往往在某一目标函数的优化上不如单目标优化结果,但是在其他目标函数的优化上却有显著优势.
表 4 采用GA与lingo所求最优解的比较
Tab.4
| 优化对象 | 决策变量 | 目标函数 | 最优化程度 | ||||||||||
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | E | Tn | C | y | |||
| GA求解结果 | 30 | 21 | 16 | 1.42 | 1.00 | 1.15 | 1.26 | 321 450 | 0.9 | 13 569 000 | 1.641 0 | ||
| lingo求解结果 | 30 | 20 | 17 | 1.33 | 1.14 | 1.33 | 1.14 | 324 109 | 0.9 | 13 441 980 | 1.639 9 | ||
3.3. 使用非支配排序遗传算法的求解
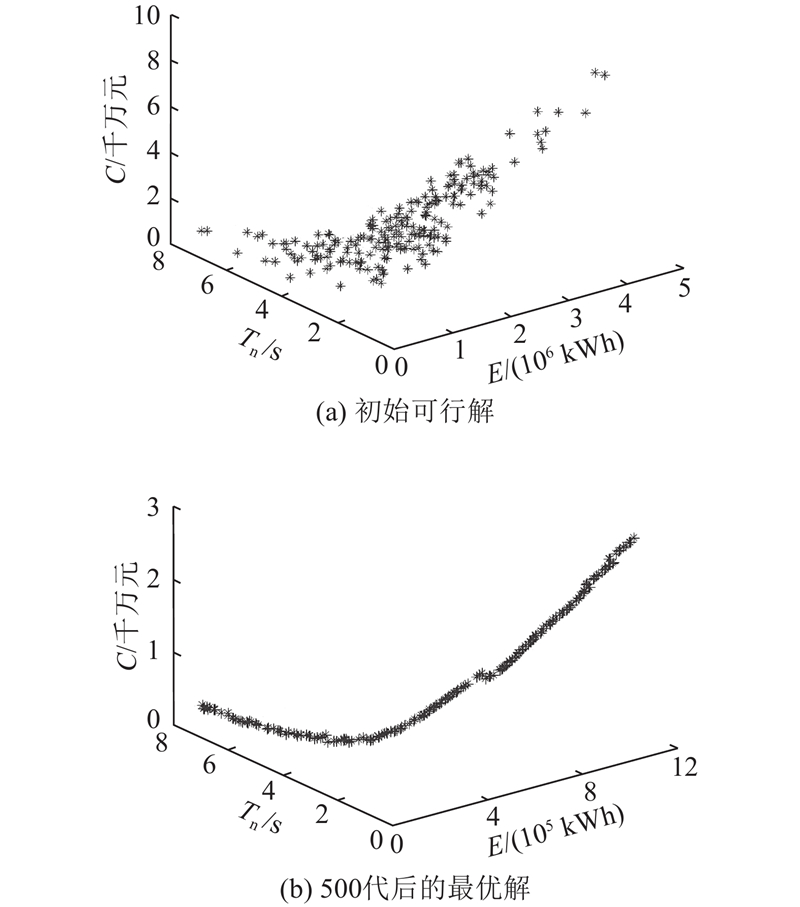
图 3
图 3 使用非支配排序遗传算法(NSGA-II)得到的pareto解
Fig.3 Pareto solution by using non-dominated sorting genetic algorithm
图 4
图 4 pareto前沿中的成本和能耗的关系
Fig.4 Relation of cost and energy consumption in pareto front
这些pareto解都是非劣解,相对于其他解,都有一定的优势. 在设计自动立库存储区时,可以根据偏好选择合适的pareto解. 部分pareto解与单目标优化结果和双目标(效率、成本)优化结果进行对比, 结果如表5所示. 表中, 括号中数值为各目标的优化百分比, 即多目标优化下与单(双)目标优化下的优化目标之差, 与单(双)目标优化下的优化目标之比. 可以发现,多目标优化结果往往在某一目标函数的优化上不如单目标优化结果,但是在其他目标函数的优化上有显著优势.
表 5 多目标优化与其他优化方法的结果比较
Tab.5
| 优化结果比较 | E | Tn | C |
| E最优化 | 202 960 | 3.464 | 5 928 484 |
| (−138.40%) | (80.66%) | (−159.49%) | |
| Tn最优化 | 1 931 153 | 0.338 | 48 345 948 |
| (74.94%) | (−98.22%) | (68.18%) | |
| C最优化 | 202 960 | 3.464 | 5 928 484 |
| (−138.40%) | (80.66%) | (2.52%) | |
| 双目标优化 | 494 400 | 0.650 | 15 782 416 |
| (2.13%) | (−3.08%) | (2.52%) | |
| 多目标优化 | 483 862 | 0.670 | 15 383 918 |
3.4. 2种求解方法的比较和应用
结合权重的遗传算法和非支配排序遗传算法都可以用于求解多目标优化问题,算例实验证明,这2种方法在求解本文的存储区设计的多目标问题时均有效. 但是这2种方法有所不同,不能直接评价好坏,且各有适用的场合.
单独使用经典遗传算法,不能求解多目标优化问题,必须结合权重法或者其他方法才能求解. 且由于权重法需要事先知晓能耗、平均吞吐时间和成本的权重,才能代入求解,而且每次只有1个最优解,权重的分配往往具有一定的主观性,事先确定的权重并不一定符合实际需要. 如果要获取许多最优解,就需要不断调整程序中的参数重新运行并收集结果,因此求解过程相对繁琐.
非支配排序遗传算法没有权重的概念,可以一次性获得大量的pareto解,可以根据实际需要从中选择合适的解. 但是难以判断非支配排序遗传算法是否陷入局部最优解,多次运行无法确保得出更好的pareto解,只能根据前人经验确定算子的大小. 而与权重法结合的遗传算法可以通过修改算子或多次运行,使得结果更趋近于最优解.
在实际应用中,如果通过德尔菲法得出了几组准确的权重的取值,可以考虑使用权重法结合遗传算法;如果事先不能确定权重,那么应该使用非支配排序遗传算法求取pareto解,再依据实际情况在众多pareto解中进行选取.
4. 结 语
本文建立了多目标优化模型,以能耗、平均吞吐时间和成本为优化目标,通过经典遗传算法和非支配排序遗传算法,求解货架数量、水平货格数量和垂直货格数量和堆垛机的运行参数(水平速度、水平加速度、垂直速度和垂直加速度),进而得到设计料箱式自动立库存储区的参数,包括存储区尺寸和设备设施的选购.
建造自动立库的成本包括固定成本和运营成本两大块. 由于时间仓促,本文对运营成本(包括人员成本、设备设施维护成本等)的考虑有所欠缺. 一方面是因为设计层面尚有许多工作未完成,许多成本不好估算;另一方面是因为这不影响本文的研究思路和结论的正确性. 只要修正模型,重新进行算例实验即可. 本文的研究方法和思路,可为建设“资源节约型”自动立库提供参考.
参考文献
Travel-time models for automated storage and retrieval systems
[J].
Travel time models considering the operating characteristics of the storage and retrieval machine
[J].DOI:10.1080/00207549008942833 [本文引用: 1]
Optimal design of AS/RS storage systems with 3-class-based assignment strategy under single and dual command operations
[J].DOI:10.1007/s00170-015-6872-1 [本文引用: 2]
多载具自动化存取系统性能评价研究
[J].DOI:10.3969/j.issn.1007-5429.2012.04.004 [本文引用: 1]
Performance evaluation for a multi-shuttle automated storage and retrieval system
[J].DOI:10.3969/j.issn.1007-5429.2012.04.004 [本文引用: 1]
烟丝原料立体仓库堆垛机出入库作业优化研究
[J].
Operation optimization of storage and retrieval for stackers in AS/RS of raw tabacco material
[J].
The impact of acceleration on travel-time models for automated storage-retrieval systems
[J].
Travel time model of a new compact storage system
[J].
Designing the optimal multi-deep AS/RS storage rack under full turnover-based storage policy based on non-approximate speed model of SR machine
[J].DOI:10.1016/j.tre.2017.05.010 [本文引用: 2]
Travel time model of the storage retrieval machine for multi-deep AS/RS based on Flexsim
[J].DOI:10.2174/1874110X01509011833 [本文引用: 1]
基于非线性规划的立体仓库存储区优化设计
[J].
Optimization design of automated warehouse storage area based on nonlinear programming
[J].
Multi-objective warehouse building design to optimize the cycle time, total cost, and carbon footprint
[J].DOI:10.1007/s00170-017-0157-9 [本文引用: 2]
Warehouse design and control: framework and literature review
[J].DOI:10.1016/S0377-2217(99)00020-X [本文引用: 3]
Research on warehouse design and performance evaluation: a comprehensive review
[J].DOI:10.1016/j.ejor.2009.07.031 [本文引用: 1]
Decision models for the design, optimization and management of warehousing and material handling systems
[J].DOI:10.1016/j.ijpe.2015.08.007
Warehouse design: A structured approach
[J].DOI:10.1016/j.ejor.2007.11.045 [本文引用: 1]
Multi-aisle AS/RS dimensions optimization for cycle time minimization
[J].DOI:10.1007/s00170-014-6709-3 [本文引用: 1]
A microcomputer-based optimization model for the design of automated warehouse
[J].
An analytical approach to design of high-rise stacker crane warehouse systems
[J].
Energy efficiency model for the mini-load automated storage and retrieval systems
[J].DOI:10.1007/s00170-013-5253-x [本文引用: 1]
A fast and elitist multiobjective genetic algorithm: NSGA-II
[J].DOI:10.1109/4235.996017 [本文引用: 1]