基于改进麻雀搜索算法的机械臂多目标轨迹优化方法

doi:10.3785/j.issn.1006-754X.2025.05.111

基于改进麻雀搜索算法的机械臂多目标轨迹优化方法

李玲^,^,¹^,², 侯玉龙¹^,², 李瑶¹^,², 罗丹¹, 解妙霞¹

1.西安建筑科技大学机电工程学院，陕西西安 710055

2.西安市重型机械装备智能化技术重点实验室，陕西西安 710311

Multi-objective trajectory optimization method for manipulator based on improved sparrow search algorithm

LI Ling^,^,¹^,², HOU Yulong¹^,², LI Yao¹^,², LUO Dan¹, XIE Miaoxia¹

1.School of Mechanical and Electrical Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China

2.Xi'an Key Laboratory of Intelligent Technology for Heavy Machinery Equipment, Xi'an 710311, China

收稿日期: 2025-03-10 修回日期: 2025-04-30

基金资助:

国家自然科学基金资助项目.  52475124
陕西省重点研发计划资助项目.  2024GX-YBXM-206
西安市“科学家+工程师”队伍建设项目.  24KGDW0026

Received: 2025-03-10 Revised: 2025-04-30

作者简介 About authors

李　玲（1981—），男，教授，博士生导师，博士，从事智能制造、机械动力学研究，E-mail:liling@xauat.edu.cn，https://orcid.org/0000-0002-4723-2613 , E-mail：liling@xauat.edu.cn

摘要

针对传统机械臂在执行任务时存在工作效率低，以及易产生冲击和振动而造成机械疲劳损坏等问题，提出了一种基于改进麻雀搜索算法（sparrow search algorithm, SSA）的机械臂多目标轨迹优化方法。以六自由度AR4机械臂为研究对象，采用分段式3-5-3多项式插值法构建其运动学模型。然后，基于融合Tent-Logistic混沌映射、改良精英反向学习策略及柯西-高斯变异策略的新型改进SSA（newly improved SSA, NISSA），对机械臂各关节的运行时间和冲击进行多目标协同优化。最后，与其他优化算法进行对比实验，以验证NISSA的有效性。实验结果表明，应用NISSA优化后，机械臂的运行时间缩短了17.8%，运行中产生的冲击减小了12.9%。研究结果为机械臂的轨迹优化提供了高效的方法。

关键词： 机械臂 ; 轨迹优化 ; 麻雀搜索算法 ; Tent-Logistic混沌映射 ; 精英反向学习策略

Abstract

Aiming at the problems such as low operational efficiency and mechanical fatigue damage caused by impact and vibration in traditional manipulators during task execution, a multi-objective trajectory optimization method based on an improved sparrow search algorithm (SSA) is proposed. Taking the six-degree-of-freedom AR4 manipulator as the research object, its kinematic model was constructed by using the segmented 3-5-3 polynomial interpolation method. Then, based on the newly improved SSA (NISSA) that integrated Tent-Logistic chaotic mapping, improved elite opposition-based learning strategy and Cauchy-Gaussian mutation strategy, the multi-objective collaborative optimization was carried out for the operation time and impact of each joint of the manipulator. Finally, comparative experiments were conducted with other optimization algorithms to verify the effectiveness of NISSA. The experimental results showed that after optimization with NISSA, the operation time of the manipulator was shortened by 17.8%, and the impact generated during operation was reduced by 12.9%. The research results provide an efficient method for the trajectory optimization of manipulators.

Keywords： manipulator ; trajectory optimization ; sparrow search algorithm ; Tent-Logistic chaotic mapping ; elite opposition-based learning strategy

PDF (4160KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李玲, 侯玉龙, 李瑶, 罗丹, 解妙霞. 基于改进麻雀搜索算法的机械臂多目标轨迹优化方法[J]. 工程设计学报, 2025, 32(5): 664-674 doi:10.3785/j.issn.1006-754X.2025.05.111

LI Ling, HOU Yulong, LI Yao, LUO Dan, XIE Miaoxia. Multi-objective trajectory optimization method for manipulator based on improved sparrow search algorithm[J]. Chinese Journal of Engineering Design, 2025, 32(5): 664-674 doi:10.3785/j.issn.1006-754X.2025.05.111

随着工业4.0和中国制造2025战略的推进^[1]，全球制造业加速转型，对自动化产线中机械臂的动力学性能提出了更严苛的要求^[2]。现阶段，机械臂已覆盖焊接、装配、测试等多个高精度场景，并逐步拓展至民生领域。然而，机械臂在执行任务时存在运动能效不足与动态载荷超标等问题，易引发关节磨损累积效应，增加系统能耗，导致动态精度漂移。为提升机械臂的综合性能，亟须开展多目标轨迹优化，聚焦作业周期压缩、动力系统能耗优化及末端冲击能量抑制等目标^[3]。其中，基于时间最优性约束的轨迹优化可显著压缩作业周期，对提升机械臂的工作效率有重大意义；动态载荷抑制策略能减少关节冲击约束，延长机械臂的疲劳寿命。因此，开展时间-冲击多目标协同的轨迹优化研究，对实现机械臂全生命周期性能的跃迁至关重要。

为实现机械臂关节空间轨迹的最优化，近年来众多国内外学者致力于研究更有效的优化方法^[4]。蔡永超^[5]采用三次样条曲线并结合膜计算与PSO（particle swarm optimization，粒子群优化）算法对机械臂的运动轨迹进行了优化，但算法的收敛速度较慢。孙颙琰等^[6]运用五次多项式插值法建立了机械臂的轨迹模型，并通过改良的蝙蝠算法进行了轨迹优化，但插值过程较为复杂且耗时。谢嘉等^[7]提出了一种基于3-5-3多项式插值法与改进PSO算法的机械臂时间最优轨迹规划方法，使得其运动轨迹更加平滑。吴继春等^[8]以3-5-3多项式插值法为基础，对机械臂关节轨迹进行了规划，采用基于Tent混沌映射的种群初始化、莱维飞行等方法并引入自适应阈值，提高了金枪鱼群算法的优化性能。Xue等^[9]提出了麻雀搜索算法（sparrow search algorithm, SSA），该算法在处理复杂的非线性问题时展现出卓越的寻优效率和收敛性能，相较于其他优化算法具有明显优势。吕鑫等^[10]提出了一种混沌麻雀搜索优化算法（chaos sparrow search optimization algorithm, CSSOA），并通过多维度基准函数的对比测试，验证了该算法能够克服SSA易陷入局部最优的缺陷。在此基础上，邱冰等^[11]提出了一种多策略改进SSA（multi-strategy improved SSA, MISSA），利用Logistic混沌映射均匀化种群，并通过重构正余弦机制来协调SSA的全局探索与局部开发的动态平衡，改进后的SSA在收敛速率与求解精度两个维度上均得到了大幅提升。季海涛等^[12]通过引入Logistic混沌映射和柯西-高斯变异原理，提出了一种基于多策略改进型SSA的水下伸缩臂轨迹定位方法，结果表明：改进后的SSA显著优于其他算法。Liu等^[13]提出了一种可动态选择步态参数的SSA改进策略，并采用基于非正弦末端滑动模式的轨迹跟踪控制策略来提高水下蛇形机器人的运动效率，但轨迹跟踪误差曲线可能会出现幅值较大的振荡现象，从而影响机器人的运动稳定性。综上所述，尽管融合混沌映射的SSA在全局探索能力和收敛效率方面表现优异，但在迭代末期仍面临种群多样性衰减和局部收敛等现象^[14]。此外，在传统SSA的收敛阶段，发现者与加入者的动态切换可能会导致局部种群的搜索效率退化^[15]，急需一种针对性的改进策略。

为克服SSA优化过程中群体多样性衰减的缺陷，抑制算法在迭代中期频繁收敛至局部极值的情况，本文创新性地构建了融合Tent-Logistic混沌映射机制与多维改进策略的新型改进SSA（newly improved SSA, NISSA），并将其应用于六自由度AR4机械臂的多目标轨迹优化，旨在提升机械臂的轨迹规划效率和减少其运行过程中的振动冲击。

1 机械臂轨迹优化问题描述

1.1　运动学模型建立

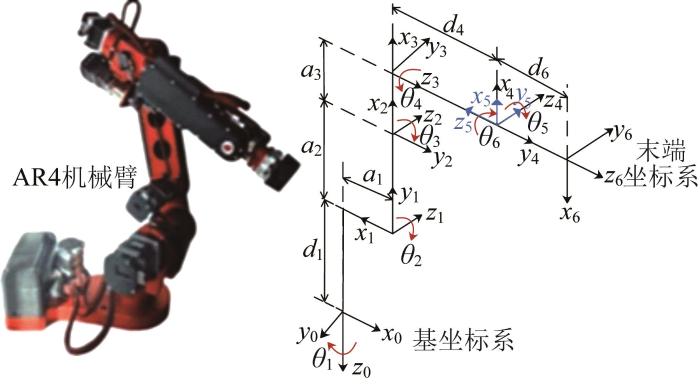
本文以六自由度AR4机械臂作为研究对象。根据串联连杆机构的特性，基于D-H参数法系统地建立机械臂各关节的连杆坐标系，如图1所示。该机械臂的D-H参数如表1所示。其中， $α_{i - 1}$ 为连杆 $i - 1$ 的扭转角， $a_{i - 1}$ 为连杆 $i - 1$ 的长度， $θ_{i}$ 为关节i的扭转角， $d_{i}$ 为关节i的偏转量。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 机械臂连杆坐标系

Fig.1 Linkage coordinate system of manipulator

表1 机械臂的D-H参数

Table 1 D-H parameters of manipulator

关节i	α_i_-1/(°)	a_i_-1/mm	d_i /mm	$θ_{i}$ /(°)
1	-90	64.2	169.77	$θ_{1}$
2	0	305.0	0	$θ_{2}$
3	90	0	0	$θ_{3}$
4	-90	0	222.63	$θ_{4}$
5	90	0	0	$θ_{5}$
6	0	0	36.25	$θ_{6}$

新窗口打开| 下载CSV

根据图1所示的坐标系，相邻坐标系{i}与{i $-$ 1}之间的位姿变换可通过2次旋转与2次平移实现，对应的齐次变换矩阵 ${}_{i}^{i - 1}$ T 可表示为：

{}_{i}^{i - 1} T = [\begin{matrix} c o s θ_{i} & - s i n θ_{i} & 0 & a_{i - 1} \\ s i n θ_{i} c o s α_{i - 1} & c o s θ_{i} c o s α_{i - 1} & - s i n α_{i - 1} & - d_{i} s i n α_{i - 1} \\ s i n θ_{i} s i n α_{i - 1} & c o s θ_{i} s i n α_{i - 1} & c o s α_{i - 1} & d_{i} c o s α_{i - 1} \\ 0 & 0 & 0 & 1 \end{matrix}]

(1)

将表1中的D-H参数代入式(1)，可得从基坐标系到各关节坐标系的6个齐次变换矩阵；随后，通过连续乘积运算，即可推导出机械臂末端的位姿变换矩阵 ${}_{6}^{0}$ T，描述了末端坐标系相对于基坐标系的位置与姿态信息，可表示为：

{}_{6}^{0} T = {}_{1}^{0}T {}_{2}^{1}T {}_{3}^{2}T {}_{4}^{3}T {}_{5}^{4}T {}_{6}^{5}T = [\begin{matrix} n_{x} & o_{x} & a_{x} & p_{x} \\ n_{y} & o_{y} & a_{y} & p_{y} \\ n_{z} & o_{z} & a_{z} & p_{z} \\ 0 & 0 & 0 & 1 \end{matrix}]

(2)

式中：(n_x, n_y, n_z )、(o_x, o_y, o_z )、(a_x, a_y, a_z )为机械臂末端坐标系x₆、y₆、z₆轴的单位方向向量，用于描述末端执行器的姿态；(p_x, p_y, p_z )为机械臂末端坐标系原点在基坐标系中的位置向量。

1.2　基于多项式插值法的轨迹规划

为确保机械臂轨迹的位置、速度和加速度的连续性，本文采用3-5-3多项式插值法^[16]进行机械臂轨迹规划，以减小其运动过程中的振动，从而保护机械结构和提高操作的精确性。

针对机械臂的各个关节，选取4个路径点 $x_{i 1}$ 、 $x_{i 2}$ 、 $x_{i 3}$ 、 $x_{i 4}$ ，相邻路径点之间构成的3个时间段可表示为0—t₁、t₁—t₂、t₂—t₃。

建立机械臂关节i的角位移与时间t的函数关系式，可表示为：

\{\begin{array}{l} θ_{i 1} (t) = b_{i 13} t_{1}^{3} + b_{i 12} t_{1}^{2} + b_{i 11} t_{1} + b_{i 10} \\ θ_{i 2} (t) = b_{i 25} t_{2}^{5} + b_{i 24} t_{2}^{4} + b_{i 23} t_{2}^{3} + b_{i 22} t_{2}^{2} + b_{i 21} t_{2} + b_{i 20} \\ θ_{i 3} (t) = b_{i 33} t_{3}^{3} + b_{i 32} t_{3}^{2} + b_{i 31} t_{3} + b_{i 30} \end{array}

(3)

式中： $b_{i \partial ε}$ 为多项式系数，下标 $\partial$ 表示关节的运动分量， $ε$ 表示多项式系数的序号。

求式(3)的一阶导数，可得到关节i的角速度与时间t的函数关系式：

\{\begin{array}{l} {\dot{θ}}_{i 1} (t) = 3 b_{i 13} t_{1}^{2} + 2 b_{i 12} t_{1} + b_{i 11} \\ {\dot{θ}}_{i 2} (t) = 5 b_{i 25} t_{2}^{4} + 4 b_{i 24} t_{2}^{3} + 3 b_{i 23} t_{2}^{2} + 2 b_{i 22} t_{2} + b_{i 21} \\ {\dot{θ}}_{i 3} (t) = 3 b_{i 33} t_{3}^{2} + 2 b_{i 32} t_{3} + b_{i 31} \end{array}

(4)

接着，求式(3)的二阶导数，得到关节i的角加速度与时间t的函数关系式：

\{\begin{array}{l} {\ddot{θ}}_{i 1} (t) = 6 b_{i 13} t_{1} + 2 b_{i 12} t_{1} \\ {\ddot{θ}}_{i 2} (t) = 20 b_{i 25} t_{2}^{3} + 12 b_{i 24} t_{2}^{2} + 6 b_{i 23} t_{2} + 2 b_{i 22} \\ {\ddot{θ}}_{i 3} (t) = 6 b_{i 33} t_{3} + 2 b_{i 32} t_{3} \end{array}

(5)

机械臂各关节在初始和结束时刻的角速度和角加速度均为0，且在经过中间点时的角速度和角加速度相等，则与时间有关的转换矩阵 A 可表示为：

A = [\begin{matrix} t_{1}^{3} & t_{1}^{2} & t_{1} & 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 & 0 & 0 & 0 \\ 3 t_{1}^{2} & 2 t_{1} & 1 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 6 t_{1} & 2 & 0 & 0 & 0 & 0 & - 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & t_{2}^{5} & t_{2}^{4} & t_{2}^{3} & t_{2}^{2} & t_{2} & 0 & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 0 & 5 t_{2}^{4} & 4 t_{2}^{3} & 3 t_{2}^{2} & 2 t_{2} & 1 & 0 & 0 & 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 20 t_{2}^{3} & 12 t_{2}^{2} & 6 t_{2} & 2 & 0 & 0 & 0 & 0 & - 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & t_{3}^{3} & t_{3}^{2} & t_{3} & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 t_{3}^{2} & 2 t_{3}^{1} & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 6 t_{3} & 2 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \end{matrix}]

(6)

机械臂关节 $i$ 的位置矩阵 θ_i 可表示为：

θ_{i} = [\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} 0 & 0 & 0 & 0 \end{matrix} & 0 & 0 & x_{i 4} \end{matrix} & 0 & 0 \end{matrix} & x_{i 1} & 0 \end{matrix} & 0 & x_{i 3} & x_{i 2} \end{matrix}]

(7)

则多项式系数矩阵 b_i 可表示为：

\begin{array}{l} b_{i} = A^{- 1} θ_{i} = [b_{i 13} b_{i 12} b_{i 11} b_{i 10} b_{i 25} b_{i 24} b_{i 23} \\ {b_{i 22} b_{i 21} b_{i 20} b_{i 33} b_{i 32} b_{i 31} b_{i 30}]}^{T} \end{array}

(8)

1.3　多目标优化函数的构建

在机械臂轨迹优化中，轨迹时间与运行冲击的

关系为：时间越短，冲击越大。因此，在对机械臂轨迹进行优化时，需在保证运行平稳性的前提下实现时间最短与冲击最小两个目标。

基于时间的目标函数可定义为：

F (t) = m i n (t_{1} + t_{2} + t_{3})

(9)

基于冲击的目标函数可定义为：

F (j) = m i n \sum_{i = 1}^{6} \sqrt[]{\frac{1}{t_{总}} \int_{0}^{t_{总}} {({\overset{⃛}{θ}}_{i} (t))}^{2} d t}

(10)

式中：t_总为总的轨迹时间，j为角加加速度。

为防止因机械臂速度过快而引发碰撞、振动及故障等，设定机械臂各关节的角速度、角加速度和角加加速度的约束条件：

\{\begin{array}{l} k_{1} (t) = |{\dot{θ}}_{i} (t)| - v_{i, m a x} \leq 0 \\ k_{2} (t) = |{\ddot{θ}}_{i} (t)| - a_{i, m a x} \leq 0 \\ k_{3} (t) = |{\overset{⃛}{θ}}_{i} (t)| - j_{i, m a x} \leq 0 \end{array}

(11)

式中：v_i_{, max}、a_i_{, max}、j_i_{, max}分别为关节i的角速度、角加速度及角加加速度的最大值。

鉴于在多目标优化问题中各目标相互冲突，单一目标的最优解可能会导致其他目标的优化效能衰减，故在工程实践中常采用线性加权组合法，即通过权重分配策略，将多目标优化转换为单目标优化，则最终的目标函数F可表示为：

F = w_{1} F (t) + w_{2} F (j)

(12)

式中： $w_{1}$ 、 $w_{2}$ 为权重系数。

由式(12)可知，当目标函数F的值减小时，机械臂的工作效率提高，碰撞产生的冲击减小。采用线性函数法对权重系数进行归一化处理：

\{\begin{array}{l} w_{1} = (F (t) - F_{m i n} (t)) / (F_{m a x} (t) - F_{m i n} (t)) \\ w_{2} = (F (j) - F_{m i n} (j)) / (F_{m a x} (j) - F_{m i n} (j)) \end{array}

(13)

式中：F_max $(t)$ 、F_min $(t)$ 、F_max $(j)$ 、F_min $(j)$ 分别为对应目标函数的最大值和最小值。

基于轨迹时间与运行冲击的动态变化特性，权重系数实时调整，以确保目标函数F能够更准确地表征机械臂运动轨迹优化的整体效能。

2 改进后的SSA（NISSA）

2.1　原始SSA

基于仿生学原理构建的SSA^[9]的核心机制为模拟麻雀觅食行为：通过构建高资源密度区域，吸引具备不同行为特征的麻雀个体形成群体协作。其中：发现者负责定位优质资源区，为后续加入者划定搜索路径与活动边界。

在迭代优化阶段，发现者群体依据自适应机制维持种群总数10%~20%的动态比例，其个体空间位置的更新方式如下：

X_{y, d}^{k + 1} = \{\begin{array}{l} X_{y, d}^{k} \cdot e x p (\frac{- y}{r k_{m a x}}), & R_{2} < S (14 ‑ 1) \\ X_{y, d}^{k} + Q H, & R_{2} \geq S (14 ‑ 2) \end{array}

式中： $X_{y, d}^{k + 1}$ 、 $X_{y, d}^{k}$ 为第k+1次、第k次迭代时第y只麻雀在第d维的位置，y=1, 2, …, N，d=1, 2, …, D；k_max为最大迭代次数，r为定义域为（0, 1）的随机数；Q为服从正态分布(0,1)的随机数； H 为1×D的全1矩阵；R₂为预警值， $R_{2} \in (0, 1)$ ；S为安全值， $S \in (0.5, 1)$ 。

对于跟随者，其个体空间位置的更新方式如下：

X_{y, d}^{k + 1} = \{\begin{array}{l} Q \cdot e x p (\frac{X_{W}^{k} - X_{y, d}^{k}}{y^{2}}), & y > N / 2 (15 ‑ 2) \\ X_{B}^{k + 1} + |X_{y, d}^{k} - X_{B}^{k + 1}| \cdot B^{+} \cdot H, & 其他 (15 ‑ 2) \end{array}

式中： $X_{W}^{k}$ 为第k次迭代时跟随者的最差位置； $X_{B}^{k + 1}$ 为第k+1次迭代时跟随者的最佳位置； $B^{+} = B^{T} {(B B^{T})}^{- 1}$ ， B 为1×D的矩阵，每个元素随机赋值1或-1。

警戒者是负责侦查和警戒的个体，约占种群的10%~20%，其个体空间位置的更新公式如下：

X_{y, d}^{k + 1} = \{\begin{array}{l} X_{B}^{k} + μ | X_{y, d}^{k} - X_{B}^{k} |, & f_{y} \neq f_{g} (16 ‑ 1) \\ X_{y, d}^{k} + c [\frac{| X_{y, d}^{k} - X_{W}^{k} |}{(f_{y} - f_{W}) + ρ}], & f_{y} = f_{g} (16 ‑ 2) \end{array}

式中： $X_{B}^{k}$ 为第k次迭代时适应度最好的个体位置， $μ$ 为服从（0,1）正态分布的随机数，c为步长控制参数， $ρ$ 为避免式子分母为0的参数，f_y 为麻雀个体当前的适应度，f_g为当前最优个体的适应度，f_W为当前最差个体的适应度。

2.2　SSA的改进策略

经典SSA通过随机采样策略在解空间内构建初始种群，然而随着迭代过程的推进，种群多样性显著衰减，这会制约算法的收敛效率与鲁棒性。此外，由于领导者位置更新机制缺乏自适应学习能力，且局部搜索与全局搜索的权重分配失衡，初始种群分布呈现高度聚集性，易陷入局部最优，同时收敛速率显著下降。因此，亟须设计一种多样性保障机制，以提升多目标优化问题中解集分布的均匀性。

针对上述局限性，本文从3个维度对SSA进行系统性改进：1）通过Tent-Logistic混沌映射初始化种群，以增强算法的全局搜索能力，有效维持种群多样性；2）引入精英反向学习策略，以实现精英反向解在有限搜索空间内的精确定位，进而促进算法有效收敛；3）融合柯西-高斯变异策略，优化当前最优个体的位置更新机制，以避免算法陷入局部最优，从而进一步提升算法性能。

2.2.1　基于Tent-Logistic混沌映射的种群初始化

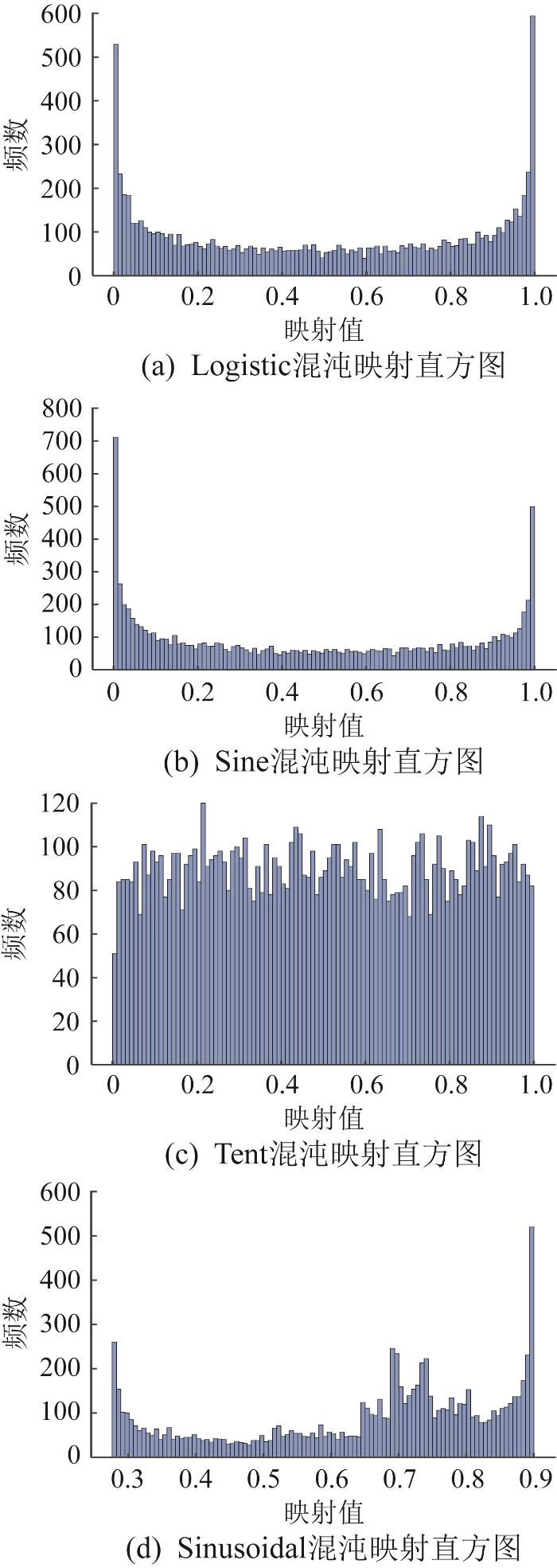
混沌理论凭借不可预测性、遍历特性及对初始值敏感的特性，在提升算法收敛效率方面具有显著优势^[17-18]。目前，主流的混沌序列生成方法包括Logistic、Sine、Tent及Sinusoidal混沌映射。图2所示为4类混沌映射迭代10 000次的混沌值域密度分布。结果显示，所有映射均约束于(0, 1)区间内：Logistic混沌映射呈现边缘聚集特征，Tent混沌映射的分布均衡性最优，而Sinusoidal混沌映射与Sine混沌映射展现出差异化非均匀模式。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 各混沌映射的频率分布直方图

Fig.2 Frequency distribution histograms of each chaotic mapping

Logistic混沌映射因两端概率密度堆积而导致时间成本增加，且参数敏感性跃迁特性易引发解空间锚定效应；Tent混沌映射虽具有高均匀性，但难以应对高维复杂的多目标优化问题。为此，通过双重混沌吸引子分裂机制来规避单一映射的伪混沌现象，以显著提升初始种群分布的多样性。

Tent混沌映射的表达式为：

x_{n + 1} = \{\begin{array}{l} η_{1} β x_{n}, & 0 \leq x_{n} \leq \frac{1}{β} \\ η_{2} β (1 - x_{n}), & \frac{1}{β} < x_{n} \leq 1 \end{array}

(17)

式中：x_n 为第n次迭代生成的混沌值；x_n₊₁为更新后的混沌值； $η_{1}$ 、 $η_{2}$ 为混沌因子；n为迭代步数； $β$ 为Tent混沌映射的参数， $β \in (0, 2)$ 。

Tent混沌映射生成的混沌序列具有周期性和混沌性质，可用于调节优化算法的参数。

Logistic混沌映射的表达式为：

x_{n + 1} = κ x_{n} (1 - x_{n})

(18)

式中： $κ$ 为控制参数， $κ \in (0, 4]$ 。

则Tent-Logistic混沌映射的表达式为：

x_{n + 1} = \{\begin{array}{l} η_{1} β x_{n}, & 0 \leq x_{n} \leq \frac{1}{β} \\ η_{2} κ x_{n} (1 - x_{n}), & \frac{1}{β} < x_{n} \leq 1 \end{array}

(19)

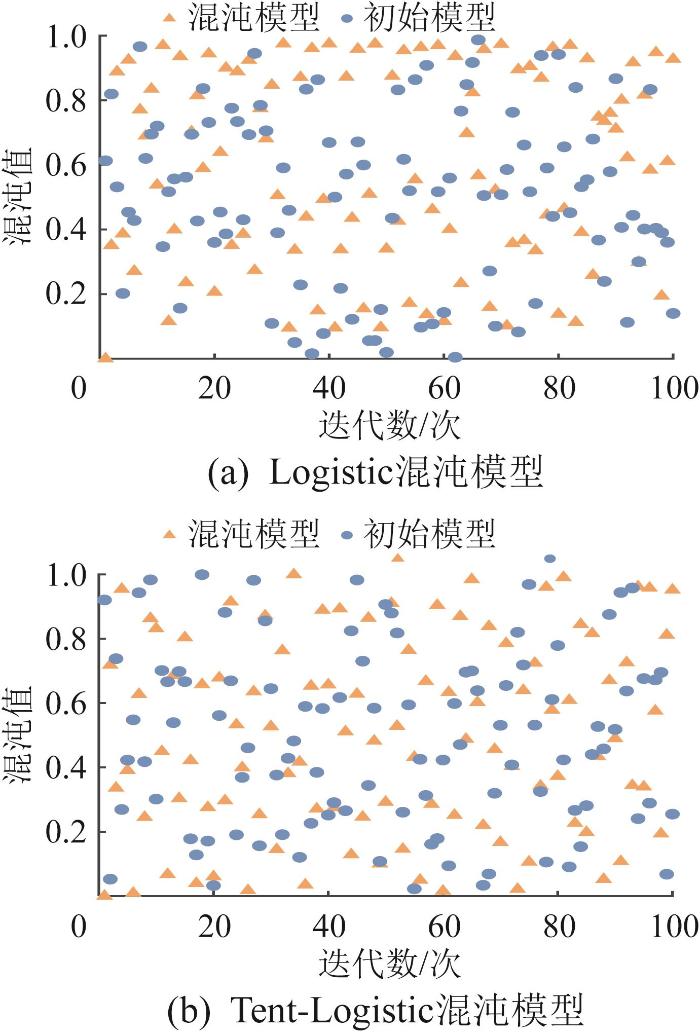
Logistic混沌映射与Tent-Logistic混沌映射的对比如图3所示。由图3(a)和图3(b)可知，与Logistic混沌映射相比，Tent-Logistic混沌映射具有更高的分布均匀性，能够有效克服单独使用Logistic混沌映射时的局限性，从而增强算法的全局搜索能力。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 Logistic混沌映射与Tent-Logistic混沌映射对比

Fig.3 Comparison between Logistic chaotic mapping and Tent-Logistic chaotic mapping

2.2.2　改良精英反向学习策略

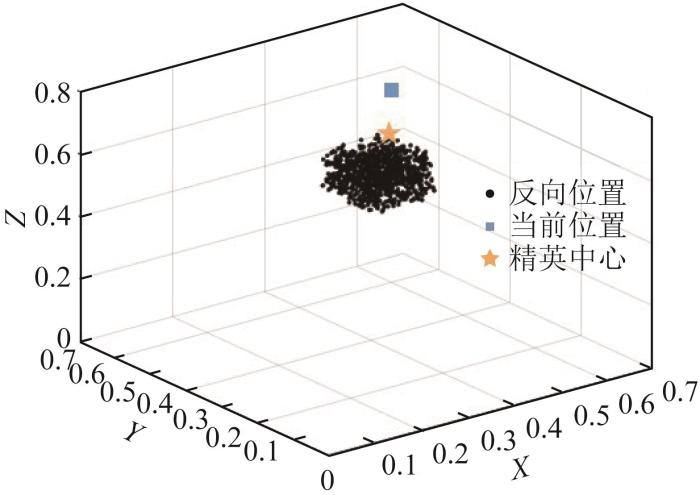
针对传统反向学习机制在复杂优化场景中存在的全局收敛性缺陷^[19]，本文提出了一种基于动态对称中心调整的改良精英反向学习策略。将反向解生成过程中的静态对称中心替换为精英种群质心坐标，通过动态追踪精英个体的空间分布特征（见图4），构建自适应反向搜索向量，以突破传统方法在非对称解空间中的寻优瓶颈。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 精英个体的空间位置分布

Fig.4 Spatial position distribution of elite individuals

设 $Z_{τ} = (z_{τ, 1}, z_{τ, 2}, \dots, z_{τ, D})$ 是D维空间中的一个普通粒子，该粒子的某个自身极值点为精英粒子，即 ${\hat{Z}}_{τ} = ({\hat{z}}_{τ, 1}, {\hat{z}}_{τ, 2}, \dots, {\hat{z}}_{τ, D})$ ，则精英反向解为：

{\hat{z}}_{τ, d} = m ({a'}_{d} + {b'}_{d}) - {\hat{z}}_{τ, d}

(20)

式中： ${\hat{z}}_{τ, d} \in [{a'}_{d}, {b'}_{d}]$ ，m为精英反向调节因子，定义域在[0, 1]内。

第d维搜索空间中的动态边界表示为 $[{a'}_{d}, {b'}_{d}]$ ，数学式如下：

{a'}_{d} = m i n (Z_{τ})

(21)

{b'}_{d} = m a x (Z_{τ})

(22)

动态边界的引入可积累搜索过程中的经验。随着搜索空间的逐渐缩减，反向解的生成会变得更加集中，从而促进算法快速收敛。当精英反向解超出既定约束区间时，往往需要进行边界修正，通过随机重定位操作来确保解的可行性，边界修改公式如下：

z_{τ, d} = r a n d ({a'}_{d} + {b'}_{d})

(23)

2.2.3　柯西-高斯变异策略

在SSA收敛阶段，个体动态切换引发的优化阻滞现象亟待解决。尤其是迭代后期，发现者与加入者的转换过度频繁会导致搜索势能显著衰减。为精确捕捉适应度演化的关键窗口期，最优个体优先迭代，引入柯西-高斯变异策略^[20-21]。变异公式如下：

Μ_{y}^{k} = X_{y}^{k} (1 + γ_{1} \cdot C (0, δ^{2}) + γ_{2} \cdot G (0, δ^{2}))

(24)

其中：

δ = \{\begin{array}{l} 1, f (X_{y}^{k}) < f (X_{τ}^{k}) \\ e x p (\frac{f (X_{y}^{k}) - f (X_{τ}^{k})}{| f (X_{s}^{k}) |}), 其他 \end{array}

\begin{array}{l} γ_{1} = \frac{k^{2}}{k_{m a x}^{2}} \\ γ_{2} = 1 - \frac{k^{2}}{k_{m a x}^{2}} \end{array}

式中： $M_{y}^{k}$ 为种群个体变异位置向量； $δ$ 为标准差，其中 $C (0, δ^{2})$ 和 $G (0, δ^{2})$ 分别为基于柯西分布和高斯分布的随机变量； $X_{s}^{k}$ 为当前全局最优解的位置； $X_{y}^{k}$ 为当前个体的位置； $X_{τ}^{k}$ 为当前临时解的位置； $γ_{1}$ 和 $γ_{2}$ 为自适应调节变量，在迭代过程中根据种群进化状态动态调整。

鉴于柯西概率密度函数曲线尾部较长，变异可能会产生更长的步长，结合高斯变异能够帮助SSA在全局探索和局部开发之间取得更好的平衡。

2.3　NISSA流程

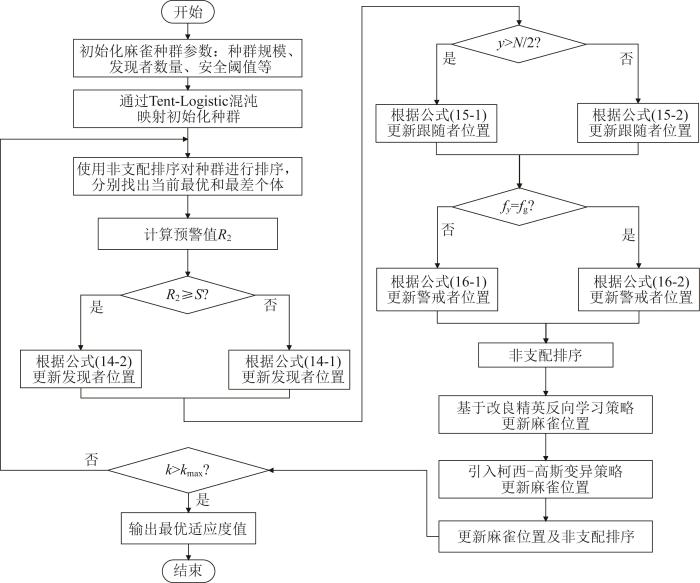
本文所提出的融合多策略的NISSA的流程如图5所示。图5系统性地展示了该算法从种群初始化到收敛输出的全过程。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 NISSA流程

Fig.5 Flow of NISSA

2.4　NISSA性能测试

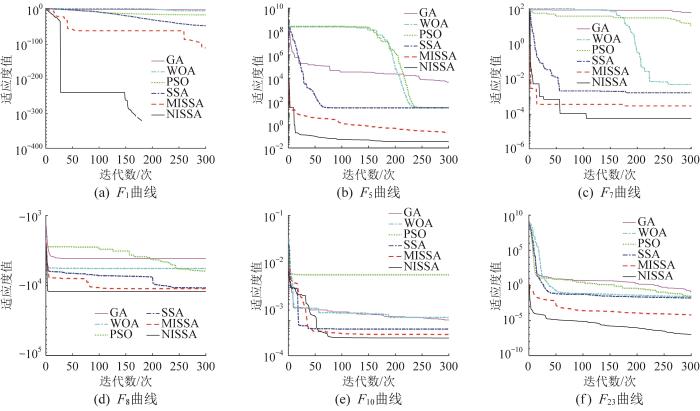
为验证NISSA的性能，选取PSO算法、GA（genetic algorithm，遗传算法）、WOA（whale optimization algorithm，鲸鱼优化算法）、SSA及MISSA^[11]作为对照，基于CEC2005基准测试集（包括测试函数F₁、F₅、F₇、F₈、F₁₀、F₂₃）^[22]，通过由单峰（F₁、F₅、F₇）与多峰（F₈、F₁₀、F₂₃）曲线来评估各算法的解空间遍历效能，结果如图6所示（适应度值取对数进行比较）。其中，算法参数统一设定如下：种群规模为100，搜索维度为3，最大迭代次数为300，发现者与警戒者各占20%，安全阈值为0.6；PSO算法的学习因子C₁=1.3，C₂=1.5，弹性系数为1。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同测试函数下各算法的收敛曲线

Fig.6 Convergence curves of various algorithms under different test functions

从图6中的F₁、F₅、F₈及F₂₃曲线中可直观看出，NISSA通过Tent-Logistic混沌映射与改良精英反向学习策略显著提升了初始种群的多样性，其解空间锚定效应抑制能力使得算法在较少迭代次数内实现多模态收敛；从F₇、F₁₀曲线中可以看出，结合柯西-高斯变异策略，NISSA展现出勘探-开采动态权衡优势，虽Pareto前沿逼近速率略低，但通过状态迁移驱动的逃逸机制，其超体积指标仍显著优于MISSA。结果表明，NISSA在多目标优化性能以及收敛性与多样性方面均展现出理论优势。

3 仿真与实验

3.1　仿真设计与分析

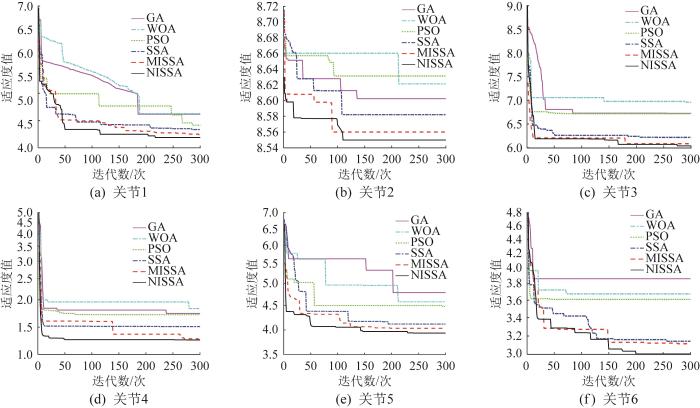
六自由度AR4机械臂作为轻量化工业机械臂，常用于精密装配或高速分拣，其轨迹优化需兼顾运动平滑性与时间效率。多目标优化的核心矛盾在于：平滑性要求低加速度，而时间效率要求高速度，两者需动态平衡。为验证NISSA在机械臂轨迹优化中的可行性，开展仿真实验。在相同工况下，利用NISSA与其他算法（PSO、GA、WOA、SSA及MISSA）分别对机械臂轨迹进行优化，并通过对比各算法的收敛曲线和机械臂的运行时间及末端冲击来评估算法性能，结果如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 机械臂各关节轨迹优化中各算法的收敛曲线对比

Fig.7 Comparison of convergence curves of various algorithms during trajectory optimization of each joint in manipulator

由图7可以看出，针对机械臂各关节的轨迹优化，PSO算法虽在单目标场景中表现良好，但在多目标协同优化时存在跨模态迁移能力不足的缺陷。MISSA与NISSA均改进了传统SSA易陷入局部最优的问题，但NISSA的Lyapunov指数导向机制使得其在机械臂动力学模型中展现出更高的覆盖率，验证了其在复杂工业场景中的有效性。在相同迭代次数下，NISSA的收敛速度显著高于其他算法，最终的超体积指标占优，说明该算法具备更优的收敛特性与精度鲁棒性。NISSA通过引入Tent-Logistic混沌映射与多维度权衡优化策略，有效地改善了自身的全局搜索能力，同时可维持高维空间勘探潜力。

3.2　实验设计与分析

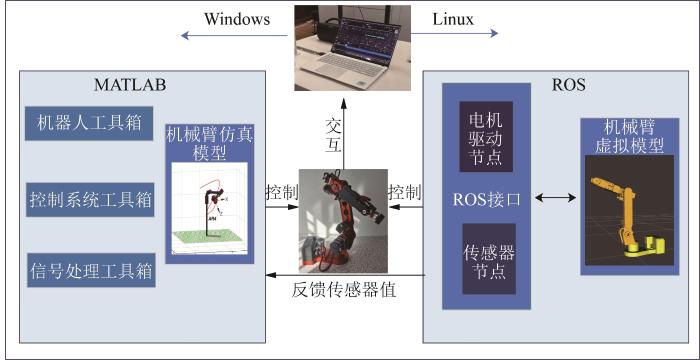
为进一步验证NISSA在实际应用中的可行性，利用六自由度AR4机械臂开展轨迹优化实验。实验用PC（personal computer，个人计算机）搭载Inter Core(TM) i5处理器，运行Linux Ubuntu 18.04操作系统。采用MATLAB-ROS（robot operating system，机器人操作系统）联合仿真平台进行算法验证。图8所示为机械臂控制系统的多层级通信架构。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 机械臂控制系统的通信架构

Fig.8 Communication architecture of manipulator control system

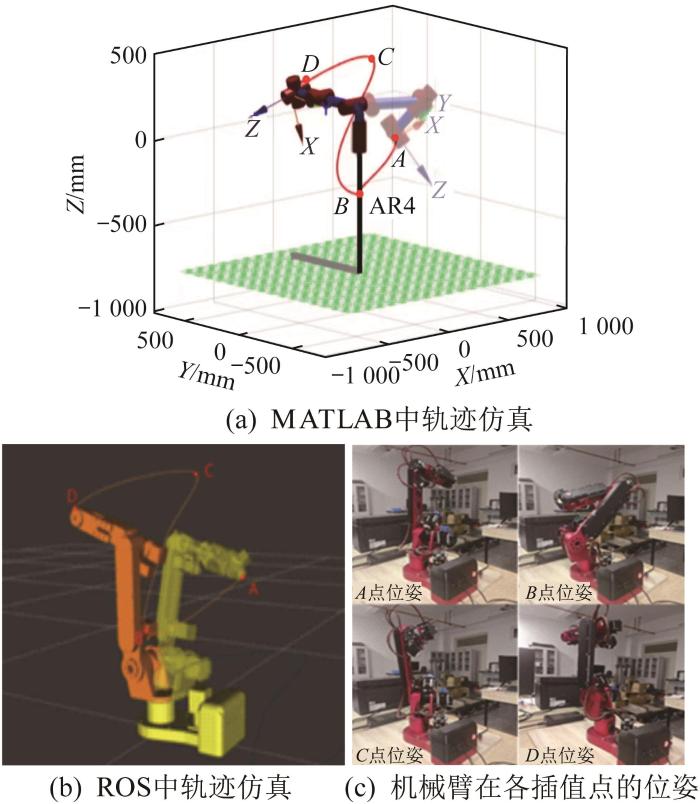
针对机械臂运行时间与末端冲击（以角加加速度表征）的多目标优化问题，在MATLAB软件中的Simulink环境下基于NISSA构建多目标轨迹优化框架，实现时间与冲击的协同优化。在虚拟样机协同仿真中，设定插值点A、B、C、D的位姿约束，并规划平滑轨迹。随后，通过MATLAB-ROS数据流同步机制，将优化轨迹部署至实际机械臂，实现实时任务调度。在实验中，ROS通过MoveIt与机械臂控制器相连，便于运动轨迹规划和控制。在配置ROS节点后，启动订阅节点以接收轨迹数据，确保从MATLAB软件向机械臂准确传输算法指令。机械臂的运动轨迹及各插值点的位姿如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 机械臂的运动轨迹

Fig.9 Motion trajectory of manipulator

通过求解机械臂的逆运动学方程，可求出关节角度。在已知机械臂末端位姿时，通过MATLAB软件中的机器人工具箱计算对应的关节角度 $θ_{1} \sim θ_{6}$ ，结果如表2所示。

表2 机械臂关节角度 (°)

Table 2 Joint angles of manipulator

关节	插值点
关节	A点	B点	C点	D点
1	-30	30	60	90
2	0	30	-30	0
3	45	-30	-60	-90
4	24	24	48	72
5	-81	27	54	81
6	-60	30	60	90

新窗口打开| 下载CSV

在实验中，分别利用不同算法（NISSA、PSO、GA、WOA、SSA及MISSA）对机械臂进行轨迹优化并记录各轨迹所需的时间均值以及各关节所受的冲击均值。结果表明，通过多模态协同优化策略，NISSA在机械臂轨迹优化中展现出显著优势：机械臂运行时间由基准值11.38 s降至9.35 s（相对降幅为17.8%），相较于GA、WOA、PSO、SSA和MISSA分别有16.6%、14.1%、12.3%、10.9%和5.8% 的提升。在运行平稳性方面，NISSA使得机械臂各关节的角加加速度从28.21 (°)/s³降低至24.57 (°)/s³（相对降幅为12.9%），相较于GA、WOA、PSO、SSA和MISSA分别有8.4%、7.9%、7.5%、5.3%、1.6%的提升。

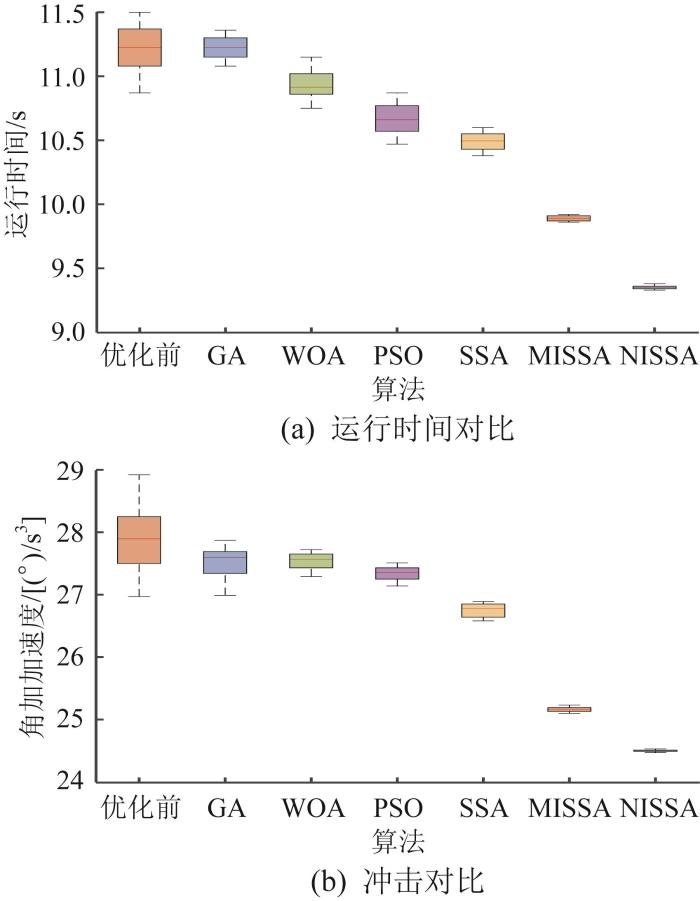
在上述实验环境下，重复进行30次轨迹优化实验并记录机械臂每次运行的时间以及末端冲击，通过箱线图对比不同算法的优化效果，如图10所示。从图10中可直观看出，NISSA的变异性显著降低，IQR（inter quartile range，四分位间距）减小，极差较小，数据集中在窄区间内，验证了NISSA在多目标轨迹优化上兼具高效性与稳定性，且柯西-高斯变异策略有效抑制了极端动态载荷。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 基于不同算法的机械臂运行时间和冲击对比

Fig.10 Comparison of operation time and impact of manipulator based on different algorithms

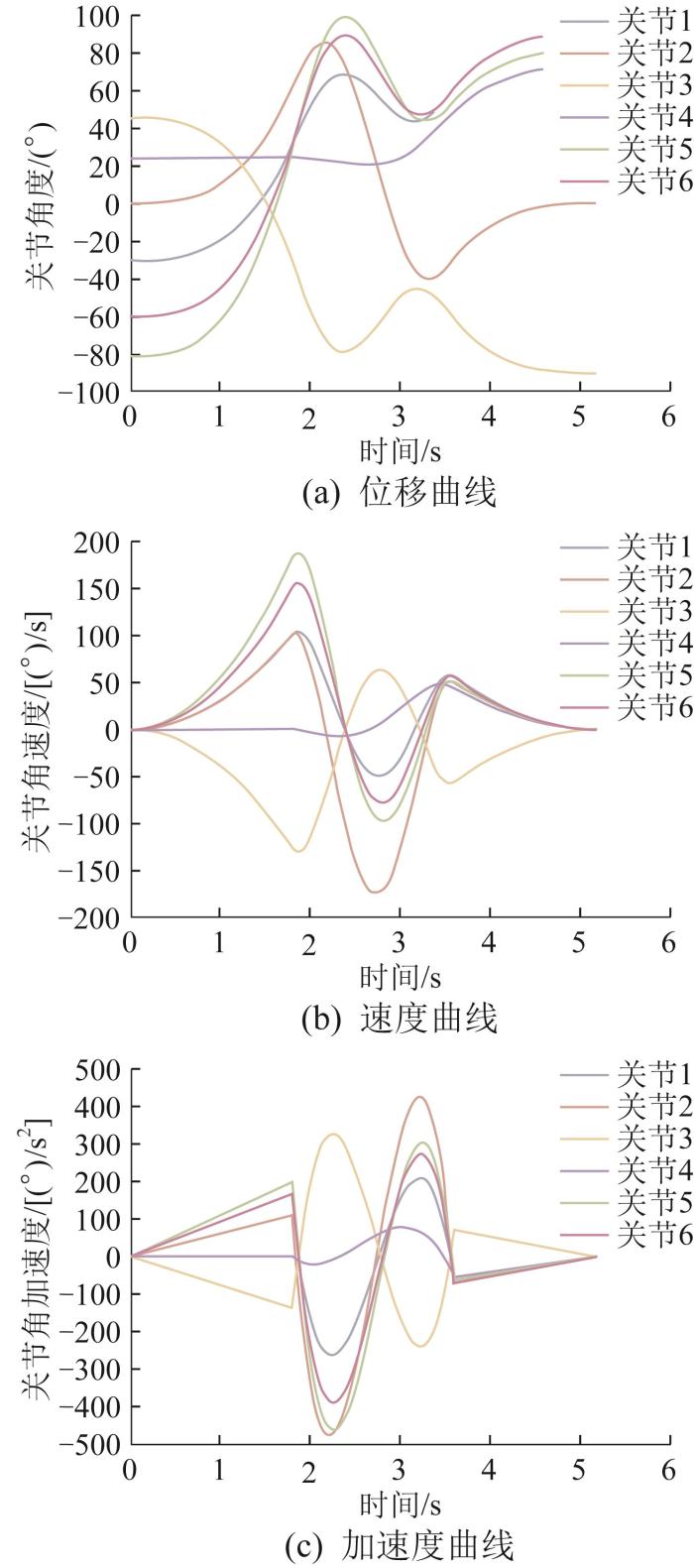
对采用NISSA优化后的机械臂轨迹进行分析，机械臂运动过程中各关节的位移、速度、加速度曲线如图11所示。由图11可以看出，利用3-5-3多项式插值得到的机械臂各关节的运动曲线光滑且连续，角速度和角加速度均满足机械臂的约束条件；机械臂可在保障本体安全性的前提下，实现17.8%的效率提升与12.9%的末端振动能量衰减，这对精密装配场景的能效增益与动态稳定性提升具有重要意义。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 优化后机械臂各关节的位移、速度和加速度曲线

Fig.11 Curves of displacement, velocity and acceleration of each joint of optimized manipulator

4 总结

本文提出了一种基于Tent-Logistic混沌映射、改良精英反向学习策略及柯西-高斯变异策略的NISSA，用于解决机械臂的多目标轨迹优化问题，通过多策略耦合提升了算法的解空间探索效能。通过与其他现有的优化算法进行对比，得到以下结论。

1）NISSA通过引入多种改进策略，显著提高了算法的全局搜索能力和收敛精度，避免了传统SSA易陷入局部最优的问题。仿真与实验结果表明，相较于其他优化算法，NISSA在复杂多目标优化问题中表现出更强的适应性和求解能力，为机械臂轨迹优化提供了更高效的方法。

2）应用NISSA优化后，机械臂的运行效率提升了17.8%，冲击减小了12.9%，实现了机械臂运行效率和稳定性的双重提升。优化后的轨迹在保持机械臂末端执行器运动连续性的同时显著减少了振动与冲击，延长了机械臂的使用寿命。

未来将针对NISSA应用于不同类型机械臂的轨迹优化展开深入研究，并通过对比不同自由度机械臂的优化效果，来验证算法在工程实际中的应用潜力。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.111

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

陆一，王萍，李书福，等.

传统制造必须向智能制造转变

［J］. 中国质量监管， 2016（10）： 70-71.