复合机器人路径规划研究

doi:10.3785/j.issn.1006-754X.2025.05.125

复合机器人路径规划研究

李宸^,, 史春景, 李金泉^,^,

沈阳理工大学机械工程学院，辽宁沈阳 110000

Research on path planning for composite robot

LI Chen^,, SHI Chunjing, LI Jinquan^,^,

School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110000, China

通讯作者: 李金泉（1965—），男，教授，博士，从事切削理论与先进制造技术等研究，E-mail: li_jinquan@163.com, http://orcid.org/0000-0002-5396-7851

收稿日期: 2025-03-31 修回日期: 2025-06-20

基金资助:

国家自然科学基金资助项目. 51775357
沈阳理工大学国防科技创新团队培育建设计划资助项目. SYLUGFTD202102

Received: 2025-03-31 Revised: 2025-06-20

作者简介 About authors

李　宸（2001—），男，硕士生，从事基于ROS的复合机器人研究，E-mail:1658881967@qq.com , E-mail：1658881967@qq.com

摘要

针对在复杂未知环境中复合机器人路径规划效率低下、路径冗余等问题，提出了一种结合改进A*算法与动态窗口法（dynamic window approach, DWA）的新型算法。首先，通过引入动态惯性权重系数，对A*算法的启发式函数进行实时调整，以实现搜索初期的加速和后期的全局最优逼近。同时，引入Open List节点访问时间阈值机制，以避免算法陷入局部最优解，并构建了不同尺寸的栅格地图，采用MATLAB软件对改进A*算法进行了仿真验证。其次，将改进A*算法与DWA进行融合，以实现动态避障与全局路径跟随的协同。最后，在ROS（robot operating system，机器人操作系统）仿真环境和真实环境中对改进A*-DWA融合算法进行了实验验证。实验结果显示，相较于传统A*-DWA融合算法，采用改进A*-DWA融合算法可使规划路径缩短27.57%，转折点减少40%，耗时缩短31.03%，复合机器人的速度变化更稳定。改进A*-DWA融合算法不仅具有全局最优路径规划性能，还具备动态适应性，使机器人具有较高的避障成功率，能够满足复杂未知环境下复合机器人路径规划的需求。

关键词： 路径规划 ; 机器人操作系统环境 ; 复合机器人 ; A*算法 ; 动态窗口法

Abstract

To address the inefficiency and path redundancy in the path planning of composite robots in complex and unknown environments, a novel algorithm integrating an improved A* algorithm with the dynamic window approach (DWA) was proposed. Firstly, by introducing a dynamic inertia weight coefficient, the heuristic function of the A* algorithm was adjusted in real time to achieve acceleration in the early stage of the search and global optimal approximation in the later stage. Meanwhile, the time threshold mechanism for accessing Open List nodes was introduced to prevent the algorithm from falling into local optimal solutions. Grid maps with different sizes were constructed, and the improved A* algorithm was verified through simulation using MATLAB software. Secondly, the improved A* algorithm was integrated with DWA to achieve the synergy of dynamic obstacle avoidance and global path following. Finally, the improved A*-DWA fusion algorithm was experimentally verified in both the ROS (robot operating system) simulation environment and the real environment. The experimental results showed that, compared with the traditional A*-DWA fusion algorithm, the use of the improved A*- DWA fusion algorithm could shorten the planned path by 27.57%, reduce the turning points by 40%, shorten the time consumption by 31.03%, and make the speed variation of the composite robot more stable. The improving A*-DWA fusion algorithm not only has the performance of global optimal path planning, but also exhibits dynamic adaptability, enabling the robot to have a high success rate in obstacle avoidance and meeting the requirements of path planning for composite robots in complex and unknown environments.

Keywords： path planning ; robot operating system (ROS) environment ; composite robot ; A* algorithm ; dynamic window approach

PDF (7673KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李宸, 史春景, 李金泉. 复合机器人路径规划研究[J]. 工程设计学报, 2025, 32(5): 623-633 doi:10.3785/j.issn.1006-754X.2025.05.125

LI Chen, SHI Chunjing, LI Jinquan. Research on path planning for composite robot[J]. Chinese Journal of Engineering Design, 2025, 32(5): 623-633 doi:10.3785/j.issn.1006-754X.2025.05.125

随着智能制造的发展，复合机器人在多领域得到广泛应用，而其在复杂环境下的自主导航与任务执行能力是核心挑战^[1]。采用传统的路径规划算法如Dijkstra算法^[2]、人工蜂群算法^[3]、A*算法^[4]等可实现静态环境下的全局路径优化，但其固定搜索策略难以适用于复杂环境；动态窗口法（dynamic window approach，DWA)^[5]擅长于局部避障，但缺乏全局引导，易偏离目标或陷入局部最优。因此，融合全局规划与局部避障优势的机器人动态路径规划成为当下研究的热点^[6]。

学者们已对路径规划算法提出了多种改进方案。如：王慧锬等^[7]根据机器鱼行进的位置，以机器鱼与障碍物之间的距离为指标来改进A*算法，但该算法仅适用于简单环境，在复杂环境中表现不佳；Allus等^[8]提出通过优化目标节点的访问顺序来改进A*算法，降低了路径搜索过程中的计算复杂性；彭斌等^[9]提出了改进A*算法，用加权欧氏距离优化启发式函数，并结合拐点识别去除冗余节点，但路径的距离变化不明显；毕竟等^[10]提出了结合方向约束的A*算法，但是规划的路径较曲折，不够平滑；曾宪阳等^[11]提出了以动态加权处理启发式函数，并利用Floyd算法去除路径中冗余点的改进A*算法，但其无法满足较大场景下路径规划的实时性要求。现有的方法存在两方面局限：传统A*算法的固定启发权重难以平衡路径规划效率与计算消耗，在动态环境下易产生冗余节点；全局规划器与局部规划器简单串联，易引发路径震荡^[12]。此外，现有研究多基于仿真验证，真实场景中的运动控制误差对算法鲁棒性的影响仍需探索^[13]。

本文提出了一种动态惯性权重改进A*算法与DWA融合的路径规划方法，旨在为复合机器人规划出既短又平滑的安全路径。利用该方法，可以在工业自动化中提高物料搬运和设备巡检的效率，降低成本；在国防侦察中，能帮助机器人快速规划安全路径，避开危险；在救灾抢险中，可以使机器人快速找到安全路径，高效救援受困人员。因此，所研究的路径规划方法不仅理论价值高，而且应用前景广阔，对复合机器人在多领域的智能化应用具有重要意义^[14]。

本研究关注复杂未知环境下复合机器人的路径规划问题，构建了研究框架。第1章主要讨论全局路径规划，提出了改进A*算法，引入动态惯性权重系数来调节启发式函数，加快搜索并逼近最优解；设计Open List节点访问时间阈值机制，避免局部最优；仿真验证了A*算法的性能；第2章探讨了局部路径规划，基于全向底盘运动学模型，分析了DWA的速度采样限制和轨迹预测，并构建了评价函数模型；第3章提出了改进A*-DWA融合策略，实现了动态避障与全局目标协同，并验证了融合算法的实时适应性；第4章进行了ROS（robot operating system，机器人操作系统）环境和真实场景中融合算法的验证，以及路径规划精度、动态避障能力及工程应用可行性等综合评估，并将改进算法与传统算法进行对比，量化分析了关键指标；最后，总结了研究成果，展望了未来研究方向。

1 全局路径规划改进A*算法

1.1　传统A*算法

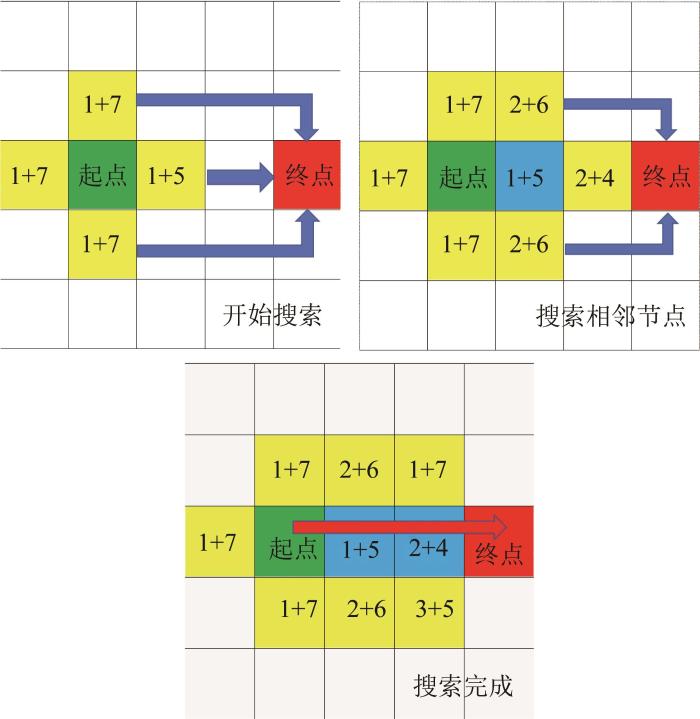
A*算法是一种结合了Dijkstra算法和贪心最佳优先搜索（启发式引导）算法优点的启发式算法^[15]。从起始点开始，通过代价函数估计每个节点的总代价，优先探索总代价最低的节点，经多次循环迭代直至到达目标点。其原理如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 传统A*算法原理示意

Fig.1 Principle schematic of traditional A* algorithm

其代价函数 $F (n)$ 的表达式为：

F (n) = G (n) + H (n)

(1)

式中： $G (n)$ 为从起点到节点n的真实距离， $H (n)$ 为采用启发式函数计算的节点n到目标点的距离。

在A*算法中，常用的启发式函数有欧氏距离^[16]、切比雪夫距离^[17]和曼哈顿距离。曼哈顿距离计算简便，更适配网格化空间，所以将曼哈顿距离作为A*算法的启发式函数。其表达式为：

H (n) = |x_{s} - x_{0}| + |y_{s} - y_{0}|

(2)

式中：x_s、y_s分别为终点的横坐标和纵坐标，x₀、y₀分别为起点的横坐标和纵坐标。

传统A*算法设计简单，在复杂环境下节点扩展多，易重复计算，效率低下^[18]。因此，改进传统A*算法，提高其在复杂环境下的路径规划效率和准确性，是非常重要的。

1.2　改进A*算法

1.2.1　引入动态惯性权重系数

鉴于传统A*算法的局限性，对其启发式函数 $H (n)$ 增加权重系数 $ω (n)$ ，以调节节点扩展优先级，减少冗余计算。改进后代价函数 $F (n)$ 的表达式为：

F (n) = G (n) + ω (n) \cdot H (n)

(3)

当权重系数 $ω (n)$ 较大时，算法搜索快，但易忽略最优路径；当 $ω (n)$ 较小时，算法搜索慢，但更精确。在实际应用中需平衡搜索速度与路径质量。

因此，通过动态调整权重系数 $ω (n)$ ，实现启发式函数的实时变化。 $ω (n)$ 随迭代次数i而动态调整，以实时优化启发式函数。A*算法的有效性取决于 $G (n)$ 与 $H (n)$ 的平衡。动态权重系数应平滑变化，采用指数递减策略可避免其突变。改进后的权重系数为：

ω (i) = ω_{s} \cdot e^{- λ \cdot \frac{i}{I}}

(4)

式中： $ω_{s}$ 为初始权重，其值大于1，以强化启发式引导； $λ$ 为衰减系数，其值大于1，用来调节权重下降速度范围；I为预设的最大迭代次数。

当 $i = 0$ 时， $ω (0) = ω_{s}$ ，启发式影响最大；当 $i \to I$ 时， $ω (I) \to ω_{s} \cdot e^{- λ}$ 。 $ω (i) \in [1, ω_{s}]$ ，既保留了启发式引导能力，又避免了 $H (n)$ 主导导致的最优性损失。

在搜索初期， $ω (i) \approx ω_{s} > 1$ ，此时 $F (n)$ 中 $H (n)$ 为主导，节点扩展偏向目标方向，减少了无效搜索。

假设传统A*算法的扩展节点优先级 $为 F_{0} (n) = G (n) + H (n)$ ，改进A*算法的扩展节点优先级为 $F_{1} (n) = G (n) + ω (i) \cdot H (n)$ ，对于任意节点 $n_{1}$ 和 $n_{2}$ ，若n₁更接近目标，即 $H (n_{1}) < H (n_{2})$ ，则：

F_{1} (n_{1}) - F_{2} (n_{2}) = [G (n_{1}) - G (n_{2})] + ω (i) [H (n_{1}) - H (n_{2})]

(5)

$ω (i)$ 放大了 $H (n)$ 的差异， $n_{1}$ 的优先级显著高于 $n_{2}$ ，减少了非目标节点扩展，提升了搜索效率。

在搜索后期， $ω (i) \to 1$ ，此时 $F (n)$ 趋近于传统A*算法的代价函数，确保算法收敛到全局最优路径。根据A*算法理论， $ω (i) \geq 1$ 时， $ω (i) \cdot H (n) \geq H (n)$ ，由于 $H (n)$ 为可采纳启发式，即 $H (n) \leq$ 实际最优代价， $ω (i) \cdot H (n)$ 仍为可采纳函数，则可保证找到全局最优路径，即得到式(6)。

H (n) \leq ω (i) \cdot H (n) \leq 实际 最优 代价

(6)

在实际应用中，取 $ω (i) \in [1, 2]$ 即可确保上述条件成立，从而维持算法初期高权重而加速搜索、后期低权重以保证最优性。

1.2.2　引入Open List节点访问时间阈值机制

在A*算法中，扩展子节点时遍历所有候选节点可能会导致效率低下^[19]。设置时间阈值T_t，若首个节点在该时间内未扩展，则优先扩展，避免局部最优，提高路径规划和搜索的效率。

T_t用于判断节点是否陷入局部最优而“停滞”。超时判定条件为：

t_{c} - t_{i} > T_{t}

(7)

式中：t_c为当前时间，t_i为节点加入Open List的时间。

实现流程：节点加入Open List时记录时间戳t_c，每次迭代前检查首个节点滞留时间t_b：

t_{b} = t_{c} - t_{i}

(8)

若t_b $\leq$ T_t，按传统规则扩展节点；若t_b>T_t，节点可能陷入局部最优，则将其设为最高优先级，进行强制扩展以探索新路径，并重新计算代价函数，更新Open List和Closed List列表，避免无限循环。

T_t的设置会直接影响算法求解效率和路径质量。若T_t过小，可能导致正常节点被误判为“停滞”，增加不必要的计算开销；若T_t过大，可能无法及时解除局部最优，导致路径冗余或搜索时间延长。通过预实验，设置T_t为3 s（小规模地图）和6 s（大规模地图），来平衡避障效率与计算消耗。

1.3　改进A*算法仿真验证

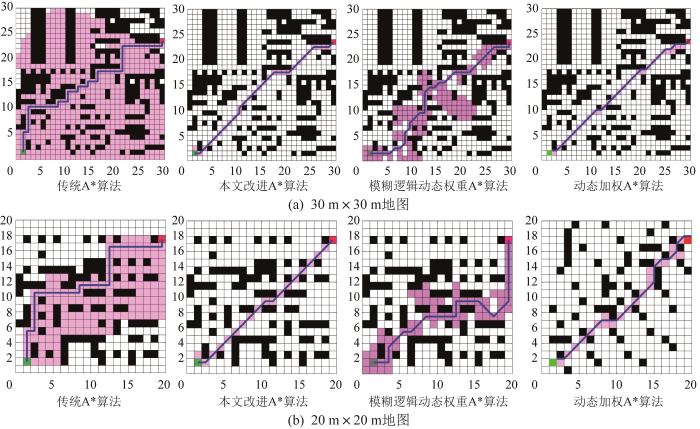
为了验证改进A*算法的优势，在MATLAB 2023b中进行仿真对比实验。搭建尺寸为30 m×30 m和20 m×20 m的栅格地图，其中：绿色、红色栅格分别为起点和终点，黑色为障碍物，白色为自由区域，粉色为搜索节点。规划的路径如图2所示，具体仿真结果如表1所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不同算法下路径规划结果

Fig.2 Path planning results under different algorithms

表1 不同算法下路径规划仿真结果

Table 1 Simulation results of path planning under different algorithms

地图尺寸	算法	转折数量/次	路径长度/m	搜索节点数量/个	搜索时间/s
30 m×30 m	传统A*算法	13	40.627	555	0.496 6
	本文改进A*算法	7	37.689	30	0.326 6
	模糊逻辑动态权重A*算法	18	39.42	143	0.665 0
	动态加权A*算法	9	37.11	30	0.577 2
20 m×20 m	传统A*算法	8	34.01	297	0.614 5
	本文改进A*算法	3	26.68	20	0.229 2
	模糊逻辑动态权重A*算法	10	30.07	67	0.643 5
	动态加权A*算法	10	26.38	24	0.485 9

新窗口打开| 下载CSV

仿真结果表明，相较其他3种算法，改进A*算法的搜索速度最快，路径最短，转折最少。在不同尺寸地图中规划路径的长度缩短了7.2%~21.6%，搜索节点最多减少了62%，搜索时间缩短了34.2%~50.9%。表明采用本文提出的改进A*算法能提升静态环境下的路径规划效率。

后续将引入局部规划算法来应对动态环境。通过全局与局部规划的结合，使复合机器人能智能适应复杂环境，实现高效安全的路径规划。

2 局部路径规划DWA算法

采用DWA，推算移动机器人在运动模型下的轨迹，确定速度采样空间；在速度空间（v, ω）中采样多组速度，并模拟一定时间内机器人在这些速度下的运动轨迹，通过评价函数对这些轨迹进行打分，选取最优的轨迹来控制机器人的运动^[20]。

2.1　运动学模型

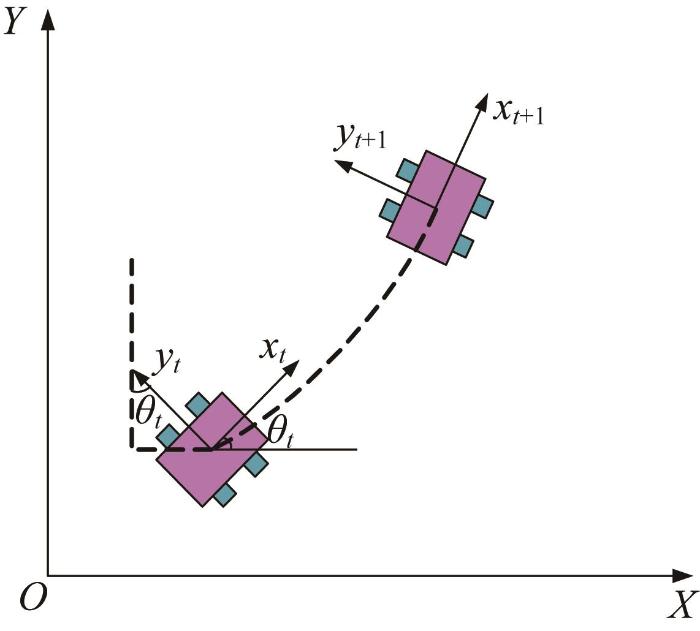
为了更好地模拟机器人的运动轨迹，需要确定机器人的运动学模型。全向底盘运动学模型如图3所示。其中：x_t 为底盘X向位移，y_t 为底盘Y向位移，θ为底盘的方位角。由于机器人在相邻时刻内的运动距离很短，可以将两相邻点之间的运动轨迹看成直线。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 全向底盘运动学模型

Fig.3 Kinematic model of omnidirectional chassis

将该段距离投影到世界坐标系下，则在t+1时刻机器人在世界坐标系下X向和Y向的移动位移 $Δ x$ 和 $Δ y$ 分别为：

\{\begin{array}{l} Δ x = v Δ t c o s θ_{t} \\ Δ y = v Δ t s i n θ_{t} \end{array}

(9)

式中： $θ_{t}$ 为变化时间 $Δ t$ 内的角度变化。

考虑X向、Y向的移动和旋转。将Y向的移动位移投影到世界坐标系下，则：

\{\begin{array}{l} Δ x = v_{y} Δ t c o s (θ_{t} + \frac{π}{2}) = - v_{y} Δ t s i n θ_{t} \\ Δ y = v_{y} Δ t s i n (θ_{t} + \frac{π}{2}) = v_{y} Δ t c o s θ_{t} \end{array}

(10)

式中：v_y 为机器人在世界坐标系下Y向的移动速度。

将式(9)与式(10)合并，即可得到机器人的运动模型：

\{\begin{array}{l} x_{t + 1} = x_{t} + v Δ t c o s θ_{t} - v_{y} Δ t c o s θ_{t} \\ y_{t + 1} = y_{t} + v Δ t s i n θ_{t} + v_{y} Δ t c o s θ_{t} \\ θ = θ_{t} + ω Δ t \end{array}

(11)

2.2　速度采样

在速度采样过程中，受到以下因素的限制。

1）本体速度约束。

v_{m} = \{(v, ω) |v \in (v_{m i n}, v_{m a x}), ω \in (ω_{m i n}, ω_{m a x})\}

(12)

式中：v_m为机器人速度空间中线速度与角速度的集合，v_min、v_max分别为机器人的最小、最大线速度，ω_min、ω_max别为机器人的最小、最大角速度。

2）加速度约束。

\begin{array}{l} v_{d} = \{(v, ω)| v \in (v_{c} - {\dot{v}}_{m i n} t_{p} + {\dot{v}}_{m a x} t_{p}), \\ ω \in (ω_{c} - {\dot{ω}}_{m i n} t_{p} + {\dot{ω}}_{m a x} t_{p})\} \end{array}

(13)

式中：v_d为机器人的实际运动速度范围；v_c和ω_c分别为机器人在当前时刻的线速度和角速度； ${\dot{v}}_{m a x}$ 和 ${\dot{ω}}_{m a x}$ 分别为机器人在当前时刻的最大线加速度和最大角加速度； ${\dot{v}}_{m i n}$ 和 ${\dot{ω}}_{m i n}$ 分别为机器人在当前时刻的最小线加速度和最小角加速度；t_p为预测时间。

3）制动约束。

需确保机器人在运动过程中不会与障碍物发生碰撞^[21]，则其制动约束为：

v_{m a x} = \{(v, ω) | v \leq {[2 d (v, ω) {\dot{v}}_{m i n}]}^{\frac{1}{2}}, ω \leq {[2 d (v, ω) {\dot{ω}}_{m i n}]}^{\frac{1}{2}}\}

(14)

式中： $d (v, ω)$ 为机器人运动轨迹中离障碍物最近的距离。当机器人绕自身转动时，机器人的转动轨迹可以等效为以旋转半径为半径的圆弧。

2.3　轨迹预测

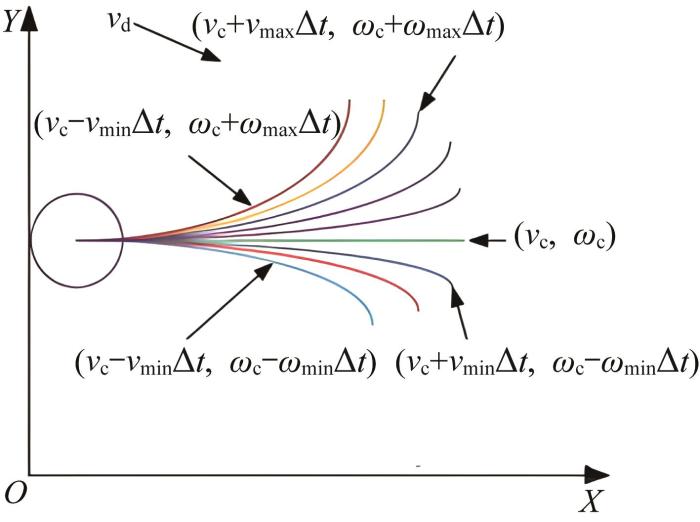
确定机器人的采样速度和运动模型后，可以对机器人的状态进行预测和更新。轨迹预测原理如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 机器人轨迹预测原理示意

Fig.4 Prediction principle schematic of robot trajectory

根据上述预测原理可预测出多条轨迹。需要对这些轨迹进行评价，按照机器人方位角、安全刹车距离、无碰撞、速度快等要求选取最优的轨迹。评价函数 $G (v, ω)$ 为：

G (v, ω) = σ [α \cdot h (v, ω) + β \cdot d (v, ω) + γ \cdot v (v, ω)]

(15)

式中：h(v, ω)为方位角评价函数，即机器人与目标点之间的角度差；d(v, ω)为机器人与障碍物之间的距离；v(v, ω)为机器人当前线速度； $α$ 、 $β$ 、 $γ$ 、 $σ$ 为各函数的权重系数。

3 改进**A*-DWA**融合算法的工作原理与仿真

3.1　融合算法的工作原理

传统A*-DWA融合算法采用“全局路径引导+局部避障”的串联模式。具体而言，A*算法基于静态环境生成全局最优路径，DWA则根据传感器实时数据在局部范围内动态调整机器人的运动轨迹，以规避动态障碍物。然而，传统融合算法存在一些局限性，如：A*算法生成的全局路径可能没有充分考虑动态环境的变化，导致机器人在运动过程中遇到不可预见的障碍物时无法灵活应对；DWA虽然可以使机器人在局部范围内动态调整运动轨迹，但其决策过程往往依赖当前瞬间的传感器数据，缺乏对未来环境的预测能力。为了消除这些局限性，本文提出了一种改进A*-DWA融合算法。该算法结合了A*算法的全局路径规划能力和DWA的局部避障优势，并通过动态调整和优化权重，来实现机器人在复杂环境下的路径规划，提高避障效率。

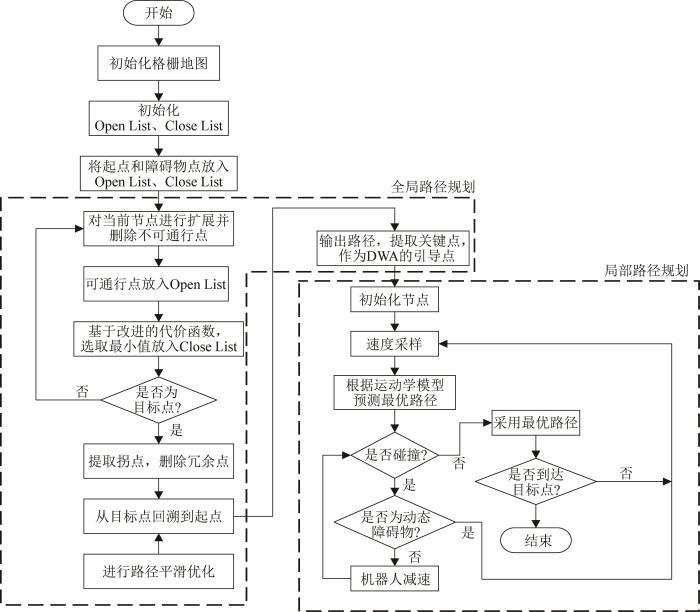
改进A*-DWA融合算法的工作原理如图5所示。该算法将A*算法中的关键路径点作为DWA中的临时目标点，确保机器人在局部避障时仍朝向全局目标。遇到动态障碍物时，通过DWA动态调整轨迹，避开障碍物，同时向全局目标前进，实现路径最优和实时避障的平衡。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 改进A*-DWA融合算法工作原理

Fig.5 Working principle of improved A*-DWA fusion algorithm

该改进算法不仅继承了传统A*算法的全局路径规划优势，还结合了DWA的局部灵活性和实时性，实现了全局与局部的更好协同。

3.2　融合算法仿真实验

在MATLAB 2023b仿真环境下，基于20 m×20 m地图添加动态障碍物，分别采用传统和改进A*-DWA融合算法进行对比实验，来验证改进融合算法的动态避障性能。机器人运动学参数如表2所示。

表2 机器人运动学参数

Table 2 Kinematic parameters of robot

参数	数值
最大线速度	0.35 m/s
最大角速度	1.57 rad/s
线加速度	0.1 m/s²
角加速度	0.785 rad/s²
规划周期	2.5 s
时间间隔	0.1 s

新窗口打开| 下载CSV

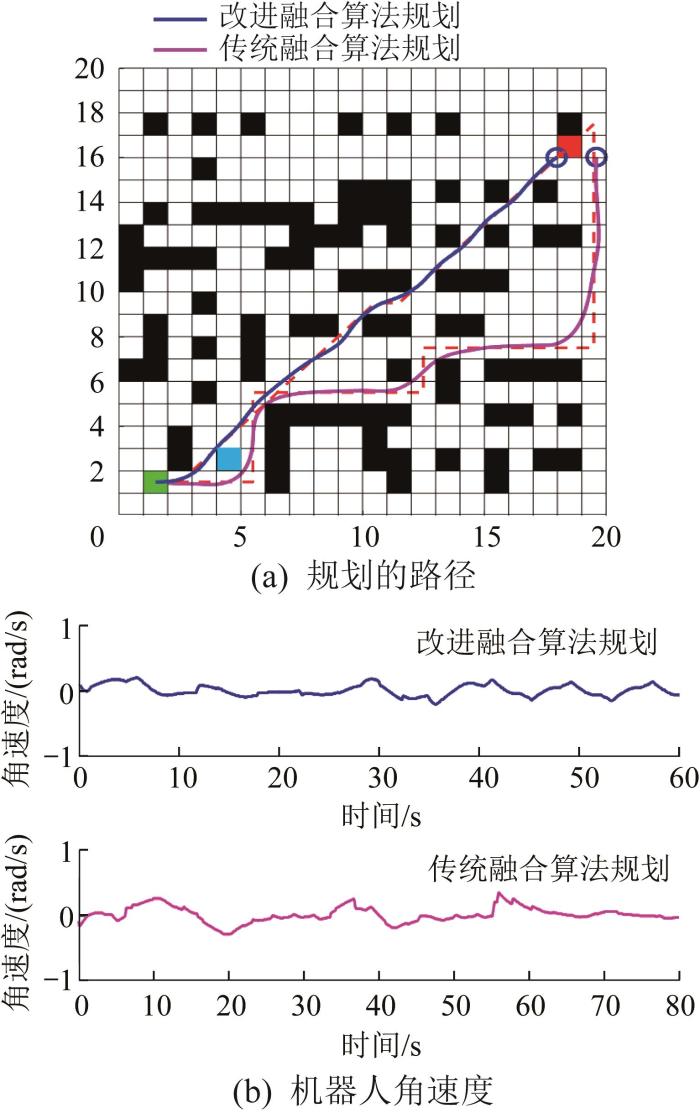
2种算法的路径规划效果如图6所示。图6(a)中，蓝色方块为添加的动态障碍物，红色虚线为全局路径。由图6(b)可知，在第10秒机器人遇到动态障碍物时，改进融合算法下机器人角速度变化比较稳定，动态避障比较安全。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 传统和改进A*-DWA融合算法路径规划效果

Fig.6 Path planning effect of traditional and improved A*-DWA fusion algorithms

2种算法的仿真结果如表3所示。由表可知，相较于传统融合算法，采用改进融合算法可使规划路径缩短27.57%，转折点减少40%，耗时缩短31.03%，在复杂环境下机器人动态避障性能更优。

表3 传统和改进A*-DWA融合算法仿真结果

Table 3 Simulation results of traditional and improved A*-DWA fusion algorithms

算法

总耗时/s

路径长度/m

转折点数量/个

传统A*-DWA

融合算法

96.301 3

改进A*-DWA

融合算法

66.419 2

24.627 4

新窗口打开| 下载CSV

4 改进**A*-DWA**融合算法实验验证

4.1　仿真环境中验证

为了验证改进A*-DWA融合算法的路径规划及动态避障性能，基于ROS环境开展仿真实验。在ROS Gazebo仿真软件中搭建地图，如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 实验地图

Fig.7 Experimental maps

指定目标点，来验证算法的路径规划性能。算法路径规划仿真结果如图8所示。由图8(a)可知，改进算法规划的路径较传统算法转折点更少、更平滑。由图8(b)可知，改进算法下机器人在避障过程中速度变化更平稳。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 融合算法路径规划仿真结果

Fig.8 Simulation results of path planning of fusion algorithms

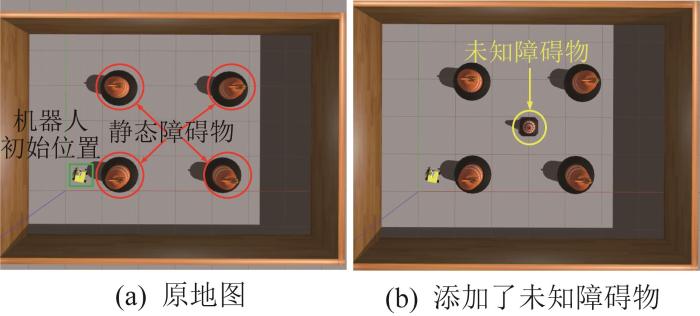
为了验证基于改进融合算法的动态避障效果，在复杂地图中设定机器人的起点、终点，并将橙色交通锥作为未知障碍物，开展机器人避障实验。运行改进融合算法后，机器人基于雷达扫描信息规划绕障路径，并沿路径持续调整方向直至靠近终点。其避障过程如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 机器人避障仿真过程

Fig.9 Simulation process of robot obstacle avoidance

仿真结果表明，本文提出的改进A*-DWA融合算法在简单及复杂动态环境中均具有较好的应用，为机器人在仿真场景下的高效安全运行提供保障，并为其在真实环境中的实验奠定了基础。

4.2　真实环境中验证

将改进A*-DWA融合算法集成到复合机器人中^[22]，在真实场景中进行实验测试。实验平台采用双层亚克力板结构，上下亚克力板的间距为25 cm，形成设备舱，底部配置麦克纳姆轮以实现全向移动，机器人顶部搭载激光雷达。

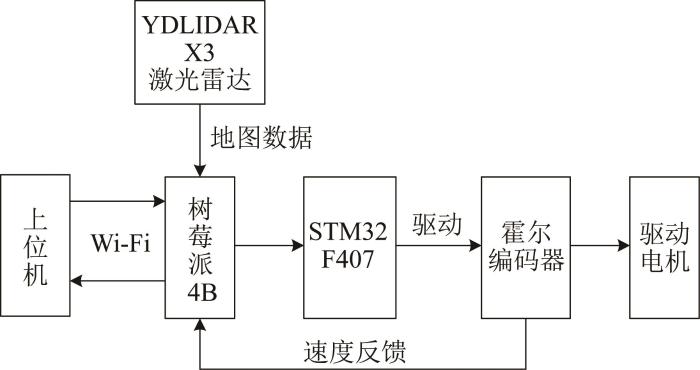
机器人控制系统的组成如图10所示。控制系统采用三级架构：上位机（ROS）执行改进A*全局规划和DWA局部避障；树莓派4B处理激光雷达数据，并构建Gmapping实时地图；底层的STM32F407控制电机驱动器，实现四轮独立PID调速。全局路径由改进A*算法生成，DWA以100 ms的周期动态采集速度空间，并结合代价地图避障，Wi-Fi指令以50 Hz的频率经树莓派转发至STM32，解算得到的线速度（0~0.8 m/s）、角速度（-1.5 ~1.5 rad/s)即为电机PWM（pulse width modulation，脉冲宽度调变）信号。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 复合机器人控制系统组成

Fig.10 Composition of composite robot control system

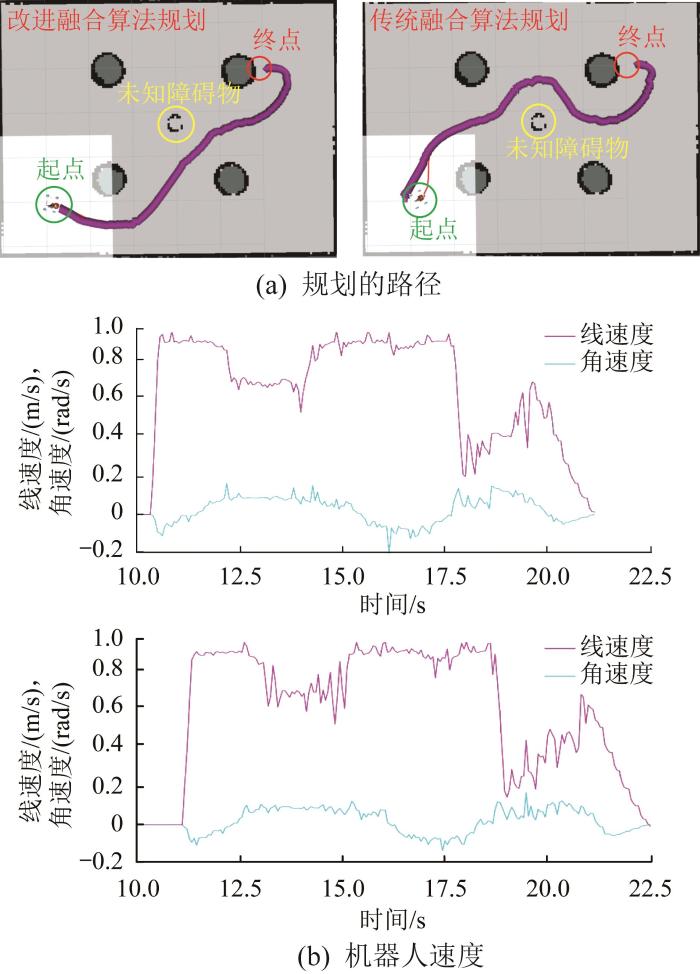
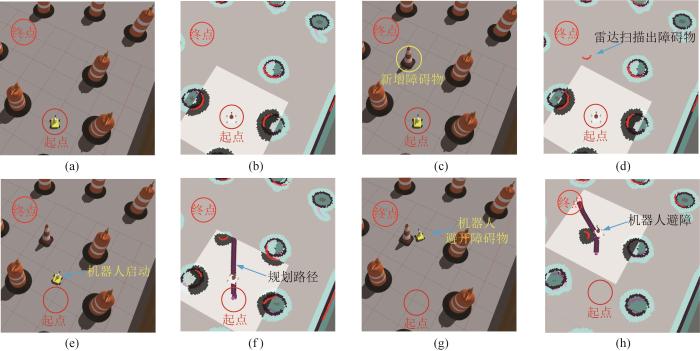
设定复合机器人从指定起点出发，依次避开障碍物A、B、C，最终到达终点，执行抓取任务。机器人避障实验过程如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 复合机器人避障实验过程

Fig.11 Experimental process of composite robot obstacle avoidance

首先，规划好机器人最优路径，如图12(a)所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

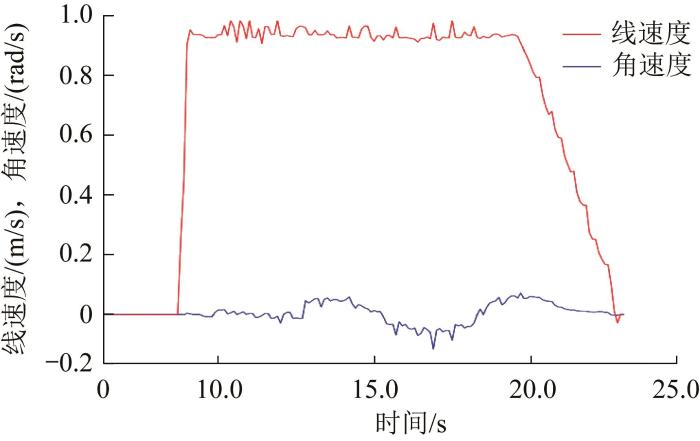
图12 路径规划过程中复合机器人的角速度和线速度

Fig.12 Angular velocity and linear velocity of composite robot during path planning process

在机器人运动过程中，通过激光雷达动态扫描环境实现环境建模更新，确保机器人始终沿着全局最优的可行运动轨迹执行导航任务。在遇到障碍物A、B、C后实时更改路径，实时选择最优路径。算法验证过程如图11(b)至图11(d)所示。

规划过程中机器人的角速度和线速度如图12所示。由图可知，在避障过程中机器人的角速度变化较平缓，线速度稳定保持在0.9~1.0 m/s。

实验结果表明，采用改进A*-DWA融合算法的机器人在复杂动态环境中具有较强的自适应能力，能够有效避开多障碍物。该算法为机器人在真实场景中的高效、安全运行提供了可靠保障。

5 结论

本文提出了改进A*-DWA融合路径规划算法。通过引入动态惯性权重系数来优化启发式函数，并引入Open List节点访问时间阈值机制，显著提升了全局路径规划效率；DWA则基于全向底盘运动学模型，通过速度采样约束和轨迹评价函数增强了机器人的动态避障能力。改进A*-DWA融合算法在ROS仿真和真实环境的实验中均能生成更平滑、转折更少的路径，验证了其在复杂动态环境中的高效性和工程可行性。该方法平衡了路径最优性、平滑性与实时避障需求之间的关系，为机器人自主导航提供了可靠的解决方案。

6 未来展望

后续，作者将结合具体应用场景进一步优化算法性能，推进其在具体应用场景的实用化进程。目前，动态权重系数是基于障碍物密度调整的，未来可结合机器学习方法，使权重随环境复杂度自适应变化，以进一步提升规划效率。在仓储、物流等应用场景中，可将算法扩展至多机协同路径规划，解决避碰和任务分配问题。在DWA的评价函数中可引入能耗指标，优化机器人在长距离任务中的运动效率。针对非结构化环境（如野外、废墟），可结合3D点云数据增强算法的地形通用性。总之，最终目标是开发出一套能够广泛应用于各类复杂场景，具备高效、智能、可靠特性的路径规划算法，推动自主导航技术的发展。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.125

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王晨旭，熊智，杨闯.

未知复杂环境下基于兴趣驱动的类脑自主导航技术

［J］. 航空科学技术， 2024， 35（2）： 1-13.