近年来，软体机器人受到越来越多的关注，其凭借卓越的柔顺性和安全性，被广泛应用于复杂环境以执行各类危险任务^[1]。与传统的刚性机械臂相比，软体机械臂在面对各种环境因素限制时展现出独特优势^[2]。在软体机械臂执行任务时，获取其连续的位姿信息至关重要。冗余自由度使软体机械臂具备良好的环境适应能力^[3-5]，但也使其形状信息的准确获取与空间运动参数的精确测量面临巨大挑战。

在软体机械臂形状信息获取方面，大多数研究采用分段常曲率（piecewise constant curvature, PCC）假设^[6]。对于弯曲程度不大、结构简单的软体机械臂，PCC假设模型能够较准确地估计出其形状^[7]，因此该假设在软体机械臂运动学建模中得到了广泛应用。然而，对于弯曲程度大、存在相互交错或部分遮挡的软体机械臂，基于PCC假设的形状估计误差较大。在软体机械臂空间运动参数测量方面，常见的方法是嵌入兼容的柔性传感器^[8-9]。Llamosi等人^[10]提出了一种基于空间分辨软传感器的测量方法，可动态测量力的强度和方向。Song等人^[11]提出了一种通过电磁传感器测量柔性机器人长度、方向和位置的方法。相比于上述方法，基于视觉传感器的测量方法更适用于软体机械臂，视觉传感器无需安装在软体机械臂上，测量成本更低且更便捷、快速^[12]。例如：Marchese等人^[13]利用视觉传感器确定了软体机械臂的弯曲曲率；Xu等人^[14]在基于柔/索驱动的软体机械臂上实现了视觉伺服控制。虽然通过视觉传感器可以获取软体机械臂上关键点的三维位置信息，进而重构出其在三维空间中的形状，但视觉传感器受光线的影响很大，因此需要对整个软体机械臂的三维位置信息进行处理。对于一些结构复杂的软体机械臂，尤其是存在部分遮挡的情况下，仅凭视觉传感器的测量效果不是很理想。

为了实现对软体机械臂复杂形状的精确测量，参数化曲线模型被应用于软体机械臂的形状估计^[15-16]。Mbakop等人^[17]提出采用五次多项式P-H（Pythagorean-Hodograph）曲线建立软体机械臂的运动学模型；Gonthina等人^[18]提出了一种基于欧拉曲线的软体机械臂建模方法，该方法的精度较高，但计算过程较为复杂；Ma等人^[19]提出了一种基于贝塞尔（Bézier）曲线的形状估计方法，解决了体积较小的软体机械臂的形状估计问题，只需少数控制点即能获取机械臂的形状，计算较为便捷，但是贝塞尔曲线的每个控制点都会影响曲线的形状，即改变任意一个控制点的位置都会导致整条曲线的形状发生改变。相比之下，B样条曲线能够很好地解决这一问题。B样条曲线中的控制点仅影响曲线的小部分形状，这意味着在进行局部修改时，B样条曲线具有更高的灵活性^[20-22]。

基于此，本文提出了一种基于双目视觉和B样条曲线的软体机械臂几何参数测量方法。首先，利用双目视觉系统捕获软体机械臂上预设标记点的三维坐标。然后，基于这些三维坐标数据，利用最小二乘法^[23]求解出B样条曲线的最优控制点，并根据这些控制点拟合得到软体机械臂的空间姿态。由于B样条曲线的构造仅需少量控制点，使得本文方法只需获取软体机械臂部分标记点的三维坐标，即可重构出其完整的三维形态。此外，即使在软体机械臂的某些部位因遮挡而无法采集相应数据的情况下，本文方法仍能够保持测量的连续性和准确性，不会对整体的几何参数测量造成影响。最后，对拟合得到的B样条曲线进行参数化处理，利用数学几何关系计算出曲线上任意点的曲率和弯曲角度，从而实现对软体机械臂各点的几何参数测量。本研究旨在为软体机械臂几何参数的测量提供一种新思路，从而为其后续的设计、控制和性能评估奠定理论基础。

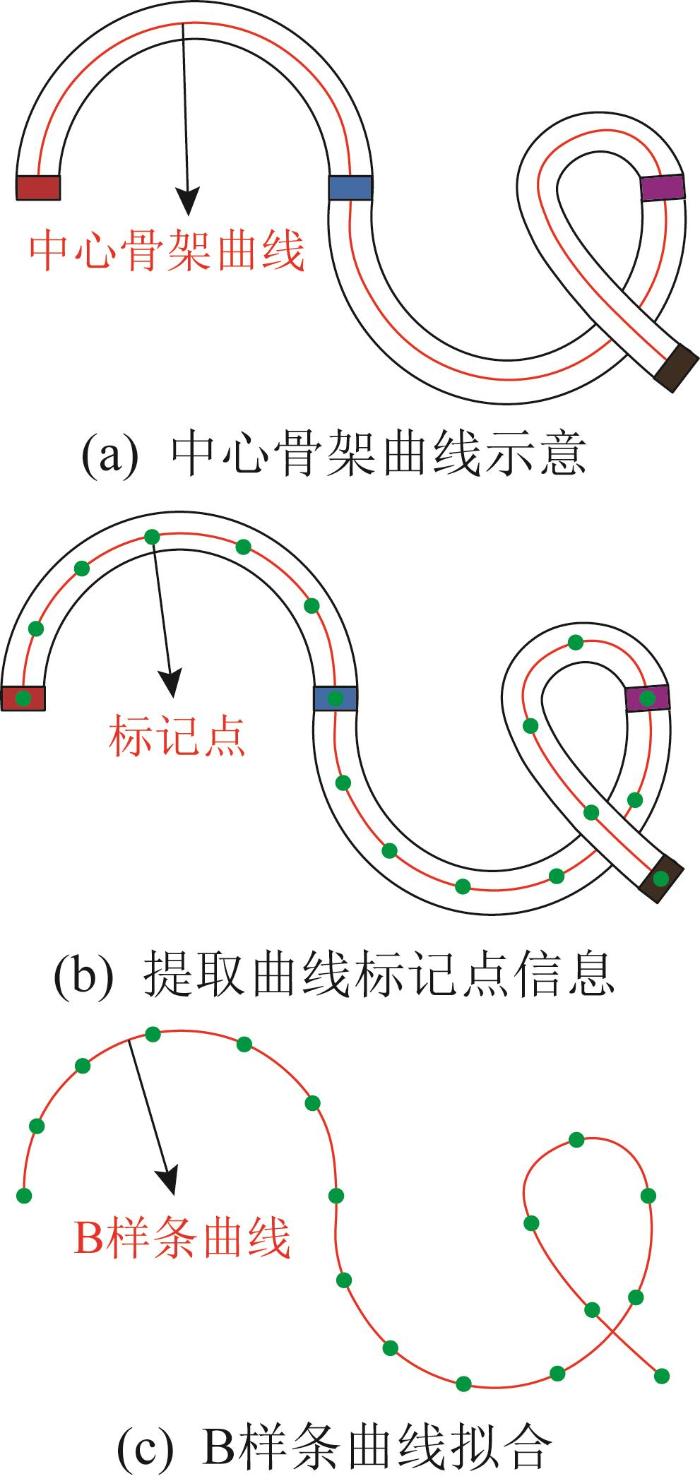
软体机械臂具有冗余自由度且形态变化复杂，其在运动过程中弯曲幅度大且相互交错，如图1(a)所示，这会导致其几何参数的测量变得十分困难。软体机械臂的空间运动主要由其中心骨架的姿态决定，通过中心骨架的姿态可以描绘出整个软体机械臂的姿态。基于此，为了简化软体机械臂的形状测量过程，利用中心骨架曲线来表示机械臂的形状。通过测量中心骨架的姿态，可间接测量整个软体机械臂的姿态，从而实现其几何参数的测量。

如图1(b)所示，软体机械臂的中心骨架曲线由一系列中心骨架点组成。为了获取这些中心骨架点的三维坐标信息，采用双目视觉系统进行数据采集与处理。在实际应用中，由于软体机械臂在三维空间中的运动姿态复杂，在未装载其他传感器的情况下，仅使用双目视觉系统无法获取所有中心骨架点的完整信息。为了解决这一问题，提出了基于少数标记点的曲线拟合方式来获取近似的软体机械臂中心骨架姿态，通过在中心骨架上添加几个有颜色的标记点，来简化坐标信息的获取过程。如此，只需获取这些标记点的坐标信息，即可实现对软体机械臂中心骨架曲线的拟合。

由于只获取了有限的标记点坐标信息，因此对曲线拟合的精度提出了更高的要求。尤其是在三维空间中，拟合曲线需要在仅有少数点的情况下精确地反映出软体机械臂中心骨架点的空间位置。B样条曲线拟合方法具备卓越的拟合性能，其能够提供连续光滑的拼接，且具有凸包性、自然连续性、局部修改不变性等特点。如图1(c)所示，仅需几个标记点，B样条曲线就能精确地逼近实际的中心骨架曲线，从而确保最终测量结果的准确性和可靠性。

通过B样条曲线拟合，不仅能够实现对软体机械臂中心骨架形状的重构，还能进一步提取得到中心骨架曲线上每个点的几何特征（如弯曲角度和曲率）。为了获取软体机械臂的几何参数，对重构得到的中心骨架曲线进行参数化处理。通过参数化处理，可以计算曲线上各个点的弯曲角度和曲率等，这可为软体机械臂几何参数的测量提供一种有效的方法。

基于上文研究思路，软体机械臂几何参数的测量过程包括3个关键步骤：中心骨架点三维坐标信息的获取、中心骨架形状重构以及中心骨架曲线参数化计算。在三维坐标信息获取阶段，通过在软体机械臂的中心骨架上附着特定标记，并运用双目视觉系统对这些标记点进行捕捉和处理，以获得中心骨架点的三维坐标。随后，进入形状重构阶段，根据所获取的中心骨架点的三维坐标，采用B样条曲线对中心骨架的形状进行三维重构。在参数化计算阶段，先对重构得到的中心骨架曲线进行参数化处理，再根据参数化曲线方程计算出中心骨架的几何参数。

在双目视觉系统中，双目相机拍摄的软体机械臂中心骨架图像是二维的。为了从二维图像中提取得到中心骨架点的三维坐标信息，必须进行精确的相机标定。标定步骤是实现像素坐标到世界坐标转换的关键环节。本文采用经典的“张氏标定法”来完成相机标定，通过左右相机拍摄标准棋盘格图案，如图2所示，以捕获一系列角点的像素坐标(u,v)和对应的世界坐标(X,Y,Z)。

基于所获取的像素坐标和世界坐标，利用投影模型来求解双目相机的内外参数，如式(1)所示。其中：内参数描述了相机镜头的畸变和焦距，外参数描述了相机在世界坐标系中的位姿。内外参数的准确获取是构建精确相机模型的基础。

式中： K 为相机的内参数矩阵； R 为旋转矩阵， T 为平移矩阵， R 和 T 组成相机的外参数矩阵；内外参数矩阵的乘积组成相机的投影矩阵。

同时，采用重投影误差这一指标来评估所获取的软体机械臂中心骨架点的位置精度。重投影误差是评价双目视觉系统精度的关键指标，它衡量了三维坐标点经相机模型投影回二维图像后的像素坐标与实际观测到的像素坐标之间的偏差。重投影误差E的数学表达式为：

式中：h为棋盘标靶数，m为标靶上的角点数，D_ab （a=1, 2, …, h，b=1, 2, …, m）为各角点的实际投影坐标与理论投影坐标之间的欧几里得距离。

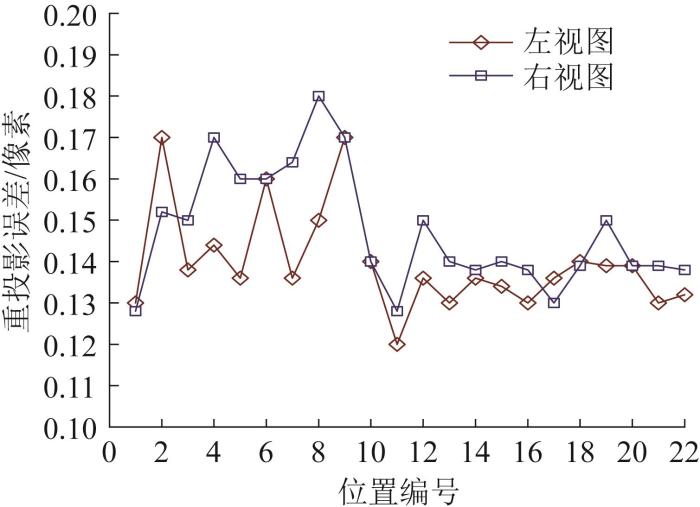
在本文的标定实验中，双目相机共采集了22组不同姿态的标定板图像。根据各角点的坐标，利用式(2)计算重投影误差，结果如图3所示。结果显示，双目相机左右视图的平均重投影误差为0.14像素，说明该双目视觉系统对软体机械臂中心骨架点位置的测量精度符合要求。

在完成相机标定后，可得到左、右相机的内参数矩阵Kl和Kr，以及外参数矩阵R和T。根据这些参数矩阵，利用式(1)将双目相机获取的软体机械臂中心骨架标记点的二维像素坐标转换为世界坐标系下的三维坐标。其中，左、右相机的内参数矩阵Kl和Kr以及外参数矩阵R和T可分别表示为：

在完成软体机械臂中心骨架标记点的三维坐标信息采集后，利用这些数据点进行中心骨架形状重构，旨在对软体机械臂在三维空间中的复杂运动轨迹进行精确建模。考虑到软体机械臂在三维空间中的复杂运动特性，需要选择一种能精确反映其形状变化的拟合方法。

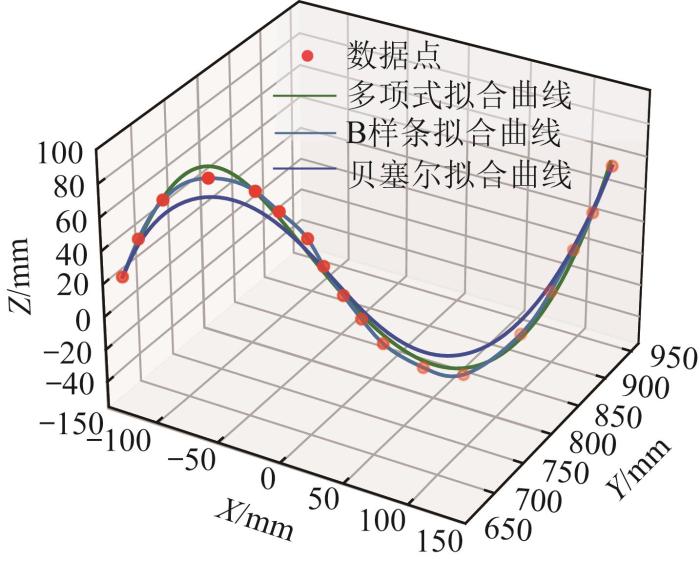
为了验证B样条曲线拟合方法的合理性，对3种常用的拟合方法（多项式曲线拟合、贝塞尔曲线拟合和B样条曲线拟合）进行了对比分析。基于上述3种拟合方法的软体机械臂中心骨架形状重构结果如图4所示。其中：多项式曲线的阶数为5，贝塞尔曲线和B样条曲线的阶数为3。

图4结果显示，由于贝塞尔曲线受每一个控制点的影响，低阶贝塞尔曲线在处理三维数据点时存在局限性，难以准确重构出软体机械臂中心骨架的形状。多项式曲线需要更高的阶数才能近似重构出软体机械臂中心骨架的形状，而更高的曲线阶数意味着后续软体机械臂几何参数的计算更加复杂困难。由此可知，贝塞尔曲线和多项式曲线在拟合精度上存在局限性，尤其是在处理复杂的三维数据点时，这2种拟合方法重构出的软体机械臂中心骨架形状与实际形状存在一定差距。相比之下，B样条曲线拟合的优势显著，即使是在较低的曲线阶数下，其仍能平滑地通过每个标记点，可为软体机械臂的形态提供一种高精度且连续的近似表示。综合考虑，B样条曲线拟合方法在精确性、平滑性和计算效率方面具有显著优势，适用于软体机械臂中心骨架形状的重构。

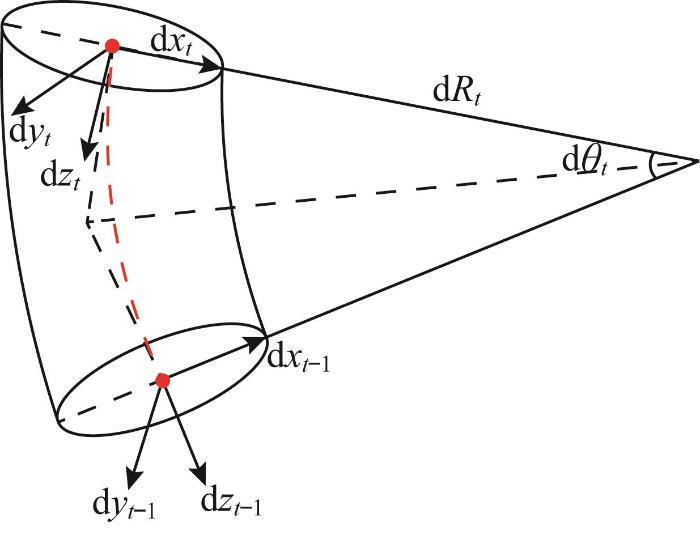
在分析软体机械臂的运动特性时，其姿态的精确测量至关重要。软体机械臂的运动主要表现为弯曲、伸长和扭转，因此弯曲角度和弯曲曲率成为评估其姿态的关键几何参数。通过对拟合得到的B样条曲线进行微分运算，可计算得到软体机械臂中心骨架曲线上各微分单元的几何参数，包括弯曲角度和弯曲曲率。如图5所示，设(dxt,dyt,dzt)和(dxt-1,dyt-1,dzt-1)为B样条曲线上2个微分单元对应的坐标点，dθt为这2个微分单元之间的弯曲角度，dRt为该区间的弯曲曲率半径。

B样条曲线的构建基于一组控制点和相应的基函数^[24]，其数学表达式为：

式中：{d0,d1,…,dn}为n+1个控制点，Ni,k(u)为基函数，k为曲线阶数，u为B样条曲线参数方程非递减的节点值。

控制点di是通过最小二乘法从软体机械臂中心骨架的实际数据点中优化得到的，而基函数Ni,k(u)通过将B样条曲线节点值代入Cox-de Boor公式递推得到的。

考虑到软体机械臂弯曲形态变化的复杂性，传统的B样条曲线拟合方法（节点均匀分布）可能无法充分捕捉其形态特征。因此，采用弦长分布节点方法，该方法可根据数据点之间的实际距离动态调整节点值，使得B样条拟合曲线更加贴合软体机械臂中心骨架的真实形态。弦长分布法的数学表达式如下：

式中：li为数据点间的实际距离；xt、yt、zt为通过双目视觉系统获取的中心骨架标记点的三维坐标；t为位置参数，t∈0,1，软体机械臂首端与末端的位置分别对应t=0和t=1；C为总弦长，C_i 为第i个点对应的弦长。

将软体机械臂中心骨架标记点的三维坐标数据代入式(4)，以计算各节点值。随后，利用式(5)递推得到B样条曲线的基函数，并运用最小二乘法确定控制点。将这些控制点和对应基函数代入式(3)，得到B样条曲线方程。

为了计算中心骨架曲线上各点的几何参数，对B样条曲线进行参数化处理。参数化后的非均匀B样条曲线方程可以表示为：

式中：wi为当前支撑区间对应的权因子，Mi为系数矩阵。

软体机械臂中心骨架的空间弯曲曲率K可通过曲线上任意一点的切向量变化率来定义，即该点处切向量的导数与切向量模长的比值，具体计算公式如下：

对于软体机械臂在三维空间中的弯曲角度θ，可通过曲线上任意一点的法向量的变化率来定义：

为了验证本文所提出的测量方法的可行性及准确性，搭建了双目视觉测量装置，用于测量软体机械臂的几何参数。该装置由三部分构成：软体机械臂、双目相机以及执行视觉测量算法的计算机，具体配置如图6所示。其中，双目相机的基线长度设为60 mm，焦距为3.4 mm。采用卷帘快门模式的相机能够实现60帧/s的实时深度图像采集。双目相机通过USB（universal serial bus，通用串行总线）接口与计算机相连，可实现高效的数据传输和串口通信。在计算机端运行的上位机软件负责接收双目相机捕获的软体机械臂中心骨架各标记点的三维坐标信息，并对其进行进一步处理。

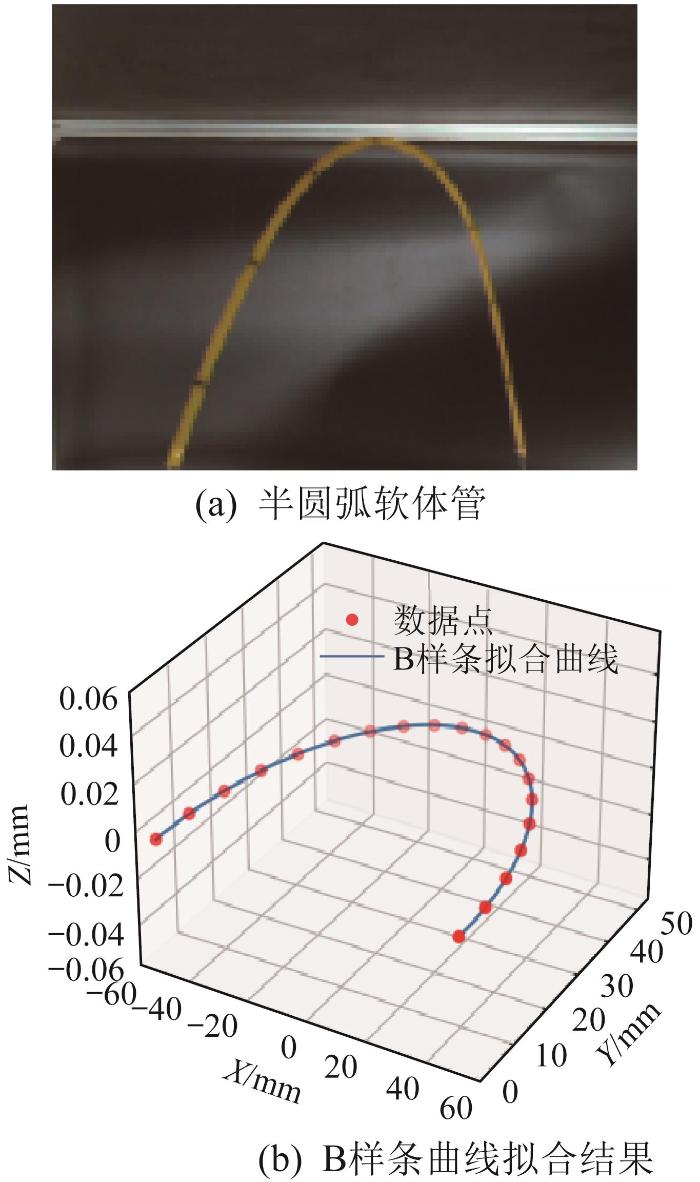
为了验证所提出的方法在平面几何参数测量中的准确性，对在平面上弯曲成圆弧形的软体机械臂进行测量实验。由于圆弧上各点具有一致的曲率特性，通过对比测量值与理论值，能够有效评估本文方法在平面测量中的精确度。考虑到软体机械臂在实际操作中难以弯曲成标准的圆弧形，选择半径为50 mm的半圆弧软体管代替软体机械臂，并在其表面标注了用于测量的标记点，如图7(a)所示。根据所提出的方法，通过双目视觉系统对半圆弧软体管中心骨架上各标记点的三维坐标数据进行采集与处理。随后，利用B样条曲线对这些数据进行拟合，实现对半圆弧软体管形状的重构，如图7(b)所示。结果显示，基于B样条曲线重构得到的半圆弧形状与实际半圆弧软体管的形状一致。

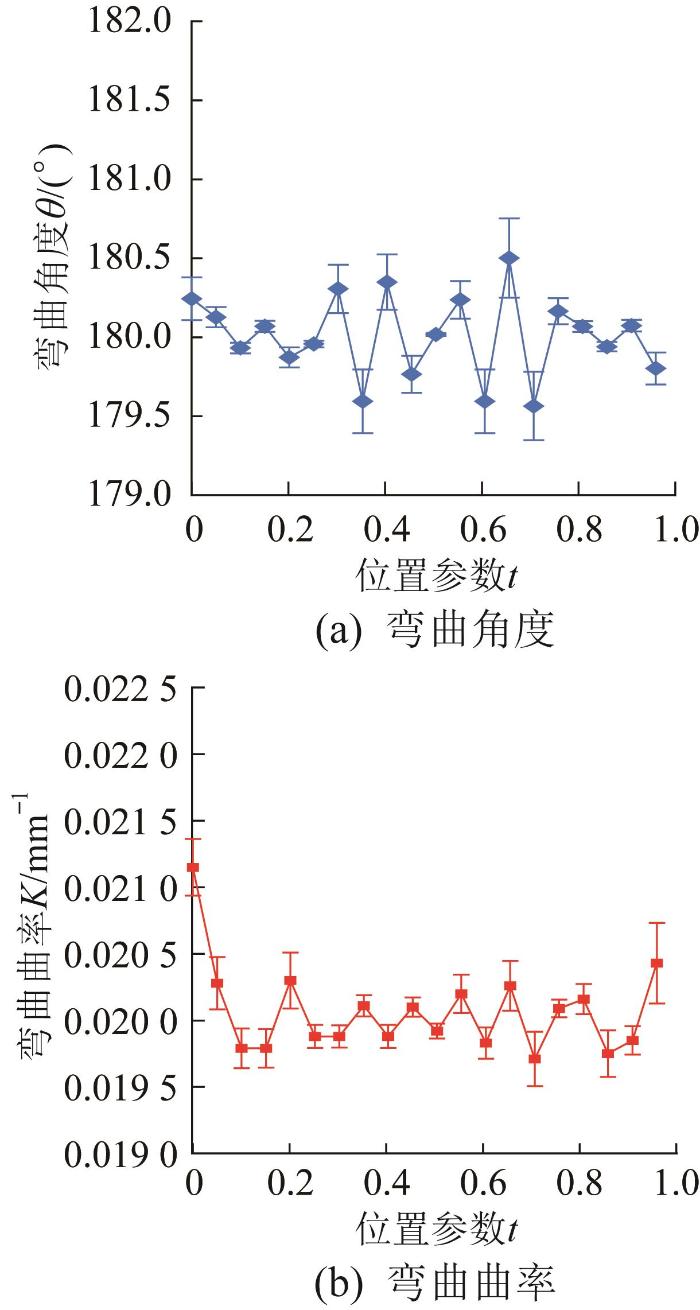
在完成半圆弧软体管形状重构后，对拟合得到的B样条曲线进行参数化处理，同时从软体管的首端到末端选取20个等间距的位置，并对这些位置的弯曲角度和弯曲曲率进行测量，结果如图8所示。由图8可知，测量得到的软体管的弯曲角度和弯曲曲率分别在180°和0.02 mm^-1附近上下波动，其中：平均弯曲角度误差为0.159%，平均弯曲曲率误差为0.198%。结果表明，该方法在平面几何参数测量上是可行的，既能准确地重构出软体机械臂的形状，又能保证测量结果与真实值接近。

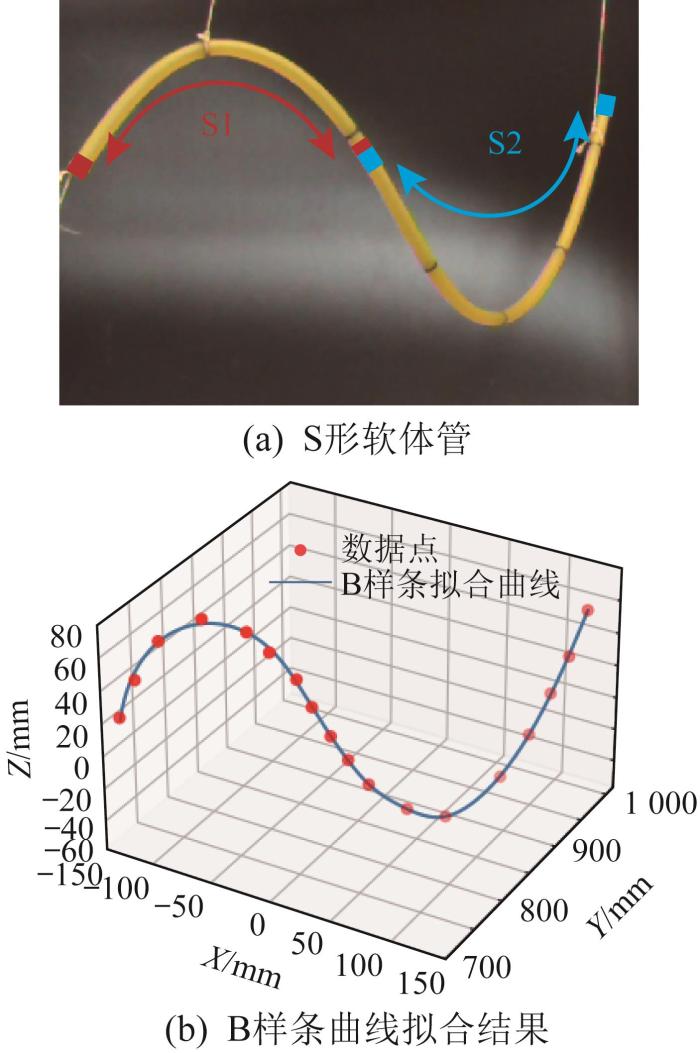
为了验证所提出的方法对空间几何参数测量的准确性，对在三维空间中弯曲成S形的软体机械臂进行测量实验。同样，为了便于测量，采用S形软体管作为测量对象，如图9(a)所示。利用所提出的方法，获取S形软体管中心骨架各标记点的三维坐标数据，并对S形软体管进行三维形状重构，结果如图9(b)所示。结果显示，重构形状与实际S形软体管的形状相吻合。

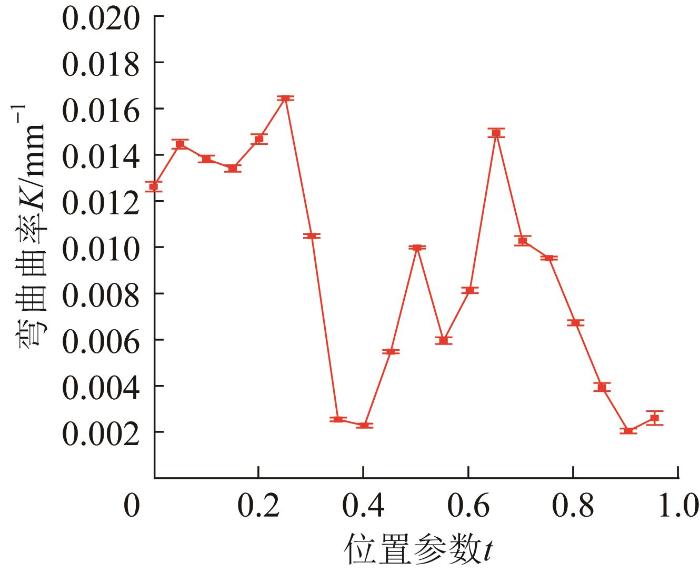
同理，对拟合得到的B样条曲线进行参数化处理（同样在软体管上取20个等间距的位置），计算得到S形软体管上各标记位置的弯曲角度和弯曲曲率，结果如图10所示。从图10中可以看出，软体管弯曲程度较大的区域对应的弯曲曲率较高，且整体的弯曲曲率变化与软体管的实际弯曲趋势吻合。由于实验用软体管是一个由上凸和下凹形状特征明显的S1和S2两部分构成的S形结构，为了进一步评估本文测量方法的准确性，对两部分的弯曲角度进行详细测量，并将测量结果与实际弯曲角度进行对比，结果如表1所示。

表1结果显示，对于在三维空间中运动的软体机械臂，本文所提出的方法也能够有效地进行几何参数测量，且测量误差保持在较小限度内。结果表明，所提出的方法不仅适用于平面测量，也适用于分析软体机械臂在三维空间中的复杂运动和形状变化。

为了进一步验证所提出的方法在动态测量中的适用性，对处于连续运动状态的L形软体机械臂进行测量实验。通过将软体机械臂的运动过程时间离散化来确保测量方法的有效性。在测量实验中，双目相机的配置为每秒捕获一帧图像，以确保对软体机械臂连续运动的准确记录。图11所示为T=0, 1, 2, 3, 4, 5 s六个时刻下双目相机捕获的软体机械臂姿态（机械臂上预先添加了不同颜色的标记点）。

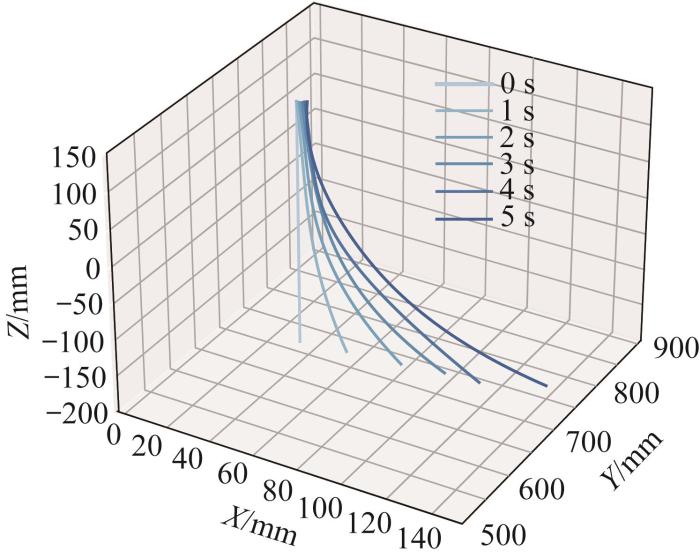
根据不同时刻下各标记点的三维坐标信息，对每个时刻下的L形软体机械臂姿态进行三维形状重构，结果如图12所示。通过形状重构，可以观察到软体机械臂随时间变化的运动姿态。实验结果验证了本文所提出的测量方法能够在时间离散化的基础上有效地对运动中的软体机械臂进行形状重构，并捕捉其运动姿态的动态变化。

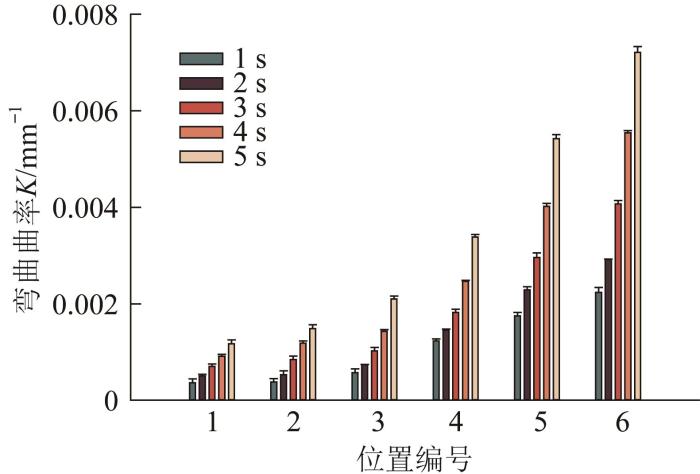
为了深入分析L形软体机械臂的动态弯曲特性，选取6个具有代表性的测量位置（如图11中编号所示），并对这些位置处随时间变化的弯曲曲率进行测量。图13所示为5个时刻下L形软体机械臂各测量位置处的弯曲曲率。结果显示，不同位置处的弯曲曲率与机械臂的实际弯曲趋势一致，且在弯曲程度较大的区域，所测得的弯曲曲率的变化幅度也较大。

上述实验结果进一步证明了本文所提出的方法具有适用性：不仅能够对静态的软体机械臂进行精确测量，还能够对连续运动的软体机械臂进行有效的动态测量。

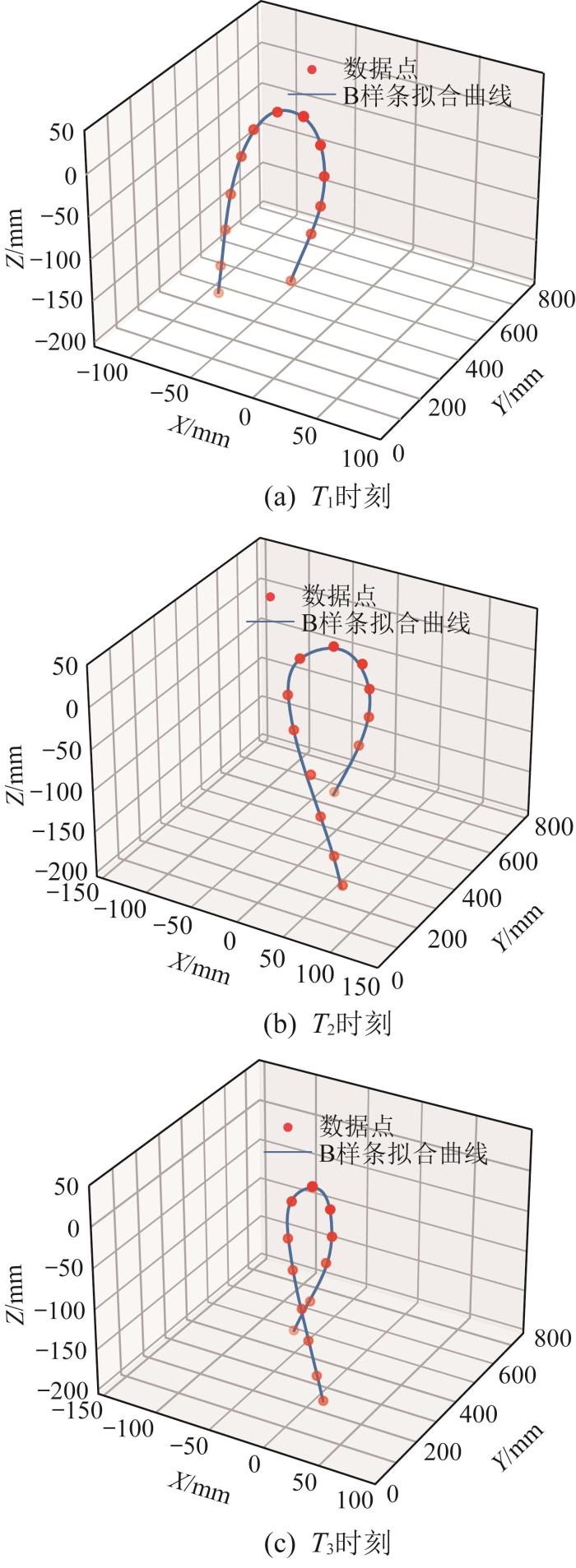
为验证所提出的方法在软体机械臂运动时出现自身遮挡场景下的测量可行性，对含部分遮挡的软体机械臂进行测量实验。同样，为便于测量，采用软体管代替软体机械臂。图14所示为双目相机捕获的T₁、T₂和T₃三个不同时刻下（随机选取3帧图像）软体管的姿态。从图14中可以看出，在T₃时刻，软体管相互交错，导致一部分区域出现了视觉遮挡。但本文方法并不依赖软体管上所有点的视觉信息，主要是利用关键标记点的三维坐标来实现形状重构。利用本文方法对不同时刻下软体管的姿态进行三维形状重构，结果如图15所示。结果显示，即使存在部分视觉遮挡，本文方法仍可利用未被遮挡处的三维坐标信息重构出软体管的形状。

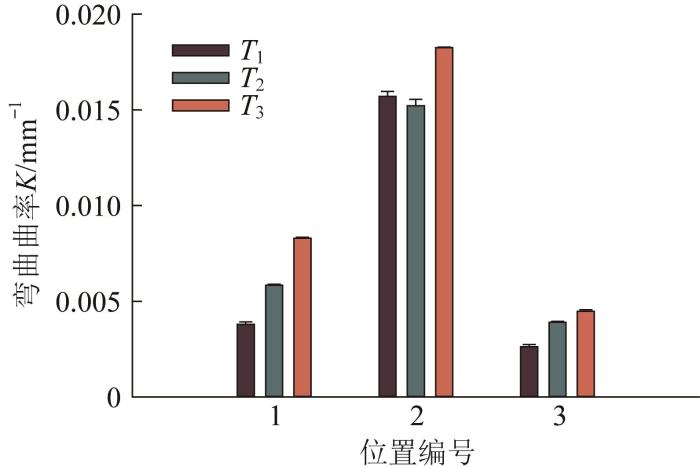
随后，对这3个时刻下软体管上具有明显特征的3个位置（如图14中编号所示）处的弯曲曲率进行了测量，结果如图16所示。测量结果显示，所测得的弯曲曲率变化趋势与软体管的实际弯曲趋势几乎完全吻合，进一步验证了所提出的方法在处理复杂运动形态测量问题上的鲁棒性与有效性。即使在视觉信息不完整的情况下，该方法仍能够实现对软体机械臂空间形状的准确重构以及关键位置处几何参数的精确测量。

本文提出了一种适用于形态变化复杂的软体机械臂的几何参数测量方法。该方法通过双目视觉系统获取软体机械臂中心骨架点的三维坐标信息，采用B样条曲线对中心骨架进行形状重构，并通过对曲线进行参数化处理来计算软体机械臂的弯曲角度和弯曲曲率等，从而实现其几何参数的准确测量。在多种复杂情况下，通过实验验证了该测量方法的适用性和准确性。在平面运动测量实验中，对弯曲成圆弧形的软体机械臂进行了测量，验证了所提出方法在平面测量中的有效性。在空间运动测量实验中，对于弯曲成S形的软体机械臂进行了测量，测量得到的弯曲角度和弯曲曲率与实际值非常接近，验证了所提出方法在空间测量中的有效性。在动态测量实验中，通过将软体机械臂的运动时间离散化，实现了对连续运动的软体机械臂的形状重构及弯曲曲率动态测量。结果表明，即使在动态运动过程中，本文方法也能够准确地重构软体机械臂的形状，并近似获取其弯曲曲率随时间的变化情况。在存在部分视觉遮挡的测量实验中，所得结果展示了本文方法在部分视觉信息缺失的情况下仍能够利用未被遮挡的特征标记点进行准确的形状重构和几何参数求解，这意味着即使在复杂或视野受限的环境中，该方法也能够实现准确、可靠的几何参数测量。综上所述，基于双目视觉和B样条曲线的测量方法为软体机械臂几何参数的测量提供了一种高效、准确的解决方案。未来的工作将聚焦于进一步提高测量精度、优化计算效率以及扩展方法适用范围等方面，以满足更广泛的应用需求。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.04.156