柔性铰链是一种依靠材料的弹性变形来传递运动和力的特殊运动副。相较于传统的刚性铰链，柔性铰链具有体积小、无间隙、无摩擦、成本低廉且无需润滑等优点。这些特性使得柔性铰链能够实现高精度运动，其被广泛应用于微机电系统、精密机械和精密测量等领域。根据转轴数量的不同，柔性铰链可分为单轴、双轴和多轴三类。多轴柔性铰链具有多个自由度，其中常见的为圆缺口型多轴柔性铰链，可用于空间柔顺精密定位机构。在柔顺机构运动过程中，柔性铰链主要承受变形和应力。对于大行程柔顺机构，柔性铰链需承受更大的变形，且易因应力过大而失效。因此，需要探索并设计新型的多轴柔性铰链，使其在一定应力约束条件下能够实现更大角度的运动，以提高综合性能。

现阶段，众多学者设计了不同缺口形状的柔性铰链，并对其柔度、精度和柔度精度比等性能进行了建模分析与研究。Paros和Weisbord ^[1]对圆弧型柔性铰链进行了理论建模研究。Lobontiu等^[2]基于卡式第二定理，通过有限元仿真对比了不同圆锥曲线型柔性铰链的柔度和精度，结果显示：椭圆型柔性铰链的柔度更好，而双曲线型柔性铰链的精度更高。Li等^[3]设计了幂函数型柔性铰链，并基于单位载荷法推导了其柔度和精度模型，通过对比幂函数型、直圆型和V型柔性铰链，发现幂函数型柔性铰链具有更高的精度。Gong等^[4]基于刚度矩阵法推导了抛物线型、角圆型和直圆型柔性铰链的柔度模型，并通过有限元仿真进行了验证，结果表明，所构建的柔度模型适用于具有复杂缺口形状的柔性铰链。Wang等^[5-6]提出了一种新颖的有限梁柔度矩阵建模（finite beam compliance matrix modeling, FBMM）法，并基于FBMM法构建了新型指数正弦型和混合不对称型柔性铰链的柔度和精度模型，同时利用有限元仿真验证了所构建的理论模型。Lin等^[7]提出了一种新型的角圆双曲线型柔性铰链，并采用卡式第二定理推导了其柔度和精度模型，该柔性铰链的柔度和柔度精度比均优于双曲线型柔性铰链。Chen等^[8]设计了椭圆弧倒角型柔性铰链，并基于材料力学变截面梁弯曲理论建立了其柔度和精度模型。Wei等^[9-10]设计了混合型多轴柔性铰链和椭圆截面型双轴柔性铰链，并推导了2种柔性铰链的柔度、精度和最大应力模型。Li等^[11-13]提出了三段混合型单轴、混合型单轴和混合型多轴柔性铰链，并利用柔度矩阵法建立了其柔度和精度模型。王传礼等^[14]设计了椭圆导角混合型柔性铰链，并以卡氏第二定理为基础推导了其柔度和精度模型，结果表明，该柔性铰链具有大柔度和低应力性能。Wang等^[15-16]设计了新型的正弦型柔性铰链和非对称二阶贝塞尔曲线型柔性铰链，与圆锥曲线型柔性铰链相比，所设计的2种新型柔性铰链均具有较大的柔度精度比。杨春辉等^[17]提出了一种圆弧型柔性球铰，并基于卡式第二定理推导了柔性球铰的柔度模型。Li等^[18]设计了幂三角函数型多轴柔性铰链，并基于卡式第二定理推导了其柔度和精度模型，与其他柔性铰链相比，所设计的柔性铰链具有更高的柔度精度比。谢超等^[19]设计了正交簧片型大行程柔性球铰，基于柔度矩阵法推导了其柔度模型，并利用有限元仿真和实验验证了柔度模型的准确性。Ling等^[20]基于传递矩阵法建立了单轴和多轴柔性铰链的柔度和精度模型，并通过与其他文献中的柔度和精度理论计算结果对比，验证了所提出方法的可行性。

由于现有柔性铰链在应对复杂载荷和大角度运动时，其最小厚度处容易因应力过大而失效，本文设计了一种新型的嵌套余弦函数型多轴柔性铰链。这一设计源于嵌套余弦函数的独特轮廓特性，嵌套余弦函数曲线的根部较厚，而中间部分相对较细。这种结构特性有助于分散复杂载荷下的应力，减少应力集中，降低柔性铰链的失效风险，从而使柔性铰链在相同应力约束下能够实现更大的柔性变形和更强的转动能力。本文将对所设计的新型柔性铰链进行详细的建模分析与研究。首先，利用FBMM法分别建立柔性铰链的柔度和精度模型；然后，通过有限元仿真分析来验证柔度和精度模型的有效性；接着，对不同结构参数下柔性铰链的性能进行分析与比较；最后，搭建柔性铰链实验平台并开展变形测量，以进一步验证柔度模型的有效性。

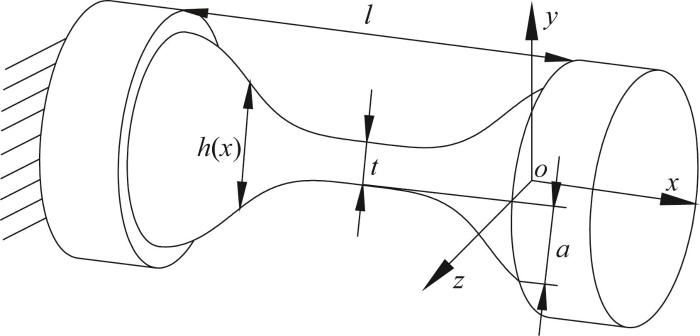
图1所示为嵌套余弦函数型多轴柔性铰链的结构（以柔性铰链自由端圆心o为原点构建坐标系）。图中：l为缺口长度，a为缺口深度，t为最小截面直径。该柔性铰链任意截面处的厚度h(x)可表示为：

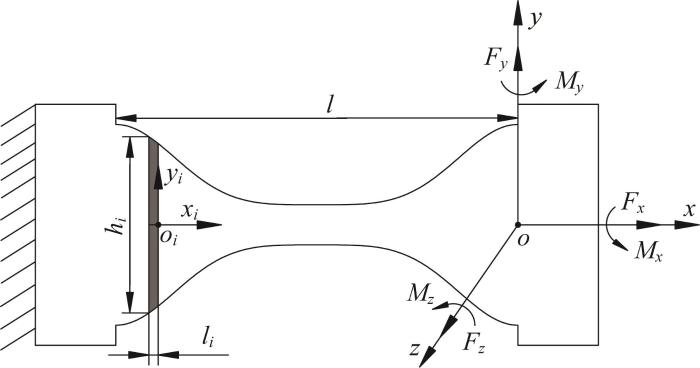
嵌套余弦函数型多轴柔性铰链的受力示意如图2所示。根据胡克定律和多轴柔性铰链的运动特点，该柔性铰链自由端点o处的位移与载荷的关系如下^[19]：

其中：

式中： Δ 为柔性铰链自由端点o处的变形， Δ =[Δx₁ Δy₁ Δz₁θ_xθ_yθ_z ]^T，其中，Δx₁、Δy₁、Δz₁分别表示点o处沿x、y和z方向的位移，θ_x 、θ_y 、θ_z 分别表示点o处沿x、y和z方向的转角； F 为柔性铰链自由端点o处的载荷， F =[F_xF_yF_zM_xM_yM_z ]^T，其中，F_x 、F_y 、F_z 和M_x 、M_y 、M_z 分别表示点o处所承受的力和力矩分量； C 为柔性铰链的柔度矩阵，其中，C_{x1, Fx} 、C_{y1, Fy} 、C_{z1, Fz} 、C_{y1, Mz} 、C_{z1, My} 、C_{θx, Mx} 、C_{θy, My} 、C_{θy, Fz} 、C_{θz, Fy} 和C_{θz, Mz} 表示柔度，即自由端点o处在载荷作用下的变形。

本文基于FBMM法对嵌套余弦函数型多轴柔性铰链进行柔度建模，该方法的基本原理是将柔性铰链切分为若干个串联的微型梁。则该柔性铰链的柔度矩阵可表示为：

式中： C_i 为第i个微型梁在其局部坐标系o_i-x_iy_iz_i 内的柔度矩阵， T_i 为第i个微型梁的局部坐标系o_i-x_iy_iz_i 相对于柔性铰链全局坐标系o-xyz的转换矩阵。

第i个微型梁的柔度矩阵 C_i 的具体表达式如下：

式中：E为材料的弹性模量，G为材料的剪切模量，l_i 、h_i 分别为第i个微型梁的长度和高度。

第i个微型梁对应的转换矩阵 T_i 可表示为：

其中：

式中： R_i 为第i个微型梁的局部坐标系o_i-x_iy_iz_i 相对于柔性铰链全局坐标系o-xyz的旋转矩阵；S(ri)为第i个微型梁的局部坐标系o_i-x_iy_iz_i 相对于柔性铰链全局坐标系o-xyz的位置变换矩阵，其中 r_i 表示原点o_i 在全局坐标系o-xyz中的位置向量， r_i=[x_iy_i z_i ]，多轴柔性铰链的位置向量 r_i=[x_i 0 0]； O 为三阶零矩阵。

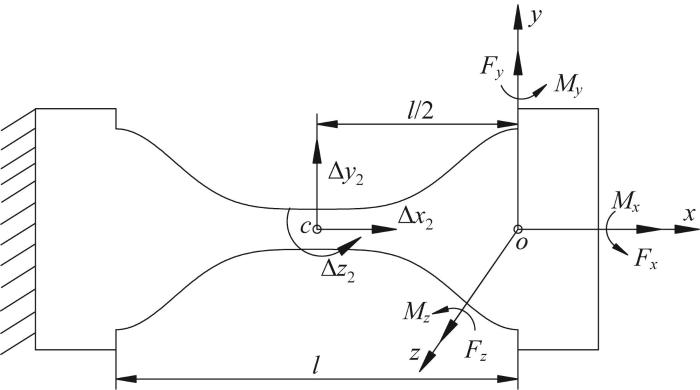
在理想情况下，柔性铰链的旋转中心不会随变形而发生移动。但在实际应用中，当柔性铰链承受载荷时，其旋转中心会不可避免地发生漂移。对于纵向和横向均对称的柔性铰链，其几何中心可看作旋转中心。为实现对柔性铰链旋转中心不漂移能力的评估，通常定义精度来表示柔性铰链约束旋转中心漂移的能力：漂移越大，精度越差。柔性铰链的精度可用其旋转中心的柔度来表示。在自由端载荷的作用下，嵌套余弦函数型多轴柔性铰链旋转中心的变形如图3所示。

根据图3，在自由端载荷 F 的作用下，该柔性铰链旋转中心c的位移 X 可表示为：

式中：Δx₂、Δy₂、Δz₂分别为旋转中心处沿x、y和z方向的位移。

则该柔性铰链旋转中心c的位移与自由端载荷的关系如下：

式中：C_{x2, Fx} 、C_{y2, Fy} 、C_{z2, Fz} 、C_{y2, Mz} 、C_{z2, My} 为柔性铰链旋转中心c处在自由端载荷作用下的柔度。

按上文分析，柔性铰链的精度矩阵可用其旋转中心的柔度矩阵 Θ 来表示。与自由端处柔度矩阵 C 类似，使用FBMM法进行建模，计算固定端到旋转中心的柔度，即可得柔度矩阵 Θ ：

式中：L₀为固定端到旋转中点的距离。

则可得：

式中： Θ (m, n)为柔度矩阵中第m行第n列的元素。

为了验证所构建的柔度和精度模型的有效性，使用ANSYS Workbench软件对嵌套余弦函数型多轴柔性铰链的柔度和精度进行有限元仿真。该柔性铰链的有限元模型如图4所示，其左端固定，在自由端施加如下载荷：F_x=F_y=1 N，M_z=0.01 N·m。网格尺寸设置为0.25 mm，并对柔性铰链缺口部分的网格进行加密处理。

柔性铰链的材料选择7075铝合金，其弹性模量E=71 GPa，泊松比μ=0.33。分别利用FBMM法和有限元仿真法求解柔性铰链的柔度和精度（N=1 000），共选取4组柔性铰链进行计算，具体尺寸参数如表1所示。

将4组柔性铰链的柔度和精度的理论值与仿真值进行对比并计算相对误差，结果如表2所示。分析表2可知，该柔性铰链柔度和精度的理论值与仿真值的最大相对误差分别为4.89%和4.97%，说明理论计算结果与有限元仿真结果的吻合度较高，验证了所构建的理论模型的有效性。

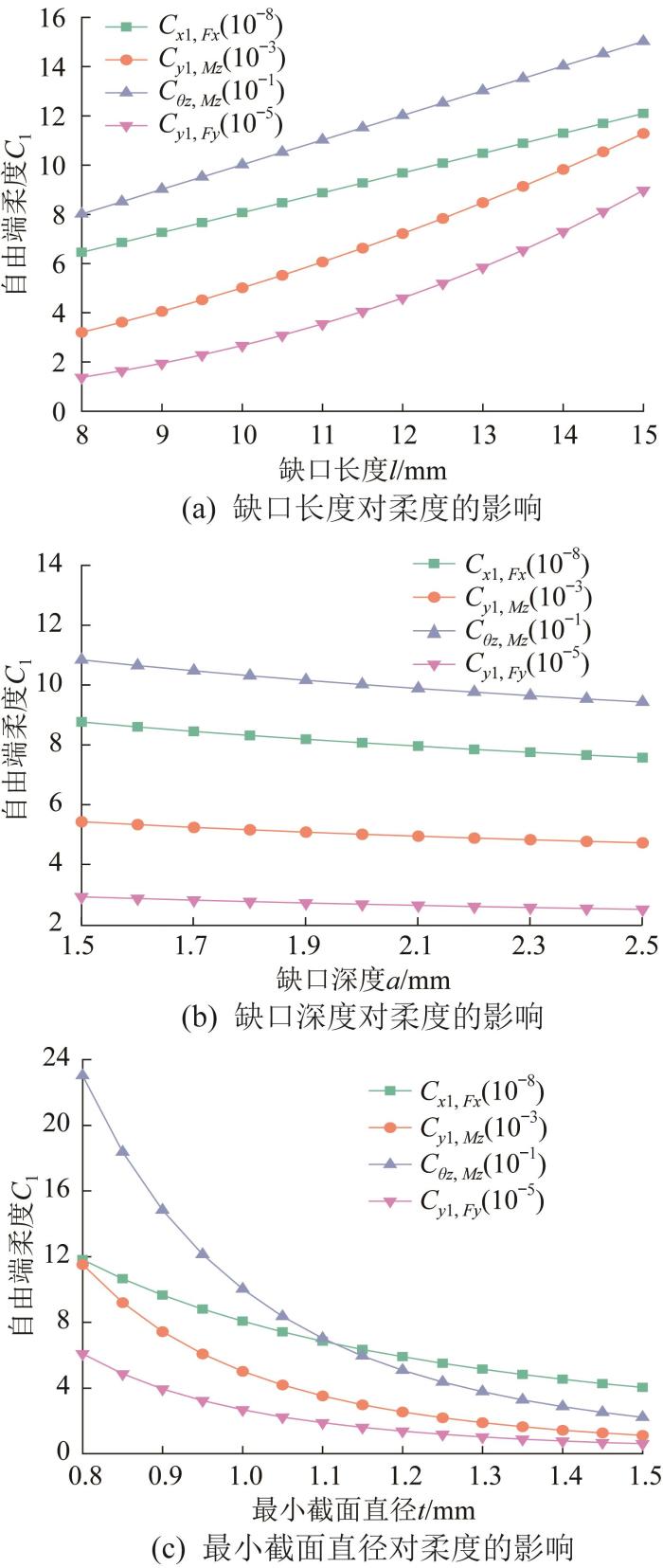
在设计柔性铰链时，柔度是一个重要的性能指标。柔性铰链的性能受材料和结构参数的共同影响^[21]。嵌套余弦函数型多轴柔性铰链的主要结构参数为缺口长度l、缺口深度a和最小截面直径t。采用控制变量法，分析各结构参数对该柔性铰链柔度的影响：1）分析缺口长度l的影响时，取l=8~15 mm，a=2 mm，t=1 mm；2）分析缺口深度a的影响时，取a=1.5~2.5 mm，l=10 mm，t=1 mm；3）分析最小截面直径t的影响时，取t=0.8~1.5 mm，l=10 mm，a=2 mm。根据不同条件下的分析结果，绘制柔性铰链柔度随结构参数的变化曲线，如图5所示。

由图5(a)可知，C_{x1, Fx} 、C_{θz, Mz} 、C_{y1, Mz} 、C_{y1, Fy} 随缺口长度l的增大而增大，其中C_{y1, Mz} 受l的影响最大。由图5(b)可知，C_{x1, Fx} 、C_{θz, Mz} 、C_{y1, Mz} 和C_{y1, Fy} 随缺口深度a的增大而减小，且递减速率较平缓。由图5(c)可知，C_{x1, Fx} 、C_{θz, Mz} 、C_{y1, Mz} 和C_{y1, Fy} 随最小截面直径t的增大而减小，其中C_{θz, Mz} 受t的影响最大。综上可知，最小截面直径对嵌套余弦函数型多轴柔性铰链柔度的影响最大。

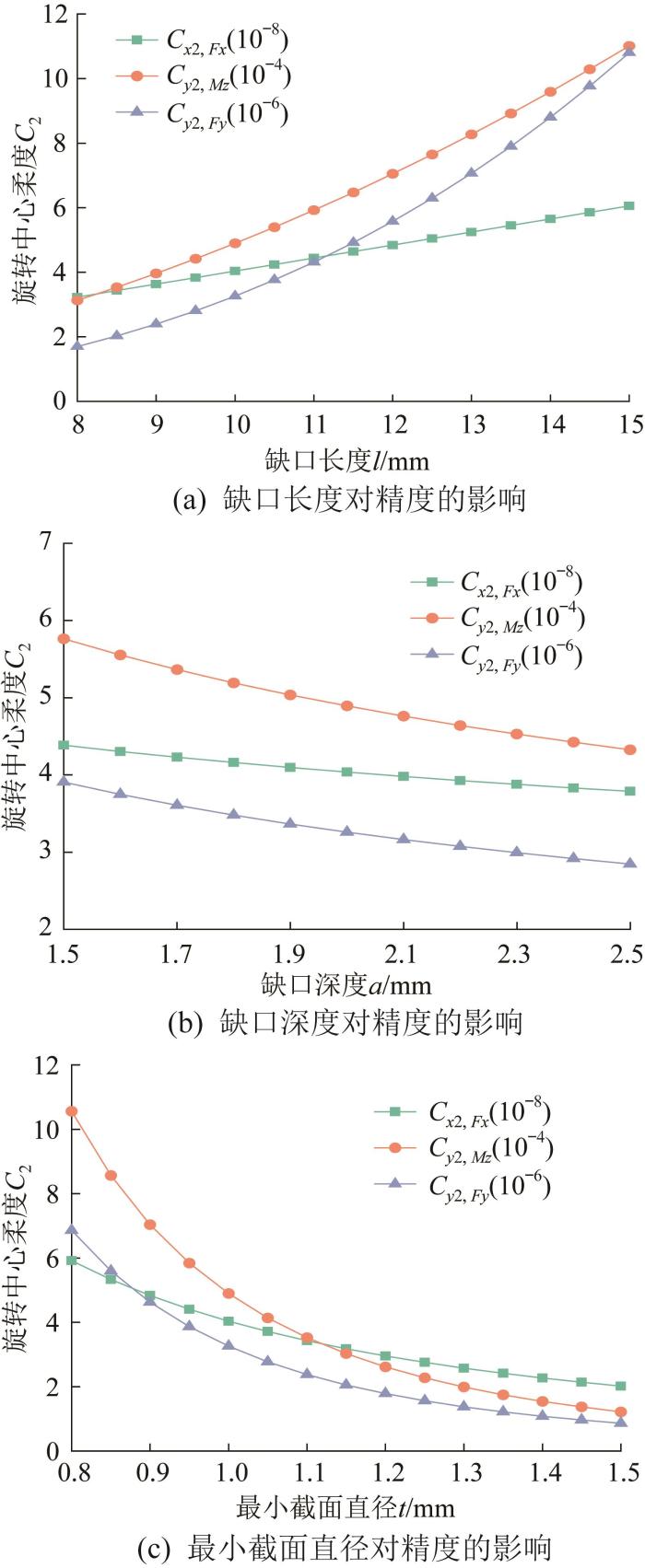
精度也是评估柔性铰链性能的一个重要指标。根据嵌套余弦函数型多轴柔性铰链的精度模型，可知其精度与缺口长度l、缺口深度a和最小截面直径t均有关。同样采用控制变量法，研究各结构参数对该柔性铰链精度的影响，结果如图6所示。图6(a)：l=8~15 mm，a=2 mm，t=1 mm；图6(b)：a=1.5~2.5 mm，l=10 mm，t=1 mm；图6(c)：t=0.8~1.5 mm，l=10 mm，a=2 mm。

由图6(a)可知，C_{x2, Fx} 、C_{y2, Mz} 、C_{y2, Fy} 随缺口长度l的增大而增大，其中C_{y2, Fy} 受l的影响最大。这是因为增大缺口长度会使柔性铰链旋转中心沿x、y方向的漂移量均增加，导致柔性铰链的精度降低。由图6(b)和图6(c)可知，C_{x2, Fx} 、C_{y2, Mz} 和C_{y2, Fy} 随缺口深度a和最小截面直径t的增大而减小。由此可知，增大缺口深度和最小截面直径可减小柔性铰链旋转中心沿x、y方向的漂移量，使得柔性铰链的精度提高。综合图6结果可知，最小截面直径对嵌套余弦函数型多轴柔性铰链精度的影响最大。

一般情况下，柔性铰链的柔度与精度的变化趋势相反，即柔度越大，精度越低。因此，在设计柔性铰链时，需要综合考虑柔度和精度。由于存在多个柔度和精度，为了有效评估柔性铰链的整体性能，定义整体柔度精度比β，表示为：

其中：

式中：C_1t为自由端圆心o处的整体柔度，C_2t为旋转中心c处的整体柔度。

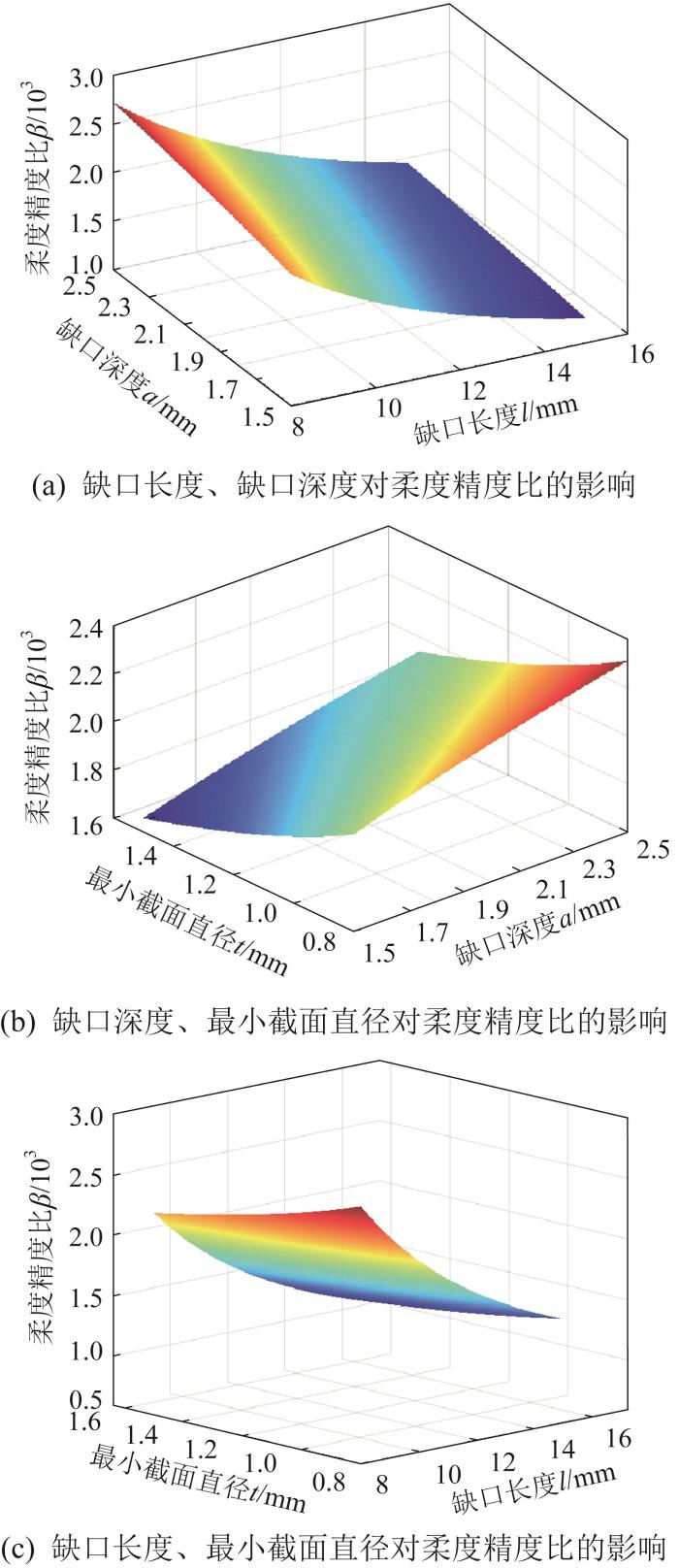
当柔性铰链具有相同柔度时，柔度精度比越大，说明其具有更高的精度。同样采用控制变量法，研究缺口长度l、缺口深度a和最小截面直径t对嵌套余弦函数型多轴柔性铰链柔度精度比β的影响：1）分析缺口长度l和缺口深度a的影响时，取l=8~15 mm，a=1.5~2.5 mm，t=1 mm；2）分析缺口深度a和最小截面直径t的影响时，取a=1.5~2.5 mm，t=0.8~1.5 mm，l=10 mm；3）分析缺口长度l和最小截面直径t的影响时，取l=8~15 mm，t=0.8~1.5 mm，a=2 mm。根据不同条件下的分析结果，绘制柔性铰链柔度精度比随结构参数的变化曲线，如图7所示。由图7可知，柔度精度比随缺口长度的增大而减小，随缺口深度的增大而增大，随最小截面直径的增大而减小。此外，综合所有结果来看，最小截面直径对柔度精度比的影响大于缺口长度和缺口深度，进一步说明最小截面直径对嵌套余弦函数型多轴柔性铰链性能的影响最大。

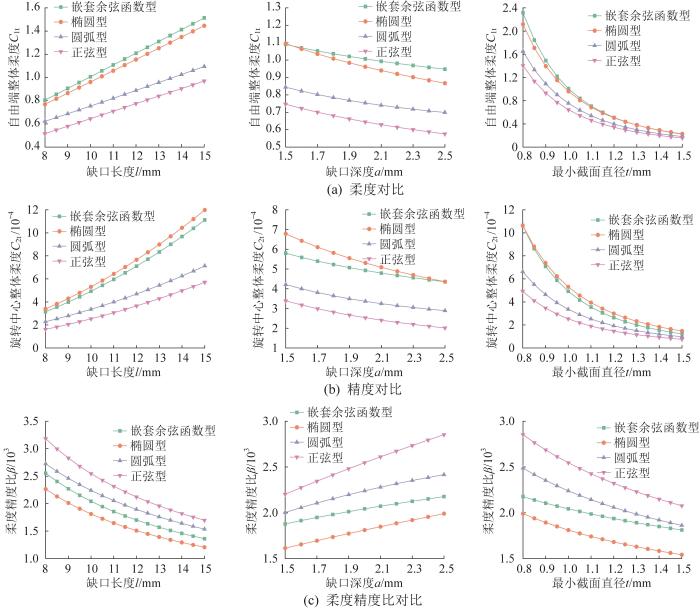
为了更深入分析嵌套余弦函数型多轴柔性铰链的性能，将其与椭圆型、圆弧型、正弦型多轴柔性铰链进行比较。在比较不同类型柔性铰链的性能时，结构参数均取以下3种情况：1）l=8~15 mm，a=2 mm，t=1 mm；2）a=1.5~2.5 mm，l=10 mm，t=1 mm；3）t=0.8~1.5 mm，l=10 mm，a=2 mm。4种柔性铰链的柔度、精度和柔度精度比随结构参数的变化情况如图8所示。由图8(a)可知，在保证缺口深度a与最小截面直径t不变的情况下，4种柔性铰链的柔度均随缺口长度l的增大而增大，精度随l的增大而减小，而柔度精度比随l的增大而减小。由图8(b)可知，在保证缺口长度l与最小截面直径t不变的情况下，4种柔性铰链的柔度均随缺口深度a的增大而减小，精度随a的增大而增大，而柔度精度比随a的增大而增大。由图8(c)可知，在保证缺口长度l与缺口深度a不变的情况下，4种柔性铰链的柔度均随最小截面直径t的增大而减小，精度随t的增大而增大，柔度精度比β也随t的增大而减小。

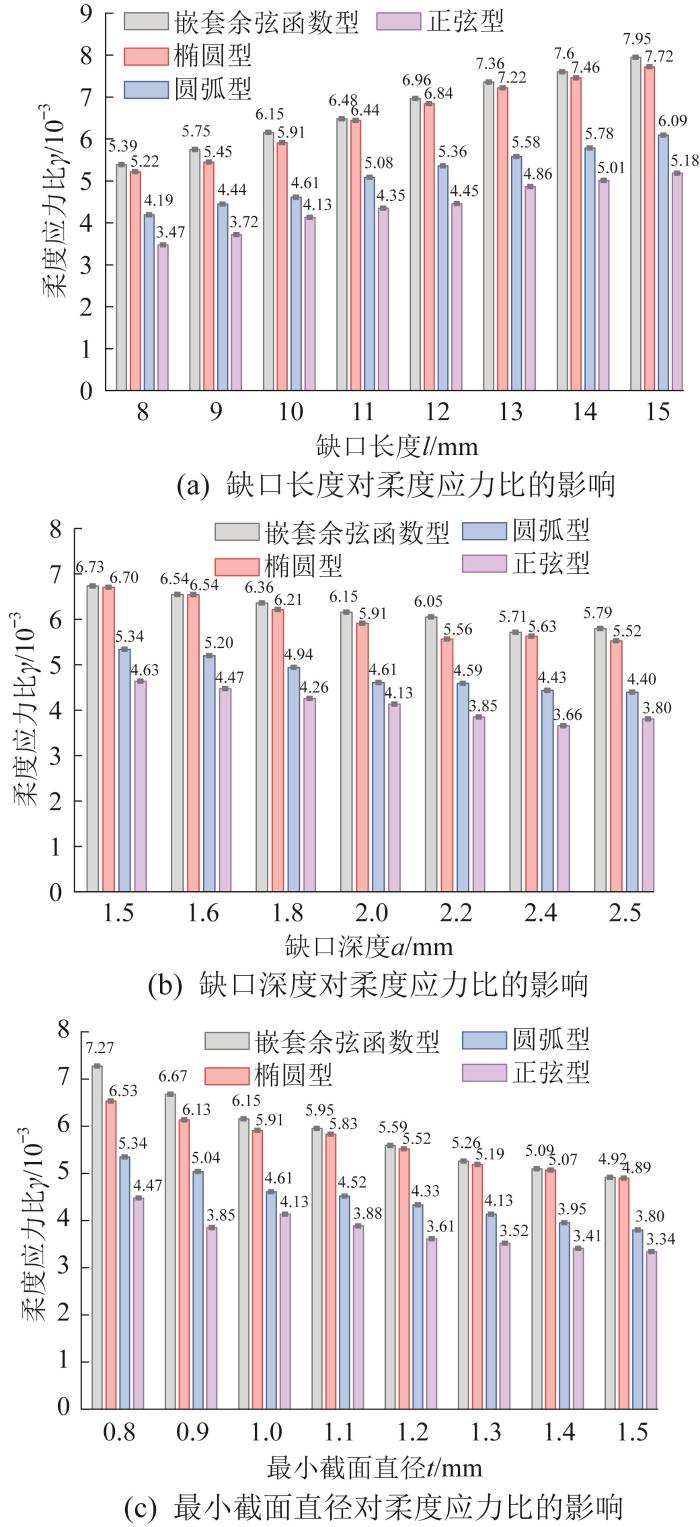
由于柔性铰链任意横截面内的应力主要由正应力和切应力组成，其中切应力通常较小，可忽略不计。此外，考虑到柔性铰链一端固定，另一端施加轴向力、纯弯矩和由末端横力引起的弯矩的组合载荷，其最大正应力出现在缺口最薄处的外表面。通过有限元仿真分别得到不同结构尺寸下4种柔性铰链的最大正应力，并计算不同结构尺寸下柔性铰链自由端圆心处整体柔度与最大正应力的比值（简称柔度应力比，用γ表示），结果如图9所示。

分析图8和图9可知，4种柔性铰链按柔度与柔度应力比从大到小的排序为：嵌套余弦函数型、椭圆型、圆弧型、正弦型；按精度和柔度精度比从高到低的排序为：正弦型、圆弧型、嵌套余弦函数型、椭圆型。结果显示：嵌套余弦函数型多轴柔性铰链的柔度应力比相对于椭圆型、圆弧型、正弦型多轴柔性铰链分别提高了8.81%、36.14%和73.25%。由此说明，在相同应力约束下，嵌套余弦函数型多轴柔性铰链可实现更大的柔性变形及更强的转动能力，该柔性铰链可为大行程柔顺精密定位平台的设计提供理论依据。

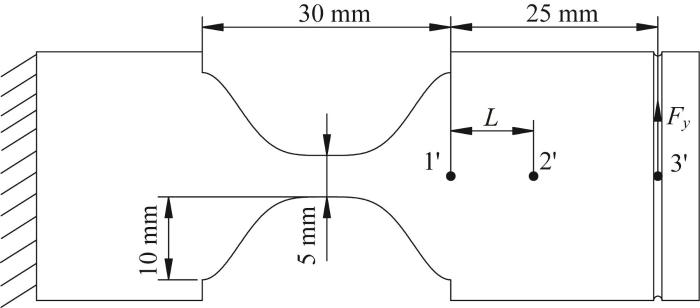
为了进一步验证本文基于FBMM法建立的嵌套余弦函数型多轴柔性铰链柔度理论模型的有效性，采用CNC（computer numerical control，计算机数值控制）技术加工柔性铰链试样，材料为7075铝合金，其结构参数如下：l=30 mm，a=10 mm，t=5 mm。该柔性铰链试样的结构尺寸如图10所示。

搭建柔性铰链柔度测试实验平台，如图11所示，实验设备主要包括24 V电源、砝码、柔性铰链试样、激光位移传感器控制器、激光位移传感器（基恩士，LK-H025，重复精度为0.02 µm）。

实验步骤为：在柔性铰链试样自由端施加沿y方向的拉力，并使用2个激光位移传感器测量柔性铰链点1'和点2'处的位移y₁和y₂，由此计算得到点2'处的旋转角度∆θ：

其中：

Δy=|y₁-y₂|

式中：L为点1'到点2'的距离，L=10 mm。

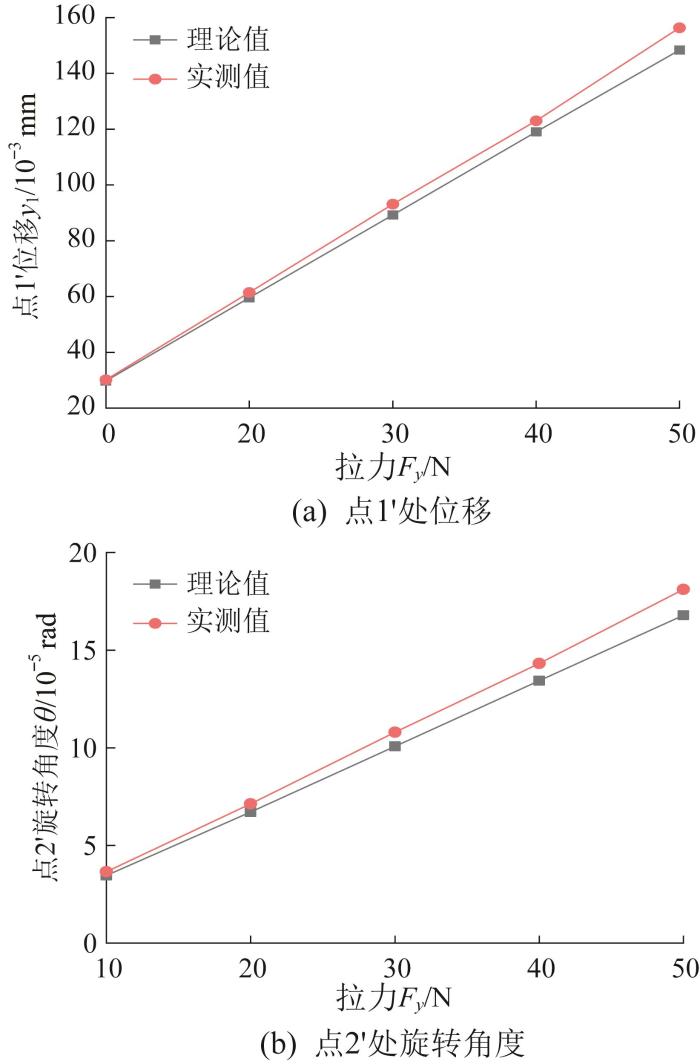
在实验过程中，通过在柔性铰链点3'处逐步施加拉力，拉力范围为10~50 N，每次增加10 N，并记录单个载荷作用下点1'和点2'处的位移。为确保准确性，每个拉力下的位移均测量10次，并取平均值作为最终的测量结果。所加工的柔性铰链试样点1'处位移和点2'处旋转角度的理论值与实测值如图12所示。结果显示，位移、旋转角度的理论值与实测值的相对误差分别小于5.13%和7.29%，均小于8%，由此验证了所构建的柔度理论模型的有效性。出现误差的原因可能为：理论建模时对柔性铰链模型进行了简化，而实验中柔性铰链试样存在制造误差以及激光位移传感器存在安装误差。

本文设计了一种嵌套余弦函数型多轴柔性铰链，并基于FBMM法构建了其柔度和精度的理论模型，通过将柔度和精度的理论计算结果与有限元仿真结果进行对比，验证了理论模型的有效性。然后，分析了结构参数对嵌套余弦函数型多轴柔性铰链柔度和精度的影响，并与椭圆型、圆弧型、正弦型多轴柔性铰链进行了性能比较。最后，通过实验进一步验证了所构建的柔度理论模型的有效性。主要结论如下：

1）嵌套余弦函数型多轴柔性铰链柔度和精度的理论计算结果与有限元仿真结果的最大相对误差分别为4.89%和4.97%，说明所构建的理论模型有效且准确。通过实验测量得到的该柔性铰链自由端的变形量与理论结果的相对误差小于8%，进一步验证了柔度理论模型的有效性。

2）结构参数对嵌套余弦函数型多轴柔性铰链柔度、精度和柔度精度比的影响结果表明：柔度和精度随各结构参数的变化呈相反趋势。若想通过改变结构参数的方式来提高柔度，则可能会导致其精度降低。其中：最小截面直径对该柔性铰链柔度、精度和柔度精度比的影响最为显著，而缺口深度和缺口长度的影响相对较小。

3）嵌套余弦函数型、椭圆型、圆弧型、正弦型多轴柔性铰链的性能比较结果显示：嵌套余弦函数型多轴柔性铰链的柔度应力比相较于椭圆型、圆弧型、正弦型分别提高了8.81%、36.14%和73.25%，说明嵌套余弦函数型多轴柔性铰链在相同应力条件下可提供更大的柔性变形量及更优的转动性能。