随着机器人技术的快速发展，机器人运动过程中的避障问题受到了学者们的广泛关注。高效的路径规划可以提高机器人的执行效率。因此，研究如何降低避障路径规划的时间成本和长度成本具有重要意义。

近年来，国内外学者针对机器人的路径规划算法做了大量研究。Fan等^[1]提出的人工势场法引入了力场原理，即：将障碍物附近区域定义为斥力场，将目标点附近区域定义为引力场。基于该算法规划的路径虽能实现有效避障，但当引力和斥力的合力为0 N时，易陷入局部最小值，导致无法规划出一条无碰撞路径。Dolgov等^[2]提出的A*算法是一种图形遍历算法，该算法在简单环境中易找到最优路径，但随着环境复杂程度的提高，每一个节点处的运算量增大，导致路径规划效率大幅下降^[3-4]。相较于上述算法，LaValle等^[5]提出的快速搜索随机树（rapidly-exploring random tree, RRT）算法具有在空间内随机快速采样的特点，且无需建模，具备空间搜索的完整性^[6-7]。但是，由于搜索方向的随机性，RRT算法的收敛速度慢，且在复杂环境中会产生大量无效节点，导致所规划路径的平滑度较差^[8-10]。

针对RRT算法在路径规划效率上的不足，许多学者对其进行了改进优化。Yuan等^[11]提出的Bias-RRT算法是在RRT算法的基础上引入目标偏置策略，利用偏置概率使随机树朝目标点方向拓展。在障碍物较少的环境中，Bias-RRT算法能快速规划出无碰撞路径，但在复杂环境中过大的偏置概率会降低规划速度^[12-13]。Karaman等^[14]提出的RRT*算法在RRT算法的基础上增加了重选父节点以及重新布线两大策略，以增加时间成本的方式来规划一条接近最优的路径。Luo等^[15]基于RRT*算法提出了一种Informed-RRT*算法，通过将采样区域限制在椭圆内的方式对规划路径进行优化。相比于RRT*算法，Informed-RRT*算法获取渐进最优路径的速度有所提升^[16]。Kuffner等^[17]提出了RRT-Connect算法，该算法是在RRT算法的基础上以目标点为根节点增加了1棵随机树，2棵随机树同时朝对方进行生长。相较于RRT算法，RRT-Connect算法在路径规划速度上有所提升，但其规划的路径仍不够平滑^[18-21]。

综上所述，已有研究虽通过改进使RRT算法在路径规划效率上得到了一定程度的提升，但仍存在环境适应性差、收敛速度慢和规划路径质量差等问题。为解决上述问题，笔者提出了一种新的改进RRT算法。首先，在传统RRT算法中引入地图复杂程度评估策略，以计算得到最适合相应地图的步长和偏置概率；然后，利用采样区域动态更新策略和采样点优化策略来提高采样点的有效性及质量，以实现在保留传统RRT算法随机性的同时获取渐进最优采样点，从而确保随机树朝目标点附近正向生长；最后，基于节点重连策略，在重新连接初始路径节点后进行碰撞检测，以删除冗余节点，使得避障路径更加优化。

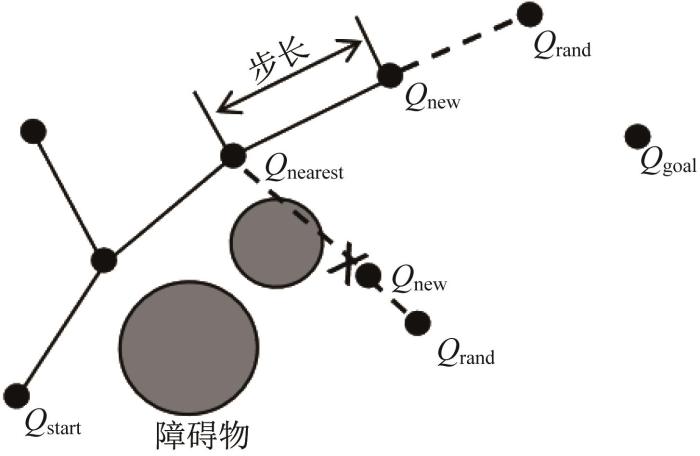
RRT算法的核心思想是建立一棵随机树，并从起点开始随机拓展随机树，直到树枝生长至目标点^[5]，其原理如图1所示。随机树从起点Q_start开始生长，令起点Q_start为随机树的根节点，在地图中随机生成一个采样点Q_rand。遍历随机树中的节点，找到距离采样点Q_rand最近的节点Q_nearest；将节点Q_nearest沿采样点Q_rand方向生长一个步长，从而得到新节点Q_new。随后，遍历障碍物，判断节点Q_nearest与节点Q_new的连线是否与障碍物发生碰撞：若碰撞，则放弃节点Q_new，并重新随机生成采样点Q_rand；若无碰撞，则将节点Q_new加入随机树，并定义节点Q_new的父节点为Q_nearest。同时，计算节点Q_new与目标点Q_goal之间的距离，若计算距离小于步长，且两点连线与障碍物无碰撞，则判定为已到达目标点Q_goal。将目标点Q_goal加入随机树，并通过反向追溯随机树中具有父节点的所有节点，将其连接后得到无碰撞路径。若计算距离大于步长，则随机树继续生长。

令M表示地图，T表示随机树，k表示迭代次数，则RRT算法的伪代码如下：

传统RRT算法不能充分利用地图中的障碍物信息来自适应调整步长，导致即使面向障碍物较少的简单地图，也难以快速规划出一条渐进最优的路径。Bias-RRT算法采用目标偏置策略，通过设定偏置概率P来选取目标点作为采样点，在简单地图中可以有效提高路径规划的收敛效率^[11]。但偏置概率P的取值采用主观定义，当面向不同环境时，Bias-RRT算法的适用性不足，尤其是对于障碍物较多的复杂地图，过大的偏置概率P会增加路径规划的时间成本，有时甚至可能会导致路径规划失败^[12-13]。

此外，传统RRT算法中随机树生长的步长为定值，而同一步长无法适应不同地图。当在障碍物较少的简单地图中进行路径规划时，若步长过短，则会增加节点数量，导致规划时间延长。当在障碍物较多的复杂地图中进行路径规划时，若步长过长，则会增大与障碍物碰撞的概率，导致难以得到一条无碰撞的路径。

针对上述问题，本文提出了一种地图复杂程度评估策略，即基于地图中的障碍物信息计算地图复杂程度系数C₁，从而得到最合适的偏置概率P和步长S。假设地图的复杂程度主要与地图中障碍物的总面积及分布情况有关，且两者对应的权重相等（均为0.5），则地图的复杂程度系数C₁可表示为：

式中：A_obstacle表示障碍物面积；A_map表示地图面积；D_obstacle表示障碍物分布情况，将地图划分为100个均等格子，障碍物所占格子数与100之比即为障碍物的分布情况。

地图复杂程度系数C₁越趋近于1，说明地图的复杂程度越高，则偏置概率P和步长S的取值应越小。合适的步长S应考虑偏置概率P以及起点到目标点的距离。本文将步长S设为偏置概率P与起点到目标点的距离之积。为确定偏置概率P的最佳取值，在传统RRT算法中引入偏置概率P和步长S，并将偏置概率P分别取为1-C₁、1-C12、1-C13和1-C14，在同一地图中分别进行50次路径规划仿真实验，整理相关数据并对比，结果如表1所示。由表1可知，当偏置概率P过大时，会导致路径规划失败；当偏置概率P过小时，偏置效果变差，导致路径规划的时间成本增加；当偏置概率P=1-C13时，路径规划的时间成本和长度成本均最低。综上，偏置概率P和步长S的计算式可表示为：

传统RRT算法规划的无碰撞路径通常不具有方向性，甚至可能会出现逆向生长，导致路径规划的时间成本和长度成本过高。出现上述问题的主要原因在于传统RRT算法会在无效区域内进行采样，使得随机树生长出过多的无效树枝。为了避免该情况发生，本文提出了采样区域动态更新策略，其核心思想是随着随机树的生长，不断向目标点所在区域缩小采样范围，以逐渐逼近目标点。

随机树节点的正向生长是指朝当前节点与目标点之间的区域生长，可不断缩小当前节点与目标点的距离，即有效生长；逆向生长是指朝当前节点与起点之间的区域生长，会不断扩大当前节点与目标点的距离，即无效生长。如图2所示，在二维地图中，根据随机树上最新增加的节点Q_new，将搜索空间分为2块区域，其中目标点所在区域定义为有效区域，即区域Ⅱ，另一块区域定义为无效区域，即区域Ⅰ。在下一次随机采样时，仅在区域Ⅱ内进行采样，随着随机树节点的增加，有效区域不断向目标点收缩，这样可以保证随机树正向生长。但如图2(a)所示，当节点Q_new生长到障碍物附近且正向生长基本被障碍物阻挡时，由于仅可在有效区域内采样，RRT算法易陷入局部无解，使得随机树无法继续生长。为解决该问题，在动态更新采样区域的基础上引入节点拒绝策略。当随机树在当前节点经过50次迭代后仍然无法继续生长时，即认为该节点无效，将其从随机树中删除，如图2(b)所示的节点Q_void即为无效节点。此时，随机树的有效采样区域为基于无效节点的父节点Q_parent分割得到的区域Ⅱ，随机树在更新后的有效采样区域内重新开始生长，如图2(c)所示。

传统RRT算法在地图中随机生成的采样点不具有导向性，导致随机树的树枝生长得杂乱无章。大量低质量采样点的产生，不仅会增加路径规划的时间成本，而且会导致节点冗余，使得路径规划的长度成本增加。

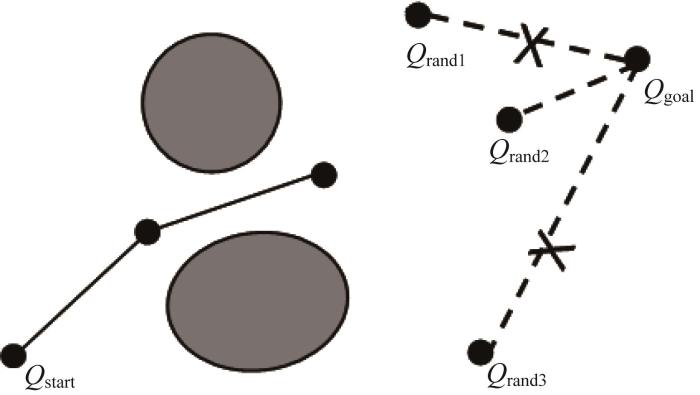
为此，本文设计了一种采样点优化策略。如图3所示，在每一次采样时，同时随机产生3个待定采样点Q_rand1、Q_rand2、Q_rand3并构成集合，计算集合中每个待定采样点到目标点的距离，选取距离目标点最近的待定采样点作为最终采样点。该优化方法的核心思想在于：从待定采样点集合中选取距离目标点最近的采样点来确定节点生长的方向，以保证随机树朝目标点附近生长。通过提高采样点的质量，既避免了随机树生长的长度成本过高，又保留了RRT算法搜索方向的完整性。

基于上述策略改进的RRT算法虽能快速规划得到初始路径，但该初始路径存在节点冗余现象，导致路径的弯折次数较多。为解决该问题，本文提出了节点重连策略，即通过对初始路径上的节点进行重新连接来减少转折点，从而优化路径。

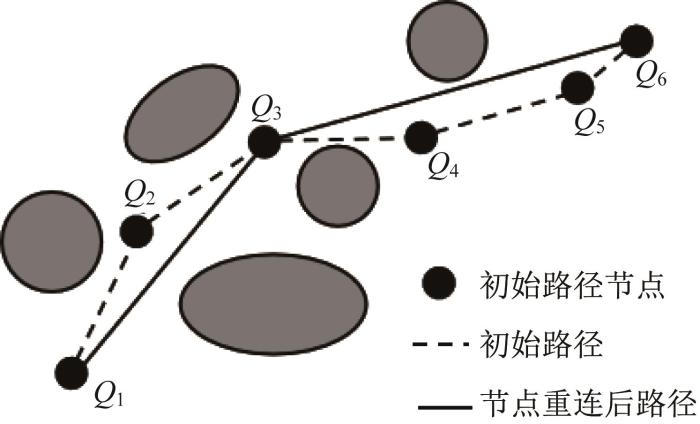
节点重连策略的原理如图4所示。图中：虚线所示路径为未引入节点重连策略的改进RRT算法规划的初始路径，该路径由初始节点集合{Q₁, Q₂, Q₃, Q₄, Q₅, Q₆}中的节点依次连接而成，其中Q₁和Q₆分别代表起点和目标点。引入节点重连策略后，将目标点Q₆作为随机树的根节点，基于Q₆依次连接初始节点集合中的各个节点并进行碰撞检测。通过检测发现，线段Q₆Q₁和线段Q₆Q₂均会与障碍物发生碰撞，但Q₆直接连接Q₃时没有发生碰撞，故将Q₃加入优化节点集合。然后，以Q₃作为碰撞检测的起点，依次连接初始节点集合中的各个节点并进行新一轮的碰撞检测。结果显示，Q₃直接连接Q₁时没有发生碰撞，故将Q₁加入优化节点集合。当起点被加入到优化节点集合中时，表明节点重连结束。将优化节点集合中的节点按顺序依次连接，获得优化路径，如图4中实线所示路径。相较于初始路径而言，节点重连后路径的节点数量明显减少，有效降低了路径规划的长度成本。

为验证本文改进RRT算法在避障路径规划中的可行性及其规划效率的提升效果，分别利用传统RRT算法、Bias-RRT算法、RRT-Connect算法和改进RRT算法进行路径规划仿真并对比。本文仿真环境为Intel(R) Core(TM) i5-7200U CPU @ 2.50 GHz，其内存为4 GB。各RRT算法均采用Python3.6和MATLAB 2017a软件来实现。

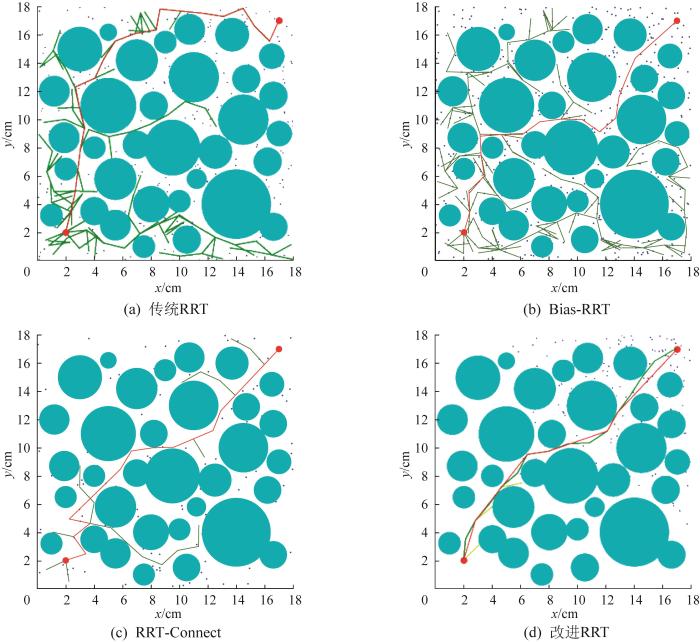
为验证本文改进RRT算法在二维空间中规划避障路径的可行性，分别利用传统RRT算法、Bias-RRT算法、RRT-Connect算法和改进RRT算法在3种复杂程度不同的二维地图中进行50次路径规划仿真实验。其中：二维地图的大小均为18 cm×18 cm；路径的起点为(2，2) cm，终点为(17，17) cm。在本文中，传统RRT算法、Bias-RRT算法、RRT-Connect算法的固定步长均取1.5 cm；Bias-RRT算法的偏置概率取20%。

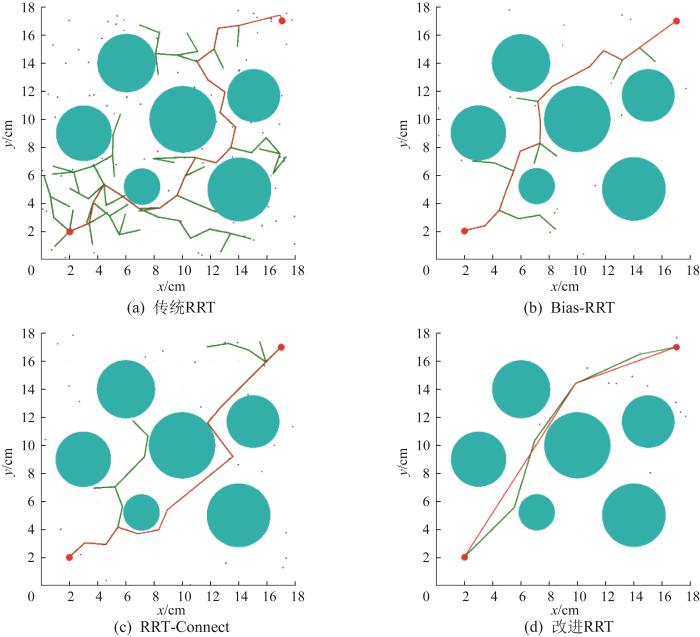
4种RRT算法在3种二维地图中的路径规划效果分别如图5至图7所示。从图5(a)、图6(a)、图7(a)中可以看出，传统RRT算法生长的随机树没有方向性，产生了大量无效节点，且规划的路径较为曲折。从图5(b)、图6(b)、图7(b)中可以看出，偏置概率取20%的Bias-RRT算法在简单环境中可以使随机树的生长具有方向性，但在复杂环境中无法实现。从图5(c)、图6(c)、图7(c)中可以看出，RRT-Connect算法中2棵随机树的双向生长虽提高了路径规划效率，但仍存在不少无效节点且路径质量较差。从图5(d)、图6(d)、图7(d)中可以看出，本文的改进RRT算法基于对地图复杂程度的自动评估得到的步长相比于其他3种RRT算法的固定步长具有明显优势，尤其在复杂程度不高的地图1和地图2中，合适的偏置概率和步长大幅提高了路径规划效率；在复杂程度较高的地图3中，当随机树生长到障碍物附近无法继续正向生长时，节点拒绝策略有助于随机树摆脱局部无解，有效地提高了路径规划效率。综上所述，相较于其他3种RRT算法，本文的改进RRT算法生长的随机树的树枝大幅减少，采样点数量减少且均向目标点收缩，经过节点重连后获得的无碰撞路径的质量明显优于其他RRT算法。

对4种RRT算法在3种复杂程度不同的地图中的路径规划数据（耗时、节点数、路径长度）进行均值处理并对比，结果分别如表2至表4所示。

由表2可得，相较于传统RRT算法、Bias-RRT算法和RRT-Connect算法，本文的改进RRT算法在复杂程度较低的地图1中的路径规划耗时分别下降了96.24%，90.08%，81.93%，路径长度分别缩短了18.89%，13.74%，16.12%。

由表3可得，相较于传统RRT算法、Bias-RRT算法和RRT-Connect算法，本文的改进RRT算法在复杂程度一般的地图2中的路径规划耗时分别下降了93.28%，88.52%，62.29%，路径长度分别缩短了26.64%，21.66%，13.44%。

由表4可得，相较于传统RRT算法、Bias-RRT算法和RRT-Connect算法，本文的改进RRT算法在复杂程度较高的地图3中的路径规划耗时分别下降了93.11%，92.49%，73.41%，路径长度分别缩短了24.25%，23.05%，21.16%。

综上所述，相较于传统RRT算法、Bias-RRT算法和RRT-Connect算法，在复杂程度不同的二维地图中，本文的改进RRT算法的避障路径规划速度更快，且路径的节点更少，长度更短。

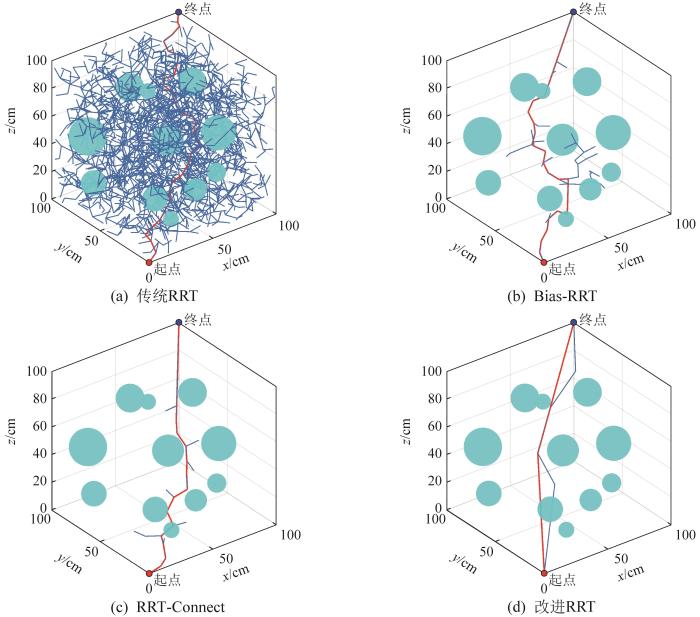
为验证本文的改进RRT算法在更加复杂的三维空间中规划路径的可行性，分别利用传统RRT算法、Bias-RRT算法、RRT-Connect算法和改进RRT算法在三维地图中进行50次路径规划仿真实验。其中，三维地图的大小为100 cm×100 cm ×100 cm，起点为(0，0，0) cm，终点为(100，100，100) cm。在本文中，传统RRT算法、Bias-RRT算法、RRT-Connect算法的固定步长取5 cm，其中Bias-RRT算法的偏置概率取20%。

4种RRT算法在三维地图中的路径规划效果如图8所示。通过对比可知，在三维地图中，传统RRT算法因搜索空间扩大且随机树的生长不具有方向性，生长出了大量的无效树枝，其规划的路径质量较差。偏置概率取20%的Bias-RRT算法的随机树生长具有一定的导向性，但仍存在较多冗余节点。相较于Bias-RRT算法，RRT-Connect算法中2棵随机树的双向生长更具有导向性，但也存在冗余节点，最终的避障路径质量较差。与上述3种RRT算法相比，本文的改进RRT算法具有更适合三维地图的步长以及其随机树生长的导向性更优，使得无效节点的数量大大减少，经节点重连后得到的避障路径也更加平滑。

将4种RRT算法在三维地图中的路径规划数据（耗时、节点数、路径长度）进行均值处理并对比，结果如表5所示。由表5可知，相较于传统RRT算法、Bias-RRT算法和RRT-Connect算法，本文的改进RRT算法在三维地图中的路径规划耗时分别下降了99.74%，90.77%，88.47%，路径长度分别缩短了26.71%，14.43%，13.19%。

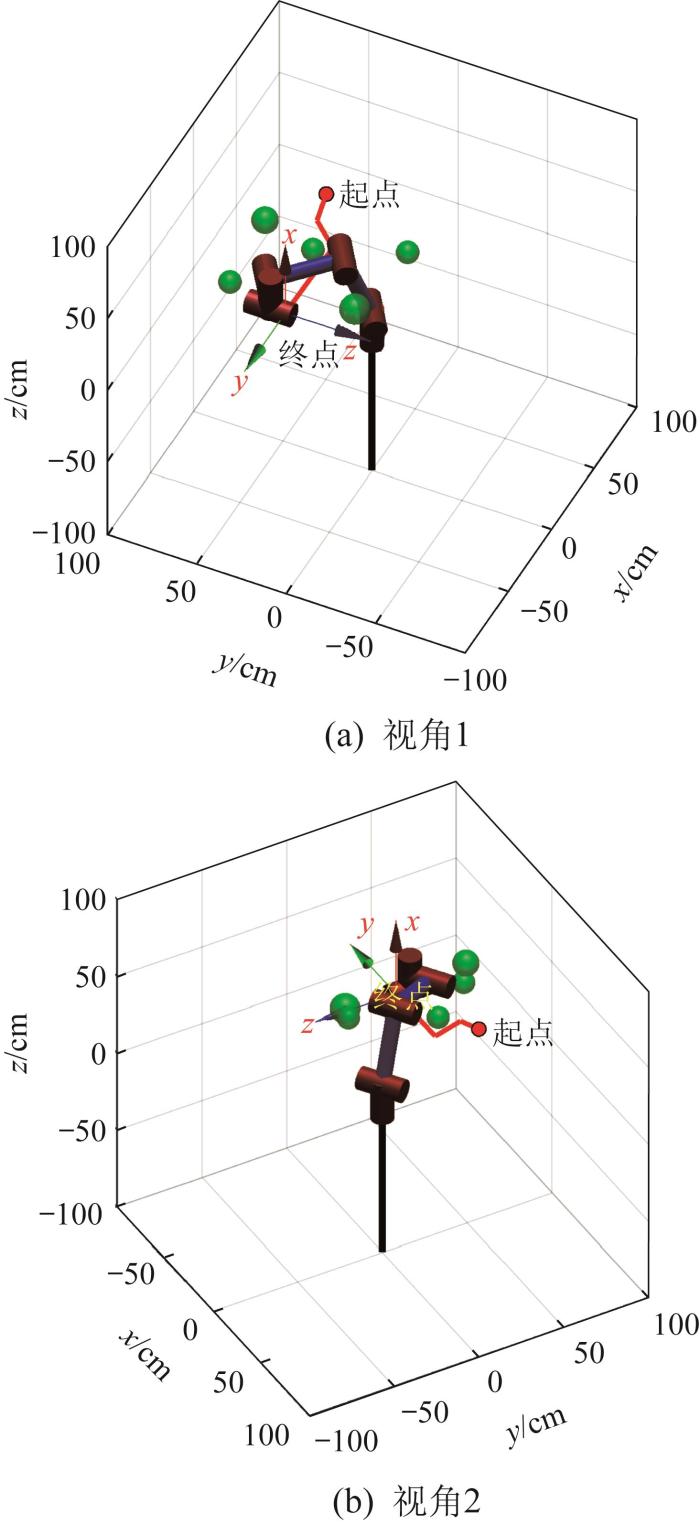
为验证本文提出的改进RRT算法在机械臂避障路径规划中的适用性，在MATLAB 2017a软件中开展仿真实验，本文以六自由度机械臂为研究对象。首先，对机械臂的工作空间进行分析，若起点和目标点均在工作空间内，则可直接开展机械臂末端的避障路径规划。机械臂末端避障路径的规划过程为：先利用改进RRT算法规划初始避障路径，并将初始避障路径分解为若干路径点；然后，将路径点的坐标依次代入机械臂的逆运动学方程，以求解得到8组关节转角。若某路径点对应的8组关节转角中有满足机械臂各连杆与障碍物无碰撞且各连杆之间无碰撞的关节转角，则认为该路径点有效。但若8组关节转角均不能满足上述要求，则将该路径点的前一个路径点作为新的起点，重新规划路径并进行连杆碰撞检测，直到获得一条无碰撞路径。

基于改进RRT算法的机械臂末端避障路径规划结果（规划50次）如图9所示。其中：起点为(30，40，50) cm，终点为(-40，30，30) cm，圆球表示障碍物，实线为机械臂末端的避障路径。与此同时，分别利用传统RRT算法、Bias-RRT算法、RRT-Connect算法对机械臂末端的避障路径规划50次（起点、终点以及障碍物位置等均相同），并对4种RRT算法的避障路径规划数据进行均值处理和对比，结果如表6所示。结果表明，利用本文的改进RRT算法对机械臂末端的避障路径进行规划时，所得路径的质量更高，时间成本更低，验证了其适用性。

针对传统RRT算法在避障路径规划时存在效率低的问题，本文提出了一种新的改进RRT算法，该算法引入了以下4个策略：1）地图复杂程度评估策略，即根据地图中的障碍物信息，计算适合相应地图的步长和偏置概率；2）采样区域动态更新策略，令RRT算法仅在有效区域内采样，以确保随机树正向生长；3）采样点优化策略，从待定采样点集合中选取距离目标点最近的采样点作为最终采样点，提高了随机树朝目标点附近生长的概率；4）节点重连策略，由于初始规划路径的弯折次数较多，通过对初始路径节点进行优选和重新连接，可去除冗余节点，实现了路径优化。最后，通过在二维、三维地图中以及对机械臂开展避障路径规划仿真实验，验证了改进RRT算法对环境的适应性比传统RRT算法、Bias-RRT算法、RRT-Connect算法强，其规划无碰撞路径的耗时更短，质量更高且更适用于机械臂。