机器人在军事领域中的应用越来越广泛。在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划。在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] 。综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] 。算法的优劣性在路径规划中起着关键作用。现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等。无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能。
遗传算法是一种智能搜索算法。它以生物进化为原型,相较于传统的路径规划算法具有较好的全局搜索能力和收敛性,但局部搜索能力差。其具有良好的可扩展性,易与其他算法结合,因此是融合算法中常用的一种算法。杨博等[16 ] 采用中间插值法,通过改进交叉算子、变异算子和适应度函数来优化遗传算法,避免了早熟现象发生,但是未考虑动态障碍物环境下算法的适应性。陈亮等[17 ] 将遗传算法与鲸鱼算法相结合,使得融合算法能在短时间内完成进化,但是当规划空间规模较大时仍存在迭代次数较大的问题。徐兴等[18 ] 提出了基于灾变策略的遗传算法,相对于传统遗传算法,可避免早熟现象且缩短寻优时间。Zhou等[19 ] 研究后发现,面对现实复杂地形和环境,采用单一的遗传算法因受到算法本身的限制而不能得到理想的结果。
遗传算法借用达尔文进化理论以算法的形式表现出来就是遗传算法的运行过程。遗传算法在计算种群适应度函数时具有较大的计算量,导致算法执行处理时间较长,搜索效率低下[20 ] 。J P S A * A * [21 ] 。
基于遗传算法效率低、运行时间长和J P S J P S
本研究采用栅格法对自主移动机器人在静态和动态环境下的路径规划进行分析,进而验证J P S G 算法
1 栅格建模
1)在环境空间中分布着有限个静态障碍物和动态障碍物,每个障碍物大小相等且不考虑高度因素,但需考虑动态障碍物的移动速度大小和方向;
2)自主移动机器人仅仅考虑移动方向,不考虑移动速度大小;
3)用黑白网格区分障碍物和自由移动空间,连续坐标代表移动路径,不重复连续相邻坐标的距离之和代表路径长度。
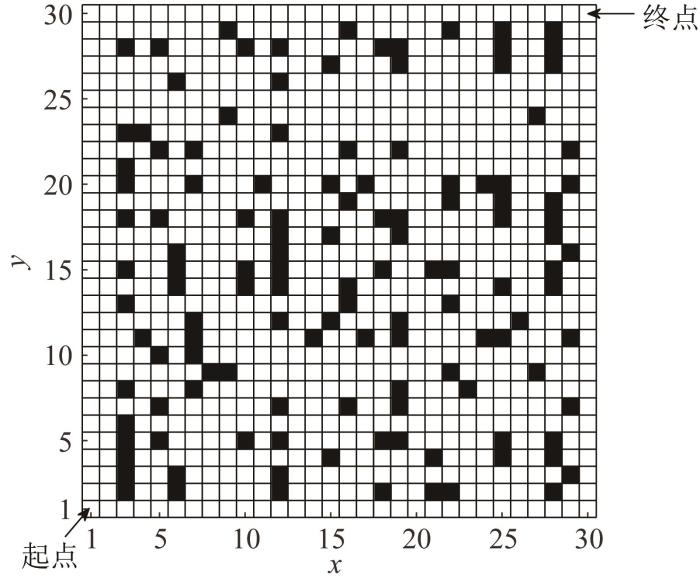
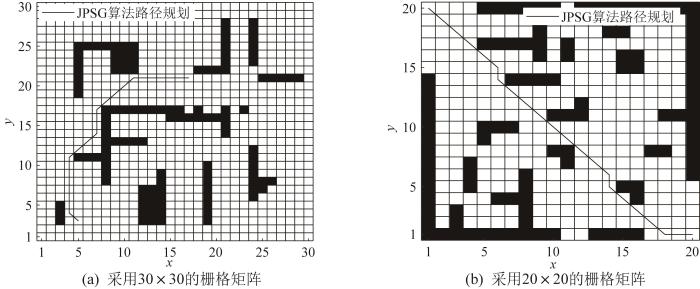
设自主移动机器人的运动环境空间为A 30 × 30 30 × 30 图1 所示。由图可知,自主移动机器人在非规则边界区域的移动方向共有8个。
图1
图1
30 × 30
Fig.1
Schematic diagram of 30×30 grid matrix
栅格矩阵中存在若干静态障碍物和动态障碍物。对于任意位置的栅格都有唯一的坐标x , y 30 × 30 s x , y
x = f i x s / 30 + 1 y = m o d s , 30 + 1
G x , y
式中:f i x m o d G
由栅格的坐标x , y
2 JPSG 算法原理
J P S G 算法 J P S J P S G 算法
2.1 改进遗传算法
改进遗传算法主要通过采用自适应交叉概率、变异概率和改进适应度函数计算方法来加快算法的收敛速度。
2.1.1 选择算子
轮盘赌法的选择方式是根据概率且将概率大小与适应度相关联,从而使有较高适应度的个体具有更大优势。表示为:
p i = f i ∑ j = i M f j (3)
式中:p i 为 f i 为 j 为种群数量,j =1, 2, …, M 。
2.1.2 交叉算子
交叉算子的主要作用是产生新的个体。交叉概率越大,新个体产生速度越快,同时种群中最优个体被破坏的概率越大;交叉概率越小,遗传算法的收敛速度越慢。表示为:
p c = 1 , p m a x ≥ 3 p m i n 0.2 s i n π 2 2 + p m a x p m i n + 0.8 , 其他 (4)
式中:p c 为 p m a x 、 p m i n
由式(4)可知:若当前种群的最大路径长度与最小路径长度的比值变大时,交叉概率随之变大。通过不断交叉使种群路径长度加速向当前迭代种群最优路径长度靠拢;当交叉概率较小时,可以避免种群中最优路径长度被破坏。
2.1.3 变异算子
变异运算是使遗传算法突破局部最优解的重要方法。变异概率太小,则产生新个体的几率较小,且容易出现早熟现象;变异概率太大,则随机概率较大。表示为:
p m = 0.05 × 1 + c o s π 2 × 1.5 × x g - x s 2 + y g - y s 2 p m a x (5)
式中:p m x s 、 y s x g 、 y g
若迭代时迭代种群内最大路径长度与起点与终点之间的距离相差较大,则当变异概率逐渐增大时,变异后得出更优的路径长度,而不至于使种群路径长度陷入局部最优路径长度。当变异概率减小时,不会破坏当前种群内路径长度的稳定性。
2.1.4 插入算子
根据式(6)可以判断路径中相邻栅格节点间是否连续。根据式(2)中 G
m a x a b s ( x n e x t - x n o w ) , a b s ( y n e x t - y n o w ) ≈ 1 (6)
x i n s e r t = f l o o r x n e x t + x n o w 2 y i n s e r t = f l o o r y n e x t + y n o w 2 (7)
式中:abs为绝对值函数,max为取最大值函数,floor为向下取整函数,x n o w 、 y n o w x n e x t 、 y n e x t x i n s e r t 、 y i n s e r t 分别
2.1.5 适应度函数
个体i 的适应度表示个体在种群生存的优势程度,用于区分个体的优劣。
F i = ∑ i = 2 n x i - x i - 1 2 + y i - y i - 1 2 (8)
F = x g - x s 2 + y g - y s 2 (9)
f i = 1 F i - F + ε , ε ∈ 0 , 1 (10)
式中:Fi 为路径长度,F 为起点与终点之间的距离,ε 为 m
原适应度值仅仅由路径长度的倒数决定,当路径长度相近并接近最优解时,适应度值相差不大而难以区分,改进后以Fi 与F
2.2 JPS 算法
通过式11
a b s ( x n o w - x p r e ) ≠ 1 a b s ( y n o w - y p r e ) ≠ 1 (11)
式中:x p r e 、 y p r e
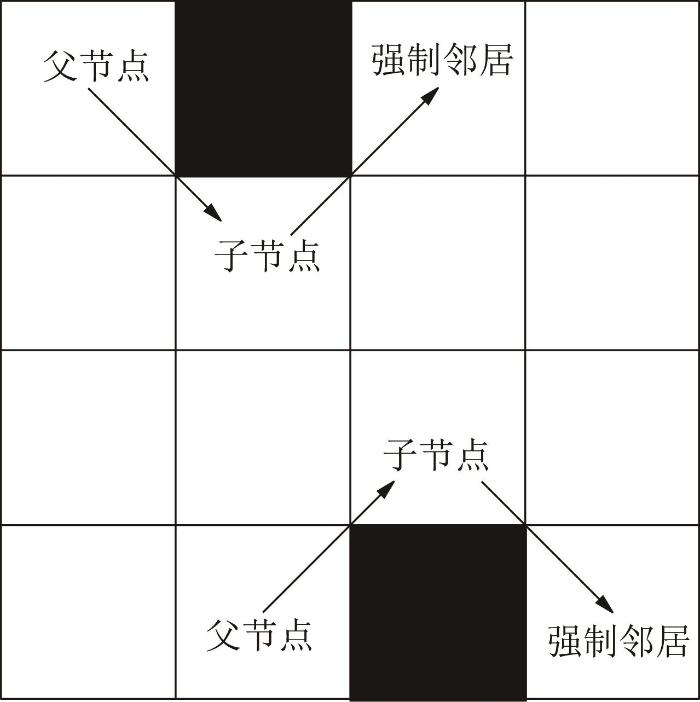
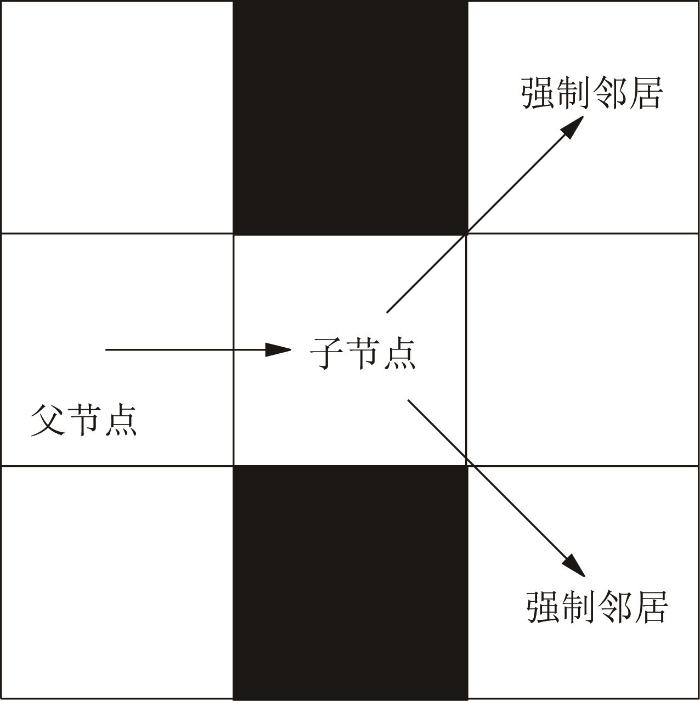
自然邻居定义为当前节点沿对角线方向上的下一个节点、水平方向上的下一个水平节点和垂直方向上的下一个垂直节点。若当前节点的邻居节点中有障碍物,且从上一节点经过当前节点到达下一节点的距离比不经过当前节点到达下一节点的距离小,则称下一节点为强制邻居,如图2 和图3 所示。
图2
图2
斜线强制邻居示意图
Fig.2
Schematic diagram of oblique line forced neighbors
图3
图3
直线强制邻居示意图
Fig.3
Schematic diagram of linear forced neighbors
2.2.1 跳点评估函数
通过搜索规则对跳点进行评估,选择出最优跳点以组成最优路径。评估函数如下:
f c o s t = ∑ i = 2 m x m - x m - 1 2 + y m - y m - 1 2 (12)
f v a l u e = x g - x n o w 2 + y g - y n o w 2 (13)
f j p s = f c o s t + f v a l u e (14)
式中:f c o s t 为 f v a l u e 为 f j p s 为
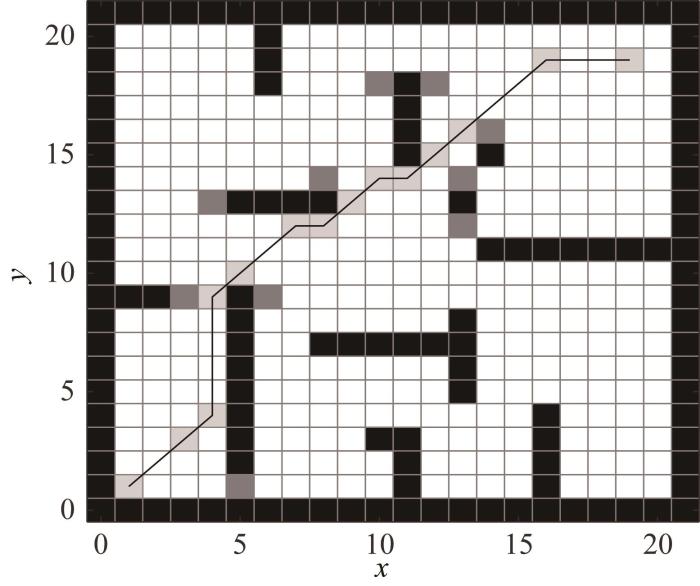
通过路径评估函数可以评判起点、跳点和终点依次连接后的路径是否为最佳路径。跳点搜索如图4 所示。图中深灰色和浅灰色栅格为跳点,其中将最优跳点(浅灰色栅格)连接后,可以构成一条由起点到终点的最优路径。
图4
图4
跳点搜索示意图
Fig.4
Schematic diagram of j u m p p o i n t s e a r c h
2.2.2 o p e n l i s t
在o p e n l i s t o p e n l i s t
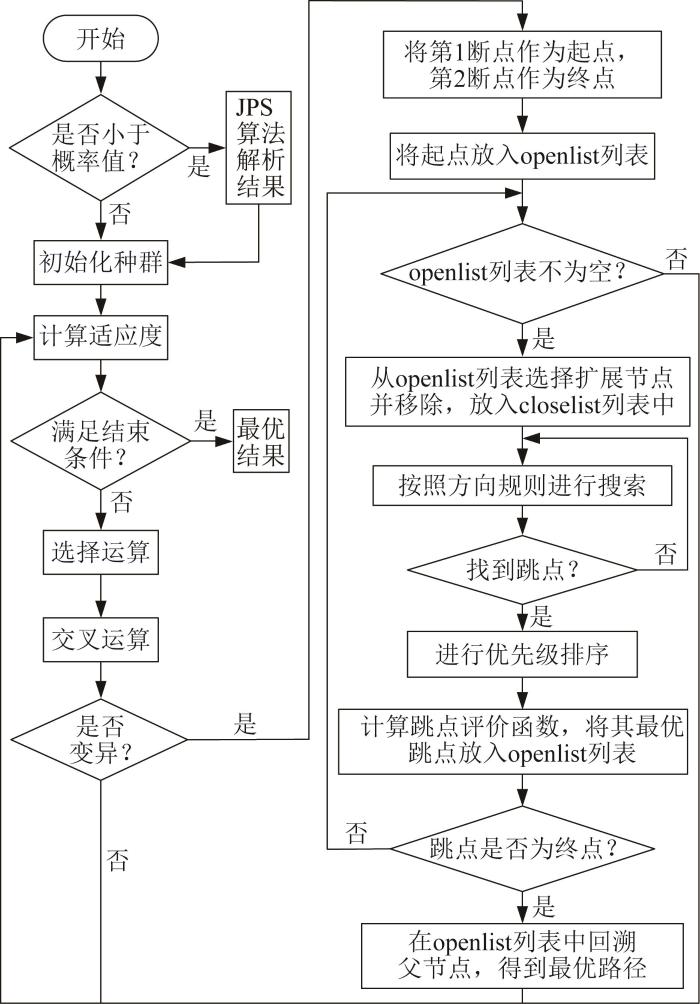
3 JPSG 算法流程
J P S G 算法 流程 如图 5 所示 。 J P S J P S J P S
图5
图5
J P S G
Fig.5
Flow chart of J P S G
4 路径规划仿真研究
在所建立的栅格矩阵上进行自主移动机器人路径规划仿真。
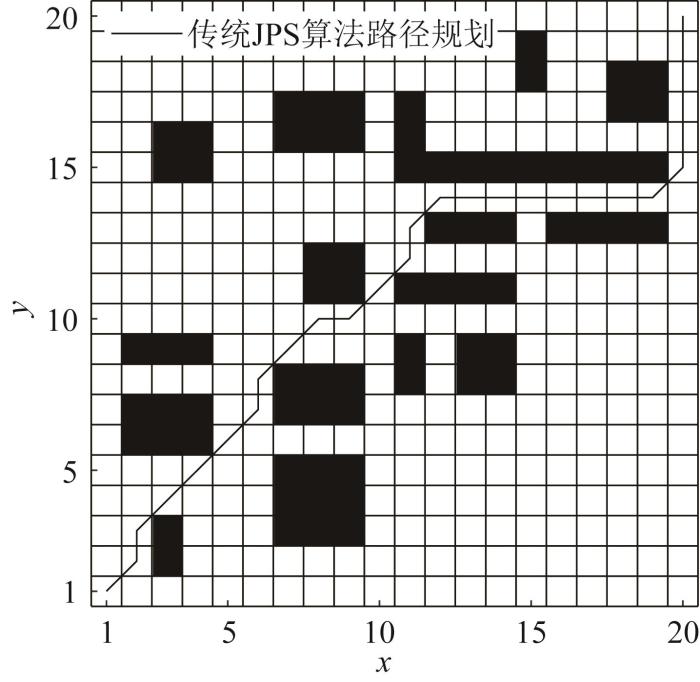
4.1 基于JPS算法的路径规划
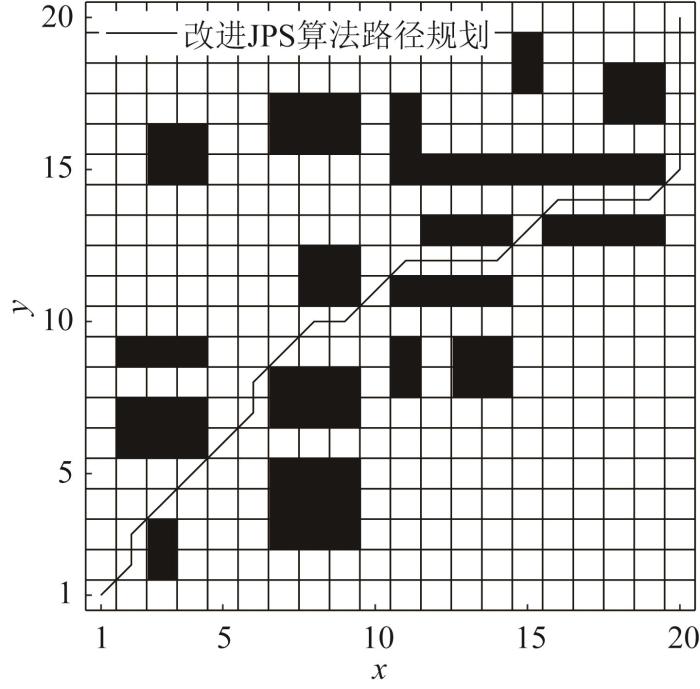
基于传统 J P S 图6 所示。将算法 中 o p e n l i s t 图7 所示。图6 中的路径长度为31.556 3,图7 中的路径长度为30.970 5,可见图7 中的路径为最优路径。图7 中,在栅格坐标(11, 12)处存在2条到下一节点的函数值相同的路径,算法改进后由于o p e n l i s t
图6
图6
基于传统J P S
Fig.6
Path planning result based on traditional JPS algorithm
图7
图7
基于改进J P S
Fig.7
Path planning result based on improved JPS algorithm
4.2 静态环境下路径规划
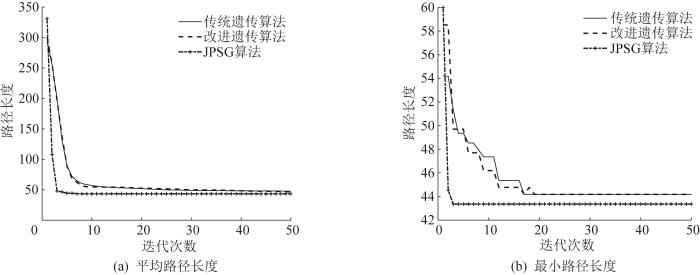
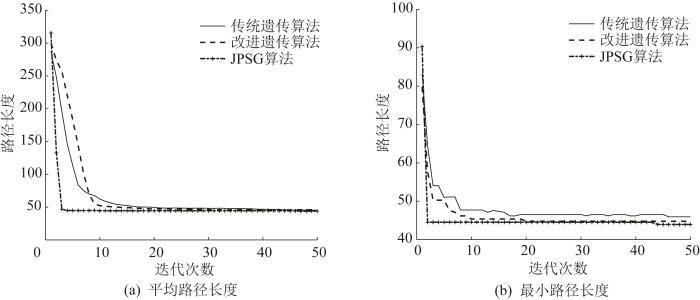
分别采用JPSG算法、改进JPS算法、改进遗传算法和传统遗传算法进行静态环境下的路径规划,并将规划结果进行对比,来验证J P S G M A T L A B 2021 b 30 × 3 0 的栅格矩阵上进行仿真。参数设置如下:M = 10 000 个 0.6 ≤ p c ≤ 1.0 0.02 ≤ p m ≤ 0.10 T = 100 次 图8 所示。采用JPSG算法、改进JPS算法、改进遗传算法和传统遗传算法得到的路径规划结果如图8 所示。J P S 图9 所示,算法性能对比如表1 所示。
图8
图8
静态环境下路径规划的仿真结果
Fig.8
S i m u l a t i o n r e s u l t s o f p a t h p l a n n i n g i n s t a t i c e n v i r o n m e n t
图9
图9
静态环境下规划路径长度的仿真结果
Fig.9
S i m u l a t i o n r e s u l t s o f p a t h p l a n n i n g l e n g t h i n s t a t i c e n v i r o n m e n t
由图8 可知:相对于改进JPS算法、改进遗传算法和传统遗传算法,JPSG算法具有更好的整体搜索能力,利用J P S J P S
由表1 可知:相较于改进遗传算法和传统遗传算法,JPSG算法的规划路径长度最短,收敛迭代次数最少;准确率分别提高了72%、90%;规划时间分别减小了12%、15%;方差值分别减小了30%、31%,表明J P S G J P S G 图10 所示。将JPSG算法与文献[22 ]和文献[23 ]提出的RRT(rapidly-exploring random tree,快速搜索随机树)算法和改进遗传-鲸鱼融合算法等进行对比,算法性能对比如表2 和表3 所示。
图10
图10
基于JPSG算法的路径规划结果
Fig.10
Path planning results based on JPSG algorithm
由表1 和表2 可知:JPSG算法和J P S 表2 得出知改进J P S R R T R R T - D i j k s t r a D i j k s t r a
由表3 可知,J P S G 23 ]中的遗传算法、改进遗传算法和改进遗传-鲸鱼融合算法在地图规模和障碍物简单的状况下的搜索效率更优。
4.3 动态环境下路径规划仿真
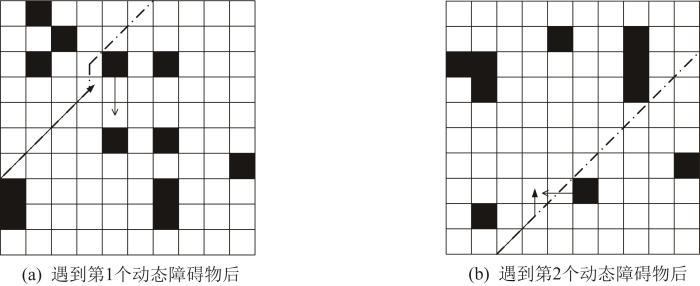
上述仿真是在静态环境下进行的,在实际中机器人所处工作环境大多是动态的,因此在动态环境下分别采用JPSG算法、改进JPS算法、改进 遗传 算法 和传 统遗 传算 法 5 ∆ t = 0.5 s 2 / s 2021 b 图11 所示。其中,当采用JPSG算法时,机器人遇到第1和第2个动态障碍物后的路径规划如图12 所示。图中带有空心箭头的实线代表动态障碍物的运动路径,带有实心箭头的实线代表静态环境下的规划路径,点划线代表动态环境下的规划路线,虚线代表动态障碍物的运动范围,箭头代表运动方向。将基于JPSG算法 遗传 算法 遗传 算法 图13 所示,算法性能对比如表4 所示。
图11
图11
在静态和动态环境下路径规划仿真结果的对比
Fig.11
Comparison of simulation results of path planning in static and dynamic environments
图12
图12
机器人遇到第1,2个动态障碍物后的路径规划示意
Fig.12
Schematic of path planning after the robot encounters the first and second dynamic obstacles
图13
图13
动态环境下规划路径长度的仿真结果
Fig.13
Simulation results of path planning in dynamic environment
由图11 可知:遗传算法对动态环境的适应性较差;在障碍物不断变化的情况下,J P S
由表4 可知:相较于改进遗传算法和传统遗传算法,JPSG算法的规划路径长度最短,收敛迭代次数最少;准确率分别提高了55%、95%;规划时间分别减小了12%、14%;方差值分别减小了50%、51%,表明J P S G
5 结 论
通过改进J P S 算法 的 o p e n l i s t J P S J P S
参考文献
View Option
[2]
[本文引用: 1]
WANG L LI M TANG D B et al Dynamic path planning for mobile robot based on improved genetic algorithm
[J]. Journal of Nanjing University of Aeronautics and Astronautics , 2016 , 48 (6 ): 841 -846 .
DOI:10.16356/j.1005-2615.2016.06.010
[本文引用: 1]
[4]
LI Y H HUANG Z H XIE Y Research status of mobile robot path planning based on genetic algorithm
[J]. Journal of Physics Conference Series , 2020 , 1544 (1 ): 012021 .
[5]
杨恒 ,李越 ,孙寒挺 ,等 路径最优的移动机器人路径规划研究
[J]. 机械设计 , 2022 , 39 (8 ): 58 -67 .
YANG H LI Y SUN H T et al Research on path planning of mobile robot with optimal path
[J]. Mechanical Design , 2022 , 39 (8 ): 58 -67 .
[6]
CHEN Z Q ZHOU J H SUN R Z et al A new evolving mechanism of genetic algorithm for multi-constraint intelligent camera path planning
[J]. Soft Computing , 2021 , 25 (27 ): 1 -20 .
[7]
LU T T FENG Y X YAN Z L A cooperative task allocation method for health management robots
[J]. Radio Engineering , 2022 , 52 (7 ): 1276 -1283 .
DOI:10.3969/j.issn.1003-3106.2022.07.022
[10]
SUN P Y HUANG Y Y PAN Y Path planning of mobile robots based on improved potential field algorithm
[J]. Journal of Military Industry , 2020 , 41 (10 ): 2106 -2121 .
DOI:10.3969/j.issn.1000-1093.2020.10.021
[11]
CHEN X A GAO P J Path planning and control of soccer robot based on genetic algorithm
[J]. Journal of Ambient Intelligence and Humanized Computing , 2019 , 11 (12 ):1 -10 .
[本文引用: 1]
[13]
[本文引用: 1]
LIU E H YAO X F AGV path planning based on improved genetic algorithm and implementation platform
[J]. Computer Integrated Manufacturing System , 2017 , 23 (3 ): 465 -472 .
DOI:10.13196/j.cims.2017.03.003
[本文引用: 1]
[14]
ZHOU K J YU L L LONG Z W et al Local path planning of driverless car navigation based on jump point search method under urban environment
[J]. Future Internet , 2017 , 9 (3 ): 51 -51 .
[本文引用: 1]
[15]
张许有 ,刘有余 基于位置代价A*算法的机械臂避障路径规划
[J]. 机械设计 , 2021 , 38 (2 ): 108 -113 .
[本文引用: 1]
ZHANG X Y LIU Y Y Path planning of obstacle avoidance for manipulators based on position cost A* algorithm
[J]. Mechanical Design , 2021 , 38 (2 ): 108 -113 .
[本文引用: 1]
[16]
杨博 ,刘树东 ,鲁维佳 ,等 改进遗传算法在机器人路径规划中的应用
[J]. 现代制造工程 , 2022 (6 ): 9 -16 .
[本文引用: 1]
YANG B LIU S D LU W J et al Application of improved genetic algorithm in robot path planning
[J]. Modern Manufacturing Engineering , 2022 , 6 : 9 -16 .
[本文引用: 1]
[17]
陈亮 ,姚懿轩 基于AGA-WOA算法融合的移动机器人路径规划
[J]. 今日制造与升级 , 2021 , 12 : 41 -43 .
[本文引用: 1]
CHEN L YAO Y X Path planning of mobile robot based on AGA-WOA algorithm fusion
[J]. Manufacturing and upgrading today , 2021 , 12 : 41 -43 .
[本文引用: 1]
[18]
[本文引用: 1]
XU X YU X Y ZHAO Y et al Global path planning of mobile robot based on improved genetic algorithm
[J]. Computer Integrated Manufacturing System , 2022 , 6 : 1659 -1672 .
DOI:10.13196/j.cims.2022.06.006
[本文引用: 1]
[19]
ZHOU L F YANG L N FANG H Lunar rover path planning based on comprehensive genetic algorithm based on slip prediction
[J]. Journal of Physics: Conference Series , 2019 , 1267 .
[本文引用: 1]
[21]
黄智榜 ,胡立坤 ,张宇 ,等 基于改进跳点搜索策略的安全路径研究
[J]. 计算机工程与应用 , 2021 , 57 (1 ): 56 -61 .
[本文引用: 1]
HUANG Z B HU L K ZHANG Y et al Research on security path based on improved hop search strategy
[J]. Computer Engineering and Application , 2021 , 57 (1 ): 56 -61 .
[本文引用: 1]
[22]
马新国 ,马希青 融合改进RRT和Dijkstra算法的机器人动态路径规划
[J]. 组合机床与自动化加工技术 , 2023 , 2 : 5 -9 .
[本文引用: 2]
MA X G MA X Q Robot path planning based on improved RRT and Dijkstra approach
[J]. Combined Machine Tool and Automated Processing Technology , 2023 , 2 : 5 -9 .
[本文引用: 2]
[23]
[本文引用: 3]
XIE C C LI Y Path planning of mobile robots based on improved algorithm
[J]. Journal of Chongqing University , 2021 , 45 (12 ): 140 -148 .
DOI:10.11835/j.issn.1000-582X.2021.12.012
[本文引用: 3]
改进自适应遗传算法在移动机器人路径规划中的应用
1
2017
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
改进自适应遗传算法在移动机器人路径规划中的应用
1
2017
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于改进遗传算法的机器人动态路径规划
1
2016
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于改进遗传算法的机器人动态路径规划
1
2016
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
一种基于遗传模拟退火算法的通信卫星资源规划方法
1
2021
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
一种基于遗传模拟退火算法的通信卫星资源规划方法
1
2021
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
Research status of mobile robot path planning based on genetic algorithm
0
2020
A new evolving mechanism of genetic algorithm for multi-constraint intelligent camera path planning
0
2021
基于多目标遗传算法的实验目标车底盘结构优化
1
2021
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于多目标遗传算法的实验目标车底盘结构优化
1
2021
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
人工势场引导蚁群算法的机器人导航路径规划
1
2021
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
人工势场引导蚁群算法的机器人导航路径规划
1
2021
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
Path planning and control of soccer robot based on genetic algorithm
1
2019
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于细菌觅食和蚁群算法的工艺路线优化
1
2020
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于细菌觅食和蚁群算法的工艺路线优化
1
2020
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于改进遗传算法的自动导引小车路径规划及其实现平台
1
2017
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于改进遗传算法的自动导引小车路径规划及其实现平台
1
2017
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
Local path planning of driverless car navigation based on jump point search method under urban environment
1
2017
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于位置代价A*算法的机械臂避障路径规划
1
2021
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
基于位置代价A*算法的机械臂避障路径规划
1
2021
... 机器人在军事领域中的应用越来越广泛.在军事活动中,机器人快速、高效地完成任务的第1步在于确定任务路线即路径规划.在具有若干障碍物的复杂环境下,自主移动机器人路径规划的核心是在起点与终点之间规划一条综合性能(如规划速度、路径长度、能量损耗等)最优的路径[1 ] .综合考虑复杂三维地形和动态障碍物环境等诸多因素下的路径规划是目前研究的新方向[2 ] .算法的优劣性在路径规划中起着关键作用.现有的算法包括传统算法和智能算法,其中常用的路径规划算法有遗传算法[3 -8 ] 、人工势场法[9 -11 ] 、蚁群算法[12 ] 、灰狼算法[13 ] 、跳点搜索(j u m p p o i n t s e a r c h , J P S [14 ] 和A * [15 ] 等.无论是传统算法还是智能算法都存在着自身缺陷,但可以通过融合算法弥补各算法的不足而使其呈现更优异的性能. ...
改进遗传算法在机器人路径规划中的应用
1
2022
... 遗传算法是一种智能搜索算法.它以生物进化为原型,相较于传统的路径规划算法具有较好的全局搜索能力和收敛性,但局部搜索能力差.其具有良好的可扩展性,易与其他算法结合,因此是融合算法中常用的一种算法.杨博等[16 ] 采用中间插值法,通过改进交叉算子、变异算子和适应度函数来优化遗传算法,避免了早熟现象发生,但是未考虑动态障碍物环境下算法的适应性.陈亮等[17 ] 将遗传算法与鲸鱼算法相结合,使得融合算法能在短时间内完成进化,但是当规划空间规模较大时仍存在迭代次数较大的问题.徐兴等[18 ] 提出了基于灾变策略的遗传算法,相对于传统遗传算法,可避免早熟现象且缩短寻优时间.Zhou等[19 ] 研究后发现,面对现实复杂地形和环境,采用单一的遗传算法因受到算法本身的限制而不能得到理想的结果. ...
改进遗传算法在机器人路径规划中的应用
1
2022
... 遗传算法是一种智能搜索算法.它以生物进化为原型,相较于传统的路径规划算法具有较好的全局搜索能力和收敛性,但局部搜索能力差.其具有良好的可扩展性,易与其他算法结合,因此是融合算法中常用的一种算法.杨博等[16 ] 采用中间插值法,通过改进交叉算子、变异算子和适应度函数来优化遗传算法,避免了早熟现象发生,但是未考虑动态障碍物环境下算法的适应性.陈亮等[17 ] 将遗传算法与鲸鱼算法相结合,使得融合算法能在短时间内完成进化,但是当规划空间规模较大时仍存在迭代次数较大的问题.徐兴等[18 ] 提出了基于灾变策略的遗传算法,相对于传统遗传算法,可避免早熟现象且缩短寻优时间.Zhou等[19 ] 研究后发现,面对现实复杂地形和环境,采用单一的遗传算法因受到算法本身的限制而不能得到理想的结果. ...
基于AGA-WOA算法融合的移动机器人路径规划
1
2021
... 遗传算法是一种智能搜索算法.它以生物进化为原型,相较于传统的路径规划算法具有较好的全局搜索能力和收敛性,但局部搜索能力差.其具有良好的可扩展性,易与其他算法结合,因此是融合算法中常用的一种算法.杨博等[16 ] 采用中间插值法,通过改进交叉算子、变异算子和适应度函数来优化遗传算法,避免了早熟现象发生,但是未考虑动态障碍物环境下算法的适应性.陈亮等[17 ] 将遗传算法与鲸鱼算法相结合,使得融合算法能在短时间内完成进化,但是当规划空间规模较大时仍存在迭代次数较大的问题.徐兴等[18 ] 提出了基于灾变策略的遗传算法,相对于传统遗传算法,可避免早熟现象且缩短寻优时间.Zhou等[19 ] 研究后发现,面对现实复杂地形和环境,采用单一的遗传算法因受到算法本身的限制而不能得到理想的结果. ...
基于AGA-WOA算法融合的移动机器人路径规划
1
2021
... 遗传算法是一种智能搜索算法.它以生物进化为原型,相较于传统的路径规划算法具有较好的全局搜索能力和收敛性,但局部搜索能力差.其具有良好的可扩展性,易与其他算法结合,因此是融合算法中常用的一种算法.杨博等[16 ] 采用中间插值法,通过改进交叉算子、变异算子和适应度函数来优化遗传算法,避免了早熟现象发生,但是未考虑动态障碍物环境下算法的适应性.陈亮等[17 ] 将遗传算法与鲸鱼算法相结合,使得融合算法能在短时间内完成进化,但是当规划空间规模较大时仍存在迭代次数较大的问题.徐兴等[18 ] 提出了基于灾变策略的遗传算法,相对于传统遗传算法,可避免早熟现象且缩短寻优时间.Zhou等[19 ] 研究后发现,面对现实复杂地形和环境,采用单一的遗传算法因受到算法本身的限制而不能得到理想的结果. ...
基于改进遗传算法的移动机器人全局路径规划
1
2022
... 遗传算法是一种智能搜索算法.它以生物进化为原型,相较于传统的路径规划算法具有较好的全局搜索能力和收敛性,但局部搜索能力差.其具有良好的可扩展性,易与其他算法结合,因此是融合算法中常用的一种算法.杨博等[16 ] 采用中间插值法,通过改进交叉算子、变异算子和适应度函数来优化遗传算法,避免了早熟现象发生,但是未考虑动态障碍物环境下算法的适应性.陈亮等[17 ] 将遗传算法与鲸鱼算法相结合,使得融合算法能在短时间内完成进化,但是当规划空间规模较大时仍存在迭代次数较大的问题.徐兴等[18 ] 提出了基于灾变策略的遗传算法,相对于传统遗传算法,可避免早熟现象且缩短寻优时间.Zhou等[19 ] 研究后发现,面对现实复杂地形和环境,采用单一的遗传算法因受到算法本身的限制而不能得到理想的结果. ...
基于改进遗传算法的移动机器人全局路径规划
1
2022
... 遗传算法是一种智能搜索算法.它以生物进化为原型,相较于传统的路径规划算法具有较好的全局搜索能力和收敛性,但局部搜索能力差.其具有良好的可扩展性,易与其他算法结合,因此是融合算法中常用的一种算法.杨博等[16 ] 采用中间插值法,通过改进交叉算子、变异算子和适应度函数来优化遗传算法,避免了早熟现象发生,但是未考虑动态障碍物环境下算法的适应性.陈亮等[17 ] 将遗传算法与鲸鱼算法相结合,使得融合算法能在短时间内完成进化,但是当规划空间规模较大时仍存在迭代次数较大的问题.徐兴等[18 ] 提出了基于灾变策略的遗传算法,相对于传统遗传算法,可避免早熟现象且缩短寻优时间.Zhou等[19 ] 研究后发现,面对现实复杂地形和环境,采用单一的遗传算法因受到算法本身的限制而不能得到理想的结果. ...
Lunar rover path planning based on comprehensive genetic algorithm based on slip prediction
1
2019
... 遗传算法是一种智能搜索算法.它以生物进化为原型,相较于传统的路径规划算法具有较好的全局搜索能力和收敛性,但局部搜索能力差.其具有良好的可扩展性,易与其他算法结合,因此是融合算法中常用的一种算法.杨博等[16 ] 采用中间插值法,通过改进交叉算子、变异算子和适应度函数来优化遗传算法,避免了早熟现象发生,但是未考虑动态障碍物环境下算法的适应性.陈亮等[17 ] 将遗传算法与鲸鱼算法相结合,使得融合算法能在短时间内完成进化,但是当规划空间规模较大时仍存在迭代次数较大的问题.徐兴等[18 ] 提出了基于灾变策略的遗传算法,相对于传统遗传算法,可避免早熟现象且缩短寻优时间.Zhou等[19 ] 研究后发现,面对现实复杂地形和环境,采用单一的遗传算法因受到算法本身的限制而不能得到理想的结果. ...
基于遗传算法的移动机器人的一种路径规划方法
1
2004
... 遗传算法借用达尔文进化理论以算法的形式表现出来就是遗传算法的运行过程.遗传算法在计算种群适应度函数时具有较大的计算量,导致算法执行处理时间较长,搜索效率低下[20 ] .J P S A * A * [21 ] . ...
基于遗传算法的移动机器人的一种路径规划方法
1
2004
... 遗传算法借用达尔文进化理论以算法的形式表现出来就是遗传算法的运行过程.遗传算法在计算种群适应度函数时具有较大的计算量,导致算法执行处理时间较长,搜索效率低下[20 ] .J P S A * A * [21 ] . ...
基于改进跳点搜索策略的安全路径研究
1
2021
... 遗传算法借用达尔文进化理论以算法的形式表现出来就是遗传算法的运行过程.遗传算法在计算种群适应度函数时具有较大的计算量,导致算法执行处理时间较长,搜索效率低下[20 ] .J P S A * A * [21 ] . ...
基于改进跳点搜索策略的安全路径研究
1
2021
... 遗传算法借用达尔文进化理论以算法的形式表现出来就是遗传算法的运行过程.遗传算法在计算种群适应度函数时具有较大的计算量,导致算法执行处理时间较长,搜索效率低下[20 ] .J P S A * A * [21 ] . ...
融合改进RRT和Dijkstra算法的机器人动态路径规划
2
2023
... 由表1 可知:相较于改进遗传算法和传统遗传算法,JPSG算法的规划路径长度最短,收敛迭代次数最少;准确率分别提高了72%、90%;规划时间分别减小了12%、15%;方差值分别减小了30%、31%,表明J P S G J P S G 图10 所示.将JPSG算法与文献[22 ]和文献[23 ]提出的RRT(rapidly-exploring random tree,快速搜索随机树)算法和改进遗传-鲸鱼融合算法等进行对比,算法性能对比如表2 和表3 所示. ...
... JPSG 算法与文献[22 ]中算法的性能对比 ...
融合改进RRT和Dijkstra算法的机器人动态路径规划
2
2023
... 由表1 可知:相较于改进遗传算法和传统遗传算法,JPSG算法的规划路径长度最短,收敛迭代次数最少;准确率分别提高了72%、90%;规划时间分别减小了12%、15%;方差值分别减小了30%、31%,表明J P S G J P S G 图10 所示.将JPSG算法与文献[22 ]和文献[23 ]提出的RRT(rapidly-exploring random tree,快速搜索随机树)算法和改进遗传-鲸鱼融合算法等进行对比,算法性能对比如表2 和表3 所示. ...
... JPSG 算法与文献[22 ]中算法的性能对比 ...
基于改进算法的移动机器人路径规划
3
2021
... 由表1 可知:相较于改进遗传算法和传统遗传算法,JPSG算法的规划路径长度最短,收敛迭代次数最少;准确率分别提高了72%、90%;规划时间分别减小了12%、15%;方差值分别减小了30%、31%,表明J P S G J P S G 图10 所示.将JPSG算法与文献[22 ]和文献[23 ]提出的RRT(rapidly-exploring random tree,快速搜索随机树)算法和改进遗传-鲸鱼融合算法等进行对比,算法性能对比如表2 和表3 所示. ...
... JPSG 算法与文献[23 ]中算法的性能对比 ...
... 由表3 可知,J P S G 23 ]中的遗传算法、改进遗传算法和改进遗传-鲸鱼融合算法在地图规模和障碍物简单的状况下的搜索效率更优. ...
基于改进算法的移动机器人路径规划
3
2021
... 由表1 可知:相较于改进遗传算法和传统遗传算法,JPSG算法的规划路径长度最短,收敛迭代次数最少;准确率分别提高了72%、90%;规划时间分别减小了12%、15%;方差值分别减小了30%、31%,表明J P S G J P S G 图10 所示.将JPSG算法与文献[22 ]和文献[23 ]提出的RRT(rapidly-exploring random tree,快速搜索随机树)算法和改进遗传-鲸鱼融合算法等进行对比,算法性能对比如表2 和表3 所示. ...
... JPSG 算法与文献[23 ]中算法的性能对比 ...
... 由表3 可知,J P S G 23 ]中的遗传算法、改进遗传算法和改进遗传-鲸鱼融合算法在地图规模和障碍物简单的状况下的搜索效率更优. ...