面向灰库清理的超大伸缩比机械臂结构设计与刚度优化

doi:10.3785/j.issn.1006-754X.2022.00.054

面向灰库清理的超大伸缩比机械臂结构设计与刚度优化

张嘉宁^,^,, 张明路, 李满宏^,^,, 张坦

河北工业大学机械工程学院, 天津 300401

Structural design and stiffness optimization of mechanical arm with super large telescopic ratio for ash silo cleaning

ZHANG Jia-ning^,^,, ZHANG Ming-lu, LI Man-hong^,^,, ZHANG Tan

School of Mechanical Engineering, Hebei University of Technology, Tianjin 300401, China

通讯作者: 李满宏（1987—），男，河北唐山人，副教授，博士，从事特种机器人技术研究，E-mail：lmh9181219@163.com，https：//orcid.org/0000-0001-5372-6268李满宏（1987—），男，河北唐山人，副教授，博士，从事特种机器人技术研究，E-mail：lmh9181219@163.com，https：//orcid.org/0000-0001-5372-6268

收稿日期: 2021-09-02 修回日期: 2021-10-11

基金资助:

国家重点研发计划资助项目. 2018YFB1309401

Received: 2021-09-02 Revised: 2021-10-11

作者简介 About authors

张嘉宁（1995—），男，辽宁营口人，硕士生，从事机器人结构优化设计研究，E-mail：melohebut@163.com，https：//orcid.org/0000-0002-3583-7439 , E-mail：melohebut@163.com

摘要

火电厂灰库内壁粉尘粘壁、板结、搭桥等现象严重影响火电机组的安全运营，因此须对灰库内壁积灰进行定期全域清理。针对现有灰库清理机器人作业区间有限及因机械臂伸缩比不足、刚度不大导致的清理效果不佳等问题，通过设计引入往复绳排驱动机构和多级嵌套箱型臂体，设计了大刚度、伸缩比为1∶7的机械臂整体结构，研制出一款面向灰库内壁全方位清理的高效作业机器人。基于机械臂级联臂体本征结构和内外耦合作用力系深度分析，结合Castigliano第二定理和线弹性原理，建立了在复杂交变载荷作用下变长度机械臂整体刚度模型。综合考虑在极端工况下机械臂应力分布特征，通过周期性拓扑优化低应力区各离散子域孔洞形状，提出了在严苛质量约束下机械臂全域刚度优化方法。机械臂性能仿真和测试实验表明：优化后机械臂质量大幅减小，且具备理想的伸缩区间和刚度特性；机械臂末端偏移量的测试值与仿真值存在一定偏差，系机械臂加工和装配误差所致。研究结果为灰库清理机器人的结构设计和刚度优化提供了重要参考。

关键词： 伸缩机械臂 ; 结构设计 ; 刚度优化 ; 灰库清理

Abstract

The phenomena of dust sticking, hardening and bridging on the inner wall of ash silo in thermal power plant seriously affect the safe operation of thermal power units, so it is necessary to clean the ash on the inner wall of ash silo regularly. In view of the limited working range of the existing ash silo cleaning robot and the poor cleaning effect caused by the insufficient telescopic ratio and low stiffness of its mechanical arms, reciprocating rope row drive mechanism and multi-level nested box-type arm body was introduced into the design of the overall structure of the mechanical arm with large stiffness and telescopic ratio of 1: 7. Therefore, an efficient working robot for the all-round cleaning of the inner wall of the ash silo was developed. Based on the depth analysis of the intrinsic structure of the cascade arm and the internal and external coupling force system of the mechanical arm combined with Castigliano's second theorem and the principle of linear elasticity, an overall stiffness model of the variable length mechanical arm under complex alternating loads was established. Considering the stress distribution characteristics of the mechanical arm under extreme working conditions, through the periodic topology optimization of hole shape of each discrete sub region in the low stress region, a global stiffness optimization method of the mechanical arm under severe mass constraint was proposed. The performance simulation and test results showed that the mass of the mechanical arm was greatly reduced after optimization, and the mechanical arm had ideal telescopic interval and stiffness characteristics. There was a certain deviation between the simulation value and test value of the end offset of the mechanical arm, which was caused by the machining and assembly errors of the mechanical arm. The research results provide an important reference for the structural design and stiffness optimization of ash silo cleaning robot.

Keywords： telescopic mechanical arm ; structural design ; stiffness optimization ; ash silo cleaning

PDF (4512KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张嘉宁, 张明路, 李满宏, 张坦. 面向灰库清理的超大伸缩比机械臂结构设计与刚度优化. 工程设计学报[J], 2022, 29(4): 430-437 doi:10.3785/j.issn.1006-754X.2022.00.054

ZHANG Jia-ning, ZHANG Ming-lu, LI Man-hong, ZHANG Tan. Structural design and stiffness optimization of mechanical arm with super large telescopic ratio for ash silo cleaning. Chinese Journal of Engineering Design[J], 2022, 29(4): 430-437 doi:10.3785/j.issn.1006-754X.2022.00.054

近年来，我国火电机组装机容量持续增长，燃煤发电量约占总发电量的70%^［1-3］。在燃煤发电过程中有大量毒粉尘产生，须将它经过一系列分流净化处理后暂贮存于灰库以待后续开发利用。灰库中的粉尘极易与水分子结合引发富集效应，致使粉尘粘壁、板结、搭桥现象时有发生，严重影响火电机组的安全运营^［4-6］。因此，定期清理灰库内壁的积灰已成为保障火电机组安全运营的重要举措之一。鉴于库内积灰清理区域巨大且作业环境中粉尘弥漫，传统的人工入库作业模式普遍存在作业周期长、清理效果差、作业风险高等问题，因此迫切需要研发一款适用于灰库内壁全方位清理的高效作业机器人。

目前，国内外学者针对灰库清理机器人已开展了大量探索性研究。如：罗宽等^［6］基于典型剪叉升降机构设计了桁架式灰库清理机器人，初步实现了井下煤仓内壁重点区域的局部清理；曹毅等^［7］基于绳索吊装机构研发了悬臂式灰库清理机器人，有效解决了灰库内壁全域清理难题；Dandan等^［8］融合伞状清灰机构研制了偏载式灰库清理机器人，初步解决了安装尺寸受限与灰库全域清理需求之间的技术冲突。

灰库清理机器人普遍采用伸缩机械臂作为其主体结构。由于灰库复杂结构的限制和严苛的尺寸约束，现有清理机器人普遍存在作业范围有限、清理效果不佳等问题^［9］，其主要原因为：1）机械臂伸缩比不足，在回转作业模式下机械臂达到最大行程时还无法与远端壁面充分接触，在最小行程时会与近端壁面产生极大干涉，以致在库顶偏置安装的情况下难以进行全方位清理；2）机械臂刚度性能欠佳，在清理机器人超长伸长作业状态下其末端偏移量较大，难以保证良好的清理效果。

针对上述问题，笔者通过设计引入往复绳排驱动机构和多级嵌套箱型臂体，设计了大刚度、超大伸缩比的机械臂整体结构，研制了一款面向灰库内壁全方位清理的高效作业机器人。基于机械臂本征结构及作用力系深度分析，结合Castigliano第二定理和线弹性原理，建立在复杂载荷作用下变长度机械臂整体刚度模型；综合考虑在极端工况下机械臂应力分布特征，通过周期性拓扑优化低应力区各离散子域孔洞形状，提出在严苛质量约束下机械臂全域刚度优化方法，并系统地开展灰库清理机器人样机性能测试实验。

1 机械臂结构优化设计

火电厂灰库通常呈立式仓筒状，其内腔直径及高度均接近15 m，而位于库顶的机器人安装孔直径仅为500 mm，且处于严重的偏置状态，安装孔中心距灰库内壁最近端仅1.3 m，因此存在机器人安装尺寸受限与库壁全域清理需求之间的技术冲突。为此，笔者在深度剖析现有清理机器人构型原理的基础上，通过设计引入绳排驱动机构和嵌套箱型臂体，设计了一款大刚度、超大伸缩比的机械臂，以实现库壁积灰安全、高效、智能清理。

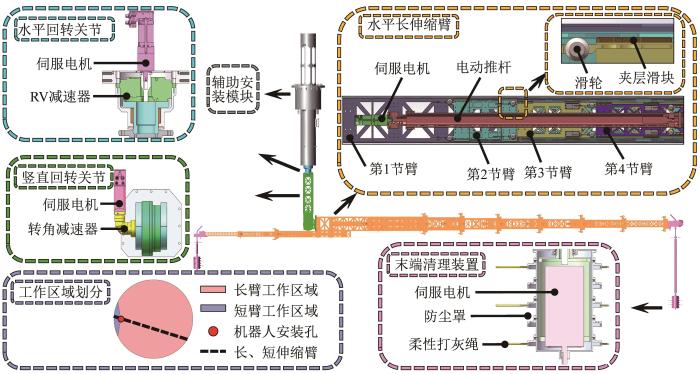
灰库清理机器人的整体结构如图1所示。其主要包括辅助安装模块、水平回转关节、竖直回转关节、水平长伸缩臂和末端清理装置等。辅助安装模块设置于机器人与库顶安装孔之间，用于机器人的辅助拆装与可靠固定；由伺服电机和RV （rotational vector）减速器组成的水平回转关节与竖直回转关节正交连接于辅助安装模块的正下方，水平回转关节用于驱动机械臂在水平面内360°回转，竖直回转关节用于实现机械臂竖直与水平状态间的切换；清理装置搭载于长、短机械臂的末端，通过与机械臂的协同配合，驱动柔性打灰绳实现库壁积灰柔顺接触式清理。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 灰库清理机器人整体结构

Fig.1 Overall structure of ash silo cleaning robot

灰库清理机器人的主要技术参数如表1所示。

表1 灰库清理机器人主要技术参数

Table 1 Main technical parameters of ash silo cleaning robot

技术参数	数值
长伸缩臂数量/节	8
长伸缩臂单节长度/m	2
短伸缩臂数量/节	3
短伸缩臂单节长度/m	2
长伸缩臂臂长变化范围/m	3.28~13.70
短伸缩臂臂长变化范围/m	1.30~3.28
竖直回转关节旋转角度/(°)	0~90
水平回转关节旋转角度/(°)	0~200
竖向清理区间长度/m	0~13.5

新窗口打开| 下载CSV

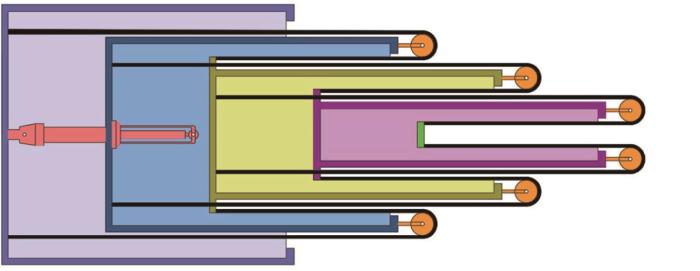
综合考虑机械臂的安装约束、导向要求、刚度特性和加工性能等，采用标准规格的铝合金方管制作机械臂。鉴于绳排机构具有较大伸缩范围和同比伸缩特性，选择其作为机械臂伸缩驱动机构。伸缩臂内部绳排布置方式如图2所示。当精密直线执行器外伸长度为 $Δ l$ 时，长伸缩臂的7节节臂在绳排机构的驱动下外伸量均为 $Δ l$ ，则长伸缩臂总体长度共增加 $7 Δ l$ ，因而伸缩比（即电动推杆轴向位移与伸缩臂整体轴向位移之比）可达1∶7。考虑到机械臂在伸缩过程中均衡受力的要求，绳排伸缩机构中外伸绳排与回缩绳排均设置2组，分别对称布置于箱型臂体的竖直与水平表面。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 伸缩臂内部绳排布置方式

Fig.2 Inner rope arrangement of telescopic arm

短伸缩臂与长伸缩臂的结构相似，绳排机构布置方式也相同。其伸缩比为1∶2。

利用超大伸缩比的机械臂和柔性末端清理装置，辅以水平回转关节与竖直回转关节的协同配合，能够有效解决机器人安装尺寸受限与库壁全域清理需求之间的技术冲突。

2 机械臂刚度特性分析

在机器人清灰过程中机械臂通常处于超长伸长状态，且承受复杂的内外交变载荷，故其刚度特性关系着机器人的运动性能及作业效果。为此，基于机械臂本征结构及作用力系深度分析，结合Castigliano第二定理和线弹性原理，建立在复杂载荷作用下变长度机械臂的整体刚度模型，以系统分析机械臂的刚度特性，为机械臂性能优化奠定基础。

为构建机械臂整体刚度模型，综合考虑机械臂的结构特征、运动特性及作用力系特点，提出如下几点合理假设：

1）鉴于箱型臂体截面尺寸远小于其长度，视各节臂体为匀质直杆，并忽略其轴向变形；

2）各节臂体的尾部外侧及头部内侧设有按周向布置的滑块支撑，因此各节臂体视作外伸简支梁；

3）由于伸缩臂整体可视作二力杆件，且其形变尺寸远小于整体尺寸，属弹性小变形范畴，故线弹性体假设成立。

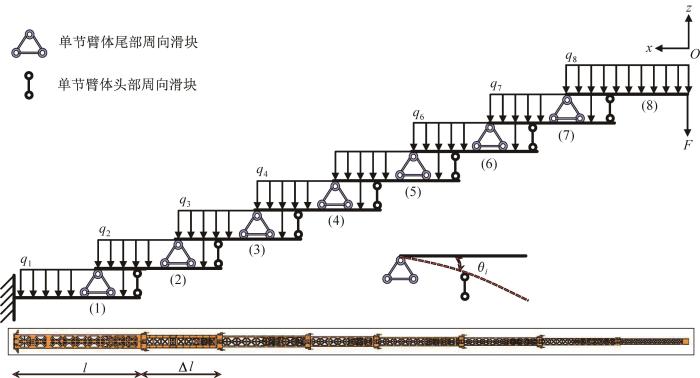
根据上述假设，伸缩臂整体可以简化为在复杂外部荷载作用下的变长度悬臂梁。长伸缩臂的层叠图如3所示，图中数字为单节箱型臂体的编码。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 在复杂荷载作用下的长伸缩臂的层叠图

Fig.3 Cascade diagram of long telescopic arm under complex load

单节臂体末端偏移量可近似由末端竖向位移与转角位移组成。伸缩臂总体偏移量可基于叠加原理进行求解，则：

f = \sum_{i = 1}^{8} δ_{i} + (7 Δ l + l) \sum_{i = 1}^{8} θ_{i}

式中：f为伸缩臂总偏移量； $δ_{i}$ 为单节臂体末端竖向位移； $θ_{i}$ 为单节臂体转角，rad；l为单节臂体长度。

当 $Δ l \geq \frac{1}{2} l$ 时，机械臂任意截面的弯矩M_x 为：

M_{x} = \{\begin{array}{l} - F x - \frac{1}{2} q_{8} x^{2}, & 0 \leq x < Δ l \\ - F x - \frac{1}{2} q_{8} x^{2} - \frac{1}{2} q_{7} {(x - Δ l)}^{2}, & Δ l \leq x < l \\ - F x - M_{i x} - \frac{1}{2} q_{(9 - i)} {[x - (i - 1) Δ l]}^{2}, & \begin{matrix} l + (i - 2) Δ l \leq x < i Δ l & (i = 2, 3, \dots, 7) \end{matrix} \\ - F x - M_{i x} - \frac{1}{2} q_{(9 - i)} {[x - (i - 1)]}^{2} - \frac{1}{2} q_{(8 - i)} {(x - i Δ l)}^{2}, & i Δ l \leq x < l + (i - 1) Δ l \\ - F x - M_{i x} - \frac{1}{2} q_{1} {(x - 7 Δ l)}^{2}, & l + 6 Δ l \leq x < l + 7 Δ l \end{array}

式中：x为机械臂末端到计算截面的距离；F为末端清理装置重量； $M_{i x}$ 为第i节臂体尾端截面前全部重力对求解截面的弯矩；q_i 为第i节臂体自重均布载荷。

根据材料力学相关理论，可以忽略轴向力和剪切力对机械臂末端偏移量的影响，主要考虑横向作用力。因此，基于Castigliano第二定理^［10-14］，结合伸缩臂任意截面的弯矩表达式，通过分段积分求得机械臂的末端竖向位移 $δ$ 及转角 $θ$ ，如式（3）和式（4）所示。

\begin{array}{l} δ = \int_{0}^{l} \frac{M_{x}}{E I_{1}} \frac{\partial M_{x}}{\partial F} d x + \sum_{i = 2}^{7} \int_{l + (i - 2) Δ l}^{l + (i - 1) Δ l} \frac{M_{x}}{E I_{i}} \frac{\partial M_{x}}{\partial F} d x + \\ \int_{l + 6 Δ l}^{l + 7 Δ l} \frac{M_{x}}{E I_{8}} \frac{\partial M_{x}}{\partial F} d x \end{array}

\begin{array}{l} θ = \int_{0}^{l} \frac{M_{x}}{E I_{1}} \frac{\partial M_{s x}}{\partial M_{e}} d x + \sum_{i = 2}^{7} \int_{l + (i - 2) Δ l}^{l + (i - 1) Δ l} \frac{M_{x}}{E I_{i}} \frac{\partial M_{s x}}{\partial M_{e}} d x + \\ \int_{l + 6 Δ l}^{l + 7 Δ l} \frac{M_{x}}{E I_{8}} \frac{\partial M_{x}}{\partial F} d x \end{array}

式中： $E I_{i}$ 为第i节臂体的抗弯刚度； $M_{s x}$ = $M_{i x}$ + $M_{e}$ ，其中 $M_{e}$ 为施加于机械臂末端的虚拟弯矩，实际取值为0。

转角 $θ$ 造成的伸缩臂末端位移 $ψ$ 可由 $ψ = (l + 7 Δ l) t a n θ$ 求取。

根据线弹性原理并联立式（3）和式（4），可得机械臂的等效刚度K为：

K = \frac{F}{δ + ψ}

当 $Δ l \leq \frac{1}{2} l$ 时，机械臂刚度的构建过程与 $Δ l \geq \frac{1}{2} l$ 时完全相同，仅仅是截面弯矩表达式不同，最后可以得到相同的等效刚度表达式。

通过以上分析可知，单节臂体长度l、外伸长度 $Δ l$ 、抗弯刚度 $E I_{i}$ 、自重q_i 相互耦合作用，共同决定着机械臂的整体刚度特性。

3 机械臂全域刚度优化

通过机械臂刚度特性分析可知，机械臂整体刚度主要由各节臂体的结构参数、外伸长度和材料参数共同决定。机械臂安装尺寸、截面形状约束严苛，且库顶承重能力有限，因此在臂体几何参数与整体质量严格受限的情况下，综合考虑在极端工况下机械臂应力分布特征，通过周期性拓扑优化低应力区各离散子域孔洞形状建立机械臂全域刚度优化方法，是至关重要的。

综合考虑机械臂在典型工况下的作业位姿，确定长、短伸缩臂在额定负载下达到最大行程时为极端工况。由于长伸缩臂自重及最大行程均大于短伸缩臂，故以长伸缩臂为例开展应力分析。

选择铝合金为臂体材料，采用扫略法将长伸缩臂划分为102 786个单元。机械臂左端设置为固定端，施加相应重力场及相应荷载，其在极端工况下的等效应力云图如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 长伸缩臂在极端工况下的等效应力云图

Fig.4 Equivalent stress cloud diagram of long telescopic arm under extreme working condition

由图4可知，在极端工况下，后四节臂体上、下翼缘板及腹板全部区域均处于低应力区，前四节臂体上、下翼缘板及腹板中间区域均处于较低应力区。因此，箱型臂体各腹板中间区域均具有极大的轻量化潜质，可通过合理优化低应力区中孔洞形状来满足在严格质量要求下的刚度最大化要求，并在优化过程中保证其具有良好的加工性能^［14-16］。

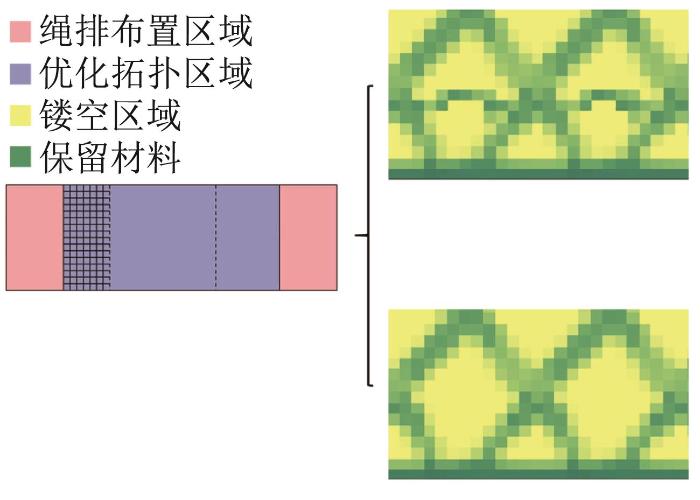
为此，将优化设计区域划分为a个子域，在各子域的孔洞拓扑优化过程中执行相同的优化准则，以确保各子域拓扑形状具有周期性。周期性拓扑优化孔洞形状的原理如图5所示。在优化初期，随着迭代次数的增加，子域内涌现孔洞，质量逐渐减小；随着优化逐步深入，孔洞发生合并现象，孔洞数量逐渐稳定。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 周期性拓扑优化孔洞形状原理示意

Fig.5 Principle schematic of periodic topology optimization of hole shape

建立合理的优化数学模型和优化准则^［17-18］，对优化设计区域内孔洞形状进行周期性拓扑优化。基于SIMP （solid isotropic material with penalization，固体各向同性材料惩罚）方法，以单节臂体中设计域单元相对密度为设计变量，以体积约束下最小柔顺度为目标函数，综合考虑长伸缩臂的力学特性和加工性能等因素，则优化数学模型为：

\{\begin{array}{l} m i n C (r_{m n}) = U^{T} K U = \sum_{m = 1}^{a} \sum_{n = 1}^{b} {(r_{m n})}^{p} u_{m n}^{T} k_{0} u_{m n} \\ s . t . K U = F \\ V = σ \cdot V_{0} = \sum_{m = 1}^{a} \sum_{n = 1}^{b} r_{m n} V_{m n} \\ r_{1 n} = r_{m n} \\ 0 \leq r_{m i n} \leq r_{m n} \leq r_{m a x} \leq 1 \end{array}

式中：C（r_mn ）为结构柔顺度； U 为结构位移向量； K 为结构刚度矩阵； $r_{m n}$ 为设计变量，即单元相对密度，初始单元的相对密度为1，无材料孔洞的相对密度为0； p为惩罚因子； u_mn 为单元位移矢量； k₀为初始单元刚度矩阵；a为子域个数；b为子域内单元个数；σ为保留体积分数；V₀为结构初始体积；V_mn 为单元体积； $r_{m a x}$ 为设计变量上限取值； $r_{m i n}$ 为设计变量下限取值。

在求解上述数学模型最优解的过程中，建立迭代次数少、求解效率高的收敛准则是极为关键的。为此，基于Lagrange乘数法及Kuhn-Tucker条件对迭代准则进行推导，构建Lagrange函数：

\begin{array}{l} L (r_{m n}, μ_{m}) = C (r_{m n}) + μ_{1} (V - σ V_{0}) + \\ μ_{2}^{T} \cdot (K U - F) + μ_{3} (r_{m i n} - r_{m n} + t_{m n}^{2}) + \\ μ_{4} (r_{m n} - r_{m a x} + s_{m n}^{2}) + \sum_{m = 1}^{a - 1} λ_{m} (r_{m n} - r_{(m + 1) n}) \end{array}

式中： $μ_{1}$ 、 $μ_{2}$ 、 $μ_{3}$ 、 $μ_{4}$ 、 $λ_{m}$ 为Lagrange乘子； $t_{m n}^{2}$ 和 $s_{m n}^{2}$ 为松弛因子。

当 $r_{m n}$ 取极值时，式（7）应满足Kuhn-Tucker条件，具体为：

\{\begin{array}{l} \frac{\partial L}{\partial r_{m n}} = \frac{\partial C}{\partial r_{m n}} + μ_{1} \frac{\partial V}{\partial r_{m n}} + μ_{2}^{T} \frac{\partial (K U)}{\partial r_{m n}} - μ_{3} + μ_{4} \\ V = σ V_{0} \\ F = K U \\ μ_{3} (r_{m i n} - r_{m n}) = 0 \\ μ_{4} (r_{m n} - r_{m a x}) = 0 \\ μ_{3 m n} > 0 \\ μ_{4 m n} > 0 \end{array}

当 $L (r_{m n}, μ_{m})$ 取极值，且 $μ_{2}$ 为任意值，将 $C = U^{T} K U$ 及 $μ_{2} = - 2 U$ 代入式（8），可得：

\frac{\partial L}{\partial r_{m n}} = - U^{T} \frac{\partial K}{\partial r_{m n}} U + μ_{1} \frac{\partial V}{\partial r_{m n}} = 0

基于人工材料密度数学模型可得 $k_{m n} = {(r_{m n})}^{p} k_{0}$ 和单元应变能 $E_{_{m n}} = \frac{1}{2} u_{m n}^{T} k_{m n} u_{m n}$ ，单元应变能与相对密度之间的关系为：

2 p E_{m n} = μ_{1} r_{m n} V_{m n}

对各子域内n单元求和即可确定优化准则，即：

g_{n}^{k} = \frac{2 p E_{n}}{μ_{1} V_{0} r_{n}} = 1

式中：k为迭代次数；拉格朗日乘子 $μ_{_{1}}$ 可基于k代与 $k + 1$ 代体积之差的泰勒展开式求解；E_n 为第n单元应变能；r_n 为第n单元相对密度。

由式（11）可推导出拓扑优化的收敛准则为：

r_{n}^{k + 1} = \{\begin{matrix} {(g_{n}^{k})}^{γ} r_{n}^{k}, & r_{m i n} < {(g_{n}^{k})}^{γ} r_{n}^{k} < r_{m a x} \\ r_{m i n}, & {(g_{n}^{k})}^{γ} r_{n}^{k} \leq r_{m i n} \\ r_{m a x}, & r_{m a x} \leq {(g_{n}^{k})}^{γ} r_{n}^{k} \end{matrix}

式中： $γ$ 为阻尼因子，其可提升计算收敛性。

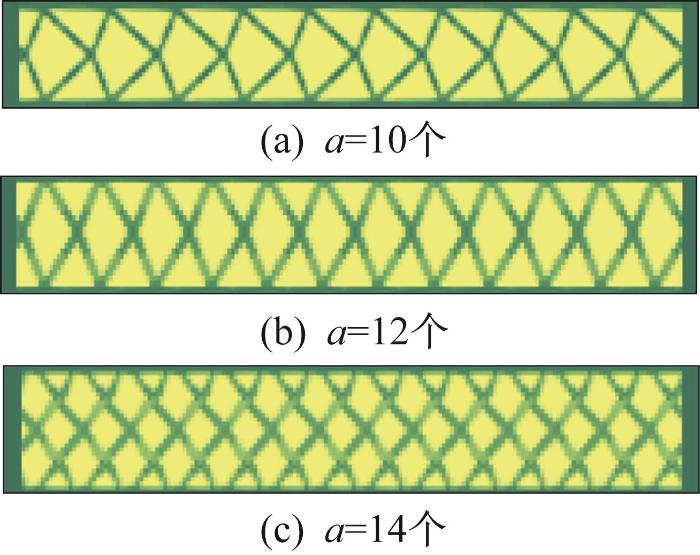
保留体积分数相同，则在不同子域数下箱型臂体孔洞周期性拓扑优化结果如6所示。由图可知，优化后材料整体呈桁架形式，且具有良好的加工性能。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 箱型臂体孔洞周期性拓扑优化结果

Fig.6 Periodic topology optimization results of box- type arm body hole

4 机械臂性能仿真和测试

为验证优化后机械臂样机的相关性能，进行机械臂性能测试实验，对在不同外伸长度下机械臂末端偏移量、刚度等关键技术指标进行测试，并将测试结果与仿真结果进行对比。机械臂性能测试实验平台如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 机械臂性能测试实验平台

Fig.7 Mechanical arm performance test platform

将机械臂水平固定于实验台上，并在其末端施加10 kg额定负载以模拟实际作业工况。箱型臂体由标准规格的6063铝合金方管加工而成。优化前机械臂质量为130.2 kg，当选取各节臂体保留体积分数σ=40%，子域数a=12个，则优化后其质量为73.6 kg，减小了43.5%。

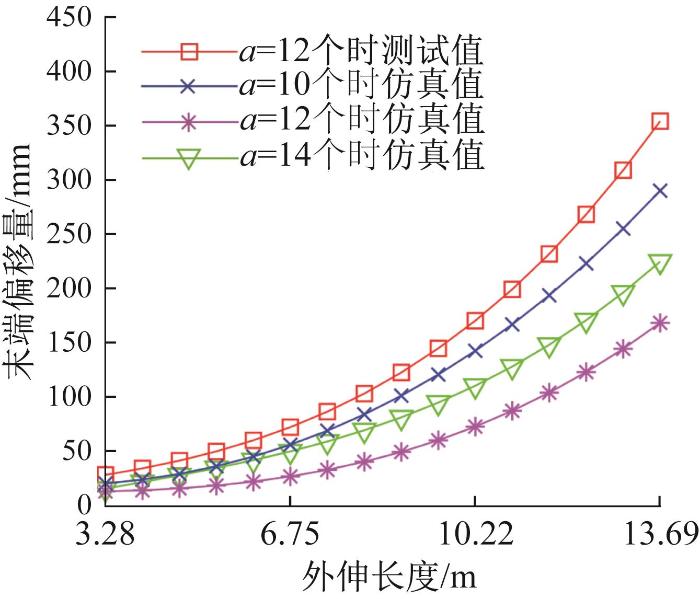
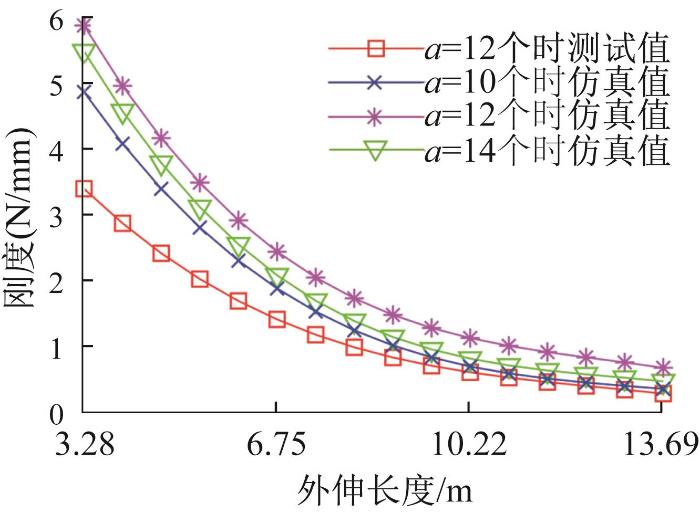
选取σ=40%，分别设置a=10，12，14个进行优化仿真。优化后机械臂在不同外伸长度下的末端偏移量和刚度的仿真和测试结果如图8和图9所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 优化后机械臂末端偏移量仿真和测试结果

Fig.8 Simulation and test results of end offset of mechanical arm after optimization

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 优化后机械臂刚度仿真和测试结果

Fig.9 Simulation and test results of stiffness of mechanical arm after optimization

由图8和图9可知：仿真中选取a=12个时，机械臂末端偏移量最小，为最优选择，与a=14个时相比末端偏移量减少25.2%；在机械臂外伸过程中，其末端偏移量呈非线性增长，刚度呈非线性下降；当机械臂外伸长度为3.28~6.75 m时，其末端偏移量的测试值与仿真值相差较小；当机械臂外伸至10.22 m后，末端偏移量的测试值与仿真值偏差较大，经分析这主要由机械臂加工和装配误差造成的。

5 结论

1）通过设计引入绳排驱动机构和嵌套箱型臂体，设计了大刚度、超大伸缩比的机械臂整体结构，成功研制出一款面向库壁全方位清理的高效作业机器人，有效解决了在应用现场机器人安装尺寸受限与库壁全域清理需求之间的技术冲突。

2）基于机械臂级联臂体本征结构和内外耦合作用力系的分析，建立了在复杂交变载荷作用下变长度机械臂的整体刚度模型。经过分析可知，机械臂整体刚度主要由各节臂体的结构参数、外伸长度和材料参数共同决定，且各参数间高度耦合，须协同优化来满足机械臂的工程应用要求。

3）综合考虑在极端作业工况下机械臂应力分布特征，通过周期性拓扑优化低应力区各离散子域孔洞形状，建立了在严苛质量约束下机械臂刚度优化方法。

4）机械臂性能仿真和测试实验表明：优化后机械臂质量大幅减小，且具备理想的伸缩区间和刚度特性；机械臂末端偏移量的测试值与仿真值存在一定偏差，系机械臂加工和装配误差所致。研究结果为灰库清理机器人的结构设计与刚度优化提供了重要参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李少华，刘冰，彭红文，等.

燃煤机组耦合生物质直燃发电技术研究

［J］.电力勘测设计，2021（6）：26-31，36.

[本文引用: 1]

Shao-hua

， LIU

Bing

， PENG

Hong-wen

， et al.

Bio-mass direct combustion of co-firing technology research in coal-fired power plants

［J］. Electric Power Survey & Design， 2021（6）： 26-31， 36.

[本文引用: 1]

[2]

潘尔生，田雪沁，徐彤，等.

火电灵活性改造的现状、关键问题与发展前景

［J］.电力建设，2020，41（9）：58-68. doi：10.12204/j.issn.1000-7229.2020.09.007

PAN

Er-sheng

， TIAN

Xue-qin

， XU

Tong

Status， crit-ical problems and prospects of flexibility retrofit of thermal power in China

［J］. Electric Power Construction， 2020， 41（9）： 58-68.

DOI:10.12204/j.issn.1000-7229.2020.09.007

[3]

SINGH

O K

， KAUSHIK

S C

Energy and exergy analysis and optimization of Kalina cycle coupled with a coal fired steam power plant

［J］. Applied Thermal Engineering， 2013， 51（1/2）： 787-800. doi：10.1016/j.applthermaleng.2012.10.006

[本文引用: 1]

[4]

王宝存，侯泽健，李鹏飞.

电厂粉煤灰筛选除湿设备的设计与研究

［J］.粉煤灰综合利用，2018（2）：29-30，34. doi：10.3969/j.issn.1005-8249.2018.02.007

[本文引用: 1]

WANG

Bao-cun

， HOU

Ze-jian

， LI

Peng-fei

Design and research of screening dehumidification equipment with power plant fly ash

［J］. Fly Ash Comprehensive Utilization， 2018（2）： 29-30， 34.

DOI:10.3969/j.issn.1005-8249.2018.02.007 [本文引用: 1]

[5]

刘建民，陈国庆，黄启龙，等.

燃煤脱硝机组空气预热器蓄热片表面飞灰沉积板结机理研究

［J］.中国电机工程学报，2016，36（S1）：132-139.

LIU

Jian-min

， CHEN

Guo-qing

， HUANG

Qi-long

， et al.

Study on mechanism of fly ash deposition and hardening on the air preheater regenerative piece surface of the coal-fired and denitration unit

［J］. Proceedings of the CSEE， 2016， 36（S1）： 132-139.

[6]

罗宽

井下煤仓清仓机器人机械臂的设计与分析

［J］.煤炭技术，2013，32（8）：41-43. doi：10.3969/j.issn.1008-8725.2013.08.021

[本文引用: 2]

LUO

Kuan

Design and analysis of underound bunker clearing robot manipulator

［J］. Coal Technology， 2013， 32（8）： 41-43.

DOI:10.3969/j.issn.1008-8725.2013.08.021 [本文引用: 2]

[7]

曹毅，臧义，刁伟华.

柔性驱动立筒仓清理机器人转动控制系统建模及简化

［J］.现代制造工程，2014（4）：24-29. doi：10.3969/j.issn.1671-3133.2014.04.006

[本文引用: 1]

CAO

， ZANG

， DIAO

Wei-hua

Systematic modeling and simplification on revolving control of flexible drive silo cleaning robot

［J］. Modern Manufacturing Engineering， 2014（4）： 24-29.

DOI:10.3969/j.issn.1671-3133.2014.04.006 [本文引用: 1]

[8]

DANDAN

， ALBITAR

， ANANIEV

， et al.

Motion control of siro： The silo cleaning robot

［J］. International Journal of Advanced Robotic Systems， 2015， 12： 184.

[本文引用: 1]

[9]

孙龙飞，房立金，梁风勇.

新型工业机器人结构设计及其全域刚度预估方法

［J］.机器人，2018，40（5）： 673-684. doi：10.1109/iisr.2018.8535652

[本文引用: 1]

SUN

Long-fei

， FANG

Li-jin

， LIANG

Feng-yong

Str-ucture design and global stiffness protection method of a novel industrial robot

［J］. Robot， 2018， 40（5）： 673-684.

DOI:10.1109/iisr.2018.8535652 [本文引用: 1]

[10]

刘双杰，郝永平.

S型折叠式微悬臂梁刚度计算

［J］.光学精密工程，2013，21（2）：388-393.

[本文引用: 1]

LIU

Shuang-jie

， HAO

Yong-ping

Calculation for spr-ing constants of folded serpentine microcantilevers

［J］.Optics and Precision Engineering， 2013， 21（2）： 388-393.

[本文引用: 1]

[11]

关立文，陈志雄，刘春，等.

钻铆机器人静刚度建模及优化

［J］.清华大学学报（自然科学版），2021，61（9）：965-971.

GUAN

Li-wen

， CHEN

Zhi-xiong

， LIU

Chun

， et al.

Static stiffness modeling for optimizing drilling and riveting robots

［J］. Journal of Tsinghua University （Science and Technology）， 2021， 61（9）： 965-971.

[12]

MEMAR

A H

， ESFAHANI

E T

A robot gripper with variable stiffness actuation for enhancing collision safety

［J］. IEEE Transactions on Industrial Electronics， 2020， 67（8）： 6607-6616. doi：10.1109/tie.2019.2938475

[13]

邵忠喜，吴石磊，富宏亚.

一种新型大口径光栅拼接柔性定位机构刚度分析

［J］.机械工程学报，2018，54（13）：117-125. doi：10.3901/jme.2018.13.117

SHAO

Zhong-xi

， WU

Shi-lei

， FU

Hong-ya

Stiffness analysis of a novel flexible positioning mechanism for large-aperture grating tiling

［J］. Journal of Mechanical Engineering， 2018， 54（13）： 117-125.

DOI:10.3901/jme.2018.13.117

[14]

吴青龙，周奇才，熊肖磊，等.

塔式起重机臂架腹杆布局及尺寸优化设计

［J］.东北大学学报（自然科学版），2018，39（9）：1309-1314.

[本文引用: 2]

Qing-long

， ZHOU

Qi-cai

， XIONG

Xiao-lei

， et al.

Layout and size optimization design of tower crane boom webs

［J］. Journal of Northeastern University （Natural Science）， 2018， 39（9）： 1309-1314.

[本文引用: 2]

[15]

周奇才，吴青龙，熊肖磊，等.

塔式起重机臂架周期性拓扑优化设计

［J］.同济大学学报（自然科学版），2017，45（10）：1498-1505.

ZHOU

Qi-cai

， WU

Qing-long

， XIONG

Xiao-lei

， et al.

Periodic topology optimization design of tower crane boom

［J］. Journal of Tongji University （Natural Science）， 2017， 45（10）： 1498-1505.

[16]

毛艳，成凯.

基于Hopfield神经网络的单缸插销式伸缩臂伸缩路径优化

［J］.吉林大学学报（工学版），2020，50（1）：53-65.

[本文引用: 1]

MAO

Yan

， CHENG

Kai

Telescopic path optimization of a single-cylinder pin-type multi-section boom based on Hopfield neural network

［J］. Journal of Jilin University （Engineering and Technology Edition）， 2020， 50（1）： 53-65.

[本文引用: 1]

[17]

魏雅君，邱国梁，丁广和，等.

一种重载码垛机器人结构优化设计方法

［J］.工程设计学报，2020，27（3）：332-339. doi：10.3785/j.issn.1006-754X.2020.00.040

[本文引用: 1]

WEI

Ya-jun

， QIU

Guo-liang

， DING

Guang-he

， et al.

A structural optimization design method for heavy-duty palletizing robot

［J］. Chinese Journal of Engineering Design， 2020， 27（3）： 332-339.

DOI:10.3785/j.issn.1006-754X.2020.00.040 [本文引用: 1]

[18]

刘昊，周成，于存贵.

随车起重机伸缩臂截面多目标优化

［J］.机械设计与研究，2020，36（1）：173-176.

[本文引用: 1]

LIU

Hao

， ZHOU

Cheng

， YU

Cun-gui

Multi-objective optimization of telescopic boom section of truckmounted crane

［J］. Machine Design & Research， 2020， 36（1）： 173-176.

[本文引用: 1]

燃煤机组耦合生物质直燃发电技术研究

2021

... 近年来，我国火电机组装机容量持续增长，燃煤发电量约占总发电量的70%^［1-3］.在燃煤发电过程中有大量毒粉尘产生，须将它经过一系列分流净化处理后暂贮存于灰库以待后续开发利用.灰库中的粉尘极易与水分子结合引发富集效应，致使粉尘粘壁、板结、搭桥现象时有发生，严重影响火电机组的安全运营^［4-6］.因此，定期清理灰库内壁的积灰已成为保障火电机组安全运营的重要举措之一.鉴于库内积灰清理区域巨大且作业环境中粉尘弥漫，传统的人工入库作业模式普遍存在作业周期长、清理效果差、作业风险高等问题，因此迫切需要研发一款适用于灰库内壁全方位清理的高效作业机器人. ...

燃煤机组耦合生物质直燃发电技术研究

2021

火电灵活性改造的现状、关键问题与发展前景

2020

火电灵活性改造的现状、关键问题与发展前景

2020

Energy and exergy analysis and optimization of Kalina cycle coupled with a coal fired steam power plant

2013

电厂粉煤灰筛选除湿设备的设计与研究

2018

电厂粉煤灰筛选除湿设备的设计与研究

2018

燃煤脱硝机组空气预热器蓄热片表面飞灰沉积板结机理研究

2016

燃煤脱硝机组空气预热器蓄热片表面飞灰沉积板结机理研究

2016

井下煤仓清仓机器人机械臂的设计与分析

2013

... 目前，国内外学者针对灰库清理机器人已开展了大量探索性研究.如：罗宽等^［6］基于典型剪叉升降机构设计了桁架式灰库清理机器人，初步实现了井下煤仓内壁重点区域的局部清理；曹毅等^［7］基于绳索吊装机构研发了悬臂式灰库清理机器人，有效解决了灰库内壁全域清理难题；Dandan等^［8］融合伞状清灰机构研制了偏载式灰库清理机器人，初步解决了安装尺寸受限与灰库全域清理需求之间的技术冲突. ...

井下煤仓清仓机器人机械臂的设计与分析

2013

柔性驱动立筒仓清理机器人转动控制系统建模及简化

2014

柔性驱动立筒仓清理机器人转动控制系统建模及简化

2014

Motion control of siro： The silo cleaning robot

2015

新型工业机器人结构设计及其全域刚度预估方法

2018

... 灰库清理机器人普遍采用伸缩机械臂作为其主体结构.由于灰库复杂结构的限制和严苛的尺寸约束，现有清理机器人普遍存在作业范围有限、清理效果不佳等问题^［9］，其主要原因为：1）机械臂伸缩比不足，在回转作业模式下机械臂达到最大行程时还无法与远端壁面充分接触，在最小行程时会与近端壁面产生极大干涉，以致在库顶偏置安装的情况下难以进行全方位清理；2）机械臂刚度性能欠佳，在清理机器人超长伸长作业状态下其末端偏移量较大，难以保证良好的清理效果. ...

新型工业机器人结构设计及其全域刚度预估方法

2018

S型折叠式微悬臂梁刚度计算

2013

... 根据材料力学相关理论，可以忽略轴向力和剪切力对机械臂末端偏移量的影响，主要考虑横向作用力.因此，基于Castigliano第二定理^［10-14］，结合伸缩臂任意截面的弯矩表达式，通过分段积分求得机械臂的末端竖向位移

δ

及转角

θ

，如式（3）和式（4）所示. ...

S型折叠式微悬臂梁刚度计算

2013

δ

及转角

θ

，如式（3）和式（4）所示. ...

钻铆机器人静刚度建模及优化

2021

钻铆机器人静刚度建模及优化

2021

A robot gripper with variable stiffness actuation for enhancing collision safety

2020

一种新型大口径光栅拼接柔性定位机构刚度分析

2018

一种新型大口径光栅拼接柔性定位机构刚度分析

2018

塔式起重机臂架腹杆布局及尺寸优化设计

2018

δ

及转角

θ

，如式（3）和式（4）所示. ...

... 由图4可知，在极端工况下，后四节臂体上、下翼缘板及腹板全部区域均处于低应力区，前四节臂体上、下翼缘板及腹板中间区域均处于较低应力区.因此，箱型臂体各腹板中间区域均具有极大的轻量化潜质，可通过合理优化低应力区中孔洞形状来满足在严格质量要求下的刚度最大化要求，并在优化过程中保证其具有良好的加工性能^［14-16］. ...

塔式起重机臂架腹杆布局及尺寸优化设计

2018

δ

及转角

θ

，如式（3）和式（4）所示. ...

塔式起重机臂架周期性拓扑优化设计

2017

塔式起重机臂架周期性拓扑优化设计

2017

基于Hopfield神经网络的单缸插销式伸缩臂伸缩路径优化

2020

基于Hopfield神经网络的单缸插销式伸缩臂伸缩路径优化

2020

一种重载码垛机器人结构优化设计方法

2020

... 建立合理的优化数学模型和优化准则^［17-18］，对优化设计区域内孔洞形状进行周期性拓扑优化.基于SIMP （solid isotropic material with penalization，固体各向同性材料惩罚）方法，以单节臂体中设计域单元相对密度为设计变量，以体积约束下最小柔顺度为目标函数，综合考虑长伸缩臂的力学特性和加工性能等因素，则优化数学模型为： ...

一种重载码垛机器人结构优化设计方法

2020

随车起重机伸缩臂截面多目标优化

2020

随车起重机伸缩臂截面多目标优化

2020

〈

〉