[1]
ZHANG C, YANG T, WENG J, et al. Unsupervised pre-training for temporal action localization tasks [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . New Orleans: IEEE, 2022: 14011–14021.
[本文引用: 1]
[2]
CHEN H, HE J Y, XIANG W, et al. Hdformer: high-order directed transformer for 3d human pose estimation [C]//Proceedings of the 32nd International Joint Conference on Artificial Intelligence . Macao: ACM, 2023: 581-589.
[3]
LIU M, YUAN J. Recognizing human actions as the evolution of pose estimation maps [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 1159–1168.
[本文引用: 1]
[4]
ZHANG Q, BAO X, WU R, et al A skeleton temporal fusion graph convolutional network for elderly action recognition
[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences , 2025 , 108 (5 ): 704 - 713
[本文引用: 1]
[5]
MEHTA D, SRIDHAR S, SOTNYCHENKO O, et al VNect: real-time 3D human pose estimation with a single RGB camera
[J]. ACM Transactions on Graphics , 2017 , 36 (4 ): 1 - 14
[本文引用: 1]
[6]
MOON G, LEE K M. I2L-MeshNet: image-to-lixel prediction network for accurate 3D human pose and mesh estimation from a single RGB image [C]//Proceedings of the European Conference on Computer Vision . Cham: Springer, 2020: 752–768.
[本文引用: 1]
[7]
PAVLAKOS G, ZHOU X, DANIILIDIS K. Ordinal depth supervision for 3D human pose estimation [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 7307–7316.
[本文引用: 2]
[8]
CHEN T, FANG C, SHEN X, et al Anatomy-aware 3D human pose estimation with bone-based pose decomposition
[J]. IEEE Transactions on Circuits and Systems for Video Technology , 2022 , 32 (1 ): 198 - 209
DOI:10.1109/TCSVT.2021.3057267
[本文引用: 3]
[9]
LIU R, SHEN J, WANG H, et al. Attention mechanism exploits temporal contexts: real-time 3D human pose reconstruction [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 5063–5072.
[本文引用: 2]
[10]
WANG J, YAN S, XIONG Y, et al. Motion guided 3D pose estimation from videos [C]// Proceedings of the European Conference on Computer Vision . Cham: Springer, 2020: 764–780.
[11]
ZENG A, SUN X, HUANG F, et al. SRNet: improving generalization in 3D human pose estimation with a split-and-recombine approach [C]// Proceedings of the European Conference on Computer Vision . Cham: Springer, 2020: 507–523.
[本文引用: 2]
[12]
CAO Z, SIMON T, WEI S E, et al. Realtime multi-person 2d pose estimation using part affinity fields [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 7291-7299.
[本文引用: 1]
[13]
ZHENG C, ZHU S, MENDIETA M, et al. 3D human pose estimation with spatial and temporal transformers [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2022: 11636–11645.
[本文引用: 8]
[14]
LI W, LIU H, DING R, et al Exploiting temporal contexts with strided transformer for 3D human pose estimation
[J]. IEEE Transactions on Multimedia , 2023 , 25 : 1282 - 1293
DOI:10.1109/TMM.2022.3141231
[本文引用: 3]
[15]
ZHANG J, TU Z, YANG J, et al. MixSTE: seq2seq mixed spatio-temporal encoder for 3D human pose estimation in video [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . New Orleans: IEEE, 2022: 13222–13232.
[本文引用: 4]
[16]
ZHU W, MA X, LIU Z, et al. MotionBERT: a unified perspective on learning human motion representations [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision . Paris: IEEE, 2024: 15039–15053.
[17]
TANG Z, QIU Z, HAO Y, et al. 3D human pose estimation with spatio-temporal criss-cross attention [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Vancouver: IEEE, 2023: 4790–4799.
[18]
CHEN X, HAN Y, WANG X, et al Action keypoint network for efficient video recognition
[J]. IEEE Transactions on Image Processing , 2022 , 31 : 4980 - 4993
DOI:10.1109/TIP.2022.3191461
[本文引用: 1]
[19]
EINFALT M, LUDWIG K, LIENHART R. Uplift and upsample: efficient 3D human pose estimation with uplifting transformers [C]//Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision . Waikoloa: IEEE, 2023: 2902–2912.
[本文引用: 1]
[20]
FAN Q, HUANG H, CHEN M, et al. Rmt: retentive networks meet vision transformers [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2024: 5641-5651.
[本文引用: 2]
[21]
LI W, LIU H, TANG H, et al. MHFormer: multi-hypothesis transformer for 3D human pose estimation [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . New Orleans: IEEE, 2022: 13137–13146.
[本文引用: 7]
[22]
SHAN W, LIU Z, ZHANG X, et al. P-STMO: pre-trained spatial temporal many-to-one model for3D human pose estimation [C]//European Conference on Computer Vision . Cham: Springer, 2022: 461–478.
[本文引用: 1]
[23]
FAN Q, HUANG H, CHEN M, et al. RMT: retentive networks meet vision transformers [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2024: 5641–5651.
[本文引用: 1]
[24]
IONESCU C, PAPAVA D, OLARU V, et al Human3.6M: large scale datasets and predictive methods for 3D human sensing in natural environments
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2014 , 36 (7 ): 1325 - 1339
DOI:10.1109/TPAMI.2013.248
[本文引用: 1]
[25]
MEHTA D, RHODIN H, CASAS D, et al. Monocular 3D human pose estimation in the wild using improved CNN supervision [C]//Proceedings of the International Conference on 3D Vision . Qingdao: IEEE, 2018: 506–516.
[本文引用: 1]
[26]
ZHENG C, WU W, CHEN C, et al Deep learning-based human pose estimation: a survey
[J]. ACM Computing Surveys , 2024 , 56 (1 ): 1 - 37
[本文引用: 1]
[27]
MARGOSSIAN C C A review of automatic differentiation and its efficient implementation
[J]. WIREs Data Mining and Knowledge Discovery , 2019 , 9 (4 ): e1305
DOI:10.1002/widm.1305
[本文引用: 1]
[28]
FINDER S E, AMOYAL R, TREISTER E, et al. Wavelet convolutions for large receptive fields [C]//European Conference on Computer Vision. Cham: Springer, 2024: 363-380.
[本文引用: 1]
[29]
CHEN Y, WANG Z, PENG Y, et al. Cascaded pyramid network for multi-person pose estimation [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 7103–7112.
[本文引用: 1]
[30]
PENG J, ZHOU Y, MOK P Y. KTPFormer: kinematics and trajectory prior knowledge-enhanced transformer for 3D human pose estimation [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2024: 1123–1132.
[本文引用: 3]
[31]
LIU J, LIU M, LIU H, et al. Tcpformer: Learning temporal correlation with implicit pose proxy for 3d human pose estimation [C]//Proceedings of the AAAI Conference on Artificial Intelligence . Washington: AAAI, 2025, 39(5): 5478−5486.
[本文引用: 3]
[32]
PAVLLO D, FEICHTENHOFER C, GRANGIER D, et al. 3D human pose estimation in video with temporal convolutions and semi-supervised training [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2020: 7745–7754.
[本文引用: 1]
[33]
YEH R, HU Y T, SCHWING A. Chirality nets for human pose regression [J]. Advances in Neural Information Processing Systems , 2019, 32: 8161–8171.
[本文引用: 1]
[34]
WANG J, YAN S, XIONG Y, et al. Motion guided 3d pose estimation from videos [C]//European Conference on Computer Vision . Cham: Springer, 2020: 764−780.
[本文引用: 3]
[35]
CAI Y, GE L, LIU J, et al. Exploiting spatial-temporal relationships for 3D pose estimation via graph convolutional networks [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision . Seoul: IEEE, 2020: 2272–2281.
[本文引用: 1]
[36]
LI H, SHI B, DAI W, et al Pose-oriented transformer with uncertainty-guided refinement for 2D-to-3D human pose estimation
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2023 , 37 (1 ): 1296 - 1304
DOI:10.1609/aaai.v37i1.25213
[本文引用: 1]
[37]
WANG H, LUO D, IKENAGA T. Image information assistance neural network for VideoPose3D-based monocular 3D pose estimation [C]//Proceedings of the 17th International Conference on Machine Vision and Applications . Aichi: IEEE, 2021: 1–4.
[本文引用: 1]
1
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
1
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
A skeleton temporal fusion graph convolutional network for elderly action recognition
1
2025
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
VNect: real-time 3D human pose estimation with a single RGB camera
1
2017
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
1
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
2
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
Anatomy-aware 3D human pose estimation with bone-based pose decomposition
3
2022
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... Detailed quantitative comparison result of three indicators under MPI-INF-3DHP
Tab.3 方法 PCK/% AUC/% MPJPE/mm VideoPose3D [37 ] 86.0 51.9 84.0 UGCN [34 ] 86.9 62.1 68.1 Anatomy3D [8 ] 87.9 54.0 78.8 MixSTE [15 ] 94.4 66.5 54.9 Poseformer [13 ] 95.4 63.2 57.7 MHFormer [21 ] 93.8 63.3 58.0 P-STMO [22 ] 97.9 75.8 32.2 MSEFN 99.1 76.4 31.2
为了评估关键帧选择模块对模型效率的优化作用,在表4 中列出了计算量、参数量、精度的对比实验结果. 可以看出,MSEFN在参数量为MHFormer一半的情况下,MPJPE指标优于MHFormer. ...
2
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... 文献[
9 ] (
f = 243)
CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0 表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
2
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
1
... 三维人体姿态估计(3D human pose estimation, 3D HPE)旨在从视频或图像序列中恢复人体在三维空间的结构与运动信息,广泛应用于动作识别[1 –3 ] 、人机交互[4 ] 和虚拟现实[5 ] 等领域. 当前的主流方法主要包括基于单目视频的直接三维估计[6 –7 ] 和基于二维关节点序列的二维到三维提升方法[8 –11 ] . 随着二维人体姿态估计技术的成熟[12 ] ,后者因其较高的稳定性与通用性成为研究热点. ...
8
... 近年来,Transformer架构在3D HPE领域取得了显著突破. Zheng等[13 ] 将长序列特征提取分解为空间与时间2个阶段,显著优于基于卷积的方法. 此后,Li等[14 -18 ] 进一步改进了基于Transformer的时空建模方式,但普遍面临以下两大挑战. 1)高频序列冗余问题. 在高帧率视频中,相邻帧间的骨架变化极小,导致模型重复处理无效信息,浪费计算资源并积累噪声. 简单降采样(如Einfalt等[19 ] 所用)虽能减轻冗余,却会显著降低精度. 2)全局时空依赖建模困难. 由于长序列自注意力的计算代价高昂,主流方法往往采用时空分解或双阶段策略,从而丢失跨帧全局依赖信息. 在长序列建模方面,Fan等[20 ] 提出的保留网络(retentive network, RetNet)通过显式衰减矩阵,有效降低了复杂度(由O (n 2 )降低至O (n )),增强了长距离依赖建模能力. 该机制已在语言建模与视觉任务中展现出优异的性能[20 -23 ] ,但其在骨架序列建模中的潜力尚未充分挖掘. ...
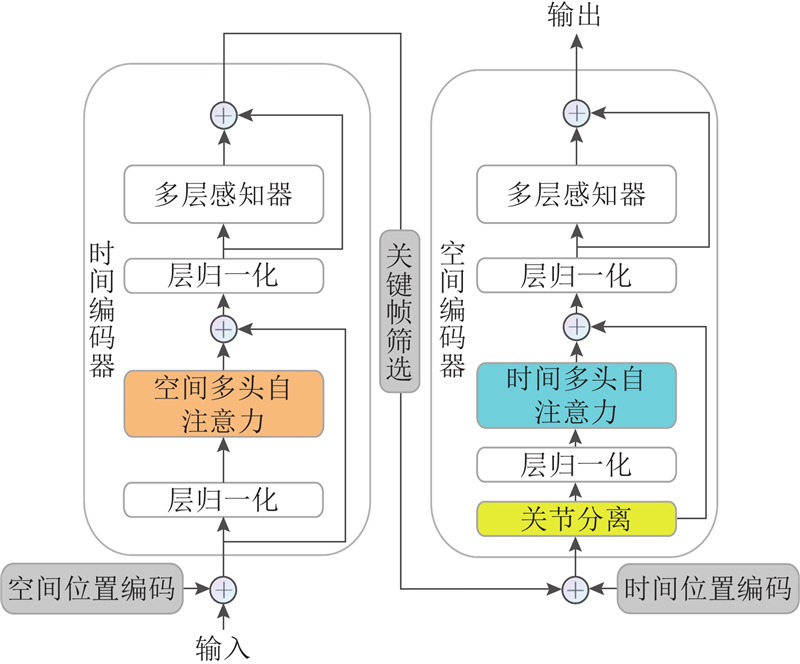
... 根据文献[13 ]可知,时间编码器能够有效地对关键特征空间编码器的输出进行时间特征的提取,从而进行跨帧人体运动建模. TTE的设计结构如图3 的右半部分所示. 具体来说,将帧选择器的输出$ {{\boldsymbol{x}}}_{1} $ $ {{\boldsymbol{E}}}_{{\mathrm{Spos}}}\in {\mathbf{R}}^{1 \times J\times c} $ M 层的时间编码器利用时间多头自注意力(temporal-MSA)模拟整个序列的帧对帧的依赖关系. 在该阶段,每个时间编码层的令牌号是N ,这是经过关键帧时空编码后的输入序列的长度. 时间编码器的时间建模过程如下: ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... [
13 ] (
f =81)
ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0 表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 on Human3.6M dataset (based on GT-detected pose input)
Tab.2 GT 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 PoseFormer [13 ] (f = 81) ICCV’21 30.0 33.6 29.9 31.0 30.2 33.3 34.8 31.4 37.8 38.6 31.7 31.5 29.0 23.3 23.1 31.3 MHFormer [21 ] (f =351) CVPR’22 27.7 32.1 29.1 28.9 30.0 33.9 33.0 31.2 37 39.3 30.0 31.0 29.4 22.2 23.0 30.5 POT[36 ] (f = 81) AAAI’23 32.9 38.3 28.3 33.8 34.9 38.7 37.2 30.7 34.5 39.7 33.9 34.7 34.3 26.1 28.9 33.8 MSEFN (f =81,k f — 27.1 28.0 25.3 26.5 24.6 27.7 29.8 26.0 31.3 33.6 26.5 28.7 28.1 16.3 18.3 26.5
如表1 所示为测试集的所有15个动作结果. 最后一列提供了在所有测试集上的平均性能. 其中,加粗表示最好,下划线表示次好. 具体来说,在实验中采用CPN网络来提取二维姿态,并将该二维姿态作为输入. 提出的模型在协议1(protocol 1)下获得39.8 mm的平均MPJPE,比Poseformer低3.6 mm,比MixSTE低1.6 mm,取得最佳的结果. 此外,比较协议2下的方法,使用刚性对齐. 本文方法在平均MPJPE上优于KTPFormer,从31.9 mm减小到31.0 mm. ...
... Detailed quantitative comparison result of three indicators under MPI-INF-3DHP
Tab.3 方法 PCK/% AUC/% MPJPE/mm VideoPose3D [37 ] 86.0 51.9 84.0 UGCN [34 ] 86.9 62.1 68.1 Anatomy3D [8 ] 87.9 54.0 78.8 MixSTE [15 ] 94.4 66.5 54.9 Poseformer [13 ] 95.4 63.2 57.7 MHFormer [21 ] 93.8 63.3 58.0 P-STMO [22 ] 97.9 75.8 32.2 MSEFN 99.1 76.4 31.2
为了评估关键帧选择模块对模型效率的优化作用,在表4 中列出了计算量、参数量、精度的对比实验结果. 可以看出,MSEFN在参数量为MHFormer一半的情况下,MPJPE指标优于MHFormer. ...
... Quantitative comparison result of FLOPs,
N p and MPJPE indicator on Human3.6M
Tab.4 方法 f FLOPs/106 N p /106 MPJPE/mm Poseformer [13 ] 27 542.1 9.65 47.0 StridedTran [14 ] 81 392 4.06 45.4 MHFormer [21 ] 27 1031.8 18.92 45.9 MSEFN 81(k f 553 9.97 39.8
综上所述,与目前的先进方法相比,MSEFN取得了具有竞争力的三维人体姿态估计结果. MSEFN不仅在精度上有着较强的竞争力,而且在训练推理效率上有着明显的优势. ...
... Quantitative comparison result of ablation study on selection of frame rate
Tab.6 方法 f k f FLOPs/106 N p v /(帧·s−1 )MPJPE/mm Poseformer[13 ] 27 27 542.1 9.65 428 47.0 StridedTran[14 ] 81 81 392 4.06 199 45.4 MHFormer[21 ] 27 27 1031.8 18.92 33 45.9 MSEFN 27 3 409 6.23 470 47.8 MSEFN 27 9 467 7.55 450 45.5 MSEFN 81 3 458 7.11 455 42.8 MSEFN 81 9 521 7.96 449 40.1 MSEFN 81 27 553 9.97 403 39.8
如表7 所示为时间维度t c 和时间编码器层数t l 的组合. 在Poseformer中,空间编码器的最优维度参数为32,空间编码器的个数为4. 只对时间维度参数和时间编码器的个数进行对比实验. 从实验结果可知,模型的最优t c 为32,t l 为4. ...
Exploiting temporal contexts with strided transformer for 3D human pose estimation
3
2023
... 近年来,Transformer架构在3D HPE领域取得了显著突破. Zheng等[13 ] 将长序列特征提取分解为空间与时间2个阶段,显著优于基于卷积的方法. 此后,Li等[14 -18 ] 进一步改进了基于Transformer的时空建模方式,但普遍面临以下两大挑战. 1)高频序列冗余问题. 在高帧率视频中,相邻帧间的骨架变化极小,导致模型重复处理无效信息,浪费计算资源并积累噪声. 简单降采样(如Einfalt等[19 ] 所用)虽能减轻冗余,却会显著降低精度. 2)全局时空依赖建模困难. 由于长序列自注意力的计算代价高昂,主流方法往往采用时空分解或双阶段策略,从而丢失跨帧全局依赖信息. 在长序列建模方面,Fan等[20 ] 提出的保留网络(retentive network, RetNet)通过显式衰减矩阵,有效降低了复杂度(由O (n 2 )降低至O (n )),增强了长距离依赖建模能力. 该机制已在语言建模与视觉任务中展现出优异的性能[20 -23 ] ,但其在骨架序列建模中的潜力尚未充分挖掘. ...
... Quantitative comparison result of FLOPs,
N p and MPJPE indicator on Human3.6M
Tab.4 方法 f FLOPs/106 N p /106 MPJPE/mm Poseformer [13 ] 27 542.1 9.65 47.0 StridedTran [14 ] 81 392 4.06 45.4 MHFormer [21 ] 27 1031.8 18.92 45.9 MSEFN 81(k f 553 9.97 39.8
综上所述,与目前的先进方法相比,MSEFN取得了具有竞争力的三维人体姿态估计结果. MSEFN不仅在精度上有着较强的竞争力,而且在训练推理效率上有着明显的优势. ...
... Quantitative comparison result of ablation study on selection of frame rate
Tab.6 方法 f k f FLOPs/106 N p v /(帧·s−1 )MPJPE/mm Poseformer[13 ] 27 27 542.1 9.65 428 47.0 StridedTran[14 ] 81 81 392 4.06 199 45.4 MHFormer[21 ] 27 27 1031.8 18.92 33 45.9 MSEFN 27 3 409 6.23 470 47.8 MSEFN 27 9 467 7.55 450 45.5 MSEFN 81 3 458 7.11 455 42.8 MSEFN 81 9 521 7.96 449 40.1 MSEFN 81 27 553 9.97 403 39.8
如表7 所示为时间维度t c 和时间编码器层数t l 的组合. 在Poseformer中,空间编码器的最优维度参数为32,空间编码器的个数为4. 只对时间维度参数和时间编码器的个数进行对比实验. 从实验结果可知,模型的最优t c 为32,t l 为4. ...
4
... 为了验证提出的MSEFN网络的有效性和竞争性, 在Human3.6M 数据集上,对MSEFN与多个先进的3D HPE方法进行比较,包括Mhformer[21 ] 、MixSTE[15 ] 、KTPFormer[30 ] 、 TCPFormer[31 ] 等. 上述方法的数据来源均出自近年来公开的实验结果或作者提供的开源代码测试生成的实验结果,相关数据如表1 、2 所示. ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... [
15 ] (
f =243)
CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0 表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... Detailed quantitative comparison result of three indicators under MPI-INF-3DHP
Tab.3 方法 PCK/% AUC/% MPJPE/mm VideoPose3D [37 ] 86.0 51.9 84.0 UGCN [34 ] 86.9 62.1 68.1 Anatomy3D [8 ] 87.9 54.0 78.8 MixSTE [15 ] 94.4 66.5 54.9 Poseformer [13 ] 95.4 63.2 57.7 MHFormer [21 ] 93.8 63.3 58.0 P-STMO [22 ] 97.9 75.8 32.2 MSEFN 99.1 76.4 31.2
为了评估关键帧选择模块对模型效率的优化作用,在表4 中列出了计算量、参数量、精度的对比实验结果. 可以看出,MSEFN在参数量为MHFormer一半的情况下,MPJPE指标优于MHFormer. ...
Action keypoint network for efficient video recognition
1
2022
... 近年来,Transformer架构在3D HPE领域取得了显著突破. Zheng等[13 ] 将长序列特征提取分解为空间与时间2个阶段,显著优于基于卷积的方法. 此后,Li等[14 -18 ] 进一步改进了基于Transformer的时空建模方式,但普遍面临以下两大挑战. 1)高频序列冗余问题. 在高帧率视频中,相邻帧间的骨架变化极小,导致模型重复处理无效信息,浪费计算资源并积累噪声. 简单降采样(如Einfalt等[19 ] 所用)虽能减轻冗余,却会显著降低精度. 2)全局时空依赖建模困难. 由于长序列自注意力的计算代价高昂,主流方法往往采用时空分解或双阶段策略,从而丢失跨帧全局依赖信息. 在长序列建模方面,Fan等[20 ] 提出的保留网络(retentive network, RetNet)通过显式衰减矩阵,有效降低了复杂度(由O (n 2 )降低至O (n )),增强了长距离依赖建模能力. 该机制已在语言建模与视觉任务中展现出优异的性能[20 -23 ] ,但其在骨架序列建模中的潜力尚未充分挖掘. ...
1
... 近年来,Transformer架构在3D HPE领域取得了显著突破. Zheng等[13 ] 将长序列特征提取分解为空间与时间2个阶段,显著优于基于卷积的方法. 此后,Li等[14 -18 ] 进一步改进了基于Transformer的时空建模方式,但普遍面临以下两大挑战. 1)高频序列冗余问题. 在高帧率视频中,相邻帧间的骨架变化极小,导致模型重复处理无效信息,浪费计算资源并积累噪声. 简单降采样(如Einfalt等[19 ] 所用)虽能减轻冗余,却会显著降低精度. 2)全局时空依赖建模困难. 由于长序列自注意力的计算代价高昂,主流方法往往采用时空分解或双阶段策略,从而丢失跨帧全局依赖信息. 在长序列建模方面,Fan等[20 ] 提出的保留网络(retentive network, RetNet)通过显式衰减矩阵,有效降低了复杂度(由O (n 2 )降低至O (n )),增强了长距离依赖建模能力. 该机制已在语言建模与视觉任务中展现出优异的性能[20 -23 ] ,但其在骨架序列建模中的潜力尚未充分挖掘. ...
2
... 近年来,Transformer架构在3D HPE领域取得了显著突破. Zheng等[13 ] 将长序列特征提取分解为空间与时间2个阶段,显著优于基于卷积的方法. 此后,Li等[14 -18 ] 进一步改进了基于Transformer的时空建模方式,但普遍面临以下两大挑战. 1)高频序列冗余问题. 在高帧率视频中,相邻帧间的骨架变化极小,导致模型重复处理无效信息,浪费计算资源并积累噪声. 简单降采样(如Einfalt等[19 ] 所用)虽能减轻冗余,却会显著降低精度. 2)全局时空依赖建模困难. 由于长序列自注意力的计算代价高昂,主流方法往往采用时空分解或双阶段策略,从而丢失跨帧全局依赖信息. 在长序列建模方面,Fan等[20 ] 提出的保留网络(retentive network, RetNet)通过显式衰减矩阵,有效降低了复杂度(由O (n 2 )降低至O (n )),增强了长距离依赖建模能力. 该机制已在语言建模与视觉任务中展现出优异的性能[20 -23 ] ,但其在骨架序列建模中的潜力尚未充分挖掘. ...
... [20 -23 ],但其在骨架序列建模中的潜力尚未充分挖掘. ...
7
... 为了验证提出的MSEFN网络的有效性和竞争性, 在Human3.6M 数据集上,对MSEFN与多个先进的3D HPE方法进行比较,包括Mhformer[21 ] 、MixSTE[15 ] 、KTPFormer[30 ] 、 TCPFormer[31 ] 等. 上述方法的数据来源均出自近年来公开的实验结果或作者提供的开源代码测试生成的实验结果,相关数据如表1 、2 所示. ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... [
21 ] (
f =351)
CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0 表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 on Human3.6M dataset (based on GT-detected pose input)
Tab.2 GT 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 PoseFormer [13 ] (f = 81) ICCV’21 30.0 33.6 29.9 31.0 30.2 33.3 34.8 31.4 37.8 38.6 31.7 31.5 29.0 23.3 23.1 31.3 MHFormer [21 ] (f =351) CVPR’22 27.7 32.1 29.1 28.9 30.0 33.9 33.0 31.2 37 39.3 30.0 31.0 29.4 22.2 23.0 30.5 POT[36 ] (f = 81) AAAI’23 32.9 38.3 28.3 33.8 34.9 38.7 37.2 30.7 34.5 39.7 33.9 34.7 34.3 26.1 28.9 33.8 MSEFN (f =81,k f — 27.1 28.0 25.3 26.5 24.6 27.7 29.8 26.0 31.3 33.6 26.5 28.7 28.1 16.3 18.3 26.5
如表1 所示为测试集的所有15个动作结果. 最后一列提供了在所有测试集上的平均性能. 其中,加粗表示最好,下划线表示次好. 具体来说,在实验中采用CPN网络来提取二维姿态,并将该二维姿态作为输入. 提出的模型在协议1(protocol 1)下获得39.8 mm的平均MPJPE,比Poseformer低3.6 mm,比MixSTE低1.6 mm,取得最佳的结果. 此外,比较协议2下的方法,使用刚性对齐. 本文方法在平均MPJPE上优于KTPFormer,从31.9 mm减小到31.0 mm. ...
... Detailed quantitative comparison result of three indicators under MPI-INF-3DHP
Tab.3 方法 PCK/% AUC/% MPJPE/mm VideoPose3D [37 ] 86.0 51.9 84.0 UGCN [34 ] 86.9 62.1 68.1 Anatomy3D [8 ] 87.9 54.0 78.8 MixSTE [15 ] 94.4 66.5 54.9 Poseformer [13 ] 95.4 63.2 57.7 MHFormer [21 ] 93.8 63.3 58.0 P-STMO [22 ] 97.9 75.8 32.2 MSEFN 99.1 76.4 31.2
为了评估关键帧选择模块对模型效率的优化作用,在表4 中列出了计算量、参数量、精度的对比实验结果. 可以看出,MSEFN在参数量为MHFormer一半的情况下,MPJPE指标优于MHFormer. ...
... Quantitative comparison result of FLOPs,
N p and MPJPE indicator on Human3.6M
Tab.4 方法 f FLOPs/106 N p /106 MPJPE/mm Poseformer [13 ] 27 542.1 9.65 47.0 StridedTran [14 ] 81 392 4.06 45.4 MHFormer [21 ] 27 1031.8 18.92 45.9 MSEFN 81(k f 553 9.97 39.8
综上所述,与目前的先进方法相比,MSEFN取得了具有竞争力的三维人体姿态估计结果. MSEFN不仅在精度上有着较强的竞争力,而且在训练推理效率上有着明显的优势. ...
... Quantitative comparison result of ablation study on selection of frame rate
Tab.6 方法 f k f FLOPs/106 N p v /(帧·s−1 )MPJPE/mm Poseformer[13 ] 27 27 542.1 9.65 428 47.0 StridedTran[14 ] 81 81 392 4.06 199 45.4 MHFormer[21 ] 27 27 1031.8 18.92 33 45.9 MSEFN 27 3 409 6.23 470 47.8 MSEFN 27 9 467 7.55 450 45.5 MSEFN 81 3 458 7.11 455 42.8 MSEFN 81 9 521 7.96 449 40.1 MSEFN 81 27 553 9.97 403 39.8
如表7 所示为时间维度t c 和时间编码器层数t l 的组合. 在Poseformer中,空间编码器的最优维度参数为32,空间编码器的个数为4. 只对时间维度参数和时间编码器的个数进行对比实验. 从实验结果可知,模型的最优t c 为32,t l 为4. ...
1
... Detailed quantitative comparison result of three indicators under MPI-INF-3DHP
Tab.3 方法 PCK/% AUC/% MPJPE/mm VideoPose3D [37 ] 86.0 51.9 84.0 UGCN [34 ] 86.9 62.1 68.1 Anatomy3D [8 ] 87.9 54.0 78.8 MixSTE [15 ] 94.4 66.5 54.9 Poseformer [13 ] 95.4 63.2 57.7 MHFormer [21 ] 93.8 63.3 58.0 P-STMO [22 ] 97.9 75.8 32.2 MSEFN 99.1 76.4 31.2
为了评估关键帧选择模块对模型效率的优化作用,在表4 中列出了计算量、参数量、精度的对比实验结果. 可以看出,MSEFN在参数量为MHFormer一半的情况下,MPJPE指标优于MHFormer. ...
1
... 近年来,Transformer架构在3D HPE领域取得了显著突破. Zheng等[13 ] 将长序列特征提取分解为空间与时间2个阶段,显著优于基于卷积的方法. 此后,Li等[14 -18 ] 进一步改进了基于Transformer的时空建模方式,但普遍面临以下两大挑战. 1)高频序列冗余问题. 在高帧率视频中,相邻帧间的骨架变化极小,导致模型重复处理无效信息,浪费计算资源并积累噪声. 简单降采样(如Einfalt等[19 ] 所用)虽能减轻冗余,却会显著降低精度. 2)全局时空依赖建模困难. 由于长序列自注意力的计算代价高昂,主流方法往往采用时空分解或双阶段策略,从而丢失跨帧全局依赖信息. 在长序列建模方面,Fan等[20 ] 提出的保留网络(retentive network, RetNet)通过显式衰减矩阵,有效降低了复杂度(由O (n 2 )降低至O (n )),增强了长距离依赖建模能力. 该机制已在语言建模与视觉任务中展现出优异的性能[20 -23 ] ,但其在骨架序列建模中的潜力尚未充分挖掘. ...
Human3.6M: large scale datasets and predictive methods for 3D human sensing in natural environments
1
2014
... 在2个常用的人体姿态基准数据集(Human3.6M[24 ] 和MPI-INF-3DHP[25 ] )上进行评估. 在 Human3.6M 数据集上,在不同地点的4台摄像机在室内拍摄了超过360万张视频帧,包含11个受试者,执行15个不同的动作. 评估指标包括平均关节位置误差(MPJPE)和对齐的平均关节点位置误差P-MPJPE[26 ] . 在 MPI-INF-3DHP 数据集上,在受控的室内环境和具有挑战性的室外环境中收集. 采用曲线下面积(AUC)、正确关键点百分比(PCK)和 MPJPE 作为评估指标. ...
1
... 在2个常用的人体姿态基准数据集(Human3.6M[24 ] 和MPI-INF-3DHP[25 ] )上进行评估. 在 Human3.6M 数据集上,在不同地点的4台摄像机在室内拍摄了超过360万张视频帧,包含11个受试者,执行15个不同的动作. 评估指标包括平均关节位置误差(MPJPE)和对齐的平均关节点位置误差P-MPJPE[26 ] . 在 MPI-INF-3DHP 数据集上,在受控的室内环境和具有挑战性的室外环境中收集. 采用曲线下面积(AUC)、正确关键点百分比(PCK)和 MPJPE 作为评估指标. ...
Deep learning-based human pose estimation: a survey
1
2024
... 在2个常用的人体姿态基准数据集(Human3.6M[24 ] 和MPI-INF-3DHP[25 ] )上进行评估. 在 Human3.6M 数据集上,在不同地点的4台摄像机在室内拍摄了超过360万张视频帧,包含11个受试者,执行15个不同的动作. 评估指标包括平均关节位置误差(MPJPE)和对齐的平均关节点位置误差P-MPJPE[26 ] . 在 MPI-INF-3DHP 数据集上,在受控的室内环境和具有挑战性的室外环境中收集. 采用曲线下面积(AUC)、正确关键点百分比(PCK)和 MPJPE 作为评估指标. ...
A review of automatic differentiation and its efficient implementation
1
2019
... MSEFN在Pytorch [27 ] 框架上进行训练及测试,所有的过程都在NVIDIA RTX 3090 上进行. 此外,MSEFN使用AdamW[28 ] 优化器对模型进行100个轮次的训练,权重衰减为0.1. 将初始学习率设置为8×10−4 ,采用指数学习率衰减计划,衰减因子为0.99. 在Human3.6M上采用CPN[29 ] 二维姿态和Ground Truth 2D检测. 对于MPI-INF- 3DHP数据集,使用Ground truth 2D检测. 在实验时,STE和TTE的编码器循环层数均设置为4,时空编码器中嵌入的特征维数c 为32. 使用 MPJPE 作为损失函数,计算关节点3D预测姿态和3D真实标签之间的平均欧几里得距离. ...
1
... MSEFN在Pytorch [27 ] 框架上进行训练及测试,所有的过程都在NVIDIA RTX 3090 上进行. 此外,MSEFN使用AdamW[28 ] 优化器对模型进行100个轮次的训练,权重衰减为0.1. 将初始学习率设置为8×10−4 ,采用指数学习率衰减计划,衰减因子为0.99. 在Human3.6M上采用CPN[29 ] 二维姿态和Ground Truth 2D检测. 对于MPI-INF- 3DHP数据集,使用Ground truth 2D检测. 在实验时,STE和TTE的编码器循环层数均设置为4,时空编码器中嵌入的特征维数c 为32. 使用 MPJPE 作为损失函数,计算关节点3D预测姿态和3D真实标签之间的平均欧几里得距离. ...
1
... MSEFN在Pytorch [27 ] 框架上进行训练及测试,所有的过程都在NVIDIA RTX 3090 上进行. 此外,MSEFN使用AdamW[28 ] 优化器对模型进行100个轮次的训练,权重衰减为0.1. 将初始学习率设置为8×10−4 ,采用指数学习率衰减计划,衰减因子为0.99. 在Human3.6M上采用CPN[29 ] 二维姿态和Ground Truth 2D检测. 对于MPI-INF- 3DHP数据集,使用Ground truth 2D检测. 在实验时,STE和TTE的编码器循环层数均设置为4,时空编码器中嵌入的特征维数c 为32. 使用 MPJPE 作为损失函数,计算关节点3D预测姿态和3D真实标签之间的平均欧几里得距离. ...
3
... 为了验证提出的MSEFN网络的有效性和竞争性, 在Human3.6M 数据集上,对MSEFN与多个先进的3D HPE方法进行比较,包括Mhformer[21 ] 、MixSTE[15 ] 、KTPFormer[30 ] 、 TCPFormer[31 ] 等. 上述方法的数据来源均出自近年来公开的实验结果或作者提供的开源代码测试生成的实验结果,相关数据如表1 、2 所示. ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... [
30 ] (
f =243)
CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0 表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
3
... 为了验证提出的MSEFN网络的有效性和竞争性, 在Human3.6M 数据集上,对MSEFN与多个先进的3D HPE方法进行比较,包括Mhformer[21 ] 、MixSTE[15 ] 、KTPFormer[30 ] 、 TCPFormer[31 ] 等. 上述方法的数据来源均出自近年来公开的实验结果或作者提供的开源代码测试生成的实验结果,相关数据如表1 、2 所示. ...
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... [
31 ] (
f =81)
CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0 表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
1
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
1
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
3
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... [
34 ] (
f = 96)
ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0 表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
... Detailed quantitative comparison result of three indicators under MPI-INF-3DHP
Tab.3 方法 PCK/% AUC/% MPJPE/mm VideoPose3D [37 ] 86.0 51.9 84.0 UGCN [34 ] 86.9 62.1 68.1 Anatomy3D [8 ] 87.9 54.0 78.8 MixSTE [15 ] 94.4 66.5 54.9 Poseformer [13 ] 95.4 63.2 57.7 MHFormer [21 ] 93.8 63.3 58.0 P-STMO [22 ] 97.9 75.8 32.2 MSEFN 99.1 76.4 31.2
为了评估关键帧选择模块对模型效率的优化作用,在表4 中列出了计算量、参数量、精度的对比实验结果. 可以看出,MSEFN在参数量为MHFormer一半的情况下,MPJPE指标优于MHFormer. ...
1
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 and protocol 2 on Human3.6M dataset (based on CPN-detected input)
Tab.1 CPN 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[32 ] (f = 243) CVPR’18 45.2 46.7 43.3 45.6 48.1 55.1 44.6 44.3 57.3 65.8 47.1 44 49 32.8 33.9 46.8 文献[33 ] NeurIPS’19 44.8 46.1 43.3 46.4 49.0 55.2 44.6 44 58.3 62.7 47.1 43.9 48.6 32.7 33.3 46.7 文献[9 ] (f = 243) CVPR’20 41.8 44.8 41.1 44.9 47.4 54.1 43.4 42.2 56.2 63.6 45.3 43.5 45.3 31.3 32.2 45.1 SRNet[11 ] ECCV’20 46.6 47.1 43.9 41.6 45.8 49.6 46.5 40.0 53.4 61.1 46.1 42.6 43.1 31.5 32.6 44.8 UGCN[34 ] (f = 96) ECCV’20 41.3 43.9 44.0 42.2 48.0 57.1 42.2 43.2 57.3 61.3 47.0 43.5 47.0 32.6 31.8 45.6 文献[8 ] (f = 81) TCSVT’21 42.1 43.8 41.0 43.8 46.1 53.5 42.4 43.1 53.9 60.5 45.7 42.1 46.2 32.2 33.8 44.6 PoseFormer[13 ] (f =81) ICCV’21 41.5 44.8 39.8 42.5 46.5 51.6 42 42 53.3 60.7 45.5 43.3 46.1 31.8 32.2 44.3 MHFormer[21 ] (f =351) CVPR’22 39.2 43.1 40.1 40.9 44.9 51.2 40.6 41.3 53.5 60.3 43.7 41.1 43.8 29.8 30.6 43.0 MixSTE[15 ] (f =243) CVPR’22 37.6 40.9 37.3 39.7 42.3 49.9 40.1 39.8 51.7 55.0 42.1 39.8 41.0 27.9 27.9 40.9 KTPFormer[30 ] (f =243) CVPR’24 37.3 39.2 35.9 37.6 42.5 48.2 38.6 39.0 51.4 55.9 41.6 39.0 40.0 27.0 27.4 40.1 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 40.5 MSEFN (f =81,k f — 36.8 39.9 35.8 39.1 41.0 47.5 37.5 37.6 51.5 47.9 39.8 38.2 42.1 25.6 26.8 39.8 CPN 协议2 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 文献[7 ] CVPR’18 34.7 39.8 41.8 38.6 42.5 47.5 38.0 36.6 50.7 56.8 42.6 39.6 43.9 32.1 36.5 41.8 文献[35 ] (f = 7) ICCV’19 35.7 37.8 36.9 40.7 39.6 45.2 37.4 34.5 46.9 50.1 40.5 36.1 41.0 29.6 32.3 39.0 文献[9 ] (f = 243) CVPR’20 32.3 35.2 33.3 35.8 35.9 41.5 33.2 32.7 44.6 50.9 37.0 32.4 37.0 25.2 27.2 35.6 UGCN[34 ] (f = 96) ECCV’20 32.9 35.,2 35.6 34.4 364 42.7 31.2 32.5 45.6 50.2 37.3 32.8 36.3 26.0 23.9 35.5 PoseFormer[13 ] (f =81) ICCV’21 32.5 34,8 32.6 34.6 35.3 39.5 32.1 32.0 42.8 48.5 34.8 32.4 35.3 24.5 26 34.6 MHFormer[21 ] (f =351) CVPR’22 31.5 34.9 32.8 33.6 35.3 39.6 32.0 32.2 43.5 48.1 36.4 32.6 34.3 23.9 25.1 34.4 MixSTE[15 ] (f =243) CVPR’22 30.8 33.1 30.3 31.8 33.1 39.1 31.1 30.5 42.5 44.5 34.0 30.8 32.7 22.1 22.9 32.6 KTPFormer[30 ] (f =243) CVPR’24 30.1 32.3 29.6 30.8 32.3 37.3 30.0 30.2 41.0 45.3 33.6 29.9 31.4 21.5 22.6 31.9 TCPFormer[31 ] (f =81) CVPR’25 — — — — — — — — — — — — — — — 33.7 MSEFN (f =81,k f — 27.5 30.5 28.5 31.8 31.5 36.4 28.5 28 41.7 46.6 32 28.3 31.8 19.8 21.3 31.0
表 2 协议1下MSEFN与不同方法在Human3.6M数据集上的MPJPE结果对比(基于GT检测姿态输入) ...
Pose-oriented transformer with uncertainty-guided refinement for 2D-to-3D human pose estimation
1
2023
... Comparison of MPJPE result of MSEFN and different methods under protocol 1 on Human3.6M dataset (based on GT-detected pose input)
Tab.2 GT 协议1 会议名 MPJPE/mm Dir. Disc. Eat. Grceet Phone Photo Pose Punch. Sit SitD. Somke Wait WalkD. Walk WalkT. 平均值 PoseFormer [13 ] (f = 81) ICCV’21 30.0 33.6 29.9 31.0 30.2 33.3 34.8 31.4 37.8 38.6 31.7 31.5 29.0 23.3 23.1 31.3 MHFormer [21 ] (f =351) CVPR’22 27.7 32.1 29.1 28.9 30.0 33.9 33.0 31.2 37 39.3 30.0 31.0 29.4 22.2 23.0 30.5 POT[36 ] (f = 81) AAAI’23 32.9 38.3 28.3 33.8 34.9 38.7 37.2 30.7 34.5 39.7 33.9 34.7 34.3 26.1 28.9 33.8 MSEFN (f =81,k f — 27.1 28.0 25.3 26.5 24.6 27.7 29.8 26.0 31.3 33.6 26.5 28.7 28.1 16.3 18.3 26.5
如表1 所示为测试集的所有15个动作结果. 最后一列提供了在所有测试集上的平均性能. 其中,加粗表示最好,下划线表示次好. 具体来说,在实验中采用CPN网络来提取二维姿态,并将该二维姿态作为输入. 提出的模型在协议1(protocol 1)下获得39.8 mm的平均MPJPE,比Poseformer低3.6 mm,比MixSTE低1.6 mm,取得最佳的结果. 此外,比较协议2下的方法,使用刚性对齐. 本文方法在平均MPJPE上优于KTPFormer,从31.9 mm减小到31.0 mm. ...
1
... Detailed quantitative comparison result of three indicators under MPI-INF-3DHP
Tab.3 方法 PCK/% AUC/% MPJPE/mm VideoPose3D [37 ] 86.0 51.9 84.0 UGCN [34 ] 86.9 62.1 68.1 Anatomy3D [8 ] 87.9 54.0 78.8 MixSTE [15 ] 94.4 66.5 54.9 Poseformer [13 ] 95.4 63.2 57.7 MHFormer [21 ] 93.8 63.3 58.0 P-STMO [22 ] 97.9 75.8 32.2 MSEFN 99.1 76.4 31.2
为了评估关键帧选择模块对模型效率的优化作用,在表4 中列出了计算量、参数量、精度的对比实验结果. 可以看出,MSEFN在参数量为MHFormer一半的情况下,MPJPE指标优于MHFormer. ...