传统的多类MI-EEG信号识别方法依赖繁琐的信号预处理和手动特征提取(如小波变换(wavelet transform, WT)[5]、独立成分分析[6])来消除噪声,在特征提取阶段采用共同空间模式[7]及其改进算法[8]. 这些传统方法耗时且高度依赖领域专家的经验,难以有效应对个体差异问题. 因此,设计端到端的学习方法,以减少人工干预并提升分类精度与鲁棒性,已成为BCI技术研究中的一大挑战. 深度学习技术快速发展,其在MI-EEG信号识别中的应用引起广泛关注. 受滤波器组共空间模式(filter bank common spatial pattern,FBCSP)算法的启发,Schirrmeister等[9]提出以卷积神经网络为核心的ConvNet模型,通过深度学习框架提取脑电信号的时间和空间特征. 尽管ConvNet在特征提取方面优势突出,但其计算复杂度高,在资源受限的设备上难以高效运行. 针对这一问题,Lawhern等[10]提出EEGNet,通过巧妙的轻量化设计,将深度可分离卷积与空间滤波结合,不仅显著降低了模型的计算复杂度,还增强了对低信噪比脑电信号的适应能力. EEG-TCNet[11]进一步扩展了EEGNet的能力,引入的时间卷积网络(temporal convolutional network, TCN)能够显著提升模型建模时间动态特性的能力,保留轻量化结构的优势. 上述方法存在瓶颈:1)传统卷积操作受限于局部感受野(receptive field size, RFS),难以全面捕捉MI-EEG信号中跨时间尺度的节律同步性,2)固定频带划分与静态参数设计导致模型对跨受试者数据泛化性能下降. 研究者开始探索注意力机制与动态建模的融合策略. Li等[12]设计融合注意力机制的卷积模型MS-AMF,通过空间和时间多尺度模块提取多脑区的特征,并结合密集融合策略和注意力模块,显著提高了信号分类性能. Altaheri等[13]提出动态注意力时间卷积网络D-ATCNet解码MI-EEG信号,模型通过动态卷积和多级注意力机制,在使用相对较少参数的同时提高模型对MI-EEG信号分类的准确性. 动态卷积的权重更新机制仍依赖离线训练,难以适应在线脑电信号的时变特性. Han等[14]引入元学习框架,实现跨受试者的动态参数调整,克服不同受试者间特异性带来的挑战. Zhang等[15]研究表明,人工设计的固定频带划分可能忽略个体特异性频段特征,其提出的动态滤波器组网络通过端到端学习频段权重,为自适应频段选择提供了新思路.
本研究提出多尺度滑窗注意力时序卷积网络(multi-scale sliding-window attention temporal convolutional network, MSWATCN). 借鉴传统卷积神经网络与注意力机制的优点,通过多尺度双流分组卷积模块提取底层时空特征,引入滑动窗口多头注意力模块精准捕捉局部关键信息,结合窗口化时间卷积模块有效建模长期依赖关系,通过多层次特征融合、动态局部和全局建模优化,实现高效精准的MI-EEG信号解码.
1. 模型介绍
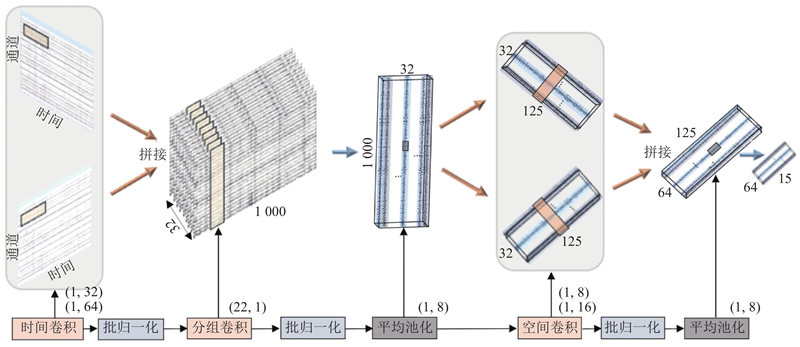
如图1所示,MSWATCN由3个主要模块构成:多尺度双流分组卷积模块、滑动窗口多头注意力模块及窗口化时间卷积模块. 多尺度双流分组卷积模块接收原始MI-EEG信号,通过多尺度时间卷积提取底层时空特征,输出维度为(64, T/64)的特征序列,其中T为采样点数量. 滑动窗口多头注意力模块将输入序列划分为多个局部窗口,
图 1
图 1 多尺度滑窗注意力时序卷积网络的整体架构图
Fig.1 Overall architecture of multi-scale sliding-window attention temporal convolutional network
1.1. 多尺度双流分组卷积模块
1.1.1. 模块输入
MI-EEG信号实验的数据由电极通道C和采样点T组成,表示为
1.1.2. 模块组成
如图2所示,多尺度双流分组卷积模块由3种卷积层构成,包括时间卷积、分组卷积和空间卷积. 1)脑电信号的采用频率为250 Hz,考虑到运动想象相关频段(4~30 Hz)的时域特性,为了提取超过4 Hz的频率相关时间信息,时间卷积层设置了2组卷积核,尺寸分别为 (1, 64) 和 (1, 32),每组卷积核的数量均为16. 这样的设计能够在时间轴上捕捉α和β波段的节律性特征,并最终生成 32 个具有多尺度信息的时间特征图. 通过多尺度卷积捕获信号的层次化时间特性,增强特征表达能力. 将2层时间卷积的输出在通道维度拼接,融合多尺度时间特征,形成包含32个特征图的丰富信息流. 2)中间层采用分组卷积以高效提取特征图的特征关系,输入特征通过大小为(C,1)的分组卷积将32张特征图分为每组2张特征图独立卷积,经批量归一化和指数线性单元(exponential linear unit,ELU)激活函数处理,以引入非线性特性并稳定训练过程. 由池化核大小为(1,8)的平均池化层进一步压缩时间维度,输出的特征图表示为
图 2
1.2. 滑动窗口多头注意力模块
1.2.1. 滑动窗口
在时间序列处理过程中,采用滑动窗口方法捕捉局部时间特征,将经过多尺度双流分组卷积和池化处理后的时间序列
滑动窗口机制将长时间序列分为多个连续的小窗口,聚焦于数据的细粒度局部特征;注意力机制自适应地调整窗口内特征的权重,增强重要特征的表示. 滑动窗口和注意力机制的结合使得模型能够适应不同长度的时间序列数据,捕捉变量间的相互依赖以及时间维度上的局部特征,多头注意力的可并行性使模型能够高效扩展到更大规模的数据.
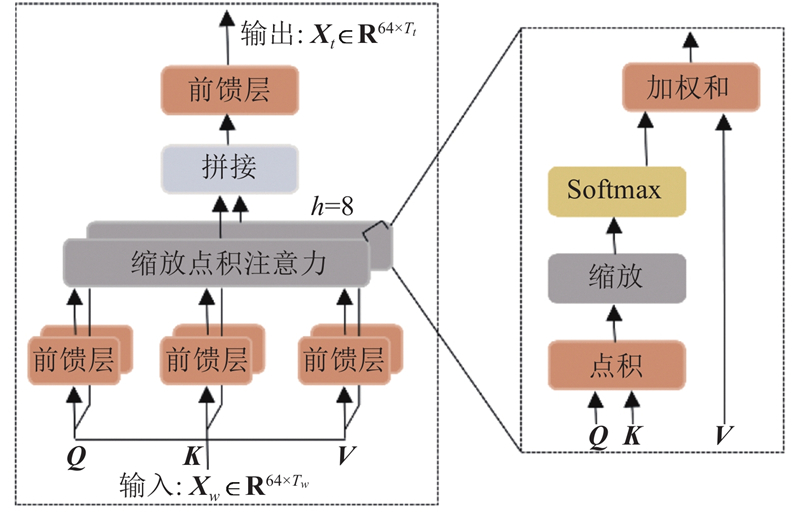
1.2.2. 多头注意力模块
图 3
输入滑动窗口后的时间序列矩阵
式中:
式中:
缩放因子
将注意力头的输出
线性映射矩阵
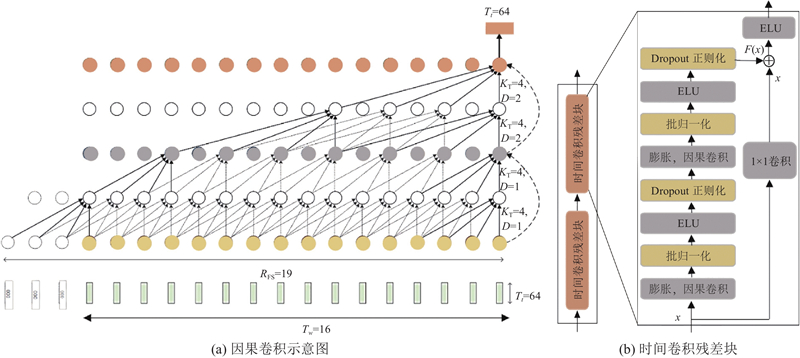
1.3. 窗口化时间卷积模块
图 4
式中:
2. 实验设计
2.1. 数据集介绍及预处理
BCI-2a是德国格拉茨理工大学于2008年发布的公共MI-EEG数据集,被广泛用于MI-EEG解码研究,是该领域的基准数据集. 选用脑机接口竞赛(BCI Competition IV)公开数据集中的2a和2b 数据集进行模型的有效性实验评估. 数据集2a包含9名受试者的脑电数据,涉及4类运动想象任务:左手、右手、双脚和舌头. 将每名受试者的实验分为训练集和测试集,分别采集于不同日期,每个阶段包含288次实验,共576次实验. 脑电数据通过22个电极采集,采样频率为250 Hz,对采集的数据进行0.50~100.00 Hz的带通滤波处理和50.00 Hz的陷波处理. 受试者的训练和测试的实验流程包括2 s的注意力集中阶段,随后1 s的任务提示时间和4 s的运动想象过程,结束后有1.5 s的休息时间. 数据集2b包含9名受试者的脑电数据,涉及2类运动想象任务:左手和右手. 实验分为无反馈和有反馈2种条件,共5个记录阶段,总计720次实验,其中前3个阶段数据作为训练集,后2个阶段数据作为测试集. 脑电数据通过3个电极采集,采样频率同样为250 Hz. 受试者的训练和测试的实验流程为受试者前2 s坐在显示屏前呈安静状态,2 s 时听到提示音后做好实验准备;3~7 s时,显示屏随机出现带有方向的箭头,同时被试做相应的想象动作,持续 4 s;受试者有2 s的休息时间,等待下一轮实验的开始. 运动想象相关的脑电活动主要集中在α波段(8~13 Hz)和β波段(14~30 Hz)[20]. 在数据预处理中,2a数据集选取2~6 s的脑电信号作为样本, 2b数据集选取3~7 s的脑电信号作为样本. 使用Hamming窗有限冲激响应(finite impulse response,FIR)滤波器[21]对信号进行1~30 Hz的带通滤波,有效保留与任务相关的关键信号. 采用公共平均参考方法(common average reference, CAR),以减少实验过程中乳突通道记录信号可能受到触变误差的影响.
2.2. 实验环境
本研究模型使用Python语言编写,基于PyTorch深度学习框架构建,实验在搭载NVIDIA GeForce RTX 3060 Laptop GPU的计算环境中完成. 训练过程中使用自适应矩估计(Adam)优化器,初始学习率设定为0.001. 在2a数据集上,模型训练进行1 000次迭代;在2b数据集上,迭代次数为500,批量大小统一为32. 使用5折交叉验证并采用分层抽样策略,确保每折中各类别样本比例与原始数据一致,准确率为5次训练准确率的平均值. 优化目标选用交叉熵损失函数,通过最小化损失来优化模型性能. 引入早停策略,当模型连续200次迭代准确率无提高时,停止训练.
2.3. 评估指标
为了全面评估模型的分类性能,选用分类准确率Acc和Kappa系数作为评价指标. 分类准确率衡量模型在测试集上的总体分类正确性,计算式为
式中:TP、TN、FP和FN分别为真阳性、真阴性、假阳性和假阴性样本数. 为了进一步排除由于随机猜测造成的偶然一致性影响,引入Kappa系数. Kappa系数是常用于分类任务的统计学一致性评价指标,计算式为
式中:
式中:
3. 实验结果与分析
3.1. 分类方法对比
为了验证MSWATCN在MI-EEG分类任务中的优势,选取多个在该数据集上表现优异的分类模型进行对比分析. 1)FBCSP[22]:将脑电信号分解为多个频带并结合共同空间模式 (common spatial pattern,CSP)提取特征,有效解决CSP依赖频带的问题. 2)浅层卷积网络架构ConvNet:时域卷积层提取频段信号,空间卷积层捕捉空间特征,较大的卷积核尺寸增强了信号转换能力,使计算复杂度降低的同时保留了关键特征. 3)紧凑高效的深度学习模型EEGNet:核心创新在于通过深度卷积逐层处理不同频段信号,点卷积整合多维信息,保持特征提取能力. 4)基于迁移学习的深度表示域适配方法DRDA[23]:通过特征提取器学习判别性特征,结合域判别器的对抗学习策略提升目标受试者的分类性能. 5)基于时空频域特征提取的深度学习网络IFBCLNet[24]:结合可解释滤波器组、CNN和长短时记忆网络(LSTM),以多维方式(时间、空间、频率)提取脑电特征. 6)Conformer[25]:结合CNN和 Transformer框架,通过CNN学习局部时间与空间特征,同时利用Transformer的自注意机制捕捉全局时间特征,实现端到端脑电信号处理. 7)结合注意力机制的滤波器组双视图图卷积网络AFB-DVGCN[26]:通过滤波器组多分支网络提取不同频段的时域和空域特征,引入有效通道注意力机制以动态加权方式增强关键特征表达.
不同方法在BCI Competition IV 2a数据集上的9名受试者(A01~A09)的分类准确率如表1所示,MSWATCN的平均分类准确率
表 1 不同分类方法在BCI Competition IV 2a数据集上的分类准确率
Tab.1
| 分类方法 | Acc/% | Kap | p | |||||||||
| A01 | A02 | A03 | A04 | A05 | A06 | A07 | A08 | A09 | ||||
| FBCSP | 76.00 | 56.50 | 81.25 | 61.00 | 55.00 | 45.25 | 82.75 | 81.25 | 70.75 | 67.75 | 0.57 | |
| ConvNet | 76.39 | 55.21 | 89.24 | 74.65 | 56.94 | 54.17 | 92.71 | 77.08 | 76.39 | 72.53 | 0.63 | |
| EEGNet | 85.76 | 61.46 | 88.54 | 67.01 | 55.90 | 52.08 | 89.58 | 83.33 | 79.51 | 74.50 | 0.66 | |
| DRDA | 83.19 | 55.14 | 87.43 | 75.28 | 62.29 | 57.15 | 86.18 | 83.61 | 82.00 | 74.75 | 0.66 | |
| IFBCLNet | 87.18 | 58.65 | 92.67 | 78.07 | 70.65 | 60.46 | 92.41 | 82.28 | 86.74 | 78.79 | 0.72 | |
| Conformer | 88.19 | 61.46 | 93.40 | 78.13 | 52.08 | 65.28 | 92.36 | 88.19 | 88.89 | 78.66 | 0.72 | |
| MSWATCN | 89.24 | 64.58 | 93.40 | 74.65 | 73.26 | 62.85 | 93.75 | 85.42 | 86.46 | 80.40 | 0.74 | — |
如表2所示为不同方法在数据集2b上的9名受试者(B01~B09)的分类准确率, MSWATCN的
表 2 不同分类方法在BCI Competition IV 2b数据集上的分类准确率
Tab.2
| 分类方法 | Acc /% | Kap | p | |||||||||
| B01 | B02 | B03 | B04 | B05 | B06 | B07 | B08 | B09 | ||||
| FBCSP | 70.00 | 60.36 | 60.94 | 97.50 | 93.12 | 80.63 | 78.13 | 92.50 | 86.88 | 80.00 | 0.60 | |
| ConvNet | 78.56 | 50.00 | 51.56 | 96.88 | 93.13 | 85.31 | 83.75 | 91.56 | 85.62 | 79.37 | 0.59 | |
| EEGNet | 75.94 | 57.64 | 58.43 | 98.13 | 81.25 | 88.75 | 84.06 | 93.44 | 89.69 | 80.48 | 0.61 | |
| DRDA | 83.37 | 62.86 | 63.63 | 95.94 | 93.56 | 88.19 | 85.00 | 95.25 | 90.00 | 83.98 | 0.68 | |
| IFBCLNet | 79.82 | 80.40 | 73.04 | 97.71 | 96.33 | 88.84 | 90.08 | 93.47 | 90.20 | 87.76 | 0.76 | |
| Conformer | 82.50 | 65.71 | 63.75 | 98.44 | 86.56 | 90.31 | 87.81 | 94.38 | 92.19 | 84.63 | 0.69 | |
| MSWATCN | 84.06 | 63.21 | 80.93 | 98.15 | 96.25 | 89.69 | 87.50 | 93.75 | 91.88 | 87.27 | 0.75 | — |
3.2. 多尺度双流分组卷积结构选择
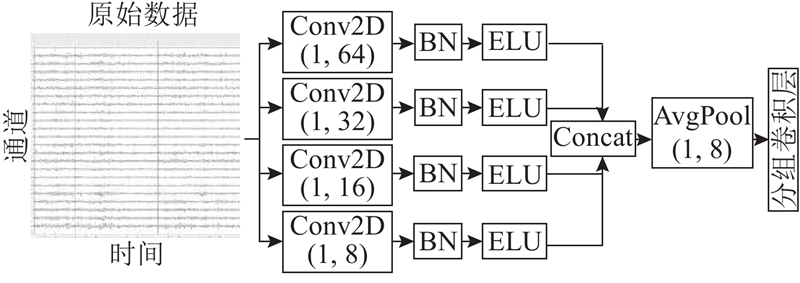
为了突出多尺度双流分组卷积模块时空特征提取能力的优势,将其与使用较多的多分支模型Inception结构进行对比. Inception结构如图5所示,在不改变其他层的基础上,使用与多尺度双流分组卷积模块相同大小的卷积核,最大程度上保持参数相同而只改变多分支结构组成. 比较2种多尺度结构对分类准确率的影响,在相同实验环境下,BCI Competition IV 2a数据集9名受试者的平均分类准确率为70.60%,BCI Competition IV 2b数据集9名受试者的平均分类准确率为83.52%,相较于多尺度双流分组卷积结构的模型平均分类准确率分别低9.8个百分点和3.75个百分点,证明所选的多尺度双流分组卷积模块在脑电信号的时空特征提取方面更具优势.
图 5
3.3. 可视化结果分析
图 6
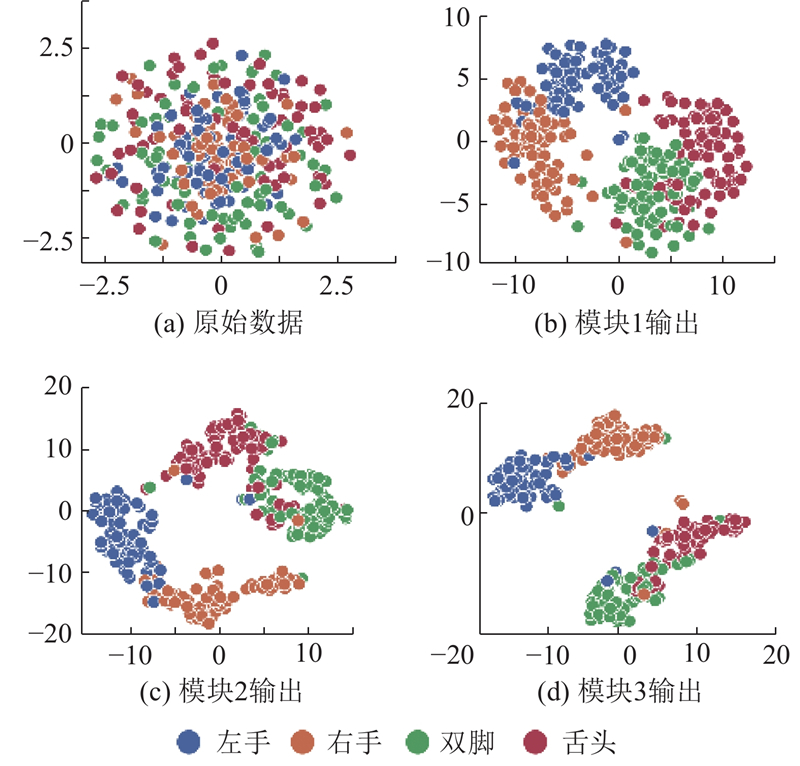
图 6 BCI Competition IV 2a数据集中不同模块的t-SNE特征可视化结果
Fig.6 Visualization results of t-SNE features of different modules for BCI Competition IV 2a dataset
图 7
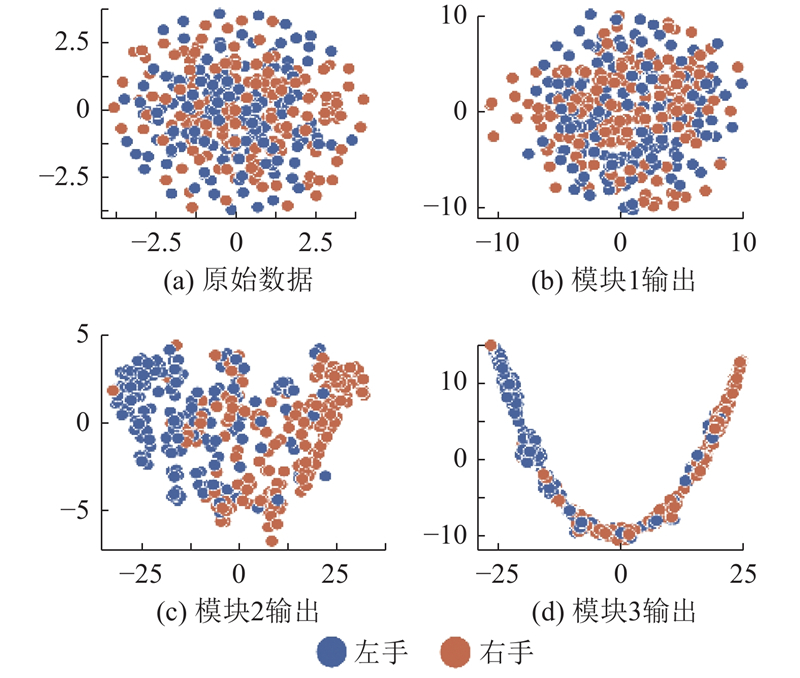
图 7 BCI Competition IV 2b数据集中不同模块的t-SNE特征可视化结果
Fig.7 Visualization results of t-SNE features of different modules for BCI Competition IV 2b dataset
BCI Competition IV 2a和2b原始数据的类别分布较为混乱,类别间重叠严重,样本的可分性较差,为此通过类间可分性指标轮廓系数量化评估各模块输出特征的可分性. 轮廓系数的计算式为
式中:
3.4. 滑动窗口数量对分类性能的影响
经多尺度双流分组卷积模块输出的时间序列
图 8
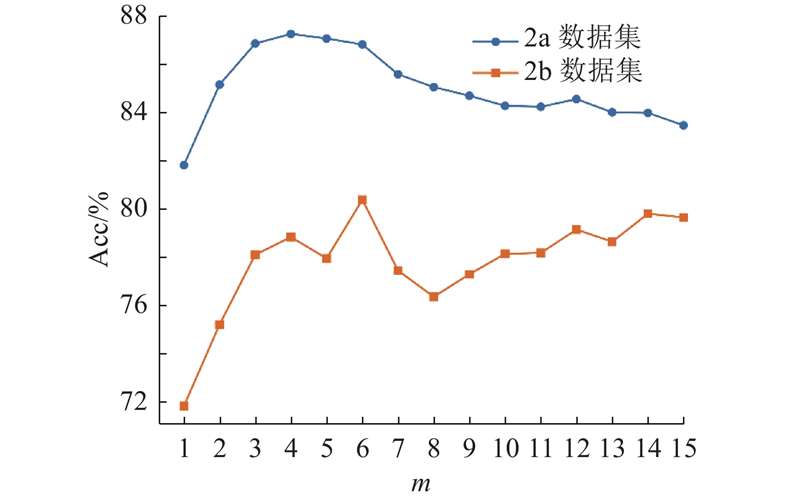
图 8 滑动窗口数量与分类准确率的关系分析
Fig.8 Analysis of relationship between number of sliding windows and classification accuracy
3.5. 消融实验
系统地移除MSWATCN中的关键模块,评估每个模块对模型整体性能的贡献,实验结果如表3所示. 移除模块包括1)滑动窗口:去除模型中处理局部时间特征的滑动窗口机制. 2)注意力机制:移除多头注意力模块在增强关键特征表示中的作用. 3)时间卷积:移除时间卷积模块在捕捉时间依赖性方面的重要性. 4)滑动窗口和注意力机制:评估模型局部时间特征处理与关键特征增强的协同作用. 5)滑动窗口和时间卷积:测试局部和全局时间特征提取的重要性. 实验结果表明,滑动窗口、多头注意力机制和时间卷积是模型性能的核心组成部分,其中滑动窗口对局部时间特征的提取起关键作用,移除后准确率大幅下降,尤其在2a数据集上影响更为显著,移除后准确率降低了接近10个百分点;多头注意力机制和时间卷积模块分别在强化关键特征表示和捕捉时间依赖性方面起重要作用,移除后均导致模型性能明显退化. 联合移除实验进一步揭示模块间的协同作用. 当滑动窗口和注意力机制同时被移除时,模型性能出现最大降幅,其中2a数据集的平均准确率降低了24.43个百分点,2b数据集降低了9个百分点,表明两者在局部时间特征提取与关键信息强化中的协作尤为重要. 相比之下,滑动窗口与时间卷积的联合移除对性能的影响略小. 综合来看,完整模型通过各模块的高效协作,实现时间特征的全面建模和关键信息的充分表达,达到最佳性能. 实验结果验证了模块设计的合理性及其协同优化的必要性,为模型的整体性能提升提供了坚实支持.
表 3 多尺度滑窗注意力时序卷积网络的模块消融实验
Tab.3
| 移除模块 | Acc/% | |
| 2a数据集 | 2b数据集 | |
| 滑动窗口 | 70.86 | 81.84 |
| 注意力机制 | 76.66 | 86.53 |
| 时间卷积 | 78.51 | 85.02 |
| 滑动窗口和注意力机制 | 55.97 | 78.27 |
| 滑动窗口和时间卷积 | 77.47 | 87.26 |
| MSWATCN | 80.40 | 87.27 |
4. 结 语
本研究提出基于多尺度滑窗注意力时序卷积网络的运动想象脑电分类模型,有效解决了多尺度时空特征提取问题. 实验结果表明,所提模型在BCI Competition IV 2a和2b数据集上表现优异,其分类准确率和一致性优于多种基准模型;滑窗注意力机制与时间卷积在局部和全局特征建模中有效. 滑窗参数对分类性能的影响因数据集而异,部分特征表征能力较弱,仍需进一步优化. 所提模型在理论上深化了对时间序列多尺度特征与注意力机制的理解,在应用上为脑机接口提供了高效、准确的分类方法. 未来研究计划优化滑窗机制,探索动态分割以减少超参数调节需求,增强模型对高噪声信号的鲁棒性,同时结合可解释性分析工具改进模型透明性,验证模型在其他生物信号分析中的通用性和扩展性.
参考文献
基于卷积神经网络的多类运动想象脑电信号识别
[J].
Recognition of multi-class motor imagery EEG signals based on convolutional neural network
[J].
An in-depth survey on deep learning-based motor imagery electroencephalogram (EEG) classification
[J].DOI:10.1016/j.artmed.2023.102738 [本文引用: 1]
A high-performance neuroprosthesis for speech decoding and avatar control
[J].DOI:10.1038/s41586-023-06443-4 [本文引用: 1]
A high-performance speech neuroprosthesis
[J].DOI:10.1038/s41586-023-06377-x [本文引用: 1]
Motor imagery EEG classification based on flexible analytic wavelet transform
[J].DOI:10.1016/j.bspc.2020.102069 [本文引用: 1]
Conceptual and empirical comparison of dimensionality reduction algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE)
[J].DOI:10.1016/j.cosrev.2021.100378 [本文引用: 1]
A new discriminative common spatial pattern method for motor imagery brain–computer interfaces
[J].DOI:10.1109/TBME.2009.2026181 [本文引用: 1]
Learning temporal information for brain-computer interface using convolutional neural networks
[J].DOI:10.1109/TNNLS.2018.2789927 [本文引用: 1]
Deep learning with convolutional neural networks for EEG decoding and visualization
[J].DOI:10.1002/hbm.23730 [本文引用: 1]
EEGNet: a compact convolutional neural network for EEG-based brain–computer interfaces
[J].DOI:10.1088/1741-2552/aace8c [本文引用: 1]
A multi-scale fusion convolutional neural network based on attention mechanism for the visualization analysis of EEG signals decoding
[J].DOI:10.1109/TNSRE.2020.3037326 [本文引用: 1]
Dynamic convolution with multilevel attention for EEG-based motor imagery decoding
[J].DOI:10.1109/JIOT.2023.3281911 [本文引用: 1]
META-EEG: meta-learning-based class-relevant EEG representation learning for zero-calibration brain–computer interfaces
[J].DOI:10.1016/j.eswa.2023.121986 [本文引用: 1]
Dynamic weighted filter bank domain adaptation for motor imagery brain–computer interfaces
[J].DOI:10.1109/TCDS.2022.3209801 [本文引用: 1]
Electroencephalography-based motor imagery classification using temporal convolutional network fusion
[J].DOI:10.1016/j.bspc.2021.102826 [本文引用: 1]
A novel time–frequency transformer based on self–attention mechanism and its application in fault diagnosis of rolling bearings
[J].DOI:10.1016/j.ymssp.2021.108616 [本文引用: 1]
Physics-informed attention temporal convolutional network for EEG-based motor imagery classification
[J].DOI:10.1109/TII.2022.3197419 [本文引用: 1]
四类运动想象脑电信号特征提取与分类算法
[J].
Feature extraction and classification of four-class motor imagery EEG data
[J].
Transfer learning for brain–computer interfaces: a euclidean space data alignment approach
[J].DOI:10.1109/TBME.2019.2913914 [本文引用: 1]
Deep representation-based domain adaptation for nonstationary EEG classification
[J].DOI:10.1109/TNNLS.2020.3010780 [本文引用: 1]
IFBCLNet: spatio-temporal frequency feature extraction-based MI-EEG classification convolutional network
[J].DOI:10.1016/j.bspc.2024.106092 [本文引用: 1]
EEG conformer: convolutional transformer for EEG decoding and visualization
[J].DOI:10.1109/TNSRE.2022.3230250 [本文引用: 1]
融合注意力的滤波器组双视图图卷积运动想象脑电分类
[J].
Attention-fused filter bank dual-view graph convolution motor imagery EEG classification
[J].
Visualizing data using t-SNE
[J].