交通流量预测在智能交通系统(intelligent transportation system，ITS)中据有至关重要的地位^[1]. 它不仅能有效减轻交通拥堵状况，还能显著提升交通系统的运行效率及安全性^[2].

近年来，随着图卷积神经网络(graph convolutional network，GCN)^[3]、图注意网络(graph attention network，GAT)^[4]以及扩散卷积递归神经网络(diffusion convolutional recurrent neural network，DCRNN)^[5]等图神经网络在处理图数据方面的显著进步，时空图神经网络逐渐应用于交通流量预测领域. 例如，Li等^[5]将交通流建模为有向图上的扩散过程，采用双向图随机游走来建模空间依赖性，并利用递归神经网络（recurrent neural network，RNN）来捕捉时间依赖性. Zhao等^[6]将GCN和门控循环单元(gated recurrent unit，GRU)组合起来，成功同时捕获了时空依赖关系. Yu等^[7]设计了融合空间图卷积和时间序列的时空卷积模块，有效模拟了交通网络的连通性与全局性. Zuo等^[8]提出的GCN-M模型结合图卷积网络和基于注意力的记忆网络，解决了交通数据中复杂的缺失值问题，并增强了对局部和全局模式的处理能力. Shin等^[9]提出的渐进图卷积网络框架（PGCN），通过构建渐进邻接矩阵来捕捉空间相关性，处理复杂的时空相关性问题.

一些研究人员将注意力机制扩展到交通预测，用于动态地对不同时间步长的重要性进行建模. 例如，Yu等^[10]提出注意时间图卷积网络（A3T-GCN），该模型在T-GCN的基础上，设计了一种注意力机制来分配不同时间步长的权重. Xu等^[11]通过叠加空间Transformer和时间Transformer的方式，有效实现了时空信息的有效融合；Jiang等^[12]引入空间自注意力模块，该模块结合了多种图掩蔽技术以捕捉局部地理信息和全局语义邻域，并专门设计了交通延迟感知特征转换模块，用于建模空间信息传播中的时间延迟. Wu等^[13]提出分解式的架构，专门用于处理长期的时间依赖性问题，并引入自相关机制，旨在提高计算效率和数据利用效率. Bai等^[14]引入新的编码器模块，旨在有效缓解处理长序列数据时常见的梯度爆炸问题. Ren等^[15]将Transformer与GRU相结合，以捕捉历史交通数据中的长期时间模式.

尽管上述方法在探索交通道路网络的时空特征上取得了一定的成效，但仍然存在一些挑战：1）先前的研究大多倾向于使用独立的模块分别捕捉空间相关性和时间相关性，随后将两者结果加以融合. 这种处理策略未能将空间和时间作为统一的整体来考虑，因而难以有效捕获交通流中复杂的时空交互关系. 2）以往工作在空间相关性建模上普遍采用基于距离度量或者地理连接关系的预定义图来刻画路网节点间的空间依赖关系. 这种静态且固定不变的图结构无法充分反映实际交通流的动态关联性. 3）大多现有方法或模型往往只关注短期内的交通变化，而没有充分考虑中长期交通数据中存在的趋势和周期性模式.

为了应对上述挑战，本研究提出多时间尺度自适应图注意Transformer模型（multi-time scale adaptive graph atttention Transformer, MSAGAFormer）. 创新点如下：1）为了更准确地处理复杂时空相关性，提出基于Transformer的交通流量预测模型. 该模型能够有效地捕获时间相关性和空间相关性. 2）为了克服预定义图的局限性，引入自适应图和节点相似度图，分别用于捕捉动态空间相关性和静态空间相关性. 此外，设计基于GAT的空间特征提取方法，以有效提取动静态的空间特征. 3）为了捕捉周期性特征，设计时空特征构建模块. 该模块由多时间尺度构建模块和时空特征聚合模块2部分组成. 多时间尺度构建模块整合了不同时间尺度的特征提取策略，以有效捕获多尺度时间特征. 时空特征聚合模块则是一种扩展至长时间序列的时间特征提取方法，能够在处理大量时间数据的同时，有效平衡数据冗余带来的精度下降风险.

交通流量预测任务是经典的时间序列预测任务. 在本研究中，使用基于最近、每日和每周周期长度为T的历史时间片作为输入序列. 具体而言，将3类输入序列融合为一个由$(a+b+g)$个子序列片段组成的输入序列. 此时，预测未来q个时间步的交通流量问题定义如下：

(1)$ [{{{Y}}_{t{\text{+1}}}}, \cdots ,{{{Y}}_{t{\text+}q}}] = f({{\boldsymbol{X}}_{\text{w}}},g,{{\boldsymbol{X}}_{\text{d}}},b,{{\boldsymbol{X}}_{\text{r}}},a). $

式中：${{\boldsymbol{X}}_{\mathrm{r}}}$为最近周期片段，$a$为最近周期片段数量，$ {{\boldsymbol{X}}_{\mathrm{d}}} $为日周期片段，$b$为日周期片段数量，$ {{\boldsymbol{X}}_{\text{w}}} $为周周期片段，$g$为周周期片段数量.

相关概念的定义如下.

定义1　交通网络. 使用无向图$ G\text{=}(V,E,{{\boldsymbol{A}}}_{\text{dis}}, {{\boldsymbol{A}}}_{\text{adp}}) $来表示交通网络，其中，V表示图中的节点集，节点总数为N；E表示节点之间的连通性；${{\boldsymbol{A}}_{{\text{dis}}}}$表示节点间静态空间相关性的预定义邻接矩阵；${{\boldsymbol{A}}_{{\text{adp}}}}$表示节点间动态空间相关性的自适应邻接矩阵.

定义2　交通流量矩阵. 交通网络${{G}}$在t时刻记录的交通流量为交通流量矩阵${{\boldsymbol{X}}_t} = [ {{\boldsymbol{x}}_{t,1}},{{\boldsymbol{x}}_{t,2}}, \cdots , {{\boldsymbol{x}}_{t,n}}]$，其中$ {{\boldsymbol{x}}_{t,v}} $表示节点v在t时刻的交通流量.

定义3　预定义邻接矩阵. 使用曼哈顿距离函数定义节点间的距离，并通过动态时间扭曲（DTW）计算每对节点的相关性，构建反映节点间静态空间相关性的预定义矩阵. 为了确保矩阵值的可比性，对矩阵进行归一化处理，并设定阈值为0.6. 当2个节点的相关性超过该阈值时，对应的矩阵元素值设为1；否则，设为0.

定义4　自适应邻接矩阵.通过节点嵌入向量的点积和Softmax归一化推断每对节点之间的空间依赖关系，并在训练过程中通过反向传播自动更新能够反映节点间动态空间相关性的自适应邻接矩阵. 与此同时，利用Gumbel-Sigmoid生成的二进制掩码确保自适应邻接矩阵的稀疏性.

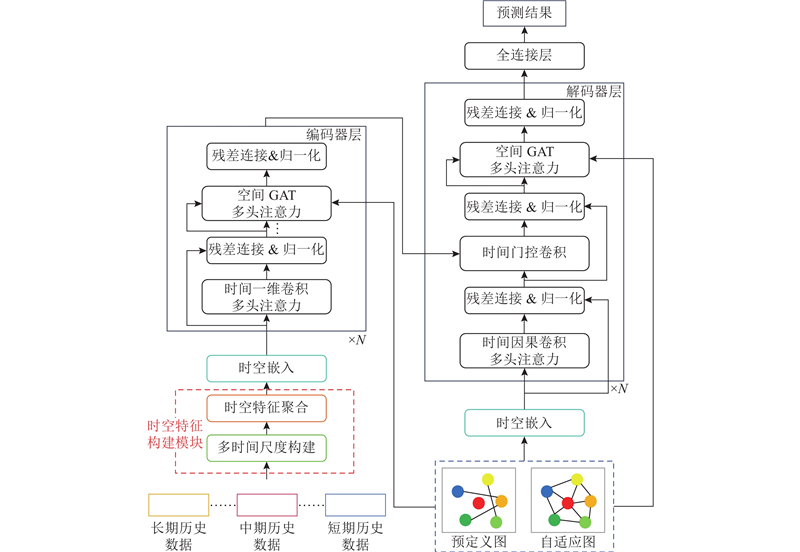
如图1所示，本研究提出的MSAGAFormer架构包含时空特征构建层、时空特征嵌入层及堆叠的编码器-解码器层. 时空特征构建层通过多时间尺度构建模块和时空特征聚合模块，分别整合不同时间尺度特征并处理长时间序列数据以平衡精度下降风险；时空特征嵌入层采用时空嵌入方法编码时空位置，提供丰富上下文信息；编码器和解码器层利用空间GAT多头注意力模块捕捉动静态空间特征，利用时间一维卷积多头注意力模块捕捉局部时间模式，利用时间因果卷积模块捕获长期时间相关性，从而全面理解时空数据中的复杂模式.

交通模式随时间演变，而不同时间尺度的特征对预测的影响各不相同. 交通数据包含瞬时变化、短期波动、中期趋势和长期依赖等多尺度的时间特征^[16-19]. 然而，现有方法通常仅关注单一的时间尺度，忽略动态的时间模式. 为了更精确地捕捉交通流的时间周期性和连续性，提出多时间尺度构建方法.

该方法将历史数据划分为短期、中期和长期，并融合这些多尺度数据以生成增强的时间序列作为后续模块的输入. 低尺度序列揭示局部变化趋势，对短期预测至关重要；中尺度序列捕捉趋势性变化，提取中期趋势特征；高尺度序列则反映周期性变化，有助于理解长期依赖. 通过串联3种尺度的序列^[20]，增强了对历史数据序列的表达能力. 此外，设置低尺度序列长度与相应的历史序列长度一致，中尺度序列长度和高尺度序列长度分别为低尺度序列长度的${1}/{2}$和${1}/{3}$.

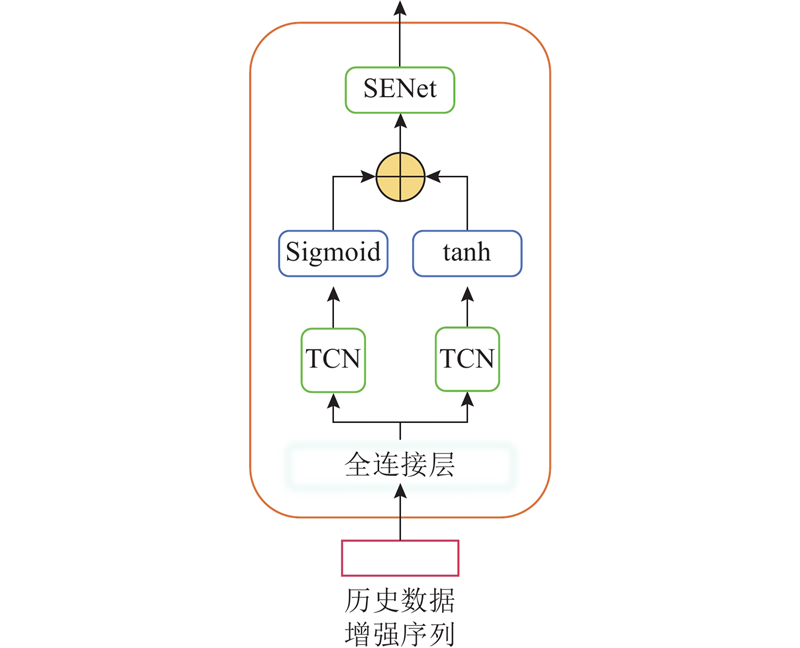
时空特征聚合模块旨在将由多时间尺度构建模块得到的历史数据增强序列压缩成较短的表现形式，从而使得模型能够在不增加计算复杂度的情况下考虑长期的时间模式. 其结构如图2所示. 具体来说，TCN通过多层膨胀卷积逐步将长时间序列的历史数据浓缩为较短的时间步表示，从而捕捉长期依赖关系而不增加计算复杂度. TCN首先处理最近的数据，随着层数加深，卷积间隔逐渐增大，覆盖更久远的历史信息，最终生成富含长期趋势信息的时间特征表示. 其表达式如下：

(2)$ \begin{split} {\text{TCN}}({\boldsymbol{X}}) =& \sum\limits_{k = 0}^{k - 1} \bigg(\sigma \Big({\boldsymbol{X}}\big[:,t - D \times k,:\big] \cdot {{\boldsymbol{W}}_{{\text{D1}}}}\big[k,:\big]\Big) \odot \\ &\tanh\; \Big({\boldsymbol{X}}\big[:t - D \times k,:\big] \cdot {{\boldsymbol{W}}_{{\text{D2}}}}\big[k,:\big]\Big)\bigg). \end{split} $

式中：$ \odot $表示元素乘法；k为卷积核大小；D为膨胀因子；W_D1、W_D2分别表示TCN中2组可学习的卷积滤波器，分别对应Sigmoid分支和tanh分支；${{\boldsymbol{W}}_{{\rm{D1}}}}[k,:] $和${{\boldsymbol{W}}_{{\rm{D2}}}}[k,:] $分别表示时间维度上第k个卷积位置处的权重向量；$ \sigma $为Sigmoid函数；$ {\boldsymbol{X}} $为历史数据增强序列经过全连接层后的结果.

SENet评估每个节点的重要性，并据此调整特征权重，强化关键位置的信息. SENet从压缩后的时间特征中提取全局信息，通过2层全连接层的非线性变换计算各节点的重要性，然后根据重要性调整原始特征，形成优化后的空间特征表示${\boldsymbol{X}}'_{\mathrm{SE}} $. 其计算方法如下：

(3)$ {\boldsymbol{X}}_{{\text{SE}}}^{'} = {\text{TCN}}({\boldsymbol{X}}) \cdot \sigma ({{\boldsymbol{W}}_{{\text{e2}}}} \cdot {\text{ReLU}}({{\boldsymbol{W}}_{{\text{e1}}}} \cdot {{\boldsymbol{X}}_{{\text{AP}}}})). $

式中：$ {{\boldsymbol{W}}_{{\text{e1}}}} $和$ {{\boldsymbol{W}}_{{\text{e2}}}} $为权重矩阵，$ {{\boldsymbol{X}}_{{\text{AP}}}} $为对$ {\text{TCN}}({\boldsymbol{X}}) $应用平均池化的结果.

与RNN不同，Transformer缺乏显式的序列顺序，因此须引入位置编码来捕获输入序列的位置信息.

MSAGAFormer从短期、中期和长期历史数据中捕捉多尺度交通模式，使模型能全面理解交通模式的变化. 这种方法不再局限于单一时间尺度的数据，还增强了对不同周期交通模式的理解. 其次，通过正弦和余弦函数生成的位置编码，模型能够有效处理序列中不同时间点的相对距离和顺序关系. 具体表达式如下：

(4)$ {{\boldsymbol{P}}_{\text{T}}}(t,2d) = \sin \left({t}\big/{{{{10\;000}^{\tfrac{{2d}}{{{d_{{\text{model}}}}}}}}}}\right), $

(5)$ {{\boldsymbol{P}}_{\text{T}}}(t,2d+1) = \cos \left({t}\big/{{{{10\;000}^{\tfrac{{2d}}{{{d_{{\text{model}}}}}}}}}}\right). $

式中：d为特征维度的索引，范围为0~${{{d_{{\text{model}}}}}}/{2} - 1$； ${d_{{\text{model}}}}$为模型特征维度的大小.

利用图拉普拉斯矩阵的特征向量来编码节点的位置信息，不仅考虑直接连接关系，还捕捉更广泛的拓扑结构信息. 具体计算公式如下：

(6)$ {\boldsymbol{\varDelta }} = {\boldsymbol{I}} - {\boldsymbol{D}}_{\text{m}}^{ - {1}/{2}}{{\boldsymbol{A}}_{{\text{adp}}}}{\boldsymbol{D}}_{\text{m}}^{ - {1}/{2}} = {{\boldsymbol{U}}^{\text{T}}} \wedge {\boldsymbol{U}}. $

式中：$ {\boldsymbol{I}} $为单位矩阵，$ {{\boldsymbol{D}}_{\text{m}}} $为度矩阵， $ {\boldsymbol{U}} $为特征向量. 此外，为每个节点选择${d_{{\text{model}}}}$个最小的非平凡特征向量作为空间位置编码$ {{\boldsymbol{P}}_{\text{S}}} $.

通过将时间特征、时间位置编码和空间位置编码进行线性组合，并引入可学习的投影矩阵，以确保模型不仅能有效捕捉时间序列中的动态演化规律，还能同时建模空间节点之间的静态与动态关联. 该设计显著增强了模型对复杂时空依赖关系的表达能力. 融合上述3类信息后所得到的统一时空表示${\boldsymbol{X}}'_{{\rm{Emb}}}$的具体表达式如下：

(7)$ {\boldsymbol{X}}_{{\text{Emb}}}^{'} = {\boldsymbol{X}}_{{\text{SE}}}^{'}+{{\boldsymbol{P}}_{\text{T}}}+{{\boldsymbol{P}}_{\text{S}}} \cdot {{\boldsymbol{W}}^{{{\boldsymbol{P}}_{\text{S}}}}}. $

式中：$ {{\boldsymbol{W}}^{{{\boldsymbol{P}}_{\text{S}}}}} $表示空间位置编码的线性投影.

通过编码器和解码器捕捉交通数据中复杂的时空相关性. 其中，编码器层由1个时间一维卷积多头注意力模块和1个空间GAT多头注意力模块组成. 解码器层包括1个因果卷积时间多头注意力模块、1个空间GAT多头注意力模块和1个时间门控卷积模块.

在编码器中，采用一维时间卷积捕捉交通数据中的局部趋势和复杂的时间依赖性. 这种方法通过参数共享提高了计算效率，减少了过拟合风险，并能同时提取时间特征和节点间的空间关系. 具体来说，输入的时空特征被分解为每个节点的时间序列，然后应用一维卷积生成增强特征表示，这些表示保留了原始序列的局部结构并提升了对时间变化的理解. 经过卷积处理的特征参与多头自注意力机制，帮助模型建模不同时间步之间的依赖关系.

解码器采用因果卷积确保预测仅依赖于当前及过去的时间步，避免泄露未来信息. 通过在前端填充零值，保持严格的因果顺序，从而更好地理解长期依赖而不引入未来偏差. 解码器接收来自编码器的输出序列，并通过因果卷积处理每一时间步. 随后，模型计算编码器输出与因果卷积多头注意力模块输出之间的关联，增强了对时间特征的理解. 最终，时间门控卷积模块有效融合局部和全局的时间依赖关系.

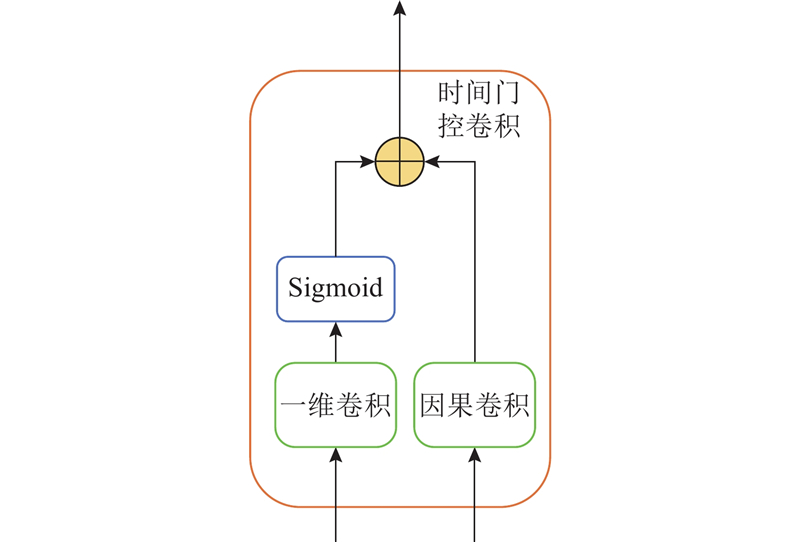
如图3所示，时间门控卷积模块旨在增强模型处理长时间序列数据的能力，通过结合一维卷积和因果卷积，确保在长序列处理中的稳定性和防止梯度爆炸或消失问题. 一维卷积捕捉局部时间模式，而因果卷积捕捉长期时间依赖性，确保预测仅基于过去信息. 这种组合使模型能够全面理解复杂的时间序列模式.

具体而言，首先，输入的时间特征表示分别为编码器的输出${{\boldsymbol{X}}_{{\text{En}}}}$和因果卷积多头注意力模块的输出${{\boldsymbol{X}}_{{\text{TC}}}}$，分别经过卷积核${{\boldsymbol{\varPhi }}_{{\text{En}}}}$和${{\boldsymbol{\varPhi }}_{{\text{TC}}}}$进行卷积操作，即${{\boldsymbol{\varPhi }}_{{\text{En}}}} \otimes {{\boldsymbol{X}}_{{\text{En}}}}$和${{\boldsymbol{\varPhi }}_{{\text{TC}}}} \otimes {{\boldsymbol{X}}_{{\text{TC}}}}$，随后使用一个函数计算门控信号$ g\odot \sigma ({{\boldsymbol{\varPhi}} }_{\text{En}}\otimes {{\boldsymbol{X}}}_{\text{En}}) $，以动态地调整不同时间步特征的重要性. 最终，将门控信号应用于因果卷积模块的输出，并与编码器输出进行加权求和，得到时间门控卷积模块的输出，具体公式如下：

(8)$ \text{TGC}({{\boldsymbol{X}}}_{\text{En}}\text{，}{{\boldsymbol{X}}}_{\text{TC}})\text=g\odot ({{\boldsymbol{\varPhi}} }_{\text{TC}}\otimes {{\boldsymbol{X}}}_{\text{TC}})\text+ ({1-}g)\odot {{\boldsymbol{X}}}_{\text{En}}. $

选用GAT作为空间依赖的捕捉策略，因其通过引入注意力机制，能够基于邻居节点特征动态分配差异化权重. GAT利用多头注意力机制在多个特征子空间中独立处理注意力分布，这不仅减轻了模型过拟合倾向，还增强了学习稳定性. 编码器结合空间GAT多头注意力模块和自适应图邻接矩阵，评估节点间的动态空间相关性，不仅限于直接连接的节点，从而能捕捉远距离节点之间的潜在联系.

解码器的任务是基于编码器输出和部分已知未来信息逐步生成精确预测. 为了确保准确性，解码器关注当前和邻近节点的状态变化. 通过空间GAT多头注意力模块和预定义图邻接矩阵提取静态空间特征，并集中处理目标节点附近的动态变化. 这种设计有助于理解局部动态特性，减少计算复杂度，并有效捕捉局部模式.

为了验证本研究提出的方法，在美国加州数据集PEMS04和PEMS08上进行实验. PEMS数据集包含3种特征，即流量、速度和占有率. 这些数据集的相关信息如表1所示. 其中，n_s为传感器数量，t_o为采样间隔. PEMS04是2018年1—2月旧金山湾区307个检测点收集到的交通数据；PEMS08是2018年7—8月圣贝纳迪诺170个检测点收集到的交通数据. 这些数据被整理成每5 min一条记录. 此外，采用标准归一化对数据进行处理，并按照6∶2∶2的比例随机划分训练集、验证集和测试集. 为了评估模型的泛化性能，生成多组不同的验证集，并在每组验证集上计算评价指标的平均值.

硬件平台如下：11th Gen Intel(R) Core(TM) i7-1195G7 @ 2.90GHz 2.92 GHz 处理器，NVIDIA GeForce MX450 GPU. 软件配置如下：Windows 10操作系统，Anaconda3资源管理，Pycharm IDE，Pytorch 2.4.0深度学习框架，Python语言开发.

采用2个评估指标以评估模型性能：均方根误差（RMSE）和平均绝对误差（MAE）. 具体计算公式如下：

(9)$ {\mathrm{RMSE}} = \left[ {\dfrac{1}{n}{{\sum\nolimits_{i = 1}^n {\left( {{{\hat Y}_i} - {Y_i}} \right)^2} }}}\right]^{1/2} , $

(10)$ {\mathrm{MAE}} = \dfrac{1}{n}\sum\nolimits_{i = 1}^n {\left| {{{\hat Y}_i} - {Y_i}} \right|} . $

式中：$ n $为样本总数；$ {Y_i} $为真实值，即实际观测到的交通流量；$ {\hat Y_i} $为预测值，即模型预测的交通流量.

为了验证所提模型的预测性能，选取以下7种基于深度学习的交通流量预测模型作为基线模型，并在PEMS04和PEMS08这2个数据集上进行对比实验.

1）STGCN^[7]：通过结合空间域的图卷积网络和时域的一维卷积网络，构建完整的卷积模块结构，用于提取时空特征.

2）T-GCN^[6]：利用GCN与GRU单元相结合，分别提取交通数据中的空间相关性与时间相关性.

3）DCRNN^[5]：采用扩散卷积网络来学习交通流数据的空间信息，并使用序列到序列模型来捕获时间序列.

4）DMSTGCN^[21]：高级的时空图卷积网络模型，专注于动态和多维度的时空数据处理.

5）Trendformer^[22]：沿用Transformer的编码器-解码器结构，其中编码器结构对输入交通流进行编码以计算出平均趋势，而解码器则基于此趋势输出预测结果.

6） STTN^[11]：构建空间Transformer与时间Transformer的神经网络架构，通过自注意力机制动态捕捉交通网络中节点间的空间依赖以及长期依赖关系.

7）ATST-GCN^[23]：采用基于注意力的双向GRU提取时间依赖，并通过多层GAT卷积模块捕获空间依赖，同时整合天气和道路属性作为辅助信息.

如表2、3所示分别展示了在PEMS04和PEMS08数据集上，不同模型使用RMSE和MAE作为评价指标的对比结果. 其中，T_p为实际预测时长. 实验结果表明，尽管STGCN、T-GCN、DCRNN和DMSTGCN等时空图卷积模型同时考虑了时间相关性和空间相关性，但它们在处理长期时间依赖方面存在局限，且忽视了动态的时空相关性. 相比之下，MSAGAFormer通过集成GAT和Transformer网络，将时空特征整体建模，显著提升了对时空特征及长期依赖关系的捕捉能力，从而提高了预测精度. 虽然Trendformer、ATST-GCN和STTN设计了时空特征提取模块以综合捕获交通流的时空相关性，但这些方法未能充分利用中长期历史数据中的趋势性和周期性特征或多时间尺度特征. MSAGAFormer不仅关注中长期历史数据，还通过多时间尺度构建模块捕获多时间尺度特征，进一步提升了预测准确性. 此外，在短期（15 min）交通流量预测中，MSAGAFormer与STTN表现相当，但在中长期预测中MSAGAFormer表现出更优性能. 在2个数据集上，MSAGAFormer始终保持最低的RMSE和MAE，尤其在PEMS08数据集上的45 min和60 min预测中性能提升更为显著，显示出其在不同数据集上的稳定性和良好的适应性.

为了探究所提模型各组件的作用，设计了5种变体，并在PEMSE04和PEMS08数据集上进行消融实验. 如表4、5所示分别展示了在PEMS04和PEMS08数据集上，不同变体使用RMSE和MAE作为评价指标的消融结果.

本研究去除时空构建模块中的多时间尺度特征，分别使用单一低时间尺度（w/o MH）、单一中时间尺度（w/o LH）和单一高时间尺度（w/o LM）进行交通流量预测，以探讨不同时间尺度对预测精度的影响. 实验结果表明，低时间尺度特征有助于捕捉瞬时变化，适用于短期预测；中时间尺度特征能够反映较长时间段内的趋势变化，适合中期预测；高时间尺度特征则擅长捕捉周期性和长期趋势，适用于长期预测. 这些结果验证了多时间尺度在提取不同类型时间特征上的重要性. 此外，本研究还评估了自适应图和预定义图的作用. 通过去除自适应图（w/o adp），仅使用传统的预定义图建模交通网络的空间相关性，以及去除预定义图（w/o dis），仅使用自适应图建模空间相关性. 实验结果表明，两者各自捕捉了不同的空间相关性. 自适应图能够动态反映节点之间的实时关联，捕捉动态的空间特征，这对于捕捉交通网络中的瞬时变化至关重要. 而预定义图提供了相对稳定的静态拓扑信息，有助于理解交通网络的基本结构关系. 通过观察这2组变体的实验结果，可以明显看出自适应图和预定义图对预测性能的重要影响.

综上所述，MSAGAFormer通过结合多时间尺度特征、自适应图以及预定义图，在所有预测时间段内保持了最佳性能，证明了这些组件在提升预测精度方面的互补作用，展示了其在处理复杂时空依赖关系上的优势.

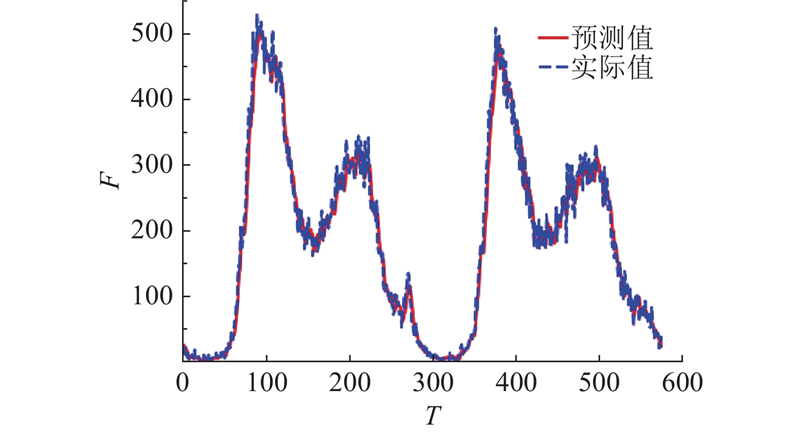
为了更直观地展示本研究所提模型在测试集上的预测表现，选择PEMS04数据集上第115号传感器作为可视化对象，展示MSAGAFormer在测试集上的预测结果与真实值的对比情况. 具体的可视化结果如图4所示. 其中，F为交通流量，T为时间段.

提出新的多时间尺度自适应图注意Transformer（MSAGAFormer），并设计了时空特征构建模块. 在PEMS数据集上的实验验证表明，所提模型在预测交通流量上表现出显著的有效性，并且相较于现有的一些先进方法，在预测精度上实现了一定提升.

所提模型仍有较大的优化空间，包括：1) 尚未考虑交通事故信息、天气信息及节假日等外部因素，限制了复杂现实场景中的预测准确性；2) 模型性能高度依赖于历史数据的质量和完整性，数据缺失或异常值可能影响预测可靠性；3) 复杂的时空特征提取和多头注意力机制导致较高的计算资源需求，限制其在资源受限环境中的应用. 计划通过持续的研究与创新来克服上述挑战，从而使所提出的模型能够在实际应用场景中发挥更卓越的性能和更高的可靠性.