人体疲劳包括生理上的疲劳和心理上的疲劳,针对上肢作业一般结合主、客观2种方法进行肌肉性疲劳、心理性疲劳、脑力性疲劳等方面的研究. 主观方法常用Borg量表,如Frasie等[3]证实了Borg CR10量表在提升作业中评估肩部疲劳的有效性;Chin等[4]将Borg RPE量表与NOISH手工提举分析、北欧身体地图问卷相结合对钣金工业中的提举作业疲劳进行评估. 客观测量方法包括表面肌电(surface electromyography,sEMG)、心率、呼吸频率和血压等生理数据的采集分析,以量化分析工作负荷和疲劳程度. 其中,sEMG技术以其高信噪比和对环境因素的低敏感性而被广泛应用,如Zhou等[5]基于sEMG研究了战斗机飞行员任务执行中的上肢肌肉疲劳状况及与作业效能的关系;徐兆等[6]结合sEMG与动作捕捉监测上肢运动疲劳;La Delfa等[7]利用sEMG评估不同手部垂直施力高度对肩部肌肉疲劳反应的影响,发现过头作业使肩部力量最大降低18%;Yang等[8]利用sEMG和上肢运动学数据评估使用坐、立两用座椅作业时的上肢疲劳改善;Musso等[9]研究了使用上肢外骨骼进行过头装配作业、砌砖和移箱作业时的上肢sEMG变化,发现肩屈肌激活减少,而非过头作业时伸肌激活增加.
以上研究探讨了不同作业场景下的上肢疲劳特性,发现其中过头作业更易增加上肢WMSDs风险. 然而,针对过头作业所致上肢肌肉疲劳的有效分类及其非线性动态演变规律的解析,仍须进一步探索. 当前,有监督学习的机器学习方法,如支持向量机(support vector machine, SVM)、k最近邻(k-nearest neighbor, KNN)、随机森林(random forest,RF)等,仍须人为对肌肉疲劳分类[10-11]. 以K-means聚类、层次聚类为代表的无监督学习虽不依赖标注数据,但前者随机的初始划分影响聚类结果且要求指定聚类数量[12],后者则对异常值和数据点密度波动较为敏感[13]. 另外,仅通过分类难以捕捉肌肉疲劳的非线性动态特征,而Hammerstein模型则能够有效描述非线性动态过程,因而被广泛应用[14-15]. Li等[15]提出基于Hammerstein结构的动态神经网络模型,应用于上肢神经康复的功能性电刺激中,实现肘关节运动的精确模拟和跟踪;Zhang等[16]针对帕金森综合征患者手腕震颤抑制性能受限问题,建立了腕部肌骨系统的Hammerstein模型,提出了自动、快速的参数辨识方法并设计了震颤抑制控制方案;杨坤等[17]基于Hammerstein系统提出航空发动机部件级辨识模型,以预测关键参数并描述航空发动机的动态特性.
针对上述问题,本研究融合Hammerstein模型和sEMG提出新的过头作业上肢肌肉疲劳评估方法. 以sEMG的中位频率(media frequency,MF)和均方根值(root mean square,RMS)作为Hammerstein模型的输入和输出,辨识动态参数,借助K-means++聚类算法对肌肉疲劳分类评估,同时利用肌电疲劳阈值(electromyographic fatigue threshold,EMGFT)确定具体肌肉疲劳时间. 设计过头作业实验并采集上肢sEMG数据,通过关键参数辨识与疲劳分类深入分析上肢肌肉疲劳的动态变化规律.
1. sEMG特征提取
为了从复杂的上肢肌肉sEMG信号中获得关键信息,须进行sEMG特征提取,常用特征包括时域特征和频域特征.
1.1. 时域特征
时域特征常用的有积分肌电值(integrated electromyography,IEMG)与RMS. IEMG表达式如下:
式中:N为sEMG总长度,xi为第i个窗口的sEMG幅值.
RMS表达式如下:
通常随着肌肉疲劳加深,IEMG幅值会增加,而RMS对信号波动和瞬时变化响应较平滑,适用于分析疲劳过程中肌肉活动的变化趋势[18].
1.2. 频域特征
频域特征主要涉及平均功率频率(mean power frequency,MPF)与MF. MPF表达式如下:
式中:Pj为第j个频率点对应的功率谱密度,M为功率谱中的总频率点数,fj为第j个频率点对应的频率.
MF的取值
2. Hammerstein模型
图 1
Hammerstein模型的输入转化如下:
式中:u(t)为t时刻系统输入,v(t)为非线性部分输出,p为基函数阶数,cl为第l个基函数的系数,
图1的动态线性模块表达式如下:
式中:Y(t)为系统输出,e(t)为均值为0的高斯白噪声.
式中:m、n分别为模型的输出、输入滞后项数目; aj为第t−j个滞后值Y(t−j)的系数;bk为第t−k个滞后值v(t−k)的系数;z−j为滞后算子,并使得z−jY(t)=Y(t−j).
联合式(5)~(7),可得
式中:ξ(t)为外界干扰. a、b、c为参数,a用以描述不同阶数的历史输出Y(t−i)对Y(t)的影响;b为非线性静态部分,将u(t)转换为v(t),并进一步影响Y(t);c反映不同阶次u(t)对v(t)的影响.
进而将式(8)简化为
其中,
式中:
采用带遗忘因子的递推最小二乘法(forgetting factor recursive least squares,FFRLS),通过降低历史数值的信息贡献,增加新数据的信息,以解决数据过载问题[22]. 表达式如下:
式中:K(t)为卡尔曼增益矩阵,P(t)为协方差矩阵,
式中:U和V为不同阶的酉矩阵,Q为对角矩阵.
式中:C、B分别为参数c、b的向量矩阵.
3. 基于K-means++算法的上肢肌肉疲劳分类
为了进一步评估肌肉疲劳状态,利用Hammerstein模型识别的参数分类检测肌肉疲劳程度,但当前缺乏对肌肉疲劳的多等级分类研究[25]. 为此,本研究利用K-means++聚类算法进行过头作业上肢肌肉疲劳分类,通过改进的初始质心选择,避免K-means算法对初始值敏感的现象,从而提高聚类结果质量. 具体步骤如下:随机选择初始质心,计算每个数据点到已选质心的最小欧氏距离,选中下一个质心的概率与该距离的平方成正比. 重复此过程直至选出K个初始质心. 之后利用标准K-means算法,将数据点分配至最近质心并更新质心位置,直至算法收敛从而完成聚类[26]. 最佳聚类数由肘部法则确定,在聚类过程中,随着K增大,误差平方和(sum of squares due to error,SSE)逐渐降低,当出现明显拐点则可确定为最佳聚类数.
为了量化a、b参数的变化规律,建立其与疲劳分类的关系,引入参数特征矩阵
式中:
4. 肌电疲劳阈值
为了更准确地确定各疲劳阶段的具体疲劳情况,采用改进的肌电疲劳阈值(electromyographic fatigue threshold,EMGFT)方法. 与以往依靠RMS单一特征不同,本研究利用Hammerstein模型参数的量化矩阵,将每个疲劳阶段的动态参数矩阵
图 2
5. 过头作业实验
5.1. 实验准备
5.1.1. 实验对象
选择10名身体健康、年龄为(23±2)岁的志愿者,身高为(174±2.5)cm,体重为(65±5)kg. 所有志愿者均无上肢肌肉骨骼疾病史,均为右利手. 实验前3个月内无肌肉骨骼损伤,且实验前72 h内无剧烈运动. 被试者在实验前都阅读实验指导书并签署同意书. 本实验得到长安大学学术委员会批准.
5.1.2. 肌肉选取
利用Anybody进行过头作业仿真,发现上肢平均肌肉激活程度大于0.1的肌肉为右臂的肱桡肌(m1)、肱二头肌(m2)、三角肌(m3)和斜方肌(m4),及左臂的斜方肌(m5)、肱二头肌(m6)、三角肌(m7)和肱桡肌(m8). 因此,选取这8块肌肉进行过头作业实验采集sEMG.
5.1.3. 实验设备
主要设备如下:电动螺丝刀、采样频率为1 000 Hz的意大利BTS Bioengineering公司的BTS FreeEMG
图 3
5.2. 实验过程
5.2.1. 最大自主收缩测量
被试者在测量最大自主收缩(maximum voluntary contraction,MVC)前进行肌肉放松,使用磨砂膏和酒精棉擦拭清洁m1~m8肌腹表面皮肤,沿肌纤维方向黏贴电极片,并按表1要求完成MVC测量. 每块肌肉测试3次,依次测量左右m1~m8肌肉. 每2次测试间休息20 min,以避免肌肉疲劳影响结果,最终取3次测量的平均值作为该肌肉的MVC.
表 1 MVC实验说明
Tab.1
| 肌肉 | 实验过程 | 示意 |
| 斜方肌 | 被试站姿,手臂伸直自然下垂,掌心朝内. 实验人员双手下按肩部,被试者用力抬肩5 s,记录肌电数据,完成一次MVC测量 | 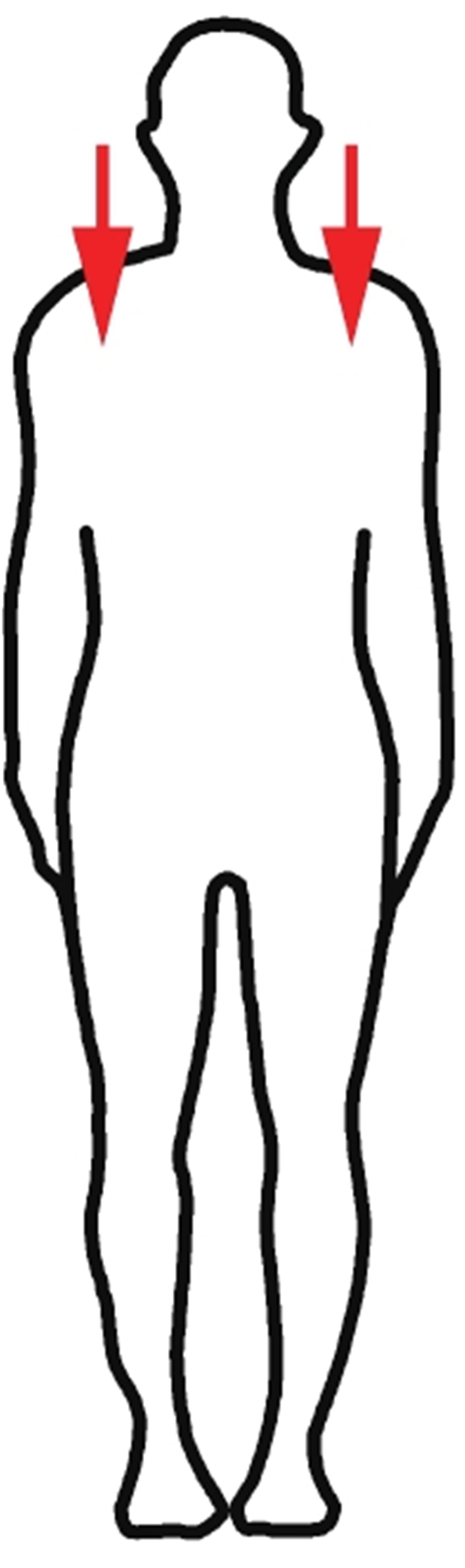 |
| 肱桡肌 | 被试者坐姿,前臂置于桌面,掌心朝下. 实验人员按住手背,被试腕关节用力抬起5 s,记录肌电数据,完成一次MVC测量 | 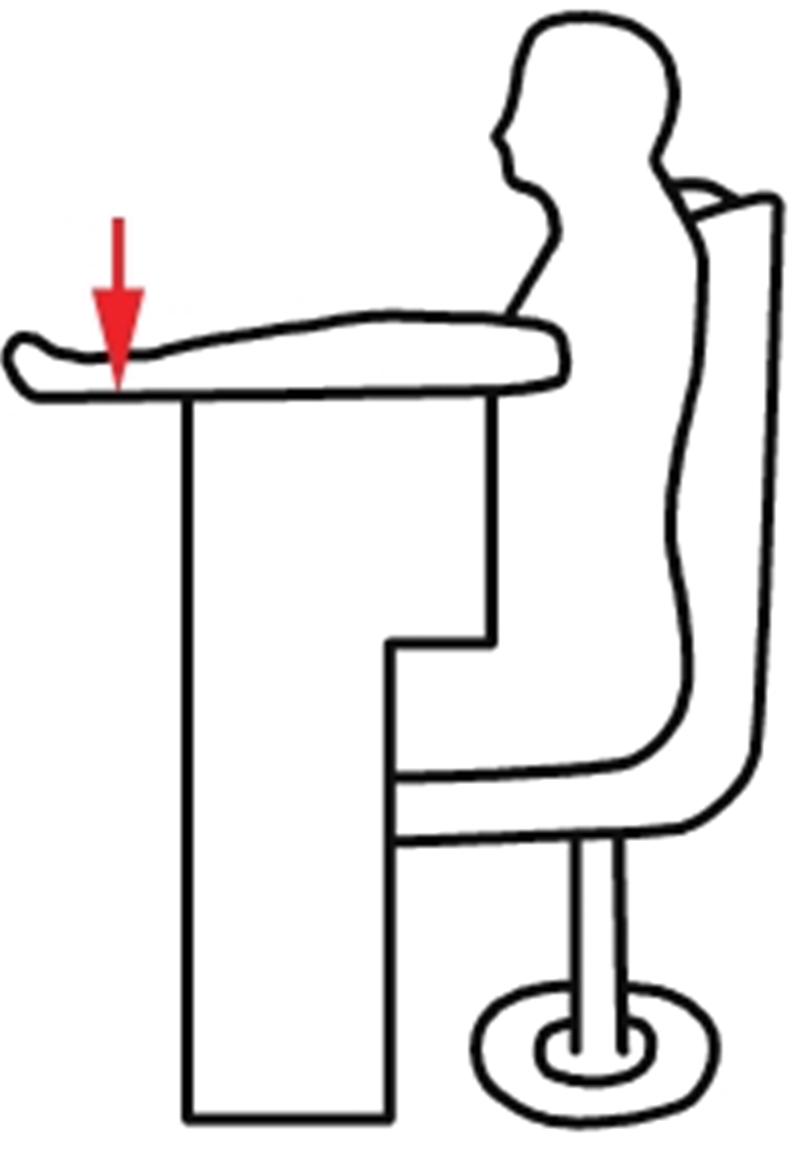 |
| 肱二头肌 | 被试者坐姿,上臂平放桌面,前臂竖直,掌心向内. 实验人员双手拉住被试者前臂,被试者紧缩肱二头肌保持5 s,记录肌电数据,完成一次MVC测量 | 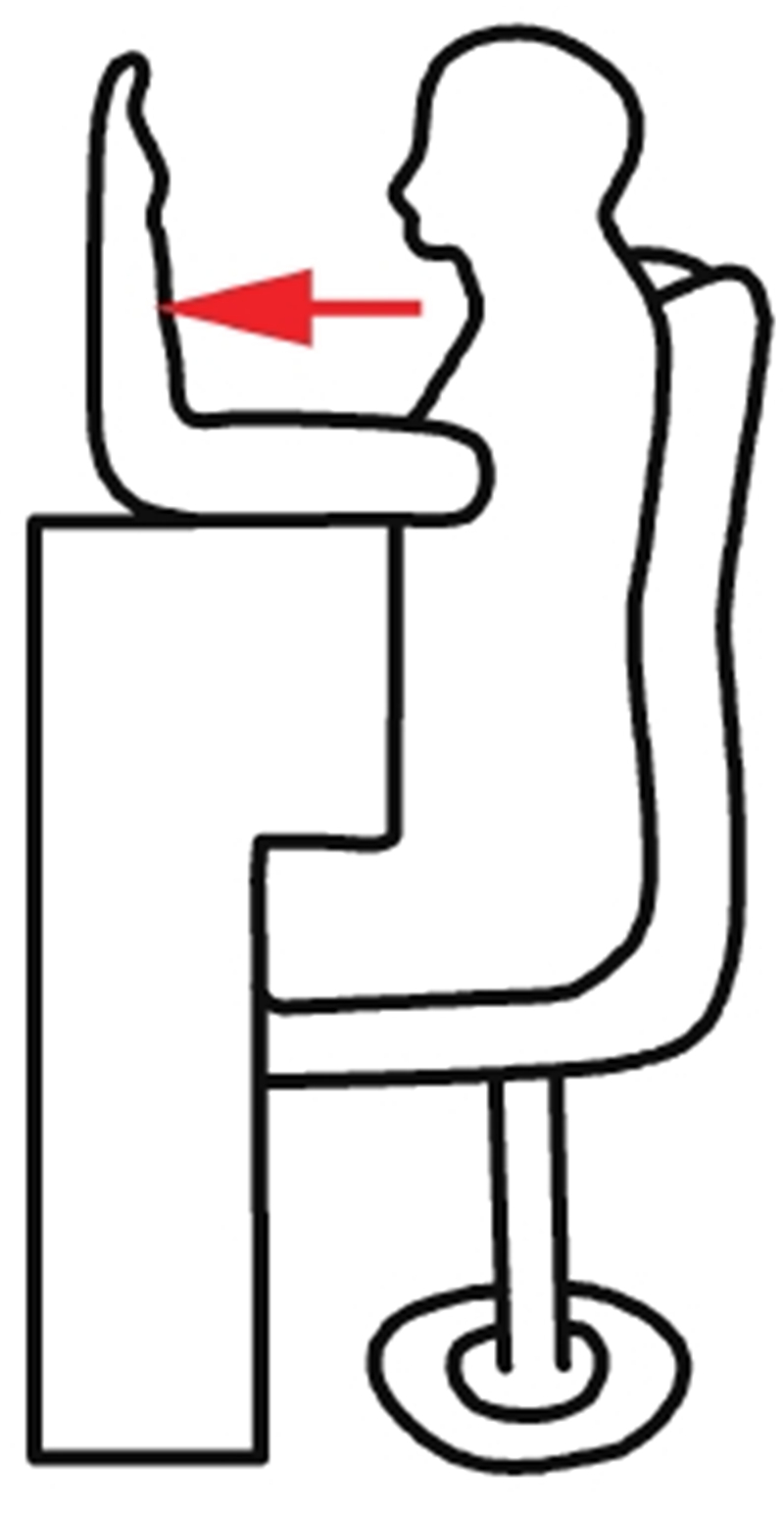 |
| 三角肌 | 被试者站姿,手臂伸直抬起与身体垂直,掌心向下. 实验人员双手下按其大臂,被试者手臂努力保持原状态5 s,记录肌电数据,完成一次MVC测量 | 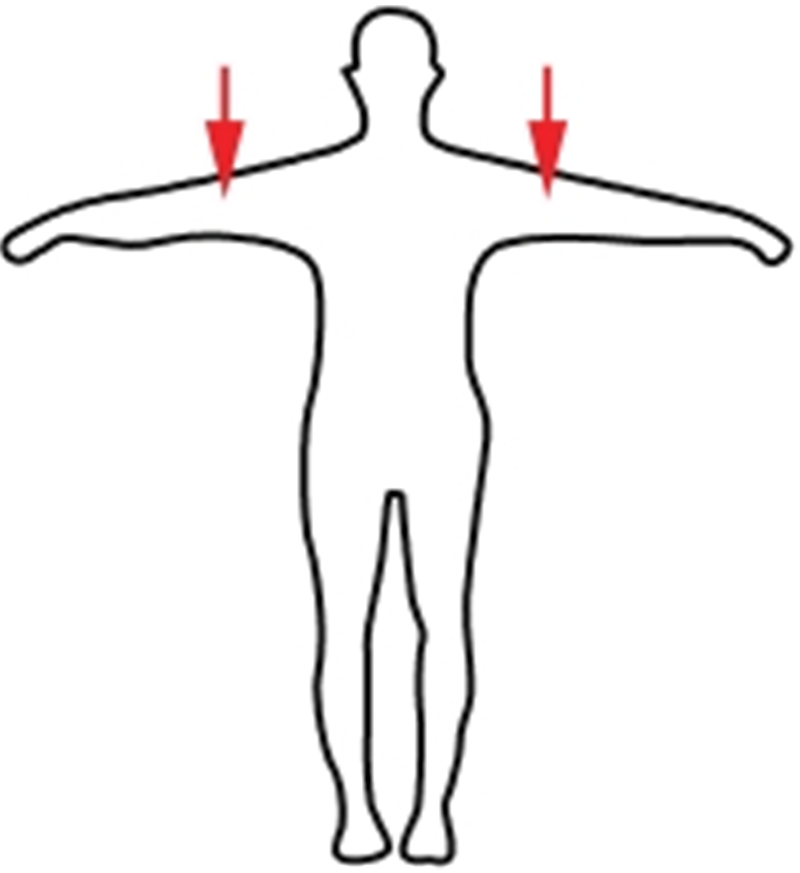 |
5.2.2. 过头作业实验流程
表 2 Borg CR10主观疲劳评估量表
Tab.2
| 数值 | 疲劳等级 |
| 0 | 完全没有 |
| 0.5 | 极其轻微,难以察觉 |
| 1 | 非常轻微,没有作业压力 |
| 2 | 轻微,感觉进入作业状态 |
| 3 | 温和,上肢有少许酸 |
| 4 | 稍稍强烈,开始出现轻微酸痛 |
| 5 | 强烈,上肢开始轻微抖动,仍能完成作业 |
| 6~8 | 非常强烈,上肢较强抖动,出现短暂无法完成作业 |
| 9 | 极其强烈,已经处于极度疲劳,无法完成作业 |
| 10 | 最大值,处于脱力状态 |
图 4
5.3. 数据预处理
5.3.1. 降噪处理
将采集的sEMG经50 Hz陷波滤波器去除工频信号干扰,再用20~500 Hz带通滤波器去除噪声保留主要sEMG,进而使用小波阈值去除通道间串扰及高斯噪声. 如图5所示为m4降噪前、后对比. 其中,Amp表示幅值.
图 5
5.3.2. 归一化
将被试者m1~m8的sEMG幅值除以其对应的MVC,对sEMG标准化,以消除个体差异和肌肉激活强度影响,确保sEMG的可比性.
5.4. 肌肉贡献率分析
表 3 各通道肌肉贡献率
Tab.3
| 被试者 | Pm/% | |||||||
| m1 | m2 | m3 | m4 | m5 | m6 | m7 | m8 | |
| 1 | 14.96 | 17.78 | 10.68 | 20.21 | 12.38 | 7.35 | 9.88 | 6.76 |
| 2 | 15.25 | 19.99 | 10.94 | 24.21 | 10.45 | 7.89 | 5.23 | 6.04 |
| 3 | 14.62 | 12.20 | 12.21 | 17.31 | 15.04 | 14.92 | 7.72 | 5.98 |
| 4 | 10.25 | 13.33 | 11.72 | 27.96 | 15.13 | 11.47 | 5.66 | 4.48 |
| 5 | 10.30 | 12.27 | 12.68 | 26.43 | 12.77 | 12.28 | 4.04 | 9.23 |
| 6 | 15.60 | 15.70 | 10.73 | 17.83 | 14.33 | 12.33 | 7.15 | 6.33 |
| 7 | 9.25 | 14.86 | 9.63 | 21.97 | 16.82 | 8.77 | 10.52 | 8.18 |
| 8 | 17.49 | 13.92 | 13.36 | 21.08 | 14.71 | 4.47 | 9.33 | 5.64 |
| 9 | 15.08 | 19.61 | 12.73 | 20.25 | 15.14 | 5.46 | 6.68 | 5.05 |
| 10 | 14.45 | 14.26 | 12.18 | 15.54 | 15.14 | 10.15 | 10.21 | 8.07 |
| 平均 | 13.73 | 15.39 | 11.68 | 21.28 | 14.19 | 9.51 | 7.64 | 6.58 |
5.5. 特征值选择
表 4 不同特征组合的判定系数R2
Tab.4
| 被试者 | R2 | |||||
| RMS-MF | RMS-MPF | IEMG-MF | IEMG-MPF | RMS-IEMG | MF-MPF | |
| 1)注:*表示为p<0.05,**表示为p<0.01. | ||||||
| 1 | 0.554**1) | 0.373* | 0.341 | 0.314 | 0.310 | 0.321 |
| 2 | 0.514** | 0.414* | 0.311 | 0.332 | 0.352* | 0.325 |
| 3 | 0.536** | 0.434* | 0.368* | 0.357* | 0.321 | 0.256 |
| 4 | 0.607** | 0.498* | 0.423* | 0.312 | 0.321 | 0.416* |
| 5 | 0.621** | 0.409* | 0.482* | 0.387* | 0.332 | 0.337 |
| 6 | 0.593** | 0.421* | 0.378* | 0.326 | 0.394* | 0.407* |
| 7 | 0.542** | 0.317 | 0.411* | 0.304 | 0.415* | 0.356* |
| 8 | 0.575** | 0.403* | 0.498* | 0.386* | 0.391* | 0.315 |
| 9 | 0.578** | 0.432* | 0.394* | 0.315 | 0.325 | 0.346 |
| 10 | 0.569** | 0.411* | 0.437* | 0.309 | 0.324 | 0.362* |
5.6. Hammerstein模型参数分析
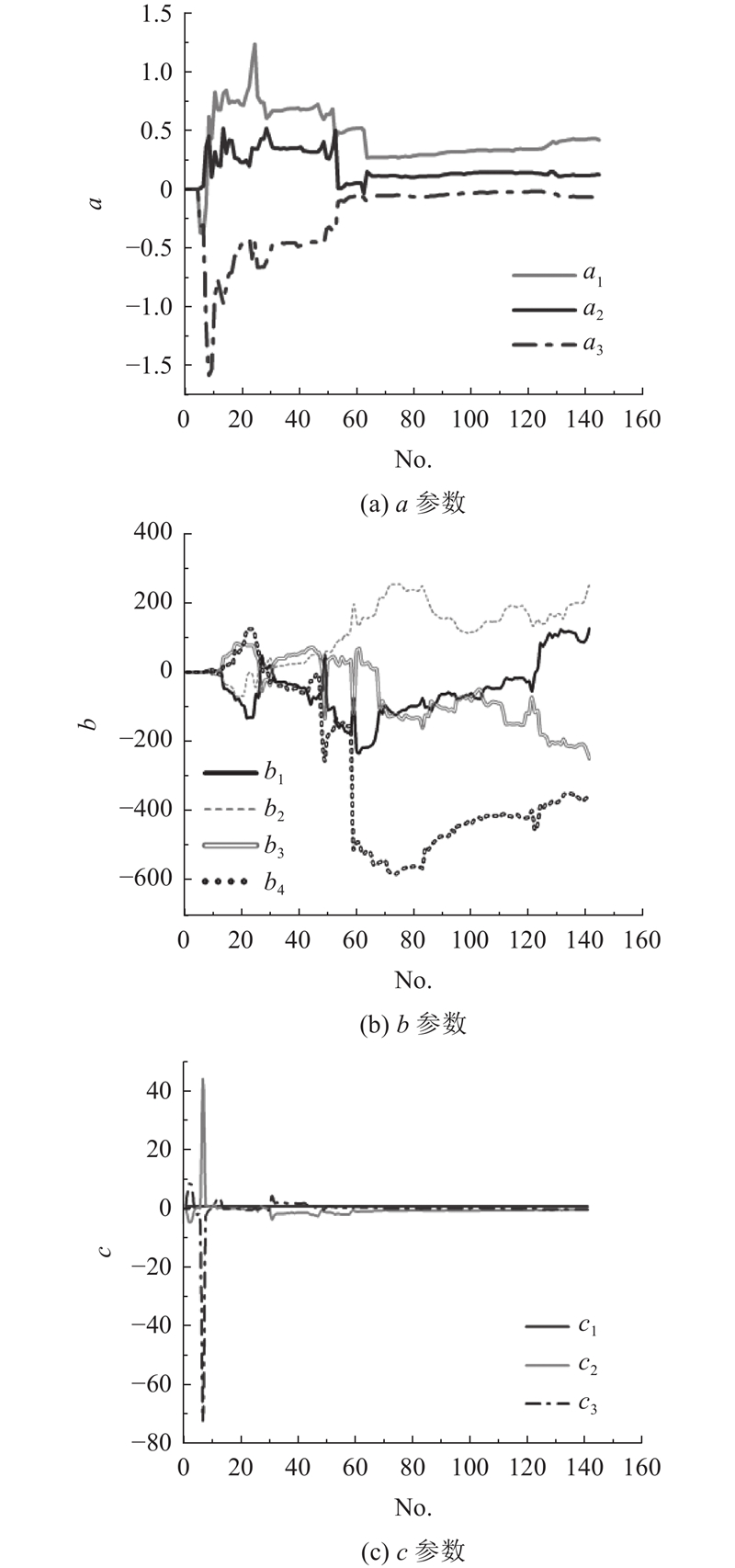
由于Hammerstein模型的输出依赖历史数据且具有记忆性,而输入具有无记忆性,选用MF和RMS分别作为Hammerstein模型的输入与输出进行建模,以描述疲劳过程中频域变化对肌肉激活水平的影响. 为了确保模型的稳定性和有效捕捉动态变化,对Hammerstein模型阶数利用最小描述长度(minimum description length,MDL)准则计算[30],当MDL取最小值时,m=3、n=4、p=3为最佳阶数组合. 根据文献[31]和[32],有λ∈[0.90,1.00],当模型残差平方和最小时,取λ=0.996. 通过式(12)~(15)辨识a、b、c参数,其中一个被试者的辨识结果如图6所示. 其中,No.为时间窗口序号. a参数随时间波动反映历史RMS对当前RMS的影响程度与趋势. 在初始阶段,系统会经历较大程度的动态调整,表现为a参数的剧烈变化,反映系统初始化过程. 随着时间推移,a参数趋于平稳,表明动态线性部分调整减少. b参数在系统初始时波动较小,表明模型非线性部分在该阶段相对平稳. 随着疲劳加剧,b参数变化变得显著,模型中的非线性效应增强. 这说明在疲劳过程中,MF和RMS的关系变得更加复杂. c参数在初期系统未稳定时表现出波动,而在后期基本保持恒定,其中微小波动主要由即时输入变化引起,符合Hammerstein模型无记忆特性[23]. 相较于简单的时、频域特征分析,Hammerstein模型参数分别描述了系统的动态与非线性变化,能够更深入地呈现肌肉疲劳过程中的复杂现象.
图 6
5.7. 肌肉疲劳分类
图 7
图 8
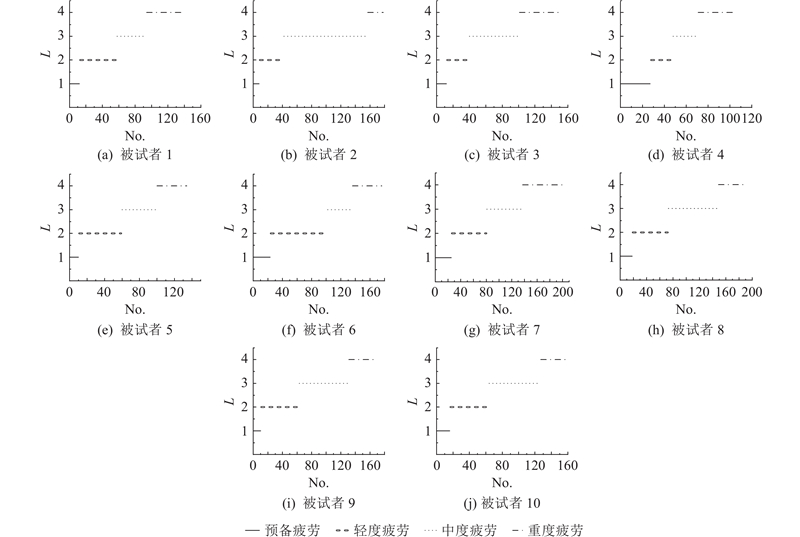
因每位被试者在完成过头作业实验任务时的Borg CR10评分均未达到9,将10名被试者的Borg CR10评分(0~8)分为4类,共计84种组合,并将每种组合均与被试者的疲劳分类进行皮尔逊相关性分析. 结果显示,6名被试者的最高皮尔逊相关系数均出现在第65组,4类疲劳等级的划分方式为{0~2,3,4,5~8},且p<0.01. 其他4名被试者,在第65组的皮尔逊相关系数大于0.86,整体平均皮尔逊相关系数为0.904(见表5),表明{0~2,3,4,5~8}的疲劳等级划分具有合理性.
表 5 第65组划分与聚类结果的皮尔逊相关系数
Tab.5
| 被试者 | 皮尔逊相关系数 | 被试者 | 皮尔逊相关系数 | |
| 1)注:**表示p<0.01 | ||||
| 1 | 0.910**1) | 7 | 0.928** | |
| 2 | 0.861** | 8 | 0.901** | |
| 3 | 0.884** | 9 | 0.894** | |
| 4 | 0.919** | 10 | 0.911** | |
| 5 | 0.889** | 平均值 | 0.904** | |
| 6 | 0.941** | — | — | |
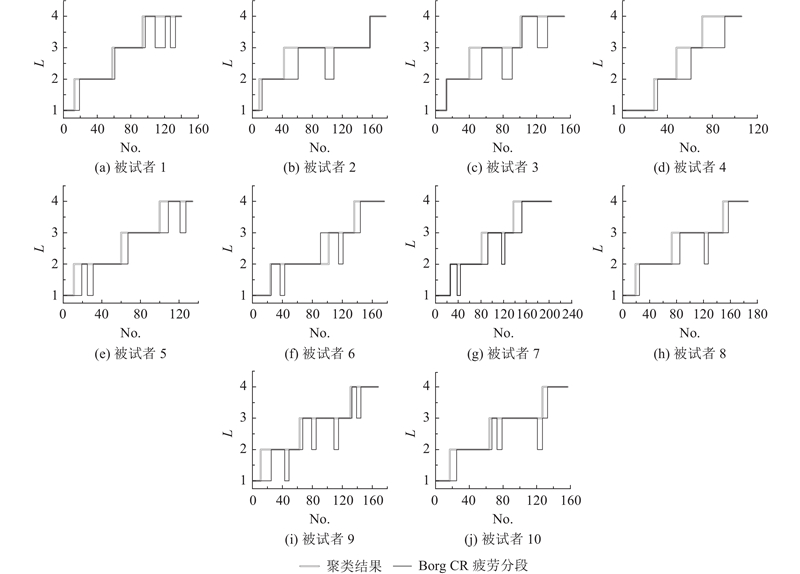
进一步对比{0~2,3,4,5~8}的疲劳等级划分和聚类结果的关系,如图9所示. 结果显示,聚类结果在肌肉疲劳阶段的划分上比主观评分更敏感,能更早检测到疲劳进展. 主观评分可能因感知滞后或判断偏差而延迟,并出现波动,如被试者9,这反映了不同被试者个体对疲劳感知的差异性.
图 9
图 9 聚类疲劳等级与第65组疲劳划分对比
Fig.9 Comparison between clustered fatigue levels and fatigue classification of group 65
6. 结果分析
6.1. Hammerstein模型参数分析
图 10
图 10 疲劳等级、MF、RMS和各参数比较分析
Fig.10 Comparison analysis of fatigue grade, MF, RMS and each parameter
图 11
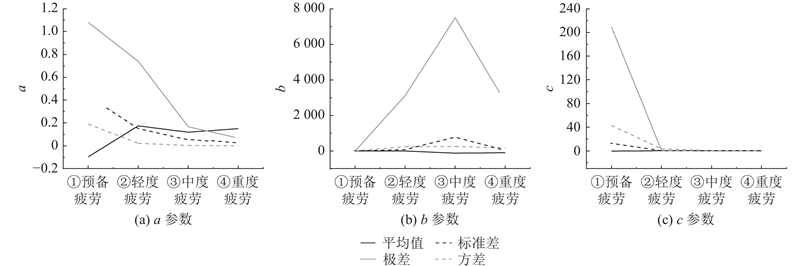
图 11 参数a、b、c在不同疲劳阶段的整体波动性统计
Fig.11 Overall fluctuation statistics of parameters a, b, and c at different fatigue stages
对于参数a,在分段①中,当肌肉刚开始收缩时,RMS较低,当前神经肌肉招募主要是慢肌纤维. a参数不确定性较高(均值:−0.097,标准差:0.438),系统初始动态响应不稳定. 在分段②中,随着肌肉工作时间延长,快肌纤维开始被动招募以补充所需肌力,a的均值从负转为正,且波动减小(标准差:0.148),方差和极差分别为0.022和0.740,说明输出对历史RMS的依赖性有所增强,动态反馈处于调整状态. 在分段③中,慢肌纤维在长时间工作后疲劳累积,贡献逐渐减少,而快肌纤维招募显著增加,以维持肌肉工作状态. 由于快肌纤维能量消耗较快且抗疲劳能力较低,导致RMS在此阶段出现波动,参数a趋于稳定(均值:0.120),但动态影响有所减弱,表现为标准差(0.055)和方差(0.003)的显著下降. 在分段④,肌肉进入重度疲劳后,慢肌纤维的工作能力明显下降,仅能维持少量基础活动,快肌纤维成为主导. 快肌纤维由于快速抽搐特性,能够维持较高的力量输出,但过多的能量消耗导致疲劳进一步加重. 此时,a的均值进一步升高(0.151),波动幅度显著降低(标准差:0.027),反映系统动态调整能力进一步减弱.
对于参数b,在分段①中MF较高,慢肌纤维为主导,快肌纤维参与较少,b数值整体稳定(均值:0.121,标准差:0.478,方差:1.710,极差:0.252),表明此阶段MF与RMS间的关系较为线性. 在分段②中,随着疲劳累积,MF下降,b的波动性增大(标准差:52.996,方差:240.540,极差:
对于参数c,在分段①的初始阶段波动较大(均值:−0.276,标准差:11.488,方差:43.010,极差:209.650),说明此时系统尚未稳定. 随着时间推移,模型的动态行为趋于平稳,因而c趋于稳定,如分段②~④的均值接近于0,标准差显著减小,方差和极差也随之降低,该稳定性反映参数c对即时输入的响应特性,与无记忆输入特征对应.
为了进一步探究上肢肌肉疲劳趋势和模型稳定性,利用式(7)的G(z)将参数对应极点绘制在极平面上,再由不同疲劳阶段划分极点. 如图12所示为所有被试者的极平面图. 在整个模型参数跟踪过程中,极点均位于单位圆内,说明当前输入输出下的Hammerstein模型具有良好稳定性. 且不同疲劳阶段的极点都随疲劳等级增加,由单位圆边缘向圆心收敛,说明随着过头作业上肢肌肉疲劳加重,肌肉动态响应能力下降,振荡逐渐减弱,系统响应速度变慢.
图 12
6.2. EMGFT分析
过头作业上肢肌肉疲劳状态的4个阶段反映了上肢肌肉疲劳的全局变化趋势,为了进一步确定具体疲劳时间,根据式(16)得到的矩阵
表 6 总时间及各疲劳阶段EMGFT
Tab.6
| 被试者 | EMGFT/s | 作业时间 | |||
| 预备疲劳 | 轻度疲劳 | 中度疲劳 | 重度疲劳 | ||
| 1 | 52.79 | 141.55 | 346.89 | 559.69 | 12 min 11 s |
| 2 | 41.69 | 168.95 | 280.42 | 830.05 | 15 min 18 s |
| 3 | 32.91 | 150.22 | 254.58 | 565.63 | 13 min 18 s |
| 4 | 150.16 | 175.49 | 290.68 | 410.60 | 10 min 11 s |
| 5 | 46.54 | 151.51 | 340.67 | 537.51 | 11 min 36 s |
| 6 | 39.89 | 163.90 | 528.18 | 647.77 | 15 min 6 s |
| 7 | 40.73 | 166.93 | 447.24 | 738.21 | 17 min 24 s |
| 8 | 36.05 | 119.29 | 287.72 | 576.94 | 15 min 54 s |
| 9 | 23.36 | 110.11 | 367.11 | 707.59 | 14 min 24 s |
| 10 | 63.42 | 145.72 | 344.16 | 685.12 | 13 min 30 s |
表 7 主体间效应
Tab.7
| 因素 | SS | MS | F | p |
| 1) 注:**表示p<0.01 | ||||
| 截距 | 597.11 | 0.000**1) | ||
| 疲劳阶段 | 110.56 | 0.000** | ||
| 被试者 | 0.99 | 0.47 | ||
| 误差 | — | — | ||
7. 结 语
通过Hammerstein模型与sEMG特征,提出新的过头作业肌肉疲劳评估方法,将sEMG的MF、RMS分别作为Hammerstein模型输入与输出,辨识模型参数,解释过头作业上肢肌肉疲劳过程并揭示其动态变化规律. 同时,将动态参数与EMGFT算法融合,识别由聚类获得的不同疲劳分段的具体疲劳阈值. 本研究不仅能够有效分离肌肉疲劳的各个阶段,且与Borg CR10主观分类具有较高一致性,有助于辅助过头作业中的上肢肌肉疲劳监测、预测与评估,为避免WMSDs、过头作业优化及助力装置设计提供理论支持. 然而,当前研究基于健康被试者在受控环境下开展,尚未充分验证所提方法在真实工业场景中长期动态作业下的鲁棒性与适用性. 下一步将拓展至复杂工况下的多任务作业人群,结合运动学数据与长期跟踪分析,进一步提升模型在实际应用中的泛化能力与实用性.
参考文献
Shoulder-support exoskeletons for overhead work: current state, challenges and future directions
[J].DOI:10.1109/TMRB.2023.3275761 [本文引用: 1]
A work-related musculoskeletal disorders (WMSDs) risk-assessment system using a single-view pose estimation model
[J].DOI:10.3390/ijerph19169803 [本文引用: 1]
Validation of the Borg CR10 Scale for the evaluation of shoulder perceived fatigue during work-related tasks
[J].DOI:10.1016/j.apergo.2023.104200 [本文引用: 1]
Workload analysis by using Nordic body map, Borg RPE and NIOSH manual lifting equation analyses: a case study in sheet metal industry
[J].DOI:10.1088/1742-6596/1424/1/012047 [本文引用: 1]
SEMG-based fighter pilot muscle fatigue analysis and operation performance research
[J].DOI:10.1016/j.medntd.2022.100189 [本文引用: 1]
基于表面肌电信号和动作捕捉的上肢运动疲劳分析
[J].
Fatigue analysis of upper limb rehabilitation based on surface electromyography signal and motion capture
[J].
The sensitivity of shoulder muscle fatigue to vertical hand location during complex manual force exertions
[J].DOI:10.1016/j.ergon.2022.103272 [本文引用: 1]
Sex-specific effects of muscle fatigue on upper body kinematics and discomfort during a repetitive point task performed on a sit-stand stool
[J].DOI:10.1016/j.ergon.2021.103188 [本文引用: 1]
Influence of an upper limb exoskeleton on muscle activity during various construction and manufacturing tasks
[J].DOI:10.1016/j.apergo.2023.104158 [本文引用: 1]
基于KPCA-SVM的表面肌电信号疲劳分类研究
[J].
Research on fatigue classification of surface EMG signal based on KPCA and SVM
[J].
MFFNet: multi-dimensional Feature Fusion Network based on attention mechanism for sEMG analysis to detect muscle fatigue
[J].DOI:10.1016/j.eswa.2021.115639 [本文引用: 1]
K-means clustering: a half-century synthesis
[J].DOI:10.1348/000711005X48266 [本文引用: 1]
Improving hierarchical cluster analysis: a new method with outlier detection and automatic clustering
[J].DOI:10.1016/j.chemolab.2007.01.005 [本文引用: 1]
Neural network based modeling and control of elbow joint motion under functional electrical stimulation
[J].DOI:10.1016/j.neucom.2019.03.003 [本文引用: 2]
Multimuscle functional-electrical-stimulation-based wrist tremor suppression using repetitive control
[J].DOI:10.1109/TMECH.2022.3150301 [本文引用: 1]
基于Hammerstein系统的航空发动机部件级辨识建模方法
[J].
Modeling and identification method for aerospace engine components based on Hammerstein systems
[J].
Motor unit reserve capacity in spinal muscular atrophy during fatiguing endurance performance
[J].DOI:10.1016/j.clinph.2020.11.044 [本文引用: 1]
基于自回归模型表面肌电信号检测肌肉疲劳研究
[J].
Detection of muscle fatigue based on sEMG signal with AR model
[J].
A simulation study to assess the factors of influence on mean and median frequency of sEMG signals during muscle fatigue
[J].DOI:10.3390/s22176360 [本文引用: 2]
多元系统耦合带遗忘因子有限数据窗递推最小二乘辨识方法
[J].
Coupled finite-data-window RLS identification approach with forgetting factors for multi-variate systems
[J].
人体肌肉状态疲劳监测及其在外骨骼交互控制中的应用
[J].
Human muscle fatigue monitoring method and its application for exoskeleton interactive control
[J].
基于SVD-K-means算法的软扩频信号伪码序列盲估计
[J].
Blind estimation of pseudo-code sequence of soft spread spectrum signal based on SVD-K-means algorithm
[J].
表面肌电信号在肌肉疲劳研究中的应用综述
[J].
Review of application of surface electromyography signals in muscle fatigue research
[J].
基于改进K-means的局部离群点检测方法
[J].
Local outlier detection method based on improved K-means
[J].
基于表面肌电与步态的外骨骼穿戴疲劳评测
[J].
Evaluation of exoskeleton wearing fatigue based on surface electromyography and gait
[J].
Electromyographic analysis of muscle activation during sit-and-reach flexibility tests
[J].DOI:10.1519/JSC.0000000000000607 [本文引用: 1]
Application of surface electromyography in exercise fatigue: a review
[J].DOI:10.3389/fnsys.2022.893275 [本文引用: 1]
FES-induced torque prediction with evoked EMG sensing for muscle fatigue tracking
[J].DOI:10.1109/TMECH.2011.2160809 [本文引用: 1]
An adaptive Hammerstein model for FES-induced torque prediction based on variable forgetting factor recursive least squares algorithm
[J].DOI:10.1109/TNSRE.2024.3371465 [本文引用: 1]
Muscle fatigue induced hand tremor clustering in dynamic laparoscopic manipulation
[J].DOI:10.1109/TSMC.2018.2882957 [本文引用: 1]