无人机空战态势评估的核心为在高对抗环境下综合分析无人机与敌方目标的位置、速度、高度及作战意图等关键要素,实时量化评估战场态势的优劣,这对于无人机的安全与高效决策至关重要. 传感器技术局限、信息传输损耗及敌方干扰常导致信息出现不确定、错误乃至缺失等情况,严重恶化评估结果. 有效融合不完备多源战场信息,实现持续准确的态势评估,已成为智能化空战亟待解决的关键难题.
目前,针对上述问题所开展的研究主要聚焦于态势信息的不确定性特征,涉及方法包括贝叶斯网络[1-3]、模糊理论[4]和证据推理[5]. 其中,贝叶斯网络和模糊理论方法依赖大量条件概率或模糊规则,在动态空战环境中难以有效应用. 相比之下,D-S证据理论引入了信度函数的概念,特别增加了对“完全未知”信息的表达,能够更全面地描述和评估不确定性命题. 作为其进阶方法,证据网络(evidential network, EN)基于树状图模型结构,在处理多源异构信息融合方面展现出卓越的能力,且对先验信息的需求低,十分适合复杂多变的空战态势评估. 李山等[5]针对空中目标威胁评估的问题,建立基于改进D-S证据理论的多时刻评估模型. Wang等[6]利用云模型构造属性信度函数,通过证据网络同时处理随机和认知不确定性,以深度感知目标意图. 近年来,随着决策信息复杂度的增加,Deng熵概念的提出将证据推理对信息特点的聚焦从不确定性推广至不完备性. Zhou等[7-9]利用空集的非零mass函数值对不完备信息建模,采用Deng熵计算不确定度以修正不完备证据,通过态势意图评估和电子转子故障诊断2个简单实例进行方法说明. 基于Deng熵的证据修正方法虽然在不完备信息融合理论研究中取得进展,但应用多局限于同源信息融合,且该方法对信息不完备性的量化缺乏泛化规则,在处理大量不完备信息的复杂决策场景,尤其多源异构信息推理的态势评估时适用性不足.
本文面向不完备信息下的空战态势评估,提出基于证据修正机制的多模式变权时空融合证据网络(multi-mode variable weight spatio-temporal fusion evidential network, MVWSF-EN). 基于深度学习与平滑指数法构建非突变型证据预测模型,设计多模式证据修正方法及自主切换流程,提升证据质量. 引入模式切换折扣因子与变权原理,设计节点权值的自适应生成公式,增强推理合理性. 针对信息类型的差异,提出3步时空融合网络推理机制,提升态势评估的准确性.
1. MVWSF-EN态势评估方法
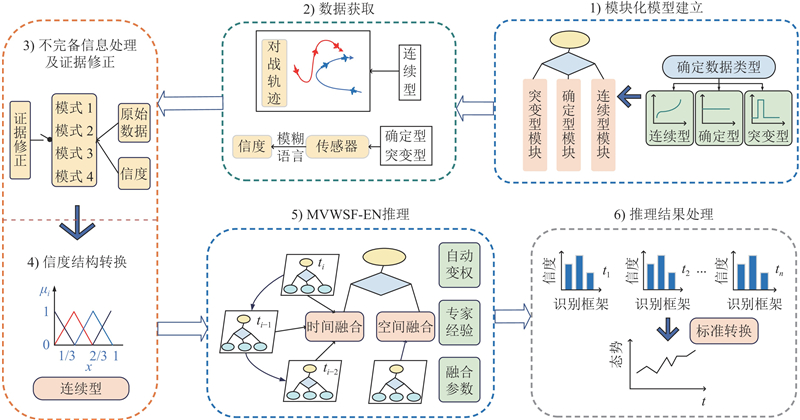
提出的MVWSF-EN方法的总体流程如图1所示.
图 1
1.1. 模块化证据网络模型的建立
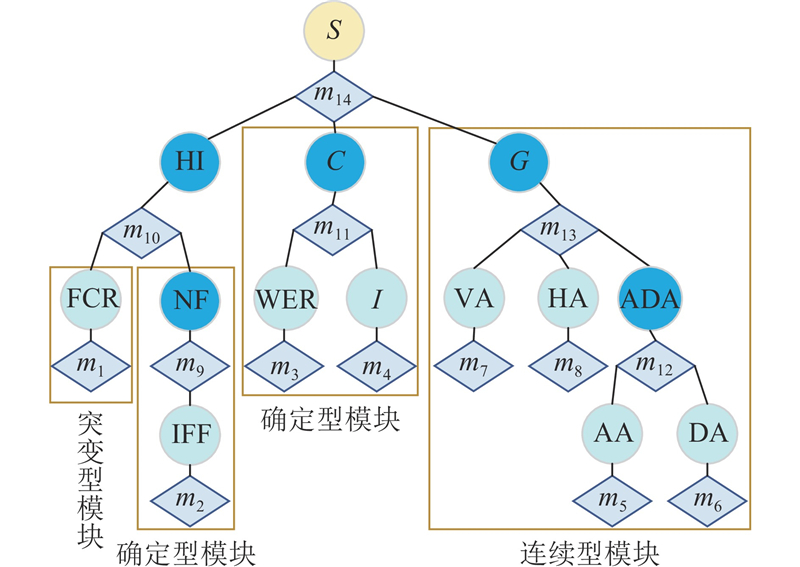
图 2
该模型依据态势信息的时间关联性,划分为突变型、确定型和连续型3类. 其中,突变型由于在时间上不相关,具有不可预测性;连续型呈现规律性时序变化,确定型是在一定时段内保持稳定或缓慢变化,两者均具有时间序列的特征,可以进行预测. 各证据节点的物理含义、识别框架、模块类型定义如表1所示,其中上层节点的识别框架和模块类型由于待融合及约简无法确定,用“—”表示.
表 1 节点变量的说明
Tab.1
| 证据节点 | 变量说明 | 识别框架 | 等级说明 |
| S | 态势等级 | — | 0_低;— |
| HI | 作战意图 | — | 0_低;— |
| C | 作战能力 | — | 0_低;— |
| G | 几何优势 | — | 0_弱;— |
| FCR | 火控雷达 | {0,1} | 0_关;1_开 |
| NF | 非友方平台 | {0,1} | 0_错;1_对 |
| IFF | 敌友识别 | {0,1} | 0_敌;1_友 |
| WER | 武器攻击范围 | {0,1,2,3} | 0_弱;3_强 |
| I | 处理危机能力 | {0,1,2,3} | 0_弱;3_强 |
| ADA | 角度距离优势 | — | 0_低;— |
| VA | 速度优势 | {0,1,2,3,4} | 0_弱;4_强 |
| AA | 角度优势 | {0,1,2,3} | 0_弱;3_强 |
| DA | 距离优势 | {0,1,2,3,4} | 0_弱;4_强 |
| HA | 高度优势 | {0,1,2,3} | 0_弱;3_强 |
表 2 初始的融合规则
Tab.2
| 信度 | 节点 | 融合规则 |
| m9 | NF、IFF | (IFF=1) (IFF=0) |
| m10 | HI、FCR、NF | HI=FCR&3NF+3NF |
| m11 | C、WER、I | C = 3WER+I |
| m12 | ADA、AA、DA | ADA = AA×DA |
| m13 | G、ADA、VA、HA | G = 3ADA+VA+2HA |
| m14 | S、HI、C、G | S = HI+C+G |
1.2. 态势评估数据的获取
为了洞悉整个作战过程中敌我双方的态势变化,在评估时刻获取图2模型中各个证据节点的实时态势信息. 其中原始定量信息主要来源于实战双方的对抗轨迹,即通过惯导传感器、激光雷达等实现对双方战机的航向角(
1.3. 不完备信息处理及证据修正
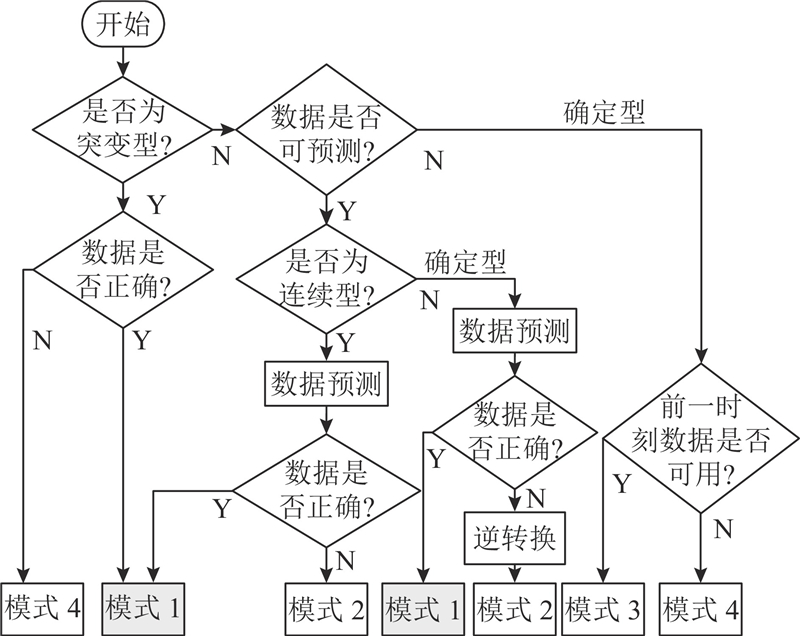
在综合分析态势信息特点的基础上,考虑证据类型和信息不完备程度,引入时序性信息预测方法,为上述3种类型证据设计4种有针对性的输入及修正模式,相关流程如图3所示.
图 3
图 3 证据输入及修正模式的选取流程
Fig.3 Selection process of evidence input and correction mode
图3中,对于各类型证据信息当前时刻是否正确的判定标准如下. 考虑到突变型证据不具备时序性,因此缺失即视为错误,反之正确. 非突变型证据(连续型和确定型)具有时序关联性,均通过判定当前检测值与预测结果的误差是否满足预设阈值进行判别,超出判定为错误,反之正确,如此,缺失证据亦会判定为错误.
提出的证据修正方法如表3所示.
表 3 证据修正方法
Tab.3
| 输入模式 | 适用类型 | 修正方案 |
| 模式1 | 全部类型 | 原始信息本身 |
| 模式2 | 确定型、连续型 | 预测数据替换 |
| 模式3 | 确定型 | 前一时刻数据替换 |
| 模式4 | 突变型、确定型 | 删除当前证据节点 |
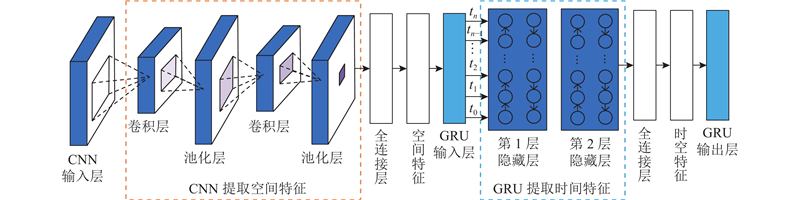
连续型和确定型证据均可通过预测获取替代数据,达到证据修正的目的. 考虑2类证据的获取方式及在时间关联度上的差异,分别采用深度学习方法和指数平均法,对2类时序性证据构建预测模型.
图 4
针对确定型证据,假设待预测证据节点的识别框架为
基于指数平均法[18],提出利用历史证据的信度期望预测当前时刻证据信度期望的计算公式:
若将式(2)计算的证据预测期望作为不完备确定型证据的修正值直接输入网络,则由于不符合网络推理所需的信度结构形式,不能进行后续融合. 采取如下思路,提出信度期望
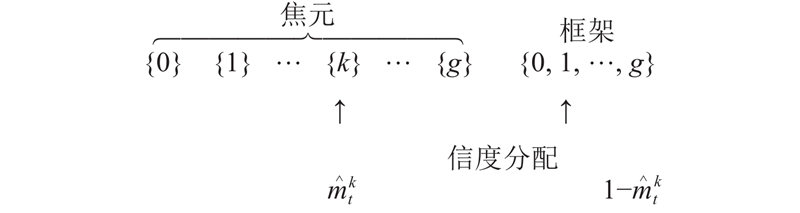
设k为预测证据前一时刻识别框架中信度最高的焦元,则选择将
图 5
图 5 预测信度期望的逆转换过程
Fig.5 Inverse conversion process of predicted belief expectation
由信度期望计算
可以推得
1.4. 证据信度结构的转换
证据网络推理要求输入信息为信度结构的形式,因此需要对图2的信息进行信度结构转换.
对于定性信息,可以将传感器检测结果采用模糊语言直接赋予信度,如判定X-47B无人机处理危机能力(I)为中高强度,则可在其划分的3个等级下进行信度赋值[0.1, 0.3, 0.5, 0.1]:0级信度为0.1,1级信度为0.3,2级信度为0.5,整个识别框架(不确定性)的信度为0.1.
式中:
1.5. MVWSF-EN推理
1.5.1. 节点自适应权值生成方法
传统态势评估方法的常权方式存在缺陷,容易引发“状态失衡”的违背实际现象. 引入变权原理[21],依据目标属性实测值的变化来优化调整经验权重,对属性值低却根据经验赋予的“高权”施加“惩罚”,对属性值高却根据经验赋予的“低权”给予“激励”(惩罚力度大于激励力度). 综合考虑不同修正模式下的证据可靠度差异对推理结果准确性的影响,提出自适应权值生成机制,具体方法如下.
1)考虑不完备信息修正方式的不同所引发的输入证据可靠度的不同及其对网络节点权重所产生的影响,为网络中的每个节点匹配模式切换折扣因子(MSF). 对于证据节点的MSF,考虑到模式1、2、3下证据可靠度逐渐递减,进行如下设定:
2)基于变权原理,设置状态变权因子SCF,用以表征实际推理结果变化对经验权值的修正. 参考文献[21],设计计算公式(相关参数数值在后续仿真中通过实验确定)如下.
式中:
3)将原始权值与上述2个因子相乘,计算动态权值:
通过下式进行整数化处理:
1.5.2. 3步时空融合机制
考虑非突变型模块各时刻推理结果的时间关联性以及选择不同证据输入模式对相邻时刻推理结果平滑性的影响,提出如下动态的3步时空融合机制.
1)在每个时间片对模块网络采用证据输入模式切换的空间融合,结果取决于当前输入证据.
2)基于1)中3个连续时间片的结果,对非突变型网络模块实施变权时间融合,如图6所示. 其中,
图 6
图 6 非突变型网络模块的变权时空融合过程
Fig.6 Variable-weight spatiotemporal fusion process of non-mutant network module
3)完成步骤1)、2)后,得到每个模块内的时空融合结果. 对当前时间片在整个网络内进行自下而上的空间推理,得到态势评估的最终信度分配.
1.5.3. 推理过程
为了解决不完备信息下的态势评估难题,MVWSF-EN在传统的EN基础上融入三大机制:不完备信息处理及证据修正﹑节点自适应权值生成以及3步时空融合. 推理过程如下.
采用1.3节的方法,对当前评估时刻的证据信息进行修正,作为叶子节点输入1.1节所建立的模块化树状网络模型. 基于1.5.2节的3步时空融合机制,依次执行网络模块内、外节点融合,融合权重由1.5.1节的自适应方法动态计算,采用不确定性融合规则实时更新信度函数. 通过循环多次的扩展、Dempster合成和边际化运算,获取目标态势等级(根节点)的信度分配函数. 利用Pignistic公式,对根节点(目标态势等级)进行概率测度计算.
上述扩展、合成及边际化等运算公式见文献[17].
1.6. 推理结果的处理
为了显示各时刻的态势评估结果,将经上述推理融合获取的态势等级的概率测度转换为态势标准值(设为p)进行输出(见式(1)、(6)). 设最终获取的态势等级S的识别框架为
2. 仿真分析
为了验证所提方法的有效性,基于建立的DDPG[16]和MADDPG[22]决策模型,分别构建1对1和2对1无人机近距对抗场景,开展态势评估实验. 主要参数如下:模式切换因子
2.1. 方法有效性及优越性的验证
1对1对抗场景如图7所示.
图 7
表 4 1对1空战信息
Tab.4
| 信息 时刻 | m | ||||||||||
| FCR | IFF | WER | I | ||||||||
| t1 | 96.07 | 98.39 | 190.61 | 190.64 | {0.8, 0, 0.2} | {0.1, 0.9, 0} | {0.5, 0.2, 0.1, 0, 0.2} | {0, 0.2, 0.5, 0.2, 0.1} | |||
| t2 | 100.50 | 103.76 | 190.16 | 191.33 | {0.5, 0, 0.5} | {0.1, 0.8, 0.1} | {0.1, 0.6, 0.1, 0, 0.2} | {0, 0.2, 0.5, 0.1, 0.2} | |||
| t3 | 92.40 | 97.48 | 188.58 | 191.63 | {0.1, 0.5, 0.4} | {0.1, 0.7, 0.2} | {0.3, 0.5, 0.1, 0, 0.1} | {0, 0.1, 0.6, 0.1, 0.2} | |||
| t4 | 83.75 | 90.05 | 187.53 | 191.05 | {0.1, 0.5, 0.4} | {0.1, 0.7, 0.2} | {0.1, 0.7, 0.1, 0, 0.1} | {0, 0.1, 0.6, 0.1, 0.2} | |||
| t5 | 83.75 | 80.41 | 186.22 | 190.85 | {0, 0.8, 0.2} | {0.3, 0.6, 0.1} | {0.1, 0.6, 0.2, 0, 0.1} | {0, 0.1, 0.6, 0.2, 0.1} | |||
| t6 | 98.03 | 53.97 | 183.45 | 183.45 | {0.1, 0.7, 0.2} | {0.3, 0.6, 0.1} | {0.1, 0.7, 0.2, 0, 0} | {0, 0.1, 0.5, 0.2, 0.2} | |||
| t7 | 115.04 | 38.25 | 182.29 | 189.02 | {0.1, 0.8, 0.1} | {0.4, 0.5, 0.1} | {0, 0.8, 0.1, 0, 0.1} | {0, 0.2, 0.5, 0.1, 0.2} | |||
| t8 | 123.44 | 31.46 | 189.02 | 188.80 | {0.8, 0, 0.2} | {0.1, 0.9, 0} | {0.5, 0.2, 0.1, 0, 0.2} | {0, 0.2, 0.5, 0.2, 0.1} | |||
| t9 | 131.10 | 26.27 | 181.26 | 188.48 | {0.5, 0, 0.5} | {0.1, 0.8, 0.1} | {0.1, 0.6, 0.1, 0, 0.2} | {0, 0.2, 0.5, 0.1, 0.2} | |||
| t10 | 143.28 | 20.77 | 180.36 | 187.13 | {0.1, 0.5, 0.4} | {0.1, 0.7, 0.2} | {0.3, 0.5, 0.1, 0, 0.1} | {0, 0.1, 0.6, 0.1, 0.2} | |||
1) 多模式证据修正.
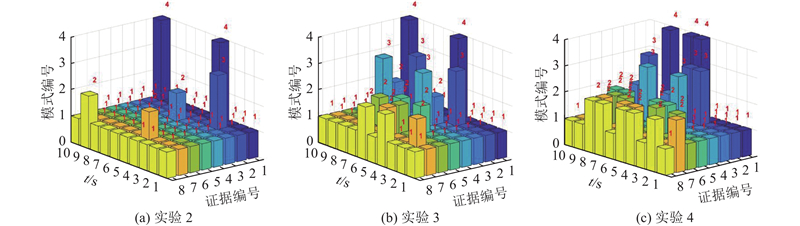
依据1.3节的证据修正方法(见图3和表3),得到不完备信息实验(实验2~4)的证据输入模式切换情况,如图8所示. 可见,随着证据信息不完备程度的加剧,非“1”的输入模式占比逐渐增大,达到了有效修正证据的目的. 从3个实验(实验2~4)中选取不同类型证据进行输入模式切换及修正过程,说明如下. 实验2中,突变型证据FCR(编号1)在t4时刻缺失,直接进行节点删除操作,因此由t3时刻的模式1切换为模式4. 实验3中确定型证据IFF(编号2)在t7时刻检测到信度为{0.1,0.5, 0.1},存在失真,但由于IFF不满足“前3个时刻信息均有效”的预测条件,将其用前一时刻的有效证据替代,由t6时刻的模式1变为模式3. 实验4中证据VA(编号7)在t5时刻的检测值为0 m/s(即数据缺失),按照1.3.1节的连续型证据预测方法进行数据预测,预测结果为186.705 2 m/s,检测值与预测值的误差超出规定阈值5 m/s. 采用预测值替代,由t4时刻的模式1变为t5时刻的模式2.
图 8
2)推理结果及方法比较.
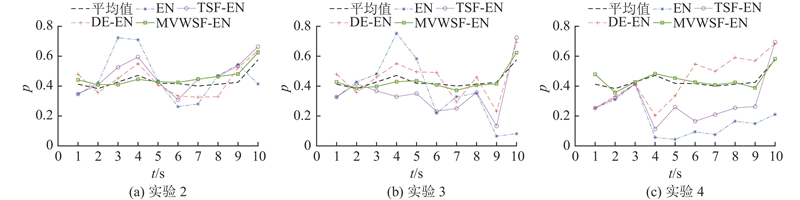
将修正后并经信度结构转换(见1.4节)的4组证据输入MVWSF-EN中,根据1.5.3节的推理操作,获取我方相对敌方的10个时刻态势等级. 为了验证本文方法的优越性,开展与EN、变权时空融合EN(TSF-EN)及基于邓熵修正证据的EN(DE-EN)在不完备信息下(实验2~4)的推理结果对比,如图9所示. 其中平均值为将实验1可靠证据输入EN和MVWSF-EN后,对推理的态势值取平均,作为态势期望衡量误差. 因DE-EN未明确不完备信息表述规则,开展如下处理:突变型信息将空集信度分配置1;非突变型信息对前两时刻信息进行不确定处理后,计算邓熵折扣系数,依据改进的合成公式[7]获取当前信息信度分配函数的修正结果.
图 9
图 9 1对1场景不完备信息下的各方法结果对比
Fig.9 Comparison of results of various methods under incomplete information in one against one scenario
从数据分析来看,信息不完备程度的加剧显著影响推理准确性. EN因缺乏对不完备信息的处理机制,平均相对误差从0.286 4激增至0.585 2,出现严重失真. 虽然TSF-EN通过信度替换和权重调整策略优化,但处理手段单一,导致平均相对误差从0.166攀升至0.376 9. DE-EN虽然基于Deng 熵理念处理不完备信息,但因缺乏通用框架与差异化校正标准,平均相对误差从0.140 7上升到0.284 1,结果不理想. 相比之下,MVWSF-EN在各实验中的平均相对误差始终约为0.05,展现出卓越的信息不完备性处理能力.
2.2. 消融实验
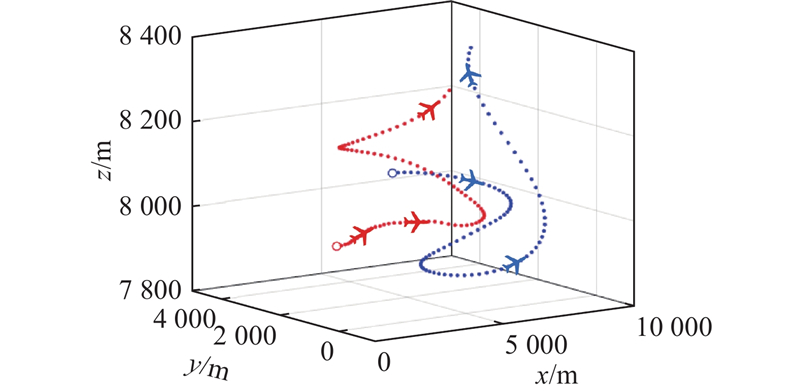
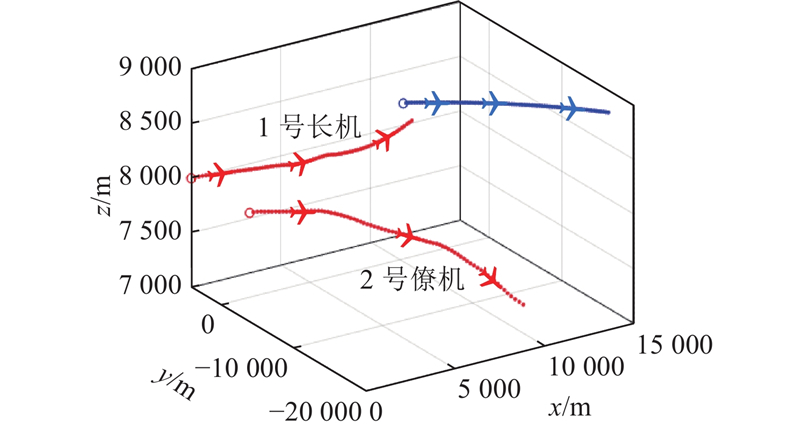
为了验证三大机制创新的有效性和必要性,构建2对1的无人机对抗场景(见图10). 假设在执行某次追击任务时,我方派出1号长机负责攻击敌机、2号僚机进行掩护支援.
图 10
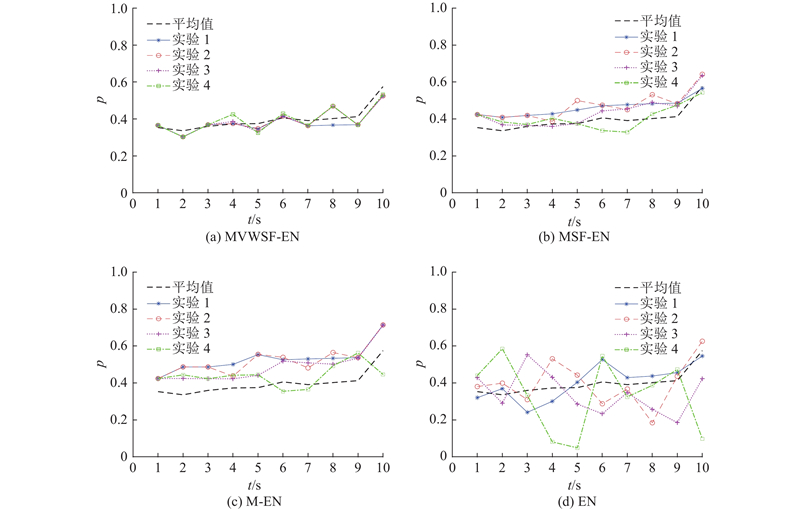
以我方1号长机相对于敌机的态势评估过程为例,开展MVWSF-EN、去掉自适应权值生成机制的MSF-EN、去掉自适应权值生成机制和时空融合的M-EN以及3种策略全部去掉的传统EN共4种方法的消融实验.4组实验(不完备信息的处理方法同2.1节)下的对比结果如图11所示.
图 11
2.3. 方法复杂度的比较
为了评估MVWSF-EN方法的实际应用能力,比较上述4种方法的推理时间. 针对所构建的1对1和2对1无人机对抗实战场景,在不完备信息缺陷率为7.5%的情况下,利用各方法分别进行200次实验,对单个推理时刻的平均运行时间tav进行比较,结果如表5所示.
表 5 4种方法的平均运行时间比较
Tab.5
| 方法 | tav/s | |||
| MVWSF-EN | DE-EN | TSF-EN | EN | |
| 1对1 | 0.17 | 0.25 | 0.26 | 0.25 |
| 2对1 | 0.32 | 0.64 | 0.72 | 0.66 |
从表5可知,MVWSF-EN算法虽然增加了证据修正、动态变权、时空融合等功能,但运行时间保持在
3. 结 语
本文提出基于证据修正机制的多模式变权时空融合证据网络方法,用于解决不完备信息下的空战态势评估问题. 通过结合数据类型与缺陷程度的多模式证据修正策略,实现缺陷信息的针对性修正,显著提升态势评估的准确度. 提出的节点权值自适应生成机制可以依据证据输入模式和推理结果自主调节权值,避免“常权”引发的推理矛盾. 针对时序信息的3步时空融合机制,区分“突变型”与“非突变型”信息的时间关联,进一步增强评估结果的合理性.1对1和2对1空战对抗场景下的多组仿真实验表明,本研究方法在多种不完备信息下表现优异,评估结果显著优于EN、TSF-EN和DE-EN等方法.
在未来研究中,将引入优化技术修正网络的主要参数,进一步提升推理结果的准确性.
参考文献
Situation assessment for air combat based on novel semi-supervised naive Bayes
[J].DOI:10.21629/JSEE.2018.04.11 [本文引用: 1]
A cloud Bayesian network approach to situation assessment of scouting under water targets with fixed-wing patrol aircraft
[J].
The situation assessment of UAVs based on an improved whale optimization Bayesian network parameter-learning algorithm
[J].DOI:10.3390/drones7110655 [本文引用: 1]
SAPFIS: a parallel fuzzy inference system for air combat situation assessment
[J].
基于改进D-S理论的多时刻空中目标威胁评估
[J].
Multi-moment aerial target threat assessment based on improved D-S theory
[J].
Evidence network inference recognition method based on cloud model
[J].DOI:10.3390/electronics12020318 [本文引用: 1]
A note on incomplete information modeling in the evidence theory
[J].DOI:10.1109/ACCESS.2019.2954132 [本文引用: 2]
An extension to Deng’s entropy in the open world assumption with an application in sensor data fusion
[J].
An improved approach of incomplete information fusion and its application in sensor data-based fault diagnosis
[J].DOI:10.3390/math9111292 [本文引用: 1]
基于变异系数法和改进TOPSIS法的空战威胁评估
[J].
Air combat threat assessment based on the coefficient of variation method and improved TOPSIS method
[J].
基于动态变权重的空战态势评估
[J].DOI:10.3969/j.issn.1000-1093.2021.07.023
Air combat situation assessment based on dynamic variable weight
[J].DOI:10.3969/j.issn.1000-1093.2021.07.023
基于集群分析的空中作战目标威胁评估技术研究
[J].
Research on air objective threat assessment technology based on cluster analysis
[J].
Anti-interference recognition for aerial infrared object based on convolutional feature inference network
[J].
Air target recognition algorithm based on mixed depth features in the interference environment
[J].DOI:10.1016/j.ijleo.2021.167535
Complex image recognition algorithm based on immune random forest model
[J].DOI:10.1007/s00500-020-04706-0 [本文引用: 1]
基于角度特征的分布式DDPG无人机追击决策
[J].DOI:10.7641/CTA.2024.30105 [本文引用: 2]
Distributed DDPG UAV pursuit decision based on angle feature
[J].DOI:10.7641/CTA.2024.30105 [本文引用: 2]
基于改进证据网络的空战动态态势估计方法
[J].
Dynamic situation assessment method of aerial warfare based on improved evidence network
[J].
湖北漳河灌区中稻气象产量变化特征及预测模型
[J].DOI:10.11988/ckyyb.20221141 [本文引用: 1]
Variation features and estimation model for meteorological yield of mid-season rice in Zhanghe irrigated area of Hubei Province
[J].DOI:10.11988/ckyyb.20221141 [本文引用: 1]
D-S证据理论在空中目标识别中的应用现状与展望
[J].DOI:10.3969/j.issn.1671-637X.2024.04.012 [本文引用: 1]
Application status and prospects of D-S evidence theory in aerial target identification
[J].DOI:10.3969/j.issn.1671-637X.2024.04.012 [本文引用: 1]
基于FD-TODIM的混杂空战多目标动态威胁评估
[J].
Multi-target dynamic threat assessment in mixed air combat based on FD-TODIM
[J].
基于轨迹预测和分布式MADDPG的无人机集群追击决策
[J].DOI:10.11772/j.issn.1001-9081.2023101538 [本文引用: 1]
Distributed UAV cluster pursuit decision-making based on trajectory prediction and MADDPG
[J].DOI:10.11772/j.issn.1001-9081.2023101538 [本文引用: 1]
An application of evidential networks to threat assessment
[J].DOI:10.1109/TAES.2009.5089545 [本文引用: 1]