列车是典型的非线性环节,具有未知和不确定的行驶阻力,其模型难以准确建立. 在实际应用中,对控制器的要求如下:列车模型的参数无须精确知道,尽可能只须测量速度和距离信息,即控制算法是无模型的. Gao等[17]设计基于残差非线性近似的模糊自适应控制方法,将位置误差和速度跟踪误差限制在规定的范围内.
1. 问题描述
1.1. 列车动力学模型
列车动力学模型[21]为
式中:
式(2)满足
1.2. 列车运行约束和控制目标
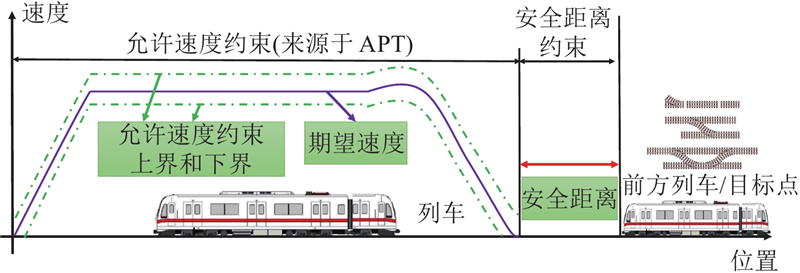
在传统ATO的基础上,添加了安全间距主动控制环节. 所设计的控制框架包含速度跟踪控制和安全距离主动控制,速度跟踪控制对ATP所规划的具有允许速度约束的速度曲线进行跟踪控制,安全距离主动控制确保在特殊情况下(信号故障、ATP误差增大)保证与前方列车的安全距离. 所考虑的列车运行示意图如图1所示.
图 1
若列车距离前方列车较远,控制器只须保证列车以期望的速度
式中:
若列车靠近前方列车或目标点,且列车间距进入ATP所设定的安全距离裕量,则距离跟踪误差
式中:
注1 速度误差
注2 由于
列车控制器设计重要的挑战是设计只依赖于距离
使得对于闭环系统,(O1)在速度控制阶段,
1.3. 预备知识
定义1(Carathéodory函数)[22] 若
1)
2)
3) 对于每个紧致集
引理1(Carathéodory函数解的存在性)[23] 定义
存在解,且每个解可以扩展为最大解. 若
定义2(C解)[22] 若
则
定义3(最大解)[22]设
2. 算法设计
2.1. 具有允许速度及安全距离约束的ATO算法
1)允许速度约束控制模块. 在速度跟踪阶段,可以忽略式(2)的第1个方程,因为它不影响输入输出行为. 此时的控制目标是跟踪预定的速度
式中:
2)安全距离约束自主控制模块. 在距离控制阶段,目标是保证列车与目标点之间的距离不得超过安全距离,并使距离误差
式中:
3)控制模块综合. 式(4)、(5)分别设计了允许速度约束控制器和安全距离约束控制器,但当
式中:
若列车远离前方列车,即
若列车在安全距离约束控制阶段,但不在允许的速度范围内(信号故障导致的ATP信息错误),即
若列车位于上述2个模块的交叉阶段,则应同时满足允许速度约束控制和安全距离约束控制,即
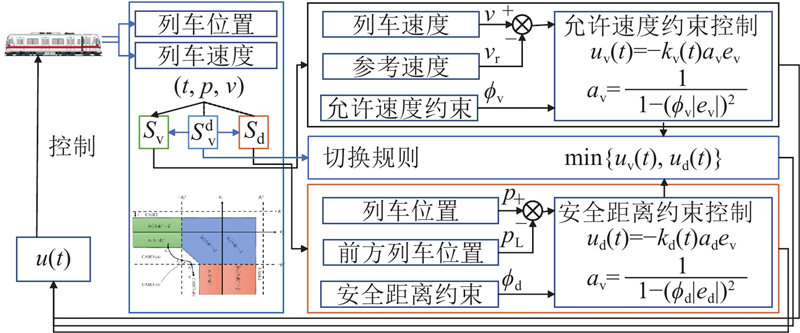
图 2
图 2 具有允许速度及安全距离约束的列车运行控制结构
Fig.2 ATO control structure with allowable speed and safety distance constraints
最终的控制器被设计为
2.2. 控制算法的稳定性分析
设计具有允许速度约束及安全间距约束的列车无模型控制算法,以实现控制目标O1、O2和O3. 以下定理证明了所提控制算法的稳定性.
定理1 考虑式(2)所描述的列车动力学系统跟随领航列车运行,领航列车位置由
证明:
步骤1:最大解的存在性证明.
定义
尽管
由于列车阻力
式中:
由于
相似地,可以推导出
(满足定义1中的条件3). 可以得出,
综上,式(11)中的
步骤2:目标O1、O2和O3的证明.
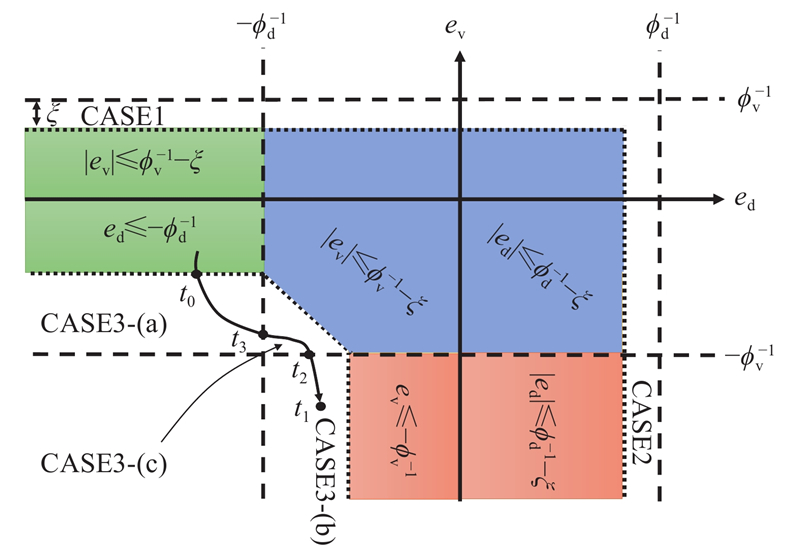
证明过程分为5种情况,通过反证法证明
图 3
设
假设对于
式中:
式中:
当
为了证明目标O1、O2和O3,需要寻找矛盾. 假设存在
情况1:假设
定义
由于
这意味着
由于
对
对式(17)积分,可得
根据
情况2:假设
采用与情况1相似的方法,可以推导得到情况2的假设不存在,目标2得证.
情况3:假设
定义
1)
2)
3)
在该情况下,对于
情况3(a):限制时间间隔,以便只考虑情况1)所示的区域. 假设存在
上述假设(19)意味着应进一步限制时间间隔,以确保
这意味着
进而,
对
对式(23)积分,可得
根据
情况3(b):与情况3(a)相似,情况3(b)可证.
情况3(c):假设存在
根据情况3(a)和情况3(b)可知,式(20)对于所有的
对于
步骤3:全局解的存在性证明.
在步骤1中,证明了最大解
情况1:
情况2:
情况3:
由于对于所有的
步骤4:
定义
在3种情况下考虑
情况1:
情况2:
情况3:
步骤5:
定义
如果
由
当
选择
3. 仿真示例
文献[24]的CRH2-A列车模型被用来验证所提出的控制算法. CRH2-A的参数设置如下.
3.1. 随机环境
在该情况下,假设自动列车远离前方列车,
图 4
图 5
图 6
3.2. 紧急刹车环境
在这种情况下,假设前方列车急刹车,在实验1的基础上,假设1 000 s时列车以
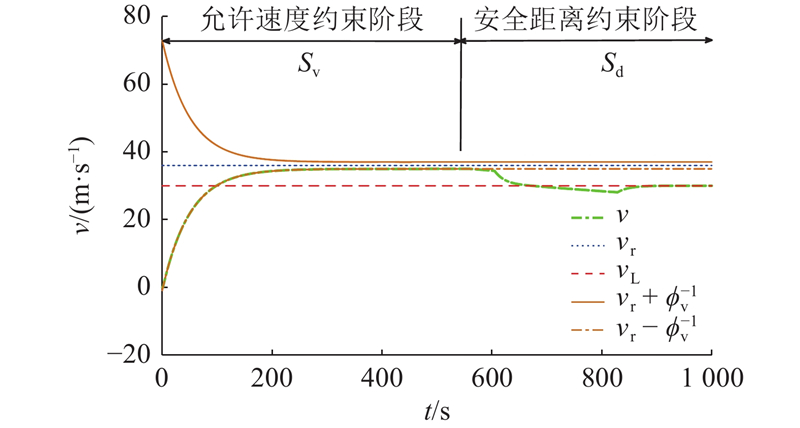
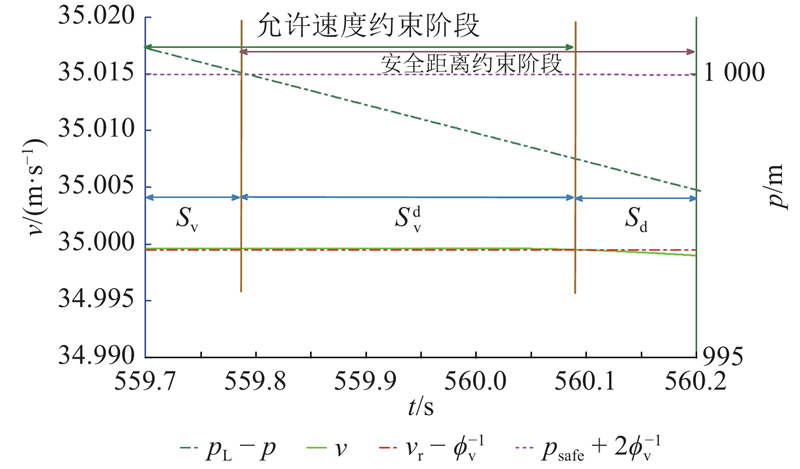
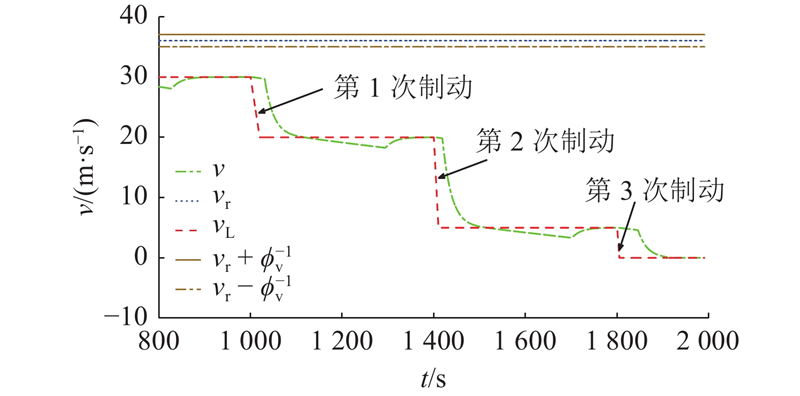
图 7
图 7 列车紧急制动时速度及允许速度的演化范围
Fig.7 Evolution range of speed and preset speed when braking
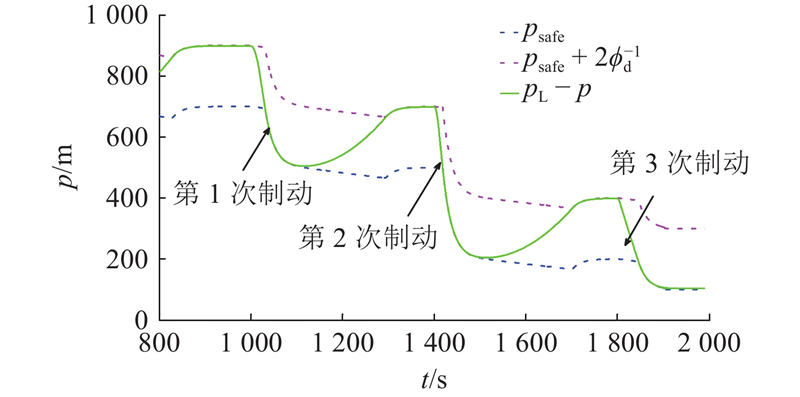
图 8
图 8 列车紧急制动时列车间距及安全间距的演化范围
Fig.8 Evolution range of distance and safety distance when suddenly braking
4. 结 语
本文提出具有允许速度约束及安全距离约束的非线性列车无模型控制方法,无需列车模型的非线性项. 构建基于Carathéodory函数的闭环系统,解析了闭环系统解的存在性、控制目标的可实现性以及控制输入的有界性和连续性,实现了控制系统的稳定性证明. 仿真结果表明,当距离前方列车较远时,所设计的算法能够实现列车在允许速度约束范围内运行. 当接近前方列车或目标点,且列车间距进入预设的安全距离裕量时,利用所设计的算法,能够保证受控列车与前方列车的安全间距. 当前方列车紧急制动时,能够保证列车的安全距离.
参考文献
一种基于策略梯度强化学习的列车智能控制方法
[J].DOI:10.3969/j.issn.1001-8360.2020.01.010 [本文引用: 1]
A policy-based reinforcement learning algorithm for intelligent train control
[J].DOI:10.3969/j.issn.1001-8360.2020.01.010 [本文引用: 1]
考虑列车混行的运行-调度一体化优化方法
[J].
Integrated optimization method of scheduling and control in express/slow train
[J].
基于自适应终端滑模的高速列车迭代学习速度控制
[J].DOI:10.3969/j.issn.1001-8360.2024.09.009 [本文引用: 1]
Adaptive terminal sliding mode based iterative learning speed control for high-speed trains
[J].DOI:10.3969/j.issn.1001-8360.2024.09.009 [本文引用: 1]
城轨列车自动驾驶积分反步线性自抗扰控制
[J].
Integral back-stepping linear active disturbance rejection control for automatic operation of urban rail trains
[J].
Tracking and collision avoidance of virtual coupling train control system
[J].DOI:10.1016/j.aej.2020.12.010 [本文引用: 1]
Energy-efficient automatic train operation for high-speed railways: considering discrete notches and neutral sections
[J].DOI:10.1016/j.trc.2022.103884 [本文引用: 1]
An analytical optimal control approach for virtually coupled high-speed trains with local and string stability
[J].DOI:10.1016/j.trc.2020.102886 [本文引用: 1]
Tracking control via sliding mode for heavy-haul trains with input saturation
[J].
Robust event-triggered model predictive control for multiple high-speed trains with switching topologies
[J].DOI:10.1109/TVT.2020.2974979 [本文引用: 1]
Modeling and energy-optimal control for high-speed trains
[J].DOI:10.1109/TTE.2020.2983855 [本文引用: 1]
Asymptotical cooperative cruise fault tolerant control for multiple high-speed trains with state constraints
[J].
Distributed event-triggered iterative learning control for multiple high-speed trains with switching topologies: a data-driven approach
[J].
Research on automatic braking and traction control of high-speed train based on neural network
[J].DOI:10.1088/1742-6596/1952/3/032048 [本文引用: 1]
An overspeed protection mechanism for virtual coupling in railway
[J].DOI:10.1109/ACCESS.2020.3029147 [本文引用: 1]
A cooperative collision-avoidance control methodology for virtual coupling trains
[J].DOI:10.1016/j.aap.2022.106703 [本文引用: 1]
Adaptive speed tracking control for high speed trains under stochastic operation environments
[J].DOI:10.1016/j.automatica.2022.110674 [本文引用: 1]
Fuzzy adaptive automatic train operation control with protection constraints: a residual nonlinearity approximation-based approach
[J].
A model predictive control approach for virtual coupling in railways
[J].DOI:10.1109/TITS.2019.2914910 [本文引用: 1]
Neural networks-based sliding mode fault-tolerant control for high-speed trains with bounded parameters and actuator faults
[J].DOI:10.1109/TVT.2019.2961409 [本文引用: 1]
High-speed trains automatic operation with protection constraints: a resilient nonlinear gain-based feedback control approach
[J].DOI:10.1109/JAS.2019.1911582 [本文引用: 1]
Fuzzy adaptive protective control for high-speed trains: an outstretched error feedback approach
[J].
Systems of controlled functional differential equations and adaptive tracking
[J].DOI:10.1137/S0363012900379704 [本文引用: 3]
Tracking with prescribed transient behaviour
[J].
Adaptive iterative learning control for high-speed trains with unknown speed delays and input saturations
[J].DOI:10.1109/TASE.2014.2371816 [本文引用: 1]