[1]
丁小欧, 于晟健, 王沐贤, 等 基于相关性分析的工业时序数据异常检测
[J]. 软件学报 , 2020 , 31 (3 ): 726 - 747
[本文引用: 2]
DING Xiaoou, YU Shengjian, WANG Muxian, et al Anomaly detection on industrial time series based on correlation analysis
[J]. Journal of Software , 2020 , 31 (3 ): 726 - 747
[本文引用: 2]
[2]
SIMMROSS-WATTENBERG F, ASENSIO-PEREZ J I, CASASECA-DE-LA-HIGUERA P, et al Anomaly detection in network traffic based on statistical inference and \alpha-stable modeling
[J]. IEEE Transactions on Dependable and Secure Computing , 2011 , 8 (4 ): 494 - 509
DOI:10.1109/TDSC.2011.14
[本文引用: 1]
[3]
张圣林, 李东闻, 孙永谦, 等 面向云数据中心多语法日志通用异常检测机制
[J]. 计算机研究与发展 , 2020 , 57 (4 ): 778 - 790
DOI:10.7544/issn1000-1239.2020.20190875
[本文引用: 2]
ZHANG Shenglin, LI Dongwen, SUN Yongqian, et al Unified anomaly detection for syntactically diverse logs in cloud datacenter
[J]. Journal of Computer Research and Development , 2020 , 57 (4 ): 778 - 790
DOI:10.7544/issn1000-1239.2020.20190875
[本文引用: 2]
[4]
苏卫星, 朱云龙, 刘芳, 等 时间序列异常点及突变点的检测算法
[J]. 计算机研究与发展 , 2014 , 51 (4 ): 781 - 788
DOI:10.7544/issn1000-1239.2014.20120542
[本文引用: 1]
SU Weixing, ZHU Yunlong, LIU Fang, et al Outliers and change-points detection algorithm for time series
[J]. Journal of Computer Research and Development , 2014 , 51 (4 ): 781 - 788
DOI:10.7544/issn1000-1239.2014.20120542
[本文引用: 1]
[7]
LI W, MAHADEVAN V, VASCONCELOS N Anomaly detection and localization in crowded scenes
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2014 , 36 (1 ): 18 - 32
DOI:10.1109/TPAMI.2013.111
[本文引用: 1]
[8]
MANEVITZ L M, YOUSEF M One-class svms for document classification
[J]. Journal of Machine Learning Research , 2002 , 2 : 139 - 154
[本文引用: 1]
[9]
LAPTEV N, AMIZADEH S, FLINT I. Generic and scalable framework for automated time-series anomaly detection [C]// Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . Sydney: ACM, 2015: 1939–1947.
[本文引用: 1]
[10]
SAKURADA M, YAIRI T. Anomaly detection using autoencoders with nonlinear dimensionality reduction [C]// Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis . Gold Coast: ACM, 2014: 4–11.
[本文引用: 1]
[11]
ZENATI H, ROMAIN M, FOO C S, et al. Adversarially learned anomaly detection [C]// Proceedings of the IEEE International Conference on Data Mining . Singapore: IEEE, 2018: 727–736.
[本文引用: 1]
[12]
BROWN A, TUOR A, HUTCHINSON B, et al. Recurrent neural network attention mechanisms for interpretable system log anomaly detection [C]// Proceedings of the First Workshop on Machine Learning for Computing Systems . Tempe: ACM, 2018: 1–8.
[本文引用: 1]
[13]
GREFF K, SRIVASTAVA R K, KOUTNÍK J, et al LSTM: a search space odyssey
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2017 , 28 (10 ): 2222 - 2232
DOI:10.1109/TNNLS.2016.2582924
[本文引用: 2]
[14]
ZHOU H, ZHANG S, PENG J, et al Informer: beyond efficient transformer for long sequence time-series forecasting
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2021 , 35 (12 ): 11106 - 11115
DOI:10.1609/aaai.v35i12.17325
[本文引用: 1]
[15]
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks [EB/OL]. (2017–02–22)[2024–08–23]. https://arxiv.org/pdf/1609.02907.
[本文引用: 1]
[16]
WEI Y, JANG-JACCARD J, XU W, et al LSTM-autoencoder-based anomaly detection for indoor air quality time-series data
[J]. IEEE Sensors Journal , 2023 , 23 (4 ): 3787 - 3800
DOI:10.1109/JSEN.2022.3230361
[本文引用: 1]
[17]
XU H, PANG G, WANG Y, et al Deep isolation forest for anomaly detection
[J]. IEEE Transactions on Knowledge and Data Engineering , 2023 , 35 (12 ): 12591 - 12604
DOI:10.1109/TKDE.2023.3270293
[本文引用: 1]
[18]
BARRIENTOS-TORRES D, MARTINEZ-RÍOS E A, NAVARRO-TUCH S A, et al Water flow modeling and forecast in a water branch of Mexico City through ARIMA and transfer function models for anomaly detection
[J]. Water , 2023 , 15 (15 ): 2792
DOI:10.3390/w15152792
[本文引用: 1]
[19]
SU Y, ZHAO Y, NIU C, et al. Robust anomaly detection for multivariate time series through stochastic recurrent neural network [C]// Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . Anchorage: ACM, 2019: 2828–2837.
[本文引用: 3]
[21]
SHEN L, LI Z, KWOK J T. Timeseries anomaly detection using temporal hierarchical one-class network [C]// Proceedings of the 34th International Conference on Neural Information Processing Systems . Vancouver: ACM, 2020: 13016–13026.
[本文引用: 2]
[22]
ZONG B, SONG Q, MIN M R, et al. Deep autoencoding gaussian mixture model for unsupervised anomaly detection [C]// International Conference on Learning Representations . Vancouver: [s.n.], 2018: 1–19.
[本文引用: 2]
[23]
ABDULAAL A, LIU Z, LANCEWICKI T. Practical approach to asynchronous multivariate time series anomaly detection and localization [C]// Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining . [S.l.]: ACM, 2021: 2485–2494.
[本文引用: 3]
[24]
ZHANG Z, LI W, DING W, et al STAD-GAN: unsupervised anomaly detection on multivariate time series with self-training generative adversarial networks
[J]. ACM Transactions on Knowledge Discovery from Data , 2023 , 17 (5 ): 1 - 18
[本文引用: 1]
[25]
ZHOU B, LIU S, HOOI B, et al. BeatGAN: anomalous rhythm detection using adversarially generated time series [C]// Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence . [S.l.]: International Joint Conferences on Artificial Intelligence Organization, 2019: 4433–4439.
[本文引用: 2]
[26]
LIU Y, DING K, LU Q, et al. Towards self-interpretable graph-level anomaly detection [EB/OL]. (2023–10–25)[2024–09–13]. https://arxiv.org/pdf/2310.16520.
[本文引用: 1]
[27]
DENG A, HOOI B. Graph neural network-based anomaly detection in multivariate time series [C]// The 34th AAAI Conference on Artificial Intelligence . [S.l.]: AAAI, 2021: 4027–4035.
[本文引用: 2]
[28]
ZHENG Y, KOH H Y, JIN M, et al Correlation-aware spatial-temporal graph learning for multivariate time-series anomaly detection
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2024 , 35 (9 ): 11802 - 11816
DOI:10.1109/TNNLS.2023.3325667
[本文引用: 1]
[29]
DING K, SHU K, SHAN X, et al Cross-domain graph anomaly detection
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2022 , 33 (6 ): 2406 - 2415
DOI:10.1109/TNNLS.2021.3110982
[本文引用: 1]
[30]
ZHAO H, WANG Y, DUAN J, et al. Multivariate time-series anomaly detection via graph attention network [C]// Proceedings of the IEEE International Conference on Data Mining . Sorrento: IEEE, 2020: 841–850.
[本文引用: 2]
[31]
GUO G, WANG H, BELL D, et al. KNN model-based approach in classification [C]// On The Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE . Berlin: Springer, 2003: 986–996.
[本文引用: 1]
[32]
PARK D, HOSHI Y, KEMP C C A multimodal anomaly detector for robot-assisted feeding using an LSTM-based variational autoencoder
[J]. IEEE Robotics and Automation Letters , 2018 , 3 (3 ): 1544 - 1551
DOI:10.1109/LRA.2018.2801475
[本文引用: 2]
[33]
WU H, HU T, LIU Y, et al. TimesNet: temporal 2D-variation modeling for general time series analysis [EB/OL]. (2023–04–12)[2024–08–21]. https://arxiv.org/pdf/2210.02186.
[本文引用: 1]
[34]
MATHUR A P, TIPPENHAUER N O. SWaT: a water treatment testbed for research and training on ICS security [C]// Proceedings of the International Workshop on Cyber-physical Systems for Smart Water Networks . Vienna: IEEE, 2016: 31–36.
[本文引用: 1]
[35]
HUNDMAN K, CONSTANTINOU V, LAPORTE C, et al. Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding [C]// Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . London: ACM, 2018: 387–395.
[本文引用: 2]
[36]
ZENG A, CHEN M, ZHANG L, et al Are transformers effective for time series forecasting?
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2023 , 37 (9 ): 11121 - 11128
DOI:10.1609/aaai.v37i9.26317
[本文引用: 1]
基于相关性分析的工业时序数据异常检测
2
2020
... 随着物联网、人工智能和云计算等新一代信息技术的迅速发展,异常检测被广泛应用于工业故障检测、交通异常事件和网络安全监测等领域[1 -3 ] . 异常检测旨在发现时序数据中不满足常态、约束和给定模式的离群数据,在保障安全、提高效率和降低成本等方面发挥着重大作用[4 ] . ...
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
基于相关性分析的工业时序数据异常检测
2
2020
... 随着物联网、人工智能和云计算等新一代信息技术的迅速发展,异常检测被广泛应用于工业故障检测、交通异常事件和网络安全监测等领域[1 -3 ] . 异常检测旨在发现时序数据中不满足常态、约束和给定模式的离群数据,在保障安全、提高效率和降低成本等方面发挥着重大作用[4 ] . ...
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
Anomaly detection in network traffic based on statistical inference and \alpha-stable modeling
1
2011
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
面向云数据中心多语法日志通用异常检测机制
2
2020
... 随着物联网、人工智能和云计算等新一代信息技术的迅速发展,异常检测被广泛应用于工业故障检测、交通异常事件和网络安全监测等领域[1 -3 ] . 异常检测旨在发现时序数据中不满足常态、约束和给定模式的离群数据,在保障安全、提高效率和降低成本等方面发挥着重大作用[4 ] . ...
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
面向云数据中心多语法日志通用异常检测机制
2
2020
... 随着物联网、人工智能和云计算等新一代信息技术的迅速发展,异常检测被广泛应用于工业故障检测、交通异常事件和网络安全监测等领域[1 -3 ] . 异常检测旨在发现时序数据中不满足常态、约束和给定模式的离群数据,在保障安全、提高效率和降低成本等方面发挥着重大作用[4 ] . ...
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
时间序列异常点及突变点的检测算法
1
2014
... 随着物联网、人工智能和云计算等新一代信息技术的迅速发展,异常检测被广泛应用于工业故障检测、交通异常事件和网络安全监测等领域[1 -3 ] . 异常检测旨在发现时序数据中不满足常态、约束和给定模式的离群数据,在保障安全、提高效率和降低成本等方面发挥着重大作用[4 ] . ...
时间序列异常点及突变点的检测算法
1
2014
... 随着物联网、人工智能和云计算等新一代信息技术的迅速发展,异常检测被广泛应用于工业故障检测、交通异常事件和网络安全监测等领域[1 -3 ] . 异常检测旨在发现时序数据中不满足常态、约束和给定模式的离群数据,在保障安全、提高效率和降低成本等方面发挥着重大作用[4 ] . ...
A survey of outlier detection methodologies
1
2004
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
Outlier detection for high dimensional data
1
2001
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
Anomaly detection and localization in crowded scenes
1
2014
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
One-class svms for document classification
1
2002
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
1
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
1
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
1
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
1
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
LSTM: a search space odyssey
2
2017
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
Informer: beyond efficient transformer for long sequence time-series forecasting
1
2021
... 由于异常检测任务中正常类与异常类的样本分布高度不平衡,且异常样本的标注成本高、获取困难,无监督异常检测成为主流方法. 无监督异常检测主要包括基于统计的方法、基于传统机器学习的方法和基于深度学习的方法. 基于统计的方法采用高斯分布[2 ] 、泊松分布[5 ] 、二项分布[6 ] 等数学模型,通过分析数据特性分布检测数据点与期望分布的偏离来检测异常值,这类方法须结合领域先验知识,不适用于未知工况和未知异常类别的时序数据. 基于传统机器学习的方法采用主成分分析[7 ] 、向量机[8 ] 、决策树[9 ] 等检测时序数据中的正常或异常类型,其建模方法较为简单,仅能捕获线性关系,不适用于具有复杂依赖关系的多变量时序数据. 基于深度学习的方法以端到端的方式从时序数据中提取非线性模式,采用如自编码器[10 ] 和生成对抗网络[11 ] 等模型计算数据重构误差,或者采用循环神经网络(recurrent neural network,RNN)[12 ] 、长短期记忆网络(long short-term memory,LSTM)[13 ] 与Transformer[14 ] 等模型比较预测值与真实值的差异进行异常检测. 现有无监督异常检测方法往往关注时序数据中变量自身的时间特征,忽略了变量之间复杂的空间关联关系(如传感器之间的变化性依赖关系),导致多变量时序数据中不同变量的异常值、异常区间和异常模式难以被准确识别和定位. 如何结合多变量时序数据的时空特征成为进一步提高异常检测性能的关键. ...
1
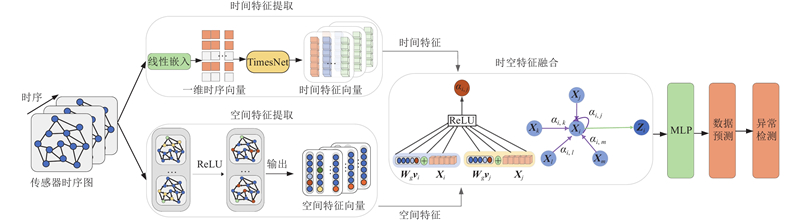
... 图深度学习在图结构数据(如交通网络、文献引用网络和知识图谱等方面)展现出强大的空间特征提取能力[15 ] ,它包括图卷积网络(graph convolutional network,GCN)、图注意力网络(graph attention network,GAT)和图变换网络(graph transformer network, GTN)等重要模型. 为了利用图深度学习提取多变量时序数据的时空特征并进行异常检测,本研究提出基于时空图注意力网络(spatiotemporal graph attention network,STGAT)的多变量时序数据异常检测方法,先将多变量时序数据转换为时序图数据,再通过STGAT提取时序图的时间和空间特征,最后根据融合后的时空特征进行时序数据预测,通过比较预测值与观测值实现异常检测. 本研究1) 针对多变量时序数据间动态依赖关系难以捕捉的问题,提出新的时序图构建方法,以各时间序列为节点,利用加权相似性度量计算变量间的依赖强度,构建动态时序图模型,实现对数据时空结构的显式表达. 2) 为了进一步融合时间演化特征与空间依赖特征,设计基于时空图注意力网络的异常检测框架,通过时序网络提取局部时间模式,结合图卷积网络捕捉变量间空间关联,引入图注意力机制实现时空特征的自适应加权融合. 3) 基于多个公开数据集开展实验验证,通过预测误差进行异常判定,评估所提方法在检测精度、异常定位能力等方面的性能. ...
LSTM-autoencoder-based anomaly detection for indoor air quality time-series data
1
2023
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
Deep isolation forest for anomaly detection
1
2023
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
Water flow modeling and forecast in a water branch of Mexico City through ARIMA and transfer function models for anomaly detection
1
2023
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
3
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
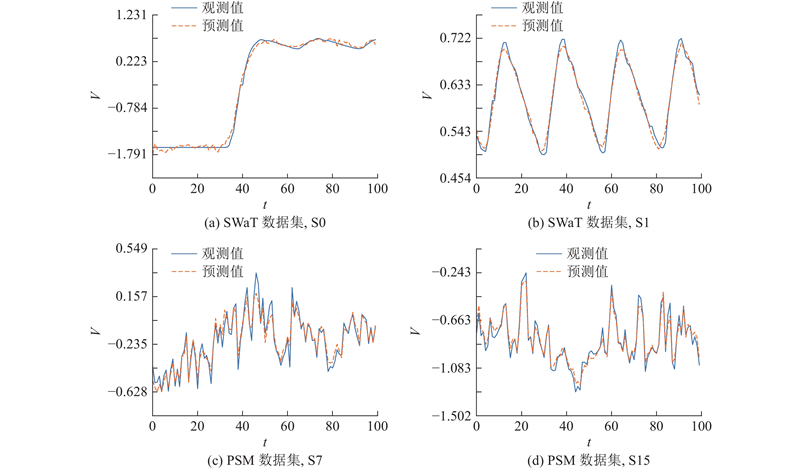
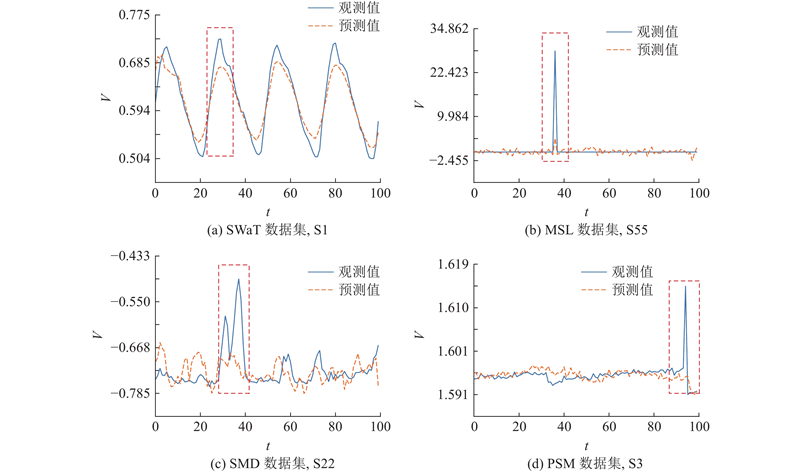
... 在4个公开数据集SWaT[34 ] 、MSL[35 ] 、SMD[19 ] 、PSM[23 ] 中开展STGAT模型性能评价实验. SWaT由连续运转的安全水处理系统中的关键传感器收集的时序数据组成,含51个变量;MSL由美国国家航天局收集的火星漫游车系统报告数据组成,含55个变量;SMD由大型互联网公司的服务器运行数据组成,含38个变量;PSM由eBay公司服务器运行数据组成,含25个变量. 实验用数据集的统计信息如表1 所示,其中n t 、n d 和n m 分别为训练集、验证集和测试集的时序数据样本数量,r a 为数据异常比例. ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
基于随机Transformer的多维时间序列异常检测模型
1
2023
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
基于随机Transformer的多维时间序列异常检测模型
1
2023
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
2
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
2
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
3
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
... 式中:ESi i 个时序数据的异常分数. 通过计算异常的均值和标准差,可以动态设定异常阈值,原因是均值和标准差分别表征数据的集中趋势和离散程度,能够有效识别显著偏离正常范围的数据点[23 ] ,计算式为 ...
... 在4个公开数据集SWaT[34 ] 、MSL[35 ] 、SMD[19 ] 、PSM[23 ] 中开展STGAT模型性能评价实验. SWaT由连续运转的安全水处理系统中的关键传感器收集的时序数据组成,含51个变量;MSL由美国国家航天局收集的火星漫游车系统报告数据组成,含55个变量;SMD由大型互联网公司的服务器运行数据组成,含38个变量;PSM由eBay公司服务器运行数据组成,含25个变量. 实验用数据集的统计信息如表1 所示,其中n t 、n d 和n m 分别为训练集、验证集和测试集的时序数据样本数量,r a 为数据异常比例. ...
STAD-GAN: unsupervised anomaly detection on multivariate time series with self-training generative adversarial networks
1
2023
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
2
... 基于深度学习的异常检测根据实现机制不同可以分为数据预测异常检测和数据重构异常检测. 数据预测异常检测采用历史时序数据对深度学习模型进行训练,以捕捉时序数据中蕴藏的如趋势和周期性的规律性知识,再将实际观测值与模型预测的规律性知识进行比较,通过计算误差进行异常检测. Wei等[16 ] 使用LSTM学习时序依赖性,通过自编码器评估重建误差以检测室内空气质量异常. Xu等[17 ] 提出深度孤立森林模型,通过随机初始化的神经网络生成多样化表示,并结合随机轴平行切割实现非线性数据分区,使异常检测性能得到提升. Barrientos-Torres等[18 ] 提出基于季节性自回归积分滑动平均模型(autoregressive integrated moving average, ARIMA)和传递函数模型的异常检测方法,通过建模水流数据实现对城市供水系统的异常检测. Su等[19 ] 提出基于随机循环神经网络的异常检测模型,利用随机变量连接和平面归一化流算法学习多变量时序的鲁棒正态表示, 通过重构输入数据并利用重构概率差异确定异常. 霍纬纲等[20 ] 提出融合Transformer 编码器和变分自编码器(variational autoencoders, VAE)的随机Transformer. Shen等[21 ] 采用具有跳跃连接的扩展循环神经网络,有效捕捉多尺度时间动态特征,通过预测结果实现异常检测,提升了检测准确率. 数据重构异常检测将重建误差作为异常分数进行异常检测. Zong等[22 ] 提出深度自动编码高斯混合模型,利用自编码器为每个输入数据点生成低维表示并进行误差重建, 再将误差输入高斯混合模型中以检测异常. Abdulaal等[23 ] 提出异常检测模型RANSynCoder,该模型对预训练自编码器(autoencoder, AE) 的潜在表示进行频谱分析,提取主要频率输入后续网络, 学习得到原始多变量的同步表示. Zhang等[24 ] 将生成对抗网络的生成器与判别器相结合,通过生成高质量伪标签和放大重构误差,提升了多变量时间序列异常检测的性能. Zhou等[25 ] 以对抗的形式执行正则化,设计翘曲方法增加训练数据进行异常检测. ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
1
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
2
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
Correlation-aware spatial-temporal graph learning for multivariate time-series anomaly detection
1
2024
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
Cross-domain graph anomaly detection
1
2022
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
2
... 有关交通网络、文献引用网络和知识图谱等图结构数据的研究表明,图深度学习具有强大的非欧空间特征学习能力[1 -3 ] ,有学者将该方法引入异常检测领域. Liu等[26 ] 等将多视图信息引入图级异常检测,通过跨视图互信息判断图的异常性. Deng等[27 ] 将学习到的图结构与时序数据同时输入多层GAT,得到各个时刻的预测值,并将异常值与预测值之间的L2距离作为异常分数. Zheng等[28 ] 提出图感知学习模型,通过图神经网络捕捉多变量时间序列的相关性,以无监督方式估计数据的异常程度. Ding等[29 ] 利用图编码器将2个不同域的属性图压缩到低维空间,利用域鉴别器和异常分类器来检测网络中出现的异常. Zhao等[30 ] 将单个时间变量数据作为特征,利用2种并行的GAT学习时序特征与特征之间的依赖关系,通过预测方法检测数据异常. 现有基于图深度学习的方法难以准确建模多变量时序数据的时空依赖关系,也不能根据融合后的时空间特征进行异常检测. ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
1
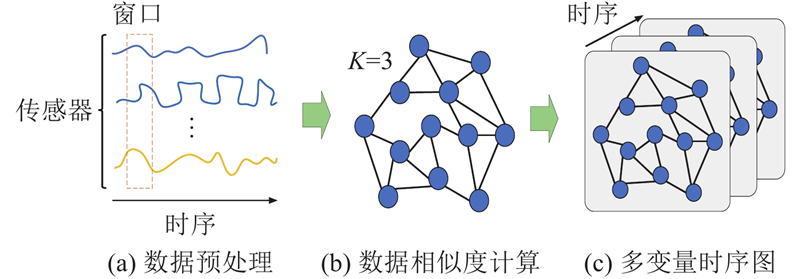
... 式中:w 为滑窗大小,x (t) 为t 时刻经滑窗处理后的数据. 在数据预处理之后,采用高斯核加权K 近邻[31 ] 构建多变量时序图模型,高斯核加权在高维空间中进行隐式数据处理,可以有效避免维度灾难问题[32 ] . 将每个时序数据值视为图的节点,数据值之间的依赖关系视为图的边,边的权重计算式为 ...
A multimodal anomaly detector for robot-assisted feeding using an LSTM-based variational autoencoder
2
2018
... 式中:w 为滑窗大小,x (t) 为t 时刻经滑窗处理后的数据. 在数据预处理之后,采用高斯核加权K 近邻[31 ] 构建多变量时序图模型,高斯核加权在高维空间中进行隐式数据处理,可以有效避免维度灾难问题[32 ] . 将每个时序数据值视为图的节点,数据值之间的依赖关系视为图的边,边的权重计算式为 ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
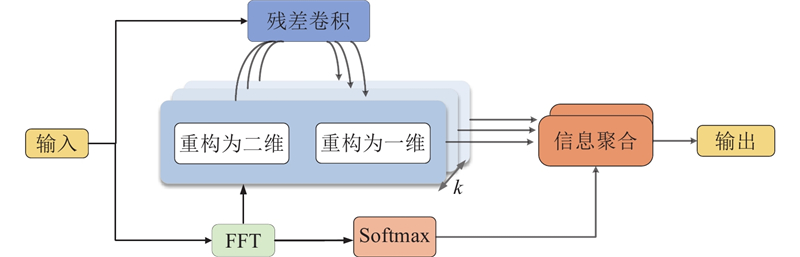
1
... STGAT模型框架如图2 所示,主要核心模块包括1)时间特征提取模块:采用TimesNet[33 ] 模型提取时序图的时间特征,得到时间特征的向量表示;2)空间特征提取模块:采用GCN提取时序图的空间特征,得到空间特征的向量表示;3)时空特征融合模块:采用图注意力机制进行时间特征向量表示和空间特征向量融合,得到统一的时空特征向量表示;4)异常检测模块:将时空特征向量表示作为输入,经过多层感知机(multilayer perceptron, MLP)进行预测,比较预测值与实际值以检测异常. ...
1
... 在4个公开数据集SWaT[34 ] 、MSL[35 ] 、SMD[19 ] 、PSM[23 ] 中开展STGAT模型性能评价实验. SWaT由连续运转的安全水处理系统中的关键传感器收集的时序数据组成,含51个变量;MSL由美国国家航天局收集的火星漫游车系统报告数据组成,含55个变量;SMD由大型互联网公司的服务器运行数据组成,含38个变量;PSM由eBay公司服务器运行数据组成,含25个变量. 实验用数据集的统计信息如表1 所示,其中n t 、n d 和n m 分别为训练集、验证集和测试集的时序数据样本数量,r a 为数据异常比例. ...
2
... 在4个公开数据集SWaT[34 ] 、MSL[35 ] 、SMD[19 ] 、PSM[23 ] 中开展STGAT模型性能评价实验. SWaT由连续运转的安全水处理系统中的关键传感器收集的时序数据组成,含51个变量;MSL由美国国家航天局收集的火星漫游车系统报告数据组成,含55个变量;SMD由大型互联网公司的服务器运行数据组成,含38个变量;PSM由eBay公司服务器运行数据组成,含25个变量. 实验用数据集的统计信息如表1 所示,其中n t 、n d 和n m 分别为训练集、验证集和测试集的时序数据样本数量,r a 为数据异常比例. ...
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...
Are transformers effective for time series forecasting?
1
2023
... 选取10个典型模型与STGAT进行对比分析,这些基线模型分属2个类别:深度学习模型和图深度学习模型. 1)DAGMM[22 ] 利用深度自编码器为每个输入数据点生成低维表示并进行误差重建;2)LSTM[13 ] 通过遗忘门、输入门和输出门控制时序数据的流动,利用序列信息学习时序数据的隐藏模式;3)LSTM-VAE[35 ] 结合LSTM与VAE,通过编码器将时序数据映射到潜在空间中,通过随机采样从潜在空间中生成重构数据以区分异常样本;4)BeatGAN[25 ] 使用对抗生成对重构误差进行正则化,使用时间序列翘曲进行数据增强;5)OminiAnomoly[19 ] 利用随机递归神经网络处理随机变量之间的显式时间依赖性,学习数据的鲁棒表示;6)THOC[21 ] 使用具有跳跃连接的扩展循环神经网络来准确捕获多个尺度下的时间动态特征进行预测;7)MTAD-GAT[30 ] 属于图深度学习模型,它利用2个并行的 GAT 学习时间序列间的时序和特征依赖关系;8)GDN[27 ] :属于图深度学习模型,它从多变量时序数据中提取高度相关的空间特征信息;9)TimesNet[32 ] 将复杂时序数据变化分解至不同周期,通过将原始一维时间序列转化至二维空间来提取时序数据周期间与周期内特征;10)DLinear[36 ] 引入 LTSF-Linear 模型,将时间序列预测问题转化为简单的线性模型,通过实验证明该模型在时序数据预测中优于基于 Transformer 的复杂模型. ...