[1]
YU L, FENG T, LI T, et al Demand prediction and optimal allocation of shared bikes around urban rail transit stations
[J]. Urban Rail Transit , 2023 , 9 (1 ): 57 - 71
DOI:10.1007/s40864-022-00183-w
[本文引用: 2]
[2]
TANG W, YANG C, WANG H, et al Spatiotemporal demand prediction for bike sharing based on WT-ConvLSTM
[J]. Advances in Civil Engineering , 2024 , 2024 (1 ): 2551687
DOI:10.1155/adce/2551687
[本文引用: 1]
[3]
XU C, JI J, LIU P The station-free sharing bike demand forecasting with a deep learning approach and large-scale datasets
[J]. Transportation Research Part C: Emerging Technologies , 2018 , 95 : 47 - 60
DOI:10.1016/j.trc.2018.07.013
[本文引用: 4]
[4]
YANG Y, SHAO X, ZHU Y, et al Short-term forecasting of dockless bike-sharing demand with the built environment and weather
[J]. Journal of Advanced Transportation , 2023 , 2023 (1 ): 7407748
[本文引用: 2]
[5]
FENG J, LIU H An adaptive spatial-temporal method capturing for short-term bike-sharing prediction
[J]. IEEE Transactions on Intelligent Transportation Systems , 2024 , 25 (11 ): 16761 - 16774
DOI:10.1109/TITS.2024.3406682
[本文引用: 2]
[6]
HE S, SHIN K G. Towards fine-grained flow forecasting: a graph attention approach for bike sharing systems [C]// Proceedings of the Proceedings of The Web Conference 2020 . [s.l.]: ACM, 2020: 88–98.
[本文引用: 2]
[7]
GALLOP C, TSE C, ZHAO J A seasonal autoregressive model of Vancouver bicycle traffic using weather variables
[J]. I-manager’s Journal on Civil Engineering , 2011 , 1 (4 ): 1694
[本文引用: 1]
[8]
KALTENBRUNNER A, MEZA R, GRIVOLLA J, et al Urban cycles and mobility patterns: exploring and predicting trends in a bicycle-based public transport system
[J]. Pervasive and Mobile Computing , 2010 , 6 (4 ): 455 - 466
DOI:10.1016/j.pmcj.2010.07.002
[9]
YOON J W, PINELLI F, CALABRESE F. Cityride: a predictive bike sharing journey advisor [C]// Proceedings of the IEEE 13th International Conference on Mobile Data Management . Bengaluru: IEEE, 2012: 306–311.
[本文引用: 2]
[10]
ASHQAR H I, ELHENAWY M, ALMANNAA M H, et al. Modeling bike availability in a bike-sharing system using machine learning [C]// Proceedings of the 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems . Naples: IEEE, 2017: 374–378.
[本文引用: 1]
[11]
SATHISHKUMAR V E, PARK J, CHO Y Using data mining techniques for bike sharing demand prediction in metropolitan city
[J]. Computer Communications , 2020 , 153 : 353 - 366
DOI:10.1016/j.comcom.2020.02.007
[本文引用: 1]
[12]
JIA R, CHAMOUN R, WALLENBRING A, et al A spatio-temporal deep learning model for short-term bike-sharing demand prediction
[J]. Electronic Research Archive , 2023 , 31 (2 ): 1031 - 1047
DOI:10.3934/era.2023051
[本文引用: 3]
[13]
LIN L, HE Z, PEETA S Predicting station-level hourly demand in a large-scale bike-sharing network: a graph convolutional neural network approach
[J]. Transportation Research Part C: Emerging Technologies , 2018 , 97 : 258 - 276
DOI:10.1016/j.trc.2018.10.011
[本文引用: 1]
[14]
DU L, WANG Y, SONG G, et al. Dynamic network embedding: an extended approach for skip-gram based network embedding [C]// Proceedings of the 27th International Joint Conference on Artificial Intelligence . Stockholm: International Joint Conferences on Artificial Intelligence Organization, 2018: 2086–2092.
[本文引用: 1]
[15]
PAREJA A, DOMENICONI G, CHEN J, et al. EvolveGCN: evolving graph convolutional networks for dynamic graphs [C]// 34th AAAI Conference on Artificial Intelligence . New York: Elsevier, 2020: 5363–5370.
[16]
WEN Z, FANG Y. TREND: temporal event and node dynamics for graph representation learning [C]// Proceedings of the ACM Web Conference 2022 . [s.l.]: ACM, 2022: 1159–1169.
[17]
YOU J, DU T, LESKOVEC J. ROLAND: graph learning framework for dynamic graphs [C]// Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining . Washington DC: ACM, 2022: 2358–2366.
[本文引用: 1]
[18]
PAN Y, ZHENG R C, ZHANG J, et al Predicting bike sharing demand using recurrent neural networks
[J]. Procedia Computer Science , 2019 , 147 : 562 - 566
DOI:10.1016/j.procs.2019.01.217
[本文引用: 1]
[19]
MEHDIZADEH DASTJERDI A, MORENCY C Bike-sharing demand prediction at community level under COVID-19 using deep learning
[J]. Sensors , 2022 , 22 (3 ): 1060
DOI:10.3390/s22031060
[本文引用: 3]
[20]
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is All you Need [C]// 31st Conference on Neural Information Processing Systems . Long Beach: 2017 : 6000–6010.
[本文引用: 3]
[21]
LIU Z, GOKON H, SEKIMOTO Y Long-term demand prediction for public bicycle sharing system: a spatio-temporal attentional graph convolution networks approach
[J]. IEEE Transactions on Intelligent Transportation Systems , 2024 , 25 (12 ): 21515 - 21527
DOI:10.1109/TITS.2024.3469169
[本文引用: 2]
[22]
LI X, ZHANG G, CUI H, et al MCANet: a joint semantic segmentation framework of optical and SAR images for land use classification
[J]. International Journal of Applied Earth Observation and Geoinformation , 2022 , 106 : 102638
DOI:10.1016/j.jag.2021.102638
[本文引用: 1]
[23]
KHAN M, GUEAIEB W, EL SADDIK A, et al MSER: multimodal speech emotion recognition using cross-attention with deep fusion
[J]. Expert Systems with Applications , 2024 , 245 : 122946
DOI:10.1016/j.eswa.2023.122946
[本文引用: 1]
[24]
GU J, ZHOU Q, YANG J, et al Exploiting interpretable patterns for flow prediction in dockless bike sharing systems
[J]. IEEE Transactions on Knowledge and Data Engineering , 2022 , 34 (2 ): 640 - 652
DOI:10.1109/TKDE.2020.2988008
[本文引用: 1]
[25]
HUA M, CHEN J, CHEN X, et al Forecasting usage and bike distribution of dockless bike-sharing using journey data
[J]. IET Intelligent Transport Systems , 2020 , 14 (12 ): 1647 - 1656
DOI:10.1049/iet-its.2020.0305
[本文引用: 2]
[26]
AI Y, LI Z, GAN M, et al Retraction note: a deep learning approach on short-term spatiotemporal distribution forecasting of dockless bike-sharing system
[J]. Neural Computing and Applications , 2024 , 36 (25 ): 15927
DOI:10.1007/s00521-024-10079-4
[本文引用: 1]
[27]
LIU Z, SHEN Y, ZHU Y. Inferring dockless shared bike distribution in new cities [C]// Proceedings of the 11th ACM International Conference on Web Search and Data Mining . Marina Del Rey: ACM, 2018: 378–386.
[本文引用: 1]
[28]
ZHANG J, ZHENG Y, QI D, et al. DNN-based prediction model for spatio-temporal data [C]// Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems . Burlingame: ACM, 2016: 1–4.
[本文引用: 1]
[29]
LIU Y, HU T, ZHANG H, et al. iTransformer: inverted transformers are effective for time series forecasting [EB/OL]. (2023-10-10)[2024-10-15]. https://arxiv.org/abs/2310.06625.
[本文引用: 1]
Demand prediction and optimal allocation of shared bikes around urban rail transit stations
2
2023
... 目前,诸多学者已开展对共享单车借还量预测的研究工作. 他们基于国内外共享单车数据集展开实验,部分学者选用无桩单车数据集(如北京市西城区[1 ] 、上海市浦西[2 ] 地区的数据),研究范围仅限于一个城市的部分区域,忽略了跨区域使用共享单车的情况;还有学者利用有桩单车数据集(如南京市[3 ] 、天津市[4 ] 地区的),然而,这些单车桩位仅仅集中在城市的局部区域,无法覆盖整个城市. 因此,这些研究在空间范围上存在着较为明显的局限性. 为了提高预测精度,在进行预测时须引入外生变量信息. 已有文献[5 -6 ] 证实了外部信息对预测精度的积极影响. 例如Feng等[5 ] 引入天气和POI变量作为外部信息. 现有研究在处理POI数据时存在局限性,不同规模的店铺或住宅常被赋予相同的POI数值,难以精准反映区域人流量. ...
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
Spatiotemporal demand prediction for bike sharing based on WT-ConvLSTM
1
2024
... 目前,诸多学者已开展对共享单车借还量预测的研究工作. 他们基于国内外共享单车数据集展开实验,部分学者选用无桩单车数据集(如北京市西城区[1 ] 、上海市浦西[2 ] 地区的数据),研究范围仅限于一个城市的部分区域,忽略了跨区域使用共享单车的情况;还有学者利用有桩单车数据集(如南京市[3 ] 、天津市[4 ] 地区的),然而,这些单车桩位仅仅集中在城市的局部区域,无法覆盖整个城市. 因此,这些研究在空间范围上存在着较为明显的局限性. 为了提高预测精度,在进行预测时须引入外生变量信息. 已有文献[5 -6 ] 证实了外部信息对预测精度的积极影响. 例如Feng等[5 ] 引入天气和POI变量作为外部信息. 现有研究在处理POI数据时存在局限性,不同规模的店铺或住宅常被赋予相同的POI数值,难以精准反映区域人流量. ...
The station-free sharing bike demand forecasting with a deep learning approach and large-scale datasets
4
2018
... 目前,诸多学者已开展对共享单车借还量预测的研究工作. 他们基于国内外共享单车数据集展开实验,部分学者选用无桩单车数据集(如北京市西城区[1 ] 、上海市浦西[2 ] 地区的数据),研究范围仅限于一个城市的部分区域,忽略了跨区域使用共享单车的情况;还有学者利用有桩单车数据集(如南京市[3 ] 、天津市[4 ] 地区的),然而,这些单车桩位仅仅集中在城市的局部区域,无法覆盖整个城市. 因此,这些研究在空间范围上存在着较为明显的局限性. 为了提高预测精度,在进行预测时须引入外生变量信息. 已有文献[5 -6 ] 证实了外部信息对预测精度的积极影响. 例如Feng等[5 ] 引入天气和POI变量作为外部信息. 现有研究在处理POI数据时存在局限性,不同规模的店铺或住宅常被赋予相同的POI数值,难以精准反映区域人流量. ...
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
... [3 ]. 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
... 3)LSTM:长短期记忆模型,专门用于解决一般 RNN的长期依赖问题[3 ] ,通过输入门、输出门和遗忘门解决隐藏状态的长期依赖问题. 该模型通过Adam优化器进行训练. 学习率为0.0001 ,批处理大小为32,隐层维度为128. ...
Short-term forecasting of dockless bike-sharing demand with the built environment and weather
2
2023
... 目前,诸多学者已开展对共享单车借还量预测的研究工作. 他们基于国内外共享单车数据集展开实验,部分学者选用无桩单车数据集(如北京市西城区[1 ] 、上海市浦西[2 ] 地区的数据),研究范围仅限于一个城市的部分区域,忽略了跨区域使用共享单车的情况;还有学者利用有桩单车数据集(如南京市[3 ] 、天津市[4 ] 地区的),然而,这些单车桩位仅仅集中在城市的局部区域,无法覆盖整个城市. 因此,这些研究在空间范围上存在着较为明显的局限性. 为了提高预测精度,在进行预测时须引入外生变量信息. 已有文献[5 -6 ] 证实了外部信息对预测精度的积极影响. 例如Feng等[5 ] 引入天气和POI变量作为外部信息. 现有研究在处理POI数据时存在局限性,不同规模的店铺或住宅常被赋予相同的POI数值,难以精准反映区域人流量. ...
... 5)GCN-LSTM-FCN:使用GCN对建成环境进行建模,使用LSTM网络提取时间特征,并使用全连接对天气影响进行建模[4 ] . 该模型通过Adam进行训练. 学习率为0.0005 ,批处理大小为 32. ...
An adaptive spatial-temporal method capturing for short-term bike-sharing prediction
2
2024
... 目前,诸多学者已开展对共享单车借还量预测的研究工作. 他们基于国内外共享单车数据集展开实验,部分学者选用无桩单车数据集(如北京市西城区[1 ] 、上海市浦西[2 ] 地区的数据),研究范围仅限于一个城市的部分区域,忽略了跨区域使用共享单车的情况;还有学者利用有桩单车数据集(如南京市[3 ] 、天津市[4 ] 地区的),然而,这些单车桩位仅仅集中在城市的局部区域,无法覆盖整个城市. 因此,这些研究在空间范围上存在着较为明显的局限性. 为了提高预测精度,在进行预测时须引入外生变量信息. 已有文献[5 -6 ] 证实了外部信息对预测精度的积极影响. 例如Feng等[5 ] 引入天气和POI变量作为外部信息. 现有研究在处理POI数据时存在局限性,不同规模的店铺或住宅常被赋予相同的POI数值,难以精准反映区域人流量. ...
... [5 ]引入天气和POI变量作为外部信息. 现有研究在处理POI数据时存在局限性,不同规模的店铺或住宅常被赋予相同的POI数值,难以精准反映区域人流量. ...
2
... 目前,诸多学者已开展对共享单车借还量预测的研究工作. 他们基于国内外共享单车数据集展开实验,部分学者选用无桩单车数据集(如北京市西城区[1 ] 、上海市浦西[2 ] 地区的数据),研究范围仅限于一个城市的部分区域,忽略了跨区域使用共享单车的情况;还有学者利用有桩单车数据集(如南京市[3 ] 、天津市[4 ] 地区的),然而,这些单车桩位仅仅集中在城市的局部区域,无法覆盖整个城市. 因此,这些研究在空间范围上存在着较为明显的局限性. 为了提高预测精度,在进行预测时须引入外生变量信息. 已有文献[5 -6 ] 证实了外部信息对预测精度的积极影响. 例如Feng等[5 ] 引入天气和POI变量作为外部信息. 现有研究在处理POI数据时存在局限性,不同规模的店铺或住宅常被赋予相同的POI数值,难以精准反映区域人流量. ...
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
A seasonal autoregressive model of Vancouver bicycle traffic using weather variables
1
2011
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
Urban cycles and mobility patterns: exploring and predicting trends in a bicycle-based public transport system
0
2010
2
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
... 1)ARIMA:差分自回归移动平均模型,通过差分之类的方法平滑时间序列,从而发现序列的自相关性并预测未来数据[9 ] . ...
1
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
Using data mining techniques for bike sharing demand prediction in metropolitan city
1
2020
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
A spatio-temporal deep learning model for short-term bike-sharing demand prediction
3
2023
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
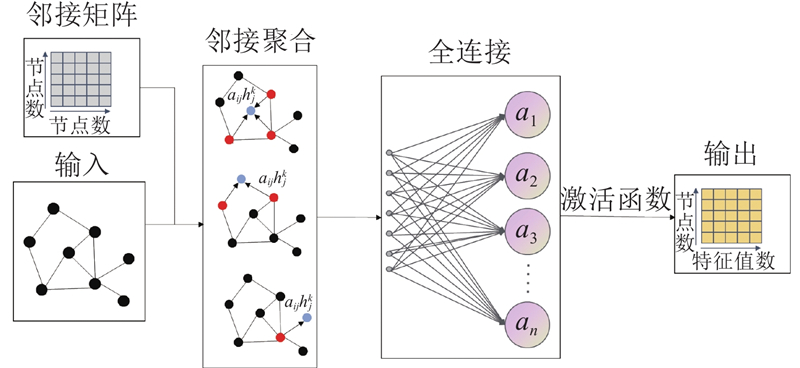
... [12 ]使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
... 2)Time-GCN:具有不同时间层的图卷积网络模型[12 ] ,应用于空间信息预测任务,为图数据挖掘提供强大的工具. 该模型通过Adam优化器进行训练. 学习率为0.0001 ,批处理大小为32. ...
Predicting station-level hourly demand in a large-scale bike-sharing network: a graph convolutional neural network approach
1
2018
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
1
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
1
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
Predicting bike sharing demand using recurrent neural networks
1
2019
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
Bike-sharing demand prediction at community level under COVID-19 using deep learning
3
2022
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
... 由于用户可以在任何允许的区域内借还单车,缺乏实际存在的站点,必须人为划定虚拟站点作为研究的基本单位. 目前研究中,虚拟站点的分类主要有2种方法. 1)利用适当的算法方法将借还车点聚类为多个类别(DBSCAN[24 ] 、K-means[25 ] 、社区发现[19 ] 等). 该方法的缺点是须预设一定的聚类参数,使用不同参数所获得的结果差异显著;聚类后区域形状不规则,不利于后续单车运营公司的管理;一些边缘点在聚类过程中容易被误判为噪声而被丢弃,无法实现对区域的全面覆盖[25 ] . 2)按区域划分,将整个研究空间均匀划分为若干等大小的区域[26 -27 ] . 这种方法的缺点是不同区域的流量差异大,影响预测的准确性. ...
... 4)CNN-bi-LSTM[19 ] :将CNN模型与LSTM后端集成的混合模型. 该架构使用CNN层对输入数据进行特征提取,并与LSTM相结合以支持序列预测. 该模型通过Adam优化器进行训练. 学习率为0.0001 ,批处理大小为32. LSTM使用双向RNN,有2个堆叠层,隐藏层维度为128. ...
3
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
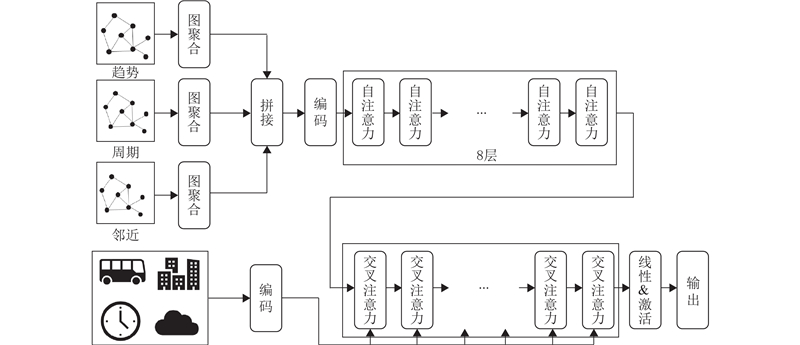
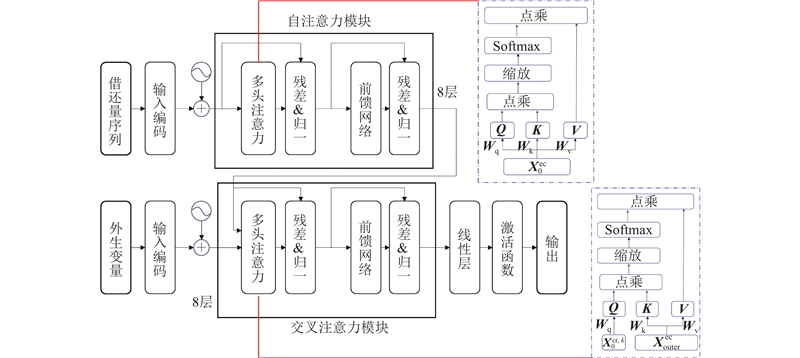
... 注意力机制借鉴Transformer模型[20 ] ,有2部分输入:车借还量的时间序列与其他外生变量. 在多源数据的学习上,传统Transformer模型存在以下问题:1)多源数据的物理意义以及分布特征存在较大的差别,天气数据和借还量数据分别代表不同的物理环境,放在同一个注意力机制中会造成权重偏差,使模型无法很好地理解不同物理量的含义;2)多源数据的采样间隔也不一致,外生变量中的天气、POI、热力值等数据在较长的时间段内变化程度较小,而借还量数据则是固定15 min时间间隔进行采样的;3)自注意力机制更关注序列内部本身的相关性,对于不同来源的交互关系捕捉能力较弱. ...
... 6)GCN-Transformer:使用原始的GCN模型和Transformer[20 ] 模型. 参数设置与本研究的相同. ...
Long-term demand prediction for public bicycle sharing system: a spatio-temporal attentional graph convolution networks approach
2
2024
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
... 8)ST-AGCN:时空注意力图卷积网络[21 ] ,该模型将概率自注意力机制和切比雪夫GCN这2个模块集成在编码器-解码器框架中. 学习率为0.0005 ,批处理大小为64. ...
MCANet: a joint semantic segmentation framework of optical and SAR images for land use classification
1
2022
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
MSER: multimodal speech emotion recognition using cross-attention with deep fusion
1
2024
... 在模型选择方面,早期研究多依赖传统时间序列分析方法[7 –9 ] 或者机器学习方法[10 -11 ] ,准确率相对较低. 深度学习的兴起推动了共享单车借还量预测领域的进步. 在空间信息捕捉方面,大多数学者使用各种图模型进行建模[12 -13 ] . Jia等[12 ] 使用图网络对数据进行预测,成功将单车站点转化为图结构,最终绝对误差约为10. 但该方法的局限在于图结构中每个节点的权重相同,导致空间信息部分损失. 在动态图模型方面,目前研究[14 -17 ] 主要采用了Hawkes过程来映射全图的链接形成过程,引入RNN学习历史的动态图结构信息来预测最新的拓扑结构. 而在共享单车借还量预测问题中,划分站点后数量不变,不存在节点增减,拓扑结构保持不变. 并且,只对站点借还量进行预测,不预测节点间的连接关系. 在时间信息捕捉方面,早期大多数学者使用LSTM模型[1 ,3 ,18 -19 ] ,最小误差约为12%[3 ] . 2017年基于注意力机制的Transformer模型[20 ] 出现后,在时序预测领域表现突出. Liu等[21 ] 以及He等[6 ] 通过构建各自的注意力机制模型,在国外一些城市数据集上进行了实验,证明了注意力机制在共享单车预测的有效性,但在外生变量与内生变量融合方面仍有不足. 针对该问题,在其他领域上,Li等[22 -23 ] 使用交叉注意力机制的方法,将图像视频和文字2种模态的数据通过交叉注意力机制融合,取得了较好的效果,证明该机制在多源数据领域能够有效捕捉相关性. ...
Exploiting interpretable patterns for flow prediction in dockless bike sharing systems
1
2022
... 由于用户可以在任何允许的区域内借还单车,缺乏实际存在的站点,必须人为划定虚拟站点作为研究的基本单位. 目前研究中,虚拟站点的分类主要有2种方法. 1)利用适当的算法方法将借还车点聚类为多个类别(DBSCAN[24 ] 、K-means[25 ] 、社区发现[19 ] 等). 该方法的缺点是须预设一定的聚类参数,使用不同参数所获得的结果差异显著;聚类后区域形状不规则,不利于后续单车运营公司的管理;一些边缘点在聚类过程中容易被误判为噪声而被丢弃,无法实现对区域的全面覆盖[25 ] . 2)按区域划分,将整个研究空间均匀划分为若干等大小的区域[26 -27 ] . 这种方法的缺点是不同区域的流量差异大,影响预测的准确性. ...
Forecasting usage and bike distribution of dockless bike-sharing using journey data
2
2020
... 由于用户可以在任何允许的区域内借还单车,缺乏实际存在的站点,必须人为划定虚拟站点作为研究的基本单位. 目前研究中,虚拟站点的分类主要有2种方法. 1)利用适当的算法方法将借还车点聚类为多个类别(DBSCAN[24 ] 、K-means[25 ] 、社区发现[19 ] 等). 该方法的缺点是须预设一定的聚类参数,使用不同参数所获得的结果差异显著;聚类后区域形状不规则,不利于后续单车运营公司的管理;一些边缘点在聚类过程中容易被误判为噪声而被丢弃,无法实现对区域的全面覆盖[25 ] . 2)按区域划分,将整个研究空间均匀划分为若干等大小的区域[26 -27 ] . 这种方法的缺点是不同区域的流量差异大,影响预测的准确性. ...
... [25 ]. 2)按区域划分,将整个研究空间均匀划分为若干等大小的区域[26 -27 ] . 这种方法的缺点是不同区域的流量差异大,影响预测的准确性. ...
Retraction note: a deep learning approach on short-term spatiotemporal distribution forecasting of dockless bike-sharing system
1
2024
... 由于用户可以在任何允许的区域内借还单车,缺乏实际存在的站点,必须人为划定虚拟站点作为研究的基本单位. 目前研究中,虚拟站点的分类主要有2种方法. 1)利用适当的算法方法将借还车点聚类为多个类别(DBSCAN[24 ] 、K-means[25 ] 、社区发现[19 ] 等). 该方法的缺点是须预设一定的聚类参数,使用不同参数所获得的结果差异显著;聚类后区域形状不规则,不利于后续单车运营公司的管理;一些边缘点在聚类过程中容易被误判为噪声而被丢弃,无法实现对区域的全面覆盖[25 ] . 2)按区域划分,将整个研究空间均匀划分为若干等大小的区域[26 -27 ] . 这种方法的缺点是不同区域的流量差异大,影响预测的准确性. ...
1
... 由于用户可以在任何允许的区域内借还单车,缺乏实际存在的站点,必须人为划定虚拟站点作为研究的基本单位. 目前研究中,虚拟站点的分类主要有2种方法. 1)利用适当的算法方法将借还车点聚类为多个类别(DBSCAN[24 ] 、K-means[25 ] 、社区发现[19 ] 等). 该方法的缺点是须预设一定的聚类参数,使用不同参数所获得的结果差异显著;聚类后区域形状不规则,不利于后续单车运营公司的管理;一些边缘点在聚类过程中容易被误判为噪声而被丢弃,无法实现对区域的全面覆盖[25 ] . 2)按区域划分,将整个研究空间均匀划分为若干等大小的区域[26 -27 ] . 这种方法的缺点是不同区域的流量差异大,影响预测的准确性. ...
1
... 共享单车借还量的时间特征包括邻近性、趋势性和周期性[28 ] . 以1个时间步长为滞后阶数,计算不同滞后阶数下借还量时间序列的自回归系数. 当天、前1天和前1周同时刻的自回归系数(0.95、0.93、0.91)大于其他时间的. 因此,使用前1周同一时刻的前10个时间步长作为趋势性(trend)特征$ {\boldsymbol{X}}_{i}^{\mathrm{t}\mathrm{r}}=\left[{P}_{i}^{T-7 \times 96},{P}_{i}^{T-7 \times 96-1},\cdots ,{P}_{i}^{T-7 \times 96-9}\right] $ $ {\boldsymbol{X}}_{i}^{\mathrm{p}\mathrm{e}}=[{P}_{i}^{T-96},{P}_{i}^{T-96-1},\cdots ,{P}_{i}^{T-96-9}] $ $ {\boldsymbol{X}}_{i}^{\mathrm{c}\mathrm{l}}= [{P}_{i}^{T-1},{P}_{i}^{T-2},\cdots ,{P}_{i}^{T-10}] $ . 30个时间步长的借还车数量共计60个数据作为输入. ...
1
... 7)GraphAgg-iTransformer:将本研究的多通道图聚合和iTransformer[29 ] 模型相结合,来验证本研究交叉注意力机制的有效性. ...