全球电力需求的持续增长加剧了能源危机,其中住宅负荷占据了总电力消耗的约40%[1]. 家庭能量管理系统(home energy management system, HEMS)作为智能电网在用户侧的延伸,能够通过优化家庭用电行为以适应电价波动,降低总体电费[2]. 随着可再生能源并网程度的提高,光伏(photovoltaic, PV)发电技术在HEMS中的应用受到了广泛关注,但其间歇性和波动性的特点对HEMS的稳定性和经济性带来了挑战[3]. 此外,电动汽车(electric vehicle, EV)与住宅之间通过能量交互(vehicle to home, V2H)技术将能量回馈给家庭或电网[4],这为家庭能量管理带来了新的机遇. 然而,EV的充电活动会加剧用电高峰,并且频繁的充放电会加速电池老化,缩短其使用寿命,从而降低家庭经济效益[5]. 因此,亟须开发一种综合性的智能家庭能量管理策略,以协调PV发电和EV充放电,智能调度家庭各类负荷,实现家庭能源的高效管理与优化.
目前,对于家庭能量管理的研究主要集中在提高经济效益和能源利用效率[6-11]. 王玉彬等[7]提出基于模型预测控制的家庭能量管理策略以降低家庭用电费用,但该策略未将EV考虑在内. Ali等[8]在考虑发电机运行成本的同时提出日前调度策略,但未关注家用不同类型电器的调度优化. Gholampour等[9]采用分层3级分布式控制方法,整合EV以优化家庭微电网的运行,但未充分考虑不同家用电器的差异需求,这会影响用户的经济效益. Prum等[10]在计及PV、储能以及EV的基础上,建立了分时电价环境下的家庭能量管理策略,但忽略了EV电池因频繁充放电带来的容量退化成本. Abdelaal等[11]考虑了EV电池退化对家庭放电活动经济性的影响,但采用的日前电价机制无法动态响应电价波动. EV的引入为HEMS带来了新的不确定性因素,如充电的随机性和用户行为的不确定性,不仅增加了系统复杂性,也对其性能提出了更高要求.
为了应对电价波动、PV发电以及用户行为的不确定性,传统模型多通过预测或场景生成结合优化算法实现调度优化[12-13]. 这些方法依赖于对电价、PV发电、电力需求等不确定性信息已知或预测假设. 但在实际中,这些系统参数受到各种因素影响呈非平稳性,导致这些信息或其先验统计知识难以精确预测或获取. 为此,研究者提出的解决方法包括深度强化学习算法[14-15]以及Lyapunov优化算法[16-17]. 尽管深度强化学习算法不需要系统参数的先验统计知识,但其过度依赖环境易陷入局部最优. Lyapunov优化算法则以其收敛快、稳定性强、能够灵活处理系统动态变化的优点,提供了更高效和鲁棒的HEMS优化方法. 然而,这些研究在模型构建时未考虑不同家电的实际需求和时延,无法针对性分配能量,且未计及EV放电及其电池容量退化成本,未充分探讨EV在HEMS中作为储能设备向家庭供能的潜力.
本研究针对含PV、EV以及家庭各类电器的智能家庭用户,充分利用EV的移动储能特性,协同PV出力的随机性、电价的时变性和智能电器用电的灵活性,提出智能家庭能量管理优化策略. 创新性工作如下:1)构建了含有EV、PV和家庭各类电器的智能家庭能量管理的新模型,通过智能控制EV的充放电、家用电器的运行调度,以及优化家庭与电网之间的双向电力交易,有效协同智能电网的实时电价、PV发电和用电需求的不确定性,以实现能源效用最大化. 2)针对传统Lyapunov优化框架无法解决EV电池约束的问题,提出改进的Lyapunov优化算法. 该算法通过构造一个衡量EV电池电量的变量和虚拟队列,以满足电池约束条件. 该算法复杂度低,且不依赖于PV出力、电网实时电价、EV充电需求和电器电力需求的统计分布信息,仅基于当前的环境状态就能做出最佳决策. 3)考虑了EV电池容量退化的成本,并分析不同类型家庭电器的用电需求和时延容忍度,提出针对性的能量分配策略,提高家庭能源利用率和分配效率.
1. 系统模型
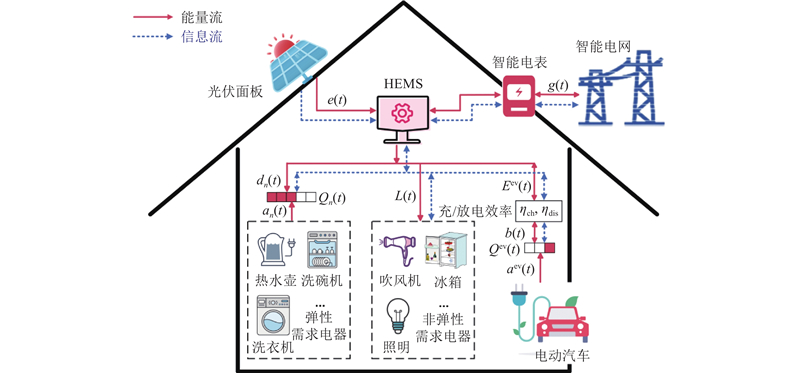
所提出的家庭能量系统模型如图1所示. 该系统由HEMS、PV发电单元、家用电器、EV以及智能电表组成. 智能电表外部与智能电网连接,以获取实时电价信息,内部则连接HEMS.
图 1
HEMS作为系统的核心控制器,采集系统数据(电费、电力需求、PV发电量等),并根据优化策略做出调度决策,下发至各设备执行. 家用电器根据用电特性分为非弹性需求电器和弹性需求电器2类. 当EV在家中插上电源时,HEMS根据其充电或放电状态,将其视为负载或储能设备来参与家庭能量管理. 系统通过HEMS与智能电网之间的双向电力交易,实现在满足家庭用电需求的同时,最大化家庭用户的售电收益.
1.1. 家用电器模型
1) 非弹性需求电器. 非弹性需求电器,如吹风机、冰箱、照明设备等,在家庭用户中属于不可调节的必须用电需求,无论何时都须优先被满足,不允许任何形式延迟. 将用户在t时隙下非弹性能量需求记为
2) 弹性需求电器. 弹性需求电器允许需求的能量有一定的时延,例如洗碗机、洗衣机. 其可以根据电价和电力供应情况进行调整,只要在一定时间范围内能满足用户要求即可. 弹性能量需求和最大能量需求分别用
式中:
1.2. EV模型
当EV在家中连接充电装置时,HEMS首先获取EV的充电信息,可以用3元组
式中:
考虑到EV用户的出行要求,出行期间EV不参与家庭能量管理,只考虑出行能量放电,在此期间有
当
式中:
进一步假设
式(5)保证了EV充电需求队列保持稳定,但不足以保证不超过充电完成时间,因此还须施加以下约束条件:
式中:
考虑EV电池在充/放电过程中存在能量转换损失,将EV的充/放电方程分别描述如下:
式中:
用
为了保证EV电池电量始终在合理水平,防止因过度放电而导致电池寿命缩短,设置约束条件:
EV电池在充放电过程中,因能量转换损失和长期循环使用,容量会逐渐退化,因此须进一步考虑这些因素对于EV电池的影响. 假设在电池容量衰减到80%时进行更换,电池容量退化成本模型参考文献[18]:
式中:CP为长期更换电池的成本,即在电池的整个使用寿命周期内,因电池容量衰减到一定阈值以下而需要更换时,每千瓦时电池容量所需支付的平均成本;
1.3. 能量平衡模型
在每个时隙t,优先使用PV发电满足家庭能量需求,并且优先满足非弹性能量需求. 当t时隙的PV发电量
2. 问题的规划及解决
基于上述模型,HEMS会根据当前时隙的智能电网的电价
用户从智能电网购买电力花费的成本:
用户向智能电网出售电力获得的利润:
用户卖给智能电网能量的总收益:
本研究的优化目标是在不超过用户可容忍时延的前提下,寻找最优决策变量
约束条件如下: 式(1)~(13),
式中:
通过求解式(17),只能得到一个宽泛的目标,因为它不包含对每个负载的延迟约束. 此外,在问题P1中存在3类时间耦合约束,即EV电池约束(式(10))、智能电器用电的最大容忍时延约束(式(19))和EV充电的最大容忍时延约束(式(6)). 因此,直接利用传统的Lyapunov优化算法无法直接求解问题P1. 为了解决上述问题,须构建相关变量和延迟感知的虚拟队列,将问题P1中的时间耦合约束转化为虚拟队列稳定性问题,对Lyapunov优化进行改进,并利用改进的Lyapunov框架求解最优化问题.
2.1. 构造虚拟延迟队列
为了确保延迟约束得到满足,引入虚拟队列
式中:
引理1 假设各队列积压均有有限的上界,即Qn
引理1的证明参考Lyapunov优化理论[19].
2.2. Lyapunov优化
为了满足上述问题规划中的约束条件(式(10)),构造衡量EV电池充/放电转换的变量
式中:V为控制参数,通过合理调节V的大小来控制变量
定义矢量
一个时隙的Lyapunov漂移函数定义为
Lyapunov“漂移加惩罚”表达式为
式中:
引理2 令
其中,
引理2的证明参考Lyapunov优化理论[19].
2.3. 实时优化算法
最小化每个时隙的“漂移加惩罚”函数等效于最小化每个时隙的不等式(式(29))右侧. 除去与决策变量
对式(31)的求解,所提算法如下.
算法1 家庭能量管理优化调度算法
1. 初始化:
2. for t = 1:1:T
观测系统状态
B(t), e(t), p(t),Qn(t), Zn(t), an(t), Qev(t), H(t), aev(t)
计算
线性规划求解式(31)
求得
根据式(16),累积用户收益
EV电池电量更新:
构造的变量更新:
根据式(2)更新EV实队列、式(21)更新EV虚拟队列:
for n = 1:1:N
根据式(1)更新电器实队列、式(20)更新电器虚拟队列
end
end
由此可见,本研究基于Lyapunov优化理论提出的实时在线算法,只须观测系统当前状态就能做出最佳决策
与动态规划(dynamic programming,DP)算法相比,理论上DP算法可以获得目标最优值,但其需要PV出力、电网时变电价以及电力需求等参数的先验信息. 然而,在实际中,这些系统参数受到各种因素的影响,其统计数据可能是非平稳的,有时候难以精确预测或获取这些参数的先验统计信息. 此外,当DP算法应用于高维度系统(例如具有多个队列的系统)时,会遇到维数灾难,其复杂度随着时隙个数的增加呈指数增长. 相比之下,所提算法不依赖于先验知识,仅根据系统当前状态就可以做出最优决策,更易于实现,复杂度较低.
3. 算法性能理论分析
定理1 假设在任意时隙
式中:
提出的算法具有以下性质.
性质1 在所有时隙t,队列
性质2 队列中任何能量需求的最大时延为
性质3 队列
性质4 所提算法的时间平均预期收益在最优值
定理1的证明参考Lyapunov优化理论[19].
由性质1,队列
4. 仿真结果分析
4.1. 仿真设置
表 1 家庭能量管理系统参数设置
Tab.1
| 参数 | 取值 |
| 时隙间隔/min | 15 |
| 总时隙数/个 | 960 |
| 能量需求 | 正态分布 |
| 电价/元 | 0.5~2.0 |
| β | 0.9 |
| CP/(元·kW−1·h−1) | |
| 0.27 |
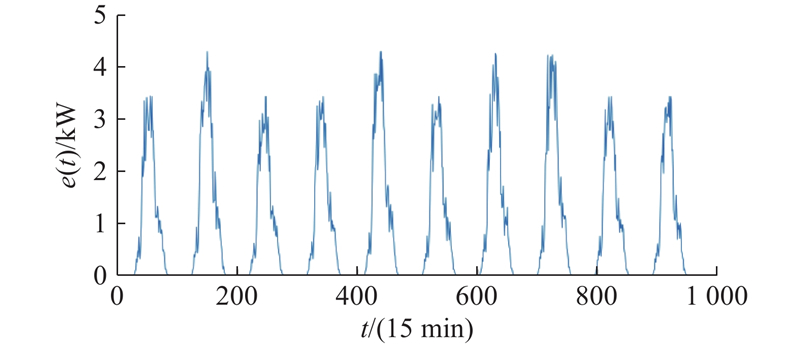
图 2
表 2 EV相关数据
Tab.2
| 参数类型 | 参数 | 数值 |
| EV参数 | EV模型 | Tesla Model 3 |
| 电池最大容量/(kW·h) | 50 | |
| 最大充/放电功率/(kW·(15 min)−1) | 11 | |
| 充/放电效率 | 0.9 | |
| 驾驶活动 | 出发时间 | 8:00 |
| 到达时间 | 19:00 | |
| 出发前的电池电量/(kW·h) | ≥40 |
4.2. 优化结果分析
基于所提算法的家庭能量管理优化结果如图3所示. 图3(a)为周末情景,此时EV全天在家. 当PV发电量超过家庭用电时(如时隙530),算法会将余电存入EV电池,以备后续使用或在电价高峰时段出售给电网(如时隙532),从而获取收益. 当PV发电无法满足家庭用电时,EV放电以补足需求(如时隙550),若EV处于低荷电状态(如时隙552),则从电网购电,一部分供应家庭用电,另一部分存入EV电池,确保家庭能源的连续供应. 图3(b)为工作日情景,EV在白天出行. 在PV发电高峰时段(如时隙48~60),算法仅使用PV电力,减少对电网的依赖. 在PV发电不足时(如时隙38和64),算法通过优化从电网购电和家电使用,提高能效和经济效益.
图 3
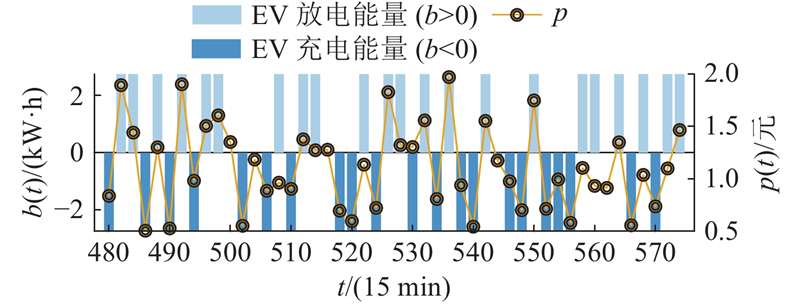
图 4
图 4 EV充放电与电网电价的关系
Fig.4 Relationship between EV charging-discharging and grid electricity price
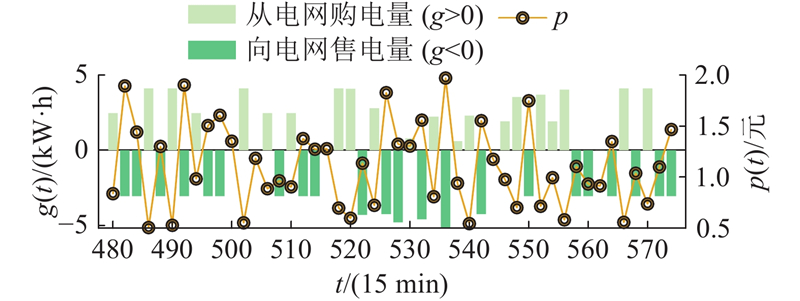
图 5
图 5 电网电力交易与电网电价的关系
Fig.5 Relationship between electricity trading with grid and grid electricity price
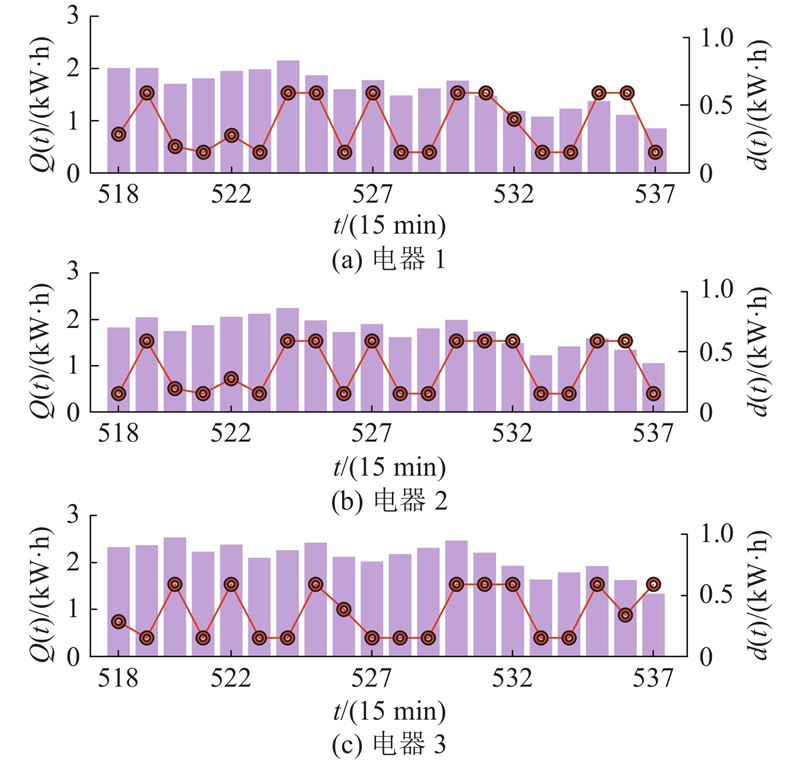
为了验证所提算法在能量分配方面的合理性,如图6所示给出了随机20个时隙(518~537)内不同电器队列积压情况与能量分配结果. 在积压量较高的时隙,如时隙520,电器3的积压量较高,须分配尽可能多的能量,而此时PV发电量不足且电价较低,HEMS从电网购电以满足用电需求. 在积压量适中的时隙,如时隙532,HEMS按照队列顺序,优先为积压量最高的电器3分配尽可能多的能量,然后将剩余的PV能量依次分配给积压量较小的电器1和电器2. 在队列积压量较小的时隙,如时隙537,HEMS在为积压量较高的电器3分配最大可能的能量后仍有剩余,此时电价较高且EV电量充足,HEMS选择将多余的电量出售给电网以实现收益,对于积压量较小的电器1和电器2,则仅分配其所需的最小能量,从而在满足家庭电力需求的同时,提高经济效益.
图 6
图 6 不同电器队列积压与能量分配
Fig.6 Backlog and energy distribution of different appliance queues
4.3. 算法性能分析
图 7
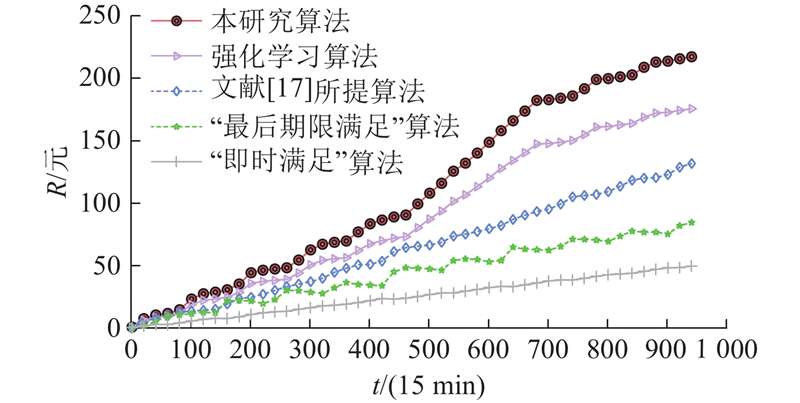
图 7 不同算法下的用户10 d累计收益对比
Fig.7 Comparison of users’ 10-day cumulative returns under different algorithms
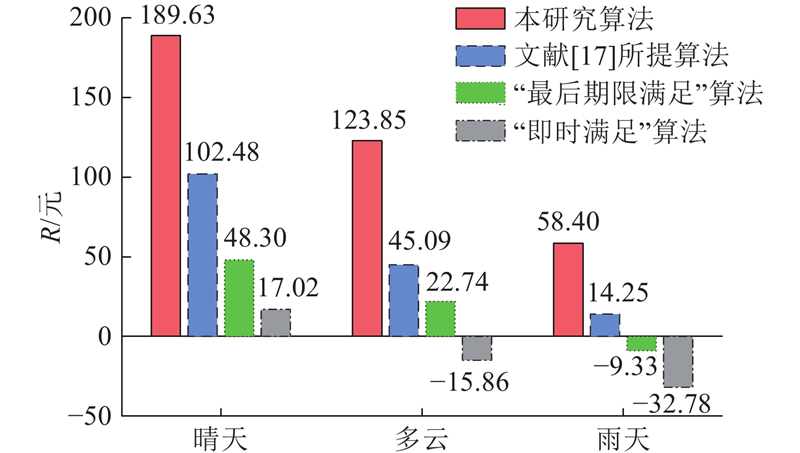
为了充分验证本研究算法的普适性,引入基于实际数据的PV发电量,设置晴朗、多云、雨天3种天气条件下的PV出力均值分别为0.678、0.475、0.226 kW·h,基于4种算法的用户10 d累计收益对比如图8所示. 结果表明,本研究算法在3种情况下均实现了最高的收益值,不依赖于PV出力的概率分布,能够更好地应对PV发电的波动性.
图 8
图 8 不同天气条件下用户10 d累计收益对比
Fig.8 Comparison of users’ 10-day cumulative returns under different weather conditions
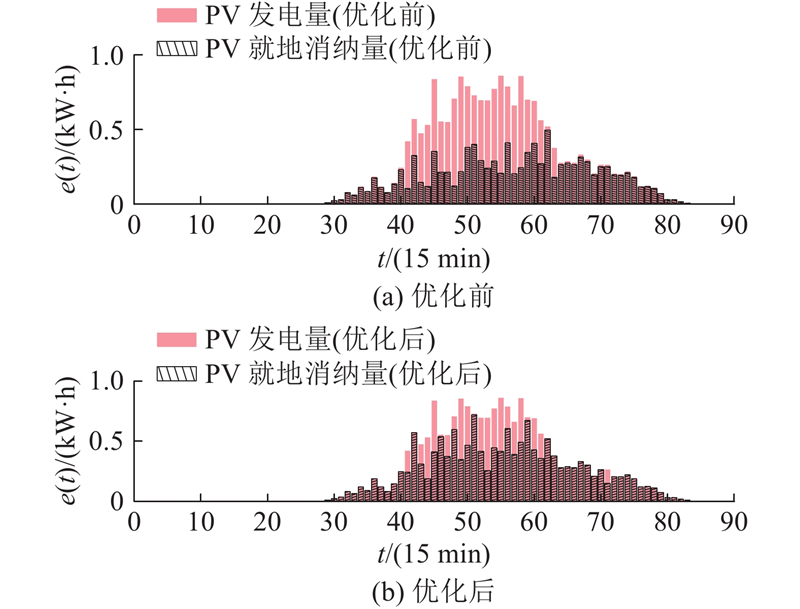
在家庭能量管理中,PV消纳率反映了PV发电量在家庭总能耗中的占比. 如图9所示对比了使用本研究算法优化前、后的PV发电就地消纳量. 由于PV发电量超过用户需求时,HEMS会将过剩电力出售给电网,而非全部自用,因此PV发电量与就地消纳量之间存在一定的差距. 结果显示,通过本研究算法优化后,PV发电与就地消纳量之间的差距有所减少,PV就地消纳率提升至81.06%,减少了能源浪费.
图 9
图 9 优化前、后PV发电就地消纳量对比
Fig.9 Comparison of local consumption of PV generation before and after optimization
为了进一步评估对用户需求等待时延的影响,将本研究算法与“最后期限满足”算法下,3种不同电器负载队列和EV充电队列的时延情况进行比较. 3种电器负载队列的最大时延分别设置为8、11、14个时隙,EV充电队列的最大时延设置为10个时隙. 2种算法下的平均时延
表 3 2种算法下平均时延对比
Tab.3
| 队列 | ||
| 本研究算法 | “最后期限满足”算法 | |
| 电器1 | 4.065 | 7.477 |
| 电器2 | 3.696 | 10.395 |
| 电器3 | 3.334 | 11.303 |
| EV | 2.860 | 6.776 |
5. 结 语
针对HEMS运行环境中的不确定性,本研究提出充分利用EV移动储能特性,结合PV发电随机性和智能电器用电灵活性的智能家庭能量管理优化策略,并对家庭内各类资源进行建模. 在此基础上,设计基于改进的Lyapunov优化理论的实时能量调度算法. 理论分析表明,该算法不依赖于PV发电和电力需求的统计分布,通过实时调度智能地响应电价波动和家庭能源需求变化,能在满足家庭电力和时延需求的前提下,实现用户收益最大化的目标. 仿真结果表明,所提算法在不同设置条件下均能实现较高的经济效益,能够就地最大化利用PV发电和EV储能,提高家庭用户PV消纳,与现有算法相比,有效降低电力需求的等待时延. 本研究聚焦于单用户家庭模型的构建与优化,能够为社区级用户模型的拓展奠定重要基础,未来将致力于研究社区级多用户协同的能量管理模型,以实现更广泛场景下的应用价值.
参考文献
A study of appliance ownership and electricity consumption determinants in urban Ghanaian households
[J].DOI:10.1016/j.scs.2018.10.019 [本文引用: 1]
Home energy management systems: a review of the concept, architecture, and scheduling strategies
[J].DOI:10.1109/ACCESS.2023.3248502 [本文引用: 1]
Intelligent energy management systems: a review
[J].DOI:10.1007/s10462-023-10441-3 [本文引用: 1]
非预测机制下计及碳交易的家庭能量低碳优化实时管理
[J].
Low-carbon optimal real-time management strategy for home energy considering carbon trading under non-prediction mechanisms
[J].
Flexible energy management protocol for cooperative EV-to-EV charging
[J].DOI:10.1109/TITS.2018.2807184 [本文引用: 1]
考虑居民用户参与度不确定性的激励型需求响应模型与评估
[J].DOI:10.7500/AEPS20210404001 [本文引用: 1]
Incentive demand response model and evaluation considering uncertainty of residential customer participation degree
[J].DOI:10.7500/AEPS20210404001 [本文引用: 1]
基于数据驱动的家庭能量实时经济调控方法
[J].DOI:10.7500/AEPS20210517013 [本文引用: 1]
Data-driven real-time economic regulation method for household energy
[J].DOI:10.7500/AEPS20210517013 [本文引用: 1]
Solving day-ahead scheduling problem with multi-objective energy optimization for demand side management in smart grid
[J].DOI:10.1016/j.jestch.2022.101135 [本文引用: 1]
Optimal hierarchical energy management system with plug-and-play capability for neighborhood home microgrids
[J].DOI:10.1109/TIE.2023.3319729 [本文引用: 1]
Energy management scheme for optimizing multiple smart homes equipped with electric vehicles
[J].DOI:10.3390/en17010254 [本文引用: 1]
Integration of electric vehicles in home energy management considering urgent charging and battery degradation
[J].DOI:10.1109/ACCESS.2021.3068421 [本文引用: 2]
Demand side management through load shifting in IoT based HEMS: overview, challenges and opportunities
[J].DOI:10.1016/j.scs.2020.102517 [本文引用: 1]
Optimal sizing of smart home renewable energy resources and battery under prosumer-based energy management
[J].
基于深度强化学习的家庭能量管理分层优化策略
[J].DOI:10.7500/AEPS20210331010 [本文引用: 1]
Hierarchical optimization strategy for home energy management based on deep reinforcement learning
[J].DOI:10.7500/AEPS20210331010 [本文引用: 1]
Deep reinforcement learning for real-time energy management in smart home
[J].DOI:10.1109/JSYST.2023.3247592 [本文引用: 1]
家庭智能电器负荷调度和能量分配优化算法
[J].
Load scheduling and energy allocation optimization algorithm for intelligent home appliances
[J].
Real-time energy optimization and scheduling of buildings integrated with renewable microgrid
[J].DOI:10.1016/j.apenergy.2023.120640 [本文引用: 2]
An economic analysis of used electric vehicle batteries integrated into commercial building microgrids
[J].DOI:10.1109/TSG.2011.2163091 [本文引用: 1]
Stochastic network optimization with application to communication and queueing systems
[J].
Local electricity markets for electric vehicles: an application study using a decentralized iterative approach
[J].DOI:10.3389/fenrg.2021.705066 [本文引用: 2]