磁共振成像(magnetic resonance imaging, MRI)具有对软组织对比度高、无侵入性和无辐射等特点,广泛应用于临床疾病的诊断、治疗和筛查. 然而, MRI具有扫描时间长的固有问题,这将可能导致患者不适和运动伪影. 因此,自磁共振成像技术出现以来,加快MRI扫描速度一直是该领域的重要研究方向之一. 并行成像(parallel imaging,PI)[1-3]和压缩感知(compressed sensing, CS)[4-5]是2种加速MRI扫描速度的常规方法. PI技术利用多个接收线圈同时采集数据,并利用多个线圈的空间灵敏度差异来编码空间信息,减少成像所必须的k空间数据从而实现加速成像. 基于灵敏度编码[6] (sensitivity encoding, SENSE)的重建算法是最常见的PI重建方法之一,此类方法须显式利用灵敏度图,因此,灵敏度图的准确估计成为这类方法的关键步骤. 通常,使用预扫描信号或者自校准信号(auto-calibration signal, ACS)进行估计[7]. CS则通过在k空间中采集部分数据并利用图像在某种变换下的稀疏性来重建图像[8-10].
目前,深度学习在去噪、压缩感知和超分辨等成像逆问题求解中取得了出色的表现[11-13]. Wu等[14]提出基于深度学习的重建方法,以端到端的方式从欠采样的k空间数据中恢复高质量的MR图像. Hammernik等[15]引入有效的可训练公式,用于加速基于PI的MRI重建,这一公式被称为变分网络(variational network, VN). 变分网络中嵌入了一个广义的CS概念,在深度学习方法中形成了一种变分模型. 其主要好处在于,变分网络能够通过学习自动调整所有自由参数,以实现对复值多通道MR数据的重建. Sriram等[16]将变分网络扩展到端到端MRI重建模型(E2E-VN). 该网络利用卷积神经网络在图像域中重建MR图像. 受这项工作的启发,Yiasemis等[17]提出递归变分网络(RecurrentVN),该网络进行多次变分迭代,以解决多线圈加速 MRI 重建的逆问题. Guo等[18]提出用于MRI重建的循环Transformer模型,即ReconFormer. ReconFormer也都采用了迭代重建的策略,通过多次迭代优化来逐渐逼近真实图像. Huang等[19]提出新的 Transformer 架构,用于重建MRI,该架构将Shifted Windows Transformer与U-Net耦合以降低网络复杂性,同时结合可变形的注意力来解释重建模型的可解释性. Huang等[20]提出基于Swin Transformer的快速MRI重建方法. 网络中的特征提取模块由多个(RSTBs)组成. 与传统Transformer不同,Swin Transformer通过移位窗口多头自注意力机制实现高效的特征提取,同时保留全局依赖信息. Wang等[21]提出的DCT-Net与上述的方法不同,在双域之间进行信息交换和优化.
为了提高MR图像的重建质量,本研究提出基于变分模型和Transformer的多尺度并行磁共振成像重建模型(multi-scale parallel MRI reconstruction model based on a variational model and Transformer, VNTM). VNTM中的灵敏度图中期增强策略(简称中期增强),使用多线圈欠采样k数据估计灵敏度图,同时在每个周期的T/2次迭代时重新估计并更新灵敏度图. 如果估计出的灵敏度图不够准确可能会产生混叠伪影,因此,本研究设计了U形多尺度重建(U-shaped multi-scale reconstruction block, UMRB)模块. UMRB模块中的网络称为UMRNet,主要是由Swin Transformer Layer构建,但是Transformer在计算过程中会产生高额的计算和内存成本,为了应对这一挑战,本研究设计了前后处理模块,其借助小波变换在空间和频率特征提取上的优势,最大限度地减少了特征信息的丢失.
1. 模型和方法
1.1. 问题表述
目前,大多数MR扫描仪都使用PI技术来加速扫描速度,具体而言,PI技术利用多个灵敏度不同的接收线圈同时采集MRI信号. 并行磁共振成像模型可以表述为
式中:
从欠采样k空间数据
式中:
式(2)为带正则化项的最小二乘问题,其近似解可使用迭代求解的梯度下降法[15]来得到:
式中:β为可学习的参数,
由于深度学习的快速发展,基于深度学习的MRI重建方法也得到了快速发展,与传统的重建方法相比,深度学习方法具有许多优势,比如:重建速度快,质量高. 文献[15]提出使用卷积神经网络(CNN)来实现正则项的梯度计算,式(3)可以重写为
式中:
式中:
式中:
1.2. VNTM结构
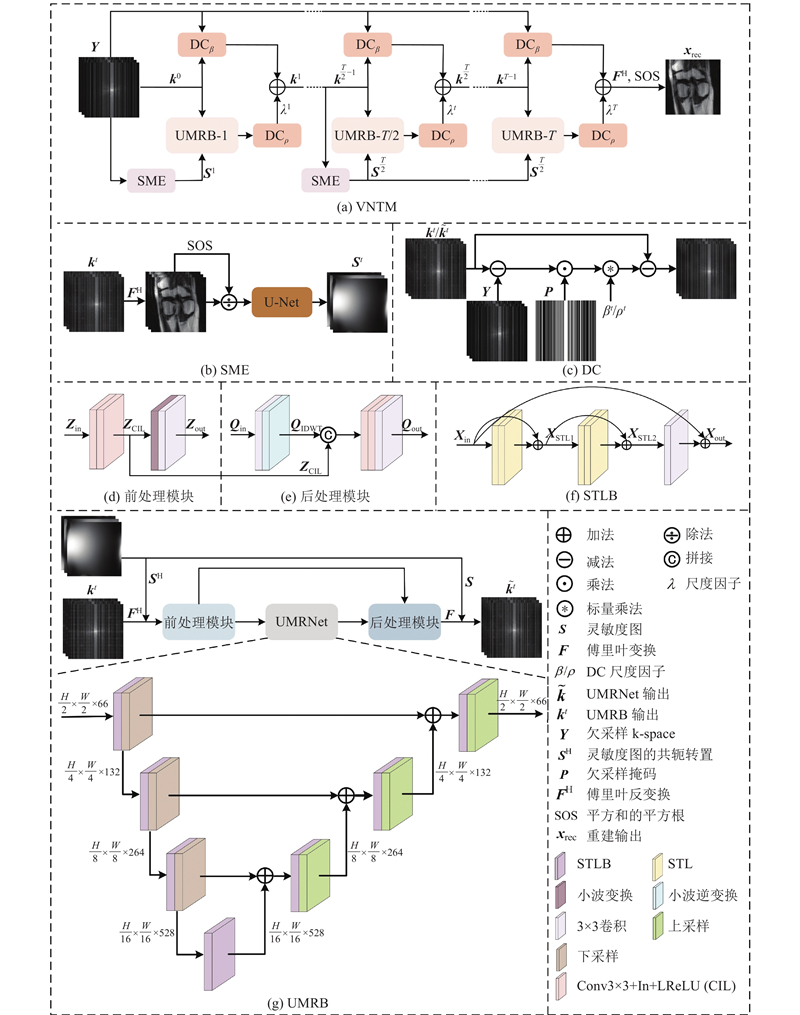
VNTM的具体结构如图1(a)所示,由灵敏度图估计(SME)模块、U形多尺度重建(UMRB)模块和数据一致性(DC)模块等子模块组成. 首先,使用多线圈欠采样k空间数据
图 1
式中:
1.2.1. 灵敏度图估计(SME)模块
对于基线模型E2E-VN中的灵敏度估计方法而言,就是将多线圈欠采样k空间的ACS区域作为输入进行一次性估计. 然而,当ACS区域有限时,灵敏度图估计的准确度将大大降低,导致传统方法(如SENSE和ESPIRiT)和深度学习方法(如E2E-VN)产生较差的重建图像. 这些方法的不足部分归因于它们依赖ACS区域数据一次性估计的灵敏度图. 为了更准确地估计每个线圈的灵敏度图,提出灵敏度图中期增强策略. 具体而言,采用多线圈欠采样k空间数据估计灵敏度图,由于一次性估计出灵敏度图不够准确,因此,当VNTM进行到T/2次迭代时,使用UMRB的输出数据作为SME的输入,进行灵敏度图的重新估计与更新,这一创新的设计旨在提高灵敏度图与重建结果的关联性,使重建结果与灵敏度图相互促进. 如图1(b)所示展示了SME模块的结构.
1.2.2. UMRB模块
UMRB结构如图1(g)所示,包含前处理模块、 UMRNet和后处理模块. 灵敏度图作为UMRB的输入之一,灵敏度图不够准确可能会导致重建图像出现混叠伪影. 为了解决这一问题,本研究设计了UMRNet,它是一种多尺度的编码器-解码器结构,其核心构建块为Swin Transformer Layer Block (STLB). 具体而言,UMRNet的输入尺寸从
在MRI重建任务中,输入图像的分辨率通常高于常用的图像数据集(32×32~256×256)[25],加上Transformer模型固有的全局时间自注意力机制所引发的二次计算成本挑战,特别是在处理更高分辨率输入时,对计算设备性能提出了更为严苛的要求. 为了在保留空间信息和减少计算资源之间取得平衡,本研究设计了前后处理模块,嵌入至UMRNet框架的两侧. 前处理模块包含小波变换(discrete wavelet transform, DWT)[26]、卷积(Conv)、实例归一化(instance normalization, IN)和LeakyReLU(LReLU)激活函数,其中小波变换不仅可以降低分辨率,还能在频域上分离图像特征,特别是高频和低频成分,从而提取边缘和纹理之类的高频细节,为网络提供更丰富的细节信息. 在小波分解过程中,每一级将图像分解为4个子图(LL、LH、HL和HH),并在通道上拼接,从而实现分辨率减半. 本实验中使用了一级小波分解. 前后处理模块显著降低了随后在UMRNet内部处理的数据的复杂性与空间占用,从而大幅提升了计算效率. 如图1(d)所示展示了前处理模块的结构,该结构可表示为如下公式:
式中:
后处理模块采用小波逆变换(inverse discrete wavelet transform, IDWT)与一系列卷积操作相结合的方式,旨在恢复数据的分辨率至与输入时相同的大小,从而确保数据在经过UMRNet处理后的完整性. 如图1(e)所示展示了后处理模块的结构,该结构可表示为如下公式:
式中:
1.2.3. 数据一致性(DC)模块
E2E-VN对前一次重建的k空间数据进行数据一致性处理,但并未对当前迭代中网络的输出数据进行数据一致性操作. 实验表明,如果对当前迭代次数的UMRNet输出值进行数据一致性处理,可提高重建质量. 在消融实验中,本研究进一步证明了对当前迭代次数的UMRNet输出值进行数据一致性操作对VNTM造成的影响.
如图1(c)所示展示了DC模块的结构,该结构可表示为如下公式:
式中:
2. 实验及结果分析
在公开的大脑和膝盖数据集上,使用不同的采样掩码和加速因子,并与当前最先进的几种方法进行比较. 本研究中所有的实验指标结果均只计算感兴趣区域(region of interest,ROI).
2.1. 实验数据
膝盖数据集是利用3T磁共振扫描仪对病人的膝盖进行全采样得到的,包含了5个不同对比度和不同解剖面的快速自旋回波(turbo spin echo, TSE)序列,每个序列采集20位不同的病人的数据. 本次实验选取了冠状面质子密度加权(Coronal-PD)序列(TR=
大脑数据集在3T或1.5T扫描仪上采集的. 原始的多线圈k空间数据经过傅立叶逆变换后,被裁剪为320×320大小. 为了标准化线圈数量,使用几何分解线圈压缩(geometric decomposition coil compression,GCC)技术,将线圈数量标准化为15. 实验过程中,从原始数据集中随机选择80名受试者进行训练,20名受试者进行验证,以及20名受试者用于测试,每个受试者包含前5个切片的数据,即每个实验样本大小为320×320×15.
2.2. 实验设置
表 1 VNTM模型参数表
Tab.1
| 参数 | 数值 |
| Batch Size | 1 |
| 卷积核大小 | 3×3 |
| 初始学习率 | 1×10−3 |
| 最小学习率 | 1×10−6 |
| Epoch | 100 |
| 级联数量T | 8 |
| 优化器 | Adam |
| 损失函数 | L1 Loss |
| 早停策略阈值 | 30 |
为了评估提出的VNTM网络的性能,在实验过程中选择了不同加速因子的采样掩码进行欠采样实验. 具体来说,采用了5种欠采样掩码,分别为一维等间隔欠采样(1DUU)、一维笛卡尔随机欠采样(1DRU)、二维随机欠采样(2DRU)、伪径向欠采样(RADU)和泊松盘欠采样(2DPU). 对于一维采样掩码,采用了2个加速因子(acceleration factor, AF),分别为3和5,而对于二维采样掩码,则选择了5和10作为加速因子,不同采样掩码的ACS大小如表2所示. 为了定量评估重建图像的质量,选择峰值信噪比(peak signal-to-noise ratio, PSNR)[29]和结构相似性指数(structural similarity, SSIM)[30]作为评价指标来定量评估重建图像,其中PSNR和SSIM的数值越高代表重建质量越好.
表 2 不同欠采样掩码的ACS大小
Tab.2
| 采样掩码 | ACS | 采样掩码 | ACS | |
| 3× 1DRU | 320×20 | 10× 2DRU | 3×6 | |
| 5× 1DRU | 320×20 | 5× RADU | 29×29 | |
| 3× 1DUU | 320×21 | 10× RADU | 19×13 | |
| 5× 1DUU | 320×22 | 5× 2DPU | 20×20 | |
| 5× 2DRU | 8×12 | 10× 2DPU | 20×20 |
2.3. 实验结果
为了验证所提出VNTM的优势,将其与当前在基于校准的欠采样MRI重建领域内的先进方法进行对比,这些方法包括E2E-VN[16]、RecurrentVN[17]、Deep-SLR[31]、Deepcomplex[32]、DONet[33]和SwinMR[20]. 其中,E2E-VN和RecurrentVN是用于多线圈MRI重建的代表性深度展开网络,都采用深度学习的方法进行灵敏度图估计. SwinMR基于Swin Transformer进行重建,损失函数部分使用ESPIRiT估计的全采样数据的灵敏度图. 而其余3种方法并未使用灵敏度图进行多个线圈图像的重建. 为了确保对比的公正性与科学性,本研究严格按照这些作者论文中设置的参数进行训练.
如表3~5所示,详尽对比了几种方法在不同数据集、采样掩码以及加速因子条件下的重建性能,并通过PSNR和SSIM指标进行定量分析,最好的结果用加粗标记. 从表3中可以观察到,在3倍加速的一维笛卡尔采样掩码应用场景下,RecurrentVN的SSIM与本研究提出VNTM的相当,但VNTM在PSNR上优于RecurrentVN. 进一步观察发现,在其他采样掩码上,VNTM不仅在PSNR上,同时在SSIM上也超越了RecurrentVN. 与其他5种方法相比,VNTM的重建质量在PSNR和SSIM上均达到了更优水平. 从表4可以观察到,在所有采样掩码的应用场景下,VNTM都具有较好的重建性能. 从表5可以观察到,虽然RecurrentVN在一维采样掩码应用场景下的SSIM与VNTM基本相同,但VNTM在PSNR上表现依旧更好,这与表1中的观察结果是一致的. 总体而言,VNTM在不同采样掩码与加速因子下都具有稳定且优异的定量结果.
表 3 不同方法在膝盖数据(冠状面质子密度加权序列)上重建结果的评价指标
Tab.3
| 评价指标 | 方法 | 3× 1DRU | 5× 1DRU | 3× 1DUU | 5× 1DUU | 5× 2DRU | 10× 2DRU | 5× RADU | 10× RADU | 5× 2DPU | 10× 2DPU |
| PSNR/dB | E2E-VN | 36.39 | 34.75 | 34.33 | 32.26 | 36.27 | 33.13 | 35.86 | 31.82 | 34.64 | 32.11 |
| RecurrentVN | 37.61 | 35.46 | 35.17 | 32.71 | 36.44 | 33.00 | 36.08 | 33.95 | 35.75 | 34.00 | |
| Deep-SLR | 33.75 | 32.22 | 31.05 | 28.74 | 36.68 | 34.23 | 36.64 | 33.20 | 35.96 | 34.29 | |
| Deepcomplex | 36.55 | 33.95 | 33.43 | 30.13 | 38.73 | 36.19 | 38.29 | 34.79 | 38.82 | 36.64 | |
| DONet | 36.85 | 34.58 | 34.08 | 31.31 | 39.02 | 36.37 | 38.52 | 35.08 | 39.34 | 36.88 | |
| SwinMR | 33.95 | 33.10 | 32.89 | 31.99 | 35.86 | 32.85 | 36.67 | 32.83 | 35.13 | 33.65 | |
| VNTM | 37.79 | 35.80 | 36.36 | 33.57 | 39.22 | 36.76 | 38.91 | 35.52 | 39.76 | 37.37 | |
| SSIM | E2E-VN | 0.938 | 0.916 | 0.921 | 0.886 | 0.940 | 0.904 | 0.934 | 0.880 | 0.933 | 0.898 |
| RecurrentVN | 0.949 | 0.920 | 0.926 | 0.885 | 0.937 | 0.899 | 0.931 | 0.896 | 0.940 | 0.907 | |
| Deep-SLR | 0.902 | 0.868 | 0.874 | 0.811 | 0.938 | 0.905 | 0.937 | 0.882 | 0.935 | 0.902 | |
| Deepcomplex | 0.938 | 0.898 | 0.899 | 0.839 | 0.953 | 0.923 | 0.949 | 0.902 | 0.956 | 0.929 | |
| DONet | 0.941 | 0.908 | 0.910 | 0.861 | 0.955 | 0.925 | 0.950 | 0.906 | 0.959 | 0.932 | |
| SwinMR | 0908 | 0.886 | 0.893 | 0.868 | 0.923 | 0.884 | 0.927 | 0.866 | 0.919 | 0.887 | |
| VNTM | 0.949 | 0.921 | 0.935 | 0.893 | 0.956 | 0.930 | 0.952 | 0.911 | 0.962 | 0.937 |
表 5 不同方法在T2大脑数据上重建结果的评价指标
Tab.5
| 评价指标 | 方法 | 3× 1DRU | 5× 1DRU | 3× 1DUU | 5× 1DUU | 5× 2DRU | 10× 2DRU | 5× RADU | 10× RADU | 5× 2DPU | 10× 2DPU |
| PSNR/dB | E2E-VN | 40.09 | 37.36 | 39.11 | 36.12 | 37.54 | 35.20 | 37.87 | 35.88 | 36.83 | 36.77 |
| RecurrentVN | 40.32 | 38.06 | 39.46 | 36.32 | 39.11 | 36.92 | 37.62 | 36.07 | 37.15 | 34.73 | |
| Deep-SLR | 36.47 | 35.26 | 34.55 | 32.79 | 37.72 | 35.25 | 37.29 | 34.45 | 37.63 | 36.04 | |
| Deepcomplex | 38.58 | 36.02 | 37.22 | 32.92 | 38.27 | 36.19 | 38.25 | 35.14 | 38.56 | 36.90 | |
| DONet | 38.81 | 36.35 | 37.47 | 33.97 | 38.44 | 36.26 | 38.47 | 35.33 | 38.61 | 36.93 | |
| SwinMR | 36.31 | 35.16 | 35.91 | 34.04 | 36.91 | 34.63 | 37.99 | 34.31 | 36.35 | 31.41 | |
| VNTM | 40.44 | 38.22 | 39.67 | 36.71 | 39.99 | 38.03 | 39.96 | 37.03 | 40.04 | 38.56 | |
| SSIM | E2E-VN | 0.972 | 0.959 | 0.968 | 0.951 | 0.964 | 0.952 | 0.966 | 0.952 | 0.962 | 0.956 |
| RecurrentVN | 0.973 | 0.962 | 0.969 | 0.951 | 0.968 | 0.958 | 0.964 | 0.952 | 0.962 | 0.947 | |
| Deep-SLR | 0.959 | 0.946 | 0.943 | 0.921 | 0.963 | 0.947 | 0.960 | 0.938 | 0.962 | 0.949 | |
| Deepcomplex | 0.966 | 0.950 | 0.957 | 0.920 | 0.964 | 0.951 | 0.963 | 0.942 | 0.964 | 0.952 | |
| DONet | 0.967 | 0.951 | 0.959 | 0.930 | 0.965 | 0.952 | 0.964 | 0.944 | 0.964 | 0.953 | |
| SwinMR | 0.950 | 0.940 | 0.948 | 0.930 | 0.952 | 0.934 | 0.959 | 0.932 | 0.947 | 0.913 | |
| VNTM | 0.973 | 0.962 | 0.969 | 0.952 | 0.971 | 0.962 | 0.970 | 0.955 | 0.971 | 0.963 |
表 4 不同方法在膝盖数据(矢状面质子密度加权序列)上重建结果的评价指标
Tab.4
| 评价指标 | 方法 | 3× 1DRU | 5× 1DRU | 3× 1DUU | 5× 1DUU | 5× 2DRU | 10× 2DRU | 5× RADU | 10× RADU | 5× 2DPU | 10× 2DPU |
| PSNR/dB | E2E-VN | 36.64 | 34.25 | 36.27 | 32.52 | 37.95 | 35.18 | 36.68 | 33.12 | 36.17 | 33.49 |
| RecurrentVN | 38.83 | 34.31 | 36.75 | 32.83 | 38.44 | 35.52 | 37.47 | 33.79 | 37.31 | 36.40 | |
| Deep-SLR | 36.27 | 33.91 | 34.69 | 30.41 | 38.68 | 36.06 | 37.92 | 34.34 | 38.40 | 35.98 | |
| Deepcomplex | 37.67 | 35.02 | 35.86 | 31.06 | 39.93 | 37.29 | 38.97 | 35.24 | 39.87 | 37.78 | |
| DONet | 38.22 | 35.75 | 36.50 | 32.07 | 39.95 | 37.58 | 39.17 | 35.63 | 40.32 | 38.00 | |
| SwinMR | 33.99 | 32.62 | 33.46 | 30.81 | 36.34 | 33.26 | 36.93 | 32.90 | 35.33 | 33.79 | |
| VNTM | 39.83 | 37.08 | 38.53 | 33.33 | 40.76 | 38.18 | 39.90 | 36.18 | 41.08 | 38.85 | |
| SSIM | E2E-VN | 0.940 | 0.911 | 0.937 | 0.875 | 0.949 | 0.921 | 0.942 | 0.891 | 0.944 | 0.913 |
| RecurrentVN | 0.954 | 0.902 | 0.938 | 0.875 | 0.949 | 0.920 | 0.939 | 0.886 | 0.944 | 0.926 | |
| Deep-SLR | 0.930 | 0.891 | 0.911 | 0.819 | 0.949 | 0.919 | 0.942 | 0.887 | 0.948 | 0.916 | |
| Deepcomplex | 0.944 | 0.908 | 0.925 | 0.837 | 0.959 | 0.933 | 0.951 | 0.902 | 0.959 | 0.937 | |
| DONet | 0.947 | 0.916 | 0.931 | 0.856 | 0.959 | 0.936 | 0.952 | 0.908 | 0.962 | 0.939 | |
| SwinMR | 0.899 | 0.869 | 0.894 | 0.830 | 0.925 | 0.888 | 0.925 | 0.860 | 0.915 | 0.882 | |
| VNTM | 0.959 | 0.931 | 0.949 | 0.881 | 0.964 | 0.942 | 0.957 | 0.916 | 0.966 | 0.946 |
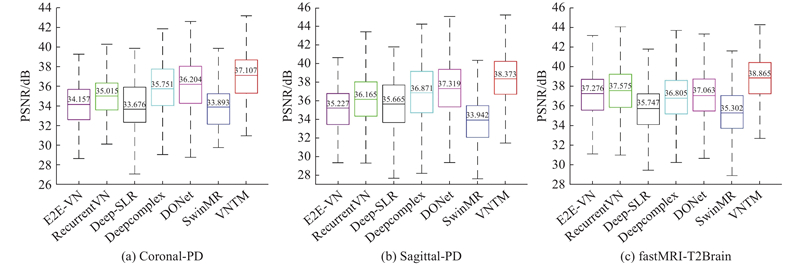
如图2所示展示了不同算法在3个数据集(Coronal-PD、Sagittal-PD 和 fastMRI-T2Brain)上的 PSNR 整体表现,反映了各算法在图像重建任务中性能的差异. 具体来看,VNTM 算法在3个数据集上的 PSNR 平均值均为最高,比次优方法分别提高了0.903、1.054、1.290 dB. DONet 在 Coronal-PD 和 Sagittal-PD 数据集上的表现虽不及 VNTM,但优于其他方法;而在 fastMRI-T2Brain 数据集中,Recurrent-VN 的表现相对较好. 相比之下,Deep-SLR 和 SwimMR 在所有数据集上的 PSNR 平均值较低,表现不佳. 总之,VNTM 在3个数据集中的定量结果最佳.
图 2
图 2 不同算法在多个数据集上PSNR 的整体表现比较
Fig.2 Overall comparison of PSNR performance of different algorithms across multiple datasets
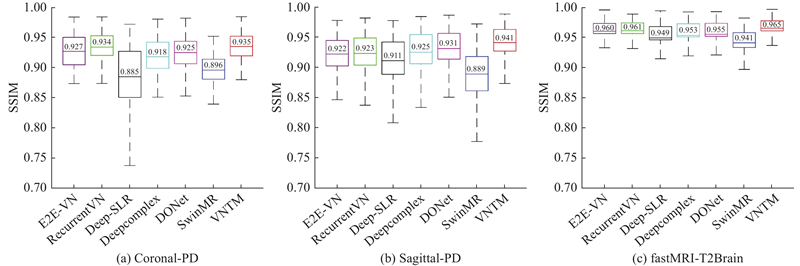
如图3所示展示了不同算法在3个数据集(Coronal-PD、Sagittal-PD 和 fastMRI-T2Brain)上的 SSIM 整体表现,反映了各算法在图像重建任务中的性能差异. 具体来看,VNTM 算法在3个数据集上的 SSIM 平均值均为最高;在 Coronal-PD 和 fastMRI-T2Brain 数据集中,Recurrent-VN 的 SSIM 表现次优,仅次于 VNTM,而在 Sagittal-PD 数据集中,DONet 表现相对较好. 相比之下,Deep-SLR 和 SwimMR 在所有数据集上的 SSIM 平均值较低,整体表现不佳. 值得注意的是,在 fastMRI-T2Brain 数据集上,各算法的 SSIM 普遍较高,且不同算法间的差距较小. 总体而言,VNTM 算法在3个数据集上的定量结果最佳.
图 3
图 3 不同算法在多个数据集上SSIM 的整体表现比较
Fig.3 Overall comparison of SSIM performance of different algorithms across multiple datasets
图 4
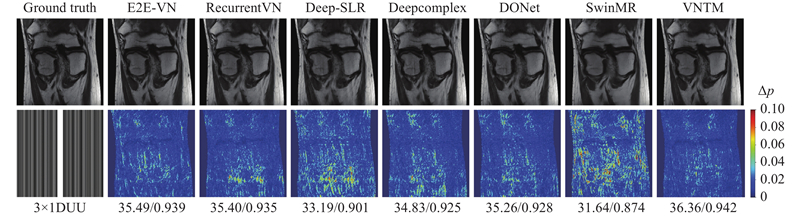
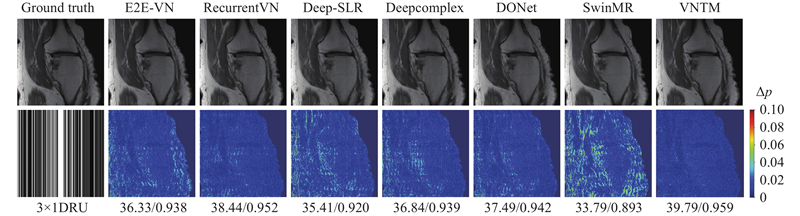
图 4 3倍加速的1DUU采样掩码下7种网络在膝关节数据(Coronal-PD)上的视觉重建效果比较
Fig.4 Visual comparison of seven networks on knee data (Coronal-PD) under 3× acceleration with a 1DUU mask
图 5
图 5 3倍加速的1DRU采样掩码下7种网络在膝关节数据(Sagittal-PD)上的视觉重建效果比较
Fig.5 Visual comparison of seven networks on knee data (Sagittal-PD) under 3× acceleration with a 1DRU mask
图 6
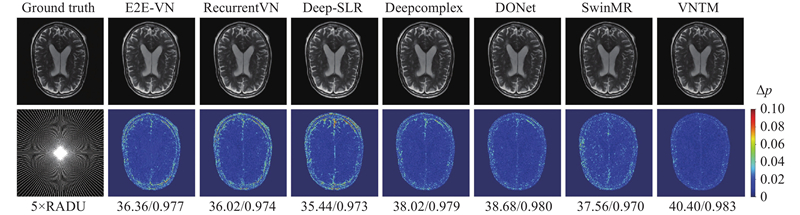
图 6 5倍加速的RADU采样掩码下7种网络在大脑数据上的视觉重建效果比较
Fig.6 Visual comparison of seven networks on fastMRI-T2Brain under 5× acceleration with a RADU sampling mask
观察图4可以发现,几乎所有的误差都集中在重建图像的中部偏下区域. 其中,Deep-SLR和SwinMR中出现了较多的块状伪影,表现相对较差. 而相比之下,本研究提出的VNTM方法表现最好. 然而,E2E-VN的误差图上仍然存在较多的误差区域,而VNTM的误差区域更少,保留了更为丰富的细节信息.
观察图5可以发现,E2E-VN、Deep-SLR、 Deepcomplex和SwinMR在误差图像的中部和左侧边缘出现了较多的伪影区域,SwinMR的误差区域最多且比较严重,相比之下,RecurrentVN、DONet和本研究提出的VNTM在边缘部分的重建细节处理的相对较好. 尤其是VNTM,相较于RecurrentVN误差区域更少.
观察图6可以发现,Deep-SLR的误差图出现了比较多的误差区域. 相比之下,E2E-VN、RecurrentVN、Deepcomplex、DONet、SwinMR和VNTM显示出的混叠伪影主要集中在重建图像的边缘区域,而VNTM的整体表现更好.
2.4. 消融实验
为了评估所提出方法的有效性,本研究设计了一系列的消融实验. 这些消融实验以E2E-VN作为基准模型(Baseline),并在Coronal-PD上使用5倍加速的二维随机的采样掩码. 在消融实验中,设计了5个算法来评估所提出方法的有效性,即:VNTM-A、VNTM-B、VNTM-C、VNTM-D和VNTM-E. 具体而言,VNTM-A与VNTM-B在基准模型中分别应用UMRNet和UMRB;VNTM-C和VNTM-D与VNTM相比,分别去除了
表 6 VNTM消融实验结果
Tab.6
| 方法 | DCρ | 中期增强 | UMRB | PSNR/dB | SSIM | |
| 前后处理 | UMRNet | |||||
| Baseline | — | — | — | — | 36.27 | 0.940 |
| VNTM-A | — | — | — | √ | 36.88 | 0.942 |
| VNTM-B | — | — | √ | √ | 37.61 | 0.946 |
| VNTM-C | — | √ | √ | √ | 39.17 | 0.955 |
| VNTM-D | √ | — | √ | √ | 37.90 | 0.947 |
| VNTM-E | √ | √ | — | √ | 38.91 | 0.953 |
| VNTM (本研究) | √ | √ | √ | √ | 39.22 | 0.956 |
从消融实验结果可以看出,所提出的改进策略均提升了模型性能. 其中,灵敏度图的中期增强提升效果最强,而
为了探究灵敏度图中期增强与非中期增强对模型重建性能的影响,针对不同的迭代点(T/4、T/2、3T/4)进行了灵敏度图增强实验,其中T/2迭代为中期增强,T/4和3T/4迭代为非中期增强. 通过对实验结果的分析(见表7)可以发现, 在T/2迭代增强时,模型性能达到了最优. 因此,本研究后续将主要聚焦于T/2迭代的深入分析,以进一步优化模型性能,而对T/4和3T/4迭代不再展开深入讨论.
表 7 灵敏度图中期增强与非中期增强实验结果
Tab.7
| 方法 | PSNR/dB | SSIM |
| VNTM-T/4 | 39.15 | 0.955 |
| VNTM-T/2 | 39.22 | 0.956 |
| VNTM-3T/4 | 39.14 | 0.955 |
为了评估处理模块对模型计算性能的影响,对其在使用前后的计算量FLOPs、参数量Para和推理时间tI进行对比. 处理模块在减少计算复杂度的同时,保持了参数量的相对稳定性,并提升了推理效率. 具体数据如表8所示,其中,VNTM-E表示没有使用处理模块,VNTM-F表示使用了处理模块. 通过处理模块,FLOPs减少了约61%,模型的计算复杂度降低;推理时间减少了约65%,推理速度提高,说明模块优化效果明显;参数量在使用处理模块后仅略微增加,表明模块的引入对模型的存储需求影响较小. 综上所述,验证了所提出处理模块的有效性.
表 8 前后处理模块使用前后计算效率比较结果
Tab.8
| 方法 | FLOPs /1012 | Para/108 | tI/s |
| VNTM-E | 1.28 | 1.27 | 0.417 |
| VNTM-F | 0.50 | 1.28 | 0.144 |
为了确定模型级联数量T对模型性能的影响,对T进行消融实验,实验中评估了不同级联数量(2, 4, 6, 8, 10, 12)对 PSNR 和 SSIM 的影响,结果如表9所示. 实验结果表明,当级联数量从2增加至8时,PSNR和SSIM均稳步提升,在 T=8时性能达到最佳. 然而,进一步增加T至10 和12时,性能提升趋于平缓,且计算量会相对增加. 因此,本研究选择T=8作为最终模型,以在性能和计算资源之间取得平衡.
表 9 级联数量对模型性能的消融实验结果
Tab.9
| 方法 | T | PSNR/dB | SSIM |
| VNTM | 2 | 38.69 | 0.953 |
| VNTM | 4 | 39.03 | 0.955 |
| VNTM | 6 | 39.16 | 0.955 |
| VNTM | 8 | 39.22 | 0.956 |
| VNTM | 10 | 39.14 | 0.955 |
| VNTM | 12 | 39.25 | 0.956 |
2.5. ACS区域大小的鲁棒性研究
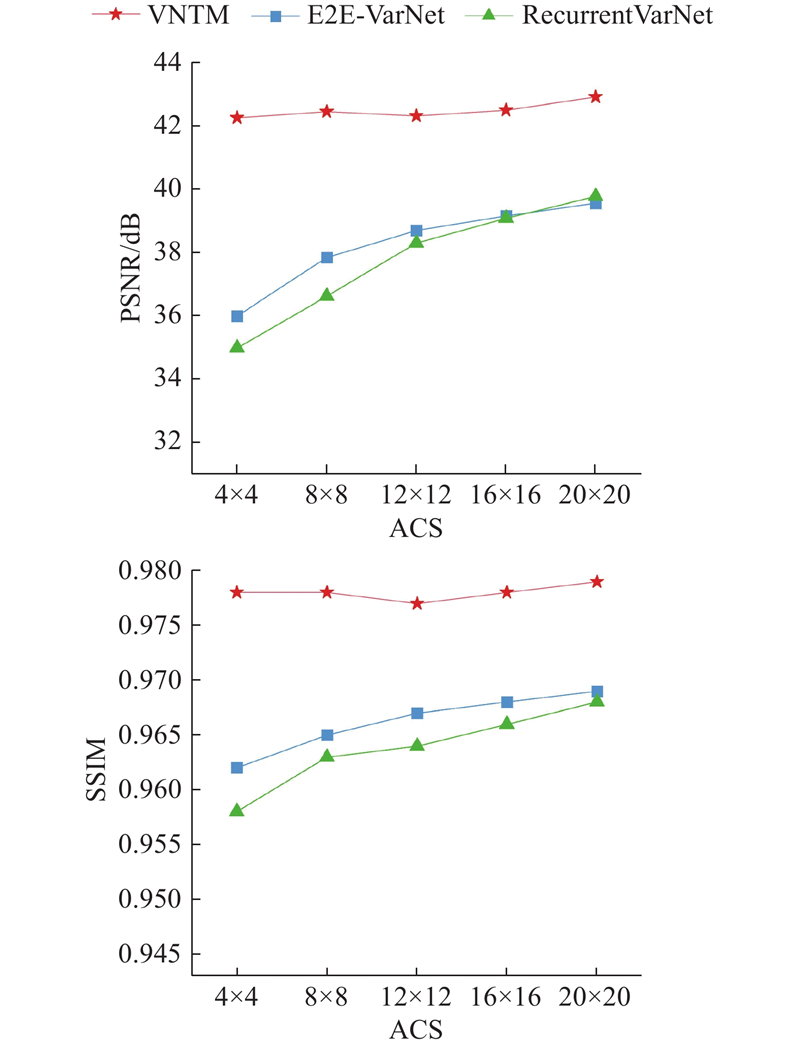
对于重建过程中需要利用ACS区域估计灵敏度图的方法,ACS区域大小尤为重要. 由于E2E-VN在估计灵敏度图时仅使用ACS区域,因此ACS区域过小,可能会产生严重的混叠伪影. 为了解决这一问题,使用欠采样多线圈k空间数据估计灵敏度图,并利用T/2次迭代时的输出数据重新估计灵敏度图,这种策略不仅加强了与重建数据之间的关联程度,而且还更新了灵敏度,进一步增加灵敏度图的准确性,并减少了对于ACS区域的依赖. 为了验证本研究的方法对于不同的ACS区域大小的鲁棒性,在Sagittal-PD上进行实验,使用3倍加速二维泊松采样掩码(3× 2DPU)进行欠采样,ACS区域大小分别设置为4×4,8×8,12×12,16×16和20×20,并将VNTM方法与E2E-VN和RecurrentVN这2种方法进行比较. 上述的消融实验结果如图7所示. 可以看出,在ACS区域从20×20降低到4×4时,本研究提出的方法在PSNR和SSIM这2种评估指标上仍然保持一个相对稳定范围,而E2E-VN和RecurrentVN则出现了较大的波动. 具体来说,当ACS从20×20降低到4×4时,VNTM的PSNR仅下降了0.31 dB,显示出良好的稳定性. 相比之下,E2E-VN和RecurrentVN的PSNR分别下降了3.57、4.79 dB. 进一步地,当ACS从20降低到4时,VNTM的SSIM下降了0.003,而E2E-VN和RecurrentVN分别下降了0.007和0.01.
图 7
图 7 不同方法对于不同ACS大小的鲁棒性实验结果
Fig.7 Robustness experimental results of different methods for various ACS sizes
图 8
图 9
3. 结 语
提出基于变分模型和Transformer的多尺度并行磁共振成像重建模型(VNTM). 该模型充分考虑了ACS区域大小对灵敏度图估计的影响,提出了灵敏度图中期增强策略,有效降低了对ACS区域大小的依赖. 为了进一步提高重建图像的质量,利用残差Swin Transformer的出色性能设计了UMRB模块. 针对Transformer模型固有的计算复杂度挑战,设计了前处理和后处理模块,以在保留空间信息和减少计算资源之间取得平衡. 通过在大脑和膝盖数据集上的实验可以看出,所提出的VNTM与最先进的重建方法相比,在定量和定性上都表现出优异的重建性能. 在之后的工作中,会继续尝试设计不同的网络架构,以获得更高的重建性能和更广泛的应用前景.
参考文献
Encoding and reconstruction in parallel MRI
[J].DOI:10.1002/nbm.1042 [本文引用: 1]
Parallel magnetic resonance imaging
[J].DOI:10.1088/0031-9155/52/7/R01
SPIRiT: iterative self-consistent parallel imaging reconstruction from arbitrary k-space
[J].DOI:10.1002/mrm.22428 [本文引用: 2]
Compressed sensing
[J].DOI:10.1109/TIT.2006.871582 [本文引用: 1]
Sparse MRI: the application of compressed sensing for rapid MR imaging
[J].DOI:10.1002/mrm.21391 [本文引用: 1]
SENSE: sensitivity encoding for fast MRI
[J].DOI:10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S [本文引用: 1]
ESPIRiT: an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA
[J].DOI:10.1002/mrm.24751 [本文引用: 1]
Compressed sensing MRI
[J].DOI:10.1109/MSP.2007.914728 [本文引用: 1]
Nonlinear total variation based noise removal algorithms
[J].
Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising
[J].DOI:10.1109/TIP.2017.2662206 [本文引用: 1]
Deep learning based MRI reconstruction with transformer
[J].DOI:10.1016/j.cmpb.2023.107452 [本文引用: 1]
Learning a variational network for reconstruction of accelerated MRI data
[J].DOI:10.1002/mrm.26977 [本文引用: 4]
ReconFormer: accelerated MRI reconstruction using recurrent transformer
[J].DOI:10.1109/TMI.2023.3314747 [本文引用: 1]
Swin transformer for fast MRI
[J].
DCT-net: dual-domain cross-fusion transformer network for MRI reconstruction
[J].DOI:10.1016/j.mri.2024.01.007 [本文引用: 1]
The NMR phased array
[J].DOI:10.1002/mrm.1910160203 [本文引用: 1]
Image reconstruction of compressed sensing MRI using graph-based redundant wavelet transform
[J].DOI:10.1016/j.media.2015.05.012 [本文引用: 1]
fastMRI: a publicly available raw k-space and DICOM dataset of knee images for accelerated MR image reconstruction using machine learning
[J].DOI:10.1148/ryai.2020190007 [本文引用: 1]
Image quality assessment: from error visibility to structural similarity
[J].DOI:10.1109/TIP.2003.819861 [本文引用: 1]
Deep generalization of structured low-rank algorithms (deep-SLR)
[J].DOI:10.1109/TMI.2020.3014581 [本文引用: 1]
Deep complexMRI: exploiting deep residual network for fast parallel MR imaging with complex convolution
[J].DOI:10.1016/j.mri.2020.02.002 [本文引用: 1]
DONet: dual-octave network for fast MR image reconstruction
[J].DOI:10.1109/TNNLS.2021.3090303 [本文引用: 1]