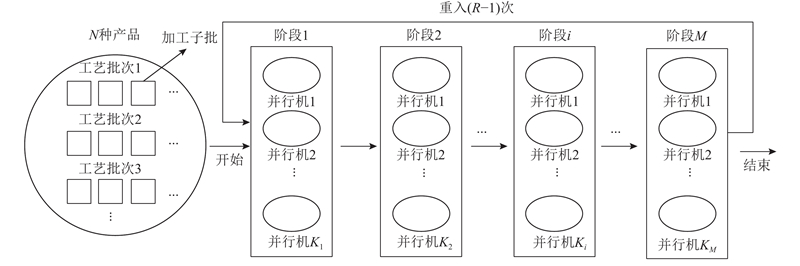
在薄膜晶体管液晶显示器(thin-film transistor-liquid crystal display, TFT-LCD)的制造流程中,阵列工艺可以被构建为可重入混合流水车间批量流调度问题(re-entrant hybrid flowshop scheduling problem with lot streaming, RHFSP-LS). 在此工艺中,玻璃基板须遵循既定流程,逐一完成所有子步骤的加工. 由于阵列工艺需要在玻璃基板上铭刻多层电路,玻璃基板须反复重入部分子步骤,致使整个问题呈现出可重入的特性. 目前,阵列车间的生产依赖手工排产,难以应对复杂多变的生产需求,因此亟需高效而精准的调度方法来完成排产工作.
RHFSP通常与特殊约束相结合进行研究. Chamnanlor等[1]提出结合蚁群优化的自适应遗传算法,求解以最小化最大完工时间为目标的带时间窗约束的RHFSP. Tong等[2]研究动态RHFSP,设计可变邻域搜索的多目标进化算法来求解问题,提出2种重调度策略来处理动态事件. Lei等[3]提出精英教与学算法,以求解带瓶颈阶段的RHFSP. 耿凯峰等[4]提出混合文化基因算法,用于求解考虑调整时间和运输时间的RHFSP,以最小化最大完工时间和总能耗. 将RHFSP与批量流(lot streaming, LS)此类特殊约束相结合进行研究的较少,仅秦红斌等[5-6]将批处理机与RHFSP结合进行研究. 在TFT-LCD的实际生产过程中,由于玻璃基板扁平的结构特性,通常采用载具装载一定数量的玻璃基板成批次的运输和加工,表现出批量流的生产特性. 本文着眼于可重入混合流水车间批量流调度的问题.
1. 问题描述与数学建模
1.1. 问题描述
研究的RHFSP-LS可以描述如下:
图 1
除了流水车间的经典假设,研究的RHFSP-LS还包括如下假设.
1) 相同工艺批次的所有加工子批在某一阶段只能选择同一台机器连续加工,即不同的工艺批次不可混插.
2) 加工子批须经过全部阶段加工后才可重入第一阶段,开始下一层次的加工.
3) 加工子批在相邻两阶段的运输时间和准备时间已包含在加工时间内.
4) 相邻两阶段的缓冲区无限.
5) 不同工艺批次的加工工艺步骤环节一致,但加工的工时参数有差异.
1.2. 数学模型
1)目标函数:最小化最大完工时间
式中:
最小化总拖期时间TFDT,如下所示:
工艺批次
式中:
2)约束函数如下:
式中:
式中:
式(6)定义了各批次的子批在某一阶段加工完成后才能进行下一阶段的加工.
式(7)定义了各批次在某一阶段进行加工时,后一子批须等前一子批加工完成后才能进行加工.
式(8)定义了各批次的子批在不同的层次进行加工时,只有在上一层次的最后一个阶段加工完成后才可以开始下一层次的首个阶段的加工.
式中:
式中:
式(13)、(14)定义了决策变量的取值范围.
2. 算法设计
2.1. MBO多目标化
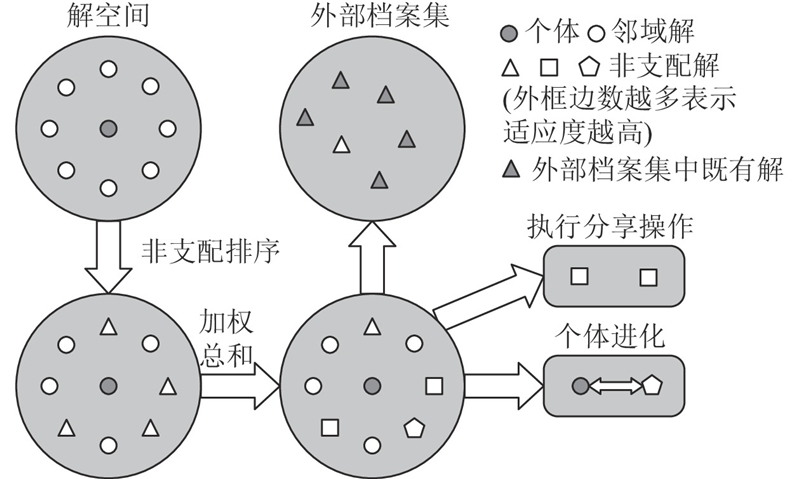
与单目标优化不同,多目标优化通常不存在单一的最优解,因为多个目标之间可能存在权衡,即在一个目标上的改善可能导致另一个目标性能的下降. 候鸟优化算法通常用于求解单目标优化问题,个体通过与邻域解集相比较,选取较优解完成进化操作. 当处理多目标问题时,如何选取邻域解集中的较优解成为MBO多目标化时需要解决的问题. 采用非支配排序、加权总和与外部档案集等操作,将MBO多目标化. 如图2所示为MBO多目标化过程的示意图.
图 2
在MBO多目标化的过程中,非支配排序被用来对搜索到的邻域解集进行层次化排序,进而精确地识别出非支配解集. 当非支配解集包含多个解时,采用加权总和方法进一步筛选出最优解. 该方法通过为目标函数分配不同的权重,计算加权和,实现排序和优选. 在本文中2个目标同等重要,因此采用相等的权重系数.
此外,为了管理和利用邻域搜索过程中产生的非支配解,引入外部档案集机制. 在个体完成进化和分享操作后,若邻域解集中存在非支配解,则将非支配解添加到外部档案集中. 此操作不仅避免了优秀个体的流失,而且通过保持多样化的非支配解集合,增强了算法的搜索能力.
2.2. 改进多目标候鸟优化算法
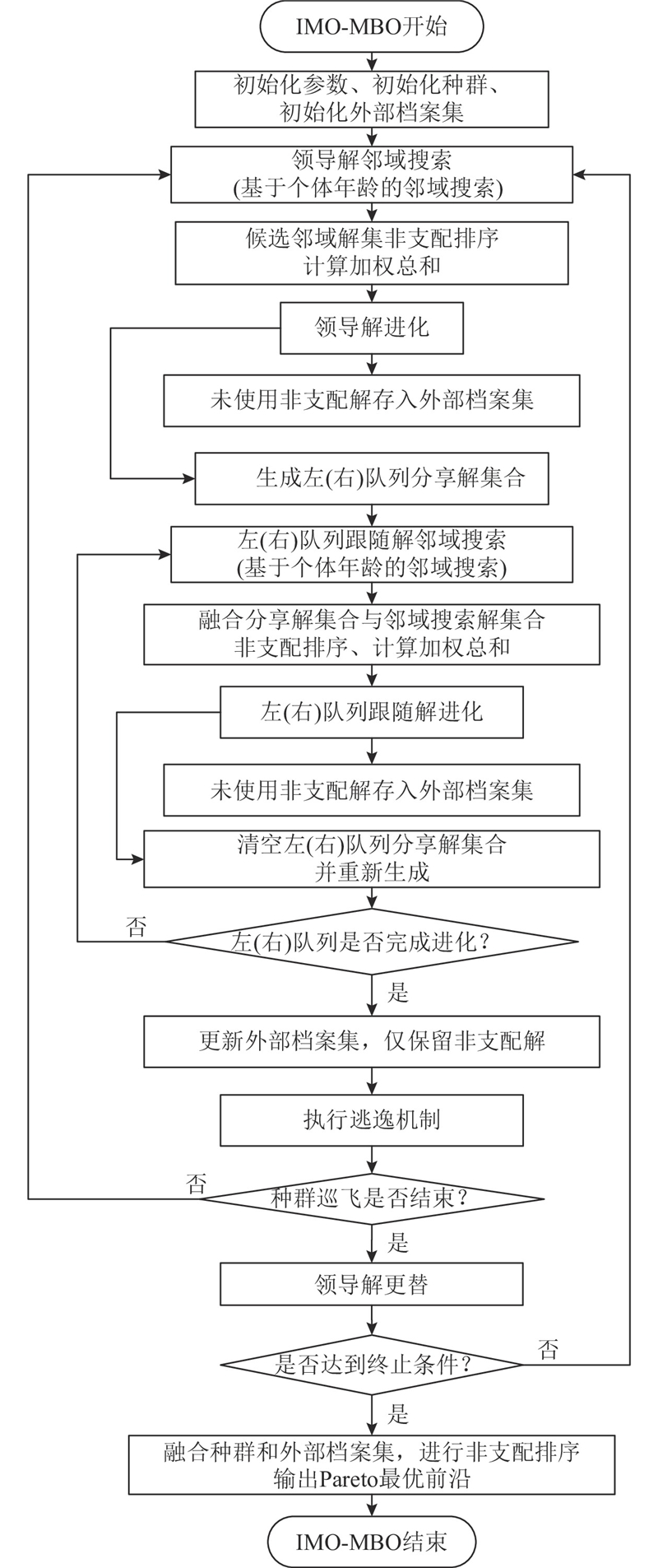
提出改进多目标候鸟优化算法(improved multi-objective migrating birds optimization, IMO-MBO),解决上述双目标可重入混合流水车间的批量流调度问题. IMO-MBO的流程如图3所示,改进之处主要包括解码机制、种群初始化、基于个体年龄的邻域搜索、逃逸机制等.
图 3
2.2.1. 编码机制和解码机制
在可重入混合流水车间调度问题中,由于工艺批次多次重入生产系统进行加工,导致利用传统的编码方法难以准确地描述该问题的复杂性,采用基于机器分配的元胞矩阵的编码方式[9]. 假设待求问题的工艺批次总数为
在编码机制中,已经确定各工艺批次在整个加工过程中的机器分配方案和首阶段的加工顺序,但在后续阶段各机器上的加工顺序未确定,因此在解码时需要解决该问题. 考虑到不同工艺批次的加工子批不可混插的情形,在已有的研究中大多采用“子批优先”或“批次优先”的解码策略. "子批优先"是基于工艺批次在前一阶段首个加工子批的完工时间来确定其在后续阶段的加工先后顺序,即首个加工子批越早完成,其在下一阶段的优先级越高. 相对地,“批次优先”依赖于工艺批次中最后一个加工子批的完工时间,优先处理在前一阶段较早完工的工艺批次.
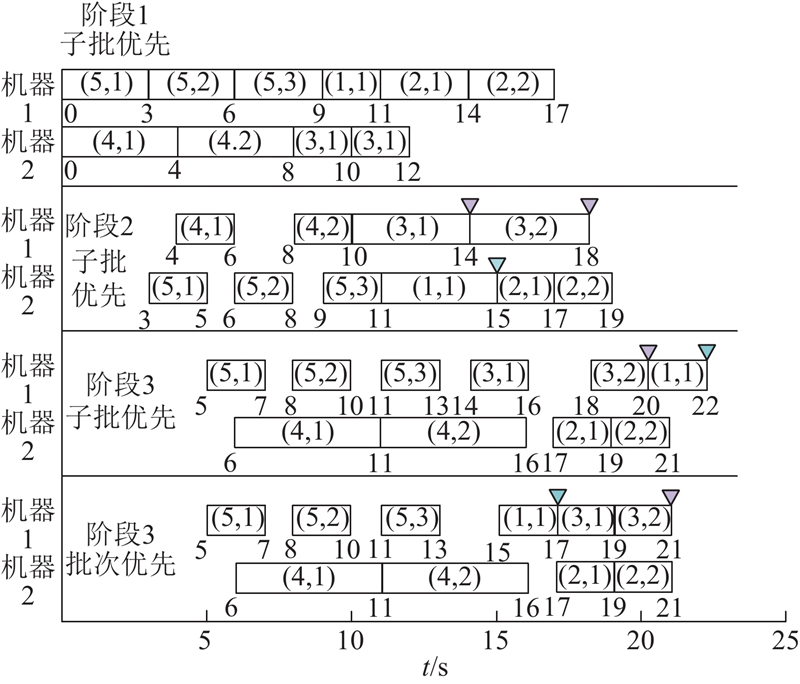
当采用“子批优先”的解码策略时,若在所有阶段都严格遵守此策略,则有可能错失较优解. 如图4所示,工艺批次1和3均被安排在阶段3的机器1上进行加工. 当在阶段3采用“子批优先”策略时,工艺批次1较早地完成了阶段2的加工,但由于工艺批次3的加工子批1在阶段2优先完工,工艺批次1须等待工艺批次3的所有子批全部完成加工后才能进行加工. 若在阶段3采用“批次优先”策略,则工艺批次1可以提前进行加工,不仅使总完工时间提前了1个单位,工艺批次1的完工时间也提前了5个单位,而代价仅仅是工艺批次3的完工时间延后了1个单位.
图 4
提出“子批优先”+“批次优先”的解码策略,在除最后一个加工层的末阶段的其余阶段采用“子批优先”策略,在最后一个加工层的末阶段分别采用“子批优先”和 “批次优先”策略进行求解,取适应度较好的方案作为最终的调度结果. 由于本文解决的是多目标优化问题,在全局各个阶段分别采用2种策略解码后,选择较优者进行下一阶段的解码,不仅缺乏比较的依据,而且得到的解可能并非最优解. 若针对各个阶段列举出所有情况再进行求解能得到最优解,但计算难度会大幅增加. 采用提出的组合策略,既不会影响整体的加工安排,也可以通过非支配排序或加权总和方法得到较优解.
2.2.2. 种群初始化
MBO算法作为基于邻域搜索的群体智能算法,主要依靠种群中的个体在搜索空间中的移动和领导解与跟随解之间的信息交互来获取最优解. 分布均匀且分散的初始种群有助于算法在解空间中进行更广泛的搜索,降低算法早熟收敛到局部最优解的风险. Logistic混沌映射是典型的混沌映射系统,具有随机性和遍历性的特点. 采用Logistic混沌映射,使初始种群在解空间中分布均匀且分散. 具体的操作方法如下.
1)构建
式中:
2)通过Logistic混沌序列映射到解空间,生成初始种群
式中:
为了避免生成质量较低的初始种群,降低算法的收敛速度,参考文献[10],采取NEH算法生成初始种群的部分个体. 利用基础NEH算法,可以解决以最小化最大完工时间为优化目标的调度问题,由于本文为多目标优化问题,优化目标为最小化最大完工时间和最小化总拖期. 对NEH算法进行改进,以工件的交货期从小到大的顺序生成序列表,作为工艺批次排序的依据,将该算法记为NEHEDD(earliest due date)算法,将基础NEH算法记为NEHLPT(long processing tim)算法. 基于上述算法生成初始种群的2个个体并与基于Logistic混沌映射生成的初始种群进行融合,将适应度最高的个体置于领导解位置,其余个体随机排列在左右队列.
2.2.3. 基于个体年龄的邻域搜索
在种群巡飞的过程中,个体通过邻域搜索实现自我进化,设计合适的邻域结构,可以使种群朝着期望的方向进行搜索. 采用贪婪插入、贪婪交换、贪婪变异和最优变异4种邻域结构. 贪婪插入和贪婪交换是针对工艺批次排序进行邻域搜索,贪婪变异和最优变异是针对机器分配方案进行邻域搜索. 对于每种操作产生的邻域解集进行适应度计算,从中挑选出适应度最好的解作为该操作生成的最终邻域解.
贪婪插入. 随机选择工艺批次
贪婪交换. 随机选择工艺批次
贪婪(最优)变异. 随机从工艺批次中选择批次
考虑到本文编码方式的特殊性,对于解空间中的一个解,其机器分配方案可生成邻域解的数量远多于工艺批次排序可生成的邻域解的数量. 设计基于个体年龄的邻域搜索机制,公式如下所示:
式中:
个体可以通过动态调整邻域搜索策略,适应问题解空间的特性. 当个体年龄较小时,由于批次排序的邻域解较少,将搜索重点放在精细调节排序上,以快速找到质量较高的解. 随着个体年龄的增大,若排序优化未能显著改善结果,则算法逐渐转向机器分配方案的邻域搜索. 此处邻域解的多样性较高,能够在广阔的搜索空间中探索新的可能性.
2.2.4. 逃逸机制
基于探索机制[11]的启发,提出结合外部档案集的逃逸机制. 由于在邻域搜索的过程中引入个体年龄的概念,设定个体年龄上限为
图 5
该机制不仅在个体陷入局部最优时提供了有效的逃逸策略,而且通过外部档案集的利用,确保算法能够继承并发掘既有解中的优秀特性,保证了解的质量和多样性.
3. 仿真实验
3.1. 数据集的描述和算法性能的评价指标
表 1 生成算例集所需参数的取值范围
Tab.1
| 参数 | 小规模 | 大规模 |
| 工艺批次数量 | [5, 10] | [10, 20] |
| 加工子批数量 | [1, 5] | [1, 10] |
| 重入层数 | [1, 2] | [1, 4] |
| 加工阶段数量 | [4, 6] | [6, 10] |
| 每个阶段并行机数量 | [1, 3] | [1, 6] |
| 加工时间 | [5, 30] | |
| 工艺批次交货期限 | ||
根据表1中参数的取值范围,随机生成5个小规模算例和5个大规模算例进行实验.
选取多目标优化问题中常用的反转世代距离[13](inverted generational distance, IGD)作为评价指标. IGD是综合性指标,能够同时衡量解集的多样性与收敛性. IGD反映的是真实帕累托(Pareto)前沿上的点到非劣解集的平均距离,IGD越小表示解集越逼近或覆盖真实Pareto前沿. 在计算IGD指标时须使用真实Pareto前沿,在本文中真实Pareto前沿是未知的,因此使用的真实Pareto前沿是通过融合所有对比算法的Pareto前沿重新非支配排序得到的.
3.2. 参数设置
参数的设置在元启发式算法的各项特性中起到了重要作用. 为了得到IMO-MBO的最优参数,采用正交实验法,设置IMO-MBO的主要参数. IMO-MBO共有7个参数需要设置,分别是
表 2 正交实验中参数水平的取值
Tab.2
| 参数水平 | 参数 | ||||
| Level1 | 31 | 3 | [0.1, 0.9] | [2,4] | 8 |
| Level2 | 51 | 5 | [0.2, 0.8] | [3,5] | 10 |
| Level3 | 81 | 8 | [0.3, 0.7] | [4,6] | 13 |
| Level4 | 101 | 10 | [0.4, 0.6] | [5,7] | 15 |
表 3 正交实验结果
Tab.3
| 实验 编号 | 参数 | IGD 平均值 | ||||
| 1 | 31 | 3 | [0.1, 0.9] | [2, 4] | 8 | |
| 2 | 31 | 5 | [0.2, 0.8] | [3, 5] | 10 | |
| 3 | 31 | 8 | [0.3, 0.7] | [4, 6] | 13 | |
| 4 | 31 | 10 | [0.4, 0.6] | [5, 7] | 15 | |
| 5 | 51 | 3 | [0.2, 0.8] | [4, 6] | 15 | |
| 6 | 51 | 5 | [0.1, 0.9] | [5, 7] | 13 | |
| 7 | 51 | 8 | [0.4, 0.6] | [2, 4] | 10 | |
| 8 | 51 | 10 | [0.3, 0.7] | [3, 5] | 8 | |
| 9 | 81 | 3 | [0.3, 0.7] | [5, 7] | 10 | |
| 10 | 81 | 5 | [0.4, 0.6] | [4, 6] | 8 | |
| 11 | 81 | 8 | [0.1, 0.9] | [3, 5] | 15 | |
| 12 | 81 | 10 | [0.2, 0.8] | [2, 4] | 13 | |
| 13 | 101 | 3 | [0.4, 0.6] | [3, 5] | 13 | |
| 14 | 101 | 5 | [0.3, 0.7] | [2, 4] | 15 | |
| 15 | 101 | 8 | [0.2, 0.8] | [5, 7] | 8 | |
| 16 | 101 | 10 | [0.1, 0.9] | [4, 6] | 10 | |
表 4 参数水平值的排序
Tab.4
| 水平 | |||||
| Level1 | |||||
| Level2 | |||||
| Level3 | |||||
| Level4 | |||||
| Delta | |||||
| 排秩 | 1 | 4 | 3 | 3 | 1 |
从表4可见,
3.3. 策略有效性的分析
为了验证所提改进策略的有效性,通过消融实验设计8种变体算法,与原算法进行对比. 各算法所采用的策略如表5所示. 表中,数字1、2和3分别表示解码策略采用“子批优先”+“批次优先”、“子批优先”和“批次优先”,字母
表 5 消融实验的策略设置
Tab.5
| 算法 | 解码策略 | 种群初始化 | 基于个体年龄 的邻域搜索 | 逃逸策略 |
| IMO-MBO | 1 | 有 | 有 | |
| MBO1 | 2 | 有 | 有 | |
| MBO2 | 3 | 有 | 有 | |
| MBO3 | 1 | 有 | 有 | |
| MBO4 | 1 | 有 | 有 | |
| MBO5 | 1 | 有 | 有 | |
| MBO6 | 1 | 无 | 有 | |
| MBO7 | 1 | 有 | 无 | |
| MBO8 | 2 | 无 | 无 |
针对生成的10个算例,每种算法独立运行20次,算法的终止条件为种群巡飞10次. 每运行一次得到一组IGD,对于每个算例所获得的20组指标取均值,结果如表6所示. 表中,数字右侧的“+”、“*”分别为IMO-MBO与MBO4、MBO3与MBO5的指标较优者的标识;对IGD所得的数据采取置信水平为95%的Wilcoxon符号秩检验,所得的p如表7所示,p≤0.05表示参与对比的2种算法间存在显著差异. 针对IGD指标而言,IMO-MBO显著优于MBO6、MBO7和MBO8,说明基于个体年龄的邻域搜索和逃逸机制有助于增强算法的鲁棒性和收敛性,将所提的各项策略组合后对于算法的性能有较大的提升. 针对解码策略,IMO-MBO、MBO1与MBO2无显著差异,但IMO-MBO在部分算例上远优于MBO1,如N7M4R1和N17M8R3,说明与“子批优先”策略相比,针对特殊问题在末阶段采取“子批优先”+“批次优先”的组合策略,有助于获得更好的最终解. 针对种群初始化策略,IMO-MBO显著优于MBO3,说明NEH算法能够为种群提供部分的优质初始解,有助于加速种群的收敛过程. IMO-MBO与MBO4、MBO3与MBO5无显著差异,但针对大部分算例的IGD指标而言,IMO-MBO略优于MBO4,MBO3略优于MBO5,说明Logistic混沌映射有助于增强算法的鲁棒性. IMO-MBO显著优于MBO5,说明种群初始化策略能够为算法的后续搜索提供优质的初始解集,有助于提高最终解的质量.
表 6 IMO-MBO与变体算法的IGD指标对比
Tab.6
| 算例 | IGD | ||||||||
| IMO-MBO | MBO1 | MBO2 | MBO3 | MBO4 | MBO5 | MBO6 | MBO7 | MBO8 | |
| N8M5R2 | |||||||||
| N10M6R2 | |||||||||
| N7M4R1 | |||||||||
| N6M6R2 | |||||||||
| N7M6R1 | |||||||||
| N18M6R2 | |||||||||
| N16M6R4 | |||||||||
| N17M8R3 | |||||||||
| N11M7R2 | |||||||||
| N13M6R1 | |||||||||
表 7 IMO-MBO与变体算法的Wilcoxon符号秩检验
Tab.7
| 对比算法 | p | 对比算法 | p | |
| IMO-MBO vs. MBO1 | 0.139 | MBO2 vs. IMO-MBO | 0.285 | |
| IMO-MBO vs. MBO5 | 0.005 | MBO2 vs. MBO1 | 0.445 | |
| IMO-MBO vs. MBO6 | 0.005 | IMO-MBO vs. MBO3 | 0.037 | |
| IMO-MBO vs. MBO7 | 0.005 | IMO-MBO vs. MBO4 | 0.005 | |
| IMO-MBO vs. MBO8 | 0.005 | MBO3 vs. MBO5 | 0.386 |
3.4. 模型验证
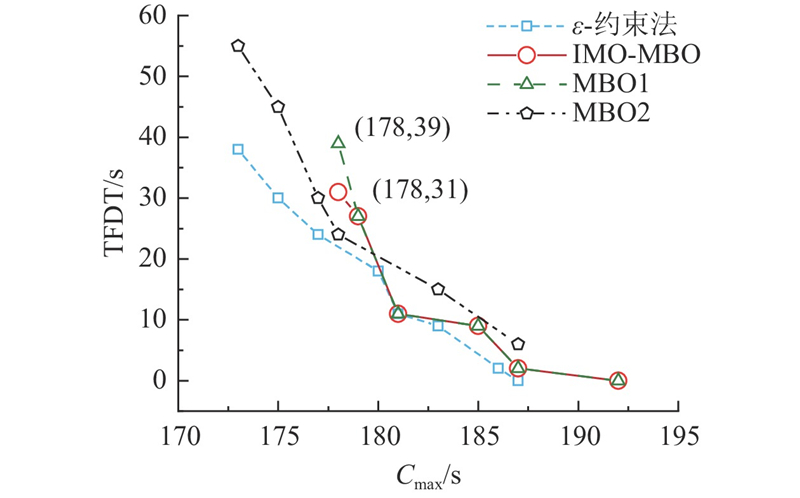
为了验证数学模型的有效性,采用
问题1:
式中:
问题2:
利用Gurobi对上述2个单目标问题进行求解,根据
图 6
图 6
Fig.6
Pareto frontier comparison of
3.5. 算法对比
为了验证IMO-MBO的有效性,将其与非支配排序遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)、多目标粒子群算法(multi-objective particle swarm algorithm, MOPSO)[14]、多目标混合遗传算法(multiple-objective hybrid genetic algorithm, MOHGA)[15]和混合多目标人工蜂群算法(hybrid multi-objective discrete artificial bee colony, HDABC)[16]等算法进行对比. 5种算法的编码、解码和种群初始化策略均相同. NSGA-II采用二元锦标赛选择算子、顺序交叉算子、贪婪变异和最优变异算子. MOPSO的邻域搜索算子采用本文的贪婪变异和最优变异算子,交叉算子采用顺序交叉算子. NSGA-II和MOPSO的其余参数如表8所示. MOHGA和HDABC采取与参考文献相同的参数和策略. 算法的终止条件为运行时间达到
表 8 NSGA-II和MOPSO的部分参数取值
Tab.8
| 算法 | 参数 | 数值 |
| NSGA-II | 种群大小 | 100 |
| 交叉概率 | 0.8 | |
| 变异概率 | 0.2 | |
| MOPSO | 粒子群规模 | 50 |
| 惯性权重 | 0.2 | |
| 个体学习因子 | 0.4 | |
| 群体学习因子 | 0.8 |
表 9 IMO-MBO与对比算法的IGD指标对比
Tab.9
| 算法 | IGD | |||||||||
| N8M5R2 | N10M6R2 | N7M4R1 | N6M6R2 | N7M6R1 | N18M6R2 | N16M6R4 | N17M8R3 | N11M7R2 | N13M6R1 | |
| IMO-MBO | ||||||||||
| NSGA-II | ||||||||||
| MOPSO | ||||||||||
| MOHGA | ||||||||||
| HDABC | ||||||||||
表 10 IMO-MBO与对比算法的Wilcoxon符号秩检验
Tab.10
| 对比算法 | p |
| IMO-MBO vs. NSGA-II | 0.005 |
| IMO-MBO vs. MOPSO | 0.005 |
| IMO-MBO vs. MOHGA | 0.028 |
| IMO-MBO vs. HDABC | 0.005 |
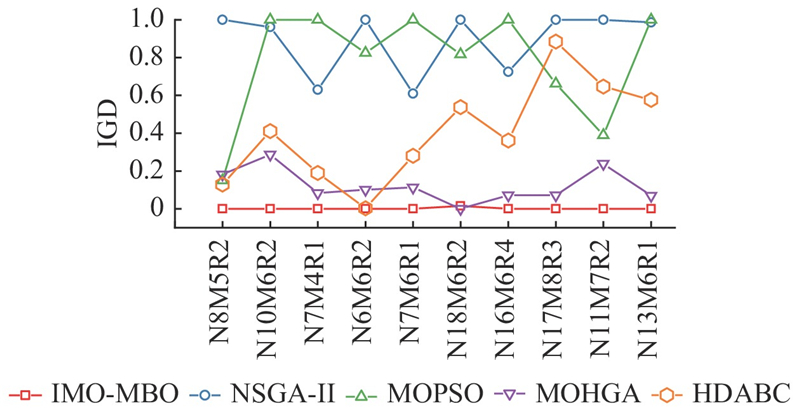
针对每个算例基于5种算法所得的IGD指标,采用最小-最大归一化方法对其进行归一化:
式中:
图 7
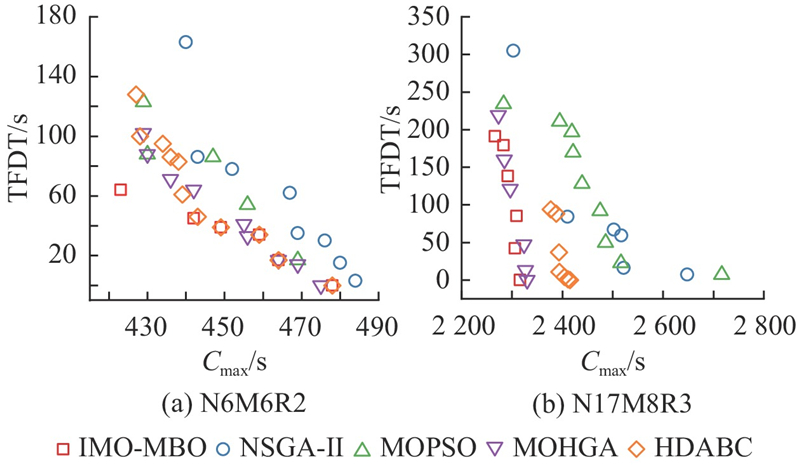
图 8
图 8 N6M6R2和N17M8R3的Pareto前沿对比图
Fig.8 Pareto frontier comparison of N6M6R2 and N17M8R3
4. 结 语
结合TFT-LCD阵列车间的生产特性,本文构建可重入混合流水车间批量流调度问题模型,设计改进多目标候鸟优化算法进行求解. 考虑到调度问题的独特性,提出“子批优先”+“批次优先”的解码策略,以增强算法在处理特殊问题时的能力. 此外,针对算法的本身特点进行改进,主要包括提升初始种群质量、优化局部搜索方向及增强全局搜索能力. 通过实验验证了改进策略的有效性和算法的优越性. 进一步的研究方向是在模型中纳入动态事件的影响,因为在实际生产中可能会遭遇机器故障或工件抽检不合格的情况. 此时通常需要将正在加工的子批进行拆分,区别不同加工状态的工件. 引入这些动态事件,将使模型更贴近生产实际.
参考文献
Embedding ant system in genetic algorithm for re-entrant hybrid flow shop scheduling problems with time window constraints
[J].DOI:10.1007/s10845-015-1078-9 [本文引用: 1]
Multi-objective evolutionary algorithm with variable neighborhood search for optimizing green scheduling in a re-entrant hybrid flow shop with dynamic events
[J].DOI:10.1088/1742-6596/2747/1/012007 [本文引用: 1]
An elite-class teaching-learning-based optimization for reentrant hybrid flow shop scheduling with bottleneck stage
[J].DOI:10.32604/cmc.2024.049481 [本文引用: 1]
考虑多时间因素的绿色可重入混合流水车间调度问题
[J].
Green re-entrant hybrid flow shop scheduling problem considering multiple time factors
[J].
基于MOMA的可重入混合流水车间调度问题研究
[J].
Reentrant hybrid flow shop scheduling problem based on MOMA
[J].
An improved multi-objective evolutionary algorithm based on decomposition for solving re-entrant hybrid flow shop scheduling problem with batch processing machines
[J].DOI:10.1016/j.cie.2022.108236 [本文引用: 1]
基于改进候鸟迁徙优化的多目标批量流混合流水车间调度
[J].
A modified migrating birds optimization for multi-objective lot streaming hybird flowshop scheduling
[J].
An improved migrating birds optimisation for a hybrid flowshop scheduling with total flowtime minimisation
[J].DOI:10.1016/j.ins.2014.02.152 [本文引用: 1]
基于总加权完成时间的可重入混合流水车间调度问题
[J].
Reentrant hybird flowshop scheduling problem based on total weighted completion time
[J].
A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem
[J].DOI:10.1016/0305-0483(83)90088-9 [本文引用: 1]
An effective modified migrating birds optimization for hybrid flowshop scheduling problem with lot streaming
[J].DOI:10.1016/j.asoc.2016.12.021 [本文引用: 1]
Bi-objective scheduling for reentrant hybrid flow shop using pareto genetic algorithm
[J].DOI:10.1016/j.cie.2011.04.008 [本文引用: 1]
多目标进化算法性能评价指标研究综述
[J].DOI:10.11897/SP.J.1016.2021.01590 [本文引用: 1]
Survey on performance indicators for multi-objective evolutionary algorithms
[J].DOI:10.11897/SP.J.1016.2021.01590 [本文引用: 1]
混合粒子群算法求解多目标柔性作业车间调调度度问题
[J].
Hybrid particle-swarm optimization for multi-objective flexible job-shop scheduling problem
[J].
A novel hybrid multi-objective artificial bee colony algorithm for blocking lot-streaming flow shop scheduling problems
[J].DOI:10.1016/j.knosys.2018.02.029 [本文引用: 1]