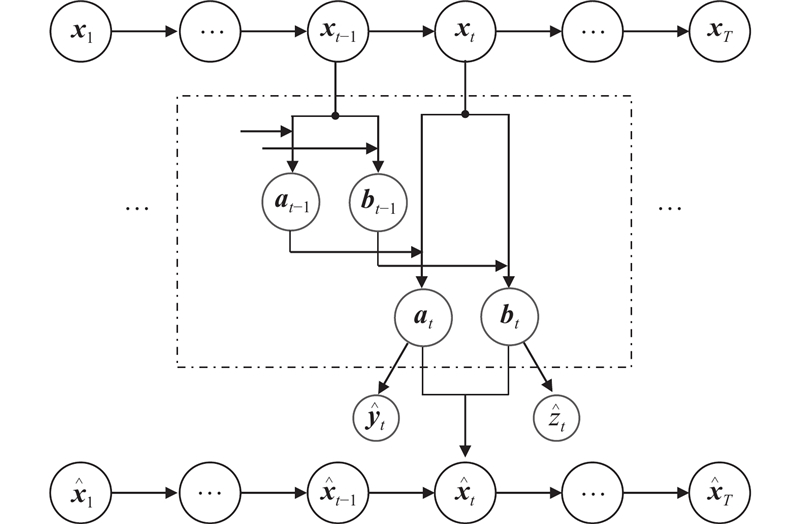
(2) $ \left. {\begin{array}{*{20}{c}} \begin{gathered} {{\boldsymbol{\alpha }}_t} \to f_t^a({{\boldsymbol{x}}_t},{{\boldsymbol{a}}_{t - 1}},{\boldsymbol{\varepsilon }}_t^a), \\ {{\boldsymbol{b}}_t} \to f_t^b({{\boldsymbol{x}}_t},{{\boldsymbol{b}}_{t - 1}},{\boldsymbol{\varepsilon }}_t^b), \\ \end{gathered} \\ {{{{\boldsymbol{\hat x}}}_t} \to f_t^x({{\boldsymbol{\alpha }}_t},{{\boldsymbol{b}}_t},{\boldsymbol{\varepsilon }}_t^x),} \\ {{{{\boldsymbol{\hat y}}}_t} \to f_t^y({{\boldsymbol{\alpha }}_t},{\boldsymbol{\varepsilon }}_t^y),} \\ {{z_t} \to f_t^z({{\boldsymbol{b}}_t},{\boldsymbol{\varepsilon }}_t^z).} \end{array}} \right\} $
后验网络的编码器$ {E_{\text{q}}} $ $ {E_{\text{r}}} $ $ p\left( {{{\boldsymbol{d}}_t}\mid {{\boldsymbol{d}}_{t - 1}},{{\boldsymbol{x}}_t}} \right) $ [19 ] 从正态分布$ N\left( {{\mu _\theta }\left( {{{\boldsymbol{d}}_{t - 1}},{{\boldsymbol{x}}_t}} \right),{\Sigma _\theta }\left( {{{\boldsymbol{d}}_{t - 1}},{{\boldsymbol{x}}_t}} \right)} \right) $ $ E_q^{{a}} $ $ E_q^{{{{b}}}} $ ${p_\theta }\left( {{{\boldsymbol{o}}_T}\mid {{\boldsymbol{d}}_{T - 1}}} \right)$ ${{\boldsymbol{a}}_T}$ ${{\boldsymbol{b}}_T}$ ${q_\phi }\left( {{{\boldsymbol{d}}_t}\mid {{\boldsymbol{d}}_{t - 1}},\;{{\boldsymbol{x}}_t}} \right)$ $ N(\mu_{\phi}(\boldsymbol{d}_{t-1},\boldsymbol{x}_t),\; \mathit{\Sigma}_{\phi} (\boldsymbol{d}_{t-1}, \boldsymbol{x}_t)) $ . 在高斯分布中采样后, VAE的解码器$ {E_{\text{r}}} $
[1]
高萍. 基于可靠性分析的复杂设备预防性维修决策研究 [D]. 北京: 清华大学, 2008: 1–119.
[本文引用: 2]
GAO Ping. The research on preventive maintenance decision of complex equipment based on reliability analysis [D]. Beijing: Tsinghua University, 2008: 1–119.
[本文引用: 2]
[2]
GAO Z, CECATI C, DING S X A survey of fault diagnosis and fault-tolerant techniques: Part II: fault diagnosis with knowledge-based and hybrid/active approaches
[J]. IEEE Transactions on Industrial Electronics , 2015 , 62 (6 ): 3768 - 3774
[本文引用: 1]
[3]
YIN S, DING S X, XIE X, et al A review on basic data-driven approaches for industrial process monitoring
[J]. IEEE Transactions on Industrial Electronics , 2014 , 61 (11 ): 6418 - 6428
DOI:10.1109/TIE.2014.2301773
[本文引用: 1]
[4]
CAI B, HUANG L, XIE M Bayesian networks in fault diagnosis
[J]. IEEE Transactions on Industrial Informatics , 2017 , 13 (5 ): 2227 - 2240
DOI:10.1109/TII.2017.2695583
[5]
周策, 白斌, 叶楠 自适应粒子群优化支持向量回归的工程系统可靠性预测
[J]. 机械工程学报 , 2023 , 59 (14 ): 328 - 338
DOI:10.3901/JME.2023.14.328
[本文引用: 1]
ZHOU Ce, BAI Bin, YE Nan Reliability prediction of engineering system based on adaptive particle swarm optimization support vector regression
[J]. Journal of Mechanical Engineering , 2023 , 59 (14 ): 328 - 338
DOI:10.3901/JME.2023.14.328
[本文引用: 1]
[6]
HAN Y, TANG B, DENG L An enhanced convolutional neural network with enlarged receptive fields for fault diagnosis of planetary gearboxes
[J]. Computers in Industry , 2019 , 107 : 50 - 58
DOI:10.1016/j.compind.2019.01.012
[本文引用: 3]
[7]
AN Z, LI S, WANG J, et al A novel bearing intelligent fault diagnosis framework under time-varying working conditions using recurrent neural network
[J]. ISA Transactions , 2020 , 100 : 155 - 170
DOI:10.1016/j.isatra.2019.11.010
[本文引用: 2]
[8]
PEI X, ZHENG X, WU J Rotating machinery fault diagnosis through a transformer convolution network subjected to transfer learning
[J]. IEEE Transactions on Instrumentation and Measurement , 2021 , 70 : 2515611
[本文引用: 2]
[9]
TZENG E, HOFFMAN J, ZHANG N, et al. Deep domain confusion: maximizing for domain invariance [EB/OL]. (2014–12–10)[2024–06–10]. https://arxiv.org/pdf/1412.3474.
[本文引用: 4]
[10]
SUN B, SAENKO K. Deep CORAL: correlation alignment for deep domain adaptation [C]// Computer Vision – ECCV 2016 Workshops . [S.l.]: Springer, 2016: 443–450.
[本文引用: 3]
[11]
GANIN Y, USTINOVA E, AJAKAN H, et al. Domain-adversarial training of neural networks [M]// CSURKA G. Domain adaptation in computer vision applications . [S.l.]: Springer, 2017: 189–209.
[本文引用: 3]
[12]
CHEN Z, HE G, LI J, et al Domain adversarial transfer network for cross-domain fault diagnosis of rotary machinery
[J]. IEEE Transactions on Instrumentation and Measurement , 2020 , 69 (11 ): 8702 - 8712
DOI:10.1109/TIM.2020.2995441
[本文引用: 2]
[13]
LONG M, CAO Z, WANG J, et al. Conditional adversarial domain adaptation [C]// Proceedings of The 32nd International Conference on Neural Information Processing Systems . Montreal: [s.n.], 2018: 1647–1657.
[本文引用: 4]
[14]
JIAO J, LI H, ZHANG T, et al Source-free adaptation diagnosis for rotating machinery
[J]. IEEE Transactions on Industrial Informatics , 2023 , 19 (9 ): 9586 - 9595
DOI:10.1109/TII.2022.3231414
[本文引用: 3]
[15]
LI Y, SONG Y, JIA L, et al Intelligent fault diagnosis by fusing domain adversarial training and maximum mean discrepancy via ensemble learning
[J]. IEEE Transactions on Industrial Informatics , 2021 , 17 (4 ): 2833 - 2841
DOI:10.1109/TII.2020.3008010
[16]
ZHAO K, JIANG H, WANG K, et al Joint distribution adaptation network with adversarial learning for rolling bearing fault diagnosis
[J]. Knowledge-Based Systems , 2021 , 222 : 106974
DOI:10.1016/j.knosys.2021.106974
[本文引用: 1]
[17]
RAS G, XIE N, VAN GERVEN M, et al Explainable deep learning: a field guide for the uninitiated
[J]. Journal of Artificial Intelligence Research , 2022 , 73 : 329 - 396
DOI:10.1613/jair.1.13200
[本文引用: 1]
[18]
LOCATELLO F, BAUER S, LUCIC M, et al. Challenging common assumptions in the unsupervised learning of disentangled representations [C]// International Conference on Learning Representations . Long Beach: [s.n.]. 2019, 97: 4114–4124.
[本文引用: 2]
[19]
KINGMA D P, WELLING M. Auto-encoding variational Bayes [EB/OL]. (2022–12–10)[2024–06–10]. https://arxiv.org/pdf/1312.6114v11.
[本文引用: 3]
[20]
HIGGINS I, MATTHEY L, PAL A, et al. β -VAE: learning basic visual concepts with a constrained variational framework [C]// International Conference on Learning Representations . Puerto Rico: [s.n.]. 2016: 1–13.
[本文引用: 1]
[21]
LI J, WU B, SUN X, et al. Causal hidden Markov model for time series disease forecasting [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Nashville: IEEE, 2021: 12100–12109.
[本文引用: 3]
[22]
LONG M, CAO Y, CAO Z, et al Transferable representation learning with deep adaptation networks
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2019 , 41 (12 ): 3071 - 3085
DOI:10.1109/TPAMI.2018.2868685
[本文引用: 2]
[23]
PEARL J. Causality: models, reasoning and inference [M]. New York: Cambridge University Press, 2000: 1–478.
[本文引用: 1]
[24]
HOU B, YANG J, WANG P, et al LSTM-based auto-encoder model for ECG arrhythmias classification
[J]. IEEE Transactions on Instrumentation and Measurement , 2020 , 69 (4 ): 1232 - 1240
DOI:10.1109/TIM.2019.2910342
[本文引用: 1]
[25]
ZHAO Z, ZHANG Q, YU X, et al Applications of unsupervised deep transfer learning to intelligent fault diagnosis: a survey and comparative study
[J]. IEEE Transactions on Instrumentation and Measurement , 2021 , 70 : 3525828
[本文引用: 2]
[26]
SMITH W A, RANDALL R B Rolling element bearing diagnostics using the Case Western Reserve University data: a benchmark study
[J]. Mechanical Systems and Signal Processing , 2015 , 64 : 100 - 131
[本文引用: 1]
[27]
QIU H, LEE J, LIN J, et al Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics
[J]. Journal of Sound and Vibration , 2006 , 289 (4/5 ): 1066 - 1090
[本文引用: 1]
[28]
RANDALL R B, ANTONI J Rolling element bearing diagnostics: a tutorial
[J]. Mechanical Systems and Signal Processing , 2011 , 25 (2 ): 485 - 520
DOI:10.1016/j.ymssp.2010.07.017
[本文引用: 1]
[29]
VAN DER MAATEN L, HINTON G Visualizing data using t-SNE
[J]. Journal of Machine Learning Research , 2008 , 9 : 2579 - 2605
[本文引用: 1]
2
... 正确识别、诊断设备故障,对确保自动化生产安全平稳地进行有重要意义. 随着设备结构的复杂化,各子系统中零部件间相互影响,构成了观测数据间的各种复杂关联关系,为故障的准确预测和设备的健康状态管理带来挑战[1 ] . ...
... 将DANN与本研究所提方法的实验结果进行可视化分析,如图6 所示为2种方法的诊断结果混淆矩阵. 为了提高结果的代表性,采用训练集上最后1个迭代轮次得到的模型,数据基于CWRU数据集上的迁移任务[3]-[1]. 图中,故障类别1为正常类,类别2~4分别表示尺寸为0.1778 mm的内圈、滚珠和外圈故障,类别5~7、8~10分别表示尺寸为0.3556 mm和0.5334 mm的3种故障. 在迁移到目标域数据后,DANN对滚珠处故障识别效果较差,较难区分不同尺寸故障(类别3、类别6和类别9)之间的差异. 滚珠在轴承运转过程中具有复杂的运动轨迹和不断变化的接触点,因而滚珠故障的振动信号表现出更多随机性和复杂频谱成分[1 , 28 ] ,在不同工况下对震动信号的域分布影响较大,导致DANN模型在迁移后没有从目标域数据中学习到清晰的决策边界. DANN采用域对抗的训练策略,需要在特征域判别性和类判别性之间寻找平衡,在不同尺寸的故障类间差异较小而域间差异较大的情况下,易受无关因素的干扰,很难达到最优的诊断结果. 本研究的解耦方法能够有效分离出与故障类直接因果相关的信息,降低其他因素的干扰,提高所学特征的类间差异,故障分类结果更好. ...
2
... 正确识别、诊断设备故障,对确保自动化生产安全平稳地进行有重要意义. 随着设备结构的复杂化,各子系统中零部件间相互影响,构成了观测数据间的各种复杂关联关系,为故障的准确预测和设备的健康状态管理带来挑战[1 ] . ...
... 将DANN与本研究所提方法的实验结果进行可视化分析,如图6 所示为2种方法的诊断结果混淆矩阵. 为了提高结果的代表性,采用训练集上最后1个迭代轮次得到的模型,数据基于CWRU数据集上的迁移任务[3]-[1]. 图中,故障类别1为正常类,类别2~4分别表示尺寸为0.1778 mm的内圈、滚珠和外圈故障,类别5~7、8~10分别表示尺寸为0.3556 mm和0.5334 mm的3种故障. 在迁移到目标域数据后,DANN对滚珠处故障识别效果较差,较难区分不同尺寸故障(类别3、类别6和类别9)之间的差异. 滚珠在轴承运转过程中具有复杂的运动轨迹和不断变化的接触点,因而滚珠故障的振动信号表现出更多随机性和复杂频谱成分[1 , 28 ] ,在不同工况下对震动信号的域分布影响较大,导致DANN模型在迁移后没有从目标域数据中学习到清晰的决策边界. DANN采用域对抗的训练策略,需要在特征域判别性和类判别性之间寻找平衡,在不同尺寸的故障类间差异较小而域间差异较大的情况下,易受无关因素的干扰,很难达到最优的诊断结果. 本研究的解耦方法能够有效分离出与故障类直接因果相关的信息,降低其他因素的干扰,提高所学特征的类间差异,故障分类结果更好. ...
A survey of fault diagnosis and fault-tolerant techniques: Part II: fault diagnosis with knowledge-based and hybrid/active approaches
1
2015
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
A review on basic data-driven approaches for industrial process monitoring
1
2014
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
Bayesian networks in fault diagnosis
0
2017
自适应粒子群优化支持向量回归的工程系统可靠性预测
1
2023
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
自适应粒子群优化支持向量回归的工程系统可靠性预测
1
2023
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
An enhanced convolutional neural network with enlarged receptive fields for fault diagnosis of planetary gearboxes
3
2019
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
... 深度神经网络能感知数据的各种关联关系,自动提取信号特征,进而判断故障类型. 在故障诊断任务中,常见的信号类型有来自单一传感器的单变量时间序列和结合多个传感器信息的多变量时间序列. 对序列数据有较强处理能力的一维卷积神经网络(one-dimensional convolutional neural network, 1DCNN)[6 ] 和循环神经网络(recurrent neural network, RNN)[7 ] 常作为特征提取的骨干网络. Han等[6 ] 基于不同大小的一维卷积核,提取、融合多尺度特征,以捕获更长时间维度上的数据关联关系. An等[7 ] 基于微元的思想,在短时序列特征的基础上利用长短时神经网络(long short-term neural network, LSTM)进行深层次处理,实现时变工况下的故障诊断. Pei等[8 ] 将1DCNN与具有捕捉长距离依赖性的Transformer结合,以增强模型在不同抽象层次上捕获数据复杂模式的能力,并将模型应用在迁移故障诊断任务中. ...
... [6 ]基于不同大小的一维卷积核,提取、融合多尺度特征,以捕获更长时间维度上的数据关联关系. An等[7 ] 基于微元的思想,在短时序列特征的基础上利用长短时神经网络(long short-term neural network, LSTM)进行深层次处理,实现时变工况下的故障诊断. Pei等[8 ] 将1DCNN与具有捕捉长距离依赖性的Transformer结合,以增强模型在不同抽象层次上捕获数据复杂模式的能力,并将模型应用在迁移故障诊断任务中. ...
A novel bearing intelligent fault diagnosis framework under time-varying working conditions using recurrent neural network
2
2020
... 深度神经网络能感知数据的各种关联关系,自动提取信号特征,进而判断故障类型. 在故障诊断任务中,常见的信号类型有来自单一传感器的单变量时间序列和结合多个传感器信息的多变量时间序列. 对序列数据有较强处理能力的一维卷积神经网络(one-dimensional convolutional neural network, 1DCNN)[6 ] 和循环神经网络(recurrent neural network, RNN)[7 ] 常作为特征提取的骨干网络. Han等[6 ] 基于不同大小的一维卷积核,提取、融合多尺度特征,以捕获更长时间维度上的数据关联关系. An等[7 ] 基于微元的思想,在短时序列特征的基础上利用长短时神经网络(long short-term neural network, LSTM)进行深层次处理,实现时变工况下的故障诊断. Pei等[8 ] 将1DCNN与具有捕捉长距离依赖性的Transformer结合,以增强模型在不同抽象层次上捕获数据复杂模式的能力,并将模型应用在迁移故障诊断任务中. ...
... [7 ]基于微元的思想,在短时序列特征的基础上利用长短时神经网络(long short-term neural network, LSTM)进行深层次处理,实现时变工况下的故障诊断. Pei等[8 ] 将1DCNN与具有捕捉长距离依赖性的Transformer结合,以增强模型在不同抽象层次上捕获数据复杂模式的能力,并将模型应用在迁移故障诊断任务中. ...
Rotating machinery fault diagnosis through a transformer convolution network subjected to transfer learning
2
2021
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
... 深度神经网络能感知数据的各种关联关系,自动提取信号特征,进而判断故障类型. 在故障诊断任务中,常见的信号类型有来自单一传感器的单变量时间序列和结合多个传感器信息的多变量时间序列. 对序列数据有较强处理能力的一维卷积神经网络(one-dimensional convolutional neural network, 1DCNN)[6 ] 和循环神经网络(recurrent neural network, RNN)[7 ] 常作为特征提取的骨干网络. Han等[6 ] 基于不同大小的一维卷积核,提取、融合多尺度特征,以捕获更长时间维度上的数据关联关系. An等[7 ] 基于微元的思想,在短时序列特征的基础上利用长短时神经网络(long short-term neural network, LSTM)进行深层次处理,实现时变工况下的故障诊断. Pei等[8 ] 将1DCNN与具有捕捉长距离依赖性的Transformer结合,以增强模型在不同抽象层次上捕获数据复杂模式的能力,并将模型应用在迁移故障诊断任务中. ...
4
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
... 由于源域和目标域之间的数据分布不同,域自适应技术须缓解域偏移的影响,学习域不变特征. Tzeng等[9 ] 提出深度领域混淆(deep domain confusion, DDC),在网络中引入自适应层对齐在2个域中学到的特征. Sun等[10 ] 提出深度相关性对齐方法(correlation alignment, CORAL),用CORAL损失替换最大均值差异(maximum mean discrepancy, MMD)距离,以对齐不同域数据分布的二阶统计特征. Ganin等[11 ] 在域自适应中引入对抗思想,提出DANN,在该网络中引入域判别器,以区分数据来自源域还是目标域,并利用梯度反转层进行对抗训练,提高特征的泛化能力. Chen等[12 ] 将DANN应用到滚动轴承的故障诊断任务中,采用交替更新特征提取器与域判别器参数的训练策略,以实现特征提取与域对齐之间的协同优化. DANN很难安全地调整域判别器,Long等[13 ] 提出CDAN,采用多线性调整和熵调整策略来处理域判别器接收的各个训练样本,提高神经网络的迁移学习效果. Jiao等[14 ] 提出无源域自适应(source-free domain adaption, SFDA)故障诊断算法,利用伪标签技术引导目标域数据的训练,避免了对源域数据的访问,同时,利用归一化对称交叉熵损失抑制伪标签噪声带来的负面影响. ...
... 测试所提方法在不同域之间的迁移性能,以分类准确率作为评估指标. 实验基于6种方法,包括作为比对的基线方法BASE,以及DDC[9 ] 、CORAL[10 ] 、DANN[11 ] 、CDAN[13 ] 、和SFDA[14 ] . 所有对比方法均采用1个1DCNN作为骨干网络,并连接1个线性分类器进行故障分类[25 ] . BASE在目标域上直接进行测试,不对域自适应任务进行专门设计. 基于CWRU数据集4种不同工作负载下的轴承数据,设计12组迁移实验,结果如表2 所示,其中[1]-[2]表示从第1种到第2种工作负载条件下的迁移,$A$
... Bearing fault diagnosis accuracy of different methods in twelve transfer tasks
Tab.2 迁移任务 A /%BASE DDC[9 ] CORAL[10 ] DANN[11 ] CDAN[13 ] SFDA[14 ] 本研究 [1]-[2] 96.53 ± 0.12 95.71 ± 0.41 94.52 ± 0.51 96.43 ± 0.23 97.59 ± 0.13 96.83 ± 0.79 98.63 ± 0.07 [1]-[3] 92.84 ± 0.49 95.48 ± 0.25 92.34 ± 1.10 96.24 ± 0.53 99.17 ± 0.17 98.63 ± 0.84 99.39 ± 0.13 [1]-[4] 88.91 ± 0.93 92.19 ± 0.58 91.56 ± 2.08 97.82 ± 0.36 98.32 ± 0.21 96.25 ± 0.66 98.69 ± 0.19 [2]-[1] 98.82 ± 0.07 98.96 ± 0.43 98.33 ± 0.24 98.65 ± 0.20 99.10 ± 0.26 98.25 ± 0.45 99.89 ± 0.06 [2]-[3] 98.56 ± 0.21 97.79 ± 0.26 98.82 ± 0.09 99.37 ± 0.18 99.53 ± 0.06 97.22 ± 0.76 99.64 ± 0.09 [2]-[4] 92.67 ± 0.18 93.48 ± 0.91 94.72 ± 1.61 99.15 ± 0.32 98.97 ± 0.21 98.62 ± 0.47 99.23 ± 0.05 [3]-[1] 96.31 ± 0.42 96.99 ± 0.72 97.53 ± 0.14 92.85 ± 0.71 99.12 ± 0.13 96.09 ± 0.77 99.15 ± 0.08 [3]-[2] 97.15 ± 0.29 98.51 ± 0.44 99.49 ± 0.11 95.47 ± 0.93 98.87 ± 0.22 97.53 ± 0.49 99.92 ± 0.03 [3]-[4] 98.88 ± 0.06 99.22 ± 0.34 98.28 ± 0.07 99.64 ± 0.09 99.95 ± 0.13 98.85 ± 0.39 100.0 ± 0.00 [4]-[1] 81.09 ± 1.13 84.35 ± 0.81 88.37 ± 0.13 88.34 ± 0.45 92.23 ± 0.18 95.62 ± 0.42 97.42 ± 0.12 [4]-[2] 84.56 ± 0.75 89.61 ± 0.74 90.43 ± 0.38 87.48 ± 0.73 91.43 ± 0.61 93.26 ± 0.72 95.34 ± 0.21 [4]-[3] 95.93 ± 0.53 96.49 ± 0.63 97.03 ± 0.16 97.42 ± 0.16 98.81 ± 0.09 97.31 ± 0.59 98.82 ± 0.16
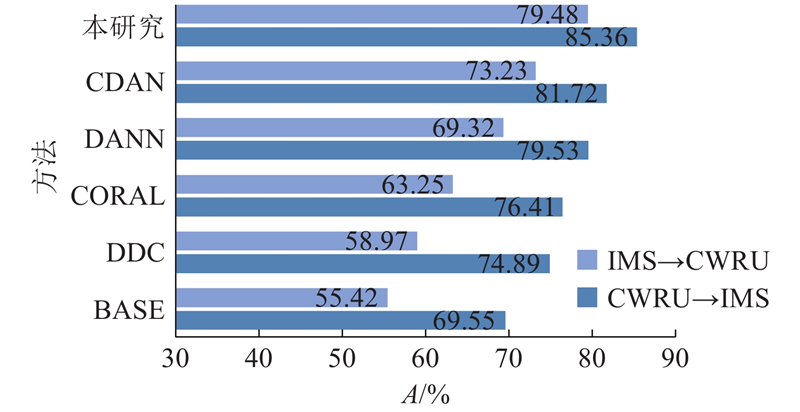
表2 中方法之间的性能差距不显著,原因是不同工作负载的数据间的域偏移不明显. 基于不同平台采集的滚动轴承数据集,轴承型号、工作条件、噪声等因素间存在差异. 为了进一步验证模型的迁移性能,在2个数据集上进行跨数据集的域迁移,实验结果如图5 所示. 相较于同一数据集中的域分布,不同轴承数据集间存在更大的域偏移,解耦后的故障相关特征能更好地找到不同数据域之间的故障共性,在所有方法中结果最好. CWRU数据集作为源域数据训练时使用了更多不同工作负载条件下的样本,训练模型的泛化性能更强,因此故障诊断的诊断准确率强于IMS数据集作为源域数据时的准确率. ...
3
... 由于源域和目标域之间的数据分布不同,域自适应技术须缓解域偏移的影响,学习域不变特征. Tzeng等[9 ] 提出深度领域混淆(deep domain confusion, DDC),在网络中引入自适应层对齐在2个域中学到的特征. Sun等[10 ] 提出深度相关性对齐方法(correlation alignment, CORAL),用CORAL损失替换最大均值差异(maximum mean discrepancy, MMD)距离,以对齐不同域数据分布的二阶统计特征. Ganin等[11 ] 在域自适应中引入对抗思想,提出DANN,在该网络中引入域判别器,以区分数据来自源域还是目标域,并利用梯度反转层进行对抗训练,提高特征的泛化能力. Chen等[12 ] 将DANN应用到滚动轴承的故障诊断任务中,采用交替更新特征提取器与域判别器参数的训练策略,以实现特征提取与域对齐之间的协同优化. DANN很难安全地调整域判别器,Long等[13 ] 提出CDAN,采用多线性调整和熵调整策略来处理域判别器接收的各个训练样本,提高神经网络的迁移学习效果. Jiao等[14 ] 提出无源域自适应(source-free domain adaption, SFDA)故障诊断算法,利用伪标签技术引导目标域数据的训练,避免了对源域数据的访问,同时,利用归一化对称交叉熵损失抑制伪标签噪声带来的负面影响. ...
... 测试所提方法在不同域之间的迁移性能,以分类准确率作为评估指标. 实验基于6种方法,包括作为比对的基线方法BASE,以及DDC[9 ] 、CORAL[10 ] 、DANN[11 ] 、CDAN[13 ] 、和SFDA[14 ] . 所有对比方法均采用1个1DCNN作为骨干网络,并连接1个线性分类器进行故障分类[25 ] . BASE在目标域上直接进行测试,不对域自适应任务进行专门设计. 基于CWRU数据集4种不同工作负载下的轴承数据,设计12组迁移实验,结果如表2 所示,其中[1]-[2]表示从第1种到第2种工作负载条件下的迁移,$A$
... Bearing fault diagnosis accuracy of different methods in twelve transfer tasks
Tab.2 迁移任务 A /%BASE DDC[9 ] CORAL[10 ] DANN[11 ] CDAN[13 ] SFDA[14 ] 本研究 [1]-[2] 96.53 ± 0.12 95.71 ± 0.41 94.52 ± 0.51 96.43 ± 0.23 97.59 ± 0.13 96.83 ± 0.79 98.63 ± 0.07 [1]-[3] 92.84 ± 0.49 95.48 ± 0.25 92.34 ± 1.10 96.24 ± 0.53 99.17 ± 0.17 98.63 ± 0.84 99.39 ± 0.13 [1]-[4] 88.91 ± 0.93 92.19 ± 0.58 91.56 ± 2.08 97.82 ± 0.36 98.32 ± 0.21 96.25 ± 0.66 98.69 ± 0.19 [2]-[1] 98.82 ± 0.07 98.96 ± 0.43 98.33 ± 0.24 98.65 ± 0.20 99.10 ± 0.26 98.25 ± 0.45 99.89 ± 0.06 [2]-[3] 98.56 ± 0.21 97.79 ± 0.26 98.82 ± 0.09 99.37 ± 0.18 99.53 ± 0.06 97.22 ± 0.76 99.64 ± 0.09 [2]-[4] 92.67 ± 0.18 93.48 ± 0.91 94.72 ± 1.61 99.15 ± 0.32 98.97 ± 0.21 98.62 ± 0.47 99.23 ± 0.05 [3]-[1] 96.31 ± 0.42 96.99 ± 0.72 97.53 ± 0.14 92.85 ± 0.71 99.12 ± 0.13 96.09 ± 0.77 99.15 ± 0.08 [3]-[2] 97.15 ± 0.29 98.51 ± 0.44 99.49 ± 0.11 95.47 ± 0.93 98.87 ± 0.22 97.53 ± 0.49 99.92 ± 0.03 [3]-[4] 98.88 ± 0.06 99.22 ± 0.34 98.28 ± 0.07 99.64 ± 0.09 99.95 ± 0.13 98.85 ± 0.39 100.0 ± 0.00 [4]-[1] 81.09 ± 1.13 84.35 ± 0.81 88.37 ± 0.13 88.34 ± 0.45 92.23 ± 0.18 95.62 ± 0.42 97.42 ± 0.12 [4]-[2] 84.56 ± 0.75 89.61 ± 0.74 90.43 ± 0.38 87.48 ± 0.73 91.43 ± 0.61 93.26 ± 0.72 95.34 ± 0.21 [4]-[3] 95.93 ± 0.53 96.49 ± 0.63 97.03 ± 0.16 97.42 ± 0.16 98.81 ± 0.09 97.31 ± 0.59 98.82 ± 0.16
表2 中方法之间的性能差距不显著,原因是不同工作负载的数据间的域偏移不明显. 基于不同平台采集的滚动轴承数据集,轴承型号、工作条件、噪声等因素间存在差异. 为了进一步验证模型的迁移性能,在2个数据集上进行跨数据集的域迁移,实验结果如图5 所示. 相较于同一数据集中的域分布,不同轴承数据集间存在更大的域偏移,解耦后的故障相关特征能更好地找到不同数据域之间的故障共性,在所有方法中结果最好. CWRU数据集作为源域数据训练时使用了更多不同工作负载条件下的样本,训练模型的泛化性能更强,因此故障诊断的诊断准确率强于IMS数据集作为源域数据时的准确率. ...
3
... 由于源域和目标域之间的数据分布不同,域自适应技术须缓解域偏移的影响,学习域不变特征. Tzeng等[9 ] 提出深度领域混淆(deep domain confusion, DDC),在网络中引入自适应层对齐在2个域中学到的特征. Sun等[10 ] 提出深度相关性对齐方法(correlation alignment, CORAL),用CORAL损失替换最大均值差异(maximum mean discrepancy, MMD)距离,以对齐不同域数据分布的二阶统计特征. Ganin等[11 ] 在域自适应中引入对抗思想,提出DANN,在该网络中引入域判别器,以区分数据来自源域还是目标域,并利用梯度反转层进行对抗训练,提高特征的泛化能力. Chen等[12 ] 将DANN应用到滚动轴承的故障诊断任务中,采用交替更新特征提取器与域判别器参数的训练策略,以实现特征提取与域对齐之间的协同优化. DANN很难安全地调整域判别器,Long等[13 ] 提出CDAN,采用多线性调整和熵调整策略来处理域判别器接收的各个训练样本,提高神经网络的迁移学习效果. Jiao等[14 ] 提出无源域自适应(source-free domain adaption, SFDA)故障诊断算法,利用伪标签技术引导目标域数据的训练,避免了对源域数据的访问,同时,利用归一化对称交叉熵损失抑制伪标签噪声带来的负面影响. ...
... 测试所提方法在不同域之间的迁移性能,以分类准确率作为评估指标. 实验基于6种方法,包括作为比对的基线方法BASE,以及DDC[9 ] 、CORAL[10 ] 、DANN[11 ] 、CDAN[13 ] 、和SFDA[14 ] . 所有对比方法均采用1个1DCNN作为骨干网络,并连接1个线性分类器进行故障分类[25 ] . BASE在目标域上直接进行测试,不对域自适应任务进行专门设计. 基于CWRU数据集4种不同工作负载下的轴承数据,设计12组迁移实验,结果如表2 所示,其中[1]-[2]表示从第1种到第2种工作负载条件下的迁移,$A$
... Bearing fault diagnosis accuracy of different methods in twelve transfer tasks
Tab.2 迁移任务 A /%BASE DDC[9 ] CORAL[10 ] DANN[11 ] CDAN[13 ] SFDA[14 ] 本研究 [1]-[2] 96.53 ± 0.12 95.71 ± 0.41 94.52 ± 0.51 96.43 ± 0.23 97.59 ± 0.13 96.83 ± 0.79 98.63 ± 0.07 [1]-[3] 92.84 ± 0.49 95.48 ± 0.25 92.34 ± 1.10 96.24 ± 0.53 99.17 ± 0.17 98.63 ± 0.84 99.39 ± 0.13 [1]-[4] 88.91 ± 0.93 92.19 ± 0.58 91.56 ± 2.08 97.82 ± 0.36 98.32 ± 0.21 96.25 ± 0.66 98.69 ± 0.19 [2]-[1] 98.82 ± 0.07 98.96 ± 0.43 98.33 ± 0.24 98.65 ± 0.20 99.10 ± 0.26 98.25 ± 0.45 99.89 ± 0.06 [2]-[3] 98.56 ± 0.21 97.79 ± 0.26 98.82 ± 0.09 99.37 ± 0.18 99.53 ± 0.06 97.22 ± 0.76 99.64 ± 0.09 [2]-[4] 92.67 ± 0.18 93.48 ± 0.91 94.72 ± 1.61 99.15 ± 0.32 98.97 ± 0.21 98.62 ± 0.47 99.23 ± 0.05 [3]-[1] 96.31 ± 0.42 96.99 ± 0.72 97.53 ± 0.14 92.85 ± 0.71 99.12 ± 0.13 96.09 ± 0.77 99.15 ± 0.08 [3]-[2] 97.15 ± 0.29 98.51 ± 0.44 99.49 ± 0.11 95.47 ± 0.93 98.87 ± 0.22 97.53 ± 0.49 99.92 ± 0.03 [3]-[4] 98.88 ± 0.06 99.22 ± 0.34 98.28 ± 0.07 99.64 ± 0.09 99.95 ± 0.13 98.85 ± 0.39 100.0 ± 0.00 [4]-[1] 81.09 ± 1.13 84.35 ± 0.81 88.37 ± 0.13 88.34 ± 0.45 92.23 ± 0.18 95.62 ± 0.42 97.42 ± 0.12 [4]-[2] 84.56 ± 0.75 89.61 ± 0.74 90.43 ± 0.38 87.48 ± 0.73 91.43 ± 0.61 93.26 ± 0.72 95.34 ± 0.21 [4]-[3] 95.93 ± 0.53 96.49 ± 0.63 97.03 ± 0.16 97.42 ± 0.16 98.81 ± 0.09 97.31 ± 0.59 98.82 ± 0.16
表2 中方法之间的性能差距不显著,原因是不同工作负载的数据间的域偏移不明显. 基于不同平台采集的滚动轴承数据集,轴承型号、工作条件、噪声等因素间存在差异. 为了进一步验证模型的迁移性能,在2个数据集上进行跨数据集的域迁移,实验结果如图5 所示. 相较于同一数据集中的域分布,不同轴承数据集间存在更大的域偏移,解耦后的故障相关特征能更好地找到不同数据域之间的故障共性,在所有方法中结果最好. CWRU数据集作为源域数据训练时使用了更多不同工作负载条件下的样本,训练模型的泛化性能更强,因此故障诊断的诊断准确率强于IMS数据集作为源域数据时的准确率. ...
Domain adversarial transfer network for cross-domain fault diagnosis of rotary machinery
2
2020
... 本研究引入基于因果关联的解耦表示学习方法[18 ] ,利用序列变分自动编码器(variational autoencoder, VAE)[19 -21 ] ,在故障标签信息的引导下将序列中与故障具有因果关系的因素提取出来,使故障模式识别更准确,让模型所学知识能够泛化到来自其他域分布的样本. 设备工况、轴承型号、外部噪声等与故障无关的因素很大程度上决定了数据样本的域分布. 在自监督域自适应任务中,样本域分布之间的偏移是模型迁移性能的主要限制因素. 基于对抗的域自适应方法,如域对抗神经网络(domain adversarial neural network, DANN)[12 ] 和条件域对抗网络(conditional domain adversarial network, CDAN)[13 ] ,在源域和目标域间的相似性和差异性中寻找平衡,以提高模型在不同域之间的迁移性能. 直接对原始特征进行对抗式训练,很难同时满足模型迁移性和特征的判别性. 本研究设计域判别损失函数,促进域相关因素的分离,从而提高故障相关因素的判别性;利用多核最大均值差异(multi-kernel maximum mean discrepancy,MK-MMD)[22 ] 来缩小不同工作条件下的数据分布偏移,增强模型的迁移能力. ...
... 由于源域和目标域之间的数据分布不同,域自适应技术须缓解域偏移的影响,学习域不变特征. Tzeng等[9 ] 提出深度领域混淆(deep domain confusion, DDC),在网络中引入自适应层对齐在2个域中学到的特征. Sun等[10 ] 提出深度相关性对齐方法(correlation alignment, CORAL),用CORAL损失替换最大均值差异(maximum mean discrepancy, MMD)距离,以对齐不同域数据分布的二阶统计特征. Ganin等[11 ] 在域自适应中引入对抗思想,提出DANN,在该网络中引入域判别器,以区分数据来自源域还是目标域,并利用梯度反转层进行对抗训练,提高特征的泛化能力. Chen等[12 ] 将DANN应用到滚动轴承的故障诊断任务中,采用交替更新特征提取器与域判别器参数的训练策略,以实现特征提取与域对齐之间的协同优化. DANN很难安全地调整域判别器,Long等[13 ] 提出CDAN,采用多线性调整和熵调整策略来处理域判别器接收的各个训练样本,提高神经网络的迁移学习效果. Jiao等[14 ] 提出无源域自适应(source-free domain adaption, SFDA)故障诊断算法,利用伪标签技术引导目标域数据的训练,避免了对源域数据的访问,同时,利用归一化对称交叉熵损失抑制伪标签噪声带来的负面影响. ...
4
... 本研究引入基于因果关联的解耦表示学习方法[18 ] ,利用序列变分自动编码器(variational autoencoder, VAE)[19 -21 ] ,在故障标签信息的引导下将序列中与故障具有因果关系的因素提取出来,使故障模式识别更准确,让模型所学知识能够泛化到来自其他域分布的样本. 设备工况、轴承型号、外部噪声等与故障无关的因素很大程度上决定了数据样本的域分布. 在自监督域自适应任务中,样本域分布之间的偏移是模型迁移性能的主要限制因素. 基于对抗的域自适应方法,如域对抗神经网络(domain adversarial neural network, DANN)[12 ] 和条件域对抗网络(conditional domain adversarial network, CDAN)[13 ] ,在源域和目标域间的相似性和差异性中寻找平衡,以提高模型在不同域之间的迁移性能. 直接对原始特征进行对抗式训练,很难同时满足模型迁移性和特征的判别性. 本研究设计域判别损失函数,促进域相关因素的分离,从而提高故障相关因素的判别性;利用多核最大均值差异(multi-kernel maximum mean discrepancy,MK-MMD)[22 ] 来缩小不同工作条件下的数据分布偏移,增强模型的迁移能力. ...
... 由于源域和目标域之间的数据分布不同,域自适应技术须缓解域偏移的影响,学习域不变特征. Tzeng等[9 ] 提出深度领域混淆(deep domain confusion, DDC),在网络中引入自适应层对齐在2个域中学到的特征. Sun等[10 ] 提出深度相关性对齐方法(correlation alignment, CORAL),用CORAL损失替换最大均值差异(maximum mean discrepancy, MMD)距离,以对齐不同域数据分布的二阶统计特征. Ganin等[11 ] 在域自适应中引入对抗思想,提出DANN,在该网络中引入域判别器,以区分数据来自源域还是目标域,并利用梯度反转层进行对抗训练,提高特征的泛化能力. Chen等[12 ] 将DANN应用到滚动轴承的故障诊断任务中,采用交替更新特征提取器与域判别器参数的训练策略,以实现特征提取与域对齐之间的协同优化. DANN很难安全地调整域判别器,Long等[13 ] 提出CDAN,采用多线性调整和熵调整策略来处理域判别器接收的各个训练样本,提高神经网络的迁移学习效果. Jiao等[14 ] 提出无源域自适应(source-free domain adaption, SFDA)故障诊断算法,利用伪标签技术引导目标域数据的训练,避免了对源域数据的访问,同时,利用归一化对称交叉熵损失抑制伪标签噪声带来的负面影响. ...
... 测试所提方法在不同域之间的迁移性能,以分类准确率作为评估指标. 实验基于6种方法,包括作为比对的基线方法BASE,以及DDC[9 ] 、CORAL[10 ] 、DANN[11 ] 、CDAN[13 ] 、和SFDA[14 ] . 所有对比方法均采用1个1DCNN作为骨干网络,并连接1个线性分类器进行故障分类[25 ] . BASE在目标域上直接进行测试,不对域自适应任务进行专门设计. 基于CWRU数据集4种不同工作负载下的轴承数据,设计12组迁移实验,结果如表2 所示,其中[1]-[2]表示从第1种到第2种工作负载条件下的迁移,$A$
... Bearing fault diagnosis accuracy of different methods in twelve transfer tasks
Tab.2 迁移任务 A /%BASE DDC[9 ] CORAL[10 ] DANN[11 ] CDAN[13 ] SFDA[14 ] 本研究 [1]-[2] 96.53 ± 0.12 95.71 ± 0.41 94.52 ± 0.51 96.43 ± 0.23 97.59 ± 0.13 96.83 ± 0.79 98.63 ± 0.07 [1]-[3] 92.84 ± 0.49 95.48 ± 0.25 92.34 ± 1.10 96.24 ± 0.53 99.17 ± 0.17 98.63 ± 0.84 99.39 ± 0.13 [1]-[4] 88.91 ± 0.93 92.19 ± 0.58 91.56 ± 2.08 97.82 ± 0.36 98.32 ± 0.21 96.25 ± 0.66 98.69 ± 0.19 [2]-[1] 98.82 ± 0.07 98.96 ± 0.43 98.33 ± 0.24 98.65 ± 0.20 99.10 ± 0.26 98.25 ± 0.45 99.89 ± 0.06 [2]-[3] 98.56 ± 0.21 97.79 ± 0.26 98.82 ± 0.09 99.37 ± 0.18 99.53 ± 0.06 97.22 ± 0.76 99.64 ± 0.09 [2]-[4] 92.67 ± 0.18 93.48 ± 0.91 94.72 ± 1.61 99.15 ± 0.32 98.97 ± 0.21 98.62 ± 0.47 99.23 ± 0.05 [3]-[1] 96.31 ± 0.42 96.99 ± 0.72 97.53 ± 0.14 92.85 ± 0.71 99.12 ± 0.13 96.09 ± 0.77 99.15 ± 0.08 [3]-[2] 97.15 ± 0.29 98.51 ± 0.44 99.49 ± 0.11 95.47 ± 0.93 98.87 ± 0.22 97.53 ± 0.49 99.92 ± 0.03 [3]-[4] 98.88 ± 0.06 99.22 ± 0.34 98.28 ± 0.07 99.64 ± 0.09 99.95 ± 0.13 98.85 ± 0.39 100.0 ± 0.00 [4]-[1] 81.09 ± 1.13 84.35 ± 0.81 88.37 ± 0.13 88.34 ± 0.45 92.23 ± 0.18 95.62 ± 0.42 97.42 ± 0.12 [4]-[2] 84.56 ± 0.75 89.61 ± 0.74 90.43 ± 0.38 87.48 ± 0.73 91.43 ± 0.61 93.26 ± 0.72 95.34 ± 0.21 [4]-[3] 95.93 ± 0.53 96.49 ± 0.63 97.03 ± 0.16 97.42 ± 0.16 98.81 ± 0.09 97.31 ± 0.59 98.82 ± 0.16
表2 中方法之间的性能差距不显著,原因是不同工作负载的数据间的域偏移不明显. 基于不同平台采集的滚动轴承数据集,轴承型号、工作条件、噪声等因素间存在差异. 为了进一步验证模型的迁移性能,在2个数据集上进行跨数据集的域迁移,实验结果如图5 所示. 相较于同一数据集中的域分布,不同轴承数据集间存在更大的域偏移,解耦后的故障相关特征能更好地找到不同数据域之间的故障共性,在所有方法中结果最好. CWRU数据集作为源域数据训练时使用了更多不同工作负载条件下的样本,训练模型的泛化性能更强,因此故障诊断的诊断准确率强于IMS数据集作为源域数据时的准确率. ...
Source-free adaptation diagnosis for rotating machinery
3
2023
... 由于源域和目标域之间的数据分布不同,域自适应技术须缓解域偏移的影响,学习域不变特征. Tzeng等[9 ] 提出深度领域混淆(deep domain confusion, DDC),在网络中引入自适应层对齐在2个域中学到的特征. Sun等[10 ] 提出深度相关性对齐方法(correlation alignment, CORAL),用CORAL损失替换最大均值差异(maximum mean discrepancy, MMD)距离,以对齐不同域数据分布的二阶统计特征. Ganin等[11 ] 在域自适应中引入对抗思想,提出DANN,在该网络中引入域判别器,以区分数据来自源域还是目标域,并利用梯度反转层进行对抗训练,提高特征的泛化能力. Chen等[12 ] 将DANN应用到滚动轴承的故障诊断任务中,采用交替更新特征提取器与域判别器参数的训练策略,以实现特征提取与域对齐之间的协同优化. DANN很难安全地调整域判别器,Long等[13 ] 提出CDAN,采用多线性调整和熵调整策略来处理域判别器接收的各个训练样本,提高神经网络的迁移学习效果. Jiao等[14 ] 提出无源域自适应(source-free domain adaption, SFDA)故障诊断算法,利用伪标签技术引导目标域数据的训练,避免了对源域数据的访问,同时,利用归一化对称交叉熵损失抑制伪标签噪声带来的负面影响. ...
... 测试所提方法在不同域之间的迁移性能,以分类准确率作为评估指标. 实验基于6种方法,包括作为比对的基线方法BASE,以及DDC[9 ] 、CORAL[10 ] 、DANN[11 ] 、CDAN[13 ] 、和SFDA[14 ] . 所有对比方法均采用1个1DCNN作为骨干网络,并连接1个线性分类器进行故障分类[25 ] . BASE在目标域上直接进行测试,不对域自适应任务进行专门设计. 基于CWRU数据集4种不同工作负载下的轴承数据,设计12组迁移实验,结果如表2 所示,其中[1]-[2]表示从第1种到第2种工作负载条件下的迁移,$A$
... Bearing fault diagnosis accuracy of different methods in twelve transfer tasks
Tab.2 迁移任务 A /%BASE DDC[9 ] CORAL[10 ] DANN[11 ] CDAN[13 ] SFDA[14 ] 本研究 [1]-[2] 96.53 ± 0.12 95.71 ± 0.41 94.52 ± 0.51 96.43 ± 0.23 97.59 ± 0.13 96.83 ± 0.79 98.63 ± 0.07 [1]-[3] 92.84 ± 0.49 95.48 ± 0.25 92.34 ± 1.10 96.24 ± 0.53 99.17 ± 0.17 98.63 ± 0.84 99.39 ± 0.13 [1]-[4] 88.91 ± 0.93 92.19 ± 0.58 91.56 ± 2.08 97.82 ± 0.36 98.32 ± 0.21 96.25 ± 0.66 98.69 ± 0.19 [2]-[1] 98.82 ± 0.07 98.96 ± 0.43 98.33 ± 0.24 98.65 ± 0.20 99.10 ± 0.26 98.25 ± 0.45 99.89 ± 0.06 [2]-[3] 98.56 ± 0.21 97.79 ± 0.26 98.82 ± 0.09 99.37 ± 0.18 99.53 ± 0.06 97.22 ± 0.76 99.64 ± 0.09 [2]-[4] 92.67 ± 0.18 93.48 ± 0.91 94.72 ± 1.61 99.15 ± 0.32 98.97 ± 0.21 98.62 ± 0.47 99.23 ± 0.05 [3]-[1] 96.31 ± 0.42 96.99 ± 0.72 97.53 ± 0.14 92.85 ± 0.71 99.12 ± 0.13 96.09 ± 0.77 99.15 ± 0.08 [3]-[2] 97.15 ± 0.29 98.51 ± 0.44 99.49 ± 0.11 95.47 ± 0.93 98.87 ± 0.22 97.53 ± 0.49 99.92 ± 0.03 [3]-[4] 98.88 ± 0.06 99.22 ± 0.34 98.28 ± 0.07 99.64 ± 0.09 99.95 ± 0.13 98.85 ± 0.39 100.0 ± 0.00 [4]-[1] 81.09 ± 1.13 84.35 ± 0.81 88.37 ± 0.13 88.34 ± 0.45 92.23 ± 0.18 95.62 ± 0.42 97.42 ± 0.12 [4]-[2] 84.56 ± 0.75 89.61 ± 0.74 90.43 ± 0.38 87.48 ± 0.73 91.43 ± 0.61 93.26 ± 0.72 95.34 ± 0.21 [4]-[3] 95.93 ± 0.53 96.49 ± 0.63 97.03 ± 0.16 97.42 ± 0.16 98.81 ± 0.09 97.31 ± 0.59 98.82 ± 0.16
表2 中方法之间的性能差距不显著,原因是不同工作负载的数据间的域偏移不明显. 基于不同平台采集的滚动轴承数据集,轴承型号、工作条件、噪声等因素间存在差异. 为了进一步验证模型的迁移性能,在2个数据集上进行跨数据集的域迁移,实验结果如图5 所示. 相较于同一数据集中的域分布,不同轴承数据集间存在更大的域偏移,解耦后的故障相关特征能更好地找到不同数据域之间的故障共性,在所有方法中结果最好. CWRU数据集作为源域数据训练时使用了更多不同工作负载条件下的样本,训练模型的泛化性能更强,因此故障诊断的诊断准确率强于IMS数据集作为源域数据时的准确率. ...
Intelligent fault diagnosis by fusing domain adversarial training and maximum mean discrepancy via ensemble learning
0
2021
Joint distribution adaptation network with adversarial learning for rolling bearing fault diagnosis
1
2021
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
Explainable deep learning: a field guide for the uninitiated
1
2022
... 相比传统的基于专家系统的方法[2 ] ,数据驱动的故障诊断方法[3 -5 ] 对先验知识(如设备运行机理)的依赖减少,应用潜力大. 深度学习方法[6 -8 ] 属于数据驱动方法,在挖掘潜层特征上有优势,但严重依赖标签数据的引导,限制了其在工业实践中的大范围应用. 一系列自监督域自适应方法[9 -16 ] 被陆续提出,它们在源域数据上有监督地进行训练后,将所学知识迁移到无标签的目标域,减少了对标签数据的依赖,降低了数据分析和标注的成本. 由于设备结构的复杂性,采集的轴承振动信号同时记录了各种与故障无关的混淆因素. 在弱监督背景下,深度神经网络的学习过程不可避免地受这些无关变量干扰,学习到错误的关联关系,抑制模型的泛化性能[17 ] . ...
2
... 本研究引入基于因果关联的解耦表示学习方法[18 ] ,利用序列变分自动编码器(variational autoencoder, VAE)[19 -21 ] ,在故障标签信息的引导下将序列中与故障具有因果关系的因素提取出来,使故障模式识别更准确,让模型所学知识能够泛化到来自其他域分布的样本. 设备工况、轴承型号、外部噪声等与故障无关的因素很大程度上决定了数据样本的域分布. 在自监督域自适应任务中,样本域分布之间的偏移是模型迁移性能的主要限制因素. 基于对抗的域自适应方法,如域对抗神经网络(domain adversarial neural network, DANN)[12 ] 和条件域对抗网络(conditional domain adversarial network, CDAN)[13 ] ,在源域和目标域间的相似性和差异性中寻找平衡,以提高模型在不同域之间的迁移性能. 直接对原始特征进行对抗式训练,很难同时满足模型迁移性和特征的判别性. 本研究设计域判别损失函数,促进域相关因素的分离,从而提高故障相关因素的判别性;利用多核最大均值差异(multi-kernel maximum mean discrepancy,MK-MMD)[22 ] 来缩小不同工作条件下的数据分布偏移,增强模型的迁移能力. ...
... 解耦表示学习旨在找到一种特别的潜层变量表示,其中每个潜层变量捕获的数据变化独立于其他潜层变量,即每个潜层变量控制数据的某个独立因素[18 ] . 解耦表示学习方法大多基于VAE架构[19 ] ,通过最大化证据下界(evidence lower bound,ELBO)进行优化,损失函数表示为 ...
3
... 本研究引入基于因果关联的解耦表示学习方法[18 ] ,利用序列变分自动编码器(variational autoencoder, VAE)[19 -21 ] ,在故障标签信息的引导下将序列中与故障具有因果关系的因素提取出来,使故障模式识别更准确,让模型所学知识能够泛化到来自其他域分布的样本. 设备工况、轴承型号、外部噪声等与故障无关的因素很大程度上决定了数据样本的域分布. 在自监督域自适应任务中,样本域分布之间的偏移是模型迁移性能的主要限制因素. 基于对抗的域自适应方法,如域对抗神经网络(domain adversarial neural network, DANN)[12 ] 和条件域对抗网络(conditional domain adversarial network, CDAN)[13 ] ,在源域和目标域间的相似性和差异性中寻找平衡,以提高模型在不同域之间的迁移性能. 直接对原始特征进行对抗式训练,很难同时满足模型迁移性和特征的判别性. 本研究设计域判别损失函数,促进域相关因素的分离,从而提高故障相关因素的判别性;利用多核最大均值差异(multi-kernel maximum mean discrepancy,MK-MMD)[22 ] 来缩小不同工作条件下的数据分布偏移,增强模型的迁移能力. ...
... 解耦表示学习旨在找到一种特别的潜层变量表示,其中每个潜层变量捕获的数据变化独立于其他潜层变量,即每个潜层变量控制数据的某个独立因素[18 ] . 解耦表示学习方法大多基于VAE架构[19 ] ,通过最大化证据下界(evidence lower bound,ELBO)进行优化,损失函数表示为 ...
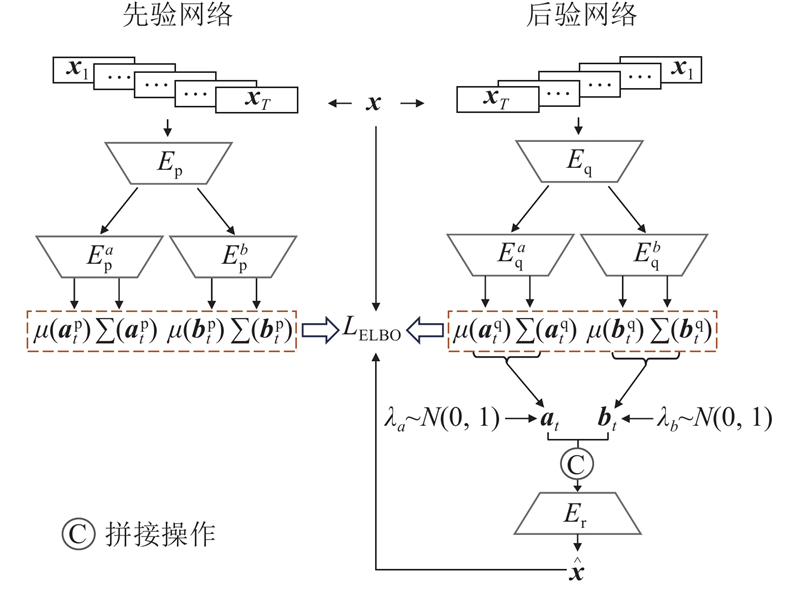
... 后验网络的编码器$ {E_{\text{q}}} $ $ {E_{\text{r}}} $ $ p\left( {{{\boldsymbol{d}}_t}\mid {{\boldsymbol{d}}_{t - 1}},{{\boldsymbol{x}}_t}} \right) $ [19 ] 从正态分布$ N\left( {{\mu _\theta }\left( {{{\boldsymbol{d}}_{t - 1}},{{\boldsymbol{x}}_t}} \right),{\Sigma _\theta }\left( {{{\boldsymbol{d}}_{t - 1}},{{\boldsymbol{x}}_t}} \right)} \right) $ $ E_q^{{a}} $ $ E_q^{{{{b}}}} $ ${p_\theta }\left( {{{\boldsymbol{o}}_T}\mid {{\boldsymbol{d}}_{T - 1}}} \right)$ ${{\boldsymbol{a}}_T}$ ${{\boldsymbol{b}}_T}$ ${q_\phi }\left( {{{\boldsymbol{d}}_t}\mid {{\boldsymbol{d}}_{t - 1}},\;{{\boldsymbol{x}}_t}} \right)$ $ N(\mu_{\phi}(\boldsymbol{d}_{t-1},\boldsymbol{x}_t),\; \mathit{\Sigma}_{\phi} (\boldsymbol{d}_{t-1}, \boldsymbol{x}_t)) $ . 在高斯分布中采样后, VAE的解码器$ {E_{\text{r}}} $
1
... 式中:$ {\boldsymbol{x}} $ $ {\boldsymbol{h}} $ $ {L_{{\text{VAE}}}} $ $ {q_\phi }({\boldsymbol{h}}|{\boldsymbol{x}}) $ $ p({\boldsymbol{h}}) $ $ {p_\theta }({\boldsymbol{x}}|{\boldsymbol{h}}) $ [20 ] 提出的β -VAE是解耦表示学习中的重要工作,通过引入超参数$\beta $ $\beta $
3
... 本研究引入基于因果关联的解耦表示学习方法[18 ] ,利用序列变分自动编码器(variational autoencoder, VAE)[19 -21 ] ,在故障标签信息的引导下将序列中与故障具有因果关系的因素提取出来,使故障模式识别更准确,让模型所学知识能够泛化到来自其他域分布的样本. 设备工况、轴承型号、外部噪声等与故障无关的因素很大程度上决定了数据样本的域分布. 在自监督域自适应任务中,样本域分布之间的偏移是模型迁移性能的主要限制因素. 基于对抗的域自适应方法,如域对抗神经网络(domain adversarial neural network, DANN)[12 ] 和条件域对抗网络(conditional domain adversarial network, CDAN)[13 ] ,在源域和目标域间的相似性和差异性中寻找平衡,以提高模型在不同域之间的迁移性能. 直接对原始特征进行对抗式训练,很难同时满足模型迁移性和特征的判别性. 本研究设计域判别损失函数,促进域相关因素的分离,从而提高故障相关因素的判别性;利用多核最大均值差异(multi-kernel maximum mean discrepancy,MK-MMD)[22 ] 来缩小不同工作条件下的数据分布偏移,增强模型的迁移能力. ...
... 因果马尔科夫条件(causal Markov condition,CMC)使得DAG中的因果变量得以解耦[21 ] . 因此,原始振动数据${{\boldsymbol{x}}_t}$ ${{\boldsymbol{a}}_t}$ ${{\boldsymbol{b}}_t}$
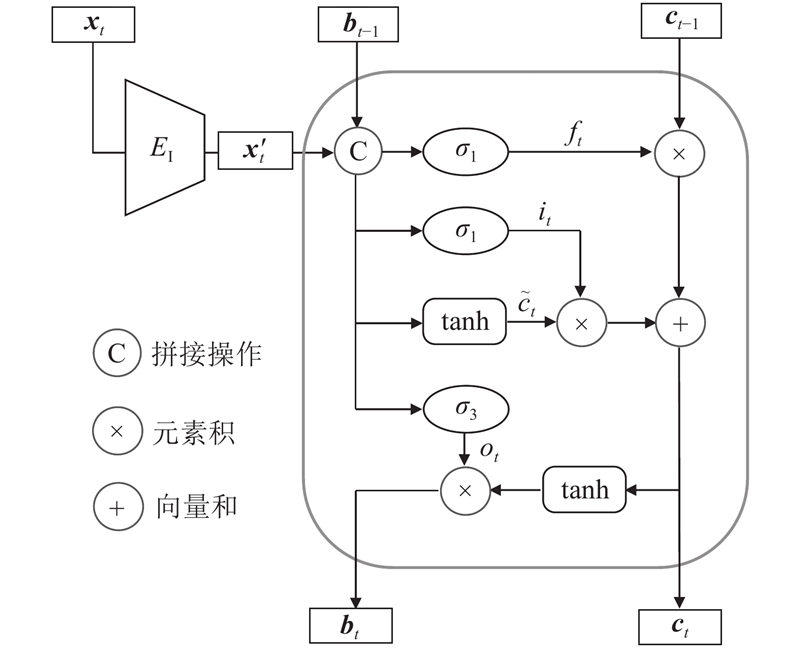
... 为了分离故障相关变量和故障无关变量,构建序列VAE[21 ] 对时间序列进行因果解耦. 如图2 所示,解耦网络包括1个先验网络和1个后验网络. 先验网络由1个基于LSTM的特征编码器$ {E_{\text{p}}} $ [24 ] 和2个基于全连接层的解耦单元$ E_{\text{p}}^{{a}} $ $ E_{\text{p}}^{{{{b}}}} $ $ {E_{\text{q}}} $ $ {E_{\text{r}}} $ $ E_{\text{q}}^{{a}} $ $ E_{\text{q}}^{{{{b}}}} $ $\theta $ $ {p_\theta }({{\boldsymbol{d}}_t}|{{\boldsymbol{d}}_{t - 1}},{{\boldsymbol{x}}_t}) $ . VAE进行信号重建,有分布$ {p_\theta }({{\boldsymbol{x}}_t}\mid {{\boldsymbol{d}}_t}) $ $\phi $ $ {q_\phi }({{\boldsymbol{d}}_t}|{{\boldsymbol{x}}_t},{{\boldsymbol{o}}_T}) $ . 故障类型和域标签的学习表示为$ {p_\theta }({{\boldsymbol{o}}_T}|{{\boldsymbol{d}}_{T - 1}}) $ . ...
Transferable representation learning with deep adaptation networks
2
2019
... 本研究引入基于因果关联的解耦表示学习方法[18 ] ,利用序列变分自动编码器(variational autoencoder, VAE)[19 -21 ] ,在故障标签信息的引导下将序列中与故障具有因果关系的因素提取出来,使故障模式识别更准确,让模型所学知识能够泛化到来自其他域分布的样本. 设备工况、轴承型号、外部噪声等与故障无关的因素很大程度上决定了数据样本的域分布. 在自监督域自适应任务中,样本域分布之间的偏移是模型迁移性能的主要限制因素. 基于对抗的域自适应方法,如域对抗神经网络(domain adversarial neural network, DANN)[12 ] 和条件域对抗网络(conditional domain adversarial network, CDAN)[13 ] ,在源域和目标域间的相似性和差异性中寻找平衡,以提高模型在不同域之间的迁移性能. 直接对原始特征进行对抗式训练,很难同时满足模型迁移性和特征的判别性. 本研究设计域判别损失函数,促进域相关因素的分离,从而提高故障相关因素的判别性;利用多核最大均值差异(multi-kernel maximum mean discrepancy,MK-MMD)[22 ] 来缩小不同工作条件下的数据分布偏移,增强模型的迁移能力. ...
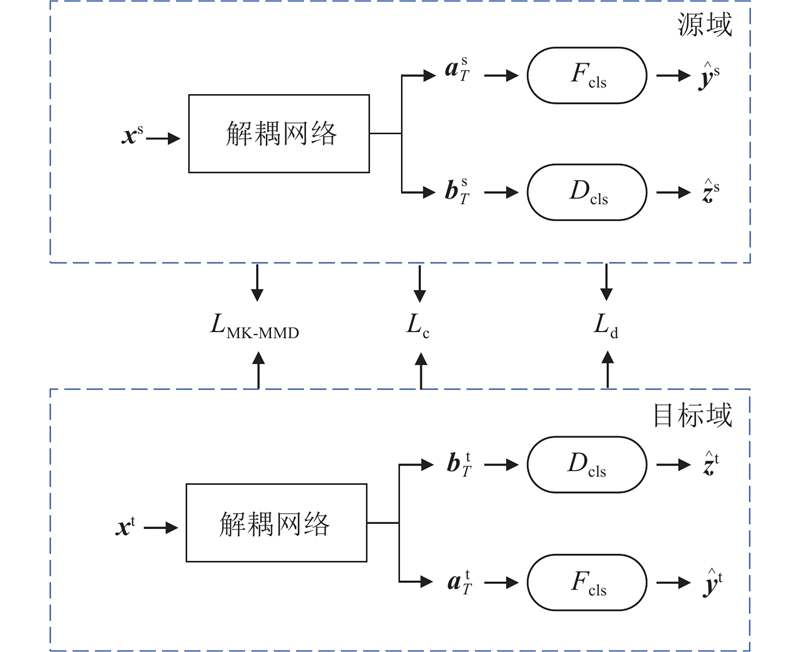
... 由于源域和目标域的设备型号、工作状态、观测条件不同,采集数据之间往往存在域偏移,限制了模型的迁移能力. 解耦学习从采集样本中分离出反映设备工况的故障无关因素${{\boldsymbol{b}}_T}$ 图4 所示,模型结合源域和目标域数据同时进行训练,在解耦出故障相关因素${{\boldsymbol{a}}_T}$ ${{\boldsymbol{b}}_T}$ ${F_{{\text{cls}}}}$ ${D_{{\text{cls}}}}$ ${F_{{\text{cls}}}}$ ${D_{{\text{cls}}}}$ [22 ] 充分衡量源域和目标域之间的差异. MK-MMD源于MMD,MMD将低维数据映射到高维的再生核希尔伯特空间(reproducing kernel Hilbert space, RKHS)中,并利用核技巧(核函数与特征映射之间的内积满足$ k({{\boldsymbol{x}}^{\text{s}}},{{\boldsymbol{x}}^{\text{t}}}) = < \varphi ({{\boldsymbol{x}}^{\text{s}}}),\varphi ({{\boldsymbol{x}}^{\text{t}}}) > $
1
... 对于DAG中任一节点变量${\boldsymbol{v}}$ $ {f_v}\; {{}^{\underline{\underline {{\mathrm{def}}}}}} \left( {{\text{pa}}\left( {\boldsymbol{v}} \right),{\varepsilon _v}} \right) $ [23 ] ,其中${\text{pa}}\left( {\boldsymbol{v}} \right)$ ${\boldsymbol{v}}$ $ {\varepsilon _v} $ 图1 中变量的相关性表示为 ...
LSTM-based auto-encoder model for ECG arrhythmias classification
1
2020
... 为了分离故障相关变量和故障无关变量,构建序列VAE[21 ] 对时间序列进行因果解耦. 如图2 所示,解耦网络包括1个先验网络和1个后验网络. 先验网络由1个基于LSTM的特征编码器$ {E_{\text{p}}} $ [24 ] 和2个基于全连接层的解耦单元$ E_{\text{p}}^{{a}} $ $ E_{\text{p}}^{{{{b}}}} $ $ {E_{\text{q}}} $ $ {E_{\text{r}}} $ $ E_{\text{q}}^{{a}} $ $ E_{\text{q}}^{{{{b}}}} $ $\theta $ $ {p_\theta }({{\boldsymbol{d}}_t}|{{\boldsymbol{d}}_{t - 1}},{{\boldsymbol{x}}_t}) $ . VAE进行信号重建,有分布$ {p_\theta }({{\boldsymbol{x}}_t}\mid {{\boldsymbol{d}}_t}) $ $\phi $ $ {q_\phi }({{\boldsymbol{d}}_t}|{{\boldsymbol{x}}_t},{{\boldsymbol{o}}_T}) $ . 故障类型和域标签的学习表示为$ {p_\theta }({{\boldsymbol{o}}_T}|{{\boldsymbol{d}}_{T - 1}}) $ . ...
Applications of unsupervised deep transfer learning to intelligent fault diagnosis: a survey and comparative study
2
2021
... 式中:$ {\beta _u} $ $u$ $ {k_u} $ $u$ $m$ [25 ] 的设置,采用高斯径向基函数,核函数数量$m$ $ {\beta _u} = 1/m $ . 为了准确识别故障,故障相关变量和故障无关变量的后验$ {\boldsymbol{a}}_T^q $ $ {\boldsymbol{b}}_T^q $
... 测试所提方法在不同域之间的迁移性能,以分类准确率作为评估指标. 实验基于6种方法,包括作为比对的基线方法BASE,以及DDC[9 ] 、CORAL[10 ] 、DANN[11 ] 、CDAN[13 ] 、和SFDA[14 ] . 所有对比方法均采用1个1DCNN作为骨干网络,并连接1个线性分类器进行故障分类[25 ] . BASE在目标域上直接进行测试,不对域自适应任务进行专门设计. 基于CWRU数据集4种不同工作负载下的轴承数据,设计12组迁移实验,结果如表2 所示,其中[1]-[2]表示从第1种到第2种工作负载条件下的迁移,$A$
Rolling element bearing diagnostics using the Case Western Reserve University data: a benchmark study
1
2015
... 为了评估所提出模型的解耦能力和迁移性能,在凯斯西储大学轴承(Case Western Reserve University,CWRU)数据集[26 ] 和智能维护系统(intelligent maintenance systems, IMS)数据集[27 ] 上进行实验验证. 1)CWRU数据集:实验基于12 kHz 的驱动端轴承传感器数据,如表1 所示为该数据集工作负载参数,其中$l$ v 为转速,N 1 为样本数. 在迁移性能验证实验中,根据轴承的工作负载(电动机负荷和电动机转速)的不同,划分为4个数据域;根据故障直径(0.1778 mm、0.3556 mm和0.5334 mm)和故障位置(轴承内圈、滚珠和外圈)的不同,划分为10种故障. 2)IMS数据集包含在一定测试条件下(轴转速为2000 r·min−1 ,径向载荷为26689.34 N)的4种轴承健康状态:正常样本,以及轴承内圈、滚珠和外圈故障. 在实验中,每个样本长度为1 200个时间步,滑动窗口宽度为400个时间步,滑动步长为200个时间步. 每个样本的时间阶数$T = 5$ . 源域和目标域均按8∶2划分训练集和测试集,实验采用Adam优化器进行训练,初始学习率为$1 \times {10^{ - 4}}$
Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics
1
2006
... 为了评估所提出模型的解耦能力和迁移性能,在凯斯西储大学轴承(Case Western Reserve University,CWRU)数据集[26 ] 和智能维护系统(intelligent maintenance systems, IMS)数据集[27 ] 上进行实验验证. 1)CWRU数据集:实验基于12 kHz 的驱动端轴承传感器数据,如表1 所示为该数据集工作负载参数,其中$l$ v 为转速,N 1 为样本数. 在迁移性能验证实验中,根据轴承的工作负载(电动机负荷和电动机转速)的不同,划分为4个数据域;根据故障直径(0.1778 mm、0.3556 mm和0.5334 mm)和故障位置(轴承内圈、滚珠和外圈)的不同,划分为10种故障. 2)IMS数据集包含在一定测试条件下(轴转速为2000 r·min−1 ,径向载荷为26689.34 N)的4种轴承健康状态:正常样本,以及轴承内圈、滚珠和外圈故障. 在实验中,每个样本长度为1 200个时间步,滑动窗口宽度为400个时间步,滑动步长为200个时间步. 每个样本的时间阶数$T = 5$ . 源域和目标域均按8∶2划分训练集和测试集,实验采用Adam优化器进行训练,初始学习率为$1 \times {10^{ - 4}}$
Rolling element bearing diagnostics: a tutorial
1
2011
... 将DANN与本研究所提方法的实验结果进行可视化分析,如图6 所示为2种方法的诊断结果混淆矩阵. 为了提高结果的代表性,采用训练集上最后1个迭代轮次得到的模型,数据基于CWRU数据集上的迁移任务[3]-[1]. 图中,故障类别1为正常类,类别2~4分别表示尺寸为0.1778 mm的内圈、滚珠和外圈故障,类别5~7、8~10分别表示尺寸为0.3556 mm和0.5334 mm的3种故障. 在迁移到目标域数据后,DANN对滚珠处故障识别效果较差,较难区分不同尺寸故障(类别3、类别6和类别9)之间的差异. 滚珠在轴承运转过程中具有复杂的运动轨迹和不断变化的接触点,因而滚珠故障的振动信号表现出更多随机性和复杂频谱成分[1 , 28 ] ,在不同工况下对震动信号的域分布影响较大,导致DANN模型在迁移后没有从目标域数据中学习到清晰的决策边界. DANN采用域对抗的训练策略,需要在特征域判别性和类判别性之间寻找平衡,在不同尺寸的故障类间差异较小而域间差异较大的情况下,易受无关因素的干扰,很难达到最优的诊断结果. 本研究的解耦方法能够有效分离出与故障类直接因果相关的信息,降低其他因素的干扰,提高所学特征的类间差异,故障分类结果更好. ...
Visualizing data using t-SNE
1
2008
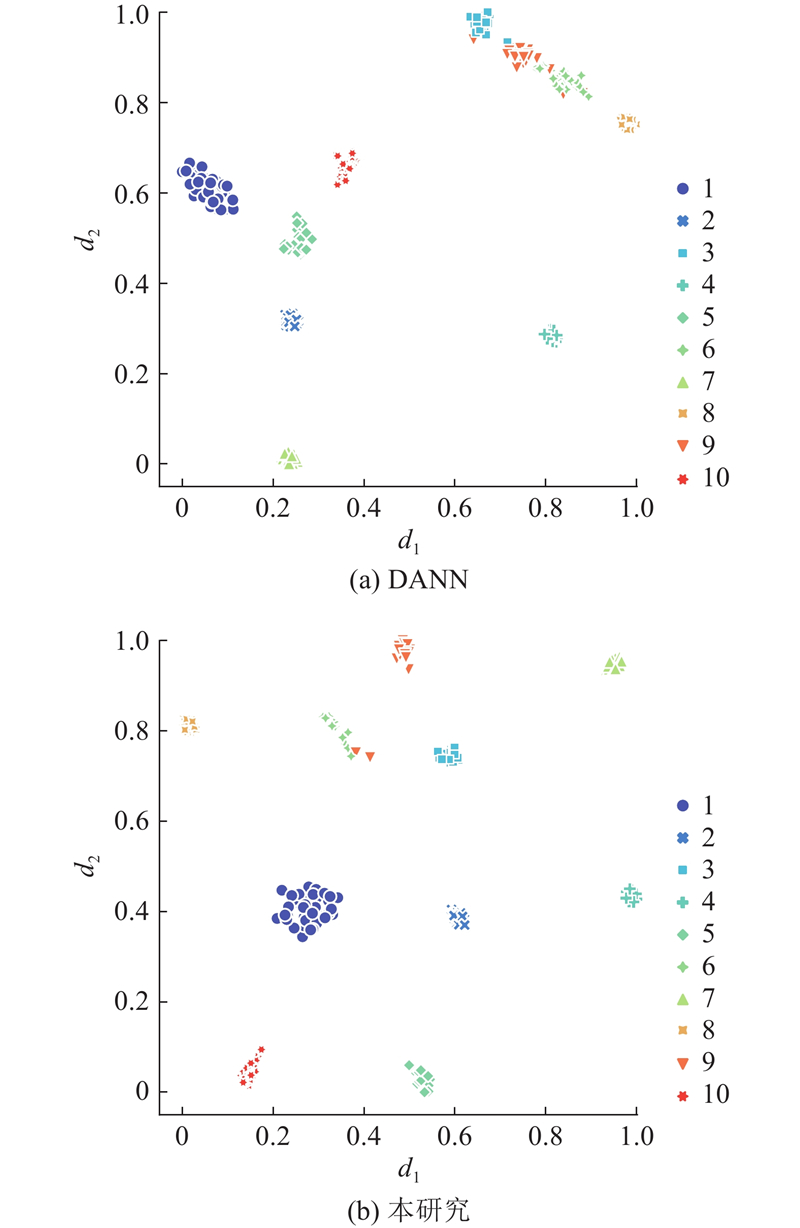
... 基于t分布随机领域嵌入(t-distributed stochastic neighbor embedding,t-SNE)降维算法[29 ] ,将迁移任务[3]-[1]中学到的特征映射到二维平面,如图7 所示,${d_1}$ ${d_2}$