[1]
TEDJOPURNOMO D A, BAO Z, ZHENG B, et al A survey on modern deep neural network for traffic prediction: trends, methods and challenges
[J]. IEEE Transactions on Knowledge and Data Engineering , 2022 , 34 (4 ): 1544 - 1561
[本文引用: 1]
[2]
KUMAR S V, VANAJAKSHI L Short-term traffic flow prediction using seasonal ARIMA model with limited input data
[J]. European Transport Research Review , 2015 , 7 (3 ): 21
DOI:10.1007/s12544-015-0170-8
[本文引用: 2]
[3]
CASTRO-NETO M, JEONG Y S, JEONG M K, et al Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions
[J]. Expert Systems with Applications , 2009 , 36 (3 ): 6164 - 6173
DOI:10.1016/j.eswa.2008.07.069
[本文引用: 2]
[4]
ZHANG J, ZHENG Y, QI D Deep spatio-temporal residual networks for citywide crowd flows prediction
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2017 , 31 (1 ): 1655 - 1661
[本文引用: 1]
[5]
YAO H, TANG X, WEI H, et al Revisiting spatial-temporal similarity: a deep learning framework for traffic prediction
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2019 , 33 (1 ): 5668 - 5675
DOI:10.1609/aaai.v33i01.33015668
[本文引用: 1]
[6]
SHI X, CHEN Z, WANG H, et al. Convolutional LSTM network [C]// Proceedings of the 29th International Conference on Neural Information Processing Systems - Volume 1 . Montreal: ACM, 2015: 802–810.
[本文引用: 2]
[7]
YAO H, WU F, KE J, et al Deep multi-view spatial-temporal network for taxi demand prediction
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2018 , 32 (1 ): 2588 - 2595
[本文引用: 1]
[8]
LI Y, YU R, SHAHABI C, et al. Diffusion convolutional recurrent neural network: data-driven traffic forecasting [EB/OL]. (2018–02–22)[2024–07–23]. https://arxiv.org/pdf/1707.01926.
[本文引用: 2]
[9]
LIN H, BAI R, JIA W, et al. Preserving dynamic attention for long-term spatial-temporal prediction [C]// Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . [S. l.]: ACM, 2020: 36–46.
[本文引用: 1]
[10]
BAI L, YAO L, LI C, et al. Adaptive graph convolutional recurrent network for traffic forecasting [C]// Proceedings of the 34th International Conference on Neural Information Processing Systems . Vancouver: ACM, 2020: 17804–17815.
[本文引用: 3]
[11]
YU B, YIN H, ZHU Z. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting [C]// Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence . Stockholm: IJCAI, 2018: 3634–3640.
[本文引用: 3]
[12]
WU Z, PAN S, LONG G, et al. Graph WaveNet for deep spatial-temporal graph modeling [C]// Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence . Macao: IJCAI, 2019: 1907−1913.
[本文引用: 3]
[13]
CHOI J, CHOI H, HWANG J, et al Graph neural controlled differential equations for traffic forecasting
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2022 , 36 (6 ): 6367 - 6374
DOI:10.1609/aaai.v36i6.20587
[本文引用: 1]
[14]
黄靖, 钟书远, 文元桥, 等 用于交通流预测的自适应图生成跳跃网络
[J]. 浙江大学学报: 工学版 , 2021 , 55 (10 ): 1825 - 1833
[本文引用: 1]
HUANG Jing, ZHONG Shuyuan, WEN Yuanqiao, et al Adaptive graph generation jump network for traffic flow prediction
[J]. Journal of Zhejiang University: Engineering Science , 2021 , 55 (10 ): 1825 - 1833
[本文引用: 1]
[15]
贺文武, 裴博彧, 李雅婷, 等 基于双向自适应门控图卷积网络的交通流预测
[J]. 交通运输系统工程与信息 , 2023 , 23 (1 ): 187 - 197
[本文引用: 1]
HE Wenwu, PEI Boyu, LI Yating, et al Traffic flow forecasting based on bi-directional adaptive gating graph convolutional networks
[J]. Journal of Transportation Systems Engineering and Information Technology , 2023 , 23 (1 ): 187 - 197
[本文引用: 1]
[16]
闫旭, 范晓亮, 郑传潘, 等 基于图卷积神经网络的城市交通态势预测算法
[J]. 浙江大学学报: 工学版 , 2020 , 54 (6 ): 1147 - 1155
[本文引用: 1]
YAN Xu, FAN Xiaoliang, ZHENG Chuanpan, et al Urban traffic flow prediction algorithm based on graph convolutional neural networks
[J]. Journal of Zhejiang University: Engineering Science , 2020 , 54 (6 ): 1147 - 1155
[本文引用: 1]
[17]
WANG B, LONG Z, SHENG J, et al Spatial–temporal similarity fusion graph adversarial convolutional networks for traffic flow forecasting
[J]. Journal of the Franklin Institute , 2024 , 361 (17 ): 107299
DOI:10.1016/j.jfranklin.2024.107299
[本文引用: 3]
[18]
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need [EB/OL]. (2023–08–02)[2024–07–23]. https://arxiv.org/pdf/1706.03762.
[本文引用: 3]
[19]
JIANG J, HAN C, ZHAO W X, et al PDFormer: propagation delay-aware dynamic long-range transformer for traffic flow prediction
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2023 , 37 (4 ): 4365 - 4373
DOI:10.1609/aaai.v37i4.25556
[本文引用: 1]
[20]
LIU H, DONG Z, JIANG R, et al. Spatio-temporal adaptive embedding makes vanilla transformer SOTA for traffic forecasting [C]// Proceedings of the 32nd ACM International Conference on Information and Knowledge Management . Birmingham: ACM, 2023: 4125–4129.
[本文引用: 1]
[21]
GAO H, JIANG R, DONG Z, et al. Spatial-temporal-decoupled masked pre-training for spatiotemporal forecasting [EB/OL]. (2024–04–28)[2024–07–23]. https://arxiv.org/pdf/2312.00516.
[本文引用: 1]
[22]
DEVLIN J, CHANG M W, LEE K, et al. BERT: pre-training of deep bidirectional transformers for language understanding [C]// Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies . Minneapolis: ACL, 2019: 4171–4186.
[本文引用: 1]
[23]
BAO H, DONG L, PIAO S, et al. BEiT: BERT pre-training of image transformers [EB/OL]. (2022–09–03)[2024–07–23]. https://arxiv.org/pdf/2106.08254.
[本文引用: 1]
[24]
NIE Y, NGUYEN N H, SINTHONG P, et al. A time series is worth 64 words: long-term forecasting with transformers [EB/OL]. (2023–03–05)[2024–07–23]. https://arxiv.org/pdf/2211.14730.
[本文引用: 1]
[25]
WANG Z, LIU J C Translating math formula images to LaTeX sequences using deep neural networks with sequence-level training
[J]. International Journal on Document Analysis and Recognition , 2021 , 24 (1/2 ): 63 - 75
[本文引用: 1]
[26]
LI M, ZHU Z Spatial-temporal fusion graph neural networks for traffic flow forecasting
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2021 , 35 (5 ): 4189 - 4196
DOI:10.1609/aaai.v35i5.16542
[本文引用: 1]
[27]
GUO S, LIN Y, FENG N, et al Attention based spatial-temporal graph convolutional networks for traffic flow forecasting
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2019 , 33 (1 ): 922 - 929
DOI:10.1609/aaai.v33i01.3301922
[本文引用: 1]
[28]
LAN S, MA Y, HUANG W, et al. DSTAGNN: dynamic spatial-temporal aware graph neural network for traffic flow forecasting [C]// Proceeding of the 39th International Conference on Machine Learning . [S. l.]: PMLR, 2022, 162: 11906–11917.
[本文引用: 2]
[29]
GUO S, LIN Y, WAN H, et al Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting
[J]. IEEE Transactions on Knowledge and Data Engineering , 2022 , 34 (11 ): 5415 - 5428
DOI:10.1109/TKDE.2021.3056502
[本文引用: 2]
[30]
CHU Z, MA W, LI M, et al Adaptive decision spatio-temporal neural ode for traffic flow forecasting with multi-kernel temporal dynamic dilation convolution
[J]. Neural Networks , 2024 , 179 : 106549
DOI:10.1016/j.neunet.2024.106549
[本文引用: 2]
A survey on modern deep neural network for traffic prediction: trends, methods and challenges
1
2022
... 智能交通的核心是交通流预测[1 ] ,它通过观测历史时空数据来预测未来的交通网络流量. 交通流预测的应用场景广泛,如智能路线规划、动态交通车辆调度、减缓交通拥堵等. ...
Short-term traffic flow prediction using seasonal ARIMA model with limited input data
2
2015
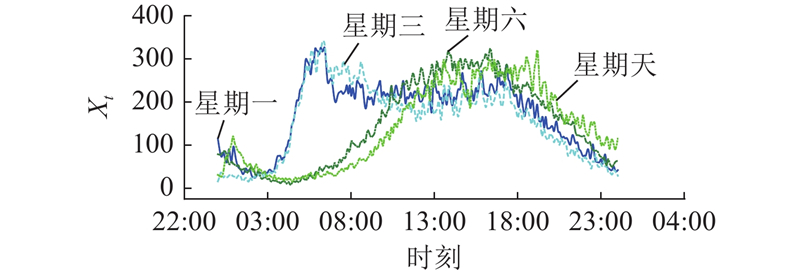
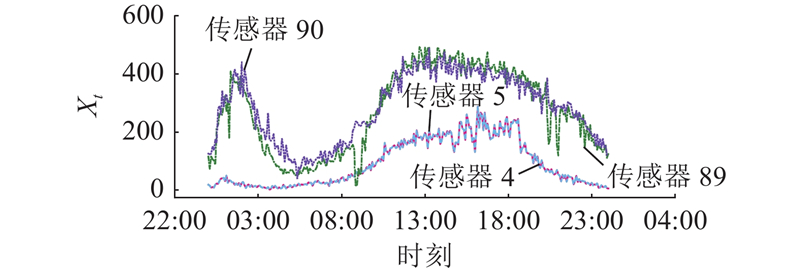
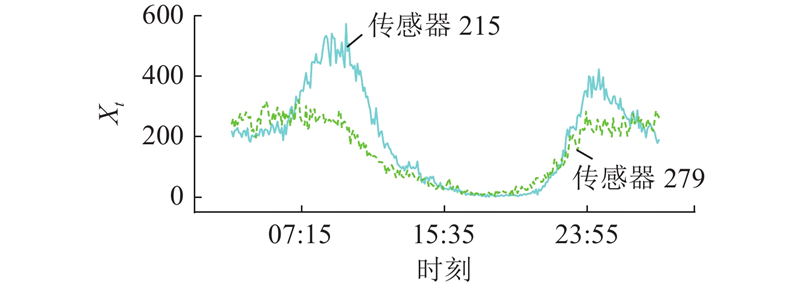
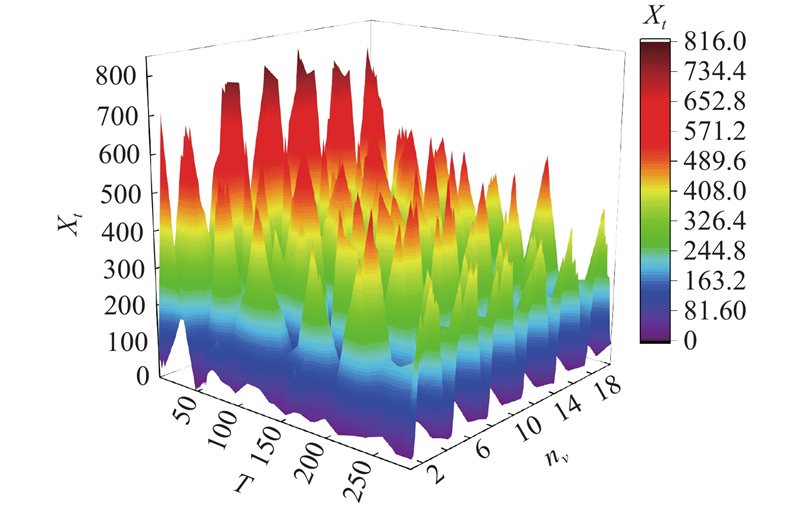
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
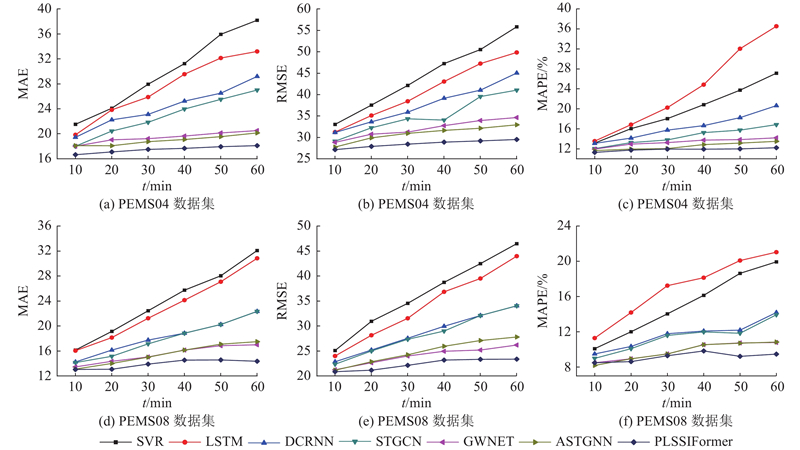
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions
2
2009
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
Deep spatio-temporal residual networks for citywide crowd flows prediction
1
2017
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
Revisiting spatial-temporal similarity: a deep learning framework for traffic prediction
1
2019
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
2
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
Deep multi-view spatial-temporal network for taxi demand prediction
1
2018
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
2
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
1
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
3
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
3
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
3
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
Graph neural controlled differential equations for traffic forecasting
1
2022
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
用于交通流预测的自适应图生成跳跃网络
1
2021
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
用于交通流预测的自适应图生成跳跃网络
1
2021
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
基于双向自适应门控图卷积网络的交通流预测
1
2023
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
基于双向自适应门控图卷积网络的交通流预测
1
2023
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
基于图卷积神经网络的城市交通态势预测算法
1
2020
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
基于图卷积神经网络的城市交通态势预测算法
1
2020
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
Spatial–temporal similarity fusion graph adversarial convolutional networks for traffic flow forecasting
3
2024
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
3
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
PDFormer: propagation delay-aware dynamic long-range transformer for traffic flow prediction
1
2023
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
1
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
1
... 20世纪末,研究者将机器学习方法用于交通流预测(如ARIMA[2 ] 、SVR[3 ] ),由卷积神经网络(convolutional neural network, CNN)捕捉空间依赖性(如STResNet[4 ] 、RSTS[5 ] ),由循环神经网络(recurrent neural networks, RNN)学习时间动态(如LSTM[6 ] 、DMVSTNet[7 ] 、DCRNN[8 ] 、DSAN[9 ] 和AGCRN[10 ] ). 图神经网络(graph neural network, GNN)比上述方法更适合模拟交通数据的底层图结构,基于GNN的方法因此被广泛应用于交通流预测中,这些方法包括STGCN[11 ] 、GWNet[12 ] 、STGNCDE[13 ] 、AGJNet[14 ] 、BAGGC[15 ] 、FASTGCN[16 ] 和STSFGACN[17 ] . Transformer[18 ] 能够在输入和输出间建立全局相关性依赖关系,该网络在交通流预测领域的应用(如PDFormer[19 ] 、STAEformer[20 ] )由此兴起. 如何运用自监督获取数据集的时空异质性指导重建短期时空特征成为交通流预测的新趋势. STDMAE[21 ] 以自监督方式分别预训练时间异质性和空间异质性;在全监督阶段,时空异质性分别指导短期序列重建,削弱时空幻影. 单独预训练的时间异质性和空间异质性不能完全挖掘多变量时空数据集的混沌,这一现象为时空异质交互性,如何挖掘这种特性是交通流预测的新难题.在交通网络中,时空异质交互性表现在单个时间片的空间维度上,城市中心与边缘郊区节点的车流量不同. 在单节点的时间维度上,工作日和周末车流量各有差异. 随着空间节点数量和时间步长增加,时间与空间交错越发复杂,某个节点的特殊事件,随着时间流逝和空间扩散,引起整个时空的涟漪波动,时空呈现混沌性,捕获和重建短期独特特征成为新的挑战. 传统预测模型输入时采用的时间步长为1 h,容易造成时空幻影(相似的历史短期时空在未来出现较大差异,或者不相似的历史短期时空在未来出现短期近似的路网交通流). ...
1
... 自监督学习利用无标注数据的自有结构和语义训练网络捕捉时空序列的复杂模式和特征,在下游任务通过未来的时空序列数据对网络进行训练时,使网络具有时空序列预测能力. 掩码预训练是自然语言处理和计算机视觉进行自监督学习的技术,它通过训练模型根据可见的上下文来预测输入中被掩码遮挡的部分. 自然语言中的BERT[22 ] 采用掩码建模预测具有双向上下文的随机掩码. 在计算机视觉领域,BEiT[23 ] 随机掩码遮挡输入图像的块,根据未被遮挡的块进行重建. STDMAE通过时间和空间掩码学习交通流数据的时空异质性,空间掩码通过剩余传感器重建部分屏蔽传感器,时间掩码通过无遮掩的时间序列恢复整个时间序列. 用${{\boldsymbol{X}}_{{\mathrm{S}}}}$ $L$ ${{\boldsymbol{X}}_{ {\mathrm{S}}}} \in {{\bf{R}}^{L \times N \times C}}$ . 定义$r$ $r$ $N \times r$ ${\hat {\boldsymbol{X}}^{{\text{S}}}}_{{\mathrm{S}}} \in {{\bf{R}}^{L \times N(1 - r) \times C}}$ $ T\times r $ ${\hat {\boldsymbol{X}}^{{\text{T}}}}_{{\mathrm{S}}} \in {{\bf{R}}^{L(1 - r) \times N \times C}}$ $1 - r$ $B(1 - r)$
1
... 自监督学习利用无标注数据的自有结构和语义训练网络捕捉时空序列的复杂模式和特征,在下游任务通过未来的时空序列数据对网络进行训练时,使网络具有时空序列预测能力. 掩码预训练是自然语言处理和计算机视觉进行自监督学习的技术,它通过训练模型根据可见的上下文来预测输入中被掩码遮挡的部分. 自然语言中的BERT[22 ] 采用掩码建模预测具有双向上下文的随机掩码. 在计算机视觉领域,BEiT[23 ] 随机掩码遮挡输入图像的块,根据未被遮挡的块进行重建. STDMAE通过时间和空间掩码学习交通流数据的时空异质性,空间掩码通过剩余传感器重建部分屏蔽传感器,时间掩码通过无遮掩的时间序列恢复整个时间序列. 用${{\boldsymbol{X}}_{{\mathrm{S}}}}$ $L$ ${{\boldsymbol{X}}_{ {\mathrm{S}}}} \in {{\bf{R}}^{L \times N \times C}}$ . 定义$r$ $r$ $N \times r$ ${\hat {\boldsymbol{X}}^{{\text{S}}}}_{{\mathrm{S}}} \in {{\bf{R}}^{L \times N(1 - r) \times C}}$ $ T\times r $ ${\hat {\boldsymbol{X}}^{{\text{T}}}}_{{\mathrm{S}}} \in {{\bf{R}}^{L(1 - r) \times N \times C}}$ $1 - r$ $B(1 - r)$
1
... 在自监督阶段,空间掩码和时间掩码进行辅助任务训练,获得交通流网络在空间和时间异质性的预训练权重. 在全监督阶段,将权重分别加载到预训练长时空分支,再次针对时空预测任务进行训练. $T_{\text{L}}$ [24 ] 解决由$T_{\text{L}}$ $ T_{\text{P}} $ $ T_{\text{P}} = T_{\text{L}}/P_{\text{S}} $ $ P_{\text{S}} $ $D_{\text{em}}$ $12 \times 1$ $12 \times 1$ . 长时空输入$ {\boldsymbol{X}}_{\text{LL}} \in {{\bf{R}}^{B \times L \times N \times C}} $ $ {\boldsymbol{X}}'_{\text{LL}} \in {{\bf{R}}^{{N} \times C \times L \times B}} $ $ {\boldsymbol{E}}_{\text{p}} \in {{\bf{R}}^{B \times N \times T_p \times D_{{\mathrm{em}}}}} $ . 空间和时间拥有共同的位置编码信息,将2个维度的编码信息[25 ] 输入块嵌入$ {\boldsymbol{E}}_{\text{p}} $ $ {\boldsymbol{E}}_{\text{pos}} \in {{\bf{R}}^{B \times N \times T_p \times D_{{\mathrm{em}}}}} $
Translating math formula images to LaTeX sequences using deep neural networks with sequence-level training
1
2021
... 在自监督阶段,空间掩码和时间掩码进行辅助任务训练,获得交通流网络在空间和时间异质性的预训练权重. 在全监督阶段,将权重分别加载到预训练长时空分支,再次针对时空预测任务进行训练. $T_{\text{L}}$ [24 ] 解决由$T_{\text{L}}$ $ T_{\text{P}} $ $ T_{\text{P}} = T_{\text{L}}/P_{\text{S}} $ $ P_{\text{S}} $ $D_{\text{em}}$ $12 \times 1$ $12 \times 1$ . 长时空输入$ {\boldsymbol{X}}_{\text{LL}} \in {{\bf{R}}^{B \times L \times N \times C}} $ $ {\boldsymbol{X}}'_{\text{LL}} \in {{\bf{R}}^{{N} \times C \times L \times B}} $ $ {\boldsymbol{E}}_{\text{p}} \in {{\bf{R}}^{B \times N \times T_p \times D_{{\mathrm{em}}}}} $ . 空间和时间拥有共同的位置编码信息,将2个维度的编码信息[25 ] 输入块嵌入$ {\boldsymbol{E}}_{\text{p}} $ $ {\boldsymbol{E}}_{\text{pos}} \in {{\bf{R}}^{B \times N \times T_p \times D_{{\mathrm{em}}}}} $
Spatial-temporal fusion graph neural networks for traffic flow forecasting
1
2021
... 与Li等[26 ] 的工作方法保持一致,将数据集PEMS03、PEMS04、PEMS07和PEMS08的训练、验证和测试集样本按照6∶2∶2划分. 数据集METR-LA和PEMS-BAY的训练、验证和测试集样本按照7∶2∶1进行划分. 在预训练过程中,PEMS03、 PEMS04、PEMS07、METR-LA和PEMS-BAY的$ T_{\text{L}} $ $ T_{\text{L}} $ $ T_{\text{in}} $ $ T_{\text{out}} $ $D_{\text{em}}$ $ P_{\text{P}} $
Attention based spatial-temporal graph convolutional networks for traffic flow forecasting
1
2019
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
2
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting
2
2022
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...
Adaptive decision spatio-temporal neural ode for traffic flow forecasting with multi-kernel temporal dynamic dilation convolution
2
2024
... 将PLSSIFormer与经典的交通流预测模型和先进的交通流预测模型进行比较. 对比模型包括基于传统时间序列预测的ARIMA、SVR模型,基于RNN的LSTM、DCRNN模型,基于图卷积的AGCRN[10 ] 、STGCN[11 ] 、GWNet[12 ] 、STSFGACN[17 ] 、ASTGCN[27 ] 、DSTAGNN [28 ] 、ASTGNN[29 ] 和 ADMSTNODE [30 ] 模型. 所提模型属于Transformer系列,因此将原始Transformer[18 ] 纳入对比模型. ...
... Performance comparison of different traffic flow prediction models in four traffic flow benchmark datasets
Tab.2 模型 PEMS03数据集 PEMS04数据集 PEMS07数据集 PEMS08数据集 MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% MAE RMSE MAPE/% ARIMA [2 ] 35.31 47.59 33.78 33.73 48.80 24.18 38.17 59.27 19.46 31.09 44.32 22.73 Transformer[18 ] 17.50 30.24 16.80 23.83 37.19 15.57 26.80 42.95 12.11 18.52 28.68 13.66 DCRNN[8 ] 18.18 30.31 18.91 24.70 38.12 17.12 25.30 38.58 11.66 17.86 27.83 11.45 STGCN[11 ] 17.49 30.12 17.15 22.70 35.55 14.59 25.38 38.78 11.08 18.02 27.83 11.40 GWNet[12 ] 19.85 32.94 19.31 25.45 39.70 17.29 26.85 42.78 12.12 19.13 31.05 12.68 SVR[3 ] 21.97 35.29 21.51 28.70 44.56 19.20 32.49 50.22 14.26 23.25 36.16 14.64 LSTM[6 ] 21.33 35.11 23.33 27.14 41.59 18.20 29.98 45.84 13.20 22.20 34.06 14.20 AGCRN[10 ] 16.06 28.49 15.85 19.83 32.26 12.97 21.29 35.12 8.97 15.95 25.22 10.09 ASTGNN[29 ] 15.07 26.88 15.80 19.26 31.16 12.65 22.23 35.95 9.25 15.98 25.67 9.97 DSTAGNN[28 ] 15.57 27.21 14.68 19.30 31.46 12.70 21.42 34.51 9.01 15.67 24.77 9.94 STSFGACN[17 ] 14.98 26.24 14.07 19.14 31.64 12.56 20.61 33.84 8.73 15.14 24.61 10.63 ADMSTNODE[30 ] 15.47 26.76 15.59 19.28 31.25 12.68 21.40 34.44 9.02 15.58 25.09 9.92 PLSSIFormer 14.67 26.36 14.92 18.11 29.51 12.22 20.29 33.39 8.62 14.35 23.37 9.48
3.5.2. 交通流数据集不同时间步长预测对比 对比不同交通流预测模型在数据集PEMS04、PEMS08上不同步长的预测性能,其中短期预测输入的序列为12,时间步长为2、4、6、8、10、12,结果如图9 所示. 可以看出,PLSSIFormer在2个数据集不同步长下,预测性能评价指标数值均低于做对比的6种先进模型,说明本研究所提模型在同领域有较高的预测精度. 还可以看出,PLSSIFormer曲线倾斜度最低,即在6个时间步长下,模型在同一数据集相同的评价指标结果变化不大,说明该模型具有较好的稳定性. ...