全球关节失能者逐年递增,目前中国已超1亿人,但关节形态通常须基于个体的医学图像进行重建,这对后续定制设计提出了更高要求. 建立不同人群的手部关节、膝关节、髋关节、肘关节、椎关节等生物力学模型,运用分层增材制造,在鼠标、矫形鞋垫、椎托及座椅等产品领域进行应用验证.
针对人体工学产品的优化设计和原型验证,本研究通过基于邻域拓扑的三维重建方法和基于Laplace-Gauss曲线的变形算法为定制设计提供数据支持,使用增材制造对定制化产品零部件提供快速原型验证,并通过深度残差网络对定制设计进行材料消耗预测,提出基于邻域拓扑重建(neighborhood topology reconstruction, NTR)的人体工学产品定制设计方法.
1. 相关工作
人体工学产品正广泛应用于各行各业,例如机械手可以模拟人手行为,执行抓取、搬运工作,人体工学设计可减小使用负担. Lindegård等[1]发现大量使用鼠标容易导致相关的上肢发生肌肉和骨骼疾病. Bleecker等[2]通过鼠标的人体工学干预减少患病率. Harih等[3]对手模型进行有限元分析,评估关节角度、肌肉力、接触面积和接触压力对人体工程学的影响,并根据有限元手部模型的结果改进人机交互. Lourenço等[4]设计新型人体工学鼠标,并通过3D打印进行原型制造. Li等[5]开发仿生机械手,可以进行网球、瓶子和电池等物体的抓取任务. Meattini等[6]设计一套可穿戴系统,可以通过人手的运动对机械手进行实时控制,能够抓取大部分常见物体. 根据Caroprese等[7]的研究,人体工学机器具有更高的效率. Zhang等[8]通过一种异步模式识别算法实现基于稳态视觉诱发电位的脑机接口系统,可以通过脑机接口对机械手进行控制.
机械手、鼠标、桌椅等人体工学产品的应用有利于提高生产产量,降低时间成本,还有助于提升残障人士的生活自理能力. 但人体工学产品根据其应用场景不同应使用不同的机械结构和机械尺寸,存在个性化定制化需要,快速准确的原型验证对于降低实验成本、提高个性化程度具有重要意义. 增材制造由于其快速生产复杂零部件的特点适合用于快速原型验证. Tumbleston等[9]通过连续液面制造技术改进立体光固化成形技术(stereo lithography appearance, SLA),将普通的逐点固化增材制造方式改进为逐面固化,提升打印速度. 数字光处理(digital light processing, DLP)也采用逐面固化的打印方式. Guo等[10]以Pickering乳状液为材料,通过数字光处理生产具有生物相容性的生物支架. Paredes等[11]使用两步烧结的方法有效提高生物相容性材料所制生物活性支架的强度和机械各向同性.
人体工学产品的定制化生产与机械尺寸的个性化调整密不可分. 作为仿生机械的典型代表,人体工学产品参考人体尺寸进行调整可有效改善人体工学产品的场景适用性. 通过三维重建获得人体模型可以更加准确方便地进行数据采集. Lorensen等[12]提出移动立方体算法(marching cube, MC),这种算法可从电子计算机断层扫描(computed tomography, CT)、核磁共振成像(magnetic resonance imaging, MRI)、正电子发射计算机断层显像(positron emission computed tomography, PET)等医学图像中提取等值面,重建目标模型,但存在二义性问题. Gueziec等[13]提出移动四面体算法(marching tetrahedrons, MT)解决二义性问题,但重建速度较慢. Kim等[14]基于移动立方体算法生成六面体网格模型,从而提高有限元模拟的求解精度和收敛速度. Chang等[15]通过移动立方体算法以及光学扫描仪的结合对口腔内牙齿形状进行三维重建,从而为牙科手术提供参考. Singh等[16]通过对CT图像的深度学习进行三维重建以及病变检测,并经过了从业医生的检查.
2. 深度残差网络
在传统的多层前馈神经网络训练中,随着网络模型层数和训练参数的增加,由于梯度消失、梯度弥散以及网络退化现象,误差在训练后期反而上升. 深度残差网络与传统多层前馈神经网络的不同点在于其采用了残差块结构叠加到原始输入,缓解了在深度神经网络中增加深度带来的梯度消失问题,使得网络模型能够学习到更多数据特征. 因此,基于模型层切面,提出基于深度残差网络的3D打印材料消耗分层预测方法.
一般的多层前馈神经网络输入输出之间的映射关系如下:
式中:
在式(1)的基础上,添加残差块结构到多层前馈神经网络,得到单层残差网络输入输出之间的映射关系:
式中:
式中:
双层残差网络输入输出之间的映射关系可以被进一步推导得出,表达式如下:
为了根据模型层切面分层预测3D打印材料消耗,采用均方差损失
式中:k为输出层神经元的个数,
对深度残差网络的训练,本质上是寻找最优的一组参数x*使得均方差损失
使用梯度下降法可以有效实现寻找最优参数的目的,本研究采用的是随机梯度下降法.
3. 人体关节三维重建及流形变形算法
为了优化人体工学产品尺寸结构,通过医学CT图像三维重建可获得人体结构三维模型. 通过采集三维模型的尺寸数据可使得人体工学产品更符合生物学规则,运行过程更加稳定.
3.1. 基于邻域拓扑的三维重建方法
基于医学图像重建三维模型,三维模型的重建精度与准确性决定了三维模型数据采集的效果,重建速度决定了数据采集的效率. 现有的移动立方体算法虽然效率较高,但存在等值线拓扑连接的二义性问题,生成的三维模型存在难以处理的错误. 移动四面体算法避免了二义性问题,但生成三维模型速度慢,不利于快速重建,三维模型数据采集时间成本高. 基于邻域拓扑的医学图像三维重建方法(NTR)利用共有面拓扑一致处理的过渡算法将效率较高、精度较低的移动立方体算法与精度较高、效率较低的移动四面体算法融合起来,从而在保证较高精度的情况下,减少医学图像三维重建所需时间,提高三维重建的效率.
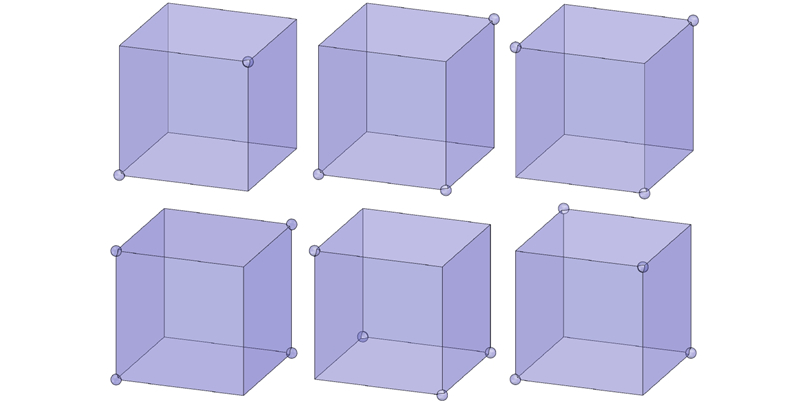
NTR首先根据医学图像建立图像坐标系,根据医学图像灰度值建立三维数值点云. 基于邻域拓扑关系可根据数值点云建立包含8个邻域点的正方体. 根据邻域点数值与目标数值的关系对邻域点进行标记,针对不同标记的邻域正方体使用不同的三维重建算法获得三维模型的各个部分,将各个部分进行平滑重组获得完整的三维模型. 当邻域正方体标记类型在移动正方体算法下存在二义性问题时,将其归类为拓扑二义型,使用移动四面体算法进行处理. 若不存在二义性问题,则采用移动立方体算法或混合算法进行处理. 如图1所示为存在二义性问题的邻域正方体. 其中,球形标记点处的数值大于目标数值.
图 1
为了保证相邻邻域正方体符合流形规则,以邻域正方体三维序号之和为标记数值,当序号之和为奇数时,采用左手方式划分的移动四面体算法进行处理,当序号之和为偶数时,采用右手方式划分的移动四面体算法进行处理. 左手方式划分的移动四面体算法与右手划分的移动四面体算法在相邻位置可以互相吻合,从而保证生成的三维模型符合流形规则. 如图2所示为其中一种标记点分布的邻域正方体的划分方式.
图 2
图 2 存在二义性问题的邻域正方体的划分方式
Fig.2 Split method of neighborhood cube with ambiguity problem
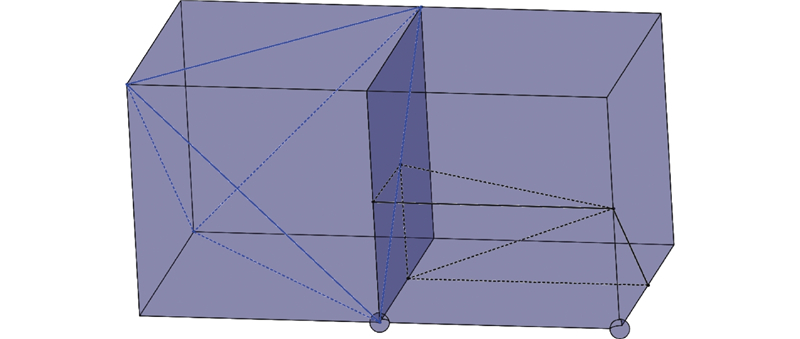
当存在二义性问题的邻域正方体与不存在二义性问题的邻域正方体相邻时,为了保证2种处理方法的邻接处符合流形规则,须对不存在二义性问题的邻域正方体采用过渡算法处理. 过渡算法示意图如图3所示. 图中,右侧的邻域立方体采用过渡算法进行处理.
图 3
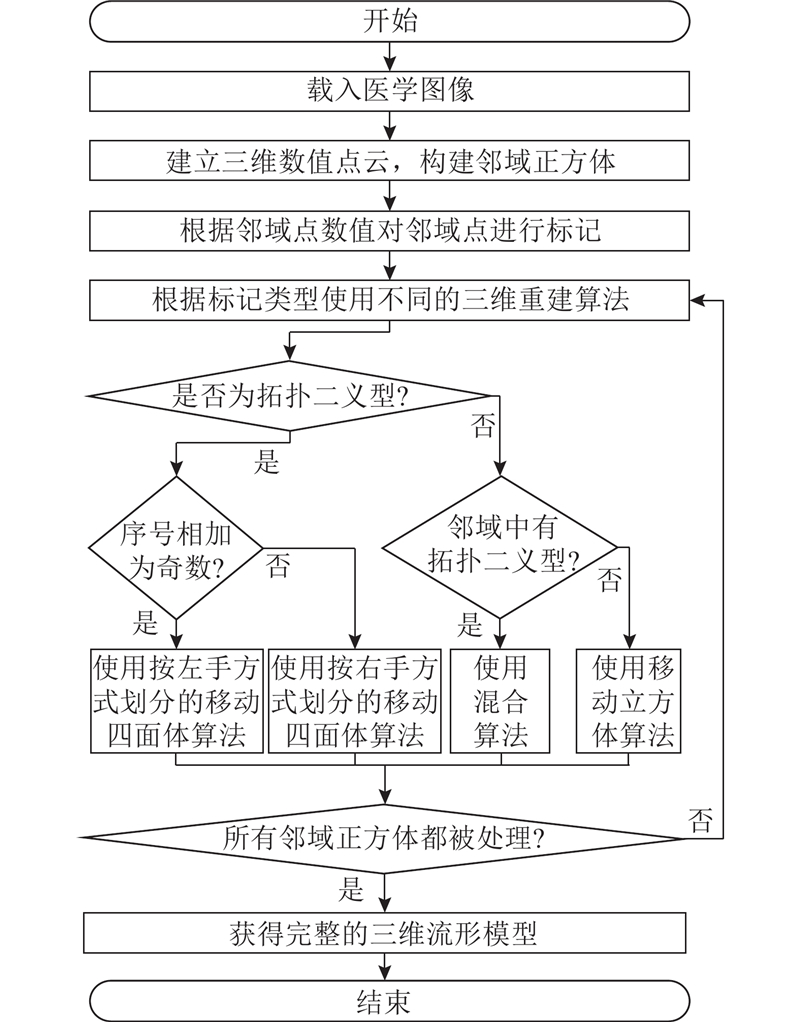
整体算法流程图如图4所示. 通过该NTR方法可以基于医学图像生成符合流形规则的三维模型,为数据采集或医学诊断提供直观和准确的数字依据.
图 4
图 4 基于邻域拓扑的医学图像三维重建方法流程图
Fig.4 Flow chart of medical image 3D reconstruction method based on neighborhood topology
3.2. 以斜椭球为凸包的柔性抓取空间
采用基于斜椭球的凸壳,构建非规则流形模型的柔性抓取空间. 利用柔性抓取空间可以方便地分析具有预定约束的多体系统. 这对于手部分析更为明显,在抓取过程中,连杆的拓扑和关节的配置不会改变,从而为变形算法提供形状约束.
给定斜椭球体包围一组点P,P为流形模型顶点集合V的子集,即P∈V. 斜椭球体的中心方程表达式如下:
式中:
将点集P划分为多个子点集,并为每个子集生成一个边界椭球. P被多个椭球体包围,并将一些顶点的刻面划分为不同的子集. 通过检测3个顶点不能在同一个椭球所覆盖的面域中,防止这些斑块不能完全椭球化. 求解log (det(A))的最小值以满足
式中:
通过计算面域的质心,得到质心与椭球之间距离最小的椭球. 根据选定椭球的原点集和面域的顶点,重新计算椭球. 通过迭代得到一系列椭球,直到误差小于给定的包络误差,最后得到的最小体积封闭椭球体可以完全包围点集P. 椭球方程定义的A是一个3×3正定矩阵. 对正定矩阵A进行奇异值分解,得到3个酉矩阵. 酉矩阵的共轭转置等于其逆矩阵门
式中:
3.3. 基于Laplace-Gauss曲线的变形算法
对于多面体概念设计原型
相比于使用Euclidean坐标,使用Laplace坐标
式中:
选择Laplace-Gauss曲线和均匀权重的组合作为权重设置函数:
式中:
如果约束在最小二乘意义上得到满足,拉伸变形和旋转变形都将表现得更好,变形能量误差方程为
式中:
对待变形顶点和剩余顶点进行差分处理,将原始概念设计原型分解为一个低频基本概念设计原型(待变形概念设计原型)和一系列高频细节簇(非变形概念设计原型),得到模型的多分辨率变形. 通过求解能量误差泛函
式中:L表示Laplace坐标系的系数矩阵,0表示零矩阵,I表示单位矩阵,
求解式(18)中稀疏线性系统的方法等价于求解超定方程的最小二乘解,令
根据式(19)计算得到原始顶点变形后的Euclidean坐标矩阵
4. 人体手部关节实例
4.1. 人体手部关节三维重建及变形
以手部(右)CT图像三维重建为例开发基于C语言的自主重建软件,根据手部扫描图像集进行NTR. CT图像和重建模型如图5所示. 根据重建后的三维模型,该手掌的大拇指远节指骨长度为23.759 mm,近节指骨为32.200 mm,第1掌骨为47.012 mm,食指远节指骨为21.201 mm,中节指骨为25.655 mm,近节指骨为43.060 mm,第2掌骨为67.559 mm,中指远节指骨为21.181 mm,中节指骨为30.363 mm,近节指骨为47.473 mm,第3掌骨为63.428 mm,无名指远节指骨为22.909 mm,中节指骨为26.592 mm,近节指骨为45.342 mm,第4掌骨为53.120 mm,小指远节指骨为20.858 mm,中节指骨为18.506 mm,近节指骨为33.674 mm,第5掌骨为49.225 mm. 根据该系列手部尺寸数据可以对人体工学鼠标的机械尺寸进行仿生化调整,从而提高按握姿势的舒适性,降低鼠标长时间使用对手部的损害.
图 5
图 5 基于邻域拓扑重建的模型及部分原始图像
Fig.5 Model based on neighborhood topology reconstruction and original image
根据人体手部尺寸数据调整低曲度普通鼠标模型尺寸. 根据手部模型流形变形结果和普通鼠标形状设计高曲度人体工学鼠标形状,并进行调整,使其更符合手部尺寸形状. 2种鼠标模型如图6所示. 低曲度普通鼠标特征线最大曲率为0.038 9 mm−1,高曲度人体工学鼠标特征线最大曲率为0.150 9 mm−1.
图 6
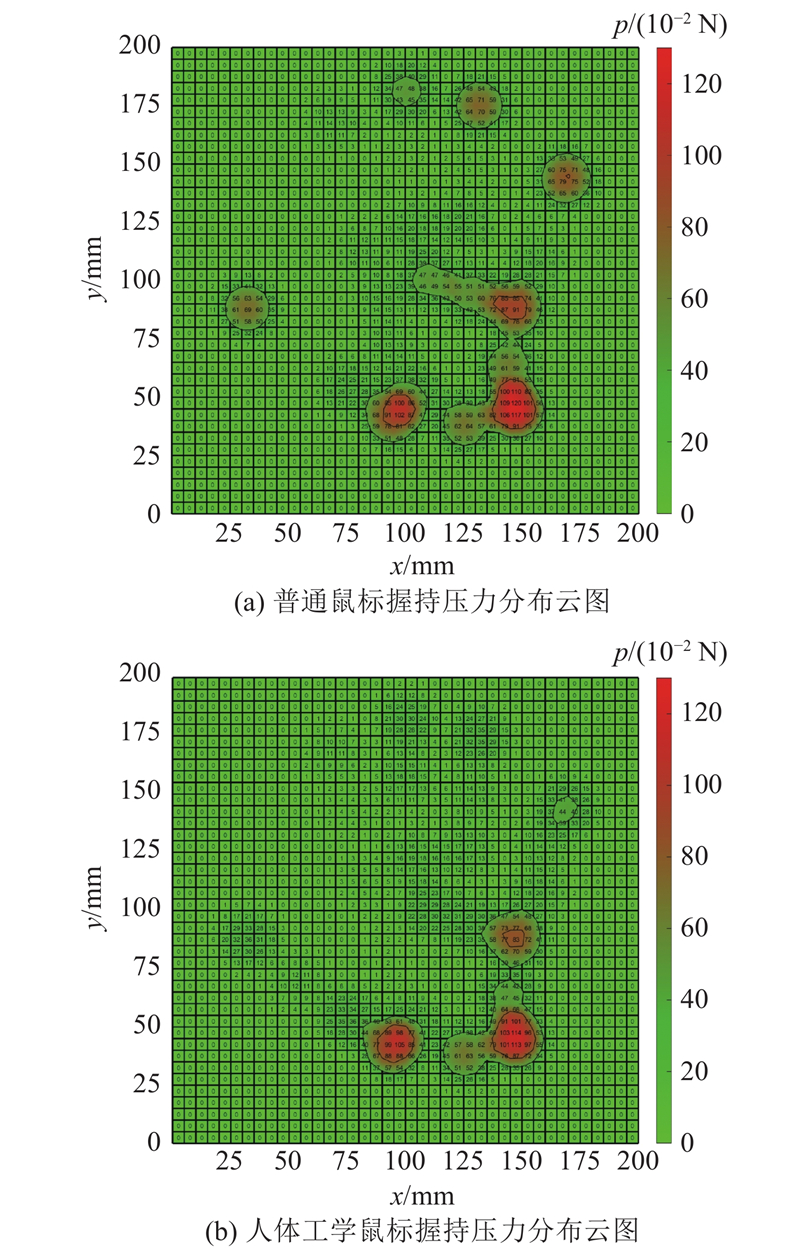
鼠标与手部流形变形模型匹配结果示意图如图7所示,人体工学鼠标握持姿势变化较大. 普通鼠标按键接触面积为1 122.74 mm2,手掌可放置面积为1 325.36 mm2. 人体工学鼠标拇指可放置面积为3 691.84 mm2,按键接触面积为2 287.97 mm2,手掌可放置面积为6 105.92 mm2. 相比于普通鼠标,高曲度人体工学鼠标的接触面积更大,接触压力更小,使用过程更加舒适.
图 7
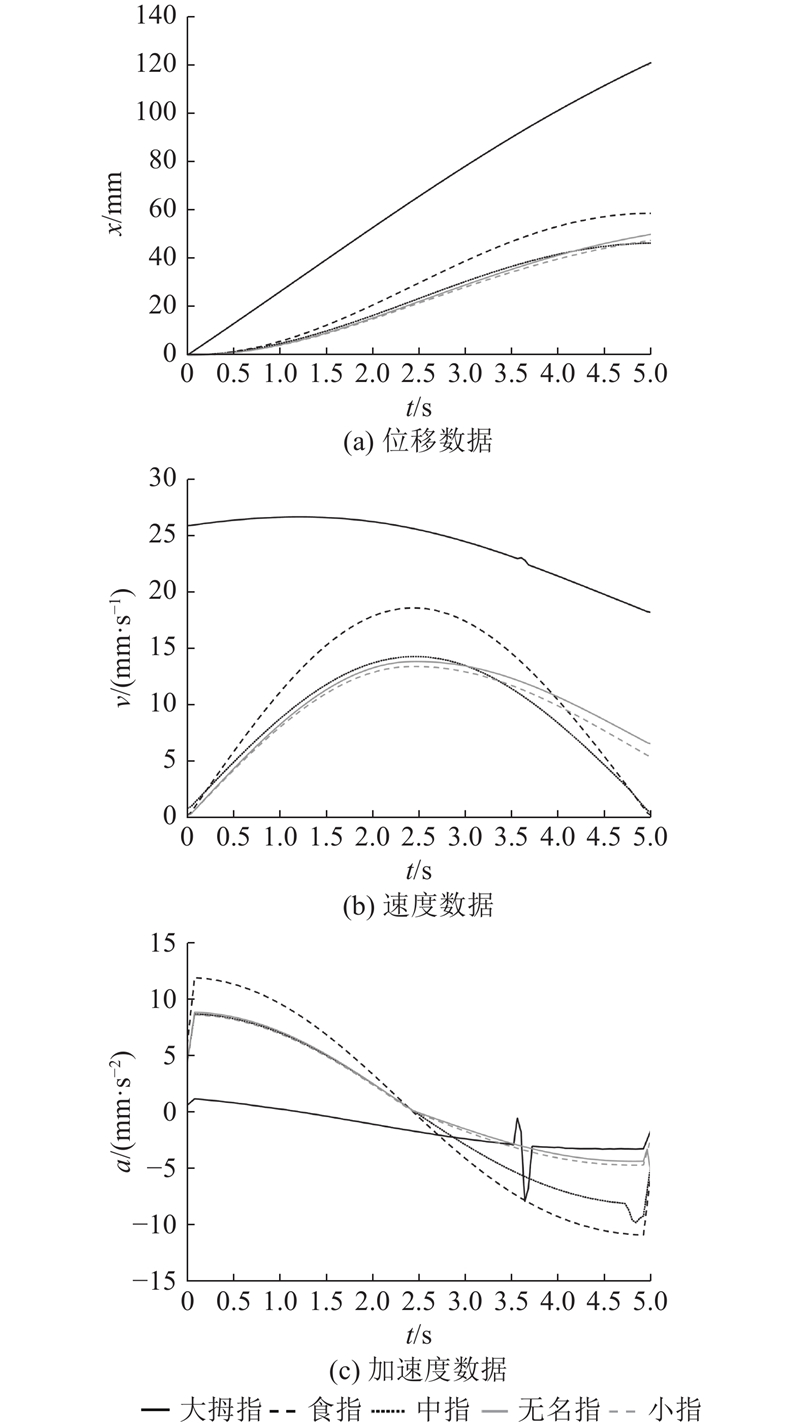
4.2. 长期按握过程运动仿真
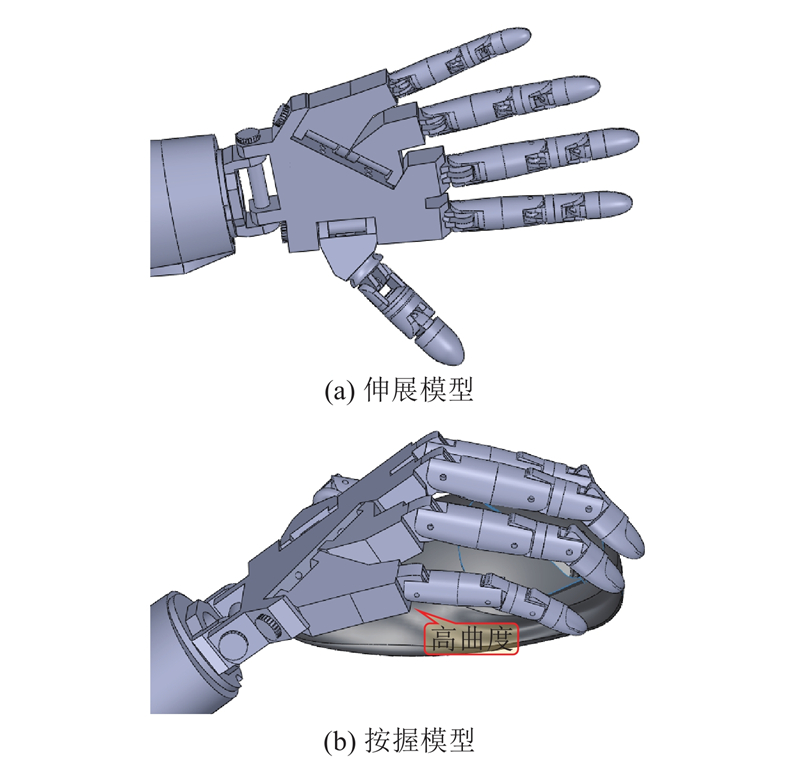
变形过程仅能模拟静态握持情况,为了验证长期按握过程,通过五指机械手进行模拟. 根据NTR获得的手部模型数据及其抓取空间,设计了五指机械手(右). 以五指机械手(右)为原型验证对象,五指机械手伸展模型和按握模型如图8所示. 该五指机械手以人类手掌为仿生对象,通过17个旋转轴充分模拟手掌的运动形式,可进行各种形状物体的按握任务. 该手掌外围盒空间尺寸为190 mm×180 mm×20 mm.
图 8
图 9
5. 物理实验
本工作中所考虑的样品是在DLP打印设备上通过使用光敏树脂作为填充材料和支撑材料制成的,如图10所示. DLP打印设备打印精度为55 μm,分层厚度为100 μm. 打印获得的人体工学鼠标可紧密贴合人体手部.
图 10
图 11
对人体工学鼠标打印模型表面进行微观观测,观测结果如图12所示. 观察视野直径为2.5 mm,可明显观察到打印层之间的过渡分割线条.
图 12
图 12 人体工学鼠标4个区域的表面微观形貌
Fig.12 Surface microscopic morphology of four areas of ergonomic mouse
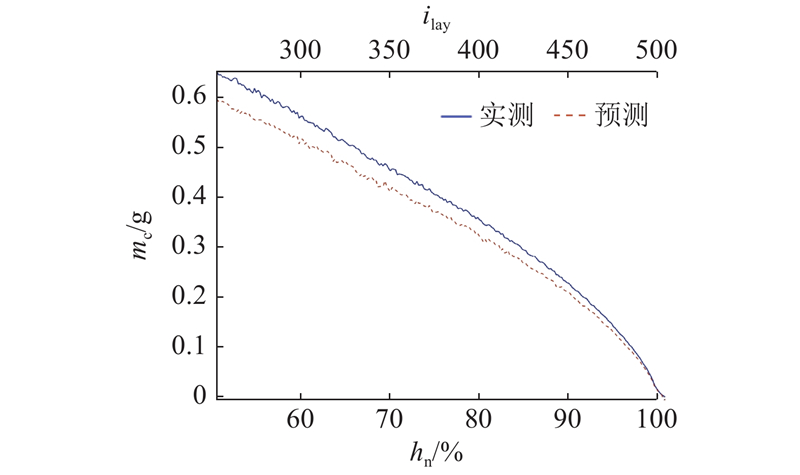
如图13所示为人体工学鼠标在3D打印过程中材料消耗的预测值和实测值. 图中,mc为材料消耗, ilay为分层序号, hn为归一化打印高度比. 使用前50%的分层数据对后50%的分层数据进行预测. 平均绝对误差(mean absolute error,MAE)为
图 13
图 13 打印过程材料消耗的预测值和实测值
Fig.13 Predicted materials consumption and measured materials consumption of printing process
为了体现本研究方法的优势,所提出的NTR方法与现有方法的对比如表1所示.
表 1 本研究方法与其他方法的对比
Tab.1
| 性能指标 | 现有方法 | 本研究方法(NTR方法) |
| 三维重建 | Lorensen等[12]的移动立方体算法存在二义性问题; Gueziec等[13]的移动四面体算法重建速度较慢 | ●在避免二义性问题的基础上,减少医学图像三维重建所需时间,提高三维 重建的效率,如 |
| 三维流形变形 | Lourenço等[4]通过手动测量尺寸以及人工建模获得 手部模型 | ●通过三维重建与流形变形方法相结合获得准确人体尺寸数据,如 ●提出柔性抓取空间,使用斜椭球作为凸壳 |
| 人体工学评价 | Harih等[3]仅考虑了静态抓握状态 | ●既考虑了静态握持状态的舒适度,又考虑了动态按握过程的平稳性, 如 |
| 快速原型制造 | Lourenço等[4]仅展示概念模型 | ●通过DLP设备进行了快速原型制造,通过微观形貌表征原型产品的 高表面精度,如 |
6. 结 论
(1)提出基于邻域拓扑重建(NTR)的人体工学产品定制设计方法. 利用邻域拓扑关系进行三维重建获得人体结构数据,有效克服了移动立方体算法的二义性问题,同时避免了移动四面体算法的高耗时问题,从而高效准确地获得符合流形规则的人体三维模型. 根据三维模型尺寸数据进行人体工学产品定制设计,从而提高人体工学产品的适用范围和工作效率.
(2)提出基于Laplace-Gauss曲线的变形算法. 采用医学CT图像进行三维重建,得到具有个性化定制信息的柔性概念设计原型的非规则原始形状. 根据原始模型获得以斜椭球为凸包的柔性抓取空间,以柔性抓取空间为约束,提出的基于Laplace-Gauss曲线的变形算法能够使柔性概念设计原型从原来的姿态变形为不同的握持姿态. 根据握持姿态及机械手按握运动学仿真可以进行人体工学鼠标设计,获得使用人体工学鼠标的运动过程信息.
(3)利用物理实验验证了所提出方法的有效性. 通过DLP设备进行人体工学鼠标和五指机械手物理模型制造并测量制造过程实际材料消耗,使用物理模型测量机械手按压压力,微观观测人体工学鼠标表面形貌. 实验结果证明,原型产品的表面精度高,人体工学鼠标可贴合人体手部,机械手按压压力分布与人体手部大致相同,且深度残差网络模型能够有效地对打印材料消耗进行分层预测,有助于增材制造的成本优化设计.
未来可以在3D打印知识库的支持下,扩展设计方法的适用范围,将其应用于槽、凸肩、匹配孔、内腔微流控通道等复杂零件结构中.
参考文献
Can biofeedback training in combination with ergonomic information reduce pain among young adult computer users with neck and upper extremity symptoms? A randomized controlled intervention study
[J].DOI:10.1016/j.apergo.2023.104155 [本文引用: 1]
A medical-ergonomic program for symptomatic keyboard/mouse users
[J].DOI:10.1097/JOM.0b013e31821719af [本文引用: 1]
Finite element human hand model: validation and ergonomic considerations
[J].DOI:10.1016/j.ergon.2021.103186 [本文引用: 2]
A design contribution to ergonomic pc mice development
[J].DOI:10.3390/ijerph19138126 [本文引用: 3]
An semg-based human–robot interface for robotic hands using machine learning and synergies
[J].DOI:10.1109/TCPMT.2018.2799987 [本文引用: 1]
Behavior, milk yield, and milk composition of machine-and hand-milked Murgese mares
[J].DOI:10.3168/jds.2006-603 [本文引用: 1]
A novel brain-controlled prosthetic hand method integrating AR-SSVEP augmentation, asynchronous control, and machine vision assistance
[J].DOI:10.1016/j.heliyon.2024.e26521 [本文引用: 1]
Continuous liquid interface production of 3D objects
[J].DOI:10.1126/science.aaa2397 [本文引用: 1]
Digital light processing bio-scaffolds of hydroxyapatite ceramic foams with multi-level pores using Pickering emulsions as the feedstock
[J].DOI:10.1016/j.jeurceramsoc.2024.01.021 [本文引用: 1]
Improving the strength of β-TCP scaffolds produced by digital light processing using two-step sintering
[J].DOI:10.1016/j.jeurceramsoc.2023.11.028 [本文引用: 1]
Exploiting triangulated surface extraction using tetrahedral decomposition
[J].DOI:10.1109/2945.485620 [本文引用: 2]
Construction of polyhedral finite element meshes based upon marching cube algorithm
[J].DOI:10.1016/j.advengsoft.2018.11.014 [本文引用: 1]
Interactive marching cubes algorithm for intraoral scanners
[J].DOI:10.1007/s00170-016-9231-y [本文引用: 1]
Image quality and lesion detection on deep learning reconstruction and iterative reconstruction of submillisievert chest and abdominal CT
[J].DOI:10.2214/AJR.19.21809 [本文引用: 1]
Autonomous in-situ correction of fused deposition modeling printers using computer vision and deep learning
[J].DOI:10.1016/j.mfglet.2019.09.005 [本文引用: 1]
Machine learning for continuous liquid interface production: Printing speed modelling
[J].DOI:10.1016/j.jmsy.2019.01.004 [本文引用: 1]
Online measurement of bead geometry in GMAW-based additive manufacturing using passive vision
[J].DOI:10.1088/0957-0233/24/11/115103 [本文引用: 1]
The effects of material property assumptions on predicted meltpool shape for laser powder bed fusion based additive manufacturing
[J].DOI:10.1088/0957-0233/27/8/085602 [本文引用: 1]
Effect of thermal deformation on part errors in metal powder based additive manufacturing processes
[J].DOI:10.1115/1.4026524 [本文引用: 1]
数智化正向设计方法及其在制造装备与过程中的应用
[J].DOI:10.3901/JME.2023.19.111 [本文引用: 1]
Digital intelligent forward design method and its application in manufacturing equipment and process
[J].DOI:10.3901/JME.2023.19.111 [本文引用: 1]
Towards support-free design for 3D printing of thin-walled composite based on stratified manufacturability reinforcement
[J].DOI:10.1016/j.cirpj.2022.05.017
Energy efficiency optimization for ecological 3D printing based on adaptive multi-layer customization
[J].DOI:10.1016/j.jclepro.2019.118826
Support diminution design for layered manufacturing of manifold surface based on variable orientation tracking
[J].
Biomechanical performance design of joint prosthesis for medical rehabilitation via generative structure optimization
[J].DOI:10.1080/10255842.2020.1789970 [本文引用: 1]