[8]
SUN Bin, XUE Yunan, CHEN Xiaohui A method for PPG signal identification based on improved neighborhood rough set
[J]. Foreign Electronic Measurement Technology , 2022 , 41 (6 ): 8 - 13
[本文引用: 1]
[9]
GU Y Y, ZHANG Y T. Photoplethysmographic authentication through fuzzy logic [C]// IEEE EMBS Asian-Pacific Conference on Biomedical Engineering . Kyoto: IEEE, 2003: 136–137.
[本文引用: 2]
[10]
SALANKE N S G R, MAHESWARI N, SAMRAJ A, et al. Enhancement in the design of biometric identification system based on photoplethysmography data [C]// International Conference on Green High Performance Computing . Nagercoil: IEEE, 2013: 1–6.
[本文引用: 2]
[11]
JEON Y J, KANG S J Multi-slice nested recurrence plot (msnrp): a robust approach for person identification using daily ECG or PPG signals
[J]. Engineering Applications of Artificial Intelligence , 2023 , 126 : 106799
DOI:10.1016/j.engappai.2023.106799
[本文引用: 2]
[12]
LEE J A, KWAK K C Personal identification using an ensemble approach of 1D-LSTM and 2D-CNN with electrocardiogram signals
[J]. Applied Sciences , 2022 , 12 (5 ): 2692
DOI:10.3390/app12052692
[本文引用: 2]
[14]
HAYES M J, SMITH P R A new method for pulse oximetry possessing inherent insensitivity toartifact
[J]. IEEE Transactions on Biomedical Engineering , 2001 , 48 (4 ): 452 - 461
DOI:10.1109/10.915711
[本文引用: 2]
[15]
KARIMIAN N, GUO Z, TEHRANIPOOR M, et al. Human recognition from photoplethysmography (PPG) based on non-fiducial features [C]// IEEE International Conference on Acoustics, Speech and Signal Processing . New Orleans: IEEE, 2017: 4636–4640.
[本文引用: 2]
[16]
ALAM R-U, ZHAO H, GOODWIN A, et al Differences in power spectral densities and phase quantities due to processing of EEG signals
[J]. Sensors , 2020 , 20 : 6285
DOI:10.3390/s20216285
[本文引用: 1]
[17]
HU J F. Biometric system based on EEG signals: a nonlinear model approach [C]// International Conference on Machine Vision and Human-machine Interface . Kaifeng: IEEE, 2010: 48–51.
[本文引用: 1]
[18]
HEJAZI M, AL-HADDAD S A R, HASHIM S J, et al. Non-fiducial based ECG biometric authentication using one-class Support Vector Machine [C]// Signal Processing: Algorithms, Architectures, Arrangements, and Applications . Poznan: IEEE, 2017: 190–194.
[本文引用: 1]
[19]
YE Z, TURNER R. Intelligent linear and nonlinear analysis for biometric fingerprint recognition [C]// 39th Southeastern Symposium on System Theory . Macon: IEEE, 2007: 315–319.
[本文引用: 1]
[1]
RAJARAM S, VOLLALA S, RAMASUBRAMANIAN N, et al Enhanced and secured random number generation for eUASBP
[J]. International Journal of System Assurance Engineering and Management , 2022 , 13 (3 ): 1135 - 1150
[本文引用: 1]
[2]
SPOOREN J, PREUVENEERS D, JOOSEN W. PPG2Live: using dual PPG for active authentication and liveness detection [C]// International Conference on Biometrics . Crete: IEEE, 2019: 1–6.
[本文引用: 1]
[20]
LEE T K M, SANEI S, CLARKE B. Fusion of nonlinear measures in fronto-normal gait recognition [C]// 5th International Multi-conference on Computing in the Global Information Technology . Valencia: IEEE, 2010: 104–109.
[本文引用: 1]
[21]
PINCUS S M Approximate entropy as a measure of system complexity
[J]. Proceedings of the National Academy of Sciences , 1991 , 88 (6 ): 2297 - 2301
DOI:10.1073/pnas.88.6.2297
[本文引用: 1]
[3]
NOWARA E M, SABHARWAL A, VEERARAGHAVAN A, et al. PPG secure: biometric presentation attack detection using photopletysmograms [C]// IEEE International Conference on Automatic Face and Gesture Recognition . Washington, DC: IEEE, 2017: 56–62.
[本文引用: 1]
[4]
GU Y Y, ZHANG Y, ZHANG Y T. A novel biometric approach in human verification by photoplethysmographic signals [C]// 4th International IEEE EMBS Special Topic Conference on Information Technology Applications in Biomedicine . Birmingham: IEEE, 2003: 13–14.
[本文引用: 1]
[22]
章思佳, 林栋, 齐诗仪, 等 基于眼电信号近似熵探讨针灸治神的临床应用
[J]. 中国针灸 , 2023 , 43 (1 ): 79 - 82
[本文引用: 1]
ZHANG Sijia, LIN Dong, QI Shiyi, et al Clinical application of acupuncture-moxibustion for the treatment of spirit based on approximate entropy of electrooculogram signal
[J]. Chinese Acupuncture and Moxibustion , 2023 , 43 (1 ): 79 - 82
[本文引用: 1]
[5]
KAVSAOGLU A R, POLAT K, BOZKURT M R A novel feature ranking algorithm for biometric recognition with PPG signals
[J]. Computers in Biology and Medicine , 2014 , 49 : 1 - 14
DOI:10.1016/j.compbiomed.2014.03.005
[本文引用: 2]
[6]
JAAFAR N A L, SIDEK K A, AZAM S N A M. Acceleration plethysmogram based biometric identification [C]// International Conference on BioSignal Analysis, Processing and Systems . Kuala Lumpur: IEEE, 2015: 16–21.
[本文引用: 2]
[7]
CHAKRABORTY S, PAL S. Photoplethysmogram signal based biometric recognition using linear discriminant classifier [C]// International Conference on Control, Instrumentation, Energy and Communication . Kolkata: IEEE, 2016: 183–187.
[本文引用: 2]
[8]
孙斌, 薛毓楠, 陈小惠 基于改进邻域粗糙集的 PPG 信号身份识别方法
[J]. 国外电子测量技术 , 2022 , 41 (6 ): 8 - 13
[本文引用: 1]
[24]
RICHMAN J S, MOORMAN J R Physiological time-series analysis using approximate entropy and sample entropy
[J]. American Journal of Physiology-Heart and Circulatory Physiology , 2000 , 278 (6 ): H2039 - H2049
DOI:10.1152/ajpheart.2000.278.6.H2039
[本文引用: 1]
[25]
CHEN W, WANG Z, XIE H, et al Characterization of surface EMG signal based on fuzzy entropy
[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering , 2007 , 15 (2 ): 266 - 272
DOI:10.1109/TNSRE.2007.897025
[本文引用: 1]
[26]
AZAMI H, ROSTAGHI M, ABÁSOLO D, et al Refined composite multiscale dispersion entropy and its application to biomedical signals
[J]. IEEE Transactions on Biomedical Engineering , 2017 , 64 (12 ): 2872 - 2879
DOI:10.1109/TBME.2017.2679136
[本文引用: 1]
[27]
郭秀花. 医学统计学与SPSS软件实现方法(第2版)[M]. 北京: 科学出版社, 2017: 33–47.
[本文引用: 1]
[28]
徐慧, 付迎春, 付朝川, 等 改进WOA算法优化SVM的网络入侵检测
[J]. 实验室研究与探索 , 2019 , 38 (8 ): 128 - 133
DOI:10.3969/j.issn.1006-7167.2019.08.031
[本文引用: 1]
XU Hui, FU Yingchun, FU Chaochuan, et al Improved whale optimization algorithm to optimize support vector machine for network intrusion detection
[J]. Research and Exploration in Laboratory , 2019 , 38 (8 ): 128 - 133
DOI:10.3969/j.issn.1006-7167.2019.08.031
[本文引用: 1]
[29]
MOODY G B, MARK R G. A database to support development and evaluation of intelligent intensive care monitoring [C]// Computers in Cardiology . Indianapolis: IEEE, 1996: 657–660.
[本文引用: 1]
[30]
GU Y Y, ZHANG Y, ZHANG Y T. A novel biometric approach in human verification by photoplethysmo-signals [C]// 4th International IEEE EMBS Special Topic Conference on Information Technology Applications in Biomedicine . Birmingham: IEEE, 2003: 13–14.
[本文引用: 1]
[31]
LEE A, KIM Y. Photoplethysmography as a form of biometric authentication [C]// 2015 IEEE Sensors . Busan: IEEE, 2015: 1–2.
[本文引用: 1]
[32]
KARIMIAN N, TEHRANIPOOR M, FORTE D. Non-fiducial PPG-based authentication for healthcare application [C]// IEEE EMBS International Conference on Biomedical and Health Informatics . Orlando: IEEE, 2017: 429–432.
[本文引用: 1]
[33]
KHAN M U, AZIZ S, NAQVI S Z H, et al. Pattern analysis towards human verification using photoplethysmograph signals [C]// International Conference on Emerging Trends in Smart Technologies . Karachi: IEEE, 2020: 1–6.
[本文引用: 1]
[34]
HWANG D Y, TAHA B, LEE D S, et al Evaluation of the time stability and uniqueness in PPG-based biometric system
[J]. IEEE Transactions on Information Forensics and Security , 2021 , 16 : 116 - 130
DOI:10.1109/TIFS.2020.3006313
[本文引用: 1]
[35]
SIAM A I, ELAZM A A, EL-BAHNASAWY N A, et al PPG-based human identification using Mel-frequency cepstral coefficients and neural networks
[J]. Multimedia Tools and Applications , 2021 , 80 (17 ): 26001 - 26019
DOI:10.1007/s11042-021-10781-8
[本文引用: 1]
基于改进邻域粗糙集的 PPG 信号身份识别方法
1
2022
... 2003年,Gu等[4 ] 提出基于PPG信号的生物识别方法. 之后,研究人员对此领域进行了广泛的探索和研究,并获得了一定的成果. Kavsaoglu等[5 ] 从PPG信号及其一阶、二阶导数中提取了40个时域特征,并提出特征排序算法对其排序,最终取得了94.4%的准确率;Jaafar等[6 ] 的研究证明了加速度体积描记信号作为生物识别系统特征的稳健性和可靠性;Chakraborty等[7 ] 从滤波后的PPG及其导数中提取了12个特征,并使用线性判别分析进行分类,该研究对15名受试者的PPG信号进行分类识别,达到了100%的准确率. 孙斌等[8 ] 对PPG信号提取了24维特征;利用寻优算法获取最佳特征子集后利用人工蜂群算法优化支持向量机算法对样本的最佳特征子集进行训练与测试,完成个体身份识别. ...
2
... 以PPG信号的特征点为基础,提取各特征点的峰值、时间间隔、斜率等时域特征来制定特征向量模板. Gu等[9 ] 的研究从受试者的PPG信号中提取了4个时域特征(波峰数、上升斜率、下降斜率、时间间隔)构成特征向量模板,然后用模糊逻辑方法来研究使用PPG信号进行生物识别的可行性. ...
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
2
... 根据PPG信号整体形态,通常通过时间或频率分析来获取统计特征,从PPG波形中提取鉴别性信息. Salanke等[10 ] 研究了PPG信号在生物识别中的适用性. 该研究运用主成分分析法对单周期PPG信号进行特征提取,以样本间的欧氏距离为判别依据. 结果表明,该方法对正常PPG信号和含有运动伪影的PPG信号都表现出良好的识别精度. ...
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
Multi-slice nested recurrence plot (msnrp): a robust approach for person identification using daily ECG or PPG signals
2
2023
... 还有一些研究将PPG信号特征与深度学习结合用于身份识别. Jeon等[11 ] 提出新的方法,称为多层嵌套递归图(multi-slice nested recurrence plot, MsNRP),这个方法主要用于解决存在噪声的PPG信号在身份识别中的问题. MsNRP展示了其对噪声的鲁棒性,从而为实际场景中的识别提供了可靠的解决方案. Lee等[12 ] 提出基于长短期记忆(long short term memory, LSTM)和卷积神经网络(convolutional neural network, CNN)的集成身份识别技术. 在预处理步骤中使用滤波器来去除噪声,并且从原始信号中提取时域特征作为LSTM的输入,获得了一定程度上的身份识别性能提升. ...
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
Personal identification using an ensemble approach of 1D-LSTM and 2D-CNN with electrocardiogram signals
2
2022
... 还有一些研究将PPG信号特征与深度学习结合用于身份识别. Jeon等[11 ] 提出新的方法,称为多层嵌套递归图(multi-slice nested recurrence plot, MsNRP),这个方法主要用于解决存在噪声的PPG信号在身份识别中的问题. MsNRP展示了其对噪声的鲁棒性,从而为实际场景中的识别提供了可靠的解决方案. Lee等[12 ] 提出基于长短期记忆(long short term memory, LSTM)和卷积神经网络(convolutional neural network, CNN)的集成身份识别技术. 在预处理步骤中使用滤波器来去除噪声,并且从原始信号中提取时域特征作为LSTM的输入,获得了一定程度上的身份识别性能提升. ...
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
On the analysis of fingertip photoplethysmogram signals
1
2012
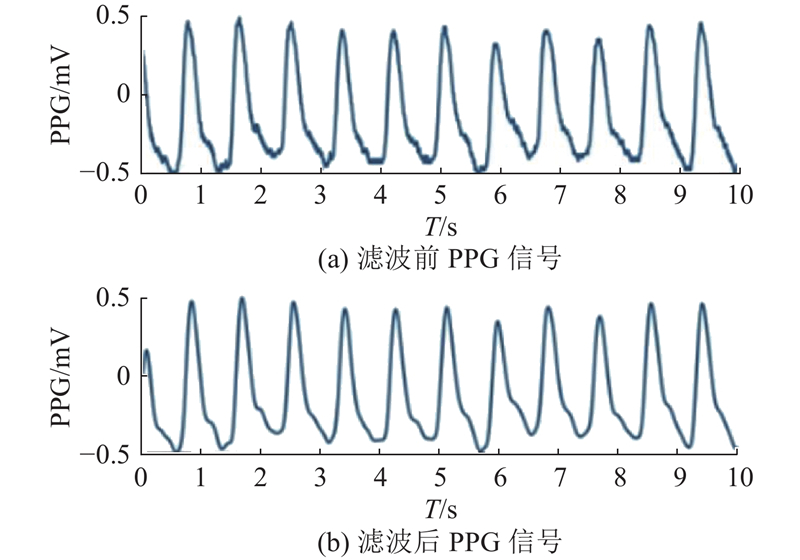
... PPG信号的噪声主要包括基线漂移、电源线干扰和运动伪影等. 其中,基线漂移是由传感器佩戴者的呼吸和移动引起的,是频率小于1 Hz的低频噪声. 电源线干扰是由于仪表放大器、采集系统拾取环境电磁信号和其他伪影造成的[13 ] ,是频率为50 Hz(或更高)的固定频率噪声. 运动伪影是由于传感器的感应点与手指之间的相对距离发生变化而造成的,其频率范围与PPG信号的频率范围重叠[14 ] ,因此极难消除. PPG信号的频率范围为0.3~20.0 Hz,大多数PPG信号的预处理依赖频率滤波来去除PPG信号频率范围之外的噪声. ...
A new method for pulse oximetry possessing inherent insensitivity toartifact
2
2001
... PPG信号的噪声主要包括基线漂移、电源线干扰和运动伪影等. 其中,基线漂移是由传感器佩戴者的呼吸和移动引起的,是频率小于1 Hz的低频噪声. 电源线干扰是由于仪表放大器、采集系统拾取环境电磁信号和其他伪影造成的[13 ] ,是频率为50 Hz(或更高)的固定频率噪声. 运动伪影是由于传感器的感应点与手指之间的相对距离发生变化而造成的,其频率范围与PPG信号的频率范围重叠[14 ] ,因此极难消除. PPG信号的频率范围为0.3~20.0 Hz,大多数PPG信号的预处理依赖频率滤波来去除PPG信号频率范围之外的噪声. ...
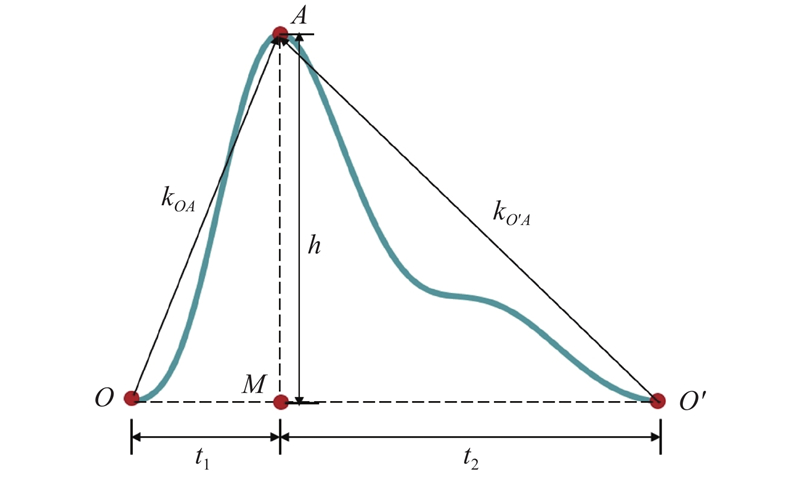
... 尽管幅值、周期、上升支斜率、下降支斜率等信息可以直观反映信号的波形特征,但为了获取更全面的身份识别特征,须对PPG信号进行频域分析[14 ] . ...
2
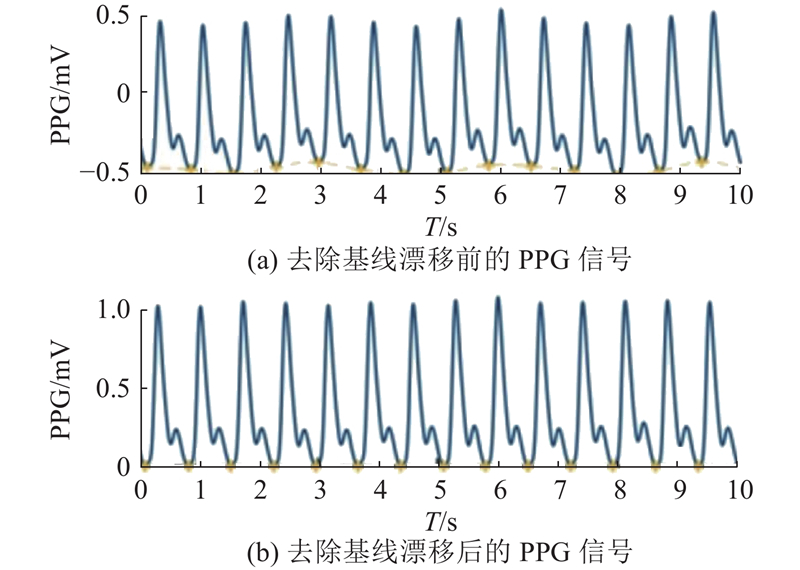
... 由于进行滤波去噪处理后的PPG信号中并不总是理想平滑的信号,使用极值法获取PPG信号波峰的方法存在误检的问题. 为此,基于PPG信号周期性的特点,采用基于滑动窗口的波峰波谷检测算法[15 ] ,具体步骤如下. ...
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
Differences in power spectral densities and phase quantities due to processing of EEG signals
1
2020
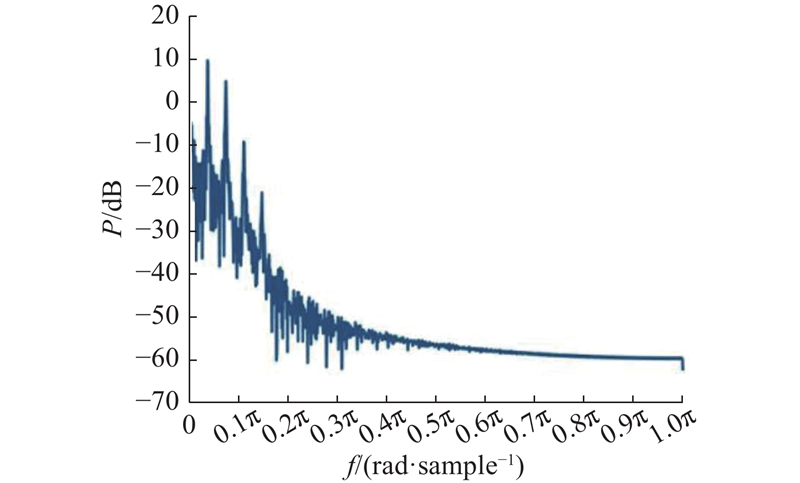
... 功率谱是功率谱密度函数(power spectral density, PSD)的简称,描述了信号功率随频率变化的情况,被广泛应用于各个领域[16 ] . 功率谱估计的方法主要有2种:一种是从给定数据集出发的非参数估计,即经典谱估计方法;另一种是基于参数模型的参数估计,即现代谱估计方法. 相较于现代谱估计方法,经典谱估计方法分辨率较低、方差性较差,但是由于其算法简单、物理意义明确,在误差范围要求不高的情况下同样可以获得较好的效果. ...
1
... 除了时域特征和频域特征之外,PPG信号还具有明显的非线性特性,这些特性与心脏、血管和微循环等部位的活动有关,不同个体PPG信号的非线性参数对于其身份识别具有重要意义. 但是,此前国内外对PPG信号的分析大多集中于其时域特性和频域特性,对于其非线性特性的研究成果相对较少. 近年来,随着对生理信号研究的深入,生理信号的非线性特性也越来越受到关注. 常见的非线性特征参数有关联维数、最大李雅普诺夫指数、近似熵、样本熵、联合熵、互信息等. 目前,已有研究基于这些非线性参数对心电信号[17 -18 ] 、指纹[19 ] 、步态[20 ] 等生理信号进行分析. 研究表明,这些非线性参数可以用于评估时序信号的复杂度和混乱程度,对于生理信号的分析具有重要意义. ...
1
... 除了时域特征和频域特征之外,PPG信号还具有明显的非线性特性,这些特性与心脏、血管和微循环等部位的活动有关,不同个体PPG信号的非线性参数对于其身份识别具有重要意义. 但是,此前国内外对PPG信号的分析大多集中于其时域特性和频域特性,对于其非线性特性的研究成果相对较少. 近年来,随着对生理信号研究的深入,生理信号的非线性特性也越来越受到关注. 常见的非线性特征参数有关联维数、最大李雅普诺夫指数、近似熵、样本熵、联合熵、互信息等. 目前,已有研究基于这些非线性参数对心电信号[17 -18 ] 、指纹[19 ] 、步态[20 ] 等生理信号进行分析. 研究表明,这些非线性参数可以用于评估时序信号的复杂度和混乱程度,对于生理信号的分析具有重要意义. ...
1
... 除了时域特征和频域特征之外,PPG信号还具有明显的非线性特性,这些特性与心脏、血管和微循环等部位的活动有关,不同个体PPG信号的非线性参数对于其身份识别具有重要意义. 但是,此前国内外对PPG信号的分析大多集中于其时域特性和频域特性,对于其非线性特性的研究成果相对较少. 近年来,随着对生理信号研究的深入,生理信号的非线性特性也越来越受到关注. 常见的非线性特征参数有关联维数、最大李雅普诺夫指数、近似熵、样本熵、联合熵、互信息等. 目前,已有研究基于这些非线性参数对心电信号[17 -18 ] 、指纹[19 ] 、步态[20 ] 等生理信号进行分析. 研究表明,这些非线性参数可以用于评估时序信号的复杂度和混乱程度,对于生理信号的分析具有重要意义. ...
Enhanced and secured random number generation for eUASBP
1
2022
... 生物识别技术是指根据个人生理特征和行为特征对其进行身份识别的技术[1 ] . 目前,基于光电容积脉搏波(photoplethysmography, PPG)的生物识别技术的研究仍处于初步阶段,但脉搏波所固有的活体检测、安全性、低成本、便利性等优点使其成为一种极具发展前景的生物识别特征[2 -3 ] . ...
1
... 生物识别技术是指根据个人生理特征和行为特征对其进行身份识别的技术[1 ] . 目前,基于光电容积脉搏波(photoplethysmography, PPG)的生物识别技术的研究仍处于初步阶段,但脉搏波所固有的活体检测、安全性、低成本、便利性等优点使其成为一种极具发展前景的生物识别特征[2 -3 ] . ...
1
... 除了时域特征和频域特征之外,PPG信号还具有明显的非线性特性,这些特性与心脏、血管和微循环等部位的活动有关,不同个体PPG信号的非线性参数对于其身份识别具有重要意义. 但是,此前国内外对PPG信号的分析大多集中于其时域特性和频域特性,对于其非线性特性的研究成果相对较少. 近年来,随着对生理信号研究的深入,生理信号的非线性特性也越来越受到关注. 常见的非线性特征参数有关联维数、最大李雅普诺夫指数、近似熵、样本熵、联合熵、互信息等. 目前,已有研究基于这些非线性参数对心电信号[17 -18 ] 、指纹[19 ] 、步态[20 ] 等生理信号进行分析. 研究表明,这些非线性参数可以用于评估时序信号的复杂度和混乱程度,对于生理信号的分析具有重要意义. ...
Approximate entropy as a measure of system complexity
1
1991
... 在1991年,Pincus[21 ] 提出新的熵测量方法,即近似熵(approximate entropy,ApEn),用于衡量非稳定时间序列的复杂程度. 熵越小,时间序列的复杂程度越低. 在生理信号的相关研究中,近似熵已经被应用于提取眼电信号[22 ] 、脑电信号[23 ] 之类的生理信号的非线性特征. 样本熵是由Richman等[24 ] 提出的对近似熵的改进. 其物理意义与近似熵相似:熵越小,时间序列的复杂程度越低. ...
1
... 生物识别技术是指根据个人生理特征和行为特征对其进行身份识别的技术[1 ] . 目前,基于光电容积脉搏波(photoplethysmography, PPG)的生物识别技术的研究仍处于初步阶段,但脉搏波所固有的活体检测、安全性、低成本、便利性等优点使其成为一种极具发展前景的生物识别特征[2 -3 ] . ...
1
... 2003年,Gu等[4 ] 提出基于PPG信号的生物识别方法. 之后,研究人员对此领域进行了广泛的探索和研究,并获得了一定的成果. Kavsaoglu等[5 ] 从PPG信号及其一阶、二阶导数中提取了40个时域特征,并提出特征排序算法对其排序,最终取得了94.4%的准确率;Jaafar等[6 ] 的研究证明了加速度体积描记信号作为生物识别系统特征的稳健性和可靠性;Chakraborty等[7 ] 从滤波后的PPG及其导数中提取了12个特征,并使用线性判别分析进行分类,该研究对15名受试者的PPG信号进行分类识别,达到了100%的准确率. 孙斌等[8 ] 对PPG信号提取了24维特征;利用寻优算法获取最佳特征子集后利用人工蜂群算法优化支持向量机算法对样本的最佳特征子集进行训练与测试,完成个体身份识别. ...
基于眼电信号近似熵探讨针灸治神的临床应用
1
2023
... 在1991年,Pincus[21 ] 提出新的熵测量方法,即近似熵(approximate entropy,ApEn),用于衡量非稳定时间序列的复杂程度. 熵越小,时间序列的复杂程度越低. 在生理信号的相关研究中,近似熵已经被应用于提取眼电信号[22 ] 、脑电信号[23 ] 之类的生理信号的非线性特征. 样本熵是由Richman等[24 ] 提出的对近似熵的改进. 其物理意义与近似熵相似:熵越小,时间序列的复杂程度越低. ...
基于眼电信号近似熵探讨针灸治神的临床应用
1
2023
... 在1991年,Pincus[21 ] 提出新的熵测量方法,即近似熵(approximate entropy,ApEn),用于衡量非稳定时间序列的复杂程度. 熵越小,时间序列的复杂程度越低. 在生理信号的相关研究中,近似熵已经被应用于提取眼电信号[22 ] 、脑电信号[23 ] 之类的生理信号的非线性特征. 样本熵是由Richman等[24 ] 提出的对近似熵的改进. 其物理意义与近似熵相似:熵越小,时间序列的复杂程度越低. ...
A novel feature ranking algorithm for biometric recognition with PPG signals
2
2014
... 2003年,Gu等[4 ] 提出基于PPG信号的生物识别方法. 之后,研究人员对此领域进行了广泛的探索和研究,并获得了一定的成果. Kavsaoglu等[5 ] 从PPG信号及其一阶、二阶导数中提取了40个时域特征,并提出特征排序算法对其排序,最终取得了94.4%的准确率;Jaafar等[6 ] 的研究证明了加速度体积描记信号作为生物识别系统特征的稳健性和可靠性;Chakraborty等[7 ] 从滤波后的PPG及其导数中提取了12个特征,并使用线性判别分析进行分类,该研究对15名受试者的PPG信号进行分类识别,达到了100%的准确率. 孙斌等[8 ] 对PPG信号提取了24维特征;利用寻优算法获取最佳特征子集后利用人工蜂群算法优化支持向量机算法对样本的最佳特征子集进行训练与测试,完成个体身份识别. ...
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
2
... 2003年,Gu等[4 ] 提出基于PPG信号的生物识别方法. 之后,研究人员对此领域进行了广泛的探索和研究,并获得了一定的成果. Kavsaoglu等[5 ] 从PPG信号及其一阶、二阶导数中提取了40个时域特征,并提出特征排序算法对其排序,最终取得了94.4%的准确率;Jaafar等[6 ] 的研究证明了加速度体积描记信号作为生物识别系统特征的稳健性和可靠性;Chakraborty等[7 ] 从滤波后的PPG及其导数中提取了12个特征,并使用线性判别分析进行分类,该研究对15名受试者的PPG信号进行分类识别,达到了100%的准确率. 孙斌等[8 ] 对PPG信号提取了24维特征;利用寻优算法获取最佳特征子集后利用人工蜂群算法优化支持向量机算法对样本的最佳特征子集进行训练与测试,完成个体身份识别. ...
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
2
... 2003年,Gu等[4 ] 提出基于PPG信号的生物识别方法. 之后,研究人员对此领域进行了广泛的探索和研究,并获得了一定的成果. Kavsaoglu等[5 ] 从PPG信号及其一阶、二阶导数中提取了40个时域特征,并提出特征排序算法对其排序,最终取得了94.4%的准确率;Jaafar等[6 ] 的研究证明了加速度体积描记信号作为生物识别系统特征的稳健性和可靠性;Chakraborty等[7 ] 从滤波后的PPG及其导数中提取了12个特征,并使用线性判别分析进行分类,该研究对15名受试者的PPG信号进行分类识别,达到了100%的准确率. 孙斌等[8 ] 对PPG信号提取了24维特征;利用寻优算法获取最佳特征子集后利用人工蜂群算法优化支持向量机算法对样本的最佳特征子集进行训练与测试,完成个体身份识别. ...
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
基于改进邻域粗糙集的 PPG 信号身份识别方法
1
2022
... 2003年,Gu等[4 ] 提出基于PPG信号的生物识别方法. 之后,研究人员对此领域进行了广泛的探索和研究,并获得了一定的成果. Kavsaoglu等[5 ] 从PPG信号及其一阶、二阶导数中提取了40个时域特征,并提出特征排序算法对其排序,最终取得了94.4%的准确率;Jaafar等[6 ] 的研究证明了加速度体积描记信号作为生物识别系统特征的稳健性和可靠性;Chakraborty等[7 ] 从滤波后的PPG及其导数中提取了12个特征,并使用线性判别分析进行分类,该研究对15名受试者的PPG信号进行分类识别,达到了100%的准确率. 孙斌等[8 ] 对PPG信号提取了24维特征;利用寻优算法获取最佳特征子集后利用人工蜂群算法优化支持向量机算法对样本的最佳特征子集进行训练与测试,完成个体身份识别. ...
基于脑电非线性动力学特征探究TEAS内关穴对焦虑的影响
1
2022
... 在1991年,Pincus[21 ] 提出新的熵测量方法,即近似熵(approximate entropy,ApEn),用于衡量非稳定时间序列的复杂程度. 熵越小,时间序列的复杂程度越低. 在生理信号的相关研究中,近似熵已经被应用于提取眼电信号[22 ] 、脑电信号[23 ] 之类的生理信号的非线性特征. 样本熵是由Richman等[24 ] 提出的对近似熵的改进. 其物理意义与近似熵相似:熵越小,时间序列的复杂程度越低. ...
基于脑电非线性动力学特征探究TEAS内关穴对焦虑的影响
1
2022
... 在1991年,Pincus[21 ] 提出新的熵测量方法,即近似熵(approximate entropy,ApEn),用于衡量非稳定时间序列的复杂程度. 熵越小,时间序列的复杂程度越低. 在生理信号的相关研究中,近似熵已经被应用于提取眼电信号[22 ] 、脑电信号[23 ] 之类的生理信号的非线性特征. 样本熵是由Richman等[24 ] 提出的对近似熵的改进. 其物理意义与近似熵相似:熵越小,时间序列的复杂程度越低. ...
Physiological time-series analysis using approximate entropy and sample entropy
1
2000
... 在1991年,Pincus[21 ] 提出新的熵测量方法,即近似熵(approximate entropy,ApEn),用于衡量非稳定时间序列的复杂程度. 熵越小,时间序列的复杂程度越低. 在生理信号的相关研究中,近似熵已经被应用于提取眼电信号[22 ] 、脑电信号[23 ] 之类的生理信号的非线性特征. 样本熵是由Richman等[24 ] 提出的对近似熵的改进. 其物理意义与近似熵相似:熵越小,时间序列的复杂程度越低. ...
Characterization of surface EMG signal based on fuzzy entropy
1
2007
... 模糊熵是由Chen等[25 ] 于2007年提出的. 模糊熵的计算过程与近似熵类似,主要的区别如下. ...
Refined composite multiscale dispersion entropy and its application to biomedical signals
1
2017
... Azami等[26 ] 的研究表明RCMDE能够区分不同的动力学,因此,将RCMDE作为PPG身份识别的特征参数是有意义的. ...
1
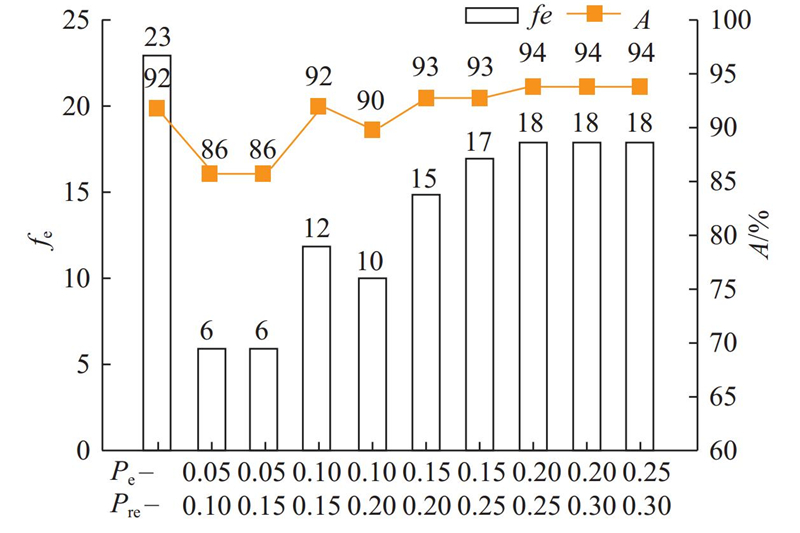
... 1) 遍历原始特征集,选择使得Wilk’s Lambda最小化的特征[27 ] . ...
改进WOA算法优化SVM的网络入侵检测
1
2019
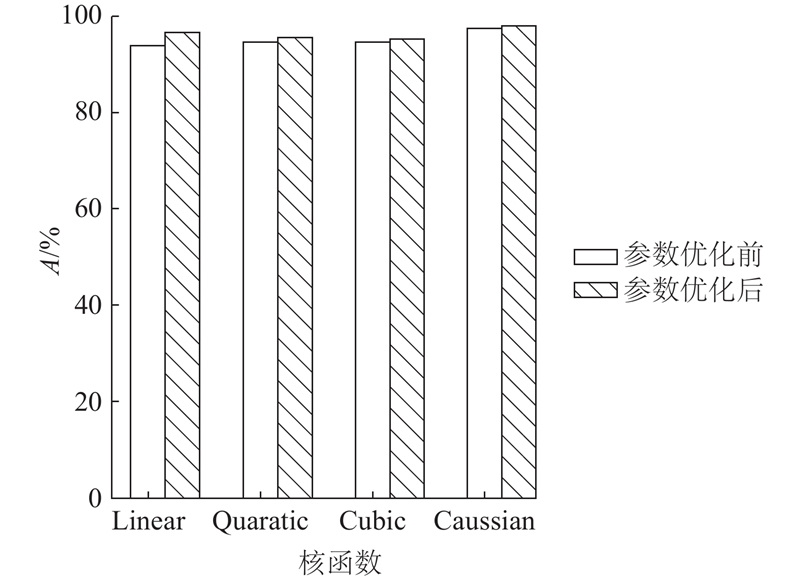
... 参数设置对于SVM分类性能具有至关重要的影响,如果选择不合适的SVM参数,所得的分类准确率可能会很差[28 ] . ...
改进WOA算法优化SVM的网络入侵检测
1
2019
... 参数设置对于SVM分类性能具有至关重要的影响,如果选择不合适的SVM参数,所得的分类准确率可能会很差[28 ] . ...
1
... 身份识别任务基于MIMIC数据库[29 ] 中的PPG信号展开. MIMIC数据库包括多名重症监护室患者的记录数据,每条记录通常包含从波士顿贝斯以色列医院的内科、外科和心脏重症监护室的病人监护仪中记录的24~48 h的连续数据,采样频率为125 Hz. 从MIMIC数据库中选择了年龄10~80岁不同性别的200个身份识别主体,每人有5条PPG数据,共1000 条数据. 此外,采用十折交叉验证的方法来评估所提出模型的泛化性能,具体地,将数据集划分为10个大小相等的子集,称为折. 然后,该算法在以下步骤中进行训练和评估: ...
1
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
1
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
1
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
1
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
Evaluation of the time stability and uniqueness in PPG-based biometric system
1
2021
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...
PPG-based human identification using Mel-frequency cepstral coefficients and neural networks
1
2021
... Comparison of proposed PPG identity recognition with relevant research
Tab.6 文献 年份 M (PPG数据)特征提取 分类器 A /%注:1) FAR为假接受率;2) FRR为假拒绝率. 文献[30 ] 2003 17 时域 KNN 94.0 文献[9 ] 2003 17 时域 模糊逻辑 94.0 文献[5 ] 2014 40 时域 KNN 94.4 文献[6 ] 2015 10 时域 贝叶斯网络 97.5 文献[31 ] 2015 10(708组) 时域 FNN FAR:4.21) 2) 文献[7 ] 2016 15 时域 LDA 100.0 文献[10 ] 2016 23 高斯参数 LDA 95.7 文献[32 ] 2017 42 小波变换 KNN 99.8 文献[15 ] 2017 42 小波变换 SVM 100.0 文献[33 ] 2020 20 时域+频域 SVM 93.1 文献[34 ] 2021 100 — CNN+LSTM 98.0 文献[35 ] 2021 35 频域 CNN 99.4 文献[12 ] 2022 100 时域+频域+小波变换 CNNLSTM 98.3 文献[11 ] 2023 50 — MsNRPNet 92.0 本研究 25(125组) 时域+频域+非线性特征 LDA 100.0 — 50(250组) 99.9 200(1000 组) 98.4
4. 结 语 提出基于PPG信号多维度特征的身份识别方法. 对获得的PPG信号进行预处理,分析PPG信号的噪声来源并基于此进行去噪. 在完成信号滤波后,对PPG信号的波峰和波谷进行检测,并基于此去除基线漂移. 随后,提取用于身份识别的新特征,构建多维度的PPG信号特征集,其中包括10个时域参数、8个频域参数和5个非线性参数,共23个特征参数. 之后,对提取的特征参数进行优化,并通过逐步回归法选出18个特征参数. 相比于没有进行特征选择的PPG身份识别模型,准确率提升了2.0%. 最后,对分类模型进行参数优化和对比分析,最终选择LDA作为分类器进行身份识别. 在200个主体、1000 条数据的身份识别任务中,该模型取得了98.4%的准确率. 与其他已有研究对比分析可知,本研究方法取得了较高的准确率. 另外,验证了构建多维度特征对于提升PPG身份识别任务准确率的作用. 本研究所提出的身份验证方法在综合考虑多个PPG信息维度的同时,还能够增加样本数量,对样本量较少的小规模数据集有着更强的适用性. ...