Multi-objective Q-learning-based hyper-heuristic with bi-criteria selection for energy-aware mixed shop scheduling
1
2022
... 作为新生代的人工智能,智能计算(intelligent computations, ICs)在过去的几十年中被广泛用于求解各种复杂的优化问题,如资源调度[1 ] 、电力系统[2 ] 、路径规划[3 ] 和无线网络[4 ] 等,并因其良好的自组织、自学习和自适应性取得了令人瞩目的成果. 其中,进化算法[5 ] 及群智能算法是ICs中的两大研究热点,代表性算法分别是差分进化(differential evolution, DE)和粒子群优化(particle swarm optimization, PSO). ...
Multi-objective optimization of a novel combined cooling, dehumidification and power system using improved M-PSO algorithm
1
2022
... 作为新生代的人工智能,智能计算(intelligent computations, ICs)在过去的几十年中被广泛用于求解各种复杂的优化问题,如资源调度[1 ] 、电力系统[2 ] 、路径规划[3 ] 和无线网络[4 ] 等,并因其良好的自组织、自学习和自适应性取得了令人瞩目的成果. 其中,进化算法[5 ] 及群智能算法是ICs中的两大研究热点,代表性算法分别是差分进化(differential evolution, DE)和粒子群优化(particle swarm optimization, PSO). ...
1
... 作为新生代的人工智能,智能计算(intelligent computations, ICs)在过去的几十年中被广泛用于求解各种复杂的优化问题,如资源调度[1 ] 、电力系统[2 ] 、路径规划[3 ] 和无线网络[4 ] 等,并因其良好的自组织、自学习和自适应性取得了令人瞩目的成果. 其中,进化算法[5 ] 及群智能算法是ICs中的两大研究热点,代表性算法分别是差分进化(differential evolution, DE)和粒子群优化(particle swarm optimization, PSO). ...
Automata based hybrid PSO–GWO algorithm for secured energy efficient optimal routing in wireless sensor network
1
2021
... 作为新生代的人工智能,智能计算(intelligent computations, ICs)在过去的几十年中被广泛用于求解各种复杂的优化问题,如资源调度[1 ] 、电力系统[2 ] 、路径规划[3 ] 和无线网络[4 ] 等,并因其良好的自组织、自学习和自适应性取得了令人瞩目的成果. 其中,进化算法[5 ] 及群智能算法是ICs中的两大研究热点,代表性算法分别是差分进化(differential evolution, DE)和粒子群优化(particle swarm optimization, PSO). ...
1
... 作为新生代的人工智能,智能计算(intelligent computations, ICs)在过去的几十年中被广泛用于求解各种复杂的优化问题,如资源调度[1 ] 、电力系统[2 ] 、路径规划[3 ] 和无线网络[4 ] 等,并因其良好的自组织、自学习和自适应性取得了令人瞩目的成果. 其中,进化算法[5 ] 及群智能算法是ICs中的两大研究热点,代表性算法分别是差分进化(differential evolution, DE)和粒子群优化(particle swarm optimization, PSO). ...
Surrogate-assisted evolutionary computation: recent advances and future challenges
1
2011
... 通常,现有关于ICs的研究大多是基于隐含的假设,即评估候选解的目标和约束条件是简单且低廉的[6 ] . 在许多实际优化问题中,这样的廉价函数不存在,目标函数只能从昂贵的物理实验、数值模拟或日常生活中收集的数据进行适应度评估[7 ] ,如翼型气动优化设计[8 ] 、药物设计[9 ] 和创伤系统设计[10 ] 等,因此计算成本非常昂贵,一次适应度评估可能需要几分钟或几小时,甚至几天的时间[11 ] . 在更极端的情况下,只有历史数据可用于执行优化,且在优化过程中不能生成新的数据,这给ICs带来了极大的挑战. 此外,随着物联网、云计算、大数据、5G和区块链等技术的发展,越来越多的昂贵优化问题(expensive optimization problems, EOPs)呈现出超多目标、大搜索空间、高可变维度、多模态、强约束等新的挑战,使得候选解的评估或约束评估成本十分高昂,ICs难以找到令人满意的解[12 ] . ...
Data-driven evolutionary optimization: an overview and case studies
4
2019
... 通常,现有关于ICs的研究大多是基于隐含的假设,即评估候选解的目标和约束条件是简单且低廉的[6 ] . 在许多实际优化问题中,这样的廉价函数不存在,目标函数只能从昂贵的物理实验、数值模拟或日常生活中收集的数据进行适应度评估[7 ] ,如翼型气动优化设计[8 ] 、药物设计[9 ] 和创伤系统设计[10 ] 等,因此计算成本非常昂贵,一次适应度评估可能需要几分钟或几小时,甚至几天的时间[11 ] . 在更极端的情况下,只有历史数据可用于执行优化,且在优化过程中不能生成新的数据,这给ICs带来了极大的挑战. 此外,随着物联网、云计算、大数据、5G和区块链等技术的发展,越来越多的昂贵优化问题(expensive optimization problems, EOPs)呈现出超多目标、大搜索空间、高可变维度、多模态、强约束等新的挑战,使得候选解的评估或约束评估成本十分高昂,ICs难以找到令人满意的解[12 ] . ...
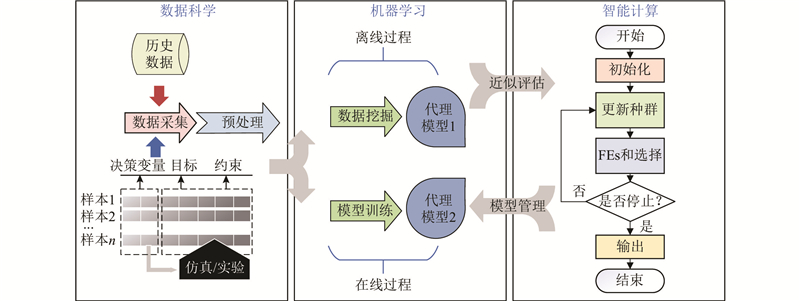
... 为了有效降低ICs优化EOPs时的计算代价,DDICs应运而生. 该框架主要涉及3个方面的内容[7 ] ,即数据科学、机器学习和ICs,具体过程如图2 所示. ...
... 对于求解EOPs-Ⅰ,算法只能根据给定的数据构建代理模型以勘探搜索空间. 因为在优化过程中不能增加新的样本点,离线DDICs比在线更复杂. 为了提高算法精度,核心的研究内容包括以下3个方面[7 ] . 1)采用集成技术,以减小代理逼近问题函数时的近似误差. 2)进行数据增强,通过生成可信度高的合成数据,提高可用历史数据的质量. 3)改进进化组件,提高算法的搜索能力与收敛效率. 此外,离线DDICs通常可以看作在线DDICs中的最佳候选点选择策略. 在某种程度上,离线DDICs研究的成果也适用于在线DDICs. 到目前为止,已经提出了许多的离线DDICs算法,本节将简要回顾相关工作,讨论它们的差异和局限性. ...
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
Offline data-driven evolutionary optimization using selective surrogate ensembles
3
2018
... 通常,现有关于ICs的研究大多是基于隐含的假设,即评估候选解的目标和约束条件是简单且低廉的[6 ] . 在许多实际优化问题中,这样的廉价函数不存在,目标函数只能从昂贵的物理实验、数值模拟或日常生活中收集的数据进行适应度评估[7 ] ,如翼型气动优化设计[8 ] 、药物设计[9 ] 和创伤系统设计[10 ] 等,因此计算成本非常昂贵,一次适应度评估可能需要几分钟或几小时,甚至几天的时间[11 ] . 在更极端的情况下,只有历史数据可用于执行优化,且在优化过程中不能生成新的数据,这给ICs带来了极大的挑战. 此外,随着物联网、云计算、大数据、5G和区块链等技术的发展,越来越多的昂贵优化问题(expensive optimization problems, EOPs)呈现出超多目标、大搜索空间、高可变维度、多模态、强约束等新的挑战,使得候选解的评估或约束评估成本十分高昂,ICs难以找到令人满意的解[12 ] . ...
... 集成学习的核心思想是通过bagging[8 ] 或boosting[39 ] 技术,将多个较弱的元模型集合成较强的组合模型,有效提高模型的泛化能力. 其中,bagging采用并行处理的方法,减小代理模型带来的方差. boosting使用串行处理技术,减小模型引入的偏差. 如图3 所示为基于bagging的集成学习过程. 此外,该技术被广泛应用于在线DDICs中. 例如,Wang等[8 ] 提出DDEA-SE算法,通过使用bagging技术离线生成大量的代理模型,且随着优化过程的进行,自适应地选择其中的一个子集进行适应度评估,减小模型的预测误差. Li等[40 ] 提出DDEA-PES算法,他们采用选择性的集成方法有效提高模型的鲁棒性,实验表明,DDEA-PES算法只需要约2%的计算预算,即可产生具有竞争力的结果. DDEA-SE和DDEA-PES分别从2 000个和200个容量的模型池中提取100个选定模型的平均输出,因此在构建模型时需要花费大量的计算时间. Huang等[41 ] 基于多核学习思想(multi-kernel learning,MLK)提出SRK-DDEA算法,主要通过随机排序(stochastic rank,SR)来组合4种不同核函数的RBFN模型,以提高预测精度. SRK-DDEA算法在高维问题上表现较好,但在低维问题上的表现不如DDEA-SE算法. 随后,Huang等[42 ] 将半监督学习和集成技术引入离线DDICs中,提出TT-DDEA算法,通过在每一代TT-DDEA的更新中使用三元训练模型,求解多达500个决策变量的大规模EOPs-Ⅰ. 虽然TT-DDEA算法的计算时间更短,但是伪标签的增加会使代理模型误导优化过程. 此外,Zheng等[43 ] 提出更高层次的离线优化框架(MS-DDEO),该框架使用4种不同的RBFNs模型,能够有效地解决不同类型的问题. 与SRK-DDEA算法不同,MS-DDEO能够提供评估代理模型的标准. 上述算法都采用相同的元模型进行同构集成学习. Fan等[44 ] 为了解决小样本离散数据的优化问题,将有限的数据分成多个子集,在每个子集上训练GP和RBFN模型进行异构集成学习,在一定程度上解决了高维优化的耗时问题. ...
... [8 ]提出DDEA-SE算法,通过使用bagging技术离线生成大量的代理模型,且随着优化过程的进行,自适应地选择其中的一个子集进行适应度评估,减小模型的预测误差. Li等[40 ] 提出DDEA-PES算法,他们采用选择性的集成方法有效提高模型的鲁棒性,实验表明,DDEA-PES算法只需要约2%的计算预算,即可产生具有竞争力的结果. DDEA-SE和DDEA-PES分别从2 000个和200个容量的模型池中提取100个选定模型的平均输出,因此在构建模型时需要花费大量的计算时间. Huang等[41 ] 基于多核学习思想(multi-kernel learning,MLK)提出SRK-DDEA算法,主要通过随机排序(stochastic rank,SR)来组合4种不同核函数的RBFN模型,以提高预测精度. SRK-DDEA算法在高维问题上表现较好,但在低维问题上的表现不如DDEA-SE算法. 随后,Huang等[42 ] 将半监督学习和集成技术引入离线DDICs中,提出TT-DDEA算法,通过在每一代TT-DDEA的更新中使用三元训练模型,求解多达500个决策变量的大规模EOPs-Ⅰ. 虽然TT-DDEA算法的计算时间更短,但是伪标签的增加会使代理模型误导优化过程. 此外,Zheng等[43 ] 提出更高层次的离线优化框架(MS-DDEO),该框架使用4种不同的RBFNs模型,能够有效地解决不同类型的问题. 与SRK-DDEA算法不同,MS-DDEO能够提供评估代理模型的标准. 上述算法都采用相同的元模型进行同构集成学习. Fan等[44 ] 为了解决小样本离散数据的优化问题,将有限的数据分成多个子集,在每个子集上训练GP和RBFN模型进行异构集成学习,在一定程度上解决了高维优化的耗时问题. ...
Artificial intelligence-enhanced drug design and development: toward a computational precision medicine
1
2022
... 通常,现有关于ICs的研究大多是基于隐含的假设,即评估候选解的目标和约束条件是简单且低廉的[6 ] . 在许多实际优化问题中,这样的廉价函数不存在,目标函数只能从昂贵的物理实验、数值模拟或日常生活中收集的数据进行适应度评估[7 ] ,如翼型气动优化设计[8 ] 、药物设计[9 ] 和创伤系统设计[10 ] 等,因此计算成本非常昂贵,一次适应度评估可能需要几分钟或几小时,甚至几天的时间[11 ] . 在更极端的情况下,只有历史数据可用于执行优化,且在优化过程中不能生成新的数据,这给ICs带来了极大的挑战. 此外,随着物联网、云计算、大数据、5G和区块链等技术的发展,越来越多的昂贵优化问题(expensive optimization problems, EOPs)呈现出超多目标、大搜索空间、高可变维度、多模态、强约束等新的挑战,使得候选解的评估或约束评估成本十分高昂,ICs难以找到令人满意的解[12 ] . ...
Data-driven surrogate-assisted multi-objective evolutionary optimization of a trauma system
6
2016
... 通常,现有关于ICs的研究大多是基于隐含的假设,即评估候选解的目标和约束条件是简单且低廉的[6 ] . 在许多实际优化问题中,这样的廉价函数不存在,目标函数只能从昂贵的物理实验、数值模拟或日常生活中收集的数据进行适应度评估[7 ] ,如翼型气动优化设计[8 ] 、药物设计[9 ] 和创伤系统设计[10 ] 等,因此计算成本非常昂贵,一次适应度评估可能需要几分钟或几小时,甚至几天的时间[11 ] . 在更极端的情况下,只有历史数据可用于执行优化,且在优化过程中不能生成新的数据,这给ICs带来了极大的挑战. 此外,随着物联网、云计算、大数据、5G和区块链等技术的发展,越来越多的昂贵优化问题(expensive optimization problems, EOPs)呈现出超多目标、大搜索空间、高可变维度、多模态、强约束等新的挑战,使得候选解的评估或约束评估成本十分高昂,ICs难以找到令人满意的解[12 ] . ...
... 1)EOPs(记为EOPs-Ⅰ)的目标或约束函数难以通过数学表达式进行显示表达,即没有明确的模型能够描述待求解目标与决策变量之间的关系. 只有从数值模拟、物理实验或日常生活中收集的数据,能够用于评估候选解的目标和约束,这类问题通常被称为离散(组合)优化问题. 例如,在许多流程工业优化[21 ] 和创伤系统设计优化问题[10 ] 中,只能通过收集的历史数据进行优化,难以构造具体的数学模型用于优化求解. 在结构设计优化问题[22 ] 中,采用非常密集的计算流体动力学(computational fluid dynamic, CFD)或有限元分析(finite element analysis, FEA)进行模拟计算,非常耗时. ...
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
... 迄今为止,很多学者致力于多目标EOPs-Ⅰ的研究. 例如,SA-NSGA-II[10 ] 和RF-CMOCO[54 ] 算法利用离线大数据产生的多个保真度水平的优势来解决多目标的创伤系统设计问题,区别在于RF-CMOCO考虑了约束处理. Mazumdar等[55 ] 提出概率选择方法的分解多目标算法,该方法利用Kriging模型提供的不确定性信息来改进离线多目标优化中的求解过程,有效地提高了解的准确性. Liu等[56 ] 采用基于指标的MOEA,设计自适应模型选择策略,提高算法的鲁棒性,减少近似误差的累积,该方法可在多达30个决策变量的多目标EOPs-Ⅰ上有效. Gong等[57 ] 构建端到端的深度学习代理用于游戏的自动团队组装(automated team assembly, ATA),开发分层修复策略来处理约束,能够帮助开发者进行游戏平衡分析,但该算法适用于涉及许多稀疏特征的ATA问题. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A systems approach to evolutionary multi-objective structural optimization and beyond
1
2009
... 通常,现有关于ICs的研究大多是基于隐含的假设,即评估候选解的目标和约束条件是简单且低廉的[6 ] . 在许多实际优化问题中,这样的廉价函数不存在,目标函数只能从昂贵的物理实验、数值模拟或日常生活中收集的数据进行适应度评估[7 ] ,如翼型气动优化设计[8 ] 、药物设计[9 ] 和创伤系统设计[10 ] 等,因此计算成本非常昂贵,一次适应度评估可能需要几分钟或几小时,甚至几天的时间[11 ] . 在更极端的情况下,只有历史数据可用于执行优化,且在优化过程中不能生成新的数据,这给ICs带来了极大的挑战. 此外,随着物联网、云计算、大数据、5G和区块链等技术的发展,越来越多的昂贵优化问题(expensive optimization problems, EOPs)呈现出超多目标、大搜索空间、高可变维度、多模态、强约束等新的挑战,使得候选解的评估或约束评估成本十分高昂,ICs难以找到令人满意的解[12 ] . ...
Evolutionary computation for expensive optimization: a survey
3
2022
... 通常,现有关于ICs的研究大多是基于隐含的假设,即评估候选解的目标和约束条件是简单且低廉的[6 ] . 在许多实际优化问题中,这样的廉价函数不存在,目标函数只能从昂贵的物理实验、数值模拟或日常生活中收集的数据进行适应度评估[7 ] ,如翼型气动优化设计[8 ] 、药物设计[9 ] 和创伤系统设计[10 ] 等,因此计算成本非常昂贵,一次适应度评估可能需要几分钟或几小时,甚至几天的时间[11 ] . 在更极端的情况下,只有历史数据可用于执行优化,且在优化过程中不能生成新的数据,这给ICs带来了极大的挑战. 此外,随着物联网、云计算、大数据、5G和区块链等技术的发展,越来越多的昂贵优化问题(expensive optimization problems, EOPs)呈现出超多目标、大搜索空间、高可变维度、多模态、强约束等新的挑战,使得候选解的评估或约束评估成本十分高昂,ICs难以找到令人满意的解[12 ] . ...
... 在过去的工作中,大多是对EOPs-Ⅰ和EOPs-Ⅱ的研究,而对EOPs-Ⅲ的探索较少. 本文主要梳理了关于EOPs-Ⅰ和EOPs-Ⅱ的最新研究内容. 为了具体刻画EOPs的关键特性,即昂贵的评估成本,Li等[12 ] 对使用ICs解决EOPs的总成本进行如下定义: ...
... DDICs为解决昂贵的优化问题提供了一种极具竞争力的方法,并被广泛应用于医疗健康、工程设计、能源能耗、环境污染和资源调度等各种EOPs问题. 对DDICs所涉及的应用领域进行总结与归纳,具体如表4 所示. 可知,很多研究者通过考虑特定问题类型和特征来应对相应EOPs的挑战,从而产生应用DDICs的方法,旨在实现计算时间成本和优化精度之间的平衡. 许多现有的优化算法通常只能应用于特定类型的EOPs,这使得研究人员在比较和测试新方法时面临困难,建立更通用的评估标准和测试平台显得尤为重要. 目前,学术界已开展多项工作,为求解EOPs提供了各种竞赛和基准测试. 如表5 所示为近6年来基于实际EOPs的竞赛. 此外,Wu等[152 ] 基于现有的开源实际车辆路线,为昂贵的人群运输优化应用程序开发了35个测试实例. 这些工作能够揭示实际应用中EOPs的困难和挑战,并评估各种最先进的方法,以弥合学术和应用之间的差距[12 ] . ...
Complementary surrogate-assisted differential evolution algorithm for expensive multi-objective problems under a limited computational budget
1
2023
... 为了应对这一挑战,机器学习的建模技术被引入优化过程,以辅助ICs解决被广泛研究的EOPs[13 ] ,形成了数据驱动优化的研究分支,或称为代理辅助优化,这是因为大多数关于数据驱动优化的工作实际上都是在代理辅助优化领域进行的. 代理模型有时也被称为元模型. 引入代理模型的目的是可以根据历史数据构建近似模型,探索问题结构的内部规律和领域知识,使得算法能够应用于目标昂贵或者没有精确目标函数的EOPs;另外,代理模型能够辅助ICs探索未知或动态的适应度形态,在不影响全局最优的前提下平滑掉局部最优,以促进知识的转移及传递. 这样能够使ICs以较少的计算时间或计算成本获得最优解,还能够尽可能地保证解的质量[14 ] . ...
A survey on handling computationally expensive multi-objective optimization problems with evolutionary algorithms
1
2019
... 为了应对这一挑战,机器学习的建模技术被引入优化过程,以辅助ICs解决被广泛研究的EOPs[13 ] ,形成了数据驱动优化的研究分支,或称为代理辅助优化,这是因为大多数关于数据驱动优化的工作实际上都是在代理辅助优化领域进行的. 代理模型有时也被称为元模型. 引入代理模型的目的是可以根据历史数据构建近似模型,探索问题结构的内部规律和领域知识,使得算法能够应用于目标昂贵或者没有精确目标函数的EOPs;另外,代理模型能够辅助ICs探索未知或动态的适应度形态,在不影响全局最优的前提下平滑掉局部最优,以促进知识的转移及传递. 这样能够使ICs以较少的计算时间或计算成本获得最优解,还能够尽可能地保证解的质量[14 ] . ...
Surrogate-assisted multicriteria optimization: complexities, prospective solutions, and business case
1
2017
... 迄今为止,数据驱动的智能计算(data-driven intelligent computations, DDICs)在解决EOPs时进行了各种研究,取得了很大的成功. 国内外已有不少学者从不同的角度围绕DDICs的研究领域进行了系统的总结与分析[15 -19 ] . 本文主要回顾了DDICs近几年的研究方法,总结了经典DDICs和自适应DDICs的最新成果,介绍了DDICs在实际生活中的应用场景及未来的发展趋势. 本文旨在综述DDICs这一新兴研究领域的最新进展,综合并参考现有的研究结果,以帮助相关领域的发展. ...
Surrogate-assisted evolutionary optimization frameworks for high-fidelity engineering design problems
0
2005
A review of techniques for handling expensive functions in evolutionary multi-objective optimization
0
2010
A survey on handling computationally expensive multi-objective optimization problems using surrogates: non-nature inspired methods
0
2015
A review of surrogate-assisted evolutionary algorithms for expensive optimization problems
1
2023
... 迄今为止,数据驱动的智能计算(data-driven intelligent computations, DDICs)在解决EOPs时进行了各种研究,取得了很大的成功. 国内外已有不少学者从不同的角度围绕DDICs的研究领域进行了系统的总结与分析[15 -19 ] . 本文主要回顾了DDICs近几年的研究方法,总结了经典DDICs和自适应DDICs的最新成果,介绍了DDICs在实际生活中的应用场景及未来的发展趋势. 本文旨在综述DDICs这一新兴研究领域的最新进展,综合并参考现有的研究结果,以帮助相关领域的发展. ...
Optimizing living material delivery during the COVID-19 outbreak
1
2021
... EOPs与其他优化问题在本质上是相同的,主要区别在于EOPs评估候选解时所花费的计算时间或计算成本十分昂贵. 这里的“昂贵”是相对的概念,在一些特殊情况下,不昂贵的优化问题可能会变得十分昂贵. 例如,当疫情或灾害突发时,交通运输和物资调度会十分紧急,因此待优化的时间和成本变得异常昂贵[20 ] . 目前,常见的EOPs主要有以下3类. ...
1
... 1)EOPs(记为EOPs-Ⅰ)的目标或约束函数难以通过数学表达式进行显示表达,即没有明确的模型能够描述待求解目标与决策变量之间的关系. 只有从数值模拟、物理实验或日常生活中收集的数据,能够用于评估候选解的目标和约束,这类问题通常被称为离散(组合)优化问题. 例如,在许多流程工业优化[21 ] 和创伤系统设计优化问题[10 ] 中,只能通过收集的历史数据进行优化,难以构造具体的数学模型用于优化求解. 在结构设计优化问题[22 ] 中,采用非常密集的计算流体动力学(computational fluid dynamic, CFD)或有限元分析(finite element analysis, FEA)进行模拟计算,非常耗时. ...
Hybrid method for inverse design of orbital angular momentum transmission fiber based on neural network and optimization algorithms
1
2022
... 1)EOPs(记为EOPs-Ⅰ)的目标或约束函数难以通过数学表达式进行显示表达,即没有明确的模型能够描述待求解目标与决策变量之间的关系. 只有从数值模拟、物理实验或日常生活中收集的数据,能够用于评估候选解的目标和约束,这类问题通常被称为离散(组合)优化问题. 例如,在许多流程工业优化[21 ] 和创伤系统设计优化问题[10 ] 中,只能通过收集的历史数据进行优化,难以构造具体的数学模型用于优化求解. 在结构设计优化问题[22 ] 中,采用非常密集的计算流体动力学(computational fluid dynamic, CFD)或有限元分析(finite element analysis, FEA)进行模拟计算,非常耗时. ...
Multi-objective surrogate-model-based neural architecture and physical design co-optimization of energy efficient neural network hardware accelerators
1
2022
... 2)EOPs(记为EOPs-Ⅱ)的目标或约束函数能够进行显示表达,但是候选解的评估或约束评估成本高昂,往往可能伴随着大规模特征、动态搜索空间、多模态、强约束、超多目标等不可预知的挑战. 这类问题通常被称作连续优化问题. 例如,在深度神经架构搜索(neural architecture search, NAS)[23 -24 ] 中存在数百万和数千万量级的结构参数待训练,使得算法的执行效率和精度大大降低. ...
Surrogate-assisted hybrid evolutionary algorithm with local estimation of distribution for expensive mixed-variable optimization problems
2
2023
... 2)EOPs(记为EOPs-Ⅱ)的目标或约束函数能够进行显示表达,但是候选解的评估或约束评估成本高昂,往往可能伴随着大规模特征、动态搜索空间、多模态、强约束、超多目标等不可预知的挑战. 这类问题通常被称作连续优化问题. 例如,在深度神经架构搜索(neural architecture search, NAS)[23 -24 ] 中存在数百万和数千万量级的结构参数待训练,使得算法的执行效率和精度大大降低. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Surrogate-assisted hybrid-model estimation of distribution algorithm for mixed-variable hyperparameters optimization in convolutional neural networks
3
2021
... 3)EOPs(记为EOPs-Ⅲ)由EOPs-Ⅰ和EOPs-Ⅱ组合而成,包含了不同的变量类型,这种混合变量特性对优化搜索提出了很大的挑战,可能具有大规模的搜索空间和昂贵的计算成本. 这类问题通常被称为混合优化问题,以卷积神经网络(convolution neural network, CNN)超参数优化问题[25 ] 为典型,其中卷积核数为整数;dropout概率为实数;激活函数的种类是离散的,因此如何有效地同时处理不同的变量类型,将是提升CNN性能的关键. ...
... b)特殊多目标EOPs. 除了上述常见的多目标优化问题,还有一些特定的MOAs用于求解特殊的多目标EOPs. 例如,Zhang等[113 ] 提出基于传递学习的代理辅助进化算法(TrSA-DMOEA),有效地解决了动态昂贵多目标问题. 具体地说,当环境发生变化时,提出基于测地线流核的膝点(keen point)流形传递学习方法,利用以往高质量膝点解的知识来增加建立高斯过程模型的训练数据,提高解的计算复杂度和质量. Li等[25 ] 提出基于代理辅助混合模型的分布估计算法(SHEDA),用于求解混合变量的大规模EOPs-III. Wang等[114 ] 将迁移学习引入到协同代理搜索中,解决评估时间不均匀的双目标EOPs-II. Wu等[115 ] 提出新的基于Kriging-SVM的进化算法,用于解决动态多模态EOPs-II. Song等[116 ] 提出求解具有不等式约束的EOPs-II通用框架(DSI),将目标和约束分别用2组不同的训练数据进行训练,提高感兴趣区域的预测精度和可靠性. 此外,Xu等[117 ] 将联邦学习引入到DDICs中,提出新的联邦学习数据驱动进化多/超多目标算法. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
1
... 一般来说,ICs主要分为单目标优化算法(single-objective optimization algorithms, SOAs)和多目标优化算法(multi-objective optimization algorithms, MOAs),用于解决存在于科学、工程、经济等许多不同领域中的优化问题[26 ] . 不失一般性,标准的无约束优化问题可以表示为如下最小化问题: ...
A neighborhood regression optimization algorithm for computationally expensive optimization problems
1
2020
... 式中: X D 维的决策向量,${\boldsymbol{X}} = {[{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2},\cdots ,{{\boldsymbol{x}}_D}]^{\mathrm{T}}}$ $f({\boldsymbol{X}})$ M 为目标函数的数量. 相应地,M = 1表示单目标优化问题,1< M ≤ 3表示多目标优化问题,M > 3表示超多目标优化问题. $\varOmega \in {{\bf{R}}^D}$ [27 ] . 近年来,随着待优化问题的复杂度越来越高,MOAs的研究逐渐占据主要地位. ...
Surrogate models in evolutionary single-objective optimization: a new taxonomy and experimental study
1
2021
... 从图2 可知,基于ICs的广义框架,DDICs由4部分组成,即种群更新、代理模型、适应度评估和模型管理(或称进化控制)[28 ] . 当前流行的元模型有传统的插值方法,如多项式回归(polynomial regression, PR),也称为响应曲面法(response surface method, RSM),以及机器学习技术,如人工神经网络(artificial neural network, ANN)、径向基函数网络(radial basis function network, RBFN)、支持向量机(support vector machine, SVM)、随机森林(random forest, RF)、K-近邻(k-nearest neighbors, KNNs)和高斯过程(Gaussian process, GP)等. 其中,RBFN和GP(也称Kriging)是研究工作中最流行的2种模型,因为RBFN处理高维问题的效率高,而GP能够提供置信水平. 此外,在最新的研究工作中,深度学习这一复杂模型被引入到DDICs中,例如CNN、高效dropout神经网络(efficient dropout neural network, EDN)和生成对抗网络(generate adversarial network, GAN)等. 如表1 所示为几种流行和最新代理模型的比较,以更好地展示不同元模型的应用特点和适用范围. 后面3.3.3节会对上述代理模型的具体应用进行进一步的详细介绍. ...
An adaptive Bayesian approach to surrogate-assisted evolutionary multi-objective optimization
2
2020
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
... 第1类是在优化过程中直接用代理模型替换昂贵的目标函数来进行环境选择,这是目前研究中的主流. 大多数算法主要是基于分解的方法,即通过3类聚合函数(权重聚合、切比雪夫和基于惩罚的边界交叉方法),将多目标问题分解为多个单目标问题,为每个目标函数建立代理模型. 如Jin等提出的AB-MOEA[29 ] 和GP-iGNG[90 ] 算法,通过参考向量(reference vector, RV)为每个目标函数建立GP模型,设计自适应管理策略,以平衡收敛性和多样性. Shen等[91 ] 提出基于分解的局部学习策略,加速多目标EOPs-II在高维搜索空间中的收敛. 采用分解方法的一个主要问题在于使用均匀分布的权重向量不一定能够实现非支配解在目标空间中的良好分布,因此可能会导致相关算法的多样性损失[92 ] . Song等[93 ] 提出基于非分解的KTA2算法,构建对影响点(即对整体预测结果产生较大影响的某些特殊数据点)不敏感的模型来逼近每个目标函数,基于收敛性、多样性或不确定性指标的自适应填充准则,提高预测精度. 此外,Lv等[94 ] 提出PAL-SAPSO算法,采用代理模型代替真实适应度函数来模拟粒子群的演化过程,使用改进的ε-PAL分类策略来识别非帕累托(Pareto)支配的候选解. 然而,第1类方式存在不足,即这种方式可能会导致元模型的近似误差逐渐累积,影响优化过程的总体准确性[95 ] . 另外,随着目标数量的增加,将产生更高的计算成本. ...
Reinforcement learning-based particle swarm optimization for sewage treatment control
2
2021
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Surrogate-assisted evolutionary deep learning using an end-to-end random forest-based performance predictor
1
2020
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
Surrogate-assisted cooperative co-evolutionary reservoir architecture search for liquid state machines
2
2023
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
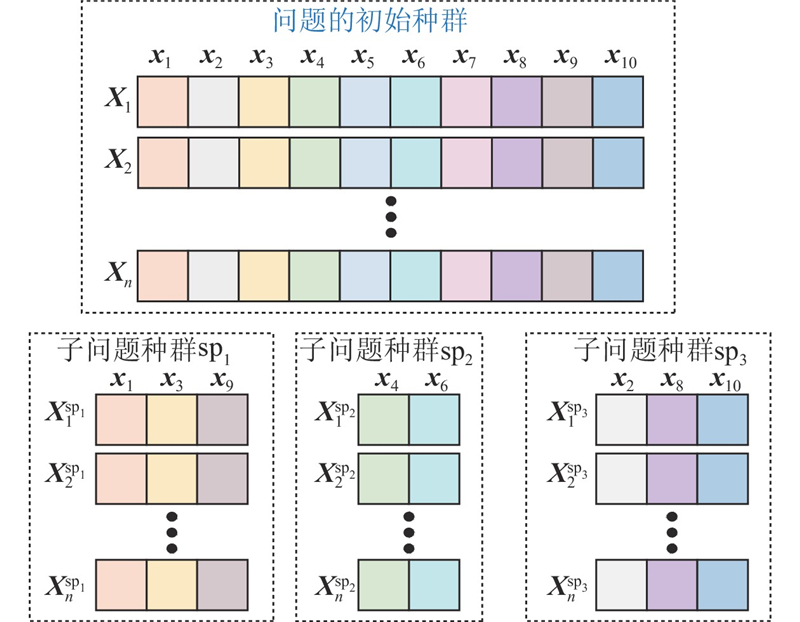
... b)协同进化搜索[64 -65 ] : 本质上是对决策变量有一个分组的过程,形成一系列子问题,如图5 所示. 通过对子问题进行寻优,将搜索到的性能表现良好的解放到当前较好的种群中进行更新,提高算法的搜索能力. 该方式通常用于优化高维和多模态EOPs-II,能够显著减少搜索空间,提高种群多样性. 子问题的解可以并行计算,因此能够减少原问题的整体求解时间. 例如,Sun等[66 ] 提出代理辅助协同群优化算法(SA-COSO),求解100维的高维耗时优化问题. Wu等[67 ] 提出基于集成代理的协同进化优化器(UNESCO),对大规模决策变量使用特征选择,使用低维数据子集训练局部代理模型,设计协同进化优化器,通过分享2个种群产生的后代信息进行辅助优化. Zhao等[68 ] 提出双群协同算法,探索和开发多模态问题. 此外,协同进化搜索能够揭示变量之间的相互作用,在优化大规模问题方面有着巨大的潜力. Chen等[69 ] 提出代理辅助的高度协同超参数优化(SHCHO)算法,通过合作优化子问题来处理原始的CNN超参数最优化问题. Zhou等[32 ] 采用RF辅助协同进化搜索,减小时间代价. Liu等[70 ] 将原始优化问题分解为置信区域内的多个子问题,在迭代中不断提高RBFN的精度. ...
Surrogate-assisted population based ACO for resource constrained job scheduling with uncertainty
2
2022
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
2
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
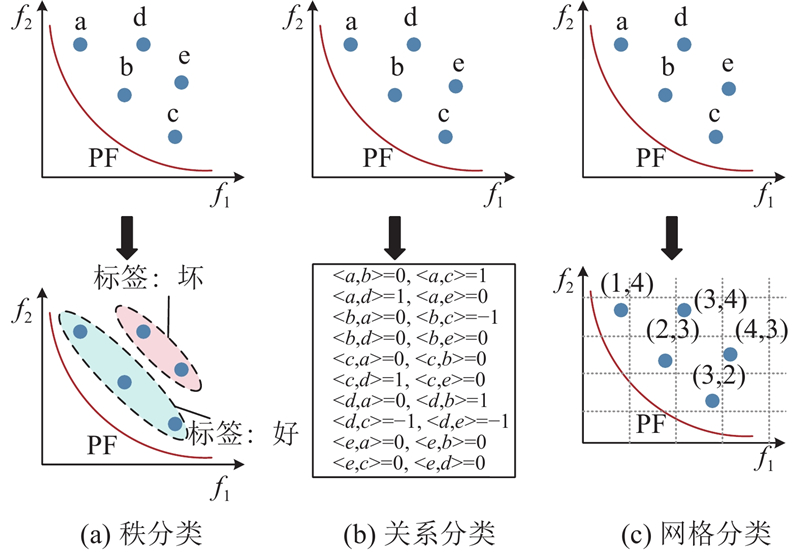
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
A convolutional neural network-based surrogate model for multi-objective optimization evolutionary algorithm based on decomposition
2
2022
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
... 此外,面对应用场景复杂的EOPs,浅层机器学习可能无法达到预期的评估精度,因此深度学习模型逐渐被引入以替换经典代理模型. Zhang等[35 ] 提出多目标并行适应度评估网络(MPFEN),采用CNN模型预测更高质量的解. Tian等[132 ] 提出MOEA/PSL算法,联合受限玻尔兹曼机(restricted Boltzmann machine, RBM)和降噪自编码器(denoising autoencoder, DAE)学习Pareto最优解为稀疏(即大多数Pareto最优解的决策变量为0)的大规模多目标问题. Liu等[133 ] 采用图神经网络(graph neural network, GNN),求解NP难的设施选址问题. Guo等[37 ] 提出计算效率高的EDN模型来取代GP模型. Liu等[134 ] 结合长短期记忆网络(long and short-term memory, LSTM)与并行近似评价模型,为多目标DDICs提供了新思路. Liang等[36 ] 提出基于RVEA框架并使用分布式对抗网络(distributed adversarial network, DAN)来生成后代的新算法,求解大规模超多目标问题. 深度学习模型的引入会增长模型的训练时间,占用计算资源,对数据量的需求更大. ...
2
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
... 此外,面对应用场景复杂的EOPs,浅层机器学习可能无法达到预期的评估精度,因此深度学习模型逐渐被引入以替换经典代理模型. Zhang等[35 ] 提出多目标并行适应度评估网络(MPFEN),采用CNN模型预测更高质量的解. Tian等[132 ] 提出MOEA/PSL算法,联合受限玻尔兹曼机(restricted Boltzmann machine, RBM)和降噪自编码器(denoising autoencoder, DAE)学习Pareto最优解为稀疏(即大多数Pareto最优解的决策变量为0)的大规模多目标问题. Liu等[133 ] 采用图神经网络(graph neural network, GNN),求解NP难的设施选址问题. Guo等[37 ] 提出计算效率高的EDN模型来取代GP模型. Liu等[134 ] 结合长短期记忆网络(long and short-term memory, LSTM)与并行近似评价模型,为多目标DDICs提供了新思路. Liang等[36 ] 提出基于RVEA框架并使用分布式对抗网络(distributed adversarial network, DAN)来生成后代的新算法,求解大规模超多目标问题. 深度学习模型的引入会增长模型的训练时间,占用计算资源,对数据量的需求更大. ...
Evolutionary optimization of high-dimensional multi-objective and many-objective expensive problems assisted by a dropout neural network
3
2021
... Comparison and analysis of several popular metamodels
Tab.1 元模型 应用范围 特点 PR/RSM[10 ] 连续问题 适合低阶非线性和小规模EOPs;不需要指定参数 GP/Kriging[29 ] 连续问题 只适合中低维EOPs;能够提供预测的不确定性 ANN[30 ] 连续问题 评估精度高,但需要人为大量试错;训练时间长;鲁棒性差 RBFN[31 ] 连续问题 适合中高维EOPs;具有较高的非线性逼近能力;鲁棒性好;可伸缩性强 RF[32 ] 连续问题和离散问题 需要调整的参数少;评估精度有待提高 KNN[33 ] 连续问题和离散问题 适合高维和多模态EOPs;对异常值不敏感;计算量大;不适合数据不平衡的问题 SVM[34 ] 连续问题和离散问题 适合中低维EOPs;鲁棒性差 CNN[35 ] 连续问题和离散问题 适合大规模多目标EOPs;能够实现模型并行 GAN[36 ] 离散问题 作为分类器,将候选解分为真实和虚假数据,适合大规模的稀疏EOPs;结构复杂,可能存在过拟合问题 EDN[37 ] 连续问题 适合高维EOPs;具有很强的可伸缩性;能够提供不确定性
不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
... 第2类是用代理模型来近似聚合函数. Luo等[96 ] 提出GCS-MOEA算法,在MOEA/D框架的基础上,使用多任务GP对多个邻域任务的聚合函数进行同时预测以提升模型精度,还提出新的填充准则来筛选候选解. Knowles[97 ] 提出ParEGO算法,该算法的主要思想是随机选择聚合函数,使用GP建立相应的代理模型,基于EGO方法找到搜索空间的下一个候选解进行评估. Tang等[98 ] 采用基于Kriging的PF估计方法来近似面向膝点(knee point)的聚合函数,取代EOPs-II中真实的适应度评估. 基于该类方式的算法大多数只适用于低维EOPs-II,特别是基于Kriging的算法. 这可能是因为当EOPs的维度增加时,需要更多的数据来训练细化的代理模型,这将显著增大训练成本(例如训练时间)[37 ] . ...
... 此外,面对应用场景复杂的EOPs,浅层机器学习可能无法达到预期的评估精度,因此深度学习模型逐渐被引入以替换经典代理模型. Zhang等[35 ] 提出多目标并行适应度评估网络(MPFEN),采用CNN模型预测更高质量的解. Tian等[132 ] 提出MOEA/PSL算法,联合受限玻尔兹曼机(restricted Boltzmann machine, RBM)和降噪自编码器(denoising autoencoder, DAE)学习Pareto最优解为稀疏(即大多数Pareto最优解的决策变量为0)的大规模多目标问题. Liu等[133 ] 采用图神经网络(graph neural network, GNN),求解NP难的设施选址问题. Guo等[37 ] 提出计算效率高的EDN模型来取代GP模型. Liu等[134 ] 结合长短期记忆网络(long and short-term memory, LSTM)与并行近似评价模型,为多目标DDICs提供了新思路. Liang等[36 ] 提出基于RVEA框架并使用分布式对抗网络(distributed adversarial network, DAN)来生成后代的新算法,求解大规模超多目标问题. 深度学习模型的引入会增长模型的训练时间,占用计算资源,对数据量的需求更大. ...
Comparative empirical study on constraint handling in offline data-driven evolutionary optimization
1
2021
... 不同类型的EOPs可能具有完全不同的数据资源和数据收集方法,因此根据优化过程中是否能够主动生成新的数据,可以进一步将DDICs分为离线和在线2种类别[38 ] . 离线DDICs主要用来解决EOPs-Ⅰ,在线DDICs主要用来解决EOPs-Ⅱ. 本文将从这2个方面简要回顾DDICs最新的研究进展. ...
Boosting data-driven evolutionary algorithm with localized data generation
2
2020
... 集成学习的核心思想是通过bagging[8 ] 或boosting[39 ] 技术,将多个较弱的元模型集合成较强的组合模型,有效提高模型的泛化能力. 其中,bagging采用并行处理的方法,减小代理模型带来的方差. boosting使用串行处理技术,减小模型引入的偏差. 如图3 所示为基于bagging的集成学习过程. 此外,该技术被广泛应用于在线DDICs中. 例如,Wang等[8 ] 提出DDEA-SE算法,通过使用bagging技术离线生成大量的代理模型,且随着优化过程的进行,自适应地选择其中的一个子集进行适应度评估,减小模型的预测误差. Li等[40 ] 提出DDEA-PES算法,他们采用选择性的集成方法有效提高模型的鲁棒性,实验表明,DDEA-PES算法只需要约2%的计算预算,即可产生具有竞争力的结果. DDEA-SE和DDEA-PES分别从2 000个和200个容量的模型池中提取100个选定模型的平均输出,因此在构建模型时需要花费大量的计算时间. Huang等[41 ] 基于多核学习思想(multi-kernel learning,MLK)提出SRK-DDEA算法,主要通过随机排序(stochastic rank,SR)来组合4种不同核函数的RBFN模型,以提高预测精度. SRK-DDEA算法在高维问题上表现较好,但在低维问题上的表现不如DDEA-SE算法. 随后,Huang等[42 ] 将半监督学习和集成技术引入离线DDICs中,提出TT-DDEA算法,通过在每一代TT-DDEA的更新中使用三元训练模型,求解多达500个决策变量的大规模EOPs-Ⅰ. 虽然TT-DDEA算法的计算时间更短,但是伪标签的增加会使代理模型误导优化过程. 此外,Zheng等[43 ] 提出更高层次的离线优化框架(MS-DDEO),该框架使用4种不同的RBFNs模型,能够有效地解决不同类型的问题. 与SRK-DDEA算法不同,MS-DDEO能够提供评估代理模型的标准. 上述算法都采用相同的元模型进行同构集成学习. Fan等[44 ] 为了解决小样本离散数据的优化问题,将有限的数据分成多个子集,在每个子集上训练GP和RBFN模型进行异构集成学习,在一定程度上解决了高维优化的耗时问题. ...
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
Data-driven evolutionary algorithm with perturbation-based ensemble surrogates
2
2020
... 集成学习的核心思想是通过bagging[8 ] 或boosting[39 ] 技术,将多个较弱的元模型集合成较强的组合模型,有效提高模型的泛化能力. 其中,bagging采用并行处理的方法,减小代理模型带来的方差. boosting使用串行处理技术,减小模型引入的偏差. 如图3 所示为基于bagging的集成学习过程. 此外,该技术被广泛应用于在线DDICs中. 例如,Wang等[8 ] 提出DDEA-SE算法,通过使用bagging技术离线生成大量的代理模型,且随着优化过程的进行,自适应地选择其中的一个子集进行适应度评估,减小模型的预测误差. Li等[40 ] 提出DDEA-PES算法,他们采用选择性的集成方法有效提高模型的鲁棒性,实验表明,DDEA-PES算法只需要约2%的计算预算,即可产生具有竞争力的结果. DDEA-SE和DDEA-PES分别从2 000个和200个容量的模型池中提取100个选定模型的平均输出,因此在构建模型时需要花费大量的计算时间. Huang等[41 ] 基于多核学习思想(multi-kernel learning,MLK)提出SRK-DDEA算法,主要通过随机排序(stochastic rank,SR)来组合4种不同核函数的RBFN模型,以提高预测精度. SRK-DDEA算法在高维问题上表现较好,但在低维问题上的表现不如DDEA-SE算法. 随后,Huang等[42 ] 将半监督学习和集成技术引入离线DDICs中,提出TT-DDEA算法,通过在每一代TT-DDEA的更新中使用三元训练模型,求解多达500个决策变量的大规模EOPs-Ⅰ. 虽然TT-DDEA算法的计算时间更短,但是伪标签的增加会使代理模型误导优化过程. 此外,Zheng等[43 ] 提出更高层次的离线优化框架(MS-DDEO),该框架使用4种不同的RBFNs模型,能够有效地解决不同类型的问题. 与SRK-DDEA算法不同,MS-DDEO能够提供评估代理模型的标准. 上述算法都采用相同的元模型进行同构集成学习. Fan等[44 ] 为了解决小样本离散数据的优化问题,将有限的数据分成多个子集,在每个子集上训练GP和RBFN模型进行异构集成学习,在一定程度上解决了高维优化的耗时问题. ...
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
1
... 集成学习的核心思想是通过bagging[8 ] 或boosting[39 ] 技术,将多个较弱的元模型集合成较强的组合模型,有效提高模型的泛化能力. 其中,bagging采用并行处理的方法,减小代理模型带来的方差. boosting使用串行处理技术,减小模型引入的偏差. 如图3 所示为基于bagging的集成学习过程. 此外,该技术被广泛应用于在线DDICs中. 例如,Wang等[8 ] 提出DDEA-SE算法,通过使用bagging技术离线生成大量的代理模型,且随着优化过程的进行,自适应地选择其中的一个子集进行适应度评估,减小模型的预测误差. Li等[40 ] 提出DDEA-PES算法,他们采用选择性的集成方法有效提高模型的鲁棒性,实验表明,DDEA-PES算法只需要约2%的计算预算,即可产生具有竞争力的结果. DDEA-SE和DDEA-PES分别从2 000个和200个容量的模型池中提取100个选定模型的平均输出,因此在构建模型时需要花费大量的计算时间. Huang等[41 ] 基于多核学习思想(multi-kernel learning,MLK)提出SRK-DDEA算法,主要通过随机排序(stochastic rank,SR)来组合4种不同核函数的RBFN模型,以提高预测精度. SRK-DDEA算法在高维问题上表现较好,但在低维问题上的表现不如DDEA-SE算法. 随后,Huang等[42 ] 将半监督学习和集成技术引入离线DDICs中,提出TT-DDEA算法,通过在每一代TT-DDEA的更新中使用三元训练模型,求解多达500个决策变量的大规模EOPs-Ⅰ. 虽然TT-DDEA算法的计算时间更短,但是伪标签的增加会使代理模型误导优化过程. 此外,Zheng等[43 ] 提出更高层次的离线优化框架(MS-DDEO),该框架使用4种不同的RBFNs模型,能够有效地解决不同类型的问题. 与SRK-DDEA算法不同,MS-DDEO能够提供评估代理模型的标准. 上述算法都采用相同的元模型进行同构集成学习. Fan等[44 ] 为了解决小样本离散数据的优化问题,将有限的数据分成多个子集,在每个子集上训练GP和RBFN模型进行异构集成学习,在一定程度上解决了高维优化的耗时问题. ...
Offline data-driven evolutionary optimization based on tri-training
2
2021
... 集成学习的核心思想是通过bagging[8 ] 或boosting[39 ] 技术,将多个较弱的元模型集合成较强的组合模型,有效提高模型的泛化能力. 其中,bagging采用并行处理的方法,减小代理模型带来的方差. boosting使用串行处理技术,减小模型引入的偏差. 如图3 所示为基于bagging的集成学习过程. 此外,该技术被广泛应用于在线DDICs中. 例如,Wang等[8 ] 提出DDEA-SE算法,通过使用bagging技术离线生成大量的代理模型,且随着优化过程的进行,自适应地选择其中的一个子集进行适应度评估,减小模型的预测误差. Li等[40 ] 提出DDEA-PES算法,他们采用选择性的集成方法有效提高模型的鲁棒性,实验表明,DDEA-PES算法只需要约2%的计算预算,即可产生具有竞争力的结果. DDEA-SE和DDEA-PES分别从2 000个和200个容量的模型池中提取100个选定模型的平均输出,因此在构建模型时需要花费大量的计算时间. Huang等[41 ] 基于多核学习思想(multi-kernel learning,MLK)提出SRK-DDEA算法,主要通过随机排序(stochastic rank,SR)来组合4种不同核函数的RBFN模型,以提高预测精度. SRK-DDEA算法在高维问题上表现较好,但在低维问题上的表现不如DDEA-SE算法. 随后,Huang等[42 ] 将半监督学习和集成技术引入离线DDICs中,提出TT-DDEA算法,通过在每一代TT-DDEA的更新中使用三元训练模型,求解多达500个决策变量的大规模EOPs-Ⅰ. 虽然TT-DDEA算法的计算时间更短,但是伪标签的增加会使代理模型误导优化过程. 此外,Zheng等[43 ] 提出更高层次的离线优化框架(MS-DDEO),该框架使用4种不同的RBFNs模型,能够有效地解决不同类型的问题. 与SRK-DDEA算法不同,MS-DDEO能够提供评估代理模型的标准. 上述算法都采用相同的元模型进行同构集成学习. Fan等[44 ] 为了解决小样本离散数据的优化问题,将有限的数据分成多个子集,在每个子集上训练GP和RBFN模型进行异构集成学习,在一定程度上解决了高维优化的耗时问题. ...
... 代理模型是DDICs的一个重要研究方向. 早期的研究[129 -130 ] 倾向于使用全局或局部的单代理模型辅助ICs,它们在简单和中低维EOPs上的优良性能得到了验证. 随着问题维度和复杂度的增加,单代理模型不能很好地辅助ICs,于是学者们开始通过建立多个代理[42 ] 或混合代理模型[131 ] 来有效解决该问题. 由于代理模型与精确目标函数之间可能存在较大的误差,上述方法无法解决各类不同形态且计算量很大的EOPs. 为了提高代理模型的预测精度和有效求解EOPs,学者们引入集成学习[100 -101 ] 的思想,以辅助DDICs. ...
Offline data-driven evolutionary optimization based on model selection
1
2022
... 集成学习的核心思想是通过bagging[8 ] 或boosting[39 ] 技术,将多个较弱的元模型集合成较强的组合模型,有效提高模型的泛化能力. 其中,bagging采用并行处理的方法,减小代理模型带来的方差. boosting使用串行处理技术,减小模型引入的偏差. 如图3 所示为基于bagging的集成学习过程. 此外,该技术被广泛应用于在线DDICs中. 例如,Wang等[8 ] 提出DDEA-SE算法,通过使用bagging技术离线生成大量的代理模型,且随着优化过程的进行,自适应地选择其中的一个子集进行适应度评估,减小模型的预测误差. Li等[40 ] 提出DDEA-PES算法,他们采用选择性的集成方法有效提高模型的鲁棒性,实验表明,DDEA-PES算法只需要约2%的计算预算,即可产生具有竞争力的结果. DDEA-SE和DDEA-PES分别从2 000个和200个容量的模型池中提取100个选定模型的平均输出,因此在构建模型时需要花费大量的计算时间. Huang等[41 ] 基于多核学习思想(multi-kernel learning,MLK)提出SRK-DDEA算法,主要通过随机排序(stochastic rank,SR)来组合4种不同核函数的RBFN模型,以提高预测精度. SRK-DDEA算法在高维问题上表现较好,但在低维问题上的表现不如DDEA-SE算法. 随后,Huang等[42 ] 将半监督学习和集成技术引入离线DDICs中,提出TT-DDEA算法,通过在每一代TT-DDEA的更新中使用三元训练模型,求解多达500个决策变量的大规模EOPs-Ⅰ. 虽然TT-DDEA算法的计算时间更短,但是伪标签的增加会使代理模型误导优化过程. 此外,Zheng等[43 ] 提出更高层次的离线优化框架(MS-DDEO),该框架使用4种不同的RBFNs模型,能够有效地解决不同类型的问题. 与SRK-DDEA算法不同,MS-DDEO能够提供评估代理模型的标准. 上述算法都采用相同的元模型进行同构集成学习. Fan等[44 ] 为了解决小样本离散数据的优化问题,将有限的数据分成多个子集,在每个子集上训练GP和RBFN模型进行异构集成学习,在一定程度上解决了高维优化的耗时问题. ...
A surrogate-assisted particle swarm optimization using ensemble learning for expensive problems with small sample datasets
1
2020
... 集成学习的核心思想是通过bagging[8 ] 或boosting[39 ] 技术,将多个较弱的元模型集合成较强的组合模型,有效提高模型的泛化能力. 其中,bagging采用并行处理的方法,减小代理模型带来的方差. boosting使用串行处理技术,减小模型引入的偏差. 如图3 所示为基于bagging的集成学习过程. 此外,该技术被广泛应用于在线DDICs中. 例如,Wang等[8 ] 提出DDEA-SE算法,通过使用bagging技术离线生成大量的代理模型,且随着优化过程的进行,自适应地选择其中的一个子集进行适应度评估,减小模型的预测误差. Li等[40 ] 提出DDEA-PES算法,他们采用选择性的集成方法有效提高模型的鲁棒性,实验表明,DDEA-PES算法只需要约2%的计算预算,即可产生具有竞争力的结果. DDEA-SE和DDEA-PES分别从2 000个和200个容量的模型池中提取100个选定模型的平均输出,因此在构建模型时需要花费大量的计算时间. Huang等[41 ] 基于多核学习思想(multi-kernel learning,MLK)提出SRK-DDEA算法,主要通过随机排序(stochastic rank,SR)来组合4种不同核函数的RBFN模型,以提高预测精度. SRK-DDEA算法在高维问题上表现较好,但在低维问题上的表现不如DDEA-SE算法. 随后,Huang等[42 ] 将半监督学习和集成技术引入离线DDICs中,提出TT-DDEA算法,通过在每一代TT-DDEA的更新中使用三元训练模型,求解多达500个决策变量的大规模EOPs-Ⅰ. 虽然TT-DDEA算法的计算时间更短,但是伪标签的增加会使代理模型误导优化过程. 此外,Zheng等[43 ] 提出更高层次的离线优化框架(MS-DDEO),该框架使用4种不同的RBFNs模型,能够有效地解决不同类型的问题. 与SRK-DDEA算法不同,MS-DDEO能够提供评估代理模型的标准. 上述算法都采用相同的元模型进行同构集成学习. Fan等[44 ] 为了解决小样本离散数据的优化问题,将有限的数据分成多个子集,在每个子集上训练GP和RBFN模型进行异构集成学习,在一定程度上解决了高维优化的耗时问题. ...
A data-driven surrogate-assisted evolutionary algorithm applied to a many-objective blast furnace optimization problem
1
2017
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
1
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
1
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
A surrogate-assisted two-stage differential evolution for expensive constrained optimization
3
2023
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
... 许多现实世界的优化问题涉及高维决策变量,其变量的维度高达100维甚至更多. 面对“维度诅咒”,集成代理协助全局搜索的能力会下降,因此需要设计更先进的进化组件保证算法在大规模、带约束或多目标空间中的高效搜索. 例如,Gong等[51 ] 基于分而治之的范式提出协同进化框架,能够实现高达1 000维的优越性能,有效解决大规模EOPs-Ⅰ. 如表2 所示为几种最新的离线数据驱动模型在不同测试函数上的性能表现. 表中,最大评估次数为11D ,其中D 为问题维度. 此外,Zhen等[52 ] 提出两阶段的搜索过程,其中第一阶段使用全局模型进行勘探,第二阶段使用具有各种搜索策略的局部模型进行开发. 这些算法都没有考虑如何处理昂贵的约束,SA-TSDE[48 ] 和eToSA-DE[53 ] 基于两阶段DE搜索方式分别用于求解带约束的EOPs-Ⅰ. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Linear subspace surrogate modeling for large-scale expensive single/multi-objective optimization
1
2023
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
Contrastive learning: An alternative surrogate for offline data-driven evolutionary computation
2
2022
... 离线DDICs的性能严重依赖可用数据的质量和数量,因为实际采集的数据可能是大数据、小数据、不平衡或存在噪声的[7 ] . 关于数据的研究是广泛的,涉及数据科学中的各种技术,如数据处理[45 ] 、数据挖掘[10 ] 和数据合成[46 ] 等. 近年来,对于小样本数据提出了一些数据增强的方法,如Guo等[47 ] 通过低阶PR生成人工数据,DDEA-PES[40 ] 和BDDEA-LDG[39 ] 进行局部数据生成. 在上述方法中,由于近似地获得了增强的数据,从而带来了困境:对于高维EOPs,少量人工合成数据对优化结果的影响非常有限,而过度使用人工数据可能降低代理精度,从而影响优化性能. 上述方法难以解决超过100维的EOPs-Ⅰ. 对于数据量很大的大规模EOPs-Ⅰ,通过聚类[48 ] 的方式,将总体聚类到一些清晰或模糊的类中,选择有代表性的个体进行近似评估,降低问题维度. L2SMEA[49 ] 将高维空间映射到多个线性子空间,根据个体到相应子空间的距离将解关联起来. 上述2种方法虽然能够有效地减少计算时间,但是都没有用到适应度,因此可解释性不强. 此外,CL-DDEA[50 ] 通过对比学习将原始数据量进行平方,在100维和200维的问题上取得了良好的效果,尤其适用于数据稀疏性高的EOPs-Ⅰ. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Offline data-driven optimization at scale: a cooperative coevolutionary approach
1
2023
... 许多现实世界的优化问题涉及高维决策变量,其变量的维度高达100维甚至更多. 面对“维度诅咒”,集成代理协助全局搜索的能力会下降,因此需要设计更先进的进化组件保证算法在大规模、带约束或多目标空间中的高效搜索. 例如,Gong等[51 ] 基于分而治之的范式提出协同进化框架,能够实现高达1 000维的优越性能,有效解决大规模EOPs-Ⅰ. 如表2 所示为几种最新的离线数据驱动模型在不同测试函数上的性能表现. 表中,最大评估次数为11D ,其中D 为问题维度. 此外,Zhen等[52 ] 提出两阶段的搜索过程,其中第一阶段使用全局模型进行勘探,第二阶段使用具有各种搜索策略的局部模型进行开发. 这些算法都没有考虑如何处理昂贵的约束,SA-TSDE[48 ] 和eToSA-DE[53 ] 基于两阶段DE搜索方式分别用于求解带约束的EOPs-Ⅰ. ...
Two-stage data-driven evolutionary optimization for high-dimensional expensive problems
1
2021
... 许多现实世界的优化问题涉及高维决策变量,其变量的维度高达100维甚至更多. 面对“维度诅咒”,集成代理协助全局搜索的能力会下降,因此需要设计更先进的进化组件保证算法在大规模、带约束或多目标空间中的高效搜索. 例如,Gong等[51 ] 基于分而治之的范式提出协同进化框架,能够实现高达1 000维的优越性能,有效解决大规模EOPs-Ⅰ. 如表2 所示为几种最新的离线数据驱动模型在不同测试函数上的性能表现. 表中,最大评估次数为11D ,其中D 为问题维度. 此外,Zhen等[52 ] 提出两阶段的搜索过程,其中第一阶段使用全局模型进行勘探,第二阶段使用具有各种搜索策略的局部模型进行开发. 这些算法都没有考虑如何处理昂贵的约束,SA-TSDE[48 ] 和eToSA-DE[53 ] 基于两阶段DE搜索方式分别用于求解带约束的EOPs-Ⅰ. ...
An efficient two-stage surrogate-assisted differential evolution for expensive inequality constrained optimization
2
2023
... 许多现实世界的优化问题涉及高维决策变量,其变量的维度高达100维甚至更多. 面对“维度诅咒”,集成代理协助全局搜索的能力会下降,因此需要设计更先进的进化组件保证算法在大规模、带约束或多目标空间中的高效搜索. 例如,Gong等[51 ] 基于分而治之的范式提出协同进化框架,能够实现高达1 000维的优越性能,有效解决大规模EOPs-Ⅰ. 如表2 所示为几种最新的离线数据驱动模型在不同测试函数上的性能表现. 表中,最大评估次数为11D ,其中D 为问题维度. 此外,Zhen等[52 ] 提出两阶段的搜索过程,其中第一阶段使用全局模型进行勘探,第二阶段使用具有各种搜索策略的局部模型进行开发. 这些算法都没有考虑如何处理昂贵的约束,SA-TSDE[48 ] 和eToSA-DE[53 ] 基于两阶段DE搜索方式分别用于求解带约束的EOPs-Ⅰ. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A random forest-assisted evolutionary algorithm for data-driven constrained multi-objective combinatorial optimization of trauma systems
2
2018
... 迄今为止,很多学者致力于多目标EOPs-Ⅰ的研究. 例如,SA-NSGA-II[10 ] 和RF-CMOCO[54 ] 算法利用离线大数据产生的多个保真度水平的优势来解决多目标的创伤系统设计问题,区别在于RF-CMOCO考虑了约束处理. Mazumdar等[55 ] 提出概率选择方法的分解多目标算法,该方法利用Kriging模型提供的不确定性信息来改进离线多目标优化中的求解过程,有效地提高了解的准确性. Liu等[56 ] 采用基于指标的MOEA,设计自适应模型选择策略,提高算法的鲁棒性,减少近似误差的累积,该方法可在多达30个决策变量的多目标EOPs-Ⅰ上有效. Gong等[57 ] 构建端到端的深度学习代理用于游戏的自动团队组装(automated team assembly, ATA),开发分层修复策略来处理约束,能够帮助开发者进行游戏平衡分析,但该算法适用于涉及许多稀疏特征的ATA问题. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Probabilistic selection approaches in decomposition-based evolutionary algorithms for offline data-driven multi-objective optimization
1
2022
... 迄今为止,很多学者致力于多目标EOPs-Ⅰ的研究. 例如,SA-NSGA-II[10 ] 和RF-CMOCO[54 ] 算法利用离线大数据产生的多个保真度水平的优势来解决多目标的创伤系统设计问题,区别在于RF-CMOCO考虑了约束处理. Mazumdar等[55 ] 提出概率选择方法的分解多目标算法,该方法利用Kriging模型提供的不确定性信息来改进离线多目标优化中的求解过程,有效地提高了解的准确性. Liu等[56 ] 采用基于指标的MOEA,设计自适应模型选择策略,提高算法的鲁棒性,减少近似误差的累积,该方法可在多达30个决策变量的多目标EOPs-Ⅰ上有效. Gong等[57 ] 构建端到端的深度学习代理用于游戏的自动团队组装(automated team assembly, ATA),开发分层修复策略来处理约束,能够帮助开发者进行游戏平衡分析,但该算法适用于涉及许多稀疏特征的ATA问题. ...
Performance indicator-based adaptive model selection for offline data-driven multi-objective evolutionary optimization
1
2022
... 迄今为止,很多学者致力于多目标EOPs-Ⅰ的研究. 例如,SA-NSGA-II[10 ] 和RF-CMOCO[54 ] 算法利用离线大数据产生的多个保真度水平的优势来解决多目标的创伤系统设计问题,区别在于RF-CMOCO考虑了约束处理. Mazumdar等[55 ] 提出概率选择方法的分解多目标算法,该方法利用Kriging模型提供的不确定性信息来改进离线多目标优化中的求解过程,有效地提高了解的准确性. Liu等[56 ] 采用基于指标的MOEA,设计自适应模型选择策略,提高算法的鲁棒性,减少近似误差的累积,该方法可在多达30个决策变量的多目标EOPs-Ⅰ上有效. Gong等[57 ] 构建端到端的深度学习代理用于游戏的自动团队组装(automated team assembly, ATA),开发分层修复策略来处理约束,能够帮助开发者进行游戏平衡分析,但该算法适用于涉及许多稀疏特征的ATA问题. ...
Automated team assembly in mobile games: a data-driven evolutionary approach using a deep learning surrogate
2
2022
... 迄今为止,很多学者致力于多目标EOPs-Ⅰ的研究. 例如,SA-NSGA-II[10 ] 和RF-CMOCO[54 ] 算法利用离线大数据产生的多个保真度水平的优势来解决多目标的创伤系统设计问题,区别在于RF-CMOCO考虑了约束处理. Mazumdar等[55 ] 提出概率选择方法的分解多目标算法,该方法利用Kriging模型提供的不确定性信息来改进离线多目标优化中的求解过程,有效地提高了解的准确性. Liu等[56 ] 采用基于指标的MOEA,设计自适应模型选择策略,提高算法的鲁棒性,减少近似误差的累积,该方法可在多达30个决策变量的多目标EOPs-Ⅰ上有效. Gong等[57 ] 构建端到端的深度学习代理用于游戏的自动团队组装(automated team assembly, ATA),开发分层修复策略来处理约束,能够帮助开发者进行游戏平衡分析,但该算法适用于涉及许多稀疏特征的ATA问题. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A hybrid cooperative co-evolution algorithm framework for optimising power take off and placements of wave energy converters
1
2020
... a)多群搜索[58 ] :通常将种群分为多个子种群,对不同的子种群分别进行代理辅助,提高种群的多样性,具体的学习过程如图4 所示. 该方式能够同时搜索不同的局部最优解,增强算法的全局搜索能力. 多种群间的信息交流可以促进优秀个体更快地传播,通常在高维EOPs-II中特别流行. 例如,Liu等[59 ] 采用亲和传播聚类来生成多个子种群,基于子种群多样性维护方案和代理辅助信赖域局部搜索技术,增强算法的探索性和开拓性. Tian等[60 ] 将总群体划分为2个子群,即粗粒度个体和细粒度个体,分别采用不同的元模型对2个子群逼近,在优化高维EOPs-II时取得了令人满意的结果. Li等[61 -62 ] 提出基于代理辅助的双种群进化算法(SAMSO和SAHSO),其中利用第1个种群来增强算法的探索性,利用第2个种群来加快收敛速度. Zhao等[63 ] 基于多群搜索聚类和预测,求解动态EOPs-II. 多群搜索方式在解决复杂优化问题时可能需要更多的计算资源和更长的运行时间. ...
Surrogate-assisted multi-population particle swarm optimizer for high-dimensional expensive optimization
3
2021
... a)多群搜索[58 ] :通常将种群分为多个子种群,对不同的子种群分别进行代理辅助,提高种群的多样性,具体的学习过程如图4 所示. 该方式能够同时搜索不同的局部最优解,增强算法的全局搜索能力. 多种群间的信息交流可以促进优秀个体更快地传播,通常在高维EOPs-II中特别流行. 例如,Liu等[59 ] 采用亲和传播聚类来生成多个子种群,基于子种群多样性维护方案和代理辅助信赖域局部搜索技术,增强算法的探索性和开拓性. Tian等[60 ] 将总群体划分为2个子群,即粗粒度个体和细粒度个体,分别采用不同的元模型对2个子群逼近,在优化高维EOPs-II时取得了令人满意的结果. Li等[61 -62 ] 提出基于代理辅助的双种群进化算法(SAMSO和SAHSO),其中利用第1个种群来增强算法的探索性,利用第2个种群来加快收敛速度. Zhao等[63 ] 基于多群搜索聚类和预测,求解动态EOPs-II. 多群搜索方式在解决复杂优化问题时可能需要更多的计算资源和更长的运行时间. ...
... 3)基于种群的管理方式[70 ] . 该方式允许多个子种群的存在,且从每个子种群中筛选候选解. 该管理方式只在多种群搜索中普遍使用,以求解高维EOPs. 例如,Liu等[59 ] 提出SAMPSO算法,从每个子群中选择最优希望的候选解,以增强种群多样性. 随着问题的维度和复杂度越来越高,基于种群的管理方式通常会与上述2种方法结合起来一起使用,提高模型的精度和稳定性. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Granularity-based surrogate-assisted particle swarm optimization for high-dimensional expensive optimization
1
2020
... a)多群搜索[58 ] :通常将种群分为多个子种群,对不同的子种群分别进行代理辅助,提高种群的多样性,具体的学习过程如图4 所示. 该方式能够同时搜索不同的局部最优解,增强算法的全局搜索能力. 多种群间的信息交流可以促进优秀个体更快地传播,通常在高维EOPs-II中特别流行. 例如,Liu等[59 ] 采用亲和传播聚类来生成多个子种群,基于子种群多样性维护方案和代理辅助信赖域局部搜索技术,增强算法的探索性和开拓性. Tian等[60 ] 将总群体划分为2个子群,即粗粒度个体和细粒度个体,分别采用不同的元模型对2个子群逼近,在优化高维EOPs-II时取得了令人满意的结果. Li等[61 -62 ] 提出基于代理辅助的双种群进化算法(SAMSO和SAHSO),其中利用第1个种群来增强算法的探索性,利用第2个种群来加快收敛速度. Zhao等[63 ] 基于多群搜索聚类和预测,求解动态EOPs-II. 多群搜索方式在解决复杂优化问题时可能需要更多的计算资源和更长的运行时间. ...
A surrogate-assisted multi-swarm optimization algorithm for high-dimensional computationally expensive problems
1
2020
... a)多群搜索[58 ] :通常将种群分为多个子种群,对不同的子种群分别进行代理辅助,提高种群的多样性,具体的学习过程如图4 所示. 该方式能够同时搜索不同的局部最优解,增强算法的全局搜索能力. 多种群间的信息交流可以促进优秀个体更快地传播,通常在高维EOPs-II中特别流行. 例如,Liu等[59 ] 采用亲和传播聚类来生成多个子种群,基于子种群多样性维护方案和代理辅助信赖域局部搜索技术,增强算法的探索性和开拓性. Tian等[60 ] 将总群体划分为2个子群,即粗粒度个体和细粒度个体,分别采用不同的元模型对2个子群逼近,在优化高维EOPs-II时取得了令人满意的结果. Li等[61 -62 ] 提出基于代理辅助的双种群进化算法(SAMSO和SAHSO),其中利用第1个种群来增强算法的探索性,利用第2个种群来加快收敛速度. Zhao等[63 ] 基于多群搜索聚类和预测,求解动态EOPs-II. 多群搜索方式在解决复杂优化问题时可能需要更多的计算资源和更长的运行时间. ...
A surrogate-assisted hybrid swarm optimization algorithm for high-dimensional computationally expensive problems
1
2022
... a)多群搜索[58 ] :通常将种群分为多个子种群,对不同的子种群分别进行代理辅助,提高种群的多样性,具体的学习过程如图4 所示. 该方式能够同时搜索不同的局部最优解,增强算法的全局搜索能力. 多种群间的信息交流可以促进优秀个体更快地传播,通常在高维EOPs-II中特别流行. 例如,Liu等[59 ] 采用亲和传播聚类来生成多个子种群,基于子种群多样性维护方案和代理辅助信赖域局部搜索技术,增强算法的探索性和开拓性. Tian等[60 ] 将总群体划分为2个子群,即粗粒度个体和细粒度个体,分别采用不同的元模型对2个子群逼近,在优化高维EOPs-II时取得了令人满意的结果. Li等[61 -62 ] 提出基于代理辅助的双种群进化算法(SAMSO和SAHSO),其中利用第1个种群来增强算法的探索性,利用第2个种群来加快收敛速度. Zhao等[63 ] 基于多群搜索聚类和预测,求解动态EOPs-II. 多群搜索方式在解决复杂优化问题时可能需要更多的计算资源和更长的运行时间. ...
A surrogate-assisted evolutionary algorithm based on multi-population clustering and prediction for solving computationally expensive dynamic optimization problems
1
2023
... a)多群搜索[58 ] :通常将种群分为多个子种群,对不同的子种群分别进行代理辅助,提高种群的多样性,具体的学习过程如图4 所示. 该方式能够同时搜索不同的局部最优解,增强算法的全局搜索能力. 多种群间的信息交流可以促进优秀个体更快地传播,通常在高维EOPs-II中特别流行. 例如,Liu等[59 ] 采用亲和传播聚类来生成多个子种群,基于子种群多样性维护方案和代理辅助信赖域局部搜索技术,增强算法的探索性和开拓性. Tian等[60 ] 将总群体划分为2个子群,即粗粒度个体和细粒度个体,分别采用不同的元模型对2个子群逼近,在优化高维EOPs-II时取得了令人满意的结果. Li等[61 -62 ] 提出基于代理辅助的双种群进化算法(SAMSO和SAHSO),其中利用第1个种群来增强算法的探索性,利用第2个种群来加快收敛速度. Zhao等[63 ] 基于多群搜索聚类和预测,求解动态EOPs-II. 多群搜索方式在解决复杂优化问题时可能需要更多的计算资源和更长的运行时间. ...
Decision space partition based surrogate-assisted evolutionary algorithm for expensive optimization
1
2023
... b)协同进化搜索[64 -65 ] : 本质上是对决策变量有一个分组的过程,形成一系列子问题,如图5 所示. 通过对子问题进行寻优,将搜索到的性能表现良好的解放到当前较好的种群中进行更新,提高算法的搜索能力. 该方式通常用于优化高维和多模态EOPs-II,能够显著减少搜索空间,提高种群多样性. 子问题的解可以并行计算,因此能够减少原问题的整体求解时间. 例如,Sun等[66 ] 提出代理辅助协同群优化算法(SA-COSO),求解100维的高维耗时优化问题. Wu等[67 ] 提出基于集成代理的协同进化优化器(UNESCO),对大规模决策变量使用特征选择,使用低维数据子集训练局部代理模型,设计协同进化优化器,通过分享2个种群产生的后代信息进行辅助优化. Zhao等[68 ] 提出双群协同算法,探索和开发多模态问题. 此外,协同进化搜索能够揭示变量之间的相互作用,在优化大规模问题方面有着巨大的潜力. Chen等[69 ] 提出代理辅助的高度协同超参数优化(SHCHO)算法,通过合作优化子问题来处理原始的CNN超参数最优化问题. Zhou等[32 ] 采用RF辅助协同进化搜索,减小时间代价. Liu等[70 ] 将原始优化问题分解为置信区域内的多个子问题,在迭代中不断提高RBFN的精度. ...
Surrogate-assisted differential evolution with region division for expensive optimization problems with discontinuous responses
1
2021
... b)协同进化搜索[64 -65 ] : 本质上是对决策变量有一个分组的过程,形成一系列子问题,如图5 所示. 通过对子问题进行寻优,将搜索到的性能表现良好的解放到当前较好的种群中进行更新,提高算法的搜索能力. 该方式通常用于优化高维和多模态EOPs-II,能够显著减少搜索空间,提高种群多样性. 子问题的解可以并行计算,因此能够减少原问题的整体求解时间. 例如,Sun等[66 ] 提出代理辅助协同群优化算法(SA-COSO),求解100维的高维耗时优化问题. Wu等[67 ] 提出基于集成代理的协同进化优化器(UNESCO),对大规模决策变量使用特征选择,使用低维数据子集训练局部代理模型,设计协同进化优化器,通过分享2个种群产生的后代信息进行辅助优化. Zhao等[68 ] 提出双群协同算法,探索和开发多模态问题. 此外,协同进化搜索能够揭示变量之间的相互作用,在优化大规模问题方面有着巨大的潜力. Chen等[69 ] 提出代理辅助的高度协同超参数优化(SHCHO)算法,通过合作优化子问题来处理原始的CNN超参数最优化问题. Zhou等[32 ] 采用RF辅助协同进化搜索,减小时间代价. Liu等[70 ] 将原始优化问题分解为置信区域内的多个子问题,在迭代中不断提高RBFN的精度. ...
Surrogate-assisted cooperative swarm optimization of high-dimensional expensive problems
2
2017
... b)协同进化搜索[64 -65 ] : 本质上是对决策变量有一个分组的过程,形成一系列子问题,如图5 所示. 通过对子问题进行寻优,将搜索到的性能表现良好的解放到当前较好的种群中进行更新,提高算法的搜索能力. 该方式通常用于优化高维和多模态EOPs-II,能够显著减少搜索空间,提高种群多样性. 子问题的解可以并行计算,因此能够减少原问题的整体求解时间. 例如,Sun等[66 ] 提出代理辅助协同群优化算法(SA-COSO),求解100维的高维耗时优化问题. Wu等[67 ] 提出基于集成代理的协同进化优化器(UNESCO),对大规模决策变量使用特征选择,使用低维数据子集训练局部代理模型,设计协同进化优化器,通过分享2个种群产生的后代信息进行辅助优化. Zhao等[68 ] 提出双群协同算法,探索和开发多模态问题. 此外,协同进化搜索能够揭示变量之间的相互作用,在优化大规模问题方面有着巨大的潜力. Chen等[69 ] 提出代理辅助的高度协同超参数优化(SHCHO)算法,通过合作优化子问题来处理原始的CNN超参数最优化问题. Zhou等[32 ] 采用RF辅助协同进化搜索,减小时间代价. Liu等[70 ] 将原始优化问题分解为置信区域内的多个子问题,在迭代中不断提高RBFN的精度. ...
... 1)基于个体的管理方式[71 ] ,即用真实目标函数评估的候选个体,这是DDICs中最灵活的管理方式. 一般来说,选择候选解进行昂贵评估的填充标准可以分为潜在的优秀个体和最不确定的个体. 对于单目标而言,个体的优劣通常由性能决定,即具有良好预测适应度的个体. 例如,SA-COSO[66 ] 和SHPSO[72 ] 都使用了这种标准. 这是大多数单目标DDICs所选取的管理方式. 对于多目标而言,优秀的个体由收敛性和多样性决定. 例如,CSEA基于收敛性选择具有更好预测值的子代[103 ] ,ACDEA采用距离回归模型和角度回归模型来选择收敛性和多样性较好的解[105 ] 等. ...
An ensemble surrogate-based coevolutionary algorithm for solving large-scale expensive optimization problems
1
2023
... b)协同进化搜索[64 -65 ] : 本质上是对决策变量有一个分组的过程,形成一系列子问题,如图5 所示. 通过对子问题进行寻优,将搜索到的性能表现良好的解放到当前较好的种群中进行更新,提高算法的搜索能力. 该方式通常用于优化高维和多模态EOPs-II,能够显著减少搜索空间,提高种群多样性. 子问题的解可以并行计算,因此能够减少原问题的整体求解时间. 例如,Sun等[66 ] 提出代理辅助协同群优化算法(SA-COSO),求解100维的高维耗时优化问题. Wu等[67 ] 提出基于集成代理的协同进化优化器(UNESCO),对大规模决策变量使用特征选择,使用低维数据子集训练局部代理模型,设计协同进化优化器,通过分享2个种群产生的后代信息进行辅助优化. Zhao等[68 ] 提出双群协同算法,探索和开发多模态问题. 此外,协同进化搜索能够揭示变量之间的相互作用,在优化大规模问题方面有着巨大的潜力. Chen等[69 ] 提出代理辅助的高度协同超参数优化(SHCHO)算法,通过合作优化子问题来处理原始的CNN超参数最优化问题. Zhou等[32 ] 采用RF辅助协同进化搜索,减小时间代价. Liu等[70 ] 将原始优化问题分解为置信区域内的多个子问题,在迭代中不断提高RBFN的精度. ...
A multi-population cooperative coevolutionary whale optimization algorithm with a two-stage orthogonal learning mechanism
1
2022
... b)协同进化搜索[64 -65 ] : 本质上是对决策变量有一个分组的过程,形成一系列子问题,如图5 所示. 通过对子问题进行寻优,将搜索到的性能表现良好的解放到当前较好的种群中进行更新,提高算法的搜索能力. 该方式通常用于优化高维和多模态EOPs-II,能够显著减少搜索空间,提高种群多样性. 子问题的解可以并行计算,因此能够减少原问题的整体求解时间. 例如,Sun等[66 ] 提出代理辅助协同群优化算法(SA-COSO),求解100维的高维耗时优化问题. Wu等[67 ] 提出基于集成代理的协同进化优化器(UNESCO),对大规模决策变量使用特征选择,使用低维数据子集训练局部代理模型,设计协同进化优化器,通过分享2个种群产生的后代信息进行辅助优化. Zhao等[68 ] 提出双群协同算法,探索和开发多模态问题. 此外,协同进化搜索能够揭示变量之间的相互作用,在优化大规模问题方面有着巨大的潜力. Chen等[69 ] 提出代理辅助的高度协同超参数优化(SHCHO)算法,通过合作优化子问题来处理原始的CNN超参数最优化问题. Zhou等[32 ] 采用RF辅助协同进化搜索,减小时间代价. Liu等[70 ] 将原始优化问题分解为置信区域内的多个子问题,在迭代中不断提高RBFN的精度. ...
A surrogate-assisted highly cooperative coevolutionary algorithm for hyperparameter optimization in deep convolutional neural network
2
2023
... b)协同进化搜索[64 -65 ] : 本质上是对决策变量有一个分组的过程,形成一系列子问题,如图5 所示. 通过对子问题进行寻优,将搜索到的性能表现良好的解放到当前较好的种群中进行更新,提高算法的搜索能力. 该方式通常用于优化高维和多模态EOPs-II,能够显著减少搜索空间,提高种群多样性. 子问题的解可以并行计算,因此能够减少原问题的整体求解时间. 例如,Sun等[66 ] 提出代理辅助协同群优化算法(SA-COSO),求解100维的高维耗时优化问题. Wu等[67 ] 提出基于集成代理的协同进化优化器(UNESCO),对大规模决策变量使用特征选择,使用低维数据子集训练局部代理模型,设计协同进化优化器,通过分享2个种群产生的后代信息进行辅助优化. Zhao等[68 ] 提出双群协同算法,探索和开发多模态问题. 此外,协同进化搜索能够揭示变量之间的相互作用,在优化大规模问题方面有着巨大的潜力. Chen等[69 ] 提出代理辅助的高度协同超参数优化(SHCHO)算法,通过合作优化子问题来处理原始的CNN超参数最优化问题. Zhou等[32 ] 采用RF辅助协同进化搜索,减小时间代价. Liu等[70 ] 将原始优化问题分解为置信区域内的多个子问题,在迭代中不断提高RBFN的精度. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Trust-region based adaptive radial basis function algorithm for global optimization of expensive constrained black-box problems
2
2021
... b)协同进化搜索[64 -65 ] : 本质上是对决策变量有一个分组的过程,形成一系列子问题,如图5 所示. 通过对子问题进行寻优,将搜索到的性能表现良好的解放到当前较好的种群中进行更新,提高算法的搜索能力. 该方式通常用于优化高维和多模态EOPs-II,能够显著减少搜索空间,提高种群多样性. 子问题的解可以并行计算,因此能够减少原问题的整体求解时间. 例如,Sun等[66 ] 提出代理辅助协同群优化算法(SA-COSO),求解100维的高维耗时优化问题. Wu等[67 ] 提出基于集成代理的协同进化优化器(UNESCO),对大规模决策变量使用特征选择,使用低维数据子集训练局部代理模型,设计协同进化优化器,通过分享2个种群产生的后代信息进行辅助优化. Zhao等[68 ] 提出双群协同算法,探索和开发多模态问题. 此外,协同进化搜索能够揭示变量之间的相互作用,在优化大规模问题方面有着巨大的潜力. Chen等[69 ] 提出代理辅助的高度协同超参数优化(SHCHO)算法,通过合作优化子问题来处理原始的CNN超参数最优化问题. Zhou等[32 ] 采用RF辅助协同进化搜索,减小时间代价. Liu等[70 ] 将原始优化问题分解为置信区域内的多个子问题,在迭代中不断提高RBFN的精度. ...
... 3)基于种群的管理方式[70 ] . 该方式允许多个子种群的存在,且从每个子种群中筛选候选解. 该管理方式只在多种群搜索中普遍使用,以求解高维EOPs. 例如,Liu等[59 ] 提出SAMPSO算法,从每个子群中选择最优希望的候选解,以增强种群多样性. 随着问题的维度和复杂度越来越高,基于种群的管理方式通常会与上述2种方法结合起来一起使用,提高模型的精度和稳定性. ...
Committee-based active learning for surrogate-assisted particle swarm optimization of expensive problems
3
2017
... c)分层搜索[71 ] : 通常构建全局模型,找到有希望的区域,利用局部代理模型进行精细搜索. 由于分层结构的设计,能够减小为高维/大规模问题构建代理模型的难度,提高算法的收敛性. 如图6 所示为分层搜索的学习过程. 例如,Yu等[72 ] 提出由标准PSO算法和社会学习PSO算法(SL-PSO)组成的代理辅助分层优化器(SHPSO),增强代理模型的全局和局部搜索性能. Chu等[73 ] 提出模糊分层的代理辅助概率PSO算法(FHSAPPSO),引入模糊聚类方法,从3个层次分别捕捉特定区域的局部景观、个体周围的适应度景观及全局景观. Zhang等[74 ] 设计混合优化算法的分层代理框架(HSAOA),在全局搜索阶段,采用RBFN来协助教学优化算法(teaching-learning-based optimization,TLBO),找出有前途的子区域,在局部搜索阶段提出新的动态集成代理方法,协助DE算法加快收敛速度. Sun等[75 ] 提出双层代理辅助PSO算法(TLSAPSO),该算法采用全局和多个局部代理模型,评估分层适应度. 此外,一些学者将降维的思想引入到高维EOPs-II中,例如Ren等[76 ] 提出增强分层的代理辅助算法(RPHSA),将训练样本随机映射到一组低维子空间中,在每个子空间中训练代理模型进行分层学习. ...
... 1)基于个体的管理方式[71 ] ,即用真实目标函数评估的候选个体,这是DDICs中最灵活的管理方式. 一般来说,选择候选解进行昂贵评估的填充标准可以分为潜在的优秀个体和最不确定的个体. 对于单目标而言,个体的优劣通常由性能决定,即具有良好预测适应度的个体. 例如,SA-COSO[66 ] 和SHPSO[72 ] 都使用了这种标准. 这是大多数单目标DDICs所选取的管理方式. 对于多目标而言,优秀的个体由收敛性和多样性决定. 例如,CSEA基于收敛性选择具有更好预测值的子代[103 ] ,ACDEA采用距离回归模型和角度回归模型来选择收敛性和多样性较好的解[105 ] 等. ...
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
Surrogate-assisted hierarchical particle swarm optimization
2
2018
... c)分层搜索[71 ] : 通常构建全局模型,找到有希望的区域,利用局部代理模型进行精细搜索. 由于分层结构的设计,能够减小为高维/大规模问题构建代理模型的难度,提高算法的收敛性. 如图6 所示为分层搜索的学习过程. 例如,Yu等[72 ] 提出由标准PSO算法和社会学习PSO算法(SL-PSO)组成的代理辅助分层优化器(SHPSO),增强代理模型的全局和局部搜索性能. Chu等[73 ] 提出模糊分层的代理辅助概率PSO算法(FHSAPPSO),引入模糊聚类方法,从3个层次分别捕捉特定区域的局部景观、个体周围的适应度景观及全局景观. Zhang等[74 ] 设计混合优化算法的分层代理框架(HSAOA),在全局搜索阶段,采用RBFN来协助教学优化算法(teaching-learning-based optimization,TLBO),找出有前途的子区域,在局部搜索阶段提出新的动态集成代理方法,协助DE算法加快收敛速度. Sun等[75 ] 提出双层代理辅助PSO算法(TLSAPSO),该算法采用全局和多个局部代理模型,评估分层适应度. 此外,一些学者将降维的思想引入到高维EOPs-II中,例如Ren等[76 ] 提出增强分层的代理辅助算法(RPHSA),将训练样本随机映射到一组低维子空间中,在每个子空间中训练代理模型进行分层学习. ...
... 1)基于个体的管理方式[71 ] ,即用真实目标函数评估的候选个体,这是DDICs中最灵活的管理方式. 一般来说,选择候选解进行昂贵评估的填充标准可以分为潜在的优秀个体和最不确定的个体. 对于单目标而言,个体的优劣通常由性能决定,即具有良好预测适应度的个体. 例如,SA-COSO[66 ] 和SHPSO[72 ] 都使用了这种标准. 这是大多数单目标DDICs所选取的管理方式. 对于多目标而言,优秀的个体由收敛性和多样性决定. 例如,CSEA基于收敛性选择具有更好预测值的子代[103 ] ,ACDEA采用距离回归模型和角度回归模型来选择收敛性和多样性较好的解[105 ] 等. ...
Fuzzy hierarchical surrogate assists probabilistic particle swarm optimization for expensive high dimensional problem
1
2021
... c)分层搜索[71 ] : 通常构建全局模型,找到有希望的区域,利用局部代理模型进行精细搜索. 由于分层结构的设计,能够减小为高维/大规模问题构建代理模型的难度,提高算法的收敛性. 如图6 所示为分层搜索的学习过程. 例如,Yu等[72 ] 提出由标准PSO算法和社会学习PSO算法(SL-PSO)组成的代理辅助分层优化器(SHPSO),增强代理模型的全局和局部搜索性能. Chu等[73 ] 提出模糊分层的代理辅助概率PSO算法(FHSAPPSO),引入模糊聚类方法,从3个层次分别捕捉特定区域的局部景观、个体周围的适应度景观及全局景观. Zhang等[74 ] 设计混合优化算法的分层代理框架(HSAOA),在全局搜索阶段,采用RBFN来协助教学优化算法(teaching-learning-based optimization,TLBO),找出有前途的子区域,在局部搜索阶段提出新的动态集成代理方法,协助DE算法加快收敛速度. Sun等[75 ] 提出双层代理辅助PSO算法(TLSAPSO),该算法采用全局和多个局部代理模型,评估分层适应度. 此外,一些学者将降维的思想引入到高维EOPs-II中,例如Ren等[76 ] 提出增强分层的代理辅助算法(RPHSA),将训练样本随机映射到一组低维子空间中,在每个子空间中训练代理模型进行分层学习. ...
A hierarchical surrogate assisted optimization algorithm using teaching-learning-based optimization and differential evolution for high-dimensional expensive problems
1
2024
... c)分层搜索[71 ] : 通常构建全局模型,找到有希望的区域,利用局部代理模型进行精细搜索. 由于分层结构的设计,能够减小为高维/大规模问题构建代理模型的难度,提高算法的收敛性. 如图6 所示为分层搜索的学习过程. 例如,Yu等[72 ] 提出由标准PSO算法和社会学习PSO算法(SL-PSO)组成的代理辅助分层优化器(SHPSO),增强代理模型的全局和局部搜索性能. Chu等[73 ] 提出模糊分层的代理辅助概率PSO算法(FHSAPPSO),引入模糊聚类方法,从3个层次分别捕捉特定区域的局部景观、个体周围的适应度景观及全局景观. Zhang等[74 ] 设计混合优化算法的分层代理框架(HSAOA),在全局搜索阶段,采用RBFN来协助教学优化算法(teaching-learning-based optimization,TLBO),找出有前途的子区域,在局部搜索阶段提出新的动态集成代理方法,协助DE算法加快收敛速度. Sun等[75 ] 提出双层代理辅助PSO算法(TLSAPSO),该算法采用全局和多个局部代理模型,评估分层适应度. 此外,一些学者将降维的思想引入到高维EOPs-II中,例如Ren等[76 ] 提出增强分层的代理辅助算法(RPHSA),将训练样本随机映射到一组低维子空间中,在每个子空间中训练代理模型进行分层学习. ...
A two-layer surrogate-assisted particle swarm optimization algorithm
1
2015
... c)分层搜索[71 ] : 通常构建全局模型,找到有希望的区域,利用局部代理模型进行精细搜索. 由于分层结构的设计,能够减小为高维/大规模问题构建代理模型的难度,提高算法的收敛性. 如图6 所示为分层搜索的学习过程. 例如,Yu等[72 ] 提出由标准PSO算法和社会学习PSO算法(SL-PSO)组成的代理辅助分层优化器(SHPSO),增强代理模型的全局和局部搜索性能. Chu等[73 ] 提出模糊分层的代理辅助概率PSO算法(FHSAPPSO),引入模糊聚类方法,从3个层次分别捕捉特定区域的局部景观、个体周围的适应度景观及全局景观. Zhang等[74 ] 设计混合优化算法的分层代理框架(HSAOA),在全局搜索阶段,采用RBFN来协助教学优化算法(teaching-learning-based optimization,TLBO),找出有前途的子区域,在局部搜索阶段提出新的动态集成代理方法,协助DE算法加快收敛速度. Sun等[75 ] 提出双层代理辅助PSO算法(TLSAPSO),该算法采用全局和多个局部代理模型,评估分层适应度. 此外,一些学者将降维的思想引入到高维EOPs-II中,例如Ren等[76 ] 提出增强分层的代理辅助算法(RPHSA),将训练样本随机映射到一组低维子空间中,在每个子空间中训练代理模型进行分层学习. ...
Enhancing hierarchical surrogate-assisted evolutionary algorithm for high-dimensional expensive optimization via random projection
1
2021
... c)分层搜索[71 ] : 通常构建全局模型,找到有希望的区域,利用局部代理模型进行精细搜索. 由于分层结构的设计,能够减小为高维/大规模问题构建代理模型的难度,提高算法的收敛性. 如图6 所示为分层搜索的学习过程. 例如,Yu等[72 ] 提出由标准PSO算法和社会学习PSO算法(SL-PSO)组成的代理辅助分层优化器(SHPSO),增强代理模型的全局和局部搜索性能. Chu等[73 ] 提出模糊分层的代理辅助概率PSO算法(FHSAPPSO),引入模糊聚类方法,从3个层次分别捕捉特定区域的局部景观、个体周围的适应度景观及全局景观. Zhang等[74 ] 设计混合优化算法的分层代理框架(HSAOA),在全局搜索阶段,采用RBFN来协助教学优化算法(teaching-learning-based optimization,TLBO),找出有前途的子区域,在局部搜索阶段提出新的动态集成代理方法,协助DE算法加快收敛速度. Sun等[75 ] 提出双层代理辅助PSO算法(TLSAPSO),该算法采用全局和多个局部代理模型,评估分层适应度. 此外,一些学者将降维的思想引入到高维EOPs-II中,例如Ren等[76 ] 提出增强分层的代理辅助算法(RPHSA),将训练样本随机映射到一组低维子空间中,在每个子空间中训练代理模型进行分层学习. ...
A surrogate assisted evolutionary multi-tasking optimization algorithm
2
2023
... d)多任务搜索[77 ] . 它是迁移优化的一个分支,旨在同时解决2个或2个以上的优化问题,以探索它们之间的相似性并加速收敛. 多任务学习可以帮助模型学习到更多的共享特征,提高泛化能力,减少计算资源的消耗. 其中大多数多任务搜索都是基于多因素进化算法(multifactorial evolutionary algorithm, MFEA)[78 ] 框架进行的,如图7 所示为该框架的信息共享过程. Wang等[79 ] 使用代理辅助多任务搜索同时寻找不同解的最坏情况,有效提高了多任务的搜索效率. Huang等[80 ] 提出基于自适应知识转移的代理辅助多任务搜索框架,基于每个任务的历史搜索信息建立代理模型,实现待解任务之间的知识转移. 此外,为了学习任务之间的相似性,即不同任务之间的共同特征,Liao等[81 ] 将全局代理和局部代理模型的建立作为2个相互关联的任务,采用多任务进化算法协同求解,利用优化2个任务得到的最优解更新全局模型和局部模型. Russo等[82 ] 提出代理辅助的多任务双层DE算法(MT-BLDE). Ji等[83 ] 将多任务搜索用于多模态问题,通过设计多代理辅助的多任务小生境PSO算法(MaMPSO),以较低的计算成本寻求问题的最优解. Zhu等[84 ] 基于多任务GA算法的优化框架,引入RBFN作为全局和局部代理进行辅助优化. 该搜索方式对相关性强的任务学习效果较好,若问题任务间的相关性较弱,则会在学习过程中产生负面影响,导致整体性能下降. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Multi-factorial evolution: toward evolutionary multi-tasking
1
2015
... d)多任务搜索[77 ] . 它是迁移优化的一个分支,旨在同时解决2个或2个以上的优化问题,以探索它们之间的相似性并加速收敛. 多任务学习可以帮助模型学习到更多的共享特征,提高泛化能力,减少计算资源的消耗. 其中大多数多任务搜索都是基于多因素进化算法(multifactorial evolutionary algorithm, MFEA)[78 ] 框架进行的,如图7 所示为该框架的信息共享过程. Wang等[79 ] 使用代理辅助多任务搜索同时寻找不同解的最坏情况,有效提高了多任务的搜索效率. Huang等[80 ] 提出基于自适应知识转移的代理辅助多任务搜索框架,基于每个任务的历史搜索信息建立代理模型,实现待解任务之间的知识转移. 此外,为了学习任务之间的相似性,即不同任务之间的共同特征,Liao等[81 ] 将全局代理和局部代理模型的建立作为2个相互关联的任务,采用多任务进化算法协同求解,利用优化2个任务得到的最优解更新全局模型和局部模型. Russo等[82 ] 提出代理辅助的多任务双层DE算法(MT-BLDE). Ji等[83 ] 将多任务搜索用于多模态问题,通过设计多代理辅助的多任务小生境PSO算法(MaMPSO),以较低的计算成本寻求问题的最优解. Zhu等[84 ] 基于多任务GA算法的优化框架,引入RBFN作为全局和局部代理进行辅助优化. 该搜索方式对相关性强的任务学习效果较好,若问题任务间的相关性较弱,则会在学习过程中产生负面影响,导致整体性能下降. ...
Surrogate-assisted evolutionary multi-tasking for expensive minimax optimization in multiple scenarios
1
2021
... d)多任务搜索[77 ] . 它是迁移优化的一个分支,旨在同时解决2个或2个以上的优化问题,以探索它们之间的相似性并加速收敛. 多任务学习可以帮助模型学习到更多的共享特征,提高泛化能力,减少计算资源的消耗. 其中大多数多任务搜索都是基于多因素进化算法(multifactorial evolutionary algorithm, MFEA)[78 ] 框架进行的,如图7 所示为该框架的信息共享过程. Wang等[79 ] 使用代理辅助多任务搜索同时寻找不同解的最坏情况,有效提高了多任务的搜索效率. Huang等[80 ] 提出基于自适应知识转移的代理辅助多任务搜索框架,基于每个任务的历史搜索信息建立代理模型,实现待解任务之间的知识转移. 此外,为了学习任务之间的相似性,即不同任务之间的共同特征,Liao等[81 ] 将全局代理和局部代理模型的建立作为2个相互关联的任务,采用多任务进化算法协同求解,利用优化2个任务得到的最优解更新全局模型和局部模型. Russo等[82 ] 提出代理辅助的多任务双层DE算法(MT-BLDE). Ji等[83 ] 将多任务搜索用于多模态问题,通过设计多代理辅助的多任务小生境PSO算法(MaMPSO),以较低的计算成本寻求问题的最优解. Zhu等[84 ] 基于多任务GA算法的优化框架,引入RBFN作为全局和局部代理进行辅助优化. 该搜索方式对相关性强的任务学习效果较好,若问题任务间的相关性较弱,则会在学习过程中产生负面影响,导致整体性能下降. ...
Surrogate-assisted evolutionary framework with adaptive knowledge transfer for multi-tasking optimization
1
2019
... d)多任务搜索[77 ] . 它是迁移优化的一个分支,旨在同时解决2个或2个以上的优化问题,以探索它们之间的相似性并加速收敛. 多任务学习可以帮助模型学习到更多的共享特征,提高泛化能力,减少计算资源的消耗. 其中大多数多任务搜索都是基于多因素进化算法(multifactorial evolutionary algorithm, MFEA)[78 ] 框架进行的,如图7 所示为该框架的信息共享过程. Wang等[79 ] 使用代理辅助多任务搜索同时寻找不同解的最坏情况,有效提高了多任务的搜索效率. Huang等[80 ] 提出基于自适应知识转移的代理辅助多任务搜索框架,基于每个任务的历史搜索信息建立代理模型,实现待解任务之间的知识转移. 此外,为了学习任务之间的相似性,即不同任务之间的共同特征,Liao等[81 ] 将全局代理和局部代理模型的建立作为2个相互关联的任务,采用多任务进化算法协同求解,利用优化2个任务得到的最优解更新全局模型和局部模型. Russo等[82 ] 提出代理辅助的多任务双层DE算法(MT-BLDE). Ji等[83 ] 将多任务搜索用于多模态问题,通过设计多代理辅助的多任务小生境PSO算法(MaMPSO),以较低的计算成本寻求问题的最优解. Zhu等[84 ] 基于多任务GA算法的优化框架,引入RBFN作为全局和局部代理进行辅助优化. 该搜索方式对相关性强的任务学习效果较好,若问题任务间的相关性较弱,则会在学习过程中产生负面影响,导致整体性能下降. ...
Multi-surrogate multi-tasking optimization of expensive problems
1
2020
... d)多任务搜索[77 ] . 它是迁移优化的一个分支,旨在同时解决2个或2个以上的优化问题,以探索它们之间的相似性并加速收敛. 多任务学习可以帮助模型学习到更多的共享特征,提高泛化能力,减少计算资源的消耗. 其中大多数多任务搜索都是基于多因素进化算法(multifactorial evolutionary algorithm, MFEA)[78 ] 框架进行的,如图7 所示为该框架的信息共享过程. Wang等[79 ] 使用代理辅助多任务搜索同时寻找不同解的最坏情况,有效提高了多任务的搜索效率. Huang等[80 ] 提出基于自适应知识转移的代理辅助多任务搜索框架,基于每个任务的历史搜索信息建立代理模型,实现待解任务之间的知识转移. 此外,为了学习任务之间的相似性,即不同任务之间的共同特征,Liao等[81 ] 将全局代理和局部代理模型的建立作为2个相互关联的任务,采用多任务进化算法协同求解,利用优化2个任务得到的最优解更新全局模型和局部模型. Russo等[82 ] 提出代理辅助的多任务双层DE算法(MT-BLDE). Ji等[83 ] 将多任务搜索用于多模态问题,通过设计多代理辅助的多任务小生境PSO算法(MaMPSO),以较低的计算成本寻求问题的最优解. Zhu等[84 ] 基于多任务GA算法的优化框架,引入RBFN作为全局和局部代理进行辅助优化. 该搜索方式对相关性强的任务学习效果较好,若问题任务间的相关性较弱,则会在学习过程中产生负面影响,导致整体性能下降. ...
1
... d)多任务搜索[77 ] . 它是迁移优化的一个分支,旨在同时解决2个或2个以上的优化问题,以探索它们之间的相似性并加速收敛. 多任务学习可以帮助模型学习到更多的共享特征,提高泛化能力,减少计算资源的消耗. 其中大多数多任务搜索都是基于多因素进化算法(multifactorial evolutionary algorithm, MFEA)[78 ] 框架进行的,如图7 所示为该框架的信息共享过程. Wang等[79 ] 使用代理辅助多任务搜索同时寻找不同解的最坏情况,有效提高了多任务的搜索效率. Huang等[80 ] 提出基于自适应知识转移的代理辅助多任务搜索框架,基于每个任务的历史搜索信息建立代理模型,实现待解任务之间的知识转移. 此外,为了学习任务之间的相似性,即不同任务之间的共同特征,Liao等[81 ] 将全局代理和局部代理模型的建立作为2个相互关联的任务,采用多任务进化算法协同求解,利用优化2个任务得到的最优解更新全局模型和局部模型. Russo等[82 ] 提出代理辅助的多任务双层DE算法(MT-BLDE). Ji等[83 ] 将多任务搜索用于多模态问题,通过设计多代理辅助的多任务小生境PSO算法(MaMPSO),以较低的计算成本寻求问题的最优解. Zhu等[84 ] 基于多任务GA算法的优化框架,引入RBFN作为全局和局部代理进行辅助优化. 该搜索方式对相关性强的任务学习效果较好,若问题任务间的相关性较弱,则会在学习过程中产生负面影响,导致整体性能下降. ...
Multi-surrogate-assisted multi-tasking particle swarm optimization for expensive multi-modal problems
1
2021
... d)多任务搜索[77 ] . 它是迁移优化的一个分支,旨在同时解决2个或2个以上的优化问题,以探索它们之间的相似性并加速收敛. 多任务学习可以帮助模型学习到更多的共享特征,提高泛化能力,减少计算资源的消耗. 其中大多数多任务搜索都是基于多因素进化算法(multifactorial evolutionary algorithm, MFEA)[78 ] 框架进行的,如图7 所示为该框架的信息共享过程. Wang等[79 ] 使用代理辅助多任务搜索同时寻找不同解的最坏情况,有效提高了多任务的搜索效率. Huang等[80 ] 提出基于自适应知识转移的代理辅助多任务搜索框架,基于每个任务的历史搜索信息建立代理模型,实现待解任务之间的知识转移. 此外,为了学习任务之间的相似性,即不同任务之间的共同特征,Liao等[81 ] 将全局代理和局部代理模型的建立作为2个相互关联的任务,采用多任务进化算法协同求解,利用优化2个任务得到的最优解更新全局模型和局部模型. Russo等[82 ] 提出代理辅助的多任务双层DE算法(MT-BLDE). Ji等[83 ] 将多任务搜索用于多模态问题,通过设计多代理辅助的多任务小生境PSO算法(MaMPSO),以较低的计算成本寻求问题的最优解. Zhu等[84 ] 基于多任务GA算法的优化框架,引入RBFN作为全局和局部代理进行辅助优化. 该搜索方式对相关性强的任务学习效果较好,若问题任务间的相关性较弱,则会在学习过程中产生负面影响,导致整体性能下降. ...
A multi-surrogate multi-tasking genetic algorithm with an adaptive training sample selection strategy for expensive optimization problems
2
2024
... d)多任务搜索[77 ] . 它是迁移优化的一个分支,旨在同时解决2个或2个以上的优化问题,以探索它们之间的相似性并加速收敛. 多任务学习可以帮助模型学习到更多的共享特征,提高泛化能力,减少计算资源的消耗. 其中大多数多任务搜索都是基于多因素进化算法(multifactorial evolutionary algorithm, MFEA)[78 ] 框架进行的,如图7 所示为该框架的信息共享过程. Wang等[79 ] 使用代理辅助多任务搜索同时寻找不同解的最坏情况,有效提高了多任务的搜索效率. Huang等[80 ] 提出基于自适应知识转移的代理辅助多任务搜索框架,基于每个任务的历史搜索信息建立代理模型,实现待解任务之间的知识转移. 此外,为了学习任务之间的相似性,即不同任务之间的共同特征,Liao等[81 ] 将全局代理和局部代理模型的建立作为2个相互关联的任务,采用多任务进化算法协同求解,利用优化2个任务得到的最优解更新全局模型和局部模型. Russo等[82 ] 提出代理辅助的多任务双层DE算法(MT-BLDE). Ji等[83 ] 将多任务搜索用于多模态问题,通过设计多代理辅助的多任务小生境PSO算法(MaMPSO),以较低的计算成本寻求问题的最优解. Zhu等[84 ] 基于多任务GA算法的优化框架,引入RBFN作为全局和局部代理进行辅助优化. 该搜索方式对相关性强的任务学习效果较好,若问题任务间的相关性较弱,则会在学习过程中产生负面影响,导致整体性能下降. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A surrogate-assisted evolutionary algorithm with knowledge transfer for expensive multi-modal optimization problems
1
2024
... e)其他新颖的搜索方式. 除了上述介绍的4种分类,其他学者提出了另外的搜索方式. 例如,Du等[85 -86 ] 将知识迁移分别引入到多模态和动态DDICs中,激发代理模型协同开发的能力. Li等[87 ] 提出结合代理辅助和无模型进化优化的新算法(SAMFEO),其中SAMFEO由局部代理辅助多算子进化优化(LSA-MoEO)和无模型单算子进化优化(MF-SoEO)组成. Cui等[88 ] 提出新颖高效的代理辅助自动编码嵌入式进化优化框架(SAEO)用于求解高维EOPs-II,利用有用的低维信息,加快优化过程. Zhao等[89 ] 提出有监督的代理辅助进化算法(SSAEA),以精确的适应度函数为监督器,将适应度评估结果作为反馈机制,帮助算法更好地选择解,还设计了新的后代生成策略及模型管理策略,以提高优化性能. ...
A data-driven evolutionary transfer optimization for expensive problems in dynamic environments
1
2024
... e)其他新颖的搜索方式. 除了上述介绍的4种分类,其他学者提出了另外的搜索方式. 例如,Du等[85 -86 ] 将知识迁移分别引入到多模态和动态DDICs中,激发代理模型协同开发的能力. Li等[87 ] 提出结合代理辅助和无模型进化优化的新算法(SAMFEO),其中SAMFEO由局部代理辅助多算子进化优化(LSA-MoEO)和无模型单算子进化优化(MF-SoEO)组成. Cui等[88 ] 提出新颖高效的代理辅助自动编码嵌入式进化优化框架(SAEO)用于求解高维EOPs-II,利用有用的低维信息,加快优化过程. Zhao等[89 ] 提出有监督的代理辅助进化算法(SSAEA),以精确的适应度函数为监督器,将适应度评估结果作为反馈机制,帮助算法更好地选择解,还设计了新的后代生成策略及模型管理策略,以提高优化性能. ...
Expensive optimization via surrogate-assisted and model-free evolutionary optimization
1
2022
... e)其他新颖的搜索方式. 除了上述介绍的4种分类,其他学者提出了另外的搜索方式. 例如,Du等[85 -86 ] 将知识迁移分别引入到多模态和动态DDICs中,激发代理模型协同开发的能力. Li等[87 ] 提出结合代理辅助和无模型进化优化的新算法(SAMFEO),其中SAMFEO由局部代理辅助多算子进化优化(LSA-MoEO)和无模型单算子进化优化(MF-SoEO)组成. Cui等[88 ] 提出新颖高效的代理辅助自动编码嵌入式进化优化框架(SAEO)用于求解高维EOPs-II,利用有用的低维信息,加快优化过程. Zhao等[89 ] 提出有监督的代理辅助进化算法(SSAEA),以精确的适应度函数为监督器,将适应度评估结果作为反馈机制,帮助算法更好地选择解,还设计了新的后代生成策略及模型管理策略,以提高优化性能. ...
Surrogate-assisted autoencoder-embedded evolutionary optimization algorithm to solve high-dimensional expensive problems
1
2021
... e)其他新颖的搜索方式. 除了上述介绍的4种分类,其他学者提出了另外的搜索方式. 例如,Du等[85 -86 ] 将知识迁移分别引入到多模态和动态DDICs中,激发代理模型协同开发的能力. Li等[87 ] 提出结合代理辅助和无模型进化优化的新算法(SAMFEO),其中SAMFEO由局部代理辅助多算子进化优化(LSA-MoEO)和无模型单算子进化优化(MF-SoEO)组成. Cui等[88 ] 提出新颖高效的代理辅助自动编码嵌入式进化优化框架(SAEO)用于求解高维EOPs-II,利用有用的低维信息,加快优化过程. Zhao等[89 ] 提出有监督的代理辅助进化算法(SSAEA),以精确的适应度函数为监督器,将适应度评估结果作为反馈机制,帮助算法更好地选择解,还设计了新的后代生成策略及模型管理策略,以提高优化性能. ...
A supervised surrogate-assisted evolutionary algorithm for complex optimization problems
1
2023
... e)其他新颖的搜索方式. 除了上述介绍的4种分类,其他学者提出了另外的搜索方式. 例如,Du等[85 -86 ] 将知识迁移分别引入到多模态和动态DDICs中,激发代理模型协同开发的能力. Li等[87 ] 提出结合代理辅助和无模型进化优化的新算法(SAMFEO),其中SAMFEO由局部代理辅助多算子进化优化(LSA-MoEO)和无模型单算子进化优化(MF-SoEO)组成. Cui等[88 ] 提出新颖高效的代理辅助自动编码嵌入式进化优化框架(SAEO)用于求解高维EOPs-II,利用有用的低维信息,加快优化过程. Zhao等[89 ] 提出有监督的代理辅助进化算法(SSAEA),以精确的适应度函数为监督器,将适应度评估结果作为反馈机制,帮助算法更好地选择解,还设计了新的后代生成策略及模型管理策略,以提高优化性能. ...
Surrogate-assisted evolutionary optimization of expensive many-objective irregular problems
1
2022
... 第1类是在优化过程中直接用代理模型替换昂贵的目标函数来进行环境选择,这是目前研究中的主流. 大多数算法主要是基于分解的方法,即通过3类聚合函数(权重聚合、切比雪夫和基于惩罚的边界交叉方法),将多目标问题分解为多个单目标问题,为每个目标函数建立代理模型. 如Jin等提出的AB-MOEA[29 ] 和GP-iGNG[90 ] 算法,通过参考向量(reference vector, RV)为每个目标函数建立GP模型,设计自适应管理策略,以平衡收敛性和多样性. Shen等[91 ] 提出基于分解的局部学习策略,加速多目标EOPs-II在高维搜索空间中的收敛. 采用分解方法的一个主要问题在于使用均匀分布的权重向量不一定能够实现非支配解在目标空间中的良好分布,因此可能会导致相关算法的多样性损失[92 ] . Song等[93 ] 提出基于非分解的KTA2算法,构建对影响点(即对整体预测结果产生较大影响的某些特殊数据点)不敏感的模型来逼近每个目标函数,基于收敛性、多样性或不确定性指标的自适应填充准则,提高预测精度. 此外,Lv等[94 ] 提出PAL-SAPSO算法,采用代理模型代替真实适应度函数来模拟粒子群的演化过程,使用改进的ε-PAL分类策略来识别非帕累托(Pareto)支配的候选解. 然而,第1类方式存在不足,即这种方式可能会导致元模型的近似误差逐渐累积,影响优化过程的总体准确性[95 ] . 另外,随着目标数量的增加,将产生更高的计算成本. ...
Surrogate-assisted evolutionary algorithm with decomposition-based local learning for high-dimensional multi-objective optimization
2
2024
... 第1类是在优化过程中直接用代理模型替换昂贵的目标函数来进行环境选择,这是目前研究中的主流. 大多数算法主要是基于分解的方法,即通过3类聚合函数(权重聚合、切比雪夫和基于惩罚的边界交叉方法),将多目标问题分解为多个单目标问题,为每个目标函数建立代理模型. 如Jin等提出的AB-MOEA[29 ] 和GP-iGNG[90 ] 算法,通过参考向量(reference vector, RV)为每个目标函数建立GP模型,设计自适应管理策略,以平衡收敛性和多样性. Shen等[91 ] 提出基于分解的局部学习策略,加速多目标EOPs-II在高维搜索空间中的收敛. 采用分解方法的一个主要问题在于使用均匀分布的权重向量不一定能够实现非支配解在目标空间中的良好分布,因此可能会导致相关算法的多样性损失[92 ] . Song等[93 ] 提出基于非分解的KTA2算法,构建对影响点(即对整体预测结果产生较大影响的某些特殊数据点)不敏感的模型来逼近每个目标函数,基于收敛性、多样性或不确定性指标的自适应填充准则,提高预测精度. 此外,Lv等[94 ] 提出PAL-SAPSO算法,采用代理模型代替真实适应度函数来模拟粒子群的演化过程,使用改进的ε-PAL分类策略来识别非帕累托(Pareto)支配的候选解. 然而,第1类方式存在不足,即这种方式可能会导致元模型的近似误差逐渐累积,影响优化过程的总体准确性[95 ] . 另外,随着目标数量的增加,将产生更高的计算成本. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Balancing convergence and diversity in decomposition-based many-objective optimizers
1
2015
... 第1类是在优化过程中直接用代理模型替换昂贵的目标函数来进行环境选择,这是目前研究中的主流. 大多数算法主要是基于分解的方法,即通过3类聚合函数(权重聚合、切比雪夫和基于惩罚的边界交叉方法),将多目标问题分解为多个单目标问题,为每个目标函数建立代理模型. 如Jin等提出的AB-MOEA[29 ] 和GP-iGNG[90 ] 算法,通过参考向量(reference vector, RV)为每个目标函数建立GP模型,设计自适应管理策略,以平衡收敛性和多样性. Shen等[91 ] 提出基于分解的局部学习策略,加速多目标EOPs-II在高维搜索空间中的收敛. 采用分解方法的一个主要问题在于使用均匀分布的权重向量不一定能够实现非支配解在目标空间中的良好分布,因此可能会导致相关算法的多样性损失[92 ] . Song等[93 ] 提出基于非分解的KTA2算法,构建对影响点(即对整体预测结果产生较大影响的某些特殊数据点)不敏感的模型来逼近每个目标函数,基于收敛性、多样性或不确定性指标的自适应填充准则,提高预测精度. 此外,Lv等[94 ] 提出PAL-SAPSO算法,采用代理模型代替真实适应度函数来模拟粒子群的演化过程,使用改进的ε-PAL分类策略来识别非帕累托(Pareto)支配的候选解. 然而,第1类方式存在不足,即这种方式可能会导致元模型的近似误差逐渐累积,影响优化过程的总体准确性[95 ] . 另外,随着目标数量的增加,将产生更高的计算成本. ...
3
... 第1类是在优化过程中直接用代理模型替换昂贵的目标函数来进行环境选择,这是目前研究中的主流. 大多数算法主要是基于分解的方法,即通过3类聚合函数(权重聚合、切比雪夫和基于惩罚的边界交叉方法),将多目标问题分解为多个单目标问题,为每个目标函数建立代理模型. 如Jin等提出的AB-MOEA[29 ] 和GP-iGNG[90 ] 算法,通过参考向量(reference vector, RV)为每个目标函数建立GP模型,设计自适应管理策略,以平衡收敛性和多样性. Shen等[91 ] 提出基于分解的局部学习策略,加速多目标EOPs-II在高维搜索空间中的收敛. 采用分解方法的一个主要问题在于使用均匀分布的权重向量不一定能够实现非支配解在目标空间中的良好分布,因此可能会导致相关算法的多样性损失[92 ] . Song等[93 ] 提出基于非分解的KTA2算法,构建对影响点(即对整体预测结果产生较大影响的某些特殊数据点)不敏感的模型来逼近每个目标函数,基于收敛性、多样性或不确定性指标的自适应填充准则,提高预测精度. 此外,Lv等[94 ] 提出PAL-SAPSO算法,采用代理模型代替真实适应度函数来模拟粒子群的演化过程,使用改进的ε-PAL分类策略来识别非帕累托(Pareto)支配的候选解. 然而,第1类方式存在不足,即这种方式可能会导致元模型的近似误差逐渐累积,影响优化过程的总体准确性[95 ] . 另外,随着目标数量的增加,将产生更高的计算成本. ...
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
... 大多数现有DDICs中设计的填充抽样标准都是使用一个指标或多个混合指标衡量其在收敛性、多样性和模型准确性方面表现的潜在效益,但是没有明确地考虑在不同搜索阶段的细微变化情况. 为此,越来越多的研究倾向于开发自适应的管理策略来指导填充采样,以充分利用有限的评估次数. Song等[93 ] 分别考虑收敛性、多样性和模型不确定性的要求,设计自适应采样策略来指导解的选择,包括1个优化状态评估和3种不同的采样策略,根据检测到的优化状态,为每个优化状态选择定制的采样策略. Chen等[142 ] 提出自适应填充策略,通过设计的突变算子,平衡代理辅助进化搜索中的勘探和开发. Wang等[150 ] 提出基于贝叶斯优化的自适应批量采集函数选择方法,可以根据不同的优化阶段和问题选择合适的采集函数,提高贝叶斯优化的精度. Yang等[151 ] 提出自适应的代理辅助优化框架(ASA-MOEA/D),即在RBFN代理的协助下,能够自适应地在多样性、可行性和收敛性之间取得平衡. ...
Surrogate-assisted particle swarm optimization algorithm with Pareto active learning for expensive multi-objective optimization
1
2019
... 第1类是在优化过程中直接用代理模型替换昂贵的目标函数来进行环境选择,这是目前研究中的主流. 大多数算法主要是基于分解的方法,即通过3类聚合函数(权重聚合、切比雪夫和基于惩罚的边界交叉方法),将多目标问题分解为多个单目标问题,为每个目标函数建立代理模型. 如Jin等提出的AB-MOEA[29 ] 和GP-iGNG[90 ] 算法,通过参考向量(reference vector, RV)为每个目标函数建立GP模型,设计自适应管理策略,以平衡收敛性和多样性. Shen等[91 ] 提出基于分解的局部学习策略,加速多目标EOPs-II在高维搜索空间中的收敛. 采用分解方法的一个主要问题在于使用均匀分布的权重向量不一定能够实现非支配解在目标空间中的良好分布,因此可能会导致相关算法的多样性损失[92 ] . Song等[93 ] 提出基于非分解的KTA2算法,构建对影响点(即对整体预测结果产生较大影响的某些特殊数据点)不敏感的模型来逼近每个目标函数,基于收敛性、多样性或不确定性指标的自适应填充准则,提高预测精度. 此外,Lv等[94 ] 提出PAL-SAPSO算法,采用代理模型代替真实适应度函数来模拟粒子群的演化过程,使用改进的ε-PAL分类策略来识别非帕累托(Pareto)支配的候选解. 然而,第1类方式存在不足,即这种方式可能会导致元模型的近似误差逐渐累积,影响优化过程的总体准确性[95 ] . 另外,随着目标数量的增加,将产生更高的计算成本. ...
A taxonomy for metamodeling frameworks for evolutionary multi-objective optimization
1
2018
... 第1类是在优化过程中直接用代理模型替换昂贵的目标函数来进行环境选择,这是目前研究中的主流. 大多数算法主要是基于分解的方法,即通过3类聚合函数(权重聚合、切比雪夫和基于惩罚的边界交叉方法),将多目标问题分解为多个单目标问题,为每个目标函数建立代理模型. 如Jin等提出的AB-MOEA[29 ] 和GP-iGNG[90 ] 算法,通过参考向量(reference vector, RV)为每个目标函数建立GP模型,设计自适应管理策略,以平衡收敛性和多样性. Shen等[91 ] 提出基于分解的局部学习策略,加速多目标EOPs-II在高维搜索空间中的收敛. 采用分解方法的一个主要问题在于使用均匀分布的权重向量不一定能够实现非支配解在目标空间中的良好分布,因此可能会导致相关算法的多样性损失[92 ] . Song等[93 ] 提出基于非分解的KTA2算法,构建对影响点(即对整体预测结果产生较大影响的某些特殊数据点)不敏感的模型来逼近每个目标函数,基于收敛性、多样性或不确定性指标的自适应填充准则,提高预测精度. 此外,Lv等[94 ] 提出PAL-SAPSO算法,采用代理模型代替真实适应度函数来模拟粒子群的演化过程,使用改进的ε-PAL分类策略来识别非帕累托(Pareto)支配的候选解. 然而,第1类方式存在不足,即这种方式可能会导致元模型的近似误差逐渐累积,影响优化过程的总体准确性[95 ] . 另外,随着目标数量的增加,将产生更高的计算成本. ...
Evolutionary optimization of expensive multi-objective problems with co-sub-Pareto front Gaussian process surrogates
1
2018
... 第2类是用代理模型来近似聚合函数. Luo等[96 ] 提出GCS-MOEA算法,在MOEA/D框架的基础上,使用多任务GP对多个邻域任务的聚合函数进行同时预测以提升模型精度,还提出新的填充准则来筛选候选解. Knowles[97 ] 提出ParEGO算法,该算法的主要思想是随机选择聚合函数,使用GP建立相应的代理模型,基于EGO方法找到搜索空间的下一个候选解进行评估. Tang等[98 ] 采用基于Kriging的PF估计方法来近似面向膝点(knee point)的聚合函数,取代EOPs-II中真实的适应度评估. 基于该类方式的算法大多数只适用于低维EOPs-II,特别是基于Kriging的算法. 这可能是因为当EOPs的维度增加时,需要更多的数据来训练细化的代理模型,这将显著增大训练成本(例如训练时间)[37 ] . ...
ParEGO: a hybrid algorithm with on-line landscape approximation for expensive multi-objective optimization problems
1
2006
... 第2类是用代理模型来近似聚合函数. Luo等[96 ] 提出GCS-MOEA算法,在MOEA/D框架的基础上,使用多任务GP对多个邻域任务的聚合函数进行同时预测以提升模型精度,还提出新的填充准则来筛选候选解. Knowles[97 ] 提出ParEGO算法,该算法的主要思想是随机选择聚合函数,使用GP建立相应的代理模型,基于EGO方法找到搜索空间的下一个候选解进行评估. Tang等[98 ] 采用基于Kriging的PF估计方法来近似面向膝点(knee point)的聚合函数,取代EOPs-II中真实的适应度评估. 基于该类方式的算法大多数只适用于低维EOPs-II,特别是基于Kriging的算法. 这可能是因为当EOPs的维度增加时,需要更多的数据来训练细化的代理模型,这将显著增大训练成本(例如训练时间)[37 ] . ...
Surrogate-assisted multi-objective optimization via knee-oriented Pareto front estimation
1
2023
... 第2类是用代理模型来近似聚合函数. Luo等[96 ] 提出GCS-MOEA算法,在MOEA/D框架的基础上,使用多任务GP对多个邻域任务的聚合函数进行同时预测以提升模型精度,还提出新的填充准则来筛选候选解. Knowles[97 ] 提出ParEGO算法,该算法的主要思想是随机选择聚合函数,使用GP建立相应的代理模型,基于EGO方法找到搜索空间的下一个候选解进行评估. Tang等[98 ] 采用基于Kriging的PF估计方法来近似面向膝点(knee point)的聚合函数,取代EOPs-II中真实的适应度评估. 基于该类方式的算法大多数只适用于低维EOPs-II,特别是基于Kriging的算法. 这可能是因为当EOPs的维度增加时,需要更多的数据来训练细化的代理模型,这将显著增大训练成本(例如训练时间)[37 ] . ...
A dual surrogate assisted evolutionary algorithm based on parallel search for expensive multi/many-objective optimization
2
2023
... 随着EOPs-II维度和规模的增加,单一代理辅助的预测精度降低,时间复杂度提高. 越来越多的学者投入第3类多代理辅助优化的研究中. 多代理辅助和分层搜索是有区别的,这些代理都是并行搜索,以减少训练成本. 例如,Shen等[99 ] 提出基于并行搜索的双代理辅助进化算法(DSAEA-PS),引入基于异构MOEA的并行搜索,以更好地探索决策空间. Habib等[100 ] 提出HSMEA算法,他们使用4种不同的代理模型(Krigng、一阶RSM、二阶RSM和RBFN模型)对每个目标函数进行近似,选择具有最小均方根误差(root mean square error, RMSE)的模型来近似当前的目标函数. Guo等[101 ] 提出HeE-MOEA算法,构造由SVM和RBFN组成的异构集成预测器,以确保集成模型在面对不同数据输入时,能够提供更稳定和更可信的估计结果,从而提高决策的可靠性. 前3类方法都是基于回归的DDICs,由于实际EOPs-II应用中可获得的数据量的限制,导致大多数基于回归的DDICs无法训练出高精度的代理模型. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A multiple surrogate assisted decomposition-based evolutionary algorithm for expensive multi/many-objective optimization
2
2019
... 随着EOPs-II维度和规模的增加,单一代理辅助的预测精度降低,时间复杂度提高. 越来越多的学者投入第3类多代理辅助优化的研究中. 多代理辅助和分层搜索是有区别的,这些代理都是并行搜索,以减少训练成本. 例如,Shen等[99 ] 提出基于并行搜索的双代理辅助进化算法(DSAEA-PS),引入基于异构MOEA的并行搜索,以更好地探索决策空间. Habib等[100 ] 提出HSMEA算法,他们使用4种不同的代理模型(Krigng、一阶RSM、二阶RSM和RBFN模型)对每个目标函数进行近似,选择具有最小均方根误差(root mean square error, RMSE)的模型来近似当前的目标函数. Guo等[101 ] 提出HeE-MOEA算法,构造由SVM和RBFN组成的异构集成预测器,以确保集成模型在面对不同数据输入时,能够提供更稳定和更可信的估计结果,从而提高决策的可靠性. 前3类方法都是基于回归的DDICs,由于实际EOPs-II应用中可获得的数据量的限制,导致大多数基于回归的DDICs无法训练出高精度的代理模型. ...
... 代理模型是DDICs的一个重要研究方向. 早期的研究[129 -130 ] 倾向于使用全局或局部的单代理模型辅助ICs,它们在简单和中低维EOPs上的优良性能得到了验证. 随着问题维度和复杂度的增加,单代理模型不能很好地辅助ICs,于是学者们开始通过建立多个代理[42 ] 或混合代理模型[131 ] 来有效解决该问题. 由于代理模型与精确目标函数之间可能存在较大的误差,上述方法无法解决各类不同形态且计算量很大的EOPs. 为了提高代理模型的预测精度和有效求解EOPs,学者们引入集成学习[100 -101 ] 的思想,以辅助DDICs. ...
Heterogeneous ensemble-based infill criterion for evolutionary multi-objective optimization of expensive problems
3
2018
... 随着EOPs-II维度和规模的增加,单一代理辅助的预测精度降低,时间复杂度提高. 越来越多的学者投入第3类多代理辅助优化的研究中. 多代理辅助和分层搜索是有区别的,这些代理都是并行搜索,以减少训练成本. 例如,Shen等[99 ] 提出基于并行搜索的双代理辅助进化算法(DSAEA-PS),引入基于异构MOEA的并行搜索,以更好地探索决策空间. Habib等[100 ] 提出HSMEA算法,他们使用4种不同的代理模型(Krigng、一阶RSM、二阶RSM和RBFN模型)对每个目标函数进行近似,选择具有最小均方根误差(root mean square error, RMSE)的模型来近似当前的目标函数. Guo等[101 ] 提出HeE-MOEA算法,构造由SVM和RBFN组成的异构集成预测器,以确保集成模型在面对不同数据输入时,能够提供更稳定和更可信的估计结果,从而提高决策的可靠性. 前3类方法都是基于回归的DDICs,由于实际EOPs-II应用中可获得的数据量的限制,导致大多数基于回归的DDICs无法训练出高精度的代理模型. ...
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
... 代理模型是DDICs的一个重要研究方向. 早期的研究[129 -130 ] 倾向于使用全局或局部的单代理模型辅助ICs,它们在简单和中低维EOPs上的优良性能得到了验证. 随着问题维度和复杂度的增加,单代理模型不能很好地辅助ICs,于是学者们开始通过建立多个代理[42 ] 或混合代理模型[131 ] 来有效解决该问题. 由于代理模型与精确目标函数之间可能存在较大的误差,上述方法无法解决各类不同形态且计算量很大的EOPs. 为了提高代理模型的预测精度和有效求解EOPs,学者们引入集成学习[100 -101 ] 的思想,以辅助DDICs. ...
Grid classification-based surrogate-assisted particle swarm optimization for expensive multi-objective optimization
2
2024
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
... [102 ]提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
A classification-based surrogate-assisted evolutionary algorithm for expensive many-objective optimization
2
2018
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
... 1)基于个体的管理方式[71 ] ,即用真实目标函数评估的候选个体,这是DDICs中最灵活的管理方式. 一般来说,选择候选解进行昂贵评估的填充标准可以分为潜在的优秀个体和最不确定的个体. 对于单目标而言,个体的优劣通常由性能决定,即具有良好预测适应度的个体. 例如,SA-COSO[66 ] 和SHPSO[72 ] 都使用了这种标准. 这是大多数单目标DDICs所选取的管理方式. 对于多目标而言,优秀的个体由收敛性和多样性决定. 例如,CSEA基于收敛性选择具有更好预测值的子代[103 ] ,ACDEA采用距离回归模型和角度回归模型来选择收敛性和多样性较好的解[105 ] 等. ...
A classification surrogate-assisted multi-objective evolutionary algorithm for expensive optimization
1
2022
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
A surrogate-assisted many-objective evolutionary algorithm using multi-classification and coevolution for expensive optimization problems
2
2021
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
... 1)基于个体的管理方式[71 ] ,即用真实目标函数评估的候选个体,这是DDICs中最灵活的管理方式. 一般来说,选择候选解进行昂贵评估的填充标准可以分为潜在的优秀个体和最不确定的个体. 对于单目标而言,个体的优劣通常由性能决定,即具有良好预测适应度的个体. 例如,SA-COSO[66 ] 和SHPSO[72 ] 都使用了这种标准. 这是大多数单目标DDICs所选取的管理方式. 对于多目标而言,优秀的个体由收敛性和多样性决定. 例如,CSEA基于收敛性选择具有更好预测值的子代[103 ] ,ACDEA采用距离回归模型和角度回归模型来选择收敛性和多样性较好的解[105 ] 等. ...
Evolutionary multi-objective optimization driven by generative adversarial networks (GANs)
1
2020
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
1
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
Expensive multi-objective evolutionary optimization assisted by dominance prediction
1
2021
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
Expensive multi-objective optimization by relation learning and prediction
1
2022
... 第4类是将代理模型作为分类器进行辅助优化,主要思想是候选解的选择仅取决于它们是否具有潜在的良好性能. 与上述基于回归的算法相比,基于分类的优点主要在于以下2个方面[102 ] . (a)候选解的选择不再依赖于精确的适应度,而是替换为粗略的二元关系(如好或坏),因此代理模型不再受到高预测精度的限制. (b)基于分类的代理可以由轻量级分类模型组成,这将大大降低训练成本. 在现有的基于分类的DDICs中,分类器通常以3种方式工作:秩分类、关系分类和网格分类. 图8 展示这3种分类方式. 在秩分类中(见图8 (a)),收集所有已评估的解以形成数据库,根据它们的性能(如Pareto支配秩信息)将所有解标记为好或坏. 这些标记的解用于训练分类代理,该代理可以判断没有真实适应度信息的候选解是优质解还是劣质解. 如Pan等[103 ] 提出CSEA算法,根据ANN预测的候选解与参考解的支配关系,选择相应的候选解进行评估. Zhang等[34 ] 利用个体间的支配关系训练SVM分类模型,预测后代个体质量. Li等[104 ] 提出CSA-MOEA,训练不需要额外参数的RF作为分类器,设计有效的分类准则,将收敛性好的非劣解视为优秀解,提高算法的收敛速度. Wang等[105 ] 提出代理辅助的多目标进化算法(ACDEA),利用多分类模型和回归模型的协同作用,在降低计算量的同时提高了搜索质量. He等[106 ] 提出GMOEA算法,该算法采用GAN模型将候选解分类为真实和虚假样本,利用生成器生成优秀的新子代解和鉴别器,为这些子代解提供预测标签. 在关系分类(见图8 (b))中,所有评估的候选解都是成对的,并分配一个标签来指示它们之间的关系,然后训练分类器来近似任意2个候选解之间的二元关系. 与秩分类相比,在相同数量的解下,关系分类具有更大的训练数据集,这有助于训练更精细的代理模型,适用于仅能收集少量真实评估解的EOPs-II. NSGA-II-RCPS通过二进制关系分类器来近似每个目标中的关系对[107 ] ,其中所有分类器的融合可以近似任何2个候选解之间的支配关系. θ-DEA-DP和REMO均采用FNN来近似解对之间的二元关系[108 -109 ] . 具体地说,θ-DAE-DP使用2种不同的FNN来近似θ-支配和Pareto支配关系;REMO利用FNN构建三分类器的关系模型,根据投票评分策略选择关系进行候选解评估. 上述2种分类的算法很难考虑多样性信息,因此大多数算法考虑使用复杂的网络模型作为分类器,如FNN和GAN,导致模型训练过程耗时,没有显著的优势. Yang等[102 ] 提出网格分类方法(见图8 (c))来降低训练成本,将候选解分类到目标空间的不同网格中,以保持解的收敛性(即逐渐接近最优解)和多样性(即在目标空间中的分布广泛)信息,将这些具有网格位置信息的解用来训练基于网格分类的代理模型(grid classification-based surrogate, GCS),预测新的候选解的网格位置. 该方法可以通过轻量级分类模型实现收敛性和多样性. 如表3 所示为利用10种最新算法求解3目标60维的DTLZ和WFG测试函数上的IDG值结果,其中最大评估次数为780. 实验结果表明,不同的算法在不同的测试问题上具有突出优势,但这些算法的性能大体上是相似的. ...
Offline data-driven multi-objective optimization: knowledge transfer between surrogates and generation of final solutions
1
2019
... 此外,有些研究者提出了一些其他的方法,例如,Yang等[110 ] 使用分层框架,构造粗代理模型引导算法快速定位有潜力的区域,构造细代理模型来平衡粗代理模型知识迁移过来的有希望解. Tian等[111 ] 提出基于成对比较的代理辅助进化算法,用于代价高昂的多目标优化. 随后,Tian等[112 ] 提出基于局部帕累托前沿(Pareto front, PF)评估的多目标优化算法,求解高度不规则的PF问题. 这类问题的特点是不同目标之间存在复杂关系,例如可能存在多个局部最优解,使得PF呈现出不规则的形状. 上述方法在后面介绍的特殊多目标优化中同样适用. ...
A pairwise comparison based surrogate-assisted evolutionary algorithm for expensive multi-objective optimization
1
2023
... 此外,有些研究者提出了一些其他的方法,例如,Yang等[110 ] 使用分层框架,构造粗代理模型引导算法快速定位有潜力的区域,构造细代理模型来平衡粗代理模型知识迁移过来的有希望解. Tian等[111 ] 提出基于成对比较的代理辅助进化算法,用于代价高昂的多目标优化. 随后,Tian等[112 ] 提出基于局部帕累托前沿(Pareto front, PF)评估的多目标优化算法,求解高度不规则的PF问题. 这类问题的特点是不同目标之间存在复杂关系,例如可能存在多个局部最优解,使得PF呈现出不规则的形状. 上述方法在后面介绍的特殊多目标优化中同样适用. ...
Local model-based Pareto front estimation for multi-objective optimization
1
2022
... 此外,有些研究者提出了一些其他的方法,例如,Yang等[110 ] 使用分层框架,构造粗代理模型引导算法快速定位有潜力的区域,构造细代理模型来平衡粗代理模型知识迁移过来的有希望解. Tian等[111 ] 提出基于成对比较的代理辅助进化算法,用于代价高昂的多目标优化. 随后,Tian等[112 ] 提出基于局部帕累托前沿(Pareto front, PF)评估的多目标优化算法,求解高度不规则的PF问题. 这类问题的特点是不同目标之间存在复杂关系,例如可能存在多个局部最优解,使得PF呈现出不规则的形状. 上述方法在后面介绍的特殊多目标优化中同样适用. ...
An adaptive Gaussian process based manifold transfer learning to expensive dynamic multi-objective optimization
1
2023
... b)特殊多目标EOPs. 除了上述常见的多目标优化问题,还有一些特定的MOAs用于求解特殊的多目标EOPs. 例如,Zhang等[113 ] 提出基于传递学习的代理辅助进化算法(TrSA-DMOEA),有效地解决了动态昂贵多目标问题. 具体地说,当环境发生变化时,提出基于测地线流核的膝点(keen point)流形传递学习方法,利用以往高质量膝点解的知识来增加建立高斯过程模型的训练数据,提高解的计算复杂度和质量. Li等[25 ] 提出基于代理辅助混合模型的分布估计算法(SHEDA),用于求解混合变量的大规模EOPs-III. Wang等[114 ] 将迁移学习引入到协同代理搜索中,解决评估时间不均匀的双目标EOPs-II. Wu等[115 ] 提出新的基于Kriging-SVM的进化算法,用于解决动态多模态EOPs-II. Song等[116 ] 提出求解具有不等式约束的EOPs-II通用框架(DSI),将目标和约束分别用2组不同的训练数据进行训练,提高感兴趣区域的预测精度和可靠性. 此外,Xu等[117 ] 将联邦学习引入到DDICs中,提出新的联邦学习数据驱动进化多/超多目标算法. ...
Transfer learning based co-surrogate assisted evolutionary bi-objective optimization for objectives with non-uniform evaluation times
1
2022
... b)特殊多目标EOPs. 除了上述常见的多目标优化问题,还有一些特定的MOAs用于求解特殊的多目标EOPs. 例如,Zhang等[113 ] 提出基于传递学习的代理辅助进化算法(TrSA-DMOEA),有效地解决了动态昂贵多目标问题. 具体地说,当环境发生变化时,提出基于测地线流核的膝点(keen point)流形传递学习方法,利用以往高质量膝点解的知识来增加建立高斯过程模型的训练数据,提高解的计算复杂度和质量. Li等[25 ] 提出基于代理辅助混合模型的分布估计算法(SHEDA),用于求解混合变量的大规模EOPs-III. Wang等[114 ] 将迁移学习引入到协同代理搜索中,解决评估时间不均匀的双目标EOPs-II. Wu等[115 ] 提出新的基于Kriging-SVM的进化算法,用于解决动态多模态EOPs-II. Song等[116 ] 提出求解具有不等式约束的EOPs-II通用框架(DSI),将目标和约束分别用2组不同的训练数据进行训练,提高感兴趣区域的预测精度和可靠性. 此外,Xu等[117 ] 将联邦学习引入到DDICs中,提出新的联邦学习数据驱动进化多/超多目标算法. ...
A Kriging model-based evolutionary algorithm with support vector machine for dynamic multi-modal optimization
1
2023
... b)特殊多目标EOPs. 除了上述常见的多目标优化问题,还有一些特定的MOAs用于求解特殊的多目标EOPs. 例如,Zhang等[113 ] 提出基于传递学习的代理辅助进化算法(TrSA-DMOEA),有效地解决了动态昂贵多目标问题. 具体地说,当环境发生变化时,提出基于测地线流核的膝点(keen point)流形传递学习方法,利用以往高质量膝点解的知识来增加建立高斯过程模型的训练数据,提高解的计算复杂度和质量. Li等[25 ] 提出基于代理辅助混合模型的分布估计算法(SHEDA),用于求解混合变量的大规模EOPs-III. Wang等[114 ] 将迁移学习引入到协同代理搜索中,解决评估时间不均匀的双目标EOPs-II. Wu等[115 ] 提出新的基于Kriging-SVM的进化算法,用于解决动态多模态EOPs-II. Song等[116 ] 提出求解具有不等式约束的EOPs-II通用框架(DSI),将目标和约束分别用2组不同的训练数据进行训练,提高感兴趣区域的预测精度和可靠性. 此外,Xu等[117 ] 将联邦学习引入到DDICs中,提出新的联邦学习数据驱动进化多/超多目标算法. ...
A surrogate-assisted evolutionary framework with regions of interests-based data selection for expensive constrained optimization
1
2023
... b)特殊多目标EOPs. 除了上述常见的多目标优化问题,还有一些特定的MOAs用于求解特殊的多目标EOPs. 例如,Zhang等[113 ] 提出基于传递学习的代理辅助进化算法(TrSA-DMOEA),有效地解决了动态昂贵多目标问题. 具体地说,当环境发生变化时,提出基于测地线流核的膝点(keen point)流形传递学习方法,利用以往高质量膝点解的知识来增加建立高斯过程模型的训练数据,提高解的计算复杂度和质量. Li等[25 ] 提出基于代理辅助混合模型的分布估计算法(SHEDA),用于求解混合变量的大规模EOPs-III. Wang等[114 ] 将迁移学习引入到协同代理搜索中,解决评估时间不均匀的双目标EOPs-II. Wu等[115 ] 提出新的基于Kriging-SVM的进化算法,用于解决动态多模态EOPs-II. Song等[116 ] 提出求解具有不等式约束的EOPs-II通用框架(DSI),将目标和约束分别用2组不同的训练数据进行训练,提高感兴趣区域的预测精度和可靠性. 此外,Xu等[117 ] 将联邦学习引入到DDICs中,提出新的联邦学习数据驱动进化多/超多目标算法. ...
A federated data-driven evolutionary algorithm for expensive multi-/many-objective optimization
1
2021
... b)特殊多目标EOPs. 除了上述常见的多目标优化问题,还有一些特定的MOAs用于求解特殊的多目标EOPs. 例如,Zhang等[113 ] 提出基于传递学习的代理辅助进化算法(TrSA-DMOEA),有效地解决了动态昂贵多目标问题. 具体地说,当环境发生变化时,提出基于测地线流核的膝点(keen point)流形传递学习方法,利用以往高质量膝点解的知识来增加建立高斯过程模型的训练数据,提高解的计算复杂度和质量. Li等[25 ] 提出基于代理辅助混合模型的分布估计算法(SHEDA),用于求解混合变量的大规模EOPs-III. Wang等[114 ] 将迁移学习引入到协同代理搜索中,解决评估时间不均匀的双目标EOPs-II. Wu等[115 ] 提出新的基于Kriging-SVM的进化算法,用于解决动态多模态EOPs-II. Song等[116 ] 提出求解具有不等式约束的EOPs-II通用框架(DSI),将目标和约束分别用2组不同的训练数据进行训练,提高感兴趣区域的预测精度和可靠性. 此外,Xu等[117 ] 将联邦学习引入到DDICs中,提出新的联邦学习数据驱动进化多/超多目标算法. ...
Expected improvement matrix-based infill criteria for expensive multi-objective optimization
1
2017
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
A parallel technique for multi-objective Bayesian global optimization: using a batch selection of probability of improvement
1
2022
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
A new multi-objective Bayesian optimization formulation with the acquisition function for convergence and diversity
1
2020
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
Surrogate-assisted operator-repeated evolutionary algorithm for computationally expensive multi-objective problems
3
2023
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
... 2)基于代数的管理方式[126 ] ,即在特定代数中的所有种群进行重采样以生成新数据,根据新数据更新代理模型. 例如,Yu等[127 ] 提出基于代数的最优重启策略的代理辅助优化算法(GORS-SSLPSO),该方法同时考虑基于代数和基于个体的模型管理以及最优重启策略. Cai等[121 ] 提出代理辅助的重复算子多目标进化算法(SAOR-MOEA),该算法基于算子重复后代创建策略,可以产生多个不同的候选后代个体,增强算法的全局搜索能力和有效性. Li等[128 ] 提出基于多子代生成方法和2个填充准则的代理辅助多目标进化算法(SMEA-MIC),设计每对父解生成多个后代,结合RV和非支配排序来选择后代,以增强勘探能力. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A fast surrogate-assisted particle swarm optimization algorithm for computationally expensive problems
2
2020
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
... [122 ]. 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
Ensemble of surrogates assisted particle swarm optimization of medium scale expensive problems
1
2019
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
Multi-objective infill criterion driven Gaussian process-assisted particle swarm optimization of high-dimensional expensive problems
1
2018
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
Evolutionary algorithm with individual-distribution search strategy and regression-classification surrogates for expensive optimization
2
2023
... DDICs中的不确定性通常是指适应度评估的可靠性. 当候选解的适应度评估不可靠时,该解存在较大的不确定性. 这种具有不确定性的个体会将搜索推向未探索或探索不充分的区域,避免陷入局部最优. 到目前为止,学者们提出了不同的方法来衡量适应度评估中的不确定性填充准则,以平衡优化过程中的勘探和开发. 例如,由于Kriging模型可以提供方差,在线DDICs中开发了各种基于概率代理的填充准则,具体包括期望改进(expected improvement, ExI)[118 ] 、概率改善(probability improvement, PoI)[119 ] 和置信下限(lower confidence limit, LCL)[120 ] . 尽管基于Kriging的填充标准具有良好的性能,但是存在效率低下的问题,因为通常难以在不同性能之间达成合理的平衡[121 ] . 除此之外,可以使用候选解到训练样本的距离[93 ,122 ] 及来自集成代理的预测误差[101 ,123 ] ,提供不确定性信息. 基于距离的准则的缺点之一是它不能很好地考虑Pareto最优解集的多样性,因为不同目标的尺度是不同的. 最近,许多研究都集中在将基于不确定性的标准与基于性能的标准结合起来使用,例如CALSAPSO[71 ] 和FASAPSO[122 ] . 此外,Tian等[124 ] 提出多目标填充准则,该准则将填充抽样视为同时最小化近似适应度评估和近似评估方差的多目标问题,选取第1个和最后1个非支配前沿的解作为新的填充样本. Li等[125 ] 设计基于回归-分类的预筛选机制(regression-classification-based prescreening, RCP),该机制结合回归模型和分类模型来识别高水平的后代,使用基于性能的填充标准和基于分布的填充标准,从高水平的适应度评估中合作选择最有希望的后代. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Multiple surrogates and offspring-assisted differential evolution for high-dimensional expensive problems
1
2022
... 2)基于代数的管理方式[126 ] ,即在特定代数中的所有种群进行重采样以生成新数据,根据新数据更新代理模型. 例如,Yu等[127 ] 提出基于代数的最优重启策略的代理辅助优化算法(GORS-SSLPSO),该方法同时考虑基于代数和基于个体的模型管理以及最优重启策略. Cai等[121 ] 提出代理辅助的重复算子多目标进化算法(SAOR-MOEA),该算法基于算子重复后代创建策略,可以产生多个不同的候选后代个体,增强算法的全局搜索能力和有效性. Li等[128 ] 提出基于多子代生成方法和2个填充准则的代理辅助多目标进化算法(SMEA-MIC),设计每对父解生成多个后代,结合RV和非支配排序来选择后代,以增强勘探能力. ...
A generation-based optimal restart strategy for surrogate-assisted social learning particle swarm optimization
1
2019
... 2)基于代数的管理方式[126 ] ,即在特定代数中的所有种群进行重采样以生成新数据,根据新数据更新代理模型. 例如,Yu等[127 ] 提出基于代数的最优重启策略的代理辅助优化算法(GORS-SSLPSO),该方法同时考虑基于代数和基于个体的模型管理以及最优重启策略. Cai等[121 ] 提出代理辅助的重复算子多目标进化算法(SAOR-MOEA),该算法基于算子重复后代创建策略,可以产生多个不同的候选后代个体,增强算法的全局搜索能力和有效性. Li等[128 ] 提出基于多子代生成方法和2个填充准则的代理辅助多目标进化算法(SMEA-MIC),设计每对父解生成多个后代,结合RV和非支配排序来选择后代,以增强勘探能力. ...
Surrogate-assisted multi-objective evolutionary optimization with a multi-offspring method and two infill criteria
1
2023
... 2)基于代数的管理方式[126 ] ,即在特定代数中的所有种群进行重采样以生成新数据,根据新数据更新代理模型. 例如,Yu等[127 ] 提出基于代数的最优重启策略的代理辅助优化算法(GORS-SSLPSO),该方法同时考虑基于代数和基于个体的模型管理以及最优重启策略. Cai等[121 ] 提出代理辅助的重复算子多目标进化算法(SAOR-MOEA),该算法基于算子重复后代创建策略,可以产生多个不同的候选后代个体,增强算法的全局搜索能力和有效性. Li等[128 ] 提出基于多子代生成方法和2个填充准则的代理辅助多目标进化算法(SMEA-MIC),设计每对父解生成多个后代,结合RV和非支配排序来选择后代,以增强勘探能力. ...
Sequential approximation optimization assisted particle swarm optimization for expensive problems
1
2019
... 代理模型是DDICs的一个重要研究方向. 早期的研究[129 -130 ] 倾向于使用全局或局部的单代理模型辅助ICs,它们在简单和中低维EOPs上的优良性能得到了验证. 随着问题维度和复杂度的增加,单代理模型不能很好地辅助ICs,于是学者们开始通过建立多个代理[42 ] 或混合代理模型[131 ] 来有效解决该问题. 由于代理模型与精确目标函数之间可能存在较大的误差,上述方法无法解决各类不同形态且计算量很大的EOPs. 为了提高代理模型的预测精度和有效求解EOPs,学者们引入集成学习[100 -101 ] 的思想,以辅助DDICs. ...
A surrogate-assisted reference vector guided evolutionary algorithm for computationally expensive many-objective optimization
1
2018
... 代理模型是DDICs的一个重要研究方向. 早期的研究[129 -130 ] 倾向于使用全局或局部的单代理模型辅助ICs,它们在简单和中低维EOPs上的优良性能得到了验证. 随着问题维度和复杂度的增加,单代理模型不能很好地辅助ICs,于是学者们开始通过建立多个代理[42 ] 或混合代理模型[131 ] 来有效解决该问题. 由于代理模型与精确目标函数之间可能存在较大的误差,上述方法无法解决各类不同形态且计算量很大的EOPs. 为了提高代理模型的预测精度和有效求解EOPs,学者们引入集成学习[100 -101 ] 的思想,以辅助DDICs. ...
Combining global and local surrogate models to accelerate evolutionary optimization
1
2006
... 代理模型是DDICs的一个重要研究方向. 早期的研究[129 -130 ] 倾向于使用全局或局部的单代理模型辅助ICs,它们在简单和中低维EOPs上的优良性能得到了验证. 随着问题维度和复杂度的增加,单代理模型不能很好地辅助ICs,于是学者们开始通过建立多个代理[42 ] 或混合代理模型[131 ] 来有效解决该问题. 由于代理模型与精确目标函数之间可能存在较大的误差,上述方法无法解决各类不同形态且计算量很大的EOPs. 为了提高代理模型的预测精度和有效求解EOPs,学者们引入集成学习[100 -101 ] 的思想,以辅助DDICs. ...
Solving large-scale multi-objective optimization problems with sparse optimal solutions via unsupervised neural networks
1
2020
... 此外,面对应用场景复杂的EOPs,浅层机器学习可能无法达到预期的评估精度,因此深度学习模型逐渐被引入以替换经典代理模型. Zhang等[35 ] 提出多目标并行适应度评估网络(MPFEN),采用CNN模型预测更高质量的解. Tian等[132 ] 提出MOEA/PSL算法,联合受限玻尔兹曼机(restricted Boltzmann machine, RBM)和降噪自编码器(denoising autoencoder, DAE)学习Pareto最优解为稀疏(即大多数Pareto最优解的决策变量为0)的大规模多目标问题. Liu等[133 ] 采用图神经网络(graph neural network, GNN),求解NP难的设施选址问题. Guo等[37 ] 提出计算效率高的EDN模型来取代GP模型. Liu等[134 ] 结合长短期记忆网络(long and short-term memory, LSTM)与并行近似评价模型,为多目标DDICs提供了新思路. Liang等[36 ] 提出基于RVEA框架并使用分布式对抗网络(distributed adversarial network, DAN)来生成后代的新算法,求解大规模超多目标问题. 深度学习模型的引入会增长模型的训练时间,占用计算资源,对数据量的需求更大. ...
1
... 此外,面对应用场景复杂的EOPs,浅层机器学习可能无法达到预期的评估精度,因此深度学习模型逐渐被引入以替换经典代理模型. Zhang等[35 ] 提出多目标并行适应度评估网络(MPFEN),采用CNN模型预测更高质量的解. Tian等[132 ] 提出MOEA/PSL算法,联合受限玻尔兹曼机(restricted Boltzmann machine, RBM)和降噪自编码器(denoising autoencoder, DAE)学习Pareto最优解为稀疏(即大多数Pareto最优解的决策变量为0)的大规模多目标问题. Liu等[133 ] 采用图神经网络(graph neural network, GNN),求解NP难的设施选址问题. Guo等[37 ] 提出计算效率高的EDN模型来取代GP模型. Liu等[134 ] 结合长短期记忆网络(long and short-term memory, LSTM)与并行近似评价模型,为多目标DDICs提供了新思路. Liang等[36 ] 提出基于RVEA框架并使用分布式对抗网络(distributed adversarial network, DAN)来生成后代的新算法,求解大规模超多目标问题. 深度学习模型的引入会增长模型的训练时间,占用计算资源,对数据量的需求更大. ...
A parallel approximate evaluation-based model for multi-objective operation optimization of reservoir group
2
2023
... 此外,面对应用场景复杂的EOPs,浅层机器学习可能无法达到预期的评估精度,因此深度学习模型逐渐被引入以替换经典代理模型. Zhang等[35 ] 提出多目标并行适应度评估网络(MPFEN),采用CNN模型预测更高质量的解. Tian等[132 ] 提出MOEA/PSL算法,联合受限玻尔兹曼机(restricted Boltzmann machine, RBM)和降噪自编码器(denoising autoencoder, DAE)学习Pareto最优解为稀疏(即大多数Pareto最优解的决策变量为0)的大规模多目标问题. Liu等[133 ] 采用图神经网络(graph neural network, GNN),求解NP难的设施选址问题. Guo等[37 ] 提出计算效率高的EDN模型来取代GP模型. Liu等[134 ] 结合长短期记忆网络(long and short-term memory, LSTM)与并行近似评价模型,为多目标DDICs提供了新思路. Liang等[36 ] 提出基于RVEA框架并使用分布式对抗网络(distributed adversarial network, DAN)来生成后代的新算法,求解大规模超多目标问题. 深度学习模型的引入会增长模型的训练时间,占用计算资源,对数据量的需求更大. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
1
... 一般来说,构建高质量的DDIC是迭代的、复杂的和耗时的过程[135 ] ,而在该过程中通常需要大量的人为参与,如模型与算法的选择、超参数的调整、实验结果的评估等,以确保算法的有效性,如图10 所示. 代理模型的近似误差可能会产生不可靠的搜索,影响算法的整体性能. 此外,由“无免费的午餐(no free lunch, NFL)”[136 ] 定理可知,没有一种最先进的算法能够在所有类型的优化问题上都获得良好的性能表现,不同的优化算法具有解决不同优化问题的能力. 探索具有良好的泛化能力且能够自适应优化问题的高级启发式优化技术,一直是学术界密切关注的课题[137 ] . 随着自动机器学习的出现,越来越多的学者投入自适应的DDICs研究中,期望能够实现算法的自动构建、自动调参、自动优化等功能,有效降低人为设计算法和调参的主观性. 这些研究内容主要分为4个方向,即自适应算法选择、自适应模型选择、自适应超参数调整及自适应模型管理. ...
No free lunch theorems for optimization
1
1997
... 一般来说,构建高质量的DDIC是迭代的、复杂的和耗时的过程[135 ] ,而在该过程中通常需要大量的人为参与,如模型与算法的选择、超参数的调整、实验结果的评估等,以确保算法的有效性,如图10 所示. 代理模型的近似误差可能会产生不可靠的搜索,影响算法的整体性能. 此外,由“无免费的午餐(no free lunch, NFL)”[136 ] 定理可知,没有一种最先进的算法能够在所有类型的优化问题上都获得良好的性能表现,不同的优化算法具有解决不同优化问题的能力. 探索具有良好的泛化能力且能够自适应优化问题的高级启发式优化技术,一直是学术界密切关注的课题[137 ] . 随着自动机器学习的出现,越来越多的学者投入自适应的DDICs研究中,期望能够实现算法的自动构建、自动调参、自动优化等功能,有效降低人为设计算法和调参的主观性. 这些研究内容主要分为4个方向,即自适应算法选择、自适应模型选择、自适应超参数调整及自适应模型管理. ...
A general framework of surrogate-assisted evolutionary algorithms for solving computationally expensive constrained optimization problems
1
2023
... 一般来说,构建高质量的DDIC是迭代的、复杂的和耗时的过程[135 ] ,而在该过程中通常需要大量的人为参与,如模型与算法的选择、超参数的调整、实验结果的评估等,以确保算法的有效性,如图10 所示. 代理模型的近似误差可能会产生不可靠的搜索,影响算法的整体性能. 此外,由“无免费的午餐(no free lunch, NFL)”[136 ] 定理可知,没有一种最先进的算法能够在所有类型的优化问题上都获得良好的性能表现,不同的优化算法具有解决不同优化问题的能力. 探索具有良好的泛化能力且能够自适应优化问题的高级启发式优化技术,一直是学术界密切关注的课题[137 ] . 随着自动机器学习的出现,越来越多的学者投入自适应的DDICs研究中,期望能够实现算法的自动构建、自动调参、自动优化等功能,有效降低人为设计算法和调参的主观性. 这些研究内容主要分为4个方向,即自适应算法选择、自适应模型选择、自适应超参数调整及自适应模型管理. ...
1
... 由于不存在一种IC在所有优化问题上都具有最佳性能,使用一种优化算法来解决所有优化问题是不合理的. 目前,大多数算法都是依据经验比较从多个候选算子中选择最优算子,这是不切实际的. 为了解决上述问题,Tian等[138 ] 提出自动算法选择方法,用于为给定的多目标EOPs选择最合适的优化算子. 该方法基于一组候选进化算子在多个基准问题上的性能建立预测器. 其中预测器的输入是基准问题的显示特征(如问题规模、目标函数类型)和隐式特征(可能是问题的内部结构或复杂性),输出是优化算子在特定基准问题上表现的评估结果,这些评估结果包括性能评分、收敛速度、解的质量等指标,用于衡量不同算子在该问题上的优越性. Wang等[139 ] 提出基于自适应选择机制的多代理框架(MSFASM),解决生产优化问题. 该框架包含2个阶段,在第1阶段设计降维宽度学习系统(board learning system, BLS),自适应地选择当前优化阶段性能最好的进化算子;在第2阶段采用NSGA-II作为优化器,在多个代理模型上寻找一组性能良好的Pareto解. Dai等[140 ] 引入Q学习策略,实现5种PSOs的在线自适应选择,有效地提高算法的泛化能力与精度. Tian等[141 ] 提出基于强化学习(reinforcement learning, RL)的算子自适应选择方法,以解决具有挑战性的多目标优化问题. ...
Multi-surrogate framework with an adaptive selection mechanism for production optimization
1
2024
... 由于不存在一种IC在所有优化问题上都具有最佳性能,使用一种优化算法来解决所有优化问题是不合理的. 目前,大多数算法都是依据经验比较从多个候选算子中选择最优算子,这是不切实际的. 为了解决上述问题,Tian等[138 ] 提出自动算法选择方法,用于为给定的多目标EOPs选择最合适的优化算子. 该方法基于一组候选进化算子在多个基准问题上的性能建立预测器. 其中预测器的输入是基准问题的显示特征(如问题规模、目标函数类型)和隐式特征(可能是问题的内部结构或复杂性),输出是优化算子在特定基准问题上表现的评估结果,这些评估结果包括性能评分、收敛速度、解的质量等指标,用于衡量不同算子在该问题上的优越性. Wang等[139 ] 提出基于自适应选择机制的多代理框架(MSFASM),解决生产优化问题. 该框架包含2个阶段,在第1阶段设计降维宽度学习系统(board learning system, BLS),自适应地选择当前优化阶段性能最好的进化算子;在第2阶段采用NSGA-II作为优化器,在多个代理模型上寻找一组性能良好的Pareto解. Dai等[140 ] 引入Q学习策略,实现5种PSOs的在线自适应选择,有效地提高算法的泛化能力与精度. Tian等[141 ] 提出基于强化学习(reinforcement learning, RL)的算子自适应选择方法,以解决具有挑战性的多目标优化问题. ...
1
... 由于不存在一种IC在所有优化问题上都具有最佳性能,使用一种优化算法来解决所有优化问题是不合理的. 目前,大多数算法都是依据经验比较从多个候选算子中选择最优算子,这是不切实际的. 为了解决上述问题,Tian等[138 ] 提出自动算法选择方法,用于为给定的多目标EOPs选择最合适的优化算子. 该方法基于一组候选进化算子在多个基准问题上的性能建立预测器. 其中预测器的输入是基准问题的显示特征(如问题规模、目标函数类型)和隐式特征(可能是问题的内部结构或复杂性),输出是优化算子在特定基准问题上表现的评估结果,这些评估结果包括性能评分、收敛速度、解的质量等指标,用于衡量不同算子在该问题上的优越性. Wang等[139 ] 提出基于自适应选择机制的多代理框架(MSFASM),解决生产优化问题. 该框架包含2个阶段,在第1阶段设计降维宽度学习系统(board learning system, BLS),自适应地选择当前优化阶段性能最好的进化算子;在第2阶段采用NSGA-II作为优化器,在多个代理模型上寻找一组性能良好的Pareto解. Dai等[140 ] 引入Q学习策略,实现5种PSOs的在线自适应选择,有效地提高算法的泛化能力与精度. Tian等[141 ] 提出基于强化学习(reinforcement learning, RL)的算子自适应选择方法,以解决具有挑战性的多目标优化问题. ...
Deep reinforcement learning based adaptive operator selection for evolutionary multi-objective optimization
1
2022
... 由于不存在一种IC在所有优化问题上都具有最佳性能,使用一种优化算法来解决所有优化问题是不合理的. 目前,大多数算法都是依据经验比较从多个候选算子中选择最优算子,这是不切实际的. 为了解决上述问题,Tian等[138 ] 提出自动算法选择方法,用于为给定的多目标EOPs选择最合适的优化算子. 该方法基于一组候选进化算子在多个基准问题上的性能建立预测器. 其中预测器的输入是基准问题的显示特征(如问题规模、目标函数类型)和隐式特征(可能是问题的内部结构或复杂性),输出是优化算子在特定基准问题上表现的评估结果,这些评估结果包括性能评分、收敛速度、解的质量等指标,用于衡量不同算子在该问题上的优越性. Wang等[139 ] 提出基于自适应选择机制的多代理框架(MSFASM),解决生产优化问题. 该框架包含2个阶段,在第1阶段设计降维宽度学习系统(board learning system, BLS),自适应地选择当前优化阶段性能最好的进化算子;在第2阶段采用NSGA-II作为优化器,在多个代理模型上寻找一组性能良好的Pareto解. Dai等[140 ] 引入Q学习策略,实现5种PSOs的在线自适应选择,有效地提高算法的泛化能力与精度. Tian等[141 ] 提出基于强化学习(reinforcement learning, RL)的算子自适应选择方法,以解决具有挑战性的多目标优化问题. ...
Surrogate-assisted evolutionary algorithm with hierarchical surrogate technique and adaptive infill strategy
3
2023
... 在没有任何先验知识的情况下,单一的代理模型不能始终对所有EOPs都表现良好,不同模型适用的场景不同. 为了克服这一问题,自适应的模型选择策略开始被广泛研究,如图11 所示为代理模型和算法的自适应选择过程,选择策略是自适应学习的关键. 例如,Chen等[142 -143 ] 基于RMSE提出自适应代理辅助优化算法,分别求解单目标EOPs和多目标EOPs. Deb等[144 ] 提出基于自适应切换的元建模方法,通过在10种不同的元建模框架之间切换,对所有框架的元建模精度进行统计比较. Wu等[145 ] 基于均方差(mean squared error, MSE)提出自适应的RBFN模型选择策略,该策略可以动态地为每个目标建立最有前景的RBFN模型,提高预测的可靠性. Wu等[146 ] 提出基于价值和顺序2种选择机制的实时核函数自动选择方法,构建最有前途的RBFN模型. ...
... 大多数现有DDICs中设计的填充抽样标准都是使用一个指标或多个混合指标衡量其在收敛性、多样性和模型准确性方面表现的潜在效益,但是没有明确地考虑在不同搜索阶段的细微变化情况. 为此,越来越多的研究倾向于开发自适应的管理策略来指导填充采样,以充分利用有限的评估次数. Song等[93 ] 分别考虑收敛性、多样性和模型不确定性的要求,设计自适应采样策略来指导解的选择,包括1个优化状态评估和3种不同的采样策略,根据检测到的优化状态,为每个优化状态选择定制的采样策略. Chen等[142 ] 提出自适应填充策略,通过设计的突变算子,平衡代理辅助进化搜索中的勘探和开发. Wang等[150 ] 提出基于贝叶斯优化的自适应批量采集函数选择方法,可以根据不同的优化阶段和问题选择合适的采集函数,提高贝叶斯优化的精度. Yang等[151 ] 提出自适应的代理辅助优化框架(ASA-MOEA/D),即在RBFN代理的协助下,能够自适应地在多样性、可行性和收敛性之间取得平衡. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Adaptive surrogate assisted multi-objective optimization approach for highly nonlinear and complex engineering design problems
2
2023
... 在没有任何先验知识的情况下,单一的代理模型不能始终对所有EOPs都表现良好,不同模型适用的场景不同. 为了克服这一问题,自适应的模型选择策略开始被广泛研究,如图11 所示为代理模型和算法的自适应选择过程,选择策略是自适应学习的关键. 例如,Chen等[142 -143 ] 基于RMSE提出自适应代理辅助优化算法,分别求解单目标EOPs和多目标EOPs. Deb等[144 ] 提出基于自适应切换的元建模方法,通过在10种不同的元建模框架之间切换,对所有框架的元建模精度进行统计比较. Wu等[145 ] 基于均方差(mean squared error, MSE)提出自适应的RBFN模型选择策略,该策略可以动态地为每个目标建立最有前景的RBFN模型,提高预测的可靠性. Wu等[146 ] 提出基于价值和顺序2种选择机制的实时核函数自动选择方法,构建最有前途的RBFN模型. ...
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Surrogate modeling approaches for multi-objective optimization: methods, taxonomy, and results
1
2020
... 在没有任何先验知识的情况下,单一的代理模型不能始终对所有EOPs都表现良好,不同模型适用的场景不同. 为了克服这一问题,自适应的模型选择策略开始被广泛研究,如图11 所示为代理模型和算法的自适应选择过程,选择策略是自适应学习的关键. 例如,Chen等[142 -143 ] 基于RMSE提出自适应代理辅助优化算法,分别求解单目标EOPs和多目标EOPs. Deb等[144 ] 提出基于自适应切换的元建模方法,通过在10种不同的元建模框架之间切换,对所有框架的元建模精度进行统计比较. Wu等[145 ] 基于均方差(mean squared error, MSE)提出自适应的RBFN模型选择策略,该策略可以动态地为每个目标建立最有前景的RBFN模型,提高预测的可靠性. Wu等[146 ] 提出基于价值和顺序2种选择机制的实时核函数自动选择方法,构建最有前途的RBFN模型. ...
Adaptive surrogate-assisted multi-objective evolutionary algorithm using an efficient infill technique
1
2022
... 在没有任何先验知识的情况下,单一的代理模型不能始终对所有EOPs都表现良好,不同模型适用的场景不同. 为了克服这一问题,自适应的模型选择策略开始被广泛研究,如图11 所示为代理模型和算法的自适应选择过程,选择策略是自适应学习的关键. 例如,Chen等[142 -143 ] 基于RMSE提出自适应代理辅助优化算法,分别求解单目标EOPs和多目标EOPs. Deb等[144 ] 提出基于自适应切换的元建模方法,通过在10种不同的元建模框架之间切换,对所有框架的元建模精度进行统计比较. Wu等[145 ] 基于均方差(mean squared error, MSE)提出自适应的RBFN模型选择策略,该策略可以动态地为每个目标建立最有前景的RBFN模型,提高预测的可靠性. Wu等[146 ] 提出基于价值和顺序2种选择机制的实时核函数自动选择方法,构建最有前途的RBFN模型. ...
Adaptive multi-surrogate and module-based optimization algorithm for high-dimensional and computationally expensive problems
1
2023
... 在没有任何先验知识的情况下,单一的代理模型不能始终对所有EOPs都表现良好,不同模型适用的场景不同. 为了克服这一问题,自适应的模型选择策略开始被广泛研究,如图11 所示为代理模型和算法的自适应选择过程,选择策略是自适应学习的关键. 例如,Chen等[142 -143 ] 基于RMSE提出自适应代理辅助优化算法,分别求解单目标EOPs和多目标EOPs. Deb等[144 ] 提出基于自适应切换的元建模方法,通过在10种不同的元建模框架之间切换,对所有框架的元建模精度进行统计比较. Wu等[145 ] 基于均方差(mean squared error, MSE)提出自适应的RBFN模型选择策略,该策略可以动态地为每个目标建立最有前景的RBFN模型,提高预测的可靠性. Wu等[146 ] 提出基于价值和顺序2种选择机制的实时核函数自动选择方法,构建最有前途的RBFN模型. ...
Adaptive online data-driven closed-loop parameter control strategy for swarm intelligence algorithm
1
2020
... DDICs中的参数调整是困难且具有挑战性的问题,目前的参数研究侧重于ICs. 为了使DDICs中的参数能够根据不同的优化问题和算法运行情况实时变化,已经涌现出一些自适应的超参数控制策略,确保算法在求解优化问题的过程中能够时刻保持最佳性能. Lu等[147 ] 提出自适应的数据驱动闭环参数控制策略,实时控制群智能算法的优化性能. Liu等[148 ] 利用RL对PSO中的参数进行自适应控制. Gao等[149 ] 提出结合分布、对抗和平衡特性的参数自适应机制,旨在降低参数设置的算法灵敏度,提高算法的适应性. ...
1
... DDICs中的参数调整是困难且具有挑战性的问题,目前的参数研究侧重于ICs. 为了使DDICs中的参数能够根据不同的优化问题和算法运行情况实时变化,已经涌现出一些自适应的超参数控制策略,确保算法在求解优化问题的过程中能够时刻保持最佳性能. Lu等[147 ] 提出自适应的数据驱动闭环参数控制策略,实时控制群智能算法的优化性能. Liu等[148 ] 利用RL对PSO中的参数进行自适应控制. Gao等[149 ] 提出结合分布、对抗和平衡特性的参数自适应机制,旨在降低参数设置的算法灵敏度,提高算法的适应性. ...
Quadruple parameter adaptation growth optimizer with integrated distribution, confrontation, and balance features for optimization
1
2024
... DDICs中的参数调整是困难且具有挑战性的问题,目前的参数研究侧重于ICs. 为了使DDICs中的参数能够根据不同的优化问题和算法运行情况实时变化,已经涌现出一些自适应的超参数控制策略,确保算法在求解优化问题的过程中能够时刻保持最佳性能. Lu等[147 ] 提出自适应的数据驱动闭环参数控制策略,实时控制群智能算法的优化性能. Liu等[148 ] 利用RL对PSO中的参数进行自适应控制. Gao等[149 ] 提出结合分布、对抗和平衡特性的参数自适应机制,旨在降低参数设置的算法灵敏度,提高算法的适应性. ...
Batch Bayesian optimization with adaptive batch acquisition functions via multi-objective optimization
1
2023
... 大多数现有DDICs中设计的填充抽样标准都是使用一个指标或多个混合指标衡量其在收敛性、多样性和模型准确性方面表现的潜在效益,但是没有明确地考虑在不同搜索阶段的细微变化情况. 为此,越来越多的研究倾向于开发自适应的管理策略来指导填充采样,以充分利用有限的评估次数. Song等[93 ] 分别考虑收敛性、多样性和模型不确定性的要求,设计自适应采样策略来指导解的选择,包括1个优化状态评估和3种不同的采样策略,根据检测到的优化状态,为每个优化状态选择定制的采样策略. Chen等[142 ] 提出自适应填充策略,通过设计的突变算子,平衡代理辅助进化搜索中的勘探和开发. Wang等[150 ] 提出基于贝叶斯优化的自适应批量采集函数选择方法,可以根据不同的优化阶段和问题选择合适的采集函数,提高贝叶斯优化的精度. Yang等[151 ] 提出自适应的代理辅助优化框架(ASA-MOEA/D),即在RBFN代理的协助下,能够自适应地在多样性、可行性和收敛性之间取得平衡. ...
Surrogate-assisted MOEA/D for expensive constrained multi-objective optimization
1
2023
... 大多数现有DDICs中设计的填充抽样标准都是使用一个指标或多个混合指标衡量其在收敛性、多样性和模型准确性方面表现的潜在效益,但是没有明确地考虑在不同搜索阶段的细微变化情况. 为此,越来越多的研究倾向于开发自适应的管理策略来指导填充采样,以充分利用有限的评估次数. Song等[93 ] 分别考虑收敛性、多样性和模型不确定性的要求,设计自适应采样策略来指导解的选择,包括1个优化状态评估和3种不同的采样策略,根据检测到的优化状态,为每个优化状态选择定制的采样策略. Chen等[142 ] 提出自适应填充策略,通过设计的突变算子,平衡代理辅助进化搜索中的勘探和开发. Wang等[150 ] 提出基于贝叶斯优化的自适应批量采集函数选择方法,可以根据不同的优化阶段和问题选择合适的采集函数,提高贝叶斯优化的精度. Yang等[151 ] 提出自适应的代理辅助优化框架(ASA-MOEA/D),即在RBFN代理的协助下,能够自适应地在多样性、可行性和收敛性之间取得平衡. ...
SAFE: scale-adaptive fitness evaluation method for expensive optimization problems
1
2021
... DDICs为解决昂贵的优化问题提供了一种极具竞争力的方法,并被广泛应用于医疗健康、工程设计、能源能耗、环境污染和资源调度等各种EOPs问题. 对DDICs所涉及的应用领域进行总结与归纳,具体如表4 所示. 可知,很多研究者通过考虑特定问题类型和特征来应对相应EOPs的挑战,从而产生应用DDICs的方法,旨在实现计算时间成本和优化精度之间的平衡. 许多现有的优化算法通常只能应用于特定类型的EOPs,这使得研究人员在比较和测试新方法时面临困难,建立更通用的评估标准和测试平台显得尤为重要. 目前,学术界已开展多项工作,为求解EOPs提供了各种竞赛和基准测试. 如表5 所示为近6年来基于实际EOPs的竞赛. 此外,Wu等[152 ] 基于现有的开源实际车辆路线,为昂贵的人群运输优化应用程序开发了35个测试实例. 这些工作能够揭示实际应用中EOPs的困难和挑战,并评估各种最先进的方法,以弥合学术和应用之间的差距[12 ] . ...
Dual-surrogate-assisted cooperative particle swarm optimization for expensive multi-modal problems
1
2021
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Fast multi-objective optimization of multi-parameter antenna structures based on improved MOEA/D with surrogate-assisted model
1
2017
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
An efficient surrogate assisted particle swarm optimization for antenna synthesis
1
2022
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A Kriging-assisted double population differential evolution for mixed-integer expensive constrained optimization problems with mixed constraints
1
2024
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A surrogate-assisted differential evolution for expensive constrained optimization problems involving mixed-integer variables
1
2023
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
1
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A multi-strategy surrogate-assisted competitive swarm optimizer for expensive optimization problems
1
2023
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Surrogate-assisted evolutionary optimization for perishable inventory management in multi-echelon distribution systems
1
2024
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Dynamic optimal control for wastewater treatment process under multiple operating conditions
1
2022
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
A surrogate-assisted heuristic approach for the joint optimization of resource allocation and scheduling of an aircraft final assembly line
1
2023
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Application of surrogate-assisted global optimization algorithm with dimension-reduction in power optimization of floating offshore wind farm
1
2023
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...
Surrogate-assisted Phasmatodea population evolution algorithm applied to wireless sensor networks
1
2023
... Practical application of DDICs in different field
Tab.4 序号 应用领域 问题 算法 目标 约束 优化算子 代理模型 1 创伤系统设计 离散 SA-NSGA-II[10 ] 多 无 NSGA-II PR 1 创伤系统设计 离散 RF-CMOCO[54 ] 多 不等式 MOEA RF 2 建筑节能设计 连续 DSCPSO-EMM[153 ] 单 无 PSO RBFN 3 天线设计 连续 improved MOEA/D[154 ] 多 不等式 MOEA/D BPNN 3 天线设计 连续 SAEA-HAS[142 ] 单 无 GA RBFN 3 天线设计 连续 APSO-mixP[155 ] 单 无 PSO Kriging 4 张力/压缩弹簧设计 连续 MS-MTGAwA[84 ] 单 等式 GA RBFN 5 桁架结构设计 离散 KDPDE[156 ] 单 不等式+等式 DE Kriging 5 桁架结构设计 离散 SADE-MI[157 ] 单 不等式 DE RBFN 6 翼型设计 离散 SA-MPSO[59 ] 单 无 PSO RBFN 6 翼型设计 离散 SA-TSDE[48 ] 单 不等式 DE RBFN 6 翼型设计 离散 SAEA-DBLL[91 ] 多 无 RVEA RBFN 6 翼型设计 离散 DSAEA-PS[99 ] 多 无 NSGA-II Kriging+GP 6 翼型设计 离散 SAOR-MOEA[121 ] 多 无 MOEA RBFN 7 车辆设计 连续 K-CSEA[158 ] 多 无 RVEA Kriging 7 车辆设计 连续 AMOS[143 ] 多 不等式 MOEA PR+Kriging+RBFN 8 减速机设计 连续 SACOS[159 ] 单 不等式 CSO RBFN 9 船舶设计 连续 eToSA-DE[53 ] 单 不等式 DE GP 10 供应链系统优化 连续 CDE[160 ] 单 无 DE RF 11 污水处理过程优化 连续 RLPSO[30 ] 单 不等式 PSO ANN 11 污水处理过程优化 连续 DOC[161 ] 多 不等式 MOPSO FNN 12 车间与资源调度 连续 PAEM-LSTM[134 ] 多 不等式 MOEA LSTM 12 车间与资源调度 离散 SACS[33 ] 单 不等式+等式 ACO KNN 12 车间与资源调度 离散 RATSJOP[162 ] 单 不等式+等式 GA RF 13 神经网络架构搜索 离散 SHEALED[24 ] 单 无 DE+GA RBFN 13 神经网络架构搜索 离散 SHCHO[69 ] 单 无 DE CNN 13 神经网络架构搜索 混合 SHEDA[25 ] 单 无 EDA Kriging 14 能源与电力系统 连续 SAMTO[77 ] 单 无 MFEA RBFN 14 能源与电力系统 连续 SAFDR[163 ] 单 无 PSO GP 15 油藏产量 连续 IDRCEA[125 ] 单 无 DE RBFN+KNN 16 无线传感器系统 连续 SAPPE[164 ] 单 无 PPE RBFN 17 自动团队组装游戏 离散 DDEA-DLS[57 ] 单 等式 DE LSTM 18 交通信号配时 离散 CL-DDEA[50 ] 单 等式 DE 孪生RBFN
表 5 近6年基于实际应用EOPs的竞赛 ...