随着中国城市化发展越来越快,大多数城市快速路系统得到逐步完善,城市快速路已渐渐成为城市交通运行体系的重要组成部分. 交织区作为快速路系统中的关键节点,区域内部车辆运行特性复杂. 从微观角度来看,快速路交织区中复杂的交织换道行为是影响快速路通行能力的重要因素之一. 因此,研究快速路交织区内车辆的换道规律并对其进行有效的行为仿真建模,有助于明晰交织区内部交通流运行特性,提高快速路交织区的车辆通行效率.
近年来,国内外学者对快速路交织区的仿真建模研究可分为宏观交通流模型和微观交通流模型[1] 2类. 其中宏观交通流模型主要用于研究交织区交通流稳定性以及交通拥堵的转变. Nagatani等[2-3]提出多种交通流连续模型来研究交织区中交通流的拥堵转变. 叶颖俊等[4-5]基于上海市快速路汇入区的轨迹数据开发了一种交通流仿真系统,提出主线压迫式换道和并行式汇入方式会显著降低汇入区车辆通行效率. 吴中等[6]建立了基于换道时间随机性的动力学方程,对快速路交织区内车流速度在时空上的演变概率进行求解,成功将交通流速度的演变趋势表达为速度变化的概率密度. 微观交通流模型方面的研究较多,此类模型能够结合换道规则,模拟快速路交织区的交通波动以及交通拥堵对交通流运行特性的影响. Bando等[7]基于车辆速度建立刺激-反应模型(OVM),分析交通拥堵随时间变化的演变规律. Berg等[8]针对入口匝道处的汇入行为建立优化速度跟驰模型,成功再现入口匝道上游和下游处的均衡拥堵交通流现象. Nagel等[9]通过改进Wolfram的184号规则,提出了著名的NaSch元胞模型,对元胞自动机在交通领域的应用产生了深远的影响. 雷丽等[10]对主线为单车道的快速路交织区进行仿真建模并分析了交织区长度对快速路系统的影响. 彭博等[11]基于A型交织区的高精度轨迹数据,通过细化元胞尺寸和时间步长建立多级换道决策元胞模型. Marczak等[12]探究合流车辆与分流车辆对交织区交通流运行特性的影响. 谢济铭等[13]提出基于Gaussian分布模型的换道概率规则,依据换道安全风险构建了多车道交织区元胞自动机模型. 陈永恒等[14]基于KKW模型构建了附加导流岛型快速路出口的元胞自动机模型,讨论并分析了此类型出口对快速路交通流的影响. 元胞自动机作为一种微观仿真模型,聚焦于描绘交通流中每辆车的个体运动状态. 通过自定义车辆的跟驰换道规则,能够刻画出多车道交织区中复杂的换道行为,在快速路交织区以及基本路段交通流的特性研究中得到广泛应用.
上述研究针对快速路交织区的行为仿真建模提出了多种交通流模型,多数场景假设存在独立的出入口匝道. 但是,快速路长距离交织区无法设置单独的出入口匝道,其车辆的驶入驶出是通过换道来完成的,此时驶入驶出车辆须在同一路段上进行换道操作,车辆通行权难以得到保障. 由于快速路长距离交织区与常规快速路出入口在几何条件上存在明显差异,并且针对这一情况存在多种管理策略,深入研究长距离交织区内的车辆运行特性对于解决这种特殊快速路交通模式下的交通拥堵问题至关重要. 本研究旨在深入讨论这一特殊交通组织形式. 针对长距离交织区内不同位置的换道车辆,考虑其各自的换道行为和换道需求强度,引入3种不同的换道规则,并对其进行分段设定. 同时,基于动态安全间距、车流管理策略双重因素,构建多车道长距离交织区元胞模型. 通过微观仿真方法,对不同管理策略下的快速路长距离交织区的车辆运行特性进行深入分析,旨在为这一特殊交通模式下的组织和管理提供实用的参考依据.
1. 长距离交织区基本情况与管理策略
1.1. 长距离交织区基本情况
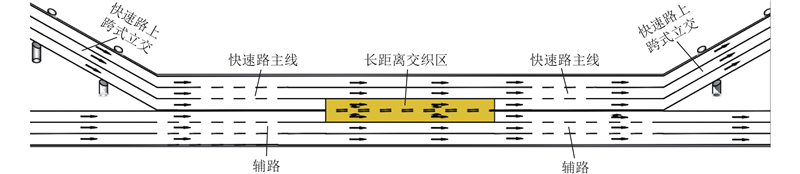
在快速路主线的建设过程中,常常须处理与快速路交通产生冲突的平面交叉口. 对于那些与快速路存在冲突但交通流量相对较小的小型交叉口,通常采用关闭或限制转弯措施来减少交通冲突. 当快速路主线须穿越大型交叉口时,通常采用上跨式立交的方式,通过上下匝道来有效分离快速路交通流和交叉口交通流. 然而,快速路主线上2个大型交叉口之间的距离较短,会导致其相邻两座上跨式立交桥之间的距离也较短,从而难以为驶入车辆和驶出车辆设置独立的驶入驶出匝道. 此时车辆不得不执行换道即驶入或换道即驶出操作,形成一种换道即驶入以及换道即驶出的特殊路段,本研究称之为快速路长距离交织区.
图 1
图 1 常规快速路出入口示意图
Fig.1 Schematic diagram of entrance and exit of typical expressway
图 2
图 2 快速路长距离交织区示意图
Fig.2 Schematic diagram of long-distance weaving zones on expressway
1.2. 长距离交织区管理策略
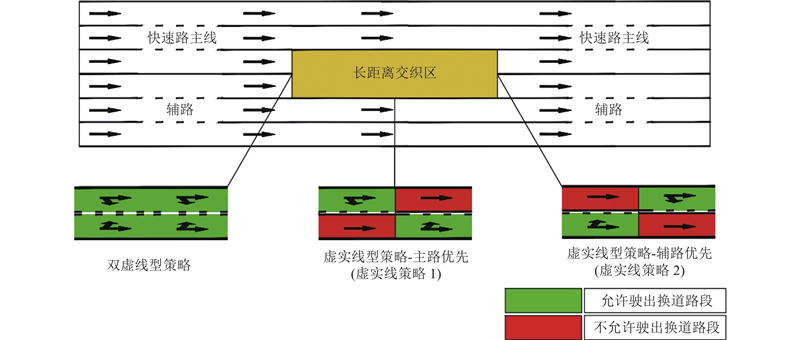
目前长距离交织区主要存在2种管理策略:双虚线型策略和虚实线型策略. 其中,双虚线型策略是指在快速路与辅路之间设置一段双虚线,在保证安全的前提下,主辅路中的驶出车辆可以自由驶出换道至目标车道. 虚实线型策略则是通过设置多段虚实线的方式,来保证虚线侧驶出车辆的换道路权. 根据主路车辆驶出顺序将虚实线型策略进一步划分为虚实线型策略1(先出后入型)和虚实线型策略2(先入后出型),如图3所示. 基于不同管理策略和车辆换道特性,构建多车道长距离交织区元胞模型.
图 3
图 3 快速路长距离交织区管理策略示意图
Fig.3 Schematic diagram of management strategies for long-distance weaving zones on urban expressway
2. 模型建立
2.1. 模型场景描述
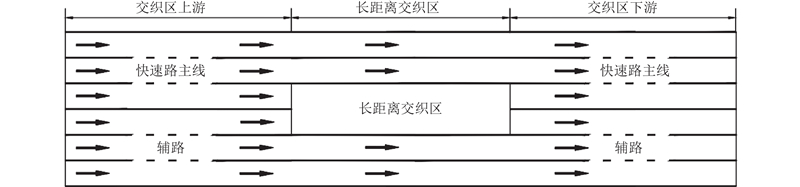
通过构建多车道元胞模型来模拟长距离交织区影响下的交通流运行情况. 考虑到长距离交织区内不同位置驾驶行为的差异性,采用分区建模的方法将整个研究路段划分为3个分区,如图4所示. 1)交织区上游:位于交织区之前,驶出车辆的换道决策受交织区影响;2)长距离交织区:车辆换道决策受交织区以及管理策略显著影响;3)交织区下游:位于交织区之后,车辆换道决策几乎不受交织区影响. 将每一个分区视作一个相对独立的实体,根据不同车辆在不同分区内的换道特性,相应地为每个分区内的车辆制定元胞规则.
图 4
2.2. 车辆跟驰规则
车辆跟驰规则采用基于动态安全间距考虑的SD模型[15],其充分考虑了车辆行驶过程中的动态安全距离,能够有效避免跟驰过程中出现不切实际的减速行为,更加符合快速路的实际交通状态. SD模型由安全距离计算和车辆速度更新2部分构成.
1)安全距离计算.
式中:
2) 车辆速度更新.
式中:
式中:
经过安全距离计算和车辆速度更新后,车辆位置更新为
2.3. 车辆换道规则
在长距离交织区内,驶出车辆面临着在有限距离内完成驶出换道的挑战,换道时机尤为紧迫. 引入3种换道规则,来匹配长距离交织区影响下车辆的不同换道行为. 为了更准确地复现这一过程,根据车辆行驶目的地将车辆划分为驶出车辆和非驶出车辆2类.
2.3.1. 自主换道规则
自由换道规则主要用于描述主辅路车辆为了追求更快的车速或者更好的行车条件而发生的换道行为. 当车辆运行速度较低且相邻车道具备更好的行驶条件时产生自主换道意图,具体为
式中:
当车辆产生自主换道意图后,须判断目标车道上的空间条件是否满足自主换道安全条件. 此时车辆发生自主换道所需满足的安全条件为
式中:
2.3.2. 强制换道规则
强制换道规则主要用于描述主辅路中的驶出车辆为了能够从交织区成功驶出而迫切寻求换道机会换道至最左/右侧车道所发生的换道行为(其中快速路中的驶出车辆迫切想要换道至快速路最右侧车道,而辅路中的驶出车辆则迫切想要换道至辅路最左侧车道). 此时,只要目标车道前方存在行驶空间,主辅路驶出车辆将产生强制换道意图,具体为
式中:
在车辆产生强制换道意图后,须判断目标车道上的空间条件是否满足强制换道安全条件来做出换道决策. 此时车辆发生强制换道所需满足的安全条件为
式中:
2.3.3. 驶出换道规则
驶出换道规则主要用于描述长距离交织区中的驶出车辆从交织区驶向目标车道所发生的换道行为. 只要目标车道前方存在行驶空间,长距离交织区中的驶出车辆就会产生驶出换道意图,具体为
当车辆产生驶出换道意图后,须判断目标车道上的空间条件是否满足驶出换道安全条件来做出换道决策. 此时车辆发生驶出换道所需满足的安全条件为
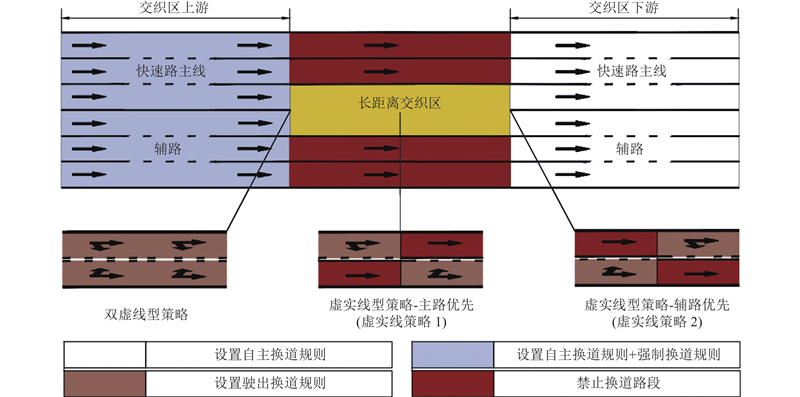
根据前文所建分区内各自的换道行为特性应用相应的换道规则,如图5所示. 长距离交织区上游段中的驶出车辆为了能够成功从交织区驶出,须换道至最左/右侧车道,此类换道行为采用强制换道规则. 如果驶出车辆直至长距离交织区前端都无法换道至最左/右侧车道,车辆将停在交织区前端处等待强制换道机会. 此外,长距离交织区上游中的非驶出车辆会为了追求更快的车速而发生换道,此类换道行为采用自主换道规则. 长距离交织区内的换道行为受管理策略的影响,应分策略设定. 其中,在双虚线型策略下,主辅路中的驶出车辆在保证安全的前提下可以自由驶出换道至目标车道,从而全段应用驶出换道规则,若直至长距离交织区末端都未能换道至目标车道,车辆将原地等待驶出换道机会. 在虚实线型策略下,只允许虚线侧的驶出车辆发生驶出换道至目标车道,因此只对虚线侧路段应用驶出换道规则,非虚线侧路段不允许发生换道. 由于长距离交织区下游段不存在驶出车辆,长距离交织区全段应用自主换道规则.
图 5
3. 仿真模拟与分析
3.1. 仿真参数定义与设置
选取长春市亚泰大街快速路上一处长距离交织区作为研究对象,如图6所示,该交织区由快速路三车道与辅路三车道组成,承载着长春市南北方向的主要交通流量. 设置每个元胞的大小为5 m,研究路段总长度L=200个元胞,即1 km. 将研究路段的车辆组成按照车辆类型分为小型车和大型车,大型车包括货车和公交车之类长度超过6 m的大型车辆. 由于长春市城市快速路禁止货车通行,假定快速路车流中不存在大型车辆,且辅路中大型车辆只存在自主换道需求,不存在驶出换道需求. 快速路的最大行驶速度以快速路设计为标准,即
图 6
表 1 仿真关键参数
Tab.1
| 参数 | 定义 | 数值 | 单位 | 参数 | 定义 | 数值 | 单位 | |
| 大型车辆所占元胞长度 | 3 | 时间步长 | 1 | |||||
| 小型车辆所占元胞长度 | 1 | 舒适加速度 | 1 | |||||
| 快速路驶出车辆比例 | 0.4 | — | 舒适减速度 | 1 | ||||
| 辅路驶出车辆比例 | 0.5 | — | 最小速度 | 略大于0 | ||||
| 快速路大型车辆比例 | 0 | — | 减速概率参数 | 0.1 | — | |||
| 辅路大型车辆比例 | 0.15 | — | 线性插值最大值 | 1 | — | |||
| 快速路最大行驶速度 | 5 | 线性插值最小值 | 0.8 | — | ||||
| 辅路最大行驶速度 | 3 | — | — | — | — |
定义驶出换道频率为
式中:
通过在元胞末端设置虚拟探头来分别采集快速路的平均流量 (
快速路、辅路的平均速度定义分别为
式中:
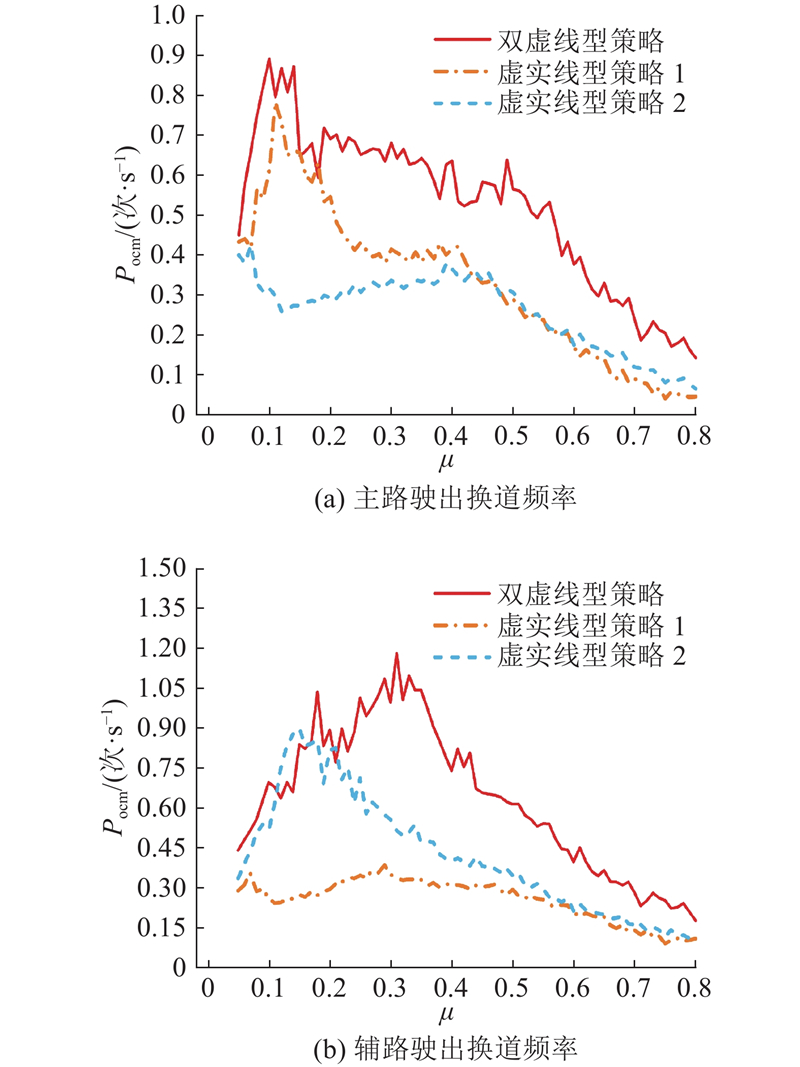
3.2. 驶出换道频率分析
主辅路驶出换道频率与元胞占有率
图 7
图 7 换道频率与占有率关系示意
Fig.7 Illustration of relationship between changeover frequency and occupancy rate
3.3. 平均流量分析
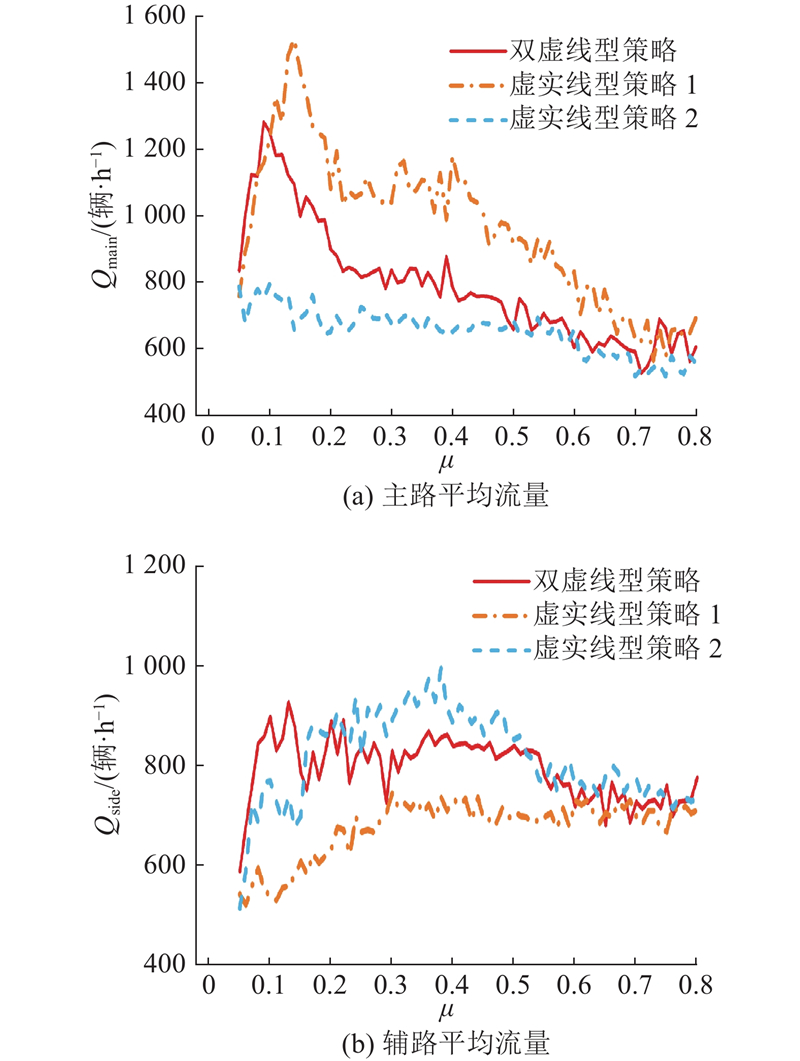
主辅路平均流量与元胞占有率的关系如图8所示. 总体趋势表明,随着元胞占有率的逐渐上升,平均流量呈现出先增加后下降,最终趋于稳定的趋势. 其中快速路平均流量相较于辅路的表现出更为显著的波动. 这表明主路车辆的通行受交织区瓶颈效应影响更大. 当元胞占有率达到0.3时,交织区的瓶颈效应凸显,此时,无论采用何种管理策略,主路流量均趋向于稳定的状态. 进一步观察可以发现,由于虚实线型策略1在一定程度上保证了主路驶出车辆的换道路权,从而导致虚实线型策略1下的主路平均流量峰值高于双虚线型策略下的.
图 8
图 8 平均流量与占有率关系示意
Fig.8 Illustration of relationship between average flow rate and occupancy rate
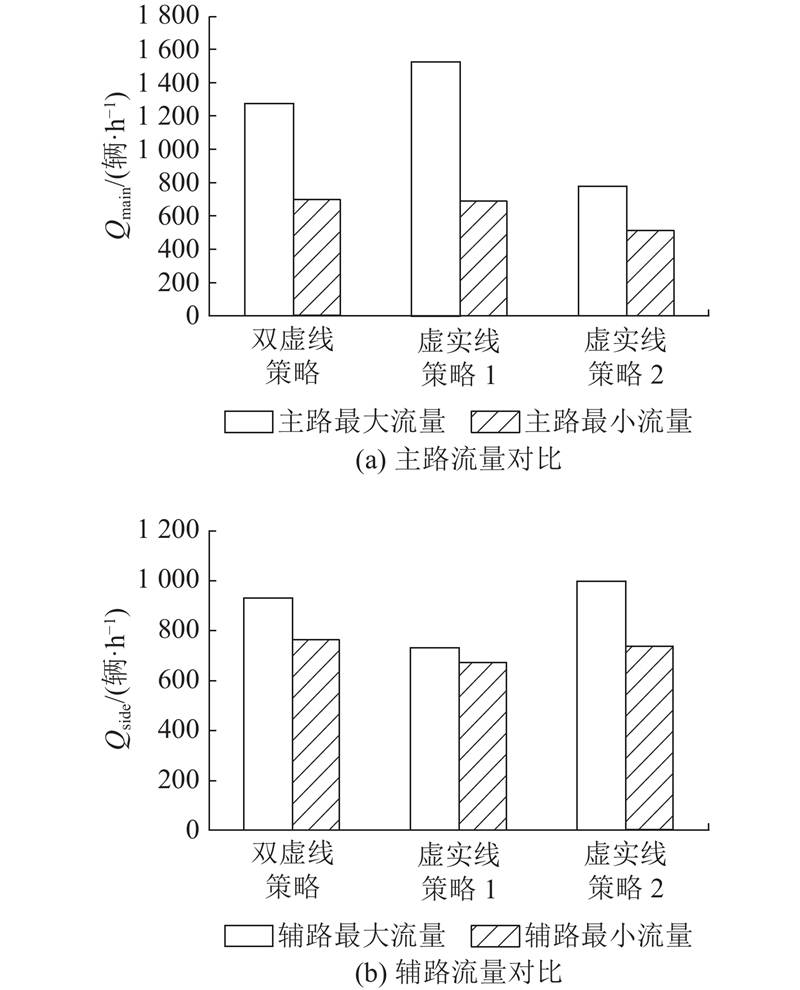
此外,不同管理策略下主辅路的最大流量(低占有率条件下各车道管理策略对应的流量最大值)和最小流量(高占有率条件下各车道管理策略对应的流量最小值)如图9所示. 其中双虚线型策略、虚实线型策略1以及虚实线型策略2对应的快速路最大流量与最小流量之间的相差百分比((最大流量−最小流量)/最大流量)分别为44.88%、55.74%和33.76%,而辅路最大流量与最小流量之间的相差百分比分别为18.02%、8.22%和26.13%. 上述结果表明,无论采用何种管理策略,主路最大流量与最小流量之间的相差百分比远大于辅路的,进一步证明长距离交织区中主路车辆较辅路车辆受管理策略影响更大.
图 9
图 9 不同管理策略下主辅路流量对比
Fig.9 Comparison of primary and secondary road flows under different lane allocation strategies
3.4. 平均速度分析
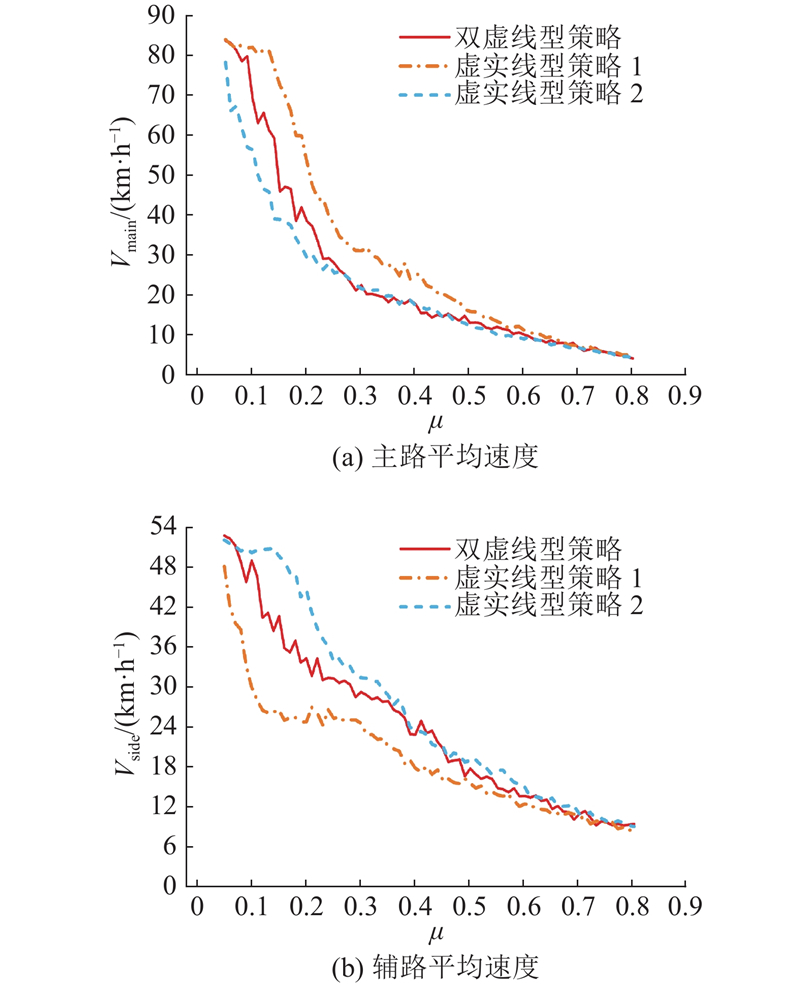
主辅路平均速度随元胞占有率的变化情况如图10所示. 由图10(a)可以发现,当元胞占有率低于0.2时,随着元胞占有率的逐渐上升,双虚线型策略下的主路平均车速变化幅度相对较小,维持在75 km/h以上,而虚实线型策略下的主路平均车速下降速度更快. 这是由于在低元胞占有率的条件下,车辆到达率较低,依靠双虚线型策略中驶出车辆的自由驶出换道能够维持长距离交织区一个相对畅通的状态. 此时虚实线型策略下换道机会的减少,将导致长距离交织区内出现减速甚至停车等待的驶出车辆,影响主路内侧车道平均速度,进而影响主路整体平均速度. 随着元胞占有率进一步增加至0.4,长距离交织区瓶颈效应逐渐显现,不同程度的拥堵现象开始在长距离交织区及交织区上游区域显现. 一方面,这直接导致3种策略下的主路平均速度迅速下降. 另一方面,强制换道车辆的干扰效应也逐渐显现. 随着停车等待车辆数目的增加,强制性换道车辆对主路外侧车道的干扰加剧,导致主路中拥堵时空范围进一步扩大. 在元胞占有率达到0.4后,长距离交织区上游陷入完全拥堵的状态,主路平均速度逐渐趋于稳定.
图 10
图 10 平均速度与占有率关系示意
Fig.10 Illustration of relationship between average speed and occupancy rate
辅路平均速度的变化趋势与主路的类似,如图10(b)所示. 当元胞占有率低于0.1时,此时不同管理策略下的辅路平均速度的差异并不太明显. 随着元胞占有率的进一步增加,受长距离交织区影响,不同管理策略下的辅路平均速度开始下降,辅路车流出现断续停滞的现象. 值得注意的是,在元胞占有率大于0.4后,长距离交织区瓶颈的影响开始凸显,3种管理策略下的辅路平均速度均呈现出相似的下降趋势,这一现象反映了三相交通流理论中所描述的交通崩塌现象.
3.5. 时空轨迹图分析
对比主辅路流量图可以观察到,不同管理策略在元胞占有率为0.4时差异较大. 为了比较分析各车道在不同管理策略下的时空轨迹图差异,选取元胞占有率为0.4时对其进行展开分析,不同管理策略下各车道时空轨迹图如表2所示. 表中,y为道路的空间位置. 对比分析辅路外侧车道(车道 5和车道 6)的时空轨迹图可以发现,在相同的元胞占有率下,不同管理策略下辅路外侧车道的时空状态呈现出明显的相似性. 这说明不同管理策略对辅路外侧车道的影响较小. 对比分析主路外侧车道(车道 1和车道 2)的时空轨迹图可以发现,尽管长距离交织区及其上游地区尚未出现大范围的拥堵,但长距离交织区所引发的道路通行能力下降已经对交织区下游产生了一定程度的影响,导致该区域频繁出现拥堵现象. 上述现象的出现主要由以下2个原因所导致:首先,由于快速路内侧车道(车道 3)中存在部分驶出车辆未能及时完成驶出换道,被迫在长距离交织区末端减速甚至停车等待驶出换道机会;其次,成功驶入快速路的辅路驶出车辆为了获得更好的行驶条件,陆续选择向快速路外侧车道(车道 2)进行换道,从而导致交织区下游频繁出现局部拥堵,并呈现向外侧车道扩散的趋势. 对比分析主辅路内侧车道(车道 3和车道 4)的时空轨迹图可以发现,虚实线型策略1下主路内侧车道(车道 3)的拥堵时空范围比双虚线型策略下的拥堵时空范围更小,而辅路内侧车道(车道 4)的拥堵情况仍优于双虚线型策略下的,稍劣于虚实线型策略2下的. 上述现象表明,主路内侧车道受车道分配策略影响较为显著. 尤其在高元胞占有率的情况下,虚实线型策略1较双虚线型策略表现出更为卓越的实施效果. 这说明在高占有率情况下,虚实线型换道策略有助于提高换道效率,进而提升整体道路通行能力. 虚实线型策略1在保证主路驶出车辆换道路权的同时,不可避免地牺牲了辅路的部分通行效率,但考虑到辅路的间断交通流特性,虚实线型策略1仍具备一定的实施价值.
表 2 不同管理策略下各车道时空轨迹图
Tab.2
| 车道 | 双虚线型策略 | 虚实线策略1 | 虚实线策略2 |
| 车道1 | 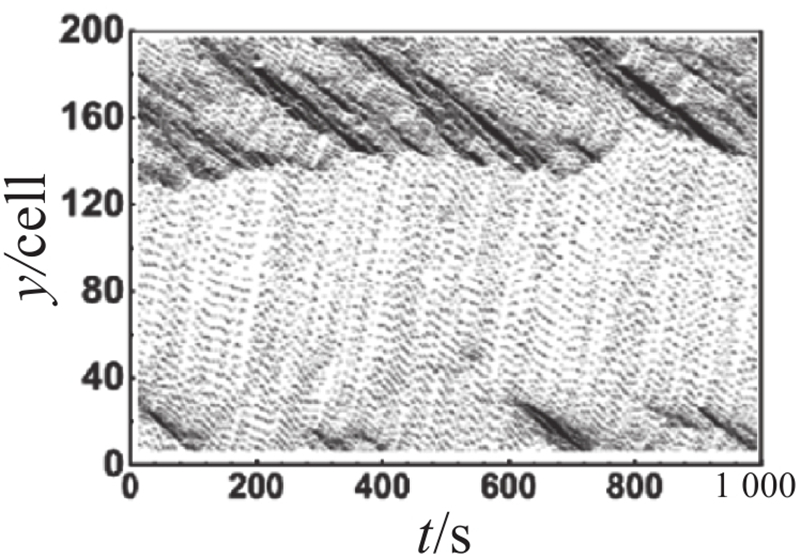 | 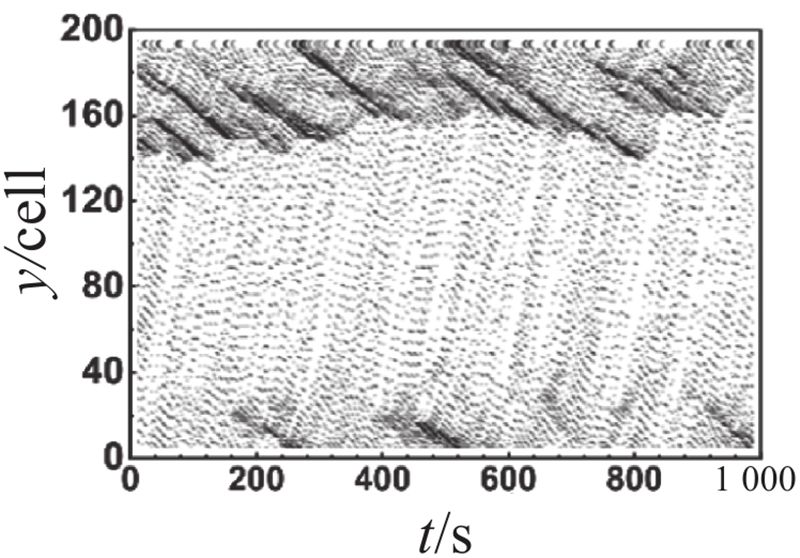 |  |
| 车道2 | 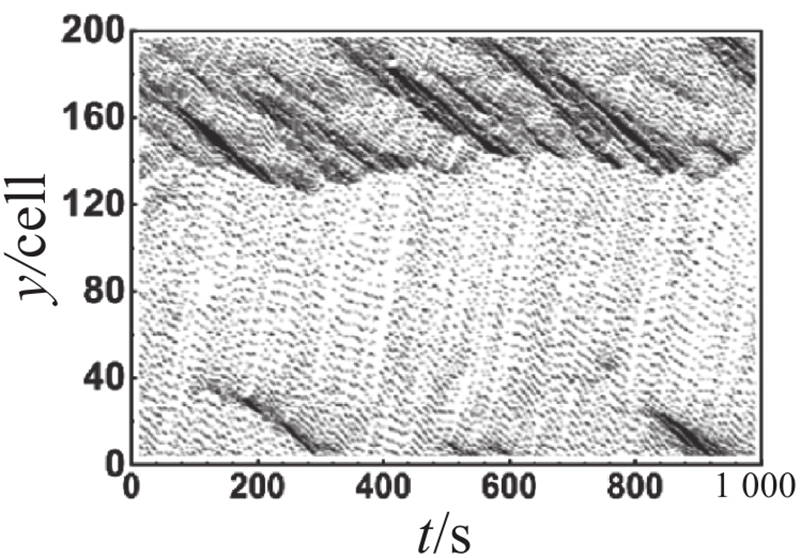 | 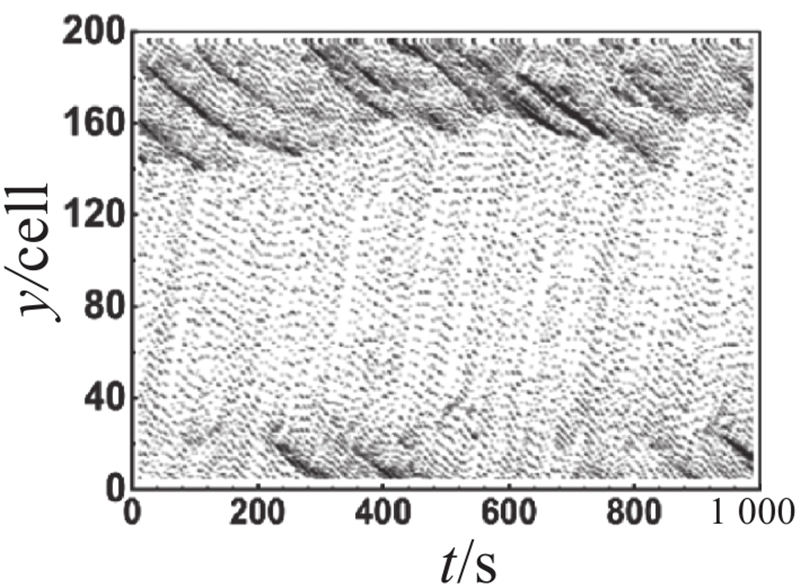 |  |
| 车道3 | 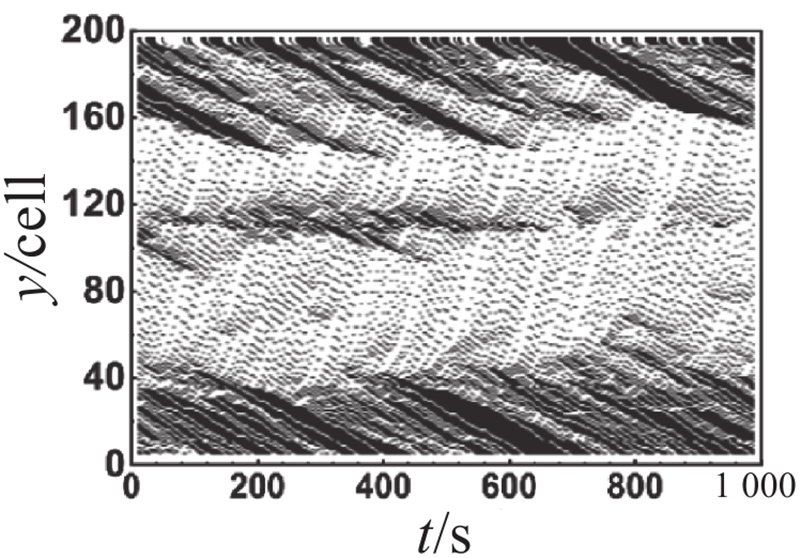 |  |  |
| 车道4 |  |  |  |
| 车道5 | 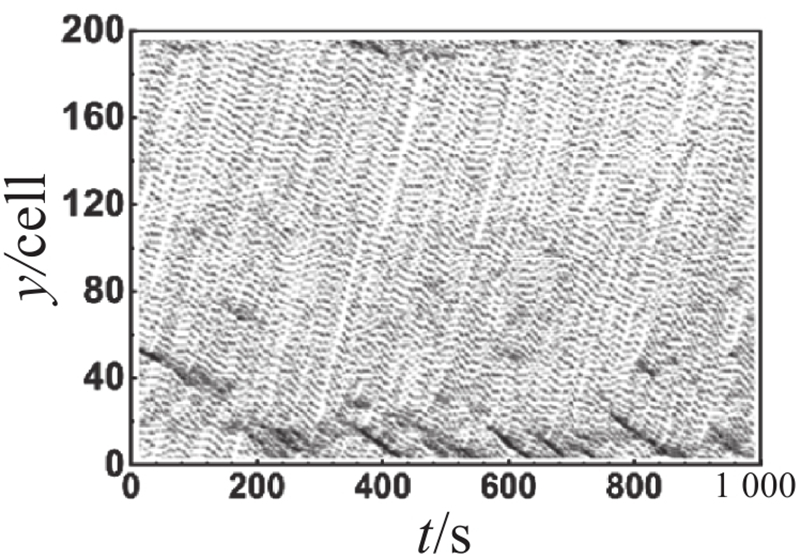 | 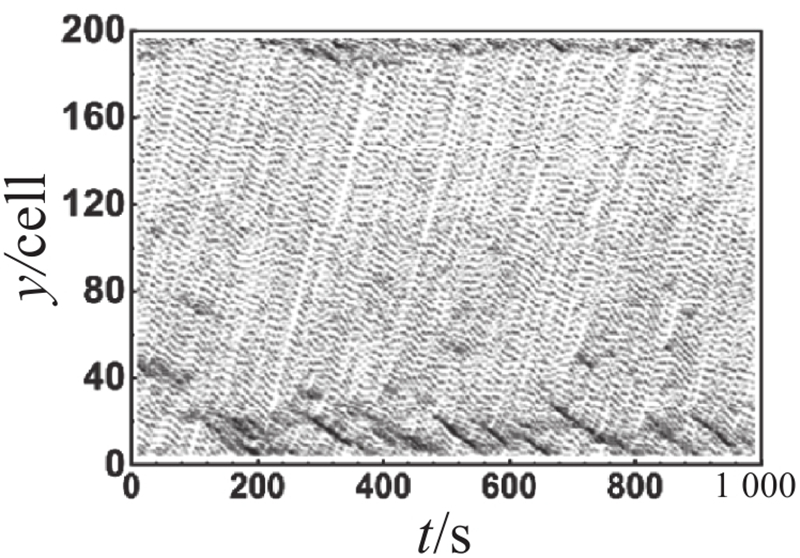 |  |
| 车道6 | 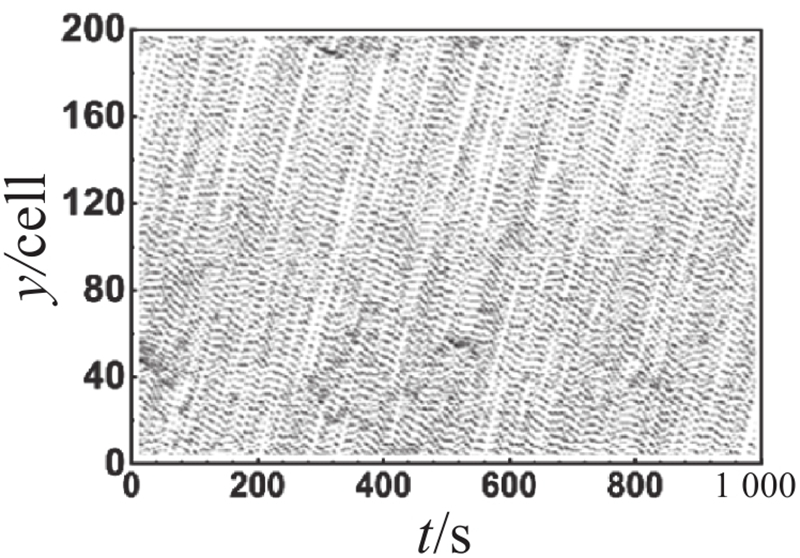 | 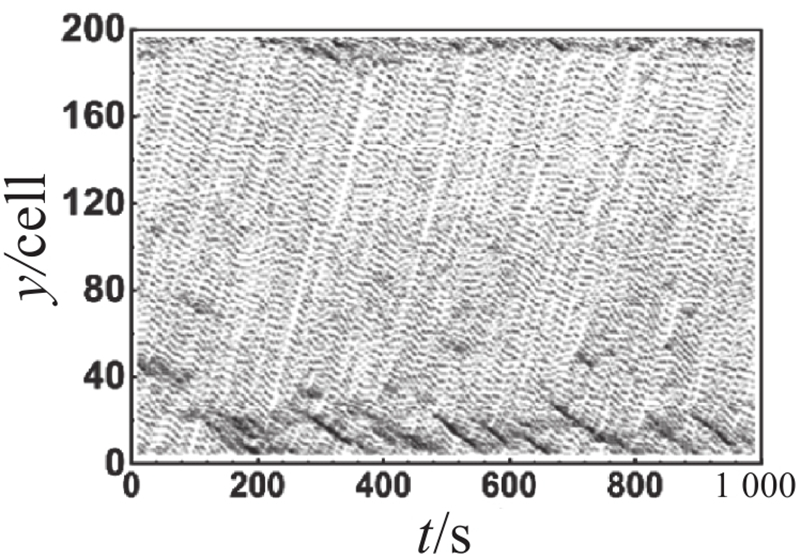 | 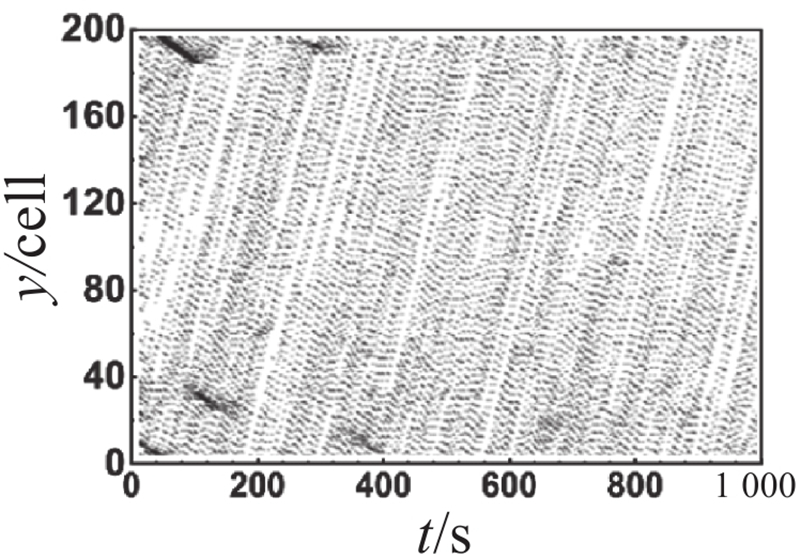 |
4. 结 论
基于快速路长距离交织区的交通组织特性,建立了不同管理策略下的多车道元胞模型,该模型相对准确地描述了不同元胞占有率下长距离交织区的交通流运行情况. 研究发现:
(1)长距离交织区内的驶出换道行为容易引发局部拥堵,影响主辅路驶出车辆的顺畅通行,进而导致平均流量和速度下降.
(2)在低占有率的情况下,可以观察到,不论是主路还是辅路,双虚线型策略下的驶出换道频率显著高于虚实线型策略下的. 这进一步验证了换道机会的多少在很大程度上决定了驶出换道频率的高低. 但是,随着占有率的逐渐增加,纯粹依赖增加换道机会来提高驶出换道频率的方法变得低效.
(3)不同管理策略对主路和辅路流量的影响较大,其中双虚线型策略、虚实线型策略1和虚实线型策略2对应的主路最大与最小流量间的相差百分比分别为44.88%、55.74%和33.76%,而辅路分别为18.02%、8.22%和26.13%. 这些数据表明,主路流量受管理策略的影响远大于辅路的,尤其在高占有率条件下,虚实线型策略的效果更为显著. 时空轨迹图的比较进一步揭示,虚实线型策略1有效减少了主路内侧车道的拥堵时空范围,尽管辅路内侧车道的拥堵情况略逊于虚实线型策略2下的,但仍优于双虚线型策略下的. 因此,虚实线型策略1确保了主路驶出车辆换道路权,虽对辅路通行效率有一定影响,但鉴于辅路的间断交通流特性,该策略仍具有实施价值.
本研究针对快速路长距离交织区的交通特性,构建了适用于不同管理策略的多车道元胞自动化模型. 模型中假定路网为静态,未考虑长距离交织区长度动态变化对流量的影响. 未来将致力于解决动态路网优化的挑战,旨在进一步改进和完善快速路长距离交织区的交通流优化策略.
参考文献
Modified KdV equation for jamming transition in the continuum models of traffic
[J].
Jamming transitions and the modified Korteweg-devries equation in a two-lane traffic flow
[J].
快速路汇入区瓶颈交通流早发性失效研究(第1部分): 建模仿真
[J].
Early-onset breakdown of bottleneck traffic at expressway merging area, part Ⅰ: modeling and simulation
[J].
快速路汇入区瓶颈交通流早发性失效研究(第2部分): 致因分析
[J].
Early-onset breakdown of bottleneck traffic at expressway merging area, part Ⅰ: causation analysis
[J].
基于换道时间分布的交通流随机微分方程
[J].
Stochastic differential equation of traffic flow model based on distribution of lane-changing duration
[J].
Dynamical model of traffic congestion and numeri cal simulation
[J].DOI:10.1103/PhysRevE.51.1035 [本文引用: 1]
On-ramp simulations and solitary waves of a car-following model
[J].DOI:10.1103/PhysRevE.64.035602 [本文引用: 1]
A cellular automaton model for freeway traffic
[J].DOI:10.1051/jp2:1992262 [本文引用: 1]
基于元胞自动机模型的高架路交织区交通流的研究
[J].DOI:10.3321/j.issn:1000-3290.2006.04.028 [本文引用: 1]
Study on the traffic flow of weaving section in elevated road system with cellular automaton model
[J].DOI:10.3321/j.issn:1000-3290.2006.04.028 [本文引用: 1]
城市干线短交织区元胞自动机多级换道决策模型
[J].
Multi-stage lane changing decision model of urban trunk road's short weaving area based on cellular automata
[J].
A macroscopic model for freeway weaving sections
[J].DOI:10.1111/mice.12119 [本文引用: 1]
基于换道概率分布的多车道交织区元胞自动机模型
[J].
Cellular automata model of multi-lane weaving area based on lane-changing probability distribution
[J].
基于元胞自动机的附加导流岛型出口仿真建模
[J].
Simulation modeling of additional channelization island type exit based on cellular automata
[J].
Cellular automaton model for traffic flow based on safe driving policies and human reactions
[J].DOI:10.1016/j.physa.2010.08.020 [本文引用: 2]