<img src="https://www.zjujournals.com/eng/images/1008-973X/images/logo.png" class="img-responsive">

图 1 双有源桥变换器的拓扑

Fig.1 Topology of dual-active-bridge converter

针对DAB在工作过程中前、后桥出现回流功率的问题，Wu等^[13]提出的CTPS控制消除了前、后桥的回流功率. 若不考虑死区，在理想情况下，CTPS控制下2种模式的理论波形如图2所示. 图中，T_hs为半个开关周期，D₁为前桥S₁与S₄半个周期内的移相比，D₂为后桥S₅与S₈半个周期内的移相比，D_φ为S₄与S₈半个周期内的移相比.

图 2

图 2 CTPS控制策略的工作波形

Fig.2 Operating waveform of CTPS control strategy

如表1所示为CTPS控制策略及功率传输模型. 表中，k为电压传输比，k = V₁/(nV₂)；p_av为标幺化后的平均传输功率，标幺化基准值为P_N=nV₁V₂/(8f_sL).

表 1 CTPS控制策略及功率传输模型

Tab.1 CTPS control strategy and power transfer model

模式	控制策略
D_φ = D₂模式	$ {D_1} = \dfrac{{{k^2}}}{{{k^2}+k+1}} - \dfrac{k}{{{k^2}+k+1}}\sqrt {1 - \dfrac{{{p_{{\text{av}}}}({k^2}+k+1)}}{{2k}}} $
	$ D_{0}=D_{2}=1+k\left(D_{1}-1\right) $
	$ D_{1} \in\left[\dfrac{k-1}{k}, \dfrac{k^{2}}{k^{2}+k+1}\right] $
	$ p_{{\mathrm{av}}}=\dfrac{2 k}{k^{2}+k+1}-2\left(k^{2}+k+1\right)\left(D_{1}-\dfrac{k^{2}}{k^{2}+k+1}\right)^{2} $
D_φ = 0模式	$ {D_1} = 1 - \sqrt {{p_{{\text{av}}}}/(2k - 2)} $
	$ D_{2}=1+k\left(D_{1}-1\right), D_{\varphi}=0 $
	$ D_{1} \in\left[\dfrac{k-1}{k}, 1\right] $
	$ p_{{\mathrm{av}}}=2(k-1)\left(1-D_{1}\right)^{2} $

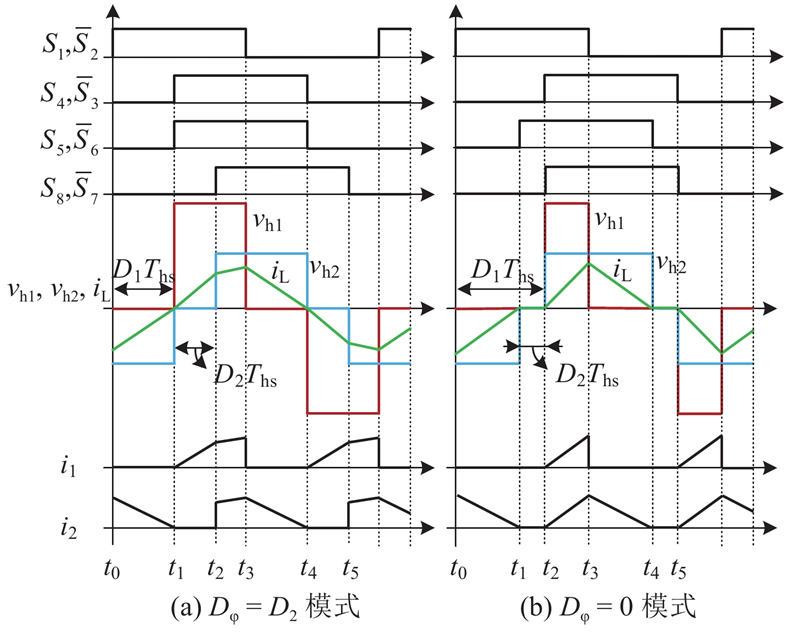
从图2可知，在CTPS控制下，DAB的v_h1、v_h2与i_L极性不会出现相反的情况，i₁、i₂始终不小于零，实现了前、后桥的无回流功率控制. 当CTPS控制处于2种模式的临界点时，D_φ = D₂ = 0，此时标幺化临界传输功率p_av,cri为

$ {p_{{\text{av,cri}}}} = \frac{{2(k - 1)}}{{{k^2}}}. $

(1)

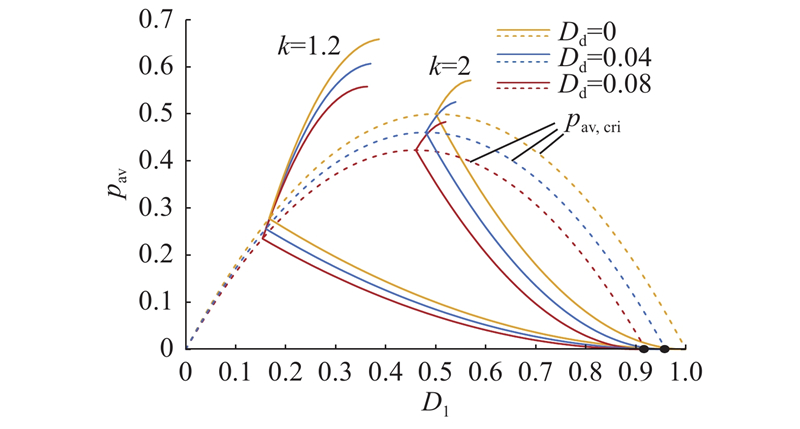
如图3所示为CTPS控制策略的移向比D₁与p_av之间的关系. 可知，随着D₁的变化，p_av在2种工作模式下非线性连续，且随着k的增大，p_av调节范围减小. 在D_φ = 0模式下，p_av会随着D₁的减小而增大，最大可增至2种工作模式的临界传输功率p_av,cri. 在D_φ=D₂模式下，p_av ≥ p_av,cri，p_av随着D₁的增大而增大. p_av,cri呈抛物线变化，标幺化峰值为0.5.

图 3

图 3 不同电压传输比下标幺后的平均传输功率与移相比的关系曲线

Fig.3 Average transmitted power versus shift ratio curve after scaling for different voltage transfer ratio

2. 桥臂死区对CTPS控制的影响

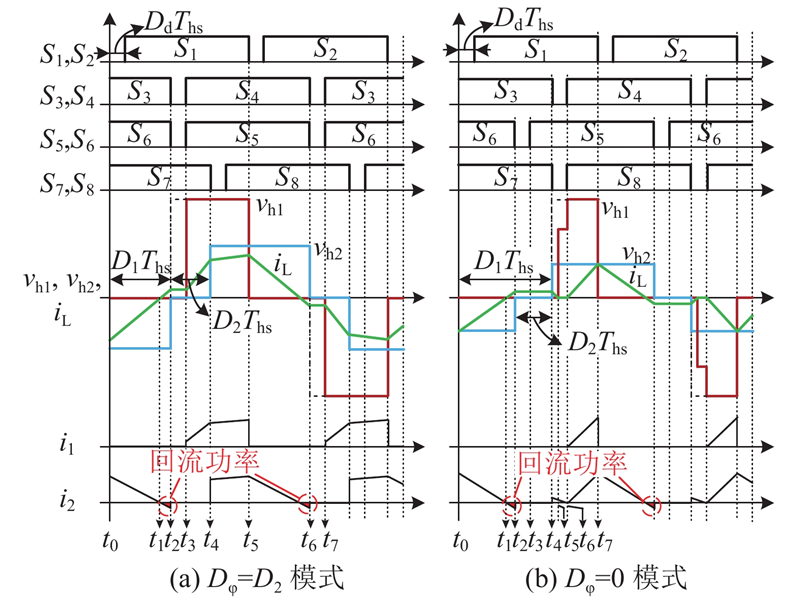
在加入桥臂死区后，各个开关管延迟导通，对CTPS控制的v_h1、v_h2及i_L波形产生影响，导致回流功率出现及部分软开关失效，降低变换器的功率传输效率及稳定性.

2.1. 死区对电压电流波形的影响

如图4所示为死区加入后CTPS控制的理论波形，虚线为理想波形，实线为实际波形. 由于死区的影响，2种模式下的v_h1脉宽与传输功率均减小，表1中的平均功率传输模型不再适用. 为了补偿缺失的功率，控制器须增大输出的控制量，但会引起i_L波形的畸变，产生回流功率；当漏感电压为零区间时，i_L波形发生偏置，开关器件的导通通态损耗增大. 分别分析2种模式下前半周期(0~T_hs)死区产生的电压电流波形畸变.

图 4

图 4 死区加入后CTPS控制的理论波形

Fig.4 Theoretical waveform of CTPS control after addition of dead band

1) D_φ = D₂模式.

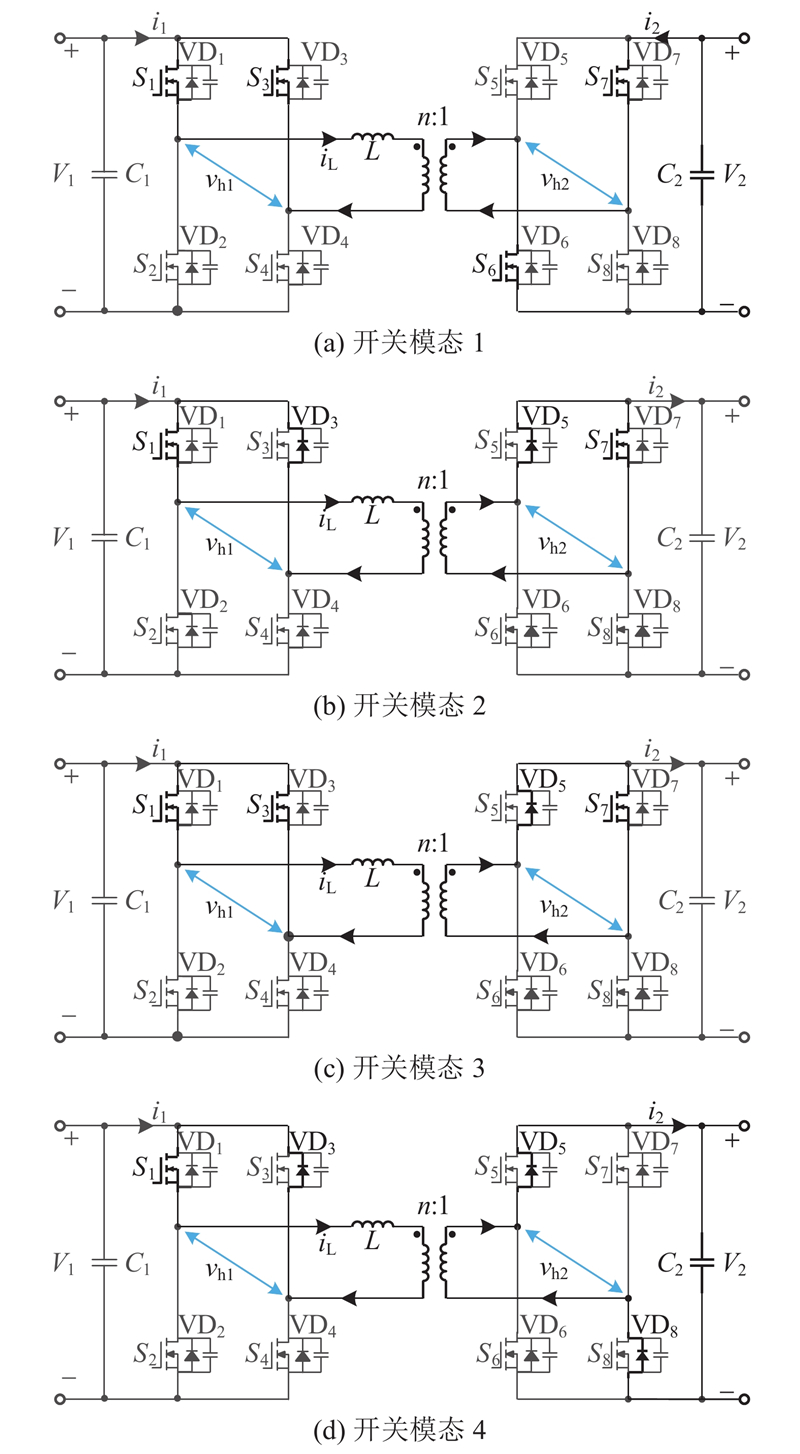
如图4(a)所示，在t₁~t₂时段内，由于输入电流平均值的增大，该时段内i_L≥0，前桥电流经S₁、S₃形成续流回路，后桥电流从电容C₂经S₇、S₆流回漏感. 在该时段，v_h2=−V₂，其极性与i_L相反，出现了回流功率，开关模态如图5(a)所示.

图 5

图 5 死区加入后CTPS控制的部分时段的开关模态

Fig.5 Switching mode of CTPS-controlled subperiod after dead band addition

在t₂~t₃时段，t₂时刻，S₃关断，而S₄未能导通，导致前桥电流经S₁、VD₃形成续流回路，v_h1为零，后桥电流经VD₅、S₇形成续流回路，漏感两端电压被钳位为零，i_L不发生变化. 开关模态如图5(b)所示.

其他时段死区未造成影响，这里不再赘述. i_L波形发生变化，改变了各个时段的电流表达式. 从图4(a)可知，各个时段的电流为

$ \begin{split} &{i_{\text{L}}}(t) = \\&\left\{ {\begin{array}{*{20}{l}} {\dfrac{{{V_1}}}{{4kL{f_{\text{s}}}}}( - 2{D_1}+k{D_{\text{d}}}) - \dfrac{{n{V_2}}}{L}t,}&{{t_0}\sim {t_2};} \\ {\dfrac{{{V_1}}}{{4L{f_{\text{s}}}}}{D_{{\mathrm{d}}} },}&{{t_2}\sim {t_3};} \\ {\dfrac{{{V_1}}}{{4L{f_{\text{s}}}}}{D_{\text{d}}}+\dfrac{{{V_1}}}{L}t,}&{{t_3}\sim {t_4};} \\ {\dfrac{{{V_1}}}{{4L{f_{\text{s}}}}}(2+2k{D_1} - 2k - {D_{\mathrm{d}}})+\dfrac{{{V_1} - n{V_2}}}{L}t,}&{{t_4}\sim {t_5}}. \end{array} } \right.\end{split} $

(2)

2) D_φ = 0模式.

如图4(b)所示，t₁~t₂时段的电路运行状态与D_φ=D₂模式下的t₁~t₂时段一致.

t₂~t₃时段，在t₂时刻，S₆关断，前桥的运行状态不变，后桥电流经VD₅、S₇形成续流回路，漏感两端电压被钳位为零，i_L不发生变化. 开关模态如图5(c)所示.

t₃~t₄时段，S₅导通，前桥电路状态不变，后桥变为经S₅、S₇形成续流回路.

t₄~t₅时段，t₄时刻，S₃、S₇关断，前桥电流经S₁、VD₃形成续流回路，后桥电流经VD₅、VD₈流向电容C₂，v_h2=V₂，漏感两端电压为−V₂. 开关模态如图5(d)所示.

其他时段死区未造成影响. 从图4(b)可知，各个时段的电流表达式为

$\begin{split} &{i_{\text{L}}}(t) = \\&\left\{ {\begin{array}{*{20}{l}} { - \dfrac{{{V_1}}}{{2kL{f_{\text{s}}}}}(k - 1)(1 - {D_1} - {D_{\text{d}}})+\dfrac{{n{V_2}}}{L}t,}&{{t_0}\sim {t_2};} \\ {\dfrac{{{V_1}}}{{4Lk{f_{\text{s}}}}}(k - 1){D_{\text{d}}},}&{{t_2}\sim {t_4};} \\ {\dfrac{{{V_1}}}{{4Lk{f_{\text{s}}}}}(k - 1){D_{\text{d}}} - \dfrac{{n{V_2}}}{L}t,}&{{t_4}\sim {t_5};} \\ 0,&{{t_5}\sim {t_6}.} \end{array} } \right.\end{split}$

(3)

2.2. 软开关分析

在DAB中，同一桥臂上的上下开关管的驱动信号互补，软开关条件相同，仅对前半周期的软开关状态进行分析.

在死区加入后，当DAB工作在D_φ=D₂模式时，t₀时刻，S₂关断，由于t₀~t₁时段内，i_L<0，S₂关断过程为硬关断，经过一个死区时间后S₁导通，但其体二极管已导通，S₁导通过程为ZVS导通. t₂时刻，S₃、S₆关断，此时i_L<0，S₃、S₆关断过程均为硬关断. t₃时刻，S₄、S₅导通，此时i_L>0，S₄导通过程为硬导通，而S₅在导通之前体二极管已导通，导通过程为ZVS导通. t₄时刻，S₇关断，i_L > 0，S₇关断过程为硬关断，经过一个死区时间后，S₈导通，其体二极管已被导通，导通过程为ZVS导通.

当工作在D_φ=0模式时，与D_φ = D₂模式类似，在t₀、t₂、t₄时刻，S₂、S₃、S₆、S₇硬关断. 当S₁开通时，i_L < 0，开通过程为ZVS开通. S₅在t₃时刻开通，i_L > 0，开通过程为ZVS开通. t₆时刻，S₄、S₈导通，i_L > 0，S₄导通过程为硬导通，S₈为ZVS导通.

从上述分析及文献[13]可知，死区加入前、后CTPS控制2种模式的软开关状态如表2所示.

表 2 死区加入前、后CTPS控制的软开关状态

Tab.2 Soft-switching state of CTPS control before and after addition of dead band

开关管	D_φ = D₂模式		D_φ = 0模式
开关管	无死区	死区加入后	无死区	死区加入后
S₁、S₂	ZVS开通硬关断	ZVS开通硬关断	ZVS开通硬关断	ZVS开通硬关断
S₃、S₄	ZCS开通 ZCS关断	硬开通硬关断	ZCS开通 ZCS关断	ZCS开通硬关断
S₅、S₆	ZCS开通 ZCS关断	ZVS开通硬关断	ZCS开通 ZCS关断	ZVS开通硬关断
S₇、S₈	ZVS开通硬关断	ZVS开通硬关断	ZCS开通 ZCS关断	ZCS开通硬关断

从表2可知，死区的加入，导致部分开关管的软开关丢失. 在D_φ=D₂模式下，前桥S₃、S₄的开通过程由ZCS开通变为硬开通，关断过程由ZCS关断变为硬关断，后桥S₅、S₆的关断过程由ZCS关断变为硬关断. 在D_φ=0模式下，除S₁、S₂外，所有开关器件的关断过程由ZCS关断变为硬关断.

3. CTPS控制的死区补偿方案

3.1. CTPS补偿原理及其实现

CTPS控制加入死区之后，导致了回流功率的发生、部分软开关失效等不良影响. 本文从无回流功率控制原理出发，对加入死区后的CTPS控制进行补偿.

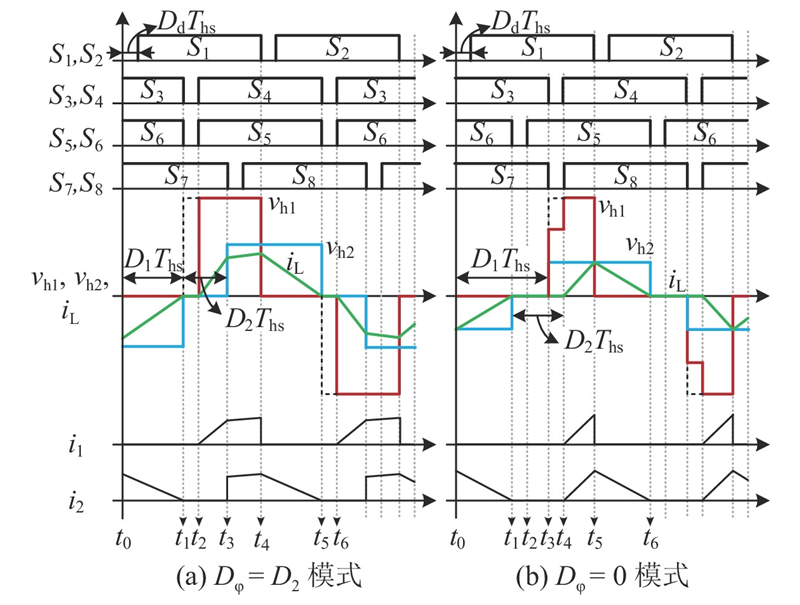
1) D_φ=D₂模式.

图4(a)中，在S₃、S₄死区时间内，v_h1缺失了脉宽，提出如图6(a)所示的补偿方案. 为了抑制v_h1、v_h2与i_L出现极性相反的情况，令t₁~t₂时段i_L=0，各时段的电流关系有

图 6

图 6 死区补偿后CTPS控制的理论波形

Fig.6 Theoretical waveform of CTPS control after compensation of dead band

$ \Delta {i_{{\text{L}}({t_2},{t_3})}}+\Delta {i_{{\text{L}}({t_3},{t_4})}} = \Delta {i_{{\text{L}}({t_4},{t_5})}}. $

(4)

式中：$ \Delta t_{\left(t_{n}, t_{n+1}\right)} (n=2,3,4) $为各时段电流的变化量，分别为

$ \left. {\begin{array}{*{20}{l}} {\Delta {i_{{\text{L}}({t_2},{t_3})}} = \dfrac{{{V_1}}}{L}({D_2} - {D_{\text{d}}})\dfrac{{{T_{\text{s}}}}}{2}}, \\ {\Delta {i_{{\text{L}}({t_3},{t_4})}} = \dfrac{{{V_1} - n{V_2}}}{L}(1 - {D_1} - {D_{\text{2}}})\dfrac{{{T_{\text{s}}}}}{2}}, \\ {\Delta {i_{{\text{L}}({t_4},{t_5})}} = \dfrac{{n{V_2}}}{L}{D_1}\dfrac{{{T_{\text{s}}}}}{2}} .\end{array} } \right\} $

(5)

将式(5)代入式(4)，可得移向比之间的耦合关系：

$ {D_2} = 1+k({D_1}+{D_{\text{d}}} - 1). $

(6)

根据图6可得标幺化平均传输功率为

$ \begin{split} {p_{{\text{av}}}} =& \frac{{{P_{{\text{av}}}}}}{{{P_{\text{N}}}}} = \frac{1}{{{P_{\text{N}}}}}\frac{2}{{{T_{\text{s}}}}}\int_0^{{{{T_{\text{s}}}} \mathord{\left/ {\vphantom {{{T_{\text{s}}}} 2}} \right. } 2}} {{V_1}{i_1}} (t){\mathrm{d}}t =\\ & \frac{{2k{{(1 - {D_{\mathrm{d}}})}^2}}}{{{k^2}+k+1}} - 2\left( {{k^2}+k+1} \right) {{{\left( {{D_1}+\frac{{{k^2}({D_{\mathrm{d}}} - 1)}}{{{k^2}+k+1}}} \right)}^2}} . \end{split}$

(7)

由此得到补偿后的D₁为

$ {{D_1} = \dfrac{{{k^2}(1 - {D_{\text{d}}})}}{{{k^2}+k+1}} - } {\sqrt {\dfrac{k}{{{k^2}+k+1}}\left( {\dfrac{{{{(1 - {D_{\text{d}}})}^2}}}{{{k^2}+k+1}} - \dfrac{{{p_{{\text{av}}}}}}{{2k}}} \right)} } . $

(8)

2) D_φ=0模式.

与D_φ=D₂模式同理，可以推出该模式下移向比的耦合关系为

$ {D_2} = 1+k({D_1}+{D_{\text{d}}} - 1) - {D_{\text{d}}}. $

(9)

标幺化平均传输功率为

$ {p_{{\mathrm{av}}}} = 2(k - 1){(1 - {D_1} - {D_{\text{d}}})^2}. $

(10)

移向比D₁的表达式为

$ {D_1} = 1 - \sqrt {\frac{{{p_{{\text{av}}}}}}{{2k - 2}}} - {D_{\text{d}}}. $

(11)

3) 模式切换条件的修正.

死区的加入改变了CTPS控制的平均传输功率和临界传输功率. 令式(6)中D₂=D_d，式(9)中D₂=0，求解可得2种模式的临界移向比：

$ {D_1} = \frac{{\left( {k - 1} \right)\left( {1 - {D_{\text{d}}}} \right)}}{k}. $

(12)

将式(12)代入式(7)、(10)，可得补偿后的标幺化临界点功率：

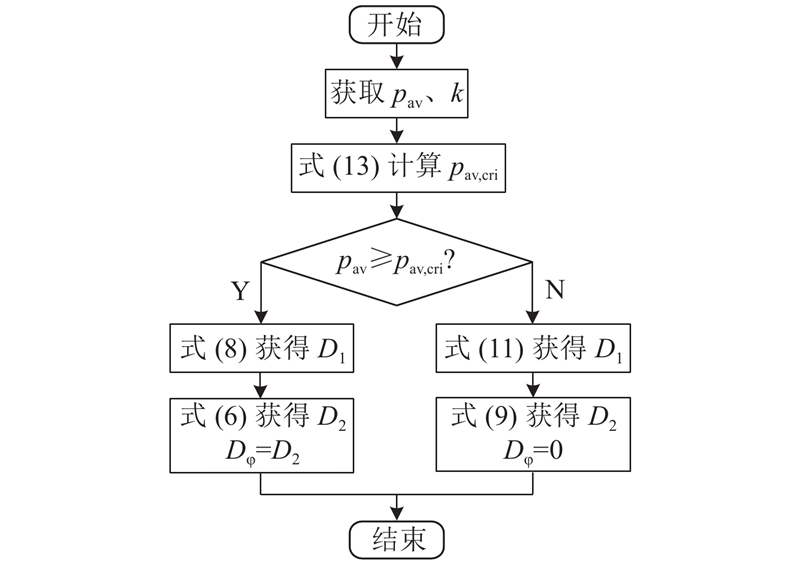
$ {p_{{\text{av,cri}}}} = \frac{{2\left( {k - 1} \right)}}{{{k^2}}}{\left( {1 - {D_{\text{d}}}} \right)^2}. $

(13)

4) CTPS控制补偿后的控制框图.

根据所提补偿算法得到DAB控制框图，如图7所示. p_av,cri由式(13)获得，通过比较p_av与p_av,cri来判断变换器的工作模式，从式(8)、(11)获取补偿后的D₁，进而获取不同模式下的D₂、D_φ来控制功率开关管S₁~S₈.

图 7

图 7 死区补偿后的CTPS控制策略

Fig.7 CTPS control strategy after compensation of dead band

3.2. 补偿算法的效果及影响分析

根据上述补偿策略得到补偿前、后的软开关状态，如表3所示. 可知，补偿后软开关性能恢复. 在D_φ = D₂模式下，S₃、S₄开通时i_L=0，其开通过程恢复为ZCS开通，后桥S₅、S₆关断时i_L=0，其关断过程恢复为ZCS关断. 在D_φ = 0模式下，t₁~t₄时段内，i_L = 0，除S₁、S₂之外，所有开关管由硬关断恢复为ZCS关断.

表 3 死区补偿前、后CTPS控制的软开关状态

Tab.3 Soft-switching state of CTPS control before and after compensation of dead band

开关管	D_φ = D₂模式		D_φ = 0模式
开关管	补偿前	补偿后	补偿前	补偿后
S₁、S₂	ZVS开通硬关断	ZVS开通硬关断	ZVS开通硬关断	ZVS开通硬关断
S₃、S₄	硬开通硬关断	ZCS开通 ZCS关断	ZCS开通硬关断	ZCS开通 ZCS关断
S₅、S₆	ZVS开通硬关断	ZCS开通 ZCS关断	ZVS开通硬关断	ZCS开通 ZCS关断
S₇、S₈	ZVS开通硬关断	ZVS开通硬关断	ZCS开通硬关断	ZCS开通 ZCS关断

如图8所示为死区补偿后不同死区时间下p_av与D₁的关系曲线. 图中，p_av,cri曲线上方为D_φ=D₂模式，下方为D_φ=0模式，p_av随着D₁的变化而连续变化. 随着死区时间的增加，p_av,cri的峰值与p_av的调节范围均减小. 在D_φ=0模式下，从式(10)可知，当变换器功率从零增加时，D₁不再从1开始减小，而是存在大小为D_d的延迟，如图8中的A、B两点.

图 8

图 8 不同死区时间下平均传输功率与移相比的关系曲线

Fig.8 Curve of average transmitted power versus shift ratio for different dead time

电流应力可以表示为

$ {I_{{\mathrm{L}}\max }} = \max\; \{ \left| {{i_{\text{L}}}(t)} \right|\} . $

(14)

从式(2)、(3)可知，死区补偿前的电流应力为

$ {i_{{\text{L}}\max }} = \dfrac{{{I_{{\text{L}}\max }}}}{{{I_{\text{N}}}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{2}{k}(2{D_1} - k{D_{\text{d}}})},&{{D_{{\text{φ}}} } = {D_2}} ;\\ {\dfrac{4}{k}(k - 1)(1 - {D_1} - {D_{\mathrm{d}}})},&{{D_{{\text{φ}}} } = 0} .\end{array} } \right. $

(15)

式中：I_N=U₁/(8f_sL_s)为漏感电流标幺化的基准值.

从图6(a)可知，死区补偿后D_φ=D₂模式下I_Lmax=i_L(t₀)，i_L(t₁)=0. 结合式(5)，可得该模式下的电流应力为

$ {I_{{\text{L}}\max }} = {i_{\text{L}}}({t_0}) = \frac{{{V_1}}}{{4kL{f_{\mathrm{s}}}}}{D_1}. $

(16)

从图6(b)可知，死区补偿后D_φ=0模式下的电流应力为

$ {I_{{\text{L}}\max }} = {i_{\text{L}}}({t_0}) = \frac{{{V_1}}}{{2kL{f_{\mathrm{s}}}}}(k - 1)(1 - {D_1} - {D_{\mathrm{d}}}). $

(17)

对式(16)、(17)标幺化，可得

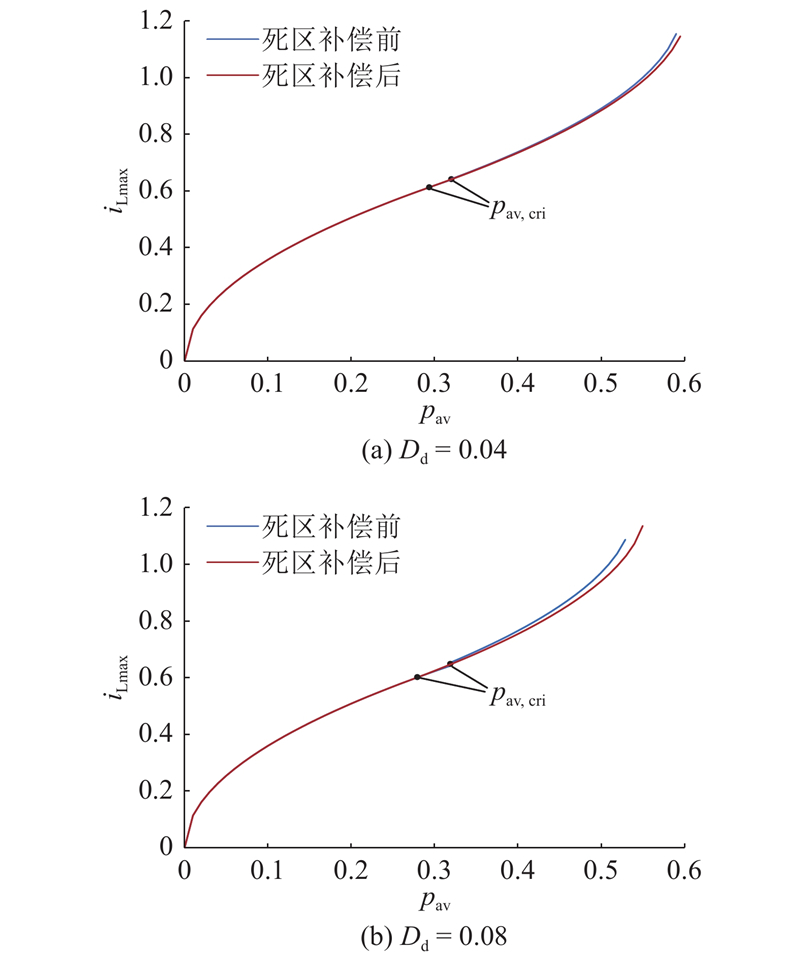
$ {i_{{\text{L}}\max }} = \dfrac{{{I_{{\text{L}}\max }}}}{{{I_{\text{N}}}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{4{D_1}}}{k}},&{{D_{{\text{φ}}} } = {D_2}} ;\\ {\dfrac{4}{k}(k - 1)(1 - {D_1} - {D_{\mathrm{d}}})},&{{D_{{\text{φ}}} } = 0} .\end{array} } \right. $

(18)

从式(15)、(18)可得死区补偿前、后不同死区的电流应力i_Lmax与p_av的关系，如图9所示.

图 9

图 9 死区补偿前、后电流应力与平均传输功率的关系曲线

Fig.9 Curve of current stress versus average transmitted power before and after dead band compensation

从图9可知，在死区补偿前、后，D_φ=0模式下的电流应力不变. 在D_φ=D₂模式下，补偿后的电流应力减小，电流应力的变化量随死区、功率的增加而增加，可见死区补偿方案对CTPS控制的电流应力有一定的优化.

4. 实验验证

为了验证所提控制方法的有效性，搭建如图10所示的双有源桥实验平台，主要参数如表4所示. 该平台由双有源桥、可调功率负载、直流电源及其他辅助设备组成，开关管选用IXYS公司IXTQ52N30P型号的Si-MOSFET，驱动电路采用驱动变压器来控制开关管的开通与关断，输入输出电容由2个1 000 µF电解电容和1个2.2 µF法拉电容并联组成. 双有源桥采用以TI公司的TMS320F28335为主控芯片的控制板进行控制.

图 10

图 10 DAB变换器的实验平台

Fig.10 Experimental platform for DAB converter

表 4 DAB实验平台的主要参数

Tab.4 Main parameter of DAB experimental platform

参数	数值	参数	数值
V₁/V	150	V₂/V	60
n	2∶1	f_s/ kHz	40
L/µH	50	死区时间/µs	1

在实验过程中，固定电压传输比k = V₁/(nV₂) = 1.25，通过改变负载侧电阻，模拟CTPS控制的不同模式. 补偿前标幺化临界传输功率p_av,cri = 0.32，补偿后p_av,cri = 0.270 8. 选取工况1(R=8 Ω，p_av=0.4)、工况2(R=20 Ω，p_av=0.16)，分别验证CTPS控制下D_φ=D₂模式与D_φ=0模式死区造成的影响及所提的补偿方案. P₁、P₂分别为v_h1与i_L、v_h2与i_L的乘积，当P₁或P₂小于零时，出现回流功率.

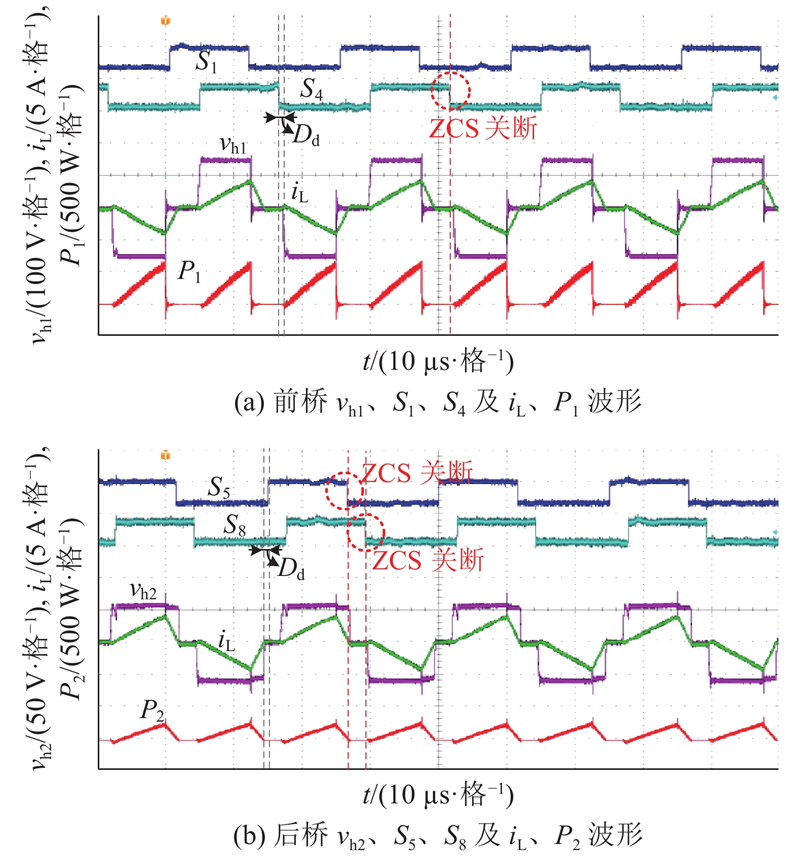
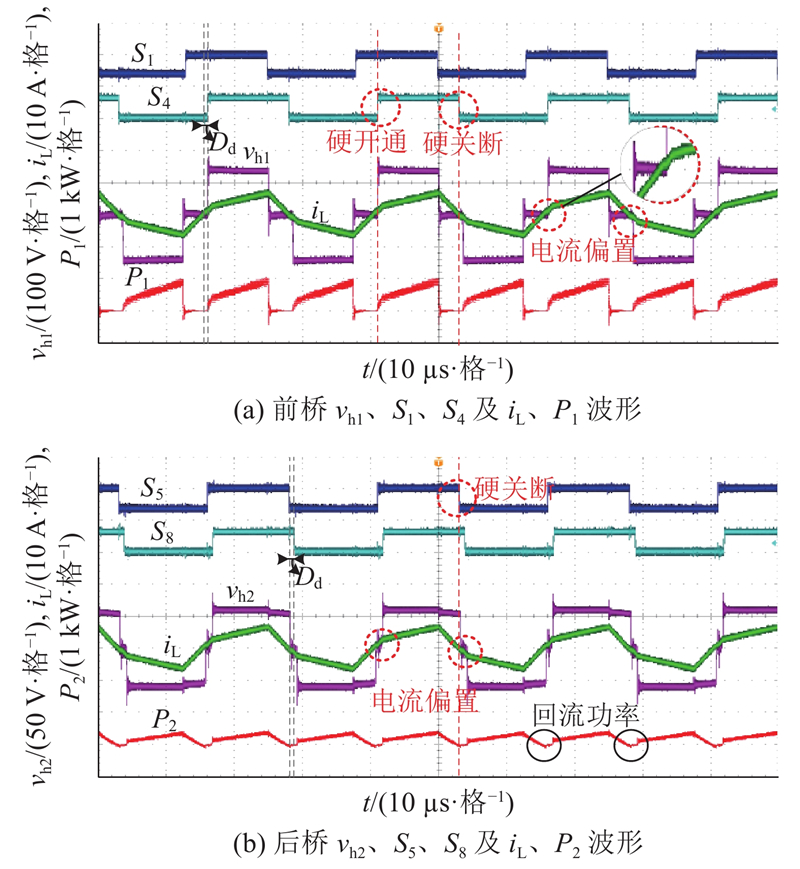
调节DAB的传输功率为450 W，此时变换器工作在工况1，原控制策略的实验波形如图11所示，所提死区补偿策略的实验波形如图12所示. 通过对比可知，在原控制策略加入1 µs死区后，开关管的导通时间变为11.5 µs，DAB后桥出现回流功率，如图11(b)中P₂小于零的部分. 在S₄所在桥臂的死区时间内，漏感电压为零，i_L出现电流偏置，S₄所在桥臂的开关管硬开通、硬关断，S₅所在桥臂的开关管硬关断. 在死区补偿后，前、后桥均不出现回流功率，S₄开通和关断时i_L均为零，i_L偏置现象消失，S₅与S₄开关状态同步，S₄、S₅所在桥臂的开关管恢复软开关性能. 与原控制策略相比，补偿后传输效率提高了0.26%. 实验结果证明了在D_φ=D₂模式下所提补偿方案的准确性.

图 11

图 11 1 µs死区，原控制策略D_φ = D₂模式下的实验波形

Fig.11 Experimental waveform of original control strategy D_φ = D₂ mode at 1 µs dead time

图 12

图 12 1 µs死区，死区补偿后D_φ = D₂模式下的实验波形

Fig.12 Experimental waveform of D_φ = D₂ mode after dead band compensation at 1 µs dead band

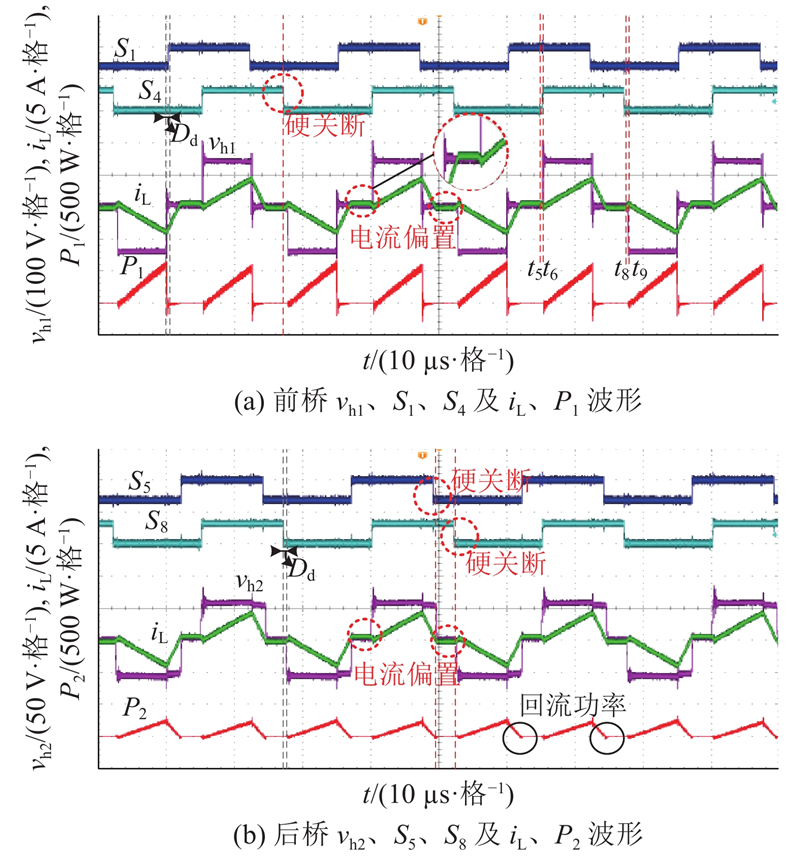
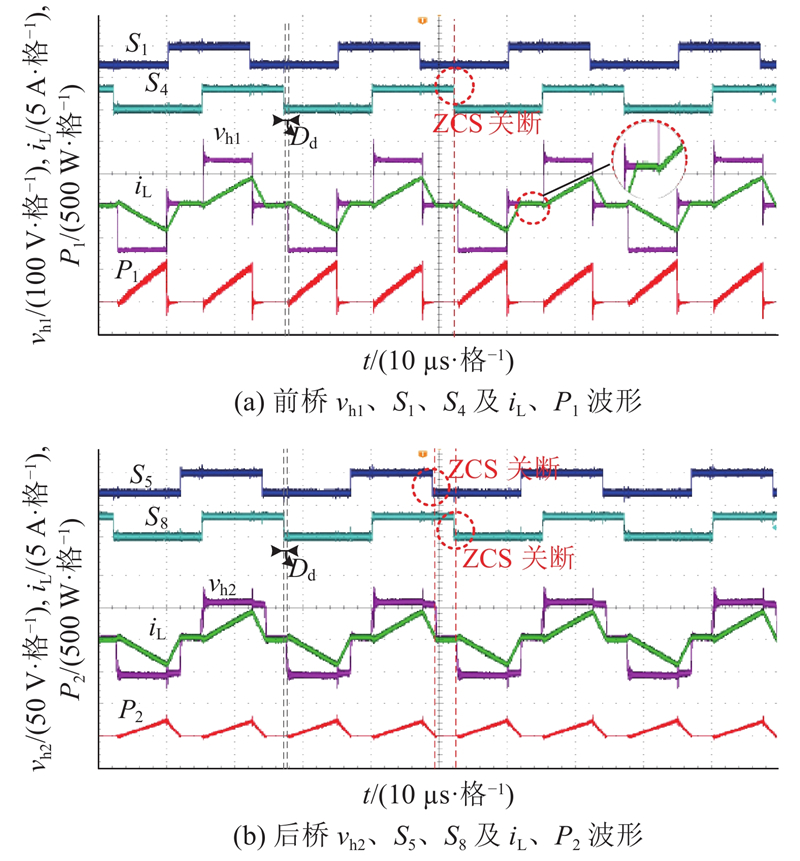
调节DAB的传输功率为180 W，此时变换器工作在工况2，原控制策略实验波形如图13所示，所提死区补偿策略的实验波形如图14所示. 对比可见，在原控制策略加入1 µs死区后，前桥回流功率基本为零，但i_L在漏感电压为零的区间内出现偏置，如图13所示. 由于该模式有较长的漏感电压为零的区间，变换器的通态损耗较大，所有开关管关断过程为硬关断，后桥出现回流功率，如图13(b)所示. 图13(a)中，在t₅~t₆、t₈~t₉时段内，v_h1=nv_h2，由于实验电路并非理想电路，存在杂散参数的影响，t₅~t₆时段内，v_h1未表现出v_h1=nv_h2的情况. 在死区补偿后，后桥回流功率被抑制，i_L在漏感电压为零区间时基本为零，软开关性能恢复，且与原算法相比，效率提升了0.54%，实验结果与理论分析基本一致.

图 13

图 13 1 µs死区，原控制策略D_φ = 0模式下的实验波形

Fig.13 Experimental waveform of original control strategy D_φ = 0 mode at 1 µs dead time

图 14

图 14 1 µs死区，死区补偿后D_φ = 0模式下的实验波形

Fig.14 Experimental waveform of D_φ = 0 mode after dead band compensation at 1 µs dead band

当桥臂死区为0.5 µs时，死区补偿策略有效. 工况1的实验波形如图15、16所示，工况2的实验波形如图17、18所示，死区补偿后p_av,cri = 0.294 9. 与1 µs死区时间相比，0.5 µs死区时间补偿前、后的i_L波形变化较小，死区越大，原控制策略造成的电流偏置现象越明显，回流功率越大.

图 15

图 15 0.5 µs死区，原控制策略D_φ = D₂模式下的实验波形

Fig.15 Experimental waveform of original control strategy D_φ = D₂ mode at 0.5 µs dead time

图 16

图 16 0.5 µs死区，死区补偿后D_φ = D₂模式下的实验波形

Fig.16 Experimental waveform of D_φ = D₂ mode after dead band compensation at 0.5 µs dead band

图 17

图 17 0.5 µs死区，原控制策略D_φ = 0模式下的实验波形

Fig.17 Experimental waveform of original control strategy D_φ = 0 mode at 0.5 µs dead time

图 18

图 18 0.5 µs死区，死区补偿后D_φ = 0模式下的实验波形

Fig.18 Experimental waveform of D_φ = 0 mode after dead band compensation at 0.5 µs dead band

综上所述，利用所提的死区补偿策略，可以有效地抑制由死区带来的回流功率，减小通态损耗，提升软开关性能.

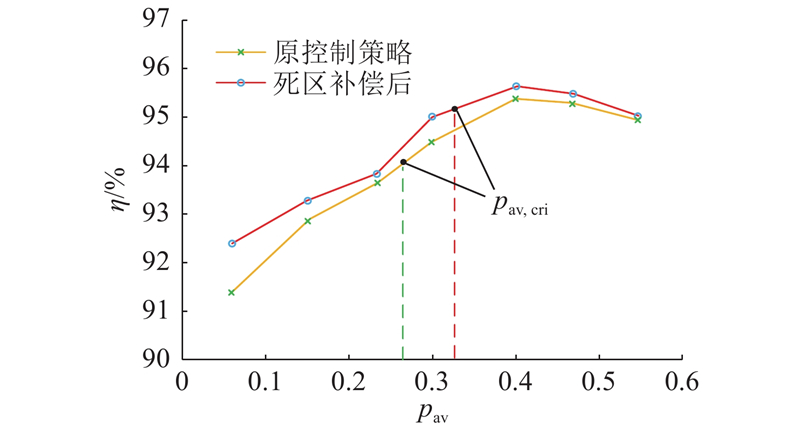
对加入1 µs死区的CTPS控制进行死区补偿后，标幺化功率调节范围减小到0~0.555. 对变换器分别采用死区补偿前、后的控制策略进行实验，通过测定补偿前、后的功率传输效率，得到死区补偿前、后的功率传输效率对比，如图19所示. 可见，当标幺化输出功率为0~0.270 8时，变换器工作在D_φ=0模式，该模式具有较长的漏感电压为零的区间，通态损耗占比较大，回流功率的占比较大，所提补偿方案的效率提升较明显，最高提升0.91%. 在标幺化输出功率为0.270 8~0.32的情况下，在原控制策略下变换器仍工作在D_φ=0模式，补偿后工作在D_φ=D₂模式，通态损耗减小，效率最高提升0.19%~0.51%. 在标幺化输出功率为0.32~0.555的情况下，变换器工作在D_φ=D₂模式，回流功率、通态损耗的占比均减小，效率提升了0.1%~0.46%.

图 19

图 19 死区补偿前、后的功率传输效率对比

Fig.19 Comparison of power transfer efficiency before and after dead band compensation

5. 结　论

（1）在加入死区后，CTPS控制产生了回流功率，i_L出现偏置电流，且CTPS控制的2种模式均会出现部分软开关失效的情况.

（2）利用所提的补偿方案，能够有效地抑制CTPS控制下死区导致的回流功率，恢复软开关状态.

（3）D_φ=D₂模式下出现了漏感电压为零的区间，D_φ= 0模式下漏感电压为零的区间增大，导致变换器的功率可调范围较补偿前有所下降.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

赵彪, 安峰, 宋强, 等

双有源桥式直流变压器发展与应用

[J]. 中国电机工程学报, 2021, 41 (1): 288- 298

ZHAO Biao, AN Feng, SONG Qiang, et al

Development and application of DC transformer based on dual-active-bridge

[J]. Proceedings of the CSEE, 2021, 41 (1): 288- 298

DOI:10.1016/j.rineng.2022.100437 [本文引用: 1]

[2]

刘健, 魏昊焜, 张志华, 等

未来配电网的主要形态: 基于储能的低压直流微电网

[J]. 电力系统保护与控制, 2018, 46 (18): 11- 16

DOI:10.7667/PSPC201852 [本文引用: 1]

LIU Jian, WEI Haokun, ZHANG Zhihua, et al

Future architecture of power distribution network: low-voltage direct current micro-grids based on energy storage

[J]. Power System Protection and Control, 2018, 46 (18): 11- 16

DOI:10.7667/PSPC201852 [本文引用: 1]

[3]

LÓPEZ-RODRÍGUEZ K, GIL-GONZÁLEZ W, ESCOBAR-MEJÍA A

Design and implementation of a PI-PBC to manage bidirectional power flow in the DAB of an SST

[J]. Results in Engineering, 2022, 14: 100437

[4]

王荣闯, 王杉杉, 高明, 等

基于LCL谐振型双有源桥的三端口DC-DC变换器及其解耦控制

[J]. 浙江大学学报: 工学版, 2021, 55 (8): 1585- 1593

WANG Rongchuang, WANG Shanshan, GAO Ming, et al

Three-port DC-DC converter based on LCL resonant dual active bridge and its decoupling control

[J]. Journal of Zhejiang University: Engineering Science, 2021, 55 (8): 1585- 1593

[5]

朱介北, 李峰, 俞露杰, 等

基于固态变压器的互联交直流微电网功率互济自主控制

[J]. 电网技术, 2023, 47 (1): 284- 295

ZHU Jiebei, LI Feng, YU Lujie, et al

Autonomous power mutual support control for AC/DC microgrid interconnected by solid state transformer

[J]. Power System Technology, 2023, 47 (1): 284- 295

DOI:10.3969/j.issn.1000-6753.2014.03.031 [本文引用: 1]

[6]

AKAGI H, KITADA R

Control and design of a modular multilevel cascade BTB system using bidirectional isolated DC/DC converters

[J]. IEEE Transactions on Power Electronics, 2011, 26 (9): 2457- 2464

DOI:10.1109/TPEL.2011.2107752 [本文引用: 1]

[7]

SHI J, GOU W, YAUN H, et al

Research on voltage and power balance control for cascaded modular solid-state transformer

[J]. IEEE Transactions on Power Electronics, 2011, 26 (4): 1154- 1166

DOI:10.1109/TPEL.2011.2106803 [本文引用: 1]

[8]

SHI H, WEN H, CHEN J, et al

Minimum-backflow-power scheme of DAB-based solid-state transformer with extended-phase-shift control

[J]. IEEE Transactions on Industry Applications, 2018, 54 (4): 3483- 3496

DOI:10.1109/TIA.2018.2819120 [本文引用: 1]

[9]

程红, 高巧梅, 朱锦标, 等

基于双重移相控制的双向全桥DC-DC变换器动态建模与最小回流功率控制

[J]. 电工技术学报, 2014, 29 (3): 245- 253

CHENG Hong, GAO Qiaomei, ZHU Jinbiao, et al

Dynamic modeling and minimum backflow power controlling of the bi-directional full-bridge DC-DC converters based on dual-phase-shifting control

[J]. Transactions of China Electrotechnical Society, 2014, 29 (3): 245- 253

DOI:10.3969/j.issn.1000-6753.2014.03.031 [本文引用: 1]

[10]

BAI H, MI C

Eliminate reactive power and increase system efficiency of isolated bidirectional dual-active-bridge DC-DC converters using novel dual-phase-shift control

[J]. IEEE Transactions on Power Electronics, 2008, 23 (6): 2905- 2914

DOI:10.1109/TPEL.2008.2005103 [本文引用: 1]

[11]

胡燕, 张天晖, 杨立新, 等

双重移相DAB变换器回流功率优化与电流应力优化的对比研究

[J]. 中国电机工程学报, 2020, 40 (Suppl.1): 243- 253

HU Yan, ZHANG Tianhui, YANG Lixin, et al

comparative study of reactive power optimization and current Stress optimization of DAB converter with dual phase shift control

[J]. Proceedings of the CSEE, 2020, 40 (Suppl.1): 243- 253

[12]

侯聂, 宋文胜, 王顺亮

全桥隔离DC/DC变换器相移控制归一化及其最小回流功率控制

[J]. 中国电机工程学报, 2016, 36 (2): 499- 506

HOU Nie, SONG Wensheng, WANG Shunliang

Normalization of phase shift control and minimum reflux power control of full-bridge isolated DC/DC converters

[J]. Proceedings of the CSEE, 2016, 36 (2): 499- 506

[13]

WU F, FENG F, GOOI H B

Cooperative triple-phase-shift control for isolated DAB DC–DC converter to improve current characteristics

[J]. IEEE Transactions on Industrial Electronics, 2019, 66 (9): 7022- 7031

DOI:10.1109/TIE.2018.2877115 [本文引用: 4]

[14]

TAKAGI K, FUJITA H. Dynamic control and dead-time compensation method of an isolated dual-active-bridge DC-DC converter [C]// Jointly Owned by EPE Association and IEEE PELS. Geneva: IEEE, 2015: 1-15.

[15]

BEHZADIRAFI S, LEÓN D F

Closed-form determination of the impedance locus plot of fault current limiters: asymmetrical faults

[J]. IEEE Transactions on Power Delivery, 2020, 35 (2): 754- 762

DOI:10.1109/TPWRD.2019.2925521 [本文引用: 1]

[16]

ZHAO B, SONG Q, LIU W, et al

Dead-time effect of the high-frequency isolated bidirectional full-bridge DC–DC converter: comprehensive theoretical analysis and experimental verification

[J]. IEEE Transactions on Power Electronics, 2014, 29 (4): 1667- 1680

DOI:10.1109/TPEL.2013.2271511 [本文引用: 2]

[17]

SONG C, CHEN A, CHEN J, et al. Dead-time effect analysis of dual active bridge DC-DC converter with dual-phase-shift control [C]// Chinese Automation Congress. Jinan: IEEE, 2017: 6545-6550.