[1]
MORENO L, GARRIDO S, BLANCO D, et al Differential evolution solution to the SLAM problem
[J]. Robotics and Autonomous Systems , 2009 , 57 (4 ): 441 - 450
DOI:10.1016/j.robot.2008.05.005
[本文引用: 1]
[2]
KHAN M U, ZAIDI S A A, ISHTIAQ A, et al. A comparative survey of lidar-slam and lidar based sensor technologies [C] // Mohammad Ali Jinnah University International Conference on Computing. Karachi: IEEE, 2021: 1-8.
[本文引用: 1]
[3]
HUANG L. Review on LiDAR-based SLAM techniques [C] // International Conference on Signal Processing and Machine Learning. Stanford: IEEE, 2021: 163-168.
[本文引用: 1]
[4]
赵洋, 刘国良, 田国会, 等 基于深度学习的视觉SLAM综述
[J]. 机器人 , 2017 , 39 (6 ): 889 - 896
[本文引用: 1]
ZHAO Yang, LIU Guoliang, TIAN Guohui, et al A survey of visual SLAM based on deep learning
[J]. Robot , 2017 , 39 (6 ): 889 - 896
[本文引用: 1]
[5]
蒋林, 刘林锐, 周安娜, 等 基于运动预测的改进ORB-SLAM算法
[J]. 浙江大学学报: 工学版 , 2023 , 57 (1 ): 170 - 177
[本文引用: 1]
JIANG Lin, LIU Linrui, ZHOU Anna, et al Improved ORB-SLAM algorithm based on motion prediction
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (1 ): 170 - 177
[本文引用: 1]
[6]
李帅鑫, 李广云, 王力, 等 LiDAR/IMU紧耦合的实时定位方法
[J]. 自动化学报 , 2021 , 47 (6 ): 1377 - 1389
[本文引用: 1]
LI Shuaixin, LI Guangyun, WANG Li, et al LiDAR/IMU tightly coupled real-time localization method
[J]. Acta Automatica Sinica , 2021 , 47 (6 ): 1377 - 1389
[本文引用: 1]
[7]
BESL P J, MCKAY N D A method for registration of 3-D shapes
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 1992 , 14 (2 ): 239 - 256
DOI:10.1109/34.121791
[本文引用: 1]
[9]
LOW K L Linear least-squares optimization for point-to-plane ICP surface registration
[J]. Chapel Hill, University of North Carolina , 2004 , 4 (10 ): 1 - 3
[本文引用: 1]
[10]
SEGAL A, HAEHNEL D, THRUN S. Generalized-ICP [C] // Robotics: Science and Systems. Seattle: MIT Press, 2009: 435.
[本文引用: 1]
[11]
ZHANG Ji, SINGH S. LOAM: lidar odometry and mapping in real-time [C] // Robotics: Science and Systems. Berkeley: RSS, 2014, 2(9): 1-9.
[本文引用: 1]
[12]
LIN Jiarong, ZHANG Fu. Loam livox: a fast, robust, high-precision LiDAR odometry and mapping package for LiDARs of small FoV [C] // IEEE International Conference on Robotics and Automation. Paris: IEEE, 2020: 3126-3131.
[本文引用: 1]
[13]
SHAN Tixiao, ENGLOT B. Lego-loam: lightweight and ground-optimized lidar odometry and mapping on variable terrain [C] // IEEE/RSJ International Conference on Intelligent Robots and Systems . Madrid: IEEE, 2018: 4758-4765.
[本文引用: 1]
[14]
WANG Han, WANG Chen, CHEN Chunlin, et al. F-loam: fast lidar odometry and mapping [C] // IEEE/RSJ International Conference on Intelligent Robots and Systems. Prague: IEEE, 2021: 4390-4396.
[本文引用: 1]
[15]
JIAO Jianhao, YE Haoyang, ZHU Yilong, et al Robust odometry and mapping for multi-lidar systems with online extrinsic calibration
[J]. IEEE Transactions on Robotics , 2021 , 38 (1 ): 351 - 371
[本文引用: 1]
[16]
YE Haoyang, CHEN Yuying, LIU Meng. Tightly coupled 3d lidar inertial odometry and mapping [C] // International Conference on Robotics and Automation. Montreal: IEEE, 2019: 3144-3150.
[本文引用: 1]
[17]
SHAN Tixiao, ENGLOT B, MEYERS D, et al. Lio-sam: tightly-coupled lidar inertial odometry via smoothing and mapping [C] // IEEE/RSJ International Conference on Intelligent Robots and Systems. Las Vegas: IEEE, 2020: 5135-5142.
[本文引用: 1]
[18]
QIN Chao, YE Haoyang, PRANATA C E, et al. Lins: a lidar-inertial state estimator for robust and efficient navigation [C] // IEEE International Conference on Robotics and Automation. Paris: IEEE, 2020: 8899-8906.
[本文引用: 1]
[19]
LV Jiajun, HU Kewei, XU Jinhang, et al. Clins: continuous-time trajectory estimation for LiDAR-inertial system [C] // IEEE/RSJ International Conference on Intelligent Robots and Systems. Prague: IEEE, 2021: 6657-6663.
[本文引用: 1]
[20]
XU Wei, ZHANG Fu Fast-LIO: a fast, robust lidar-inertial odometry package by tightly-coupled iterated Kalman filter
[J]. IEEE Robotics and Automation Letters , 2021 , 6 (2 ): 3317 - 3324
DOI:10.1109/LRA.2021.3064227
[本文引用: 1]
[21]
XU Wei, CAI Yixi, HE Dongjiao, et al Fast-lio2: fast direct lidar-inertial odometry
[J]. IEEE Transactions on Robotics , 2022 , 38 (4 ): 2053 - 2073
DOI:10.1109/TRO.2022.3141876
[本文引用: 1]
[22]
BAI Chunge, XIAO Tao, CHEN Yajie, et al Faster-LIO: lightweight tightly coupled LiDAR-inertial odometry using parallel sparse incremental voxels
[J]. IEEE Robotics and Automation Letters , 2022 , 7 (2 ): 4861 - 4868
DOI:10.1109/LRA.2022.3152830
[本文引用: 1]
[23]
罗欣, 丁晓军 地面移动作业机器人运动规划与控制研究综述
[J]. 哈尔滨工业大学学报 , 2021 , 53 (1 ): 1 - 15
[本文引用: 1]
LUO Xin, DING Xiaojun Research and prospective on motion planning and control of ground mobile manipulators
[J]. Journal of Harbin Institute of Technology , 2021 , 53 (1 ): 1 - 15
[本文引用: 1]
[24]
朱大奇, 颜明重 移动机器人路径规划技术综述
[J]. 控制与决策 , 2010 , 25 (7 ): 961 - 967
[本文引用: 1]
ZHU Daqi, YAN Mingzhong Survey on technology of mobile robot path planning
[J]. Control and Decision , 2010 , 25 (7 ): 961 - 967
[本文引用: 1]
[25]
GEIGER A, LENZ P, URTASUN R. Are we ready for autonomous driving? the kitti vision benchmark suite [C] // IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE, 2012: 3354-3361.
[本文引用: 2]
[26]
SANFOURHE M, VITTORI V, LE B G. eVO: a realtime embedded stereo odometry for MAV applications [C] // IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo: IEEE, 2013: 2107-2114.
[本文引用: 1]
Differential evolution solution to the SLAM problem
1
2009
... 实时定位与地图构建(SLAM)技术是机器人导航领域的核心技术之一[1 ] . SLAM技术作为实时定位和高精度三维点云地图构建的核心技术[2 ] ,其为机器人运动控制和轨迹规划提供了先验信息[3 ] . SLAM主要分为视觉SLAM[4 -5 ] 和激光SLAM. ...
1
... 实时定位与地图构建(SLAM)技术是机器人导航领域的核心技术之一[1 ] . SLAM技术作为实时定位和高精度三维点云地图构建的核心技术[2 ] ,其为机器人运动控制和轨迹规划提供了先验信息[3 ] . SLAM主要分为视觉SLAM[4 -5 ] 和激光SLAM. ...
1
... 实时定位与地图构建(SLAM)技术是机器人导航领域的核心技术之一[1 ] . SLAM技术作为实时定位和高精度三维点云地图构建的核心技术[2 ] ,其为机器人运动控制和轨迹规划提供了先验信息[3 ] . SLAM主要分为视觉SLAM[4 -5 ] 和激光SLAM. ...
基于深度学习的视觉SLAM综述
1
2017
... 实时定位与地图构建(SLAM)技术是机器人导航领域的核心技术之一[1 ] . SLAM技术作为实时定位和高精度三维点云地图构建的核心技术[2 ] ,其为机器人运动控制和轨迹规划提供了先验信息[3 ] . SLAM主要分为视觉SLAM[4 -5 ] 和激光SLAM. ...
基于深度学习的视觉SLAM综述
1
2017
... 实时定位与地图构建(SLAM)技术是机器人导航领域的核心技术之一[1 ] . SLAM技术作为实时定位和高精度三维点云地图构建的核心技术[2 ] ,其为机器人运动控制和轨迹规划提供了先验信息[3 ] . SLAM主要分为视觉SLAM[4 -5 ] 和激光SLAM. ...
基于运动预测的改进ORB-SLAM算法
1
2023
... 实时定位与地图构建(SLAM)技术是机器人导航领域的核心技术之一[1 ] . SLAM技术作为实时定位和高精度三维点云地图构建的核心技术[2 ] ,其为机器人运动控制和轨迹规划提供了先验信息[3 ] . SLAM主要分为视觉SLAM[4 -5 ] 和激光SLAM. ...
基于运动预测的改进ORB-SLAM算法
1
2023
... 实时定位与地图构建(SLAM)技术是机器人导航领域的核心技术之一[1 ] . SLAM技术作为实时定位和高精度三维点云地图构建的核心技术[2 ] ,其为机器人运动控制和轨迹规划提供了先验信息[3 ] . SLAM主要分为视觉SLAM[4 -5 ] 和激光SLAM. ...
LiDAR/IMU紧耦合的实时定位方法
1
2021
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
LiDAR/IMU紧耦合的实时定位方法
1
2021
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
A method for registration of 3-D shapes
1
1992
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
Object modelling by registration of multiple range images
1
1992
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
Linear least-squares optimization for point-to-plane ICP surface registration
1
2004
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
Robust odometry and mapping for multi-lidar systems with online extrinsic calibration
1
2021
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
1
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
Fast-LIO: a fast, robust lidar-inertial odometry package by tightly-coupled iterated Kalman filter
1
2021
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
Fast-lio2: fast direct lidar-inertial odometry
1
2022
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
Faster-LIO: lightweight tightly coupled LiDAR-inertial odometry using parallel sparse incremental voxels
1
2022
... 在激光SLAM方面,激光惯性里程计的发展由LiDAR和IMU松耦合的融合方式逐渐发展为紧耦合[6 ] . 松耦合方式将IMU的积分值作为当前帧与历史帧或局部地图进行配准的初值,未将IMU积分值加入到后端优化中,所以其在特征退化和旋转抖动的环境下鲁棒性较差. Besl等[7 ] 提出ICP. Chen等[8 ] 提出点到面源配准的改进ICP方法,Low[9 ] 提出基于线性最小二乘法的改进ICP方法,Segal等[10 ] 提出广义迭代最近邻G-ICP方法. Zhang等[11 ] 提出LOAM. LOAM-Livox[12 ] 、Lego-LOAM[13 ] 、F-LOAM[14 ] 、M-LOAM[15 ] 等衍生方法. 这些都是松耦合融合的激光惯性里程计方法. 紧耦合方法将IMU积分值加入后端优化中,将IMU积分值与点云配准结果进行联合优化. 利用紧耦合的方法,不仅可以抑制快速移动和旋转抖动造成的漂移,而且在半结构化或非结构化环境中相较于松耦合方式,利用紧耦合的方法能够显著提升系统的鲁棒性. Ye等[16 ] 提出第一个紧耦合的激光惯性里程计框架LIO-Mapping. Shan等[17 ] 提出LIO-SAM,通过因子图优化的方法进行多传感器的紧耦合融合. Qin等[18 ] 提出Lins,利用卡尔曼滤波的方法,实现了LiDAR和IMU的紧耦合融合. Lv等[19 ] 提出Clins,Xu等[20 ] 提出FAST-LIO. FAST-LIO通过提出的IMU反向传播方法和降维卡尔曼增益公式,提升了里程计的精度和效率. 在此基础上,FAST-LIO2[21 ] 和FASTER-LIO[22 ] 相继被提出. ...
地面移动作业机器人运动规划与控制研究综述
1
2021
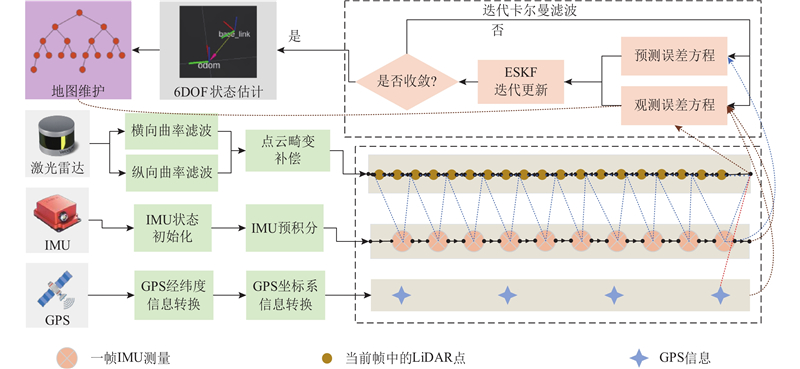
... 利用高效率和高精度的里程计,可以保证机器人运动控制和轨迹规划模块获取先验位姿的实时性和精度[23 -24 ] . 当今,激光里程计和效率的精度的优化面临如下挑战:1)利用当前的点云特征提取方法,无法精确地提取特征点并对平面和地面点进行针对性的提取和分割. 2)高效的卡尔曼滤波的方法无法同时融合LiDAR、IMU和GPS信息. 为了解决上述问题,本文提出LCG-LIO. 提出双向降维曲率滤波的高质量平面与地面点云提取和分割的方法. 提出点云伪占用的后端优化方法,平衡了平面点和地面点在后端优化中的占比. 对后端优化函数中的观测误差方程和观测误差雅可比矩阵的构建方法进行改进,在观测误差方程中加入了GPS 约束. ...
地面移动作业机器人运动规划与控制研究综述
1
2021
... 利用高效率和高精度的里程计,可以保证机器人运动控制和轨迹规划模块获取先验位姿的实时性和精度[23 -24 ] . 当今,激光里程计和效率的精度的优化面临如下挑战:1)利用当前的点云特征提取方法,无法精确地提取特征点并对平面和地面点进行针对性的提取和分割. 2)高效的卡尔曼滤波的方法无法同时融合LiDAR、IMU和GPS信息. 为了解决上述问题,本文提出LCG-LIO. 提出双向降维曲率滤波的高质量平面与地面点云提取和分割的方法. 提出点云伪占用的后端优化方法,平衡了平面点和地面点在后端优化中的占比. 对后端优化函数中的观测误差方程和观测误差雅可比矩阵的构建方法进行改进,在观测误差方程中加入了GPS 约束. ...
移动机器人路径规划技术综述
1
2010
... 利用高效率和高精度的里程计,可以保证机器人运动控制和轨迹规划模块获取先验位姿的实时性和精度[23 -24 ] . 当今,激光里程计和效率的精度的优化面临如下挑战:1)利用当前的点云特征提取方法,无法精确地提取特征点并对平面和地面点进行针对性的提取和分割. 2)高效的卡尔曼滤波的方法无法同时融合LiDAR、IMU和GPS信息. 为了解决上述问题,本文提出LCG-LIO. 提出双向降维曲率滤波的高质量平面与地面点云提取和分割的方法. 提出点云伪占用的后端优化方法,平衡了平面点和地面点在后端优化中的占比. 对后端优化函数中的观测误差方程和观测误差雅可比矩阵的构建方法进行改进,在观测误差方程中加入了GPS 约束. ...
移动机器人路径规划技术综述
1
2010
... 利用高效率和高精度的里程计,可以保证机器人运动控制和轨迹规划模块获取先验位姿的实时性和精度[23 -24 ] . 当今,激光里程计和效率的精度的优化面临如下挑战:1)利用当前的点云特征提取方法,无法精确地提取特征点并对平面和地面点进行针对性的提取和分割. 2)高效的卡尔曼滤波的方法无法同时融合LiDAR、IMU和GPS信息. 为了解决上述问题,本文提出LCG-LIO. 提出双向降维曲率滤波的高质量平面与地面点云提取和分割的方法. 提出点云伪占用的后端优化方法,平衡了平面点和地面点在后端优化中的占比. 对后端优化函数中的观测误差方程和观测误差雅可比矩阵的构建方法进行改进,在观测误差方程中加入了GPS 约束. ...
2
... 使用公开数据集KITTI[25 ] 和自采室外园区数据集,对提出的方法进行定量和定性评估. 公开数据集KITTI[25 ] 采集平台搭载了Velodyne Lidar HDL-64E 激光雷达和OXTS RT 3003 定位系统,该系统结合了GPS、GLONASS、IMU和RTK校正信号. 自己采集的数据集采集平台搭载了Velodyne VLP-16激光雷达、Xsens MTI-100 IMU和GPS系统. 分别将提出的LCG-LIO不添加GPS约束、LCG-LIO添加GPS约束和FAST-LIO2在KITTI数据集上进行纵向对比,对LCG-LIO的精度和效率进行评估. 将通过提出的伪轨迹加权方法融合GPS信息的LCG-LIO与通过因子图优化融合GPS信息的LIO-SAM在自采数据集上进行横向对比. 为了公平起见,在实验过程中关闭了LIO-SAM中的回环检测模块,分别对LCG-LIO的精度和GPS信息融合方法的可行性进行评估. 为了保证实验结果的准确性,所有实验均在Intel(R) Core(TM) i7-12700H处理器、主频为2.3 GHZ、内存为16 GB的计算机上开展. ...
... [25 ]采集平台搭载了Velodyne Lidar HDL-64E 激光雷达和OXTS RT 3003 定位系统,该系统结合了GPS、GLONASS、IMU和RTK校正信号. 自己采集的数据集采集平台搭载了Velodyne VLP-16激光雷达、Xsens MTI-100 IMU和GPS系统. 分别将提出的LCG-LIO不添加GPS约束、LCG-LIO添加GPS约束和FAST-LIO2在KITTI数据集上进行纵向对比,对LCG-LIO的精度和效率进行评估. 将通过提出的伪轨迹加权方法融合GPS信息的LCG-LIO与通过因子图优化融合GPS信息的LIO-SAM在自采数据集上进行横向对比. 为了公平起见,在实验过程中关闭了LIO-SAM中的回环检测模块,分别对LCG-LIO的精度和GPS信息融合方法的可行性进行评估. 为了保证实验结果的准确性,所有实验均在Intel(R) Core(TM) i7-12700H处理器、主频为2.3 GHZ、内存为16 GB的计算机上开展. ...
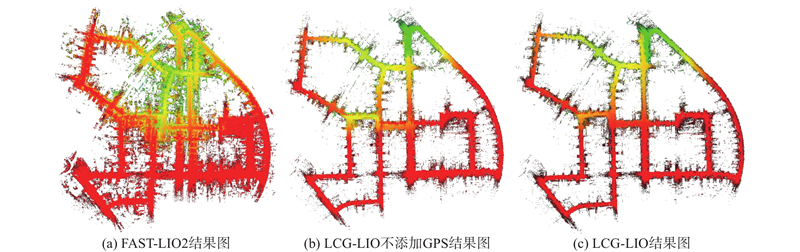
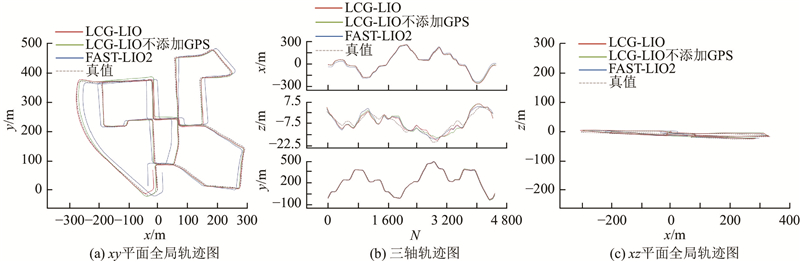
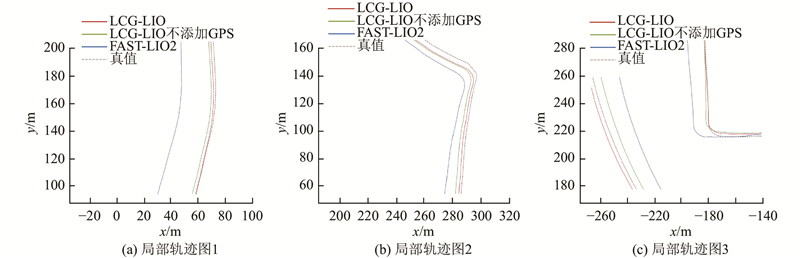
1
... 分别将LCG-LIO添加GPS约束、LCG-LIO不添加GPS约束和FAST-LIO2在KITTI数据集上进行测试. 使用EVO[26 ] 工具绘制里程计轨迹,计算不同方法的均方根误差(RMSE). 运行结果、轨迹和轨迹局部细节如图5 ~7 所示. 图中,N 为KITTI数据集的帧数. 不同方法的绝对位姿误差如表1 所示. ...