无人机在物流方面的应用得到了大量企业和研究者的关注. 2013年，亚马逊进行了无人机配送的测试；之后，谷歌、联邦物流、Zipline、顺丰、京东和美团等公司进行了相关研究^[1-3]. 不同于传统的车辆配送，无人机具有高机动性、无接触性等优点，使得其在地形复杂或人员管制的地区进行配送时表现出很大的优越性，但是无人机存在载重有限、续航时间短的不足，导致现阶段只依靠无人机无法完成大规模的配送任务. 考虑到无人机的这些特点，Murray等^[1]提出车辆-无人机协同配送问题(vehicle-drone cooperative problem, VCP). 车辆-无人机协同配送的模式极大地提高了配送效率，其应用价值吸引了越来越多研究者的关注.

近年来，考虑到实际配送中的各种约束，研究者们提出多种基于VCP的变体. Agatz等^[4]提出以最小化总配送时间为目标的带无人机的旅行商问题，使用基于局部搜索和动态规划的启发式算法进行求解. Gonzalez-R等^[5]在VCP的基础上考虑无人机单次起飞可服务多个客户的约束，提出迭代贪婪启发式方法，以最小化总配送时间. 柳伍生等^[6]研究文献[5]的问题，利用模拟退火算法来最小化总里程. Luo等^[7]在无人机单次起飞可服务多个客户的基础上，增加了同质多无人机的约束，提出多启动禁忌搜索算法，以最小化总配送时间. 伍国华等^[8]在考虑无人机单次起飞可服务多个客户的基础上，进一步考虑多车辆和多无人机协同配送，设计自适应大规模邻域搜索算法，最小化配送时间. Gu等^[9]针对无人机单次起飞可服务多个客户的多车辆VCP，提出混合了迭代局部搜索启发式算法和可变邻域下降的方法，最小化问题的总成本. Mara等^[10]针对无人机起飞后可服务多个客户的VCP，以总配送时间为优化目标，提出新的数学模型. 此外，研究者们针对含有其他约束(如多车场、动态交通环境和时间窗等)的VCP展开研究，提出多种求解方法^[11-16].

除上述研究外，研究者们开始关注道路条件和客户需求对运输工具的配送限制. 彭勇等^[17]研究以最小化总配送时间为目标的包含3类客户的VCP，利用混合邻域搜索算法求解问题. 朱晓宁等^[18]考虑区域限制，设计最短路与禁忌搜索相结合的算法，求解含有3类客户的VCP.

综上所述，现阶段VCP的研究很少涉及因区域限制或特殊事件导致运输工具配送受限的情况.本文结合客户属性和运输工具受到的限制，将客户分为3类(仅车辆可服务、仅无人机可服务以及车辆和无人机均可服务)，研究了运输工具配送受限的车辆-多投递无人机协同配送问题(multi-drop vehicle-drone cooperative problem with delivery restrictions, MDVCP-DR). 本文的主要贡献如下.

1)研究以总配送时间为优化目标的MDVCP-DR，其中综合考虑了运输工具配送范围受限、无人机单次起飞后可服务多个客户、无人机和车辆可互相等待、客户的服务时间与货物需求质量相关等约束；建立问题的数学模型，通过Gurobi验证了模型的正确性.

2) 提出混合蛙跳算法(hybrid shuffled frog leaping algorithm, HSFLA)，其中设计了预调整解码方法、个体生成方法和局部搜索策略来保证算法的可行性和搜索能力.

3) 通过在不同规模算例上的仿真和对比实验，验证了算法的有效性.

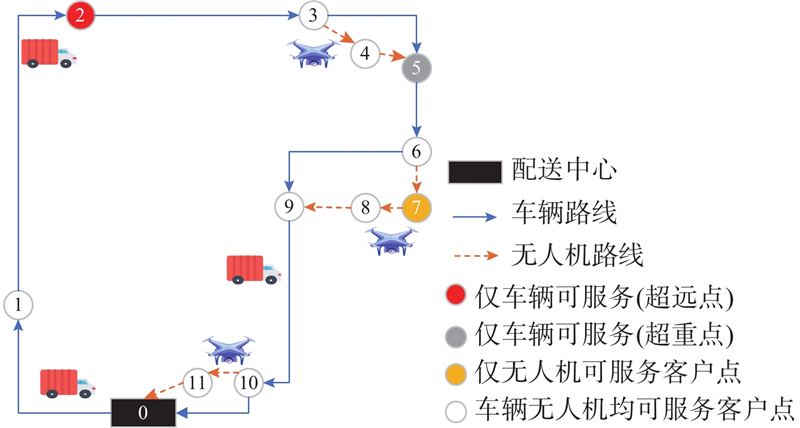
研究的MDVCP-DR包含1个配送中心和n个客户，分别记作0和1, 2$, \cdots , $ n. 配送中心有一辆车和一架无人机，配送任务由车辆和无人机共同完成，其中车辆可以携带无人机进行配送，车辆和无人机可以各自进行配送. 无人机可以在配送中心或任意客户点从车辆上起飞，在满足约束的情况下服务一个或多个客户，在服务结束后降落至车辆，即飞至车辆所在客户点更换电池以准备下次起飞配送. 无人机单次起飞的起飞和降落点不能在同一个客户. 在完成配送服务后，车辆和无人机均返回配送中心. 该问题满足以下假设和约束.

1) 配送中心位置已知，客户的位置、货物需求量和服务时间均已知. 客户集中存在因区域限制导致车辆不可到达的客户点，即只能无人机配送的客户，也存在无人机无法配送的超重点、超远点.

2) 超重点为货物需求量超出无人机载重上限的客户点. 对于一个客户点，若到最邻近2个客户点的距离和超出无人机续航上限，则称为超远点. 超重点和超远点只能由车辆配送. 除超重点、超远点和车辆不可达客户点外，其余客户点车辆和无人机均可服务.

3) 在配送过程中，每个客户只能被车辆或无人机服务一次，车辆和无人机共同访问的客户(车辆载着无人机访问或无人机在该客户点从车辆起飞或降落)由车辆进行配送服务，车辆(无人机)单独访问的客户由车辆(无人机)服务.

4) 车辆无载重和续航限制，无人机的载重限制和续航时间已知.

5) 2个客户之间的实际配送距离取决于配送工具，即无人机的配送距离为客户之间的欧式距离，车辆的配送距离为曼哈顿距离.

6) 对于仅无人机可配送的客户，货物质量不会超过无人机的载重限制.

7) 无人机从车辆起飞后，车辆和无人机均可以服务多个客户.

8) 当无人机返回车辆时，无人机(车辆)在满足约束的前提下可以等待车辆(无人机).

9) 无人机的起飞、降落、服务客户及等待降落时的悬停飞行均消耗电量.

10) 在无人机起飞前，车辆须完成对当前客户的服务，降落时允许其打断车辆对当前客户的服务.

11) 无人机无电池数量或充电次数的约束.

如图1所示为包含11个客户的车辆-无人机协同配送示意图. 车辆和无人机从配送中心出发到完成所有客户的配送服务并返回至配送中心为一次完全配送，一次完全配送由多个子配送构成. 例如，图1中车辆载着无人机从配送中心到客户1为一个子配送，车辆和无人机分别从客户3到客户5也为一个子配送.

以总配送时间为优化目标，建立MDVCP-DR的数学模型.

1) 目标函数为

(1)$ \min \sum\limits_{k \in K} {t_k^{\text{c}}} . $

式中：$t_k^{\mathrm{c}} $为第k次子配送所需的时间；K为子配送次数的集合，K = {1, 2$, \cdots , $ K_max}，其中K_max为子配送的总次数.

2) 配送约束.

根据客户属性和配送工具所受到的限制，可以将问题中的客户划分为3类：仅车辆可服务、仅无人机可服务以及车辆和无人机均可服务. 车辆和无人机服务客户须满足的约束条件如下.

(2)$ \sum\limits_{k \in K} {\sum\limits_{j \in N,j \ne i} {{x_{ij,k}}} } = 1;\; i \in \{ 0\} \cup {N_{\text{t}}}. $

(3)$ \sum\limits_{k \in K} {\sum\limits_{i \in N,i \ne j} {{x_{ij,k}}} } = 1;\; j \in \{ 0\} \cup {N_{\text{t}}}. $

(4)$ \sum\limits_{k \in K} {\sum\limits_{j \in N,j \ne i} {{y_{ij,k}}} } = 1;\; i \in \{ 0\} \cup {U_{\text{d}}}. $

(5)$ \sum\limits_{k \in K} {\sum\limits_{i \in N,i \ne j} {{y_{ij,k}}} } = 1;\; j \in \{ 0\} \cup {U_{\text{d}}}. $

(6)$ \sum\limits_{k \in K} {\sum\limits_{j \in N,j \ne i} {{y_{ij,k}}} } = 1;\; i \in {N_{\text{u}}}. $

(7)$ \sum\limits_{k \in K} {\sum\limits_{i \in N,i \ne j} {{y_{ij,k}}} } = 1;\; j \in {N_{\text{u}}}. $

(8)$ \sum\limits_{k \in K} {\sum\limits_{j \in N,j \ne i} {{x_{ij,k}}} } = 0;\; i \in {N_{\text{u}}}. $

(9)$ \sum\limits_{k \in K} {\sum\limits_{i \in N,i \ne j} {{x_{ij,k}}} } = 0;\; j \in {N_{\text{u}}}. $

(10)$ \sum\limits_{k \in K} {\sum\limits_{i \in N,i \ne j} {{y_{ij,k}}} } \leqslant \sum\limits_{k \in K} {\sum\limits_{l \in N,l \ne j} {{x_{lj,k}}} } ;\; j \in {U_{\text{m}}}. $

(11)$ 0 < \sum\limits_{k \in K} {\sum\limits_{j \in N,j \ne i} {\left( {{x_{ij,k}}+{y_{ij,k}}} \right)} } \leqslant 2;\; i \in {N_1}. $

(12)$ 0 < \sum\limits_{k \in K} {\sum\limits_{i \in N,i \ne j} {\left( {{x_{ij,k}}+{y_{ij,k}}} \right)} } \leqslant 2;\; j \in {N_1}. $

式中：x_ij,k为决策变量，x_ij,k = 1表示第k次子配送中车辆从客户点i驶往j，否则x_ij,k = 0；y_ij,k为决策变量，y_ij,k = 1表示第k次配送中无人机从客户点i飞往，否则y_ij,k = 0；N = {0, 1, 2$, \cdots , $ n}为配送中心0和客户点1$, \cdots , $ n的集合；N₁为车辆和无人机均可服务的客户集合；U_m为超重点集合；U_d为超远点集合；N_t = U_m∪U_d为仅车辆可服务的客户集合；N_u为仅无人机可服务的客户集合. 式(2)、(3)表示车辆一定会访问配送中心和仅车辆可服务的客户. 式(4)、(5)表示无人机和车辆一定会共同访问配送中心和超远点. 式(6)、(7)表示无人机一定会访问仅无人机可服务的客户. 式(8)、(9)表示车辆一定不会访问仅无人机可服务的客户. 式(10)表示无人机一定不会单独访问超重点. 式(11)、(12)表示车辆和无人机均可服务的客户既可能由车辆和无人机共同访问，也可能由车辆或无人机单独进行访问.

3) 配送点集划分如下.

(13)$ {s_1} = {e_{{K_{{\text{max}}}}}} = 0. $

(14)$ {e_k} = {s_{k+1}};\; k \in K\backslash \{ {K_{{\text{max}}}}\} . $

(15)$ S \subseteq N\backslash {N_{\text{u}}}. $

(16)$ \{ {s_1}\} \cap \{ {s_2}\} \cap \cdots \cap \{ {s_{{K_{{\text{max}}}}}}\} = \varnothing . $

(17)$ {\text{Se}}{{\text{t}}_1} \cup {\text{Se}}{{\text{t}}_2} \cup \cdots \cup {\text{Se}}{{\text{t}}_{{K_{{\text{max}}}}}} = N. $

(18)$ {\text{Se}}{{\text{t}}_1} \cap {\text{Se}}{{\text{t}}_2} \cap \cdots \cap {\text{Se}}{{\text{t}}_{{K_{{\text{max}}}}}} = S. $

(19)$ {\text{ }}N_k^{\text{t}} = \varnothing ;\; k \in K,\;\exists N_k^{\text{u}} = \varnothing . $

式中：s_k为第k次子配送的起点；e_k为第k次子配送的终点；S为所有子配送的起点集合，S = {s_k | k∈K}；N_k^u为第k次子配送中无人机单独访问的客户集合；N_k^t为第k次子配送中车辆单独访问的客户集合；Set_k为第k次子配送访问的客户集合，Set_k = {s_k}∪N_k^t∪N_k^u∪{e_k} = C_k^t∪C_k^u，其中C_k^t = {s_k}∪N_k^t∪{e_k}为第k次子配送中车辆访问的客户集合，C_k^u = {s_k}∪N_k^u∪{e_k}为第k次子配送中无人机访问的客户集合. 式(13)~(16)表示子配送的起、终点约束，其中第k+1次子配送的起点为第k次子配送的终点. 式(17)、(18)保证客户可以全部被服务，且所有子配送的交集为它们起点的集合. 式(19)保证第k次子配送由车辆携带无人机完成，或者车辆、无人机分别完成.

4) 子配送路径载重及耗时约束如下：

(20)$ t_k^{\text{u}} = \left\{ \begin{gathered} t_k^{\text{s}}+\sum\limits_{i \in N_k^{\text{u}} \cup \{ {s_k}\} } {\sum\limits_{j \in N,j \ne i} {{y_{ij,k}}\frac{{d_{ij}^{}}}{{{v^{\text{u}}}}}} } + \\ \qquad \sum\limits_{l \in N_k^{\text{u}}} {\sum\limits_{j \in N,j \ne l} {{y_{lj,k}}{f_l}} } ,\;N_k^{\text{u}} \ne \varnothing ,\;k \in K; \\ 0,{\text{ }}N_k^{\text{u}} = \varnothing ,\;k \in K.{\text{ }} \\ \end{gathered} \right.\;\;\;\;$

(21)$ t_k^{\text{t}} = \left\{ \begin{gathered} t_k^{\text{s}}+\sum\limits_{i \in N_k^{\text{t}} \cup \{ {s_k}\} } {\sum\limits_{j \in N,j \ne i}^{} {{x_{ij,k}}\frac{{d_{ij}^{\text{m}}}}{{{v^{\text{t}}}}}} } + \\ \qquad \sum\limits_{l \in N_k^{\text{t}}} {\sum\limits_{j \in N,j \ne l}^{} {{x_{lj,k}}{f_l}} ,N_k^{\text{u}} \ne \varnothing },\;k \in K; \\ \sum\limits_{i \in \{ {s_k}\} } {\sum\limits_{j \in N,j \ne i}^{} {{x_{ij,k}}\frac{{d_{ij}^{\text{m}}}}{{{v^{\text{t}}}}}} } ,{\text{ }}N_k^{\text{u}} = \varnothing ,\;k \in K. \\ \end{gathered} \right. \qquad $

(22)$ t_k^{\text{c}} = \left\{ \begin{gathered} \max \;\{ t_k^{\text{u}},t_k^{\text{t}}+{f_{{e_k}}}\} +t_k^{\text{e}},\;N_k^{\text{u}} \ne \varnothing ,\;k \in K\backslash \{ {K_{{\text{max}}}}\}; \\ t_k^{\text{t}}+{f_{{e_k}}},{\text{ }}N_k^{\text{u}} = \varnothing ,\;k \in K\backslash \{ {K_{{\text{max}}}}\}. \\ \end{gathered} \right.{\text{ }}$

(23)$ t_k^{\text{c}} = \left\{ \begin{gathered} \max\; \{ t_k^{\text{u}}+t_k^{\text{e}},t_k^{\text{t}}\} ,N_k^{\text{u}} \ne \varnothing ,\; k = {K_{{\text{max}}}}; \\ t_k^{\text{t}},{\text{ }}N_k^{\text{u}} = \varnothing ,\;k = {K_{{\text{max}}}}. \\ \end{gathered} \right. $

(24)$ \sum\limits_{i \in N_k^{\text{u}}} {\sum\limits_{j \in N,j \ne i} {{y_{ij,k}}{m_i}} } \leqslant {L_{\text{m}}};\; k \in K. $

(25)$ \left. \begin{gathered} \max \;\{ t_k^{\text{u}},t_k^{\text{t}}\} +t_k^{\text{e}} \leqslant {L_{{\text{time}}}},\;k \ne {K_{{\text{max}}}},\;N_k^{\text{u}} \ne \varnothing; \\ t_k^{\text{u}}+t_k^{\text{e}} \leqslant {L_{{\text{time}}}},{\text{ }}k = {K_{{\text{max}}}},\;N_k^{\text{u}} \ne \varnothing. \\ \end{gathered} \right\}$

式中：d_ij为客户i到j的欧式距离；d_ij^m为客户i到j的曼哈顿距离；v^t为车辆的行驶速度；v^u为无人机的飞行速度；f_i为客户i的服务时间，f_i = αm_i，其中α为常数；m_i为客户i的货物需求量；L_m为无人机的最大载重量；L_time为无人机的最大飞行时间；t_k^u为第k次子配送中无人机从开始配送到访问最后一个客户的时间；t_k^t为第k次子配送中车辆从开始配送到访问最后一个客户的时间；t_k^e为第k次子配送中无人机回收所需的时间；t_k^s为第k次子配送中无人机发射所需的时间. 式(20)、(21)分别为第k次子配送中无人机和车辆配送开始到访问最后一个客户的时间. 式(22)、(23)用于计算每次子配送所需的时间. 式(24)表示无人机携带货物不能超过最大载重量. 式(25)表示无人机须满足续航约束.

本文研究的MDVCP-DR是NP难的，且含有很多强约束条件，使用精确算法无法在短时间内求解，因此基于蛙跳算法^[19](shuffled frog leaping algorithm, SFLA)提出适于求解MDVCP-DR的HSFLA. HSFLA主要包括如下6个部分：编码与预调整解码、种群初始化、模因组搜索、自适应局部搜索、精英表更新和种群多样性检测. 在HSFLA中，令个体的适应度为目标函数值，则个体适应度越小，对应的解质量越高.

算法中的青蛙个体由序列X表示，X由客户集N\{0} = {1, 2$, \cdots , $ n}排列组成，记作X = {x₁, x₂$, \cdots , $ x_n}. 对于一个包含10个客户的MDVCP-DR， X = {9, 6, 5, 2, 8, 7, 1, 3, 4, 10}可以表示一个个体，对应的客户顺序为0→9→6→5→ 2→8→7→1→3→4→10→0.

编码过程中没有考虑无人机和车辆的具体分配，也没有考虑问题中的客户配送约束、无人机载重和续航限制等强约束，因此编码得到的个体是不可行的，即不是最终的配送路径. 本文提出预调整策略和解码策略，称为预调整解码策略，保证解的可行性，即通过对个体进行预调整解码，得到可行的配送方案. 对于算法中的个体，均须执行预调整解码.

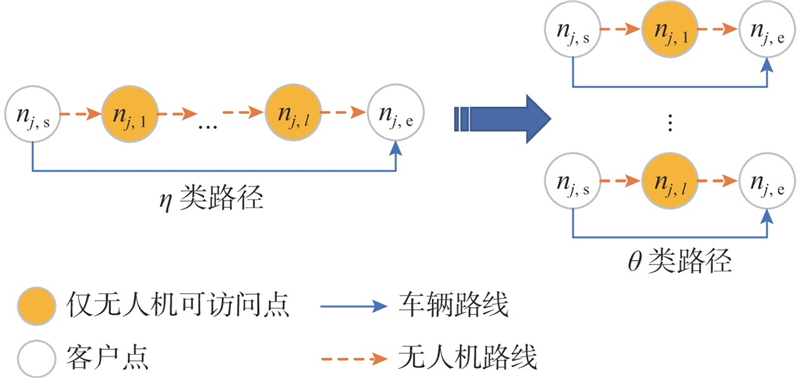
预调整策略. 由于问题中存在运输工具配送范围受限的约束，预调整策略旨在保证该约束得以满足. 为了方便说明，定义了2类路径：η类路径和θ类路径. η类路径表示为{n_j,s, n_j,1, n_j,2$, \cdots , $ n_j,l, n_j,e}，其中n_j,s和n_j,e分别为无人机的起飞和降落点且有{n_j,s, n_j,e}⊂N\N_u, n_j,1, n_j,2$, \cdots , $ n_j,l (l ≥ 1)为仅无人机可服务的客户序列. θ类路径包含3个客户点，即无人机起飞点、配送客户点和降落点，如{n_j,s, n_j,1, n_j,e}为θ类路径. 对于任意2个η(θ)类路径，只有其中的无人机起飞点、配送客户序列(客户)和降落点都相同时，它们才是相同的.

η类路径可拆分得到多个θ类路径，例如1个η类路径{n_j,s, n_j,1, n_j,2$, \cdots , $ n_j,l, n_j,e}可以拆分为l个θ类路径{n_j,s, n_j,1, n_j,e}, {n_j,s, n_j,2, n_j,e}$, \cdots , $ {n_j,s, n_j,l, n_j,e}. 此外，假如存在多个n_j,s和n_j,e相同的θ类路径{n_j,s, n_j,1, n_j,e}, {n_j,s, n_j,2, n_j,e}$, \cdots , $ {n_j,s, n_j,l, n_j,e}，它们可合并为一个η类路径{n_j,s, n_j,1, n_j,2$, \cdots , $ n_j,l, n_j,e}. 如图2所示为η和θ类路径示意图. 对于n_u∈N_u，对应的所有满足约束的θ类路径构成一个集合，记作Φ_u.

给定X，预调整策略的具体步骤如下.

1）∀n_u∈N_u，令A_u = ∅，A_u用于记录当无人机服务客户点n_u时可以作为起飞、降落点的备选客户点. 寻找n_u最邻近的一个客户n_x，令A_u = A_u∪{n_x}. 在剩余客户中找到满足续航约束的所有客户，即如果∃n_a∈N\ (N_u∪{n_x})满足d_xu+d_au ≤ v^uL_time，则A_u = A_u∪{n_a}. 在A_u中选出2个满足续航约束的客户分别作为n_j,s和n_j,e，可得θ类路径{n_j,s, n_u, n_j,e}. 类似地，可以找到所有满足约束的θ类路径，即得到Φ_u.

2）检查X中是否存在η类路径，对每个η类路径进行无人机载重、续航约束检验，若满足约束，则将η类路径拆分为θ类路径. 对于不满足约束的η类路径，为每个n_u∈N_u在Φ_u中随机选择一个θ类路径.

3）检查N_u中每个客户对应的θ类路径，若存在多个n_j,s和n_j,e相同的θ类路径，则合并其为η类路径. 当只有一个θ类路径包含n_j,s和n_j,e时，该θ类路径可以直接作为η类路径.

4）对每个η类路径进行无人机载重和续航约束检验，若满足约束，则将n_j,s和n_j′,e相同的2个η类路径进行拼接操作，即如果一个η类路径{n_j,s, n_j,1, n_j,2, n_j,e}的n_j,s(n_j,e)与另一个η类路径{n_j′,s, n_j′,1, n_j′,2, n_j′,e}的n_j′,e(n_j′,s)重合，则拼接得到η′路径{n_j′,s, n_j′,1, n_j′,2, n_j′,e, n_j,1, n_j,2, n_j,e}({n_j,s, n_j,1, n_j,2, n_j,e, n_j′,1, n_j′,2, n_j′,e})；否则，为每个n_u在Φ_u中随机选择一个θ类路径，并返回步骤3）.

5）对于每个η′路径，将其中首个客户点记为n_u′，将η′路径序列插入到X中n_u′所在位置并删除X中的冲突元素，新得到的序列记为X_new.

解码策略. 解码策略旨在保证解序列能够满足无人机的载重和续航约束，得到可行解. 为了保证解的质量，在解码过程中使用无人机优先配送原则以及子配送路径中车辆与无人机耗时尽可能相近的原则. 给定预调整得到的X_new，若其中包含配送中心0(n_j,s或n_j,e为配送中心0)，则将X_new中0之前子序列移动至最后一个元素之后，并删除0，例如由X_new = {x_n-1, x_n, 0, x₁, x₂$, \cdots , $ x_n-2}得到新的X_new = {x₁, x₂$, \cdots , $ x_n-2, x_n-1, x_n}，并令X = X_new. X的解码过程如下所示.

算法1　基于启发式规则的个体解码

算法的输出为可行解B = (ID, NA)，其中ID = {id₀, id₁$, \cdots , $ id_n+1}为客户访问顺序，NA ={na₀, na₁$, \cdots , $ na_n+1}为ID中各客户点的配送属性.

算法1中使用到的符号及对应含义如下. seq用于记录当前子配送路径中的客户，seq_t和seq_u分别用于记录子配送路径中分配给车辆和无人机的客户，td和td′用于记录t_k^u与t_k^t差的绝对值，N_temp用于记录在seq_u中最后一个客户点n_u∈N_u之后所分配的客户点n_a∈N₁. flag、flag_UF和flag_Nu的取值为{0, 1}，其中无人机配送不违反约束则flag = 0，否则flag = 1. 应用无人机优先配送原则时flag_UF = 0，否则flag_UF = 1. flag_Nu = 1表示正在规划N_u中客户的路径，flag_Nu = 0表示没有在规划N_u中客户的路径或N_u中客户在无人机上的配送顺序已确定.

种群规模为N_POP，种群初始化过程如下. 利用扫描算法生成个体，即放宽对客户的约束(假设所有客户都由车辆配送)，以配送中心为极点建立极坐标系，顺时针扫描客户，其扫描顺序构成序列X_S；随机生成N_POP−1个个体.

为了更好地引导算法进化，构建容量为Meme的精英表，以存储种群中最好的Meme个个体，将其中的个体用于种群更新.

将种群中的个体按适应度升序排序后，用精英表中的个体替换种群前Meme个个体，然后划分到Meme个模因组中. 具体过程如下：将排在第1(Meme+1, 2Meme+1, 3Meme+1,$\; \cdots \; $)的个体分配到第1个模因组，排在第2(Meme+2, 2Meme+2, 3Meme+2,$\; \cdots \; $)的个体分配到第2个模因组，以此类推，直到所有个体划分完毕.

模因组内搜索分为2个步骤.

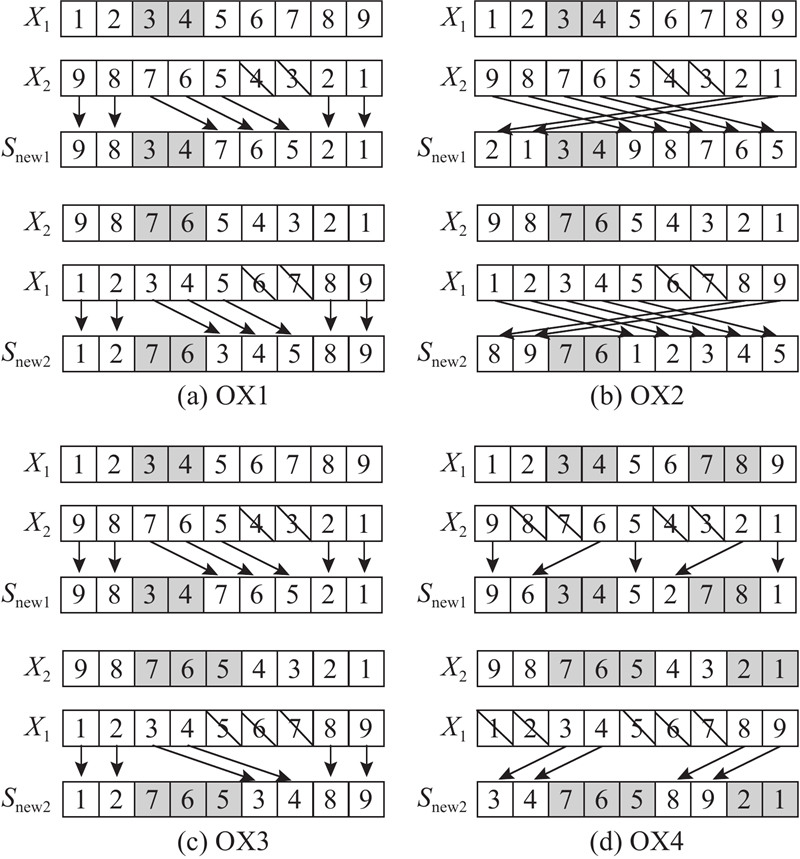
1) 新个体生成. 采用4种交叉算子(order crossover, OX)来生成新个体，其中每个模因组选定一种OX. 4种OX如图3所示，其中X₁和X₂为2个选定个体，S_new1和S_new2为新生成个体.

OX1. 在[1, n]随机生成r₁和r₂ (r₂ > r₁)作为交叉段的起点和终点. 将X₁的交叉段复制到S_new1相应的位置，对X₂进行冲突性检测，即将X₂中与交叉段相同的元素删除. 将X₂中的剩余元素从左到右依次填入S_new1. 由X₂提供交叉段，类似地，可以生成S_new2.

OX2. 在[1, n]随机生成r₁和r₂ (r₂ > r₁)，作为交叉段的起点和终点. 将X₁的交叉段复制到S_new1相应的位置，对X₂进行冲突性检测. 将X₂中的剩余元素从位置r₃+1(X₁的第r₁和r₂个元素对应X₂中的第r₁′和r₂′个元素，r₃ = max{r₁′, r₂′})开始依次填入S_new1. 类似地，由X₂提供交叉段来生成S_new2.

OX3. 在[1, n]随机生成r₁和r₂ (r₂ > r₁)，作为交叉段的起点和终点. 将X₁的交叉段复制到S_new1相应的位置，对X₂进行冲突性检测. 将X₂中的剩余元素从左到右依次填入S_new1. 在[1, n]随机生成r₃和r₄ (r₄ > r₃)作为交叉段的起点和终点，由X₂提供交叉段，类似地可生成S_new2.

OX4. 在[1, n]随机生成r₁、r₂、r₃和r₄ (r₄ > r₃> r₂> r₁)，分别将r₁和r₃(r₂和r₄)作为2个交叉段的起点(终点). 将X₁的2个交叉段复制到S_new1相应的位置，对X₂进行冲突性检测. 将X₂中的剩余元素从左到右依次填入S_new1. 采用类似的方式，由X₂提供2个交叉段，可以生成另一个新个体S_new2.

2) 个体更新. 每个模因组执行N_M次组内搜索. 在每次搜索中，基于个体适应度的倒数采用轮盘赌法选择精英表中的一个个体，记作p_l. 对p_l和模因组内最差的个体p_w执行交叉操作，得到2个新解. 若新解优于p_w，则替换p_w；否则对全局最优个体g_b与p_w执行交叉操作，得到2个新解，若新解优于p_w，则替换p_w；否则随机生成一个个体，并将其与g_b进行交叉操作，得到2个新解，若新解优于p_w，则替换p_w.

为了提升算法的搜索能力，提出自适应局部搜索策略，其中采用4种邻域搜索操作.

1) 单元素交换操作(single point swap, SPS). 随机在X中选择2个客户进行交换，如图4(a)所示.

2) 随机插入操作(random insert, RI). 随机选取一个客户，插入到其他任意位置，如图4(b)所示.

3) 最邻近插入操作(nearest insert, NI). 随机选取1—n/10个客户，将每个客户插入到其最邻近客户点的前/后一个位置，如图4(c)所示.

4) 2元素优化(2-optimization, 2-opt). 随机选取一段序列进行反转，如图4(d)所示.

在局部搜索中，精英表中的每个个体执行LS次邻域搜索操作，每次使用的操作算子自适应选定. 每次搜索后，若新个体更优，则保留，否则保留原来的个体. 具体过程如下：令ρ_h和P_h(h = 1, 2, 3, 4)分别为SPS、RI、NI和2-opt的选择权重和概率，初始化为ρ_h = 1和P_h = 0.25. 在迭代过程中，操作算子的选择概率P_h按下式更新，且采用轮盘赌法选取操作算子.

(26)$ {P_h} = \frac{{\max \left({\rho _h},0.1\displaystyle \sum\nolimits_{i = 1}^4 {{\rho _i}} \right)}}{{\displaystyle \sum\nolimits_{i = 1}^4 {{\rho _i}} }};\;h = 1,2,3,4. $

当P_h<0.1时，将其重置为P_h = 0.1，从而保证4类邻域搜索算子均能够得以应用.

此外，每个邻域搜索算子的选择权重ρ_h根据搜索操作前、后解的质量和算法的运行时间动态更新，如下所示：

(27)$ {\rho _h} = \left\{ \begin{gathered} \rho _h^{{\text{old}}}+0.01{t^*},\;{w_h} = 1; \\ 0.95\rho _h^{{\text{old}}},{\text{ }}{w_h} = 0. \\ \end{gathered} \right. $

式中：w_h表示执行一次第h种邻域搜索操作后解质量是否改善，即w_h = 1对应获得更好的新解，否则w_h = 0；ρ_h^old 为更新前的权重；t^*为当前运行时间.

精英表的更新过程如下. 当模因组每次组内搜索后得到的组内最优解p_b优于表中最差解且不在表中时，将p_b添加到精英表中. 在所有模因组完成搜索后，若种群中最优的Meme个个体优于表中的最差解且不在表中，则添加到精英表. 当经过自适应局部搜索后得到的个体优于表中最差解且不在表中时，将其添加到精英表. 当精英表超出容量时，从表中删除最差解.

为了保证种群个体的多样性，当全局最优个体在算法迭代5次后未得到改善时，检测种群中是否存在重复个体，将重复个体替换为随机生成个体.

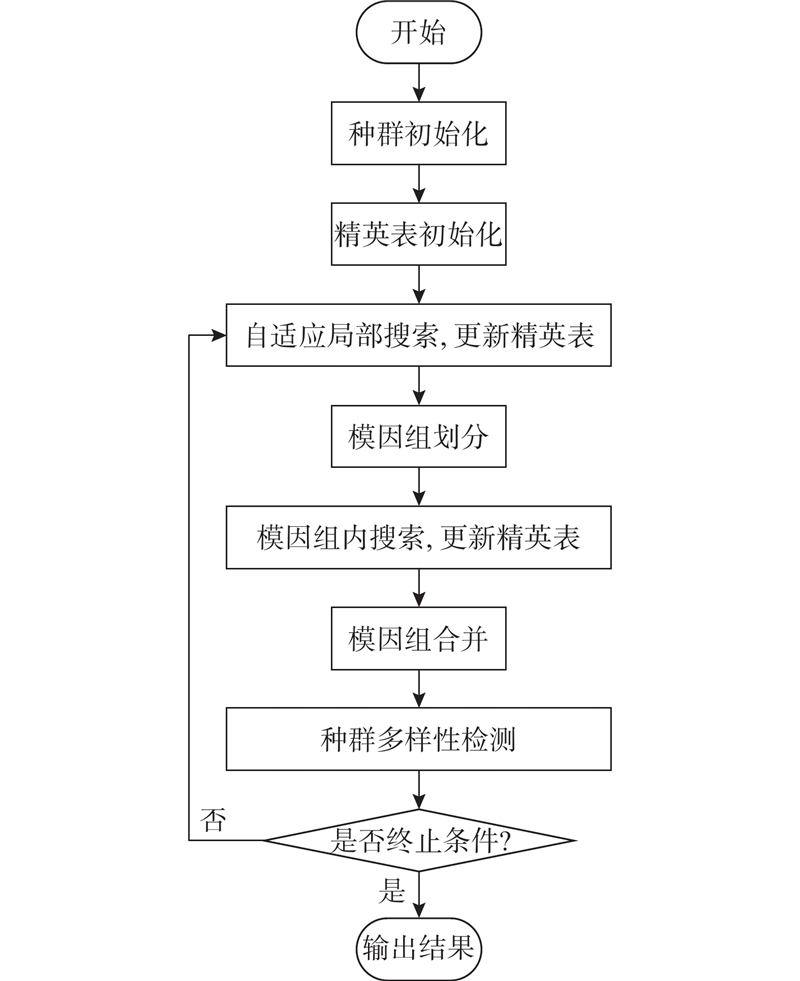
图5给出HSFLA算法的流程图，HSFLA算法的具体步骤如下.

1）初始化算法种群及精英表.

2）对精英表执行局部搜索并更新精英表.

3）模因组划分.

4）开展模因组内搜索并更新精英表.

5）模因组合并.

6）开展种群多样性检测.

7）判断终止条件是否满足，若满足，则算法终止并输出最优结果；否则转至2）.

为了测试HSFLA求解MDVCP-DR的性能，在不同算例上进行仿真实验. 与Gurobi求解器得到的最优解进行对比，再与SA^[6]、ALNS^[8]和IPGA^[20]进行对比研究. 所有的测试算法均用MATLAB 2021a编程实现，运行环境为Inter-Core i5-10500H CPU @ 2.50 GHz、内存为16 GB的PC.

由于目前无直接可用的基准算例，参考开源网站http://www.vrp-rep.org/variants/item/cvrp. html设置算例，在数据集augerat-1995中的set-a、set-p和数据集christofides-et-al-1979-cmt中共选取12个算例，对这些算例进行调整，以满足实验要求. 具体调整如下. 随机选取10%的客户，将其属性改为只能由无人机访问. 所有客户对应的包裹质量调整为原质量的10%. 为每个算例添加2个客户，即超重点(坐标为[50, 50]，包裹质量为20 kg)与超远点(坐标为[185, 185]，包裹质量为5 kg). 调整后的算例记作FP01-12¹. 问题中涉及的客户、车辆及无人机的相关参数如表1所示.

HSFLA中有4个关键参数：种群规模N_POP、模因组个数Meme、模因组内搜索次数N_M和局部搜索中邻域搜索次数LS. 采用实验设计方法(design of experiment, DOE)来确定4个关键参数的设置，选用FP08作为测试算例. 每个参数设置3个水平，参数水平设置和所使用的正交表见表2、3. 在每种参数组合下，算法在算例上独立运行10次，算法的终止条件设置为n秒(n为FP08的客户数，即为102 s). 将10次运行的平均结果作为响应值(response variable, RV)记录在表3中，其中最好RV标记为粗体. 基于表3的结果，将HSFLA算法的参数设置为N_POP = 72, Meme = 4, N_M = 4, LS = 15.

对于每个算例，每种仿真算法的终止条件均设置为最大运行时间n秒，即与问题的规模(客户点总数)相关，且算法单独运行10次. 算法在10次运行中的最好结果和平均结果分别记作BST和AVG，结果均保留2位小数.

为了验证模型的正确性和HSFLA的有效性，在不同规模的算例上开展HSFLA和Gurobi求解器的对比实验. 基于FP11生成分别含有6~17个客户点的算例，记作FP11_06~FP11_17，选择FP12和FP01为测试算例. FP11_06~FP11_17分别包含FP11中前4~15个客户点及超重点、超远点. 令L_m = 5 kg, L_time = 0.5 h，Gurobi的终止时间设置为1 800 s. 表4中，每个算例对应的最好结果用粗体标注，‘*’表示Gurobi未找到算例的最优解，‘−’表示Gurobi在运行终止时未找到可行解，t为时间.

从表4可知，Gurobi能够为FP11_06~FP11_09寻得最优解，对于其余算例都无法获得最优解. 对比发现，HSFLA可以在短时间内求得最优解或高质量解，可见其具有较高的计算效率和寻优能力.

为了验证HSFLA算法中各个策略的有效性，在不同规模算例上开展算法的消融实验，即测试了HSFLA和其他3种HSFLA (HSFLA₁、HSFLA₂和HSFLA₃)的性能. HSFLA₁是将HSFLA的初始化策略除去后获得的，HSFLA₂是将HSFLA中的自适应局部搜索策略除去后获得的，HSFLA₃是将HSFLA中的种群多样性检测策略除去后获得的.

从表5可知，HSFLA的表现明显优于HSFLA₁和HSFLA₂，验证了初始化策略、自适应局部搜索策略对于提升HSFLA性能的有效性. HSFLA和HSFLA₃均为12个算例中的8个提供了最优BST，但是HSFLA在AVG方面表现更优，即利用种群多样性检测策略提高了HSFLA的稳定性.

为了验证算法的性能，选用SA^[6]、ALNS^[8]和IPGA^[20]作为对比算法，对比算法的参数设置如表6所示. 表中，t_p为运行时间，T₀为初始温度，λ为反应参数，q为降温系数，L为链长.

考虑到MDVCP-DR中存在多种复杂约束，目前暂无其他策略可用于保证解的可行性，故对比算法中初始解的生成与编码解码均采用本文所提出的方法. SA的初始温度为T₀ = 1 000^[6]，由于文献[6]的优化目标与本文考虑的目标不同，原参数不再适用，故参考文献[8]调整为0.01. 由于本文编码未包含客户由无人机或车辆服务的信息，须解码后获取，故ALNS邻域结构不再指定插入无人机路径还是车辆路径. Zhou等^[20]采用顺序-断点的编码方式，本文仅使用顺序编码，故只采用IPGA中针对顺序的调整操作. 比较算法的其他方面与来源文献保持一致.

令L_m = 5 kg, L_time = 0.5 h，HSFLA、SA、ALNS和IPGA在FP01-12上的结果如表7所示. 每个算例对应的最好结果标记为粗体.

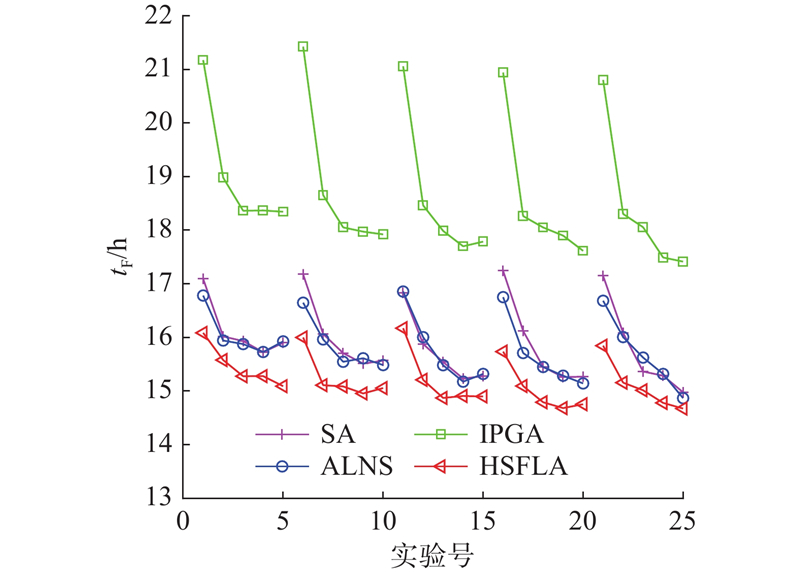
从表7可知，HSFLA在所有算例上的BST与AVG结果均优于其他比较算法，表明HSFLA对求解MDVCP-DR具有优异的性能. 随着客户规模的增大，HSFLA相较于其他算法的优势更加明显.

为了探究算法在不同无人机参数下的灵敏度，测试算法在不同的无人机续航和载重上限组合下的性能. 选取具有102个客户的大规模算例FP08作为测试算例. 所有算法在每个L_m和L_time组合下单独运行10次，10次运行的AVG记录到表8中，每个实验对应的最好结果标记为粗体. 为了更直观地展示结果，如图6所示为每个实验的AVG结果. 图中，t_F为平均总配送时间.

从表8的实验结果可知，HSFLA的结果均优于其他对比算法，说明无人机参数的变动对算法性能无干扰，即HSFLA的优化性能不会因为问题中参数的变动而受到影响. HSFLA在求解具有不同无人机参数的MDVCP-DR时有很好的稳定性，能够求得优质解.

从图6可知，随着L_m和L_time的增大，配送完成时间下降. 当一个参数值保持不变，只增大另一个参数值时，增大参数对配送时间的改善效果会逐渐下降. 结果表明，当无人机续航和载重上限同时增大时，无人机能够完成更多的配送任务，可以更大幅度地减少总配送时间.

本文解决了运输工具配送范围受到限制的无人机起飞后可服务多个客户的VCP，提出HSFLA，以最小化总配送时间.建立所研究问题的数学模型，设计HSFLA的编码与预调整解码、种群初始化、模因组搜索、自适应局部搜索、精英表更新和种群多样性检测6个部分，通过仿真实验验证了HSFLA的有效性.

本文研究的MDVCP-DR中运输工具配送范围受到的限制比较符合现实中由环境、政策及特殊事件带来的配送影响，因此具有很好的现实性和应用价值. 鉴于目前对MDVCP-DR的研究仍处于初步阶段，后续研究中将继续关注以下几个方面. 1)建立具有更好优化能力的求解算法. 2)考虑符合现实需求的其他约束，如多车辆、多无人机、时间窗约束及道路情况变动对客户的动态影响. 3)考虑优化其他性能指标，如费用、能耗.