三维目标反演是地球物理、遥感、计算机视觉等领域中的一个重要研究方向. 在地球物理领域,重磁数据被用于反演地球的内部结构,在金属矿床和油气资源勘探中广泛应用. 其中,重力反演是指利用重力数据演算地下物质分布,目前反演方法可以分为基于物理模型的反演方法和基于深度学习的反演方法. 基于物理模型的反演方法依托地球物理理论,利用线性或者非线性优化算法,使目标函数最小化. 由于地球场固有的等效性以及观测数据的离散性和误差,重力反演被视为不适定性问题,反演结果具有多解性[1]. 针对该问题,引入正则化约束,如最小体积约束[2]、深度加权[3]和最小梯度约束[4]. 引入遗传算法[5-6]、粒子群算法[7-8]和蚁群算法[9]等全局优化算法,解决了陷入局部最小值的问题,但带来了计算复杂、耗时的问题. 基于深度学习的反演方法通过数据驱动的方式建立重力数据与地下目标的映射关系,当输入的重力数据确定时,反演结果唯一. 在地球物理领域,迄今为止已有多种结构的神经网络被用于重力反演. 王逸宸等[10]使用卷积神经网络,实现了重力等值线图到异常体大小和埋深信息的映射. 阳前果[11]基于U-Net[12]重新设计了Grav-Net,端到端地实现了多异常体含噪数据的三维反演,达到了优于多约束正则化反演的效果. 为了提升三维目标的反演效果,Wang等[13]对3D U-Net进行改进,使用三维卷积实现二维异常数据到三维异常体密度分布的映射. Zhang等[14]设计GravInv,利用二维卷积和残差结构进行特征提取,维度变换后使用三维反卷积实现模型的重构. 三维卷积的引入使得网络训练和预测所需的内存和时间成本大幅增加. Zhang等[15]通过预测异常体模型的特征,设计DecNet,间接地实现了三维重力反演.
因为基于深度学习的反演方法采用较多的三维卷积运算,反演网络存在内存占用大、训练耗时久的问题. 针对该问题,本文提出面向重力反演领域的基于多特征重构的三维目标反演算法,旨在降低反演网络的训练成本,提高反演结果的准确性. 主要工作如下. 1)通过特征分解提取目标的水平区域、中心深度、垂直厚度和剩余密度4类特征,实现三维模型的压缩. 2)设计多特征重构反演网络MRNet,实现对各类特征的预测及三维模型的重构. 3)引入梯度联合,通过原始数据和梯度数据的拼接,增强目标水平区域的特征. 4)引入注意力机制分化网络中不同解码器的特征预测功能,优化反演结果.
1. 反演理论与网络结构
1.1. 重力反演
重力反演是指依据重力异常数据预测地下异常体密度模型,二者的关系满足:
式中:
基于深度学习的反演是数据驱动的方法,利用大量的先验数据优化参数化函数(神经网络),构建重力异常数据与密度模型的映射关系. 神经网络的基本形式可以表示为
式中:
式中:
常用的神经网络优化算法有随机梯度下降、小批量随机梯度下降、动量法、AdaGrad和Adam等优化算法[16].
1.2. 特征分解
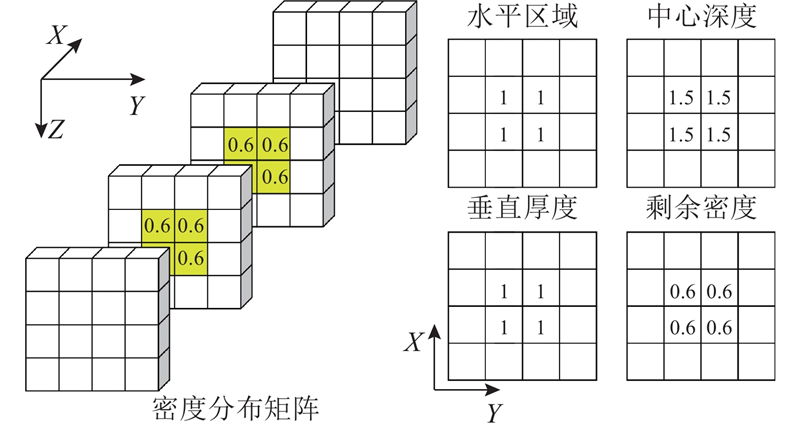
为了使神经网络直接实现二维数据到三维模型的映射,简单增加输出通道数或三维卷积的方式会大大增加网络的参数量和内存占用. 针对该问题,通过特征分解实现对三维模型的压缩,将三维反演问题分解为对多个二维特征的预测. 设异常体的空间密度模型为
式中:
图 1
1.3. 梯度联合
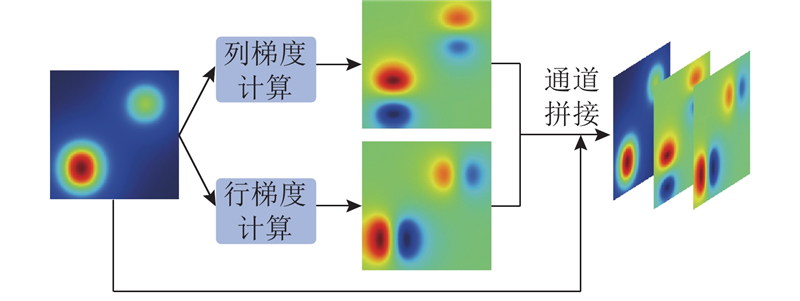
当异常体所处深度较大或者边缘复杂曲折时,在地表边缘处引起的重力异常变化较小,反演网络往往需要增加网络深度,以提高对异常体边缘的敏感度. 针对该问题,分别计算二维重力异常数据行、列方向上的梯度数据,并与原重力异常数据进行通道方向上的拼接,得到3通道的数据矩阵作为反演网络的输入,如图2所示.
图 2
1.4. 网络结构
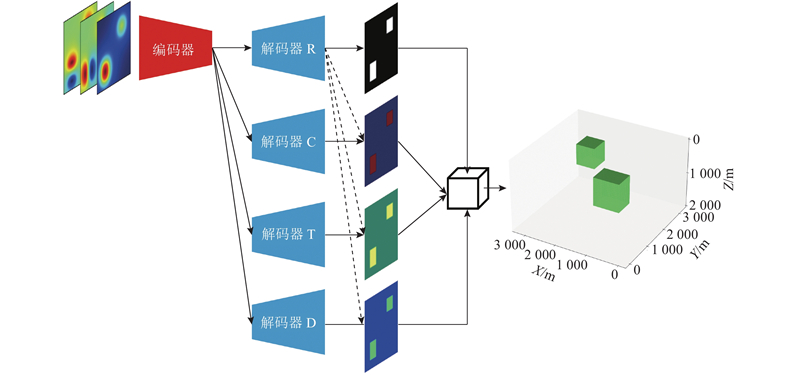
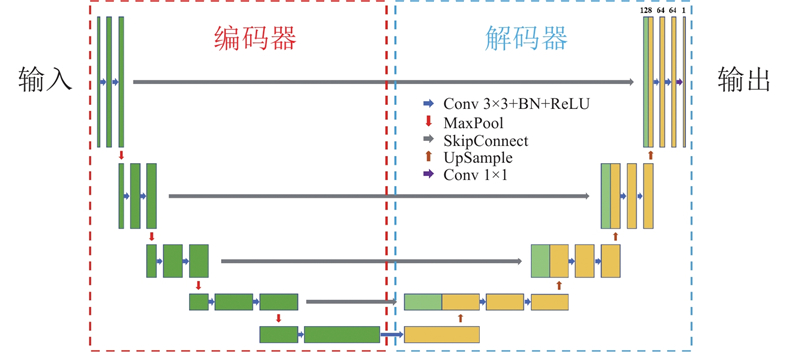
根据多特征图重构和重力梯度联合,提出基于U-Net基本架构的多任务反演网络(multi-feature reconstruction network, MRNet),如图3所示. MRNet由特征提取模块和特征映射模块组成. 特征提取模块包含1个共享编码器,负责提取共享的多层次特征. 特征映射模块包含4个解码器,分别预测三维重力异常体的4类二维特征,重构得到三维模型.
图 3
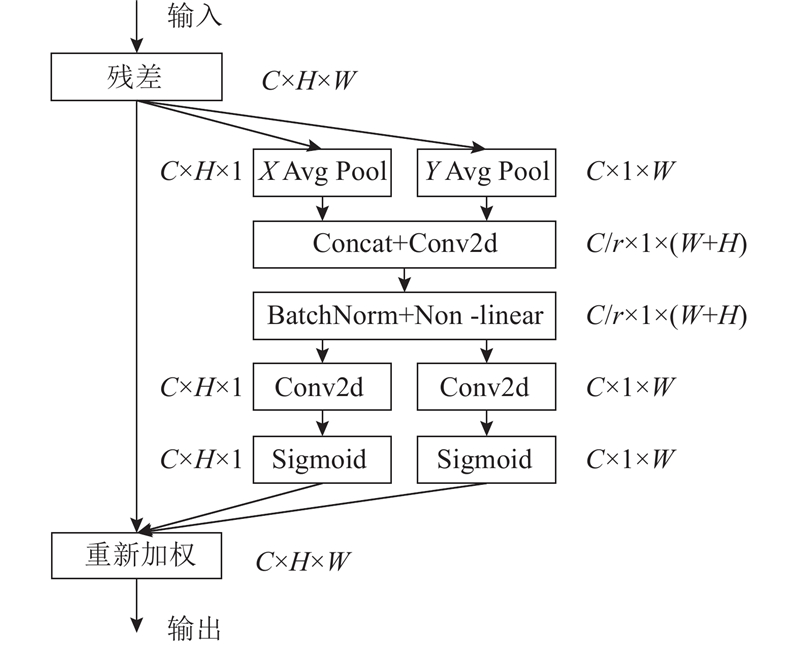
图 4
图 5
图 5 Coordinate attention模块的结构图
Fig.5 Structure diagram of coordinate attention module
MRNet将三维反演简化为对二维特征的预测,将尺寸为
在异常体的4类特征中,水平区域属于较浅层的特征,基于U-Net架构的网络较适合学习该特征. 在训练过程中,MRNet使用异常体实际的水平区域特征约束其他3类特征的学习,使特征映射模块只专注于该区域内部特征的学习. MRNet选择L2范数作为损失函数:
式中:
在预测过程中,设置水平区域特征的分类阈值为0.5. 若预测值大于0.5,则认为该区域存在异常体;反之则无. 根据预测特征重构三维模型
式中:
2. 模拟数据实验
2.1. 数据集构建
图 6
表 1 异常体各方向的尺寸参数
Tab.1
| 异常体类型 | X/grid | Y/grid | Z/grid |
| {8,12,16,20,24} | {8,12,16,20,24} | {8,12,16,20,24} | |
| 16 | 16 | 2(3层) | |
| 10 | 10 | 1(5层) |
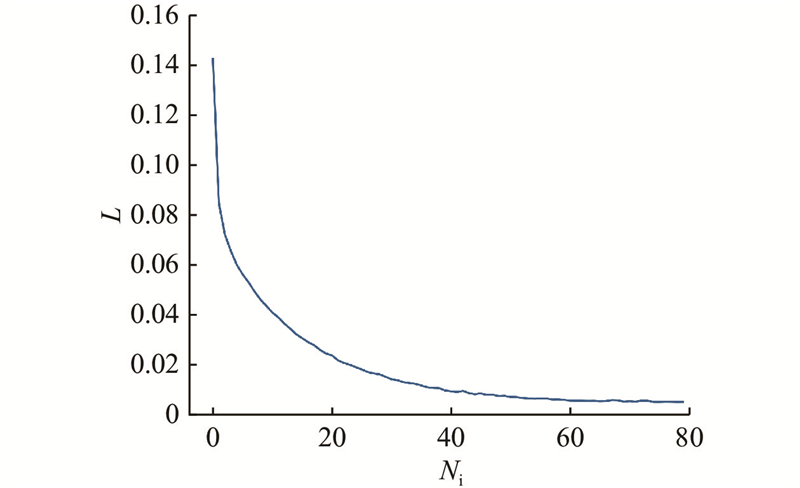
2.2. 训练参数
图 7
2.3. 反演实验
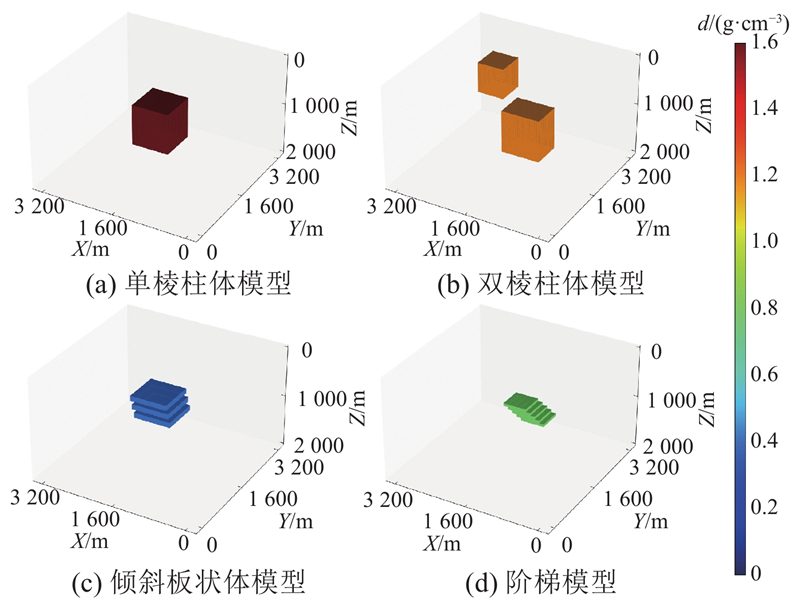
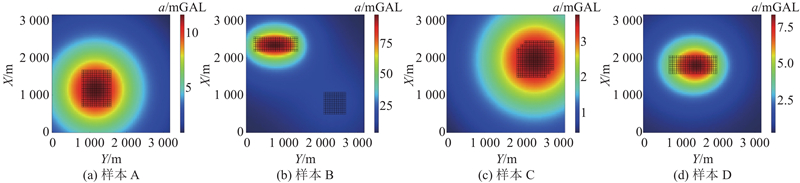
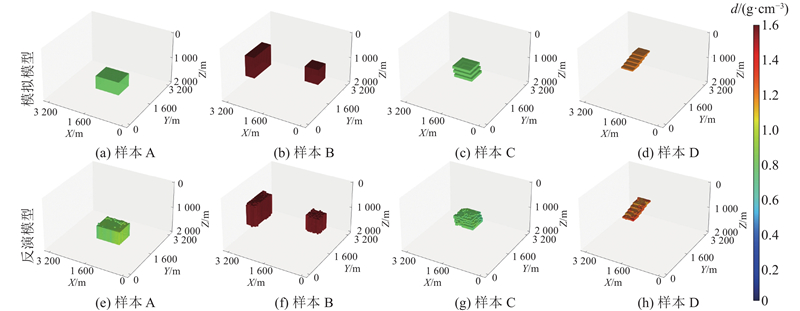
为了测试MRNet的反演效果,从测试集中随机选取4类测试样本,分别为单棱柱体模型(样本A)、双棱柱体模型(样本B)、倾斜板状体模型(样本C) 和阶梯模型(样本D). 其中样本B包含2个异常体,分别处于不同的深度,深层异常体引起的重力异常相较于浅层异常体较小,难以直接分辨. 样本C中的倾斜异常体由3层板状体组成,所处深度较大. 样本D中的薄层异常体由5层板状体组成,其厚度较小,边界曲折,难以预测. 如图8所示为各测试样本的重力异常,使用方框标注异常体的水平轮廓.
图 8
图 9
图 9 测试样本的模拟模型与MRNet的反演模型
Fig.9 Simulation model of test sample and inverse model of MRNet
表 2 测试样本各特征预测值的最大绝对误差
Tab.2
| 样本 | ||||
| A | 0 | 0.73 | 1.49 | 0.19 |
| B | 0 | 0.98 | 1.48 | 0.07 |
| C | 0 | 1.36 | 2.22 | 0.01 |
| D | 0 | 1.07 | 1.32 | 0.18 |
2.4. 对比分析
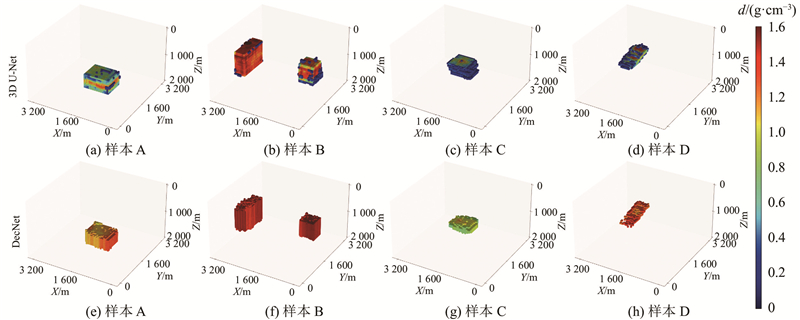
使用3D U-Net和DecNet验证MRNet的优越性,设置相同的数据集和超参数训练网络. 3D U-Net每轮训练耗时约为40 min,是MRNet的13倍,验证了特征分解在加速网络训练上的有效性,DecNet每轮训练耗时与MRNet相近. 使用相同的4种测试样本进行预测,如图10所示. 3D U-Net(见图10(a)~(d))可以预测出4类样本的大致位置和形状,但出现了较大的剩余密度偏差,且在模型边缘出现较多的异常点突起. DecNet(见图10(e)~(h))相较于3D U-Net消除了大部分的异常点突起,但异常体边缘较模糊,存在剩余密度不均的现象,对于样本A出现了严重的剩余密度偏差. MRNet(见图9(e)~(h))在DecNet的基础上大幅消除了剩余密度误差,反演模型的边缘更加清晰完整.
图 10
为了定量分析3种反演网络的优劣,使用平均绝对误差MAE、全局绝对准确率Eacc和局部相对准确率Racc衡量反演网络在测试集上的效果.
式中:
表 3 3种反演网络的平均绝对误差、全局绝对准确率和局部相对准确率
Tab.3
| 网络 | MAE/10−3 | Eacc/% | Racc/% | ||||||
| t1 = 0.001 | t1 = 0.01 | t1 = 0.1 | t2 = 1.05 | t2 = 1.10 | t2 = 1.15 | t2 = 1.20 | |||
| 3D U-Net | 1.10 | 98.86 | 98.98 | 99.61 | 21.43 | 37.55 | 49.51 | 58.33 | |
| DecNet | 1.70(+0.60) | 98.84(−0.01) | 98.95(−0.03) | 99.60(−0.01) | 20.92(−0.51) | 37.34(−0.21) | 48.97(−0.54) | 56.83(−1.50) | |
| MRNet | 0.78(−0.32) | 98.93(+0.08) | 99.25(+0.27) | 99.88(+0.27) | 53.00(+31.58) | 75.27(+37.71) | 84.67(+35.16) | 88.91(+30.58) | |
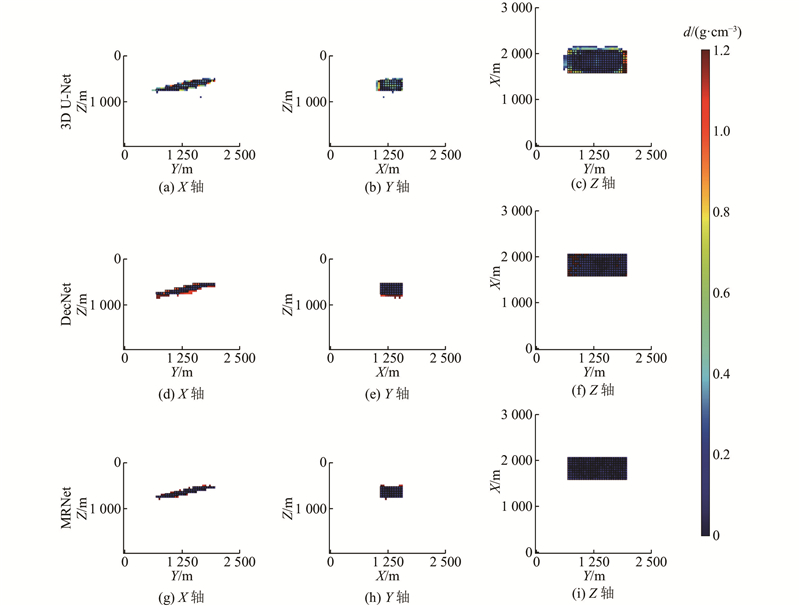
由于样本D属于薄层异常体,且具有复杂轮廓,对算法反演能力的要求更高,以样本D为例进一步分析MRNet在反演异常体轮廓上的优势. 将样本D的反演模型与模拟模型作差得到误差模型,将误差模型分别沿X、Y和Z轴进行最大值投影,结果如图11所示. 图中,黑色方框为异常体轮廓. 3D U-Net反演模型的误差主要聚集在异常体的轮廓,较多的误差点包裹着异常体,使其轮廓难以分辨. DecNet的误差点有所减少,且对于异常水平区域的反演完全准确,误差点主要存在于异常体的下表面. MRNet对于水平区域的反演完全准确,在DecNet的基础上大幅减少了误差点,对异常体整体轮廓的反演更准确.
图 11
图 11 样本D的3种误差模型投影结果
Fig.11 Projection result for three error models of sample D
3. 实测数据实验
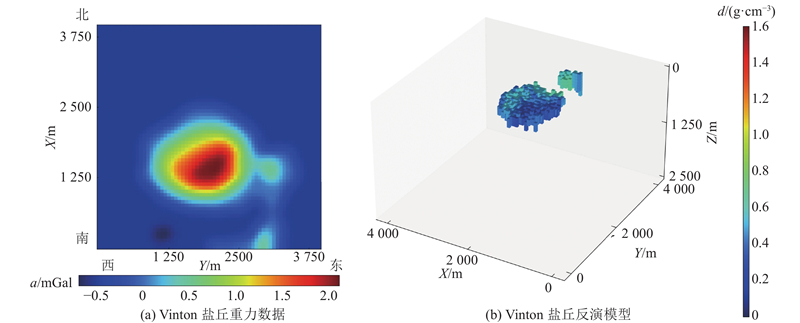
为了验证本文算法在实际反演中的效果,将MRNet应用于Vinton盐丘的重力数据反演实验中. Vinton盐丘位于美国路易斯安那州西南部,主要由大型盐核及顶部的岩盖组成. 其中岩盖主要由石灰岩和无水岩组成,平均密度约为2.75 g/cm3,剩余密度约为0.55 g/cm3. Ennen等[19-21]的研究结果显示,盖岩南北向距离约为1 100 m,东西向距离约为1 500 m,顶部所处深度为130~160 m,底部埋深为360~460 m. 2008年,Bell Geospace公司在该区域进行了航空重力数据测量,使用2.2 g/cm3的围岩密度进行地形改正,从中选取盖岩主体所在的4 000 m×4 000 m区域进行实验. 将该区域均匀划分为64×64个网格,在深度方向上划分为40个网格,网格棱长为4 000 m/64=62.5 m. 将区域内的数据进行插值获取尺寸为64×64的数据,如图12(a)所示.
图 12
图 12 Vinton盐丘的重力数据与MRNet的反演结果
Fig.12 Gravity data from Vinton salt dome and MRNet inversion result
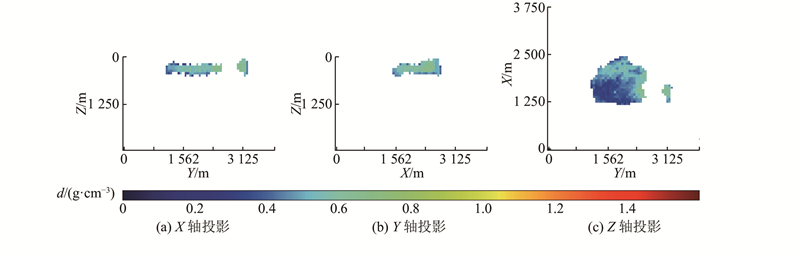
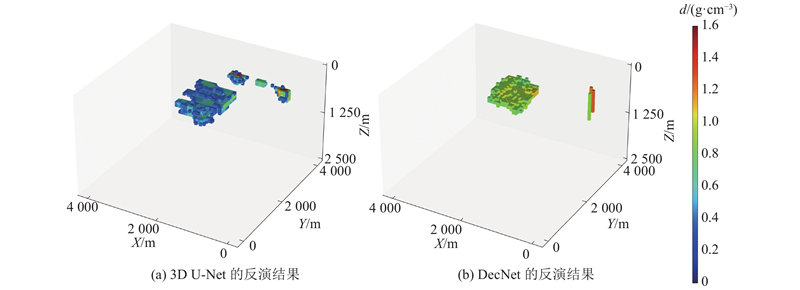
MRNet的反演模型如图12(b)所示. 将反演结果分别沿X、Y和Z轴进行投影,如图13(a)~(c)所示. 从反演结果可知,盖岩顶部埋深约为156 m,底部埋深约为468 m,在X轴方向上长约为1 250 m,在Y轴方向上长约为1 500 m,平均剩余密度约为0.48 g/cm3. 反演结果与已有成果基本一致,验证了MRNet的有效性. 此外,反演结果显示盖岩的高密度部分位于其东南部,盖岩东侧存在小型地质体,这与侯振隆等[22]的研究结果一致. 3D U-Net和DecNet的反演结果如图14所示. 3D U-Net的反演模型边缘存在大量的密度异常点,周围出现了一些散落的异常体. DecNet虽然能够得到盖岩的大致分布,但剩余密度相较于已有资料出现了明显的偏差,未能捕获盖岩东侧的小型地质体. 总体来说,MRNet对盖岩形状、位置和剩余密度的预测更准确,能够捕获主体东侧的小型地质体.
图 13
图 13 Vinton盐丘反演结果的三轴投影
Fig.13 Triaxial projection of Vinton salt dome inversion result
图 14
4. 结 语
针对基于深度学习的三维目标反演算法,加速反演网络训练过程,提出基于多特征重构的三维目标反演算法. 通过特征分解实现对三维模型的压缩,降低网络计算时的内存占用. 设计多特征重构反演网络MRNet,实现对水平区域、中心深度、垂直厚度和剩余密度4类特征的预测. 利用特征重构,得到目标的三维模型. 在MRNet的输入端,通过梯度联合增强目标的水平边界信息. 在跨层连接处,引入CA模块,使解码器自适应地关注更重要的特征,实现预测功能的分化. 在模拟数据测试集上MRNet的局部相对准确率相较于3D U-Net提升了30%以上,取得了更优的反演效果. 将MRNet应用于Vinton盐丘地区,获得盖岩的分布情况和剩余密度,且与前人的研究成果相符,验证了MRNet具有较好的泛化性能.
参考文献
Compact gravity inversion
[J].DOI:10.1190/1.1441501 [本文引用: 1]
3-D inversion of gravity data
[J].DOI:10.1190/1.1444302 [本文引用: 1]
Focusing geophysical inversion images
[J].DOI:10.1190/1.1444596 [本文引用: 1]
多尺度逐次逼近遗传算法反演大地电磁资料
[J].
Multiscale genetic algorithm and its application in magnetotelluric sounding data inversion
[J].
量子遗传算法在大地电磁反演中的应用
[J].DOI:10.1002/cjg2.1347 [本文引用: 1]
Quantum genetic algorithm and its application in magnetotelluric data inversion
[J].DOI:10.1002/cjg2.1347 [本文引用: 1]
MT-重力模拟退火联合反演研究
[J].
Study on simulated-annealing MT-gravity joint inversion
[J].
基于混沌-粒子群优化的磁法数据非线性反演方法
[J].
Nonlinear inversion of magnetic data based on chaotic and particle swarm optimization
[J].
蚁群算法在磁测资料反演解释中的应用
[J].
The application of ant colony algorithm to the inversion and interpretation of magnetic data
[J].
基于卷积神经网络识别重力异常体
[J].
The identification of gravity anomaly body based on the convolutional neural network
[J].
Three-dimensional gravity inversion based on 3D U-Net++
[J].DOI:10.1007/s11770-021-0909-z [本文引用: 1]
Deep learning for 3-D inversion of gravity data
[J].
DecNet: decomposition network for 3D gravity inversion
[J].DOI:10.1190/geo2021-0744.1 [本文引用: 1]
3-D radial gravity gradient inversion
[J].
基于阈值约束的协克里金法联合反演重力与重力梯度数据
[J].
Joint inversion of gravity and gravity gradient data based on Cokriging method with the threshold constrain
[J].