在2007年的美国规范中[6],断索计算动力放大系数(dynamic amplification factor,DAF)建议取2.0. 许多学者从结构安全性的角度研究了断索对斜拉桥的影响,并对于DAF取值的合理性进行了讨论. Wolff等[7]研究表明,斜拉桥某根拉索断索后主梁最不利位置处的弯矩DAF一般小于2.0. Mozos等[8]通过试验得知,约0.005 5 s为完好钢绞线的平均断裂时间. Zhou等[9-10]建立斜拉桥简化有限元模型,研究在随机风、汽车作用下,不同位置拉索发生断裂时的动力响应,结果表明,拉索的断索DAF取2.0是较为合理的. Hoang等[11]通过简化拉索模型实验及全桥有限元模型,研究大跨度斜拉桥不同位置拉索断裂时的动力响应,讨论了断索DAF取值的合理范围.
前期研究大多基于商业有限元软件,主要研究对象为公路斜拉桥、悬索桥. 本研究开发用于缆索承重桥梁断索计算的隐式非线性有限元动力计算程序,以G3铜陵公铁两用斜拉-悬索协作体系桥为研究对象,构建全桥计算模型,研究结构断索动力响应,以及列车-桥梁耦合动力作用下,突然断索时结构与桥上行驶列车的动力响应特性.
1. 计算方法
1.1. 断索状态的有限元非线性动力时程算法
共旋坐标系法(co-rotational formulation)是解决杆、梁结构非线性有限元计算的有效方法[22]. 在基于共旋坐标系的非线性有限元静力算法基础上,开发使用杆、梁单元的三维非线性Newmark-β动力时程算法,结构有限元模型非线性振动方程如下:
式中:x(t)为当前时间t有限元模型各个节点总体位移向量;M为总体质量矩阵,C为总体阻尼矩阵;F[x(t)]为结构振动偏离静力平衡位置时导致的节点总体内力向量,Pd[x(t)]为节点总体外部动力向量,Pw[x(t)]为恒载作用的节点总体外力向量,Pn[x(t)]为单元初始应变加恒载变形导致的节点总体内力向量,在非线性计算中它们都与位移向量x(t)相关,在有限元计算中基于x(t)计算共旋坐标系. 依据Newmark-β法计算规则,在动力时程计算中,结构由t1时刻经过小时间步长到t2时刻,t1、t2时刻位移、速度、加速度之间的关系如下:
式中:a0~a5为积分参数. 将式(2)代入式(1)得到
当桥梁结构上无外部荷载的动力作用时,Pd[x(t)]=0,同时Pw[x(t)]+Pn[x(t)]=0,结构在恒载下处于静力平衡状态,这时结构无动力响应.
当桥梁在恒载静力平衡状态下发生突然断索时,在断裂时间点将断裂单元刚度矩阵置零,达到瞬时移除结构模拟断索破坏的效果. 同时,断裂杆单元的初始张力置零,恒载产生的内力也置零,Pn(x(t))发生了变化,导致Pw[x(t)]+Pn[x(t)]≠0. 这时,式(1)中右端不为零,在对式(3)动力时程积分计算中,结构发生振动.
在本研究斜拉-悬索桥计算中,拉索以及吊索使用一根考虑初始张力的杆单元模拟. 在拉索与吊索单元刚度矩阵置零后,斜拉索断索单元的节点仍与桥塔和主梁连接,吊索断索单元的节点仍与主缆和主梁连接,不会出现节点无约束或刚度为零的情况. 因此,在动力时程计算中,当单元刚度矩阵、单元力向量置零后,重新组集的结构总体刚度矩阵不会出现矩阵奇异.
在本研究程序中,还设计了能够考虑在持续的外部动力作用,即Pd(x(t))≠0时,结构已经发生振动情况下,同时叠加断索的场景算法. 可用于模拟列车-桥梁耦合动力作用下桥梁的断索状态.
1.2. 算例验证
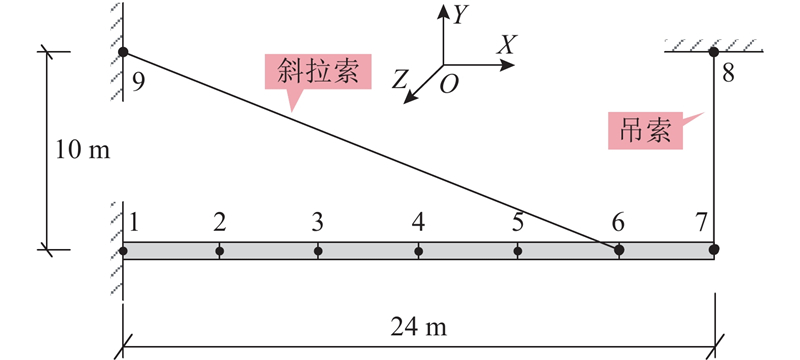
使用简单的索-梁组合结构对本研究算法进行验证,结构布置如图1所示. 梁结构分为6个三维梁单元,索结构为2个带张力的三维直杆单元.
图 1
梁的弹性模量E=2.0×1011 Pa,剪切模量G=1.0×1011 Pa,不计泊松比,材料质量密度ρ=7 800 kg/m3,截面积A=0.1 m2,抗弯惯性矩Iz=2.0×10−3 m4,Iy=2.0×10−3 m4. 吊索与斜拉索弹性模量、材料质量密度与梁相同,截面积均为A=3.0×10−4 m2,吊索初始张力H1=5.0×104 N,斜拉索初始张力H2=1.0×104 N. 模型节点1、8、9为固结约束. 重力加速度g=9.8 m/s2. 使用集中质量矩阵.
拆除连接节点7的吊索杆单元,但不移除杆单元分配给节点7的质量,静力计算得到节点6在Y方向的位移为−0.130 1 m,节点7在Y方向的位移为−0.160 8 m. 斜拉索张力为
表 1 断索工况设置
Tab.1
| 工况号 | Fc/(104 N) | Fd/(104 N) | tx/s | td/s | D6/m |
| 1 | 1.0 | 5.0 | 未断索 | 0.5 | |
| 2 | 1.0 | 20.0 | 未断索 | 2.0 | |
| 3 | 1.0 | 20.0 | 10.0 | 1.0 |
图 2
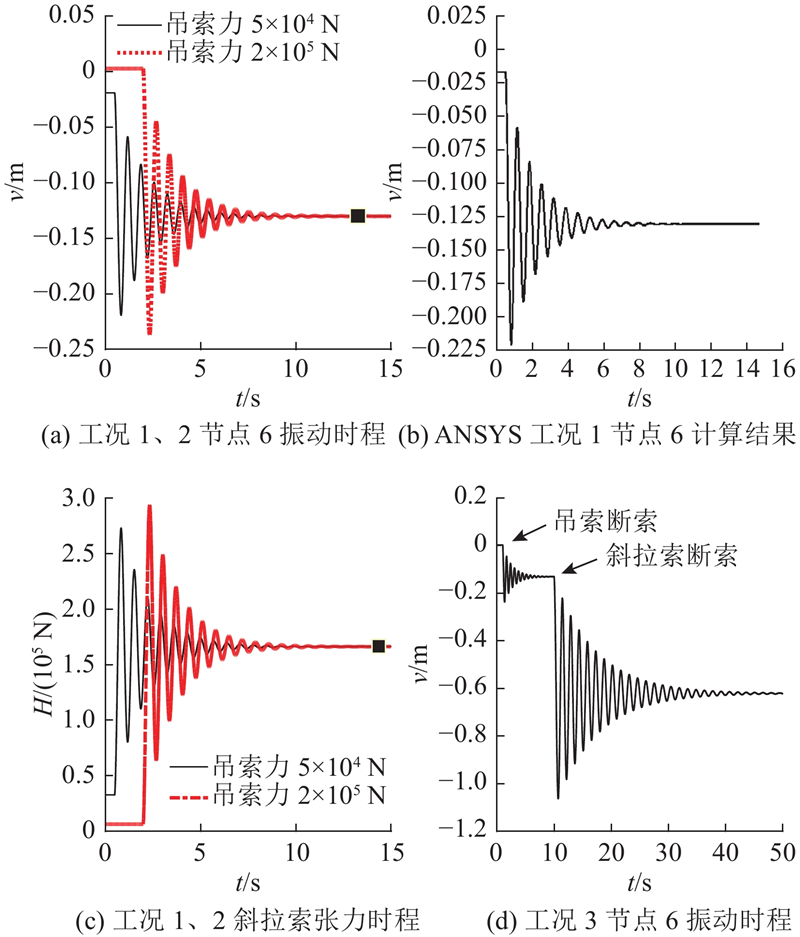
图 2 简单索-梁模型不同断索工况下位移与索力动力响应
Fig.2 Displacement and cable force dynamic response of simple cable-beam model under different cable fracture conditions
上述计算结果与物理事实规律一致,同时通过与ANSYS结果进行对比,可以验证本研究计算程序设计的正确性.
1.3. 全桥有限元模型
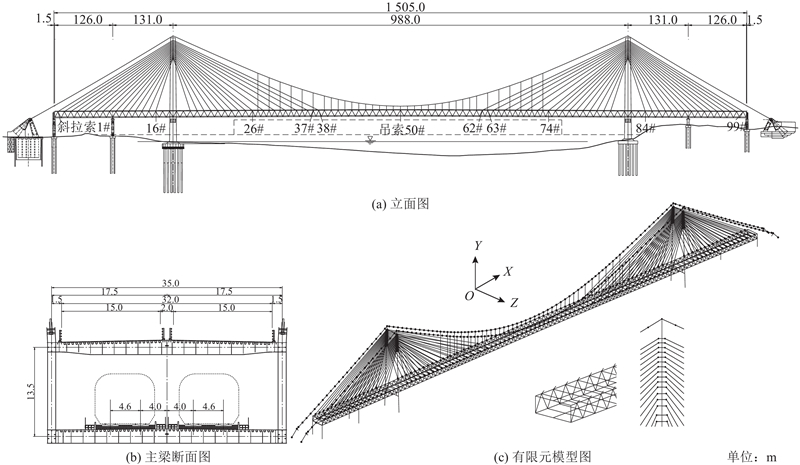
G3铜陵长江公铁大桥(主跨为988 m,全长为1 505 m)为世界首座双层斜拉-悬索协作体系公铁两用大桥(以下简称为斜拉-悬索桥). 上层桥面布置为6车道高速公路,设计时速为100 km/h. 下层桥面布置为4线铁路,最高设计时速为250 km/h. 全桥总体布置如图3所示.
图 3
图 3 斜拉-悬索桥结构总体布置与有限元模型图
Fig.3 General arrangement and FEM model diagram of cable-stayed suspension bridge
下层主梁从Z轴负方向到正方向依次为第1~4列车车道,车道中心线位置如图3(b)所示.
按照实际设计进行结构约束设置. 主梁、桥塔使用三维梁单元,主缆、斜拉索、吊索使用考虑初始张力的三维杆单元模拟,使用Ernst公式修正斜拉索弹性模量. 塔柱横梁使用梁单元刚臂延伸至主梁处,根据实际约束条件耦合主缆梁上连接节点的自由度. 钢桥阻尼比设置为0.005,重力加速度g=9.8 m/s2.
桥塔采用C60混凝土,主梁为钢桁架结构,在统计主梁上铺装质量后,采用质量点单元根据节点位置将二期恒载分配到主梁上. 如图3(c)所示,主梁上下车道的纵向桥面均使用带刚臂的“鱼刺梁模型”模拟,为了更符合实际情况,斜拉索锚固点在主梁和桥塔上使用刚臂单元进行延伸.
2. 断索状态下桥梁结构动力响应
2.1. 单根斜拉索及吊索断索动力响应
图 4
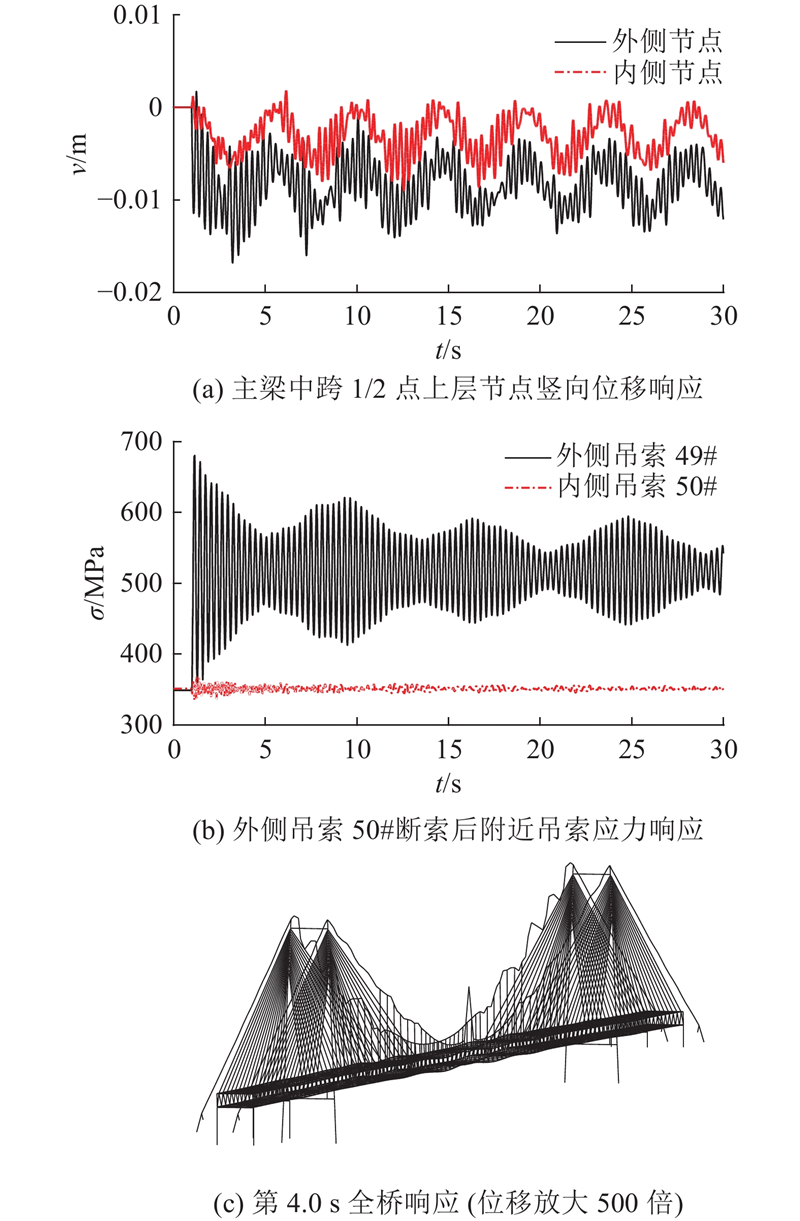
图 4 外侧吊索50#断索后桥梁结构动力响应
Fig.4 Dynamic response of bridge structure after fracture of outside suspender cable 50#
图 5
图 5 外侧斜拉索38#断索后桥梁结构动力响应
Fig.5 Dynamic response of bridge structure after outside stayed cable 38# fracture
在实际情况中,双侧同时受到极端作用导致断索的几率相对较小,所以这里计算全桥各个位置外侧断索后剩余其余斜拉索与吊索在主梁下沉动力冲击作用下的最大应力响应,如图6所示. 图中,N为拉索与吊索编号,σmax为各个剩余索的断索最大应力响应.
图 6
图 6 全桥外侧各个位置断索时剩余斜拉索、吊索最大应力响应
Fig.6 Maximum stress of other stayed cables and suspender cables with cable fracture at each position
式中:Sdmax为断索动力冲击作用下各个斜拉索与吊索的最大动应力;Ss为考虑断索后,静力计算得到的各个斜拉索与吊索的应力;S0为成桥状态下各个斜拉索与吊索的应力.
由图6(e)可以看出,在斜拉索与吊索交替区域,吊索断索后对邻近吊索的影响更为明显. 当吊索45#断裂时,吊索44#与吊索46#应力增幅较大,当吊索40#断裂时,吊索39#与吊索41#应力增幅较大,当吊索37#断裂时,临近的第1根吊索35#与吊索39#应力增幅较大,而吊索36#与吊索38#为斜拉索,其应力增幅较小.
由图6(e)、(f)可以看出,当跨中距离桥塔越近的斜拉索与吊索断索后,剩余斜拉索、吊索的最大应力响应越小.
2.2. 极限状态下的断索动力响应
斜拉-悬索桥不同区域单侧斜拉索与吊索多根同时断索后斜拉索与吊索的最大应力计算结果如图7所示.
图 7
图 7 斜拉-悬索桥不同区域外侧断索的最大应力响应
Fig.7 Maximum stress of cable fracture in different regions of cable-stayed suspension bridge
如图7(a)所示为跨中外侧吊索48#~吊索52#,共5根吊索断索的计算结果. 可以看出,由于悬索结构特性,断索后冲击力主要由靠近断索位置附近的第1根吊索承担,吊索47#与吊索53#应力增幅较大(由约350 MPa增加至接近2 000 MPa),吊索46#与吊索54#应力增幅相对较小(由约350 MPa增加至360 MPa),其他剩余吊索与斜拉索应力增幅较小. 吊索47#、53#索力增幅超过该桥吊索设计强度1 770 MPa,因此,若斜拉-悬索桥上发生极端事故,造成中跨吊索区域断索4根以上,较大可能会发生吊索连续断索,导致主梁垮塌. 跨中吊索断索极限状态计算结果与文献[19]针对悬索桥研究得到的结论接近.
如图7(b)所示为斜拉索-吊索交替区域31#~38#共8根断索的计算结果,其中单数为吊索,双数为斜拉索. 可以看出,吊索29#应力增幅较大,接近1 400 MPa,其他斜拉索应力增幅较为均匀但都较小;斜拉索30#应力增加至700 MPa;吊索39#最大应力增加至接近1 400 MPa,其他吊索应力增幅较小.
如图7(c)所示为斜拉索区域斜拉索18#~26#共9根断索计算结果. 在斜拉索区域断索后,在图中标识的剩余拉索中,应力增幅较大的17#、28#、30#~38#等均为斜拉索,断索冲击力被更均匀地分散到剩余斜拉索中,其中最大应力接近1 200 MPa. 吊索应力增幅相对较小.
综上,由于斜拉索与吊索成桥索力差别较大,且斜拉索与吊索的承力方式有所差别,斜拉索体系与吊索体系的断索动力响应耦合程度较低. 在吊索区域多根断索,主要影响剩余吊索中最靠近断索位置的第1根吊索. 斜拉索-吊索交替区域多根断索,也主要影响剩余吊索中最靠近断索位置的吊索. 斜拉索区域多根断索,主要影响剩余斜拉索,冲击力会被剩余斜拉索更均匀地分担.
斜拉-悬索桥总体上具有较高的断索安全冗余. 对于安全冗余的判断:跨中吊索区域最低,斜拉索-吊索交替区域较高,斜拉索区域最高.
3. 列车-桥梁耦合动力作用下的断索动力响应
列车的桥上位置与断索时刻必然有着复杂的工况组合,经试算,选取的工况组合如表2所示. 表中,工况1为无断索状态,是日常运营中经常发生的情况;工况2为吊索断裂后全桥处于静止状态时的列车-桥梁耦合振动;工况3~6为发生吊索断索事故时概率相对较大的情况;工况7为概率较小的情况. 为了考察桥梁结构的安全性,设置了极端工况8、9.
表 2 列车作用下发生断索时各个计算工况列表
Tab.2
| 工况编号 | 列车数量 | 列车行驶车道以及方向 | 断索时第1轮对位置 | 断裂吊索编号 | 主梁提取结果位置 |
| 1 | 1 | 第4车道正向(外侧) | — | 无斜拉索、吊索断裂 | 跨中下层双侧端节点 |
| 2 | 1 | 第4车道正向 | — | 外侧吊索50#已断裂,桥梁静止状态 | 跨中下层外侧端节点 |
| 3 | 1 | 第4车道正向 | 主梁位移最大时位置 | 吊索50#,外侧 | 跨中下层外侧端节点 |
| 4 | 1 | 第4车道正向 | 吊索50#锚点处 | 吊索50#,外侧 | 跨中下层外侧端节点 |
| 5 | 1 | 第4车道正向 | 吊索45#锚点处 | 吊索45#,外侧 | 吊索45#锚点处下层外侧节点 |
| 6 | 1 | 第4车道正向 | 斜拉索38#锚点处 | 斜拉索38#,外侧 | 斜拉索38#锚点处下层外侧节点 |
| 7 | 2 | 第3、4车道正向 | 吊索50#锚点处 | 吊索50#,外侧 | 跨中下层外侧端节点 |
| 8 | 4 | 第1、2逆向,3、4车道正向 | — | 外侧吊索50#已断裂,桥梁静止状态 | 跨中下层外侧端节点 |
| 9 | 4 | 第1、2逆向,3、4车道正向 | 吊索50#锚点处 | 吊索50#,外侧 | 跨中下层外侧端节点 |
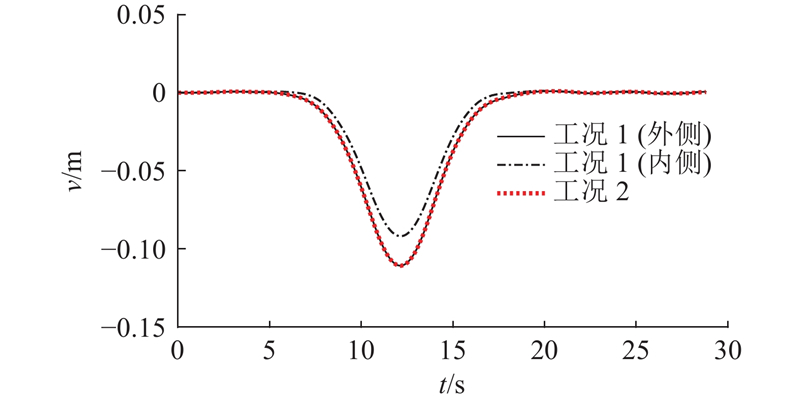
图 8
图 8 工况1、2主梁中跨1/2点位移响应
Fig.8 1/2 point displacement response of middle span of main beam under working condition 1 and 2
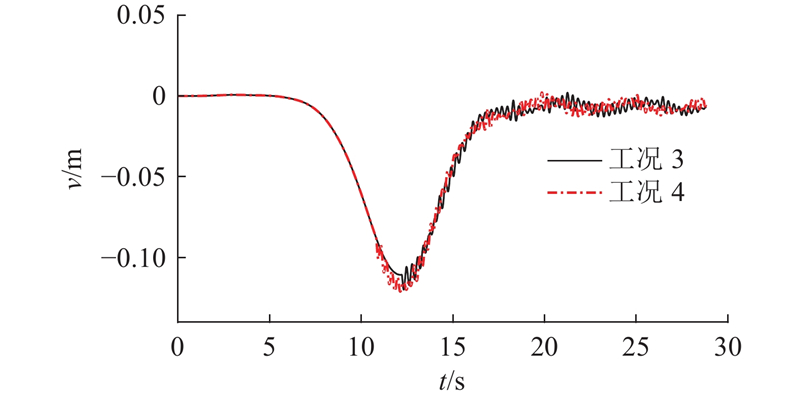
如图9所示,在工况3、4中,当列车通过桥梁时,若吊索50#发生断裂,主梁中跨1/2点在列车动力作用下的时程曲线发生了突变,最大突变响应约为0.01 m,在工况4中,列车达到吊索50#锚固位置时发生断索,较工况1(当列车使主梁位移最大时发生断索)的位移响应更为明显.
图 9
图 9 工况3、4主梁中跨1/2点位移响应
Fig.9 1/2 point displacement response of middle span of main beam under working condition 3 and 4
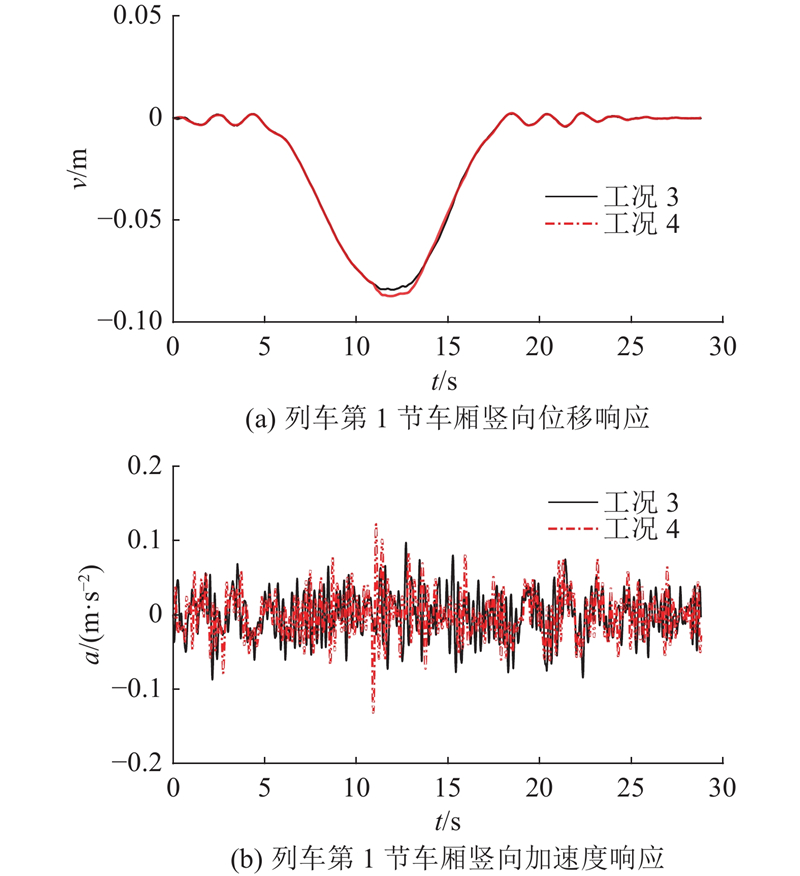
图 10
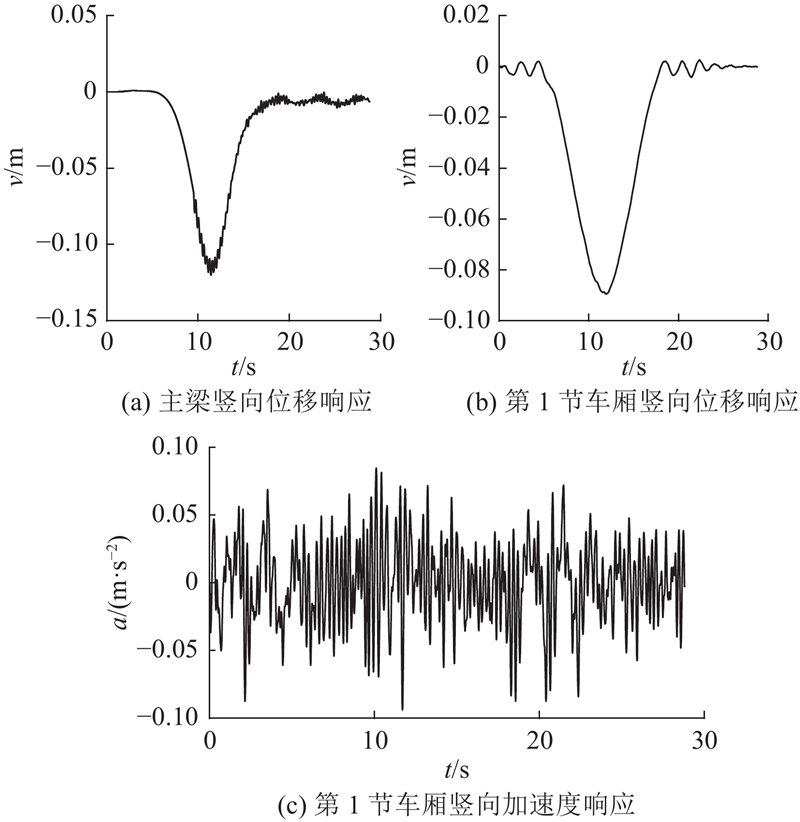
图 11
图 11 工况5桥梁与列车动力响应
Fig.11 Dynamic response of bridge and train in working condition 5
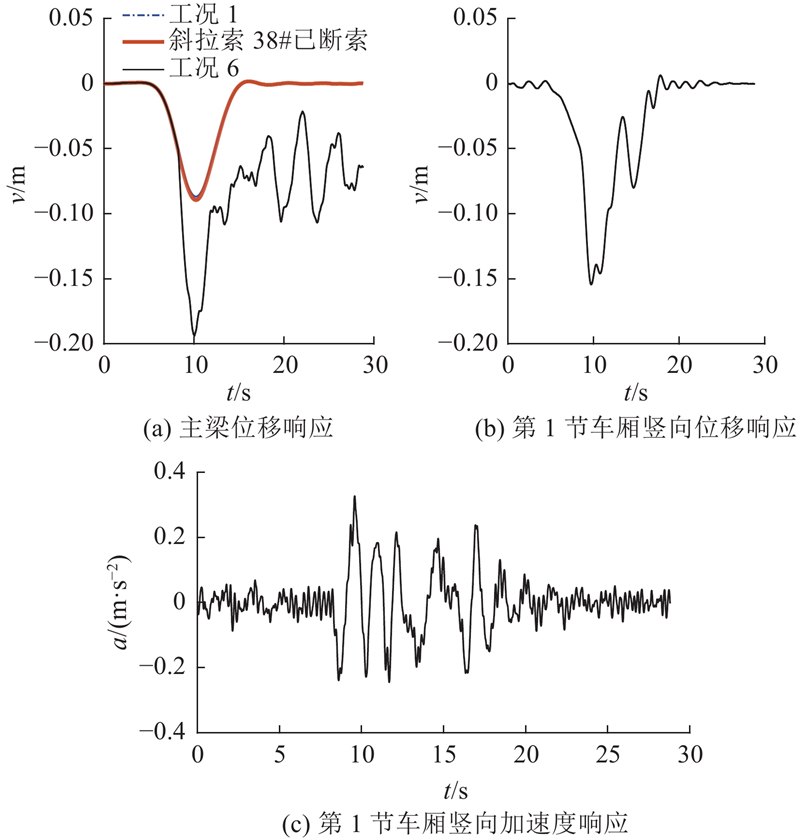
如图12所示为工况6下的桥梁与列车动力响应. 在工况6中,在列车第1轮对到达斜拉索38#时,拉索发生断索,主梁位移响应接近0.20 m,第1节车厢位移响应约为0.15 m,列车竖向加速度响应突变至约0.4 m/s2,大于单根吊索断索的工况下的. 若拉索38#已经发生断裂,与工况1中斜拉索、拉索不发生断裂的情况对比,主梁位移差别约为0.01 m,可以在保持列车通行状态下进行维修.
图 12
图 12 工况6桥梁与列车动力响应
Fig.12 Dynamic response of bridge and train in working condition 6
依据第2节的分析,在斜拉-悬索协作体系桥中,在斜拉索断索后,主梁冲击力与多余重量主要由剩余斜拉索分散承担,因此,虽然斜拉索38#位于斜拉索、吊索交替区域,但斜拉索断索后,主梁的动力响应特性更接近斜拉桥的. 由于斜拉索为斜向支撑,断索后主梁位移相对较大,这与文献[26]中得到斜拉桥的断索响应类似.
由工况6计算结果可以看出,列车车厢的竖向加速度在斜拉索断索时发生较为明显的突变,但车厢总体加速度较小,依据文献[27],车体竖向加速度小于2.45 m/s2,在安全范围内.
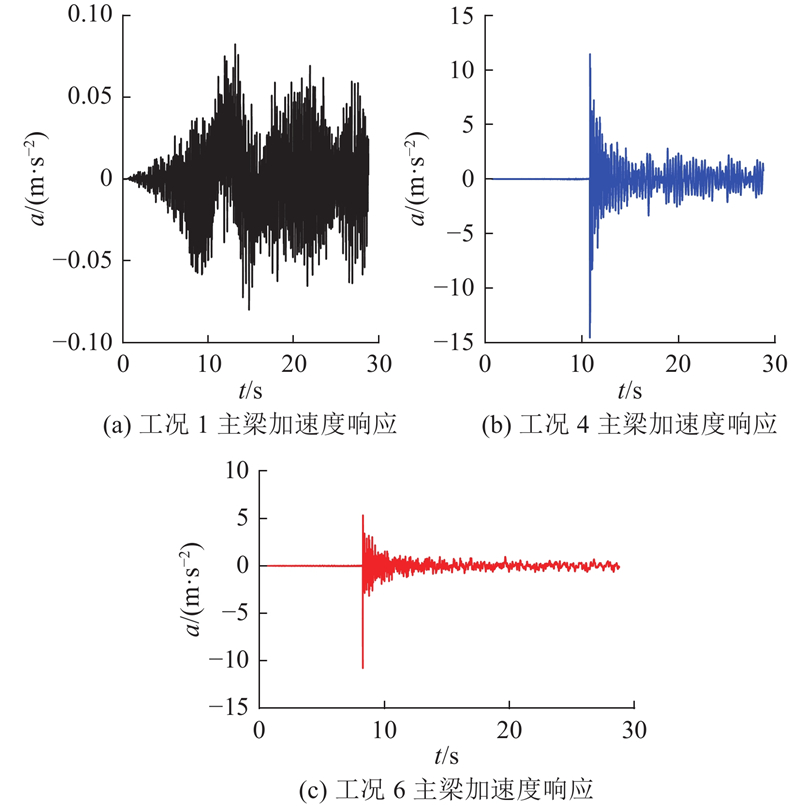
在工况1、4、6中,当斜拉索与吊索断索时,在主梁端处锚固位置,桥梁模型主梁下层靠外侧节点竖向加速度a的时程响应如图13所示. 在不断索的工况1中主梁加速度响应较小,在工况4中,吊索50#突然发生断裂,加劲梁跨中位置加速度响应绝对值突然增加至接近15 m/s2. 在工况6中,在吊索断裂瞬间,断索造成的冲击作用,导致主梁上断索处靠近轨道的局部位置发生了较高频率的微小振动. 在工况6中,当斜拉索38#断索时,主梁加速度响应绝对值接近10 m/s2.
图 13
图 13 工况1、4、6主梁竖向加速度响应
Fig.13 Acceleration response of main girder in working condition 1,4 and 6
表 3 吊索50#断索各个工况下列车作用占比
Tab.3
| 工况编号 | Q4 | Δσ1/MPa | Δσ2/MPa | B/% |
| 4 | 0.42 | 331.6 | 350.6 | 5.73 |
| 7 | 0.56 | 331.6 | 358.1 | 7.99 |
| 9 | 0.61 | 331.6 | 372.7 | 12.39 |
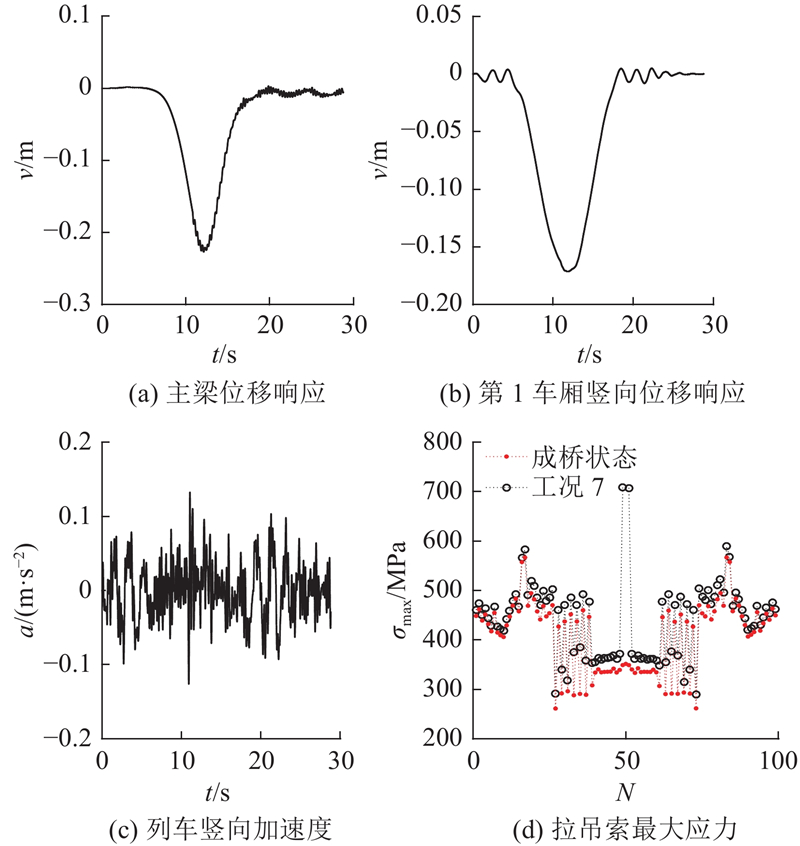
图 14
图 14 工况7桥梁与列车动力响应
Fig.14 Dynamic response of bridge and train in working condition 7
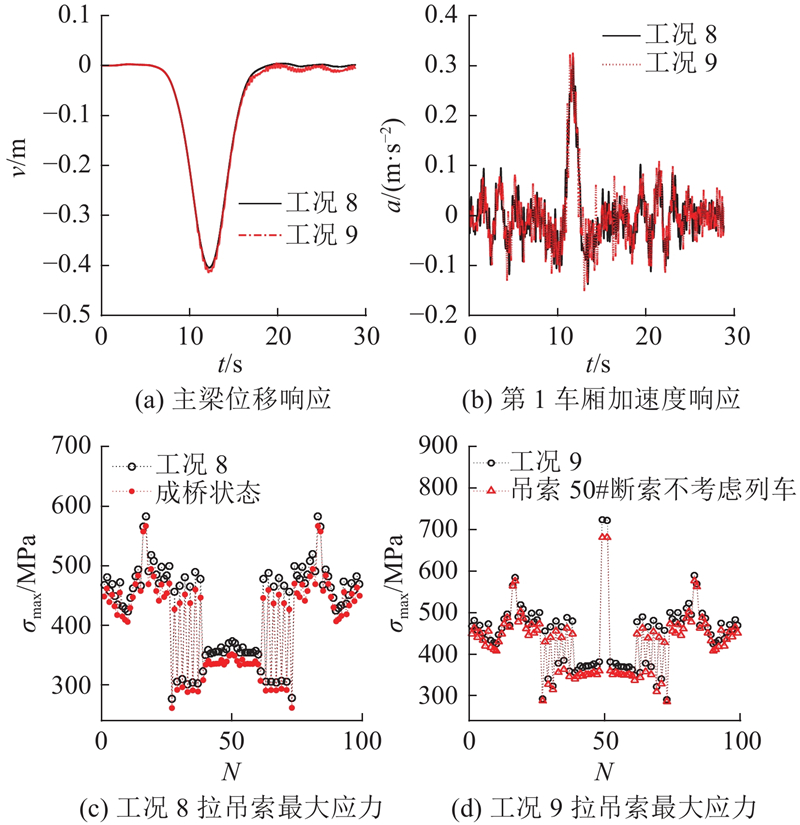
无断索的极端工况8与有断索的极端工况9结果对比如图15所示. 可以看出,断索时主梁位移响应发生了突变;工况9较工况8列车竖向加速度响应略微增加,总体上两者竖向加速度响应(最大约0.32 m/s2)较单列车的工况4计算结果(最大约0.12 m/s2)有较明显增加,说明列车竖向加速度响应变化主要影响因素为列车荷载引起的主梁竖向位移.
图 15
图 15 工况8、9桥梁与列车动力响应
Fig.15 Dynamic response of bridge and train in working condition 8 and 9
工况4与工况7中计算得到的第4车道轮重减载率相对较小,工况9中轮重减载率相对增加,略微超过0.60的安全限值[27],但工况9实际运营发生概率极低,主要用于考察桥梁的动力响应.
4. 结 论
(1)斜拉-悬索桥的主要受力结构为斜拉索,吊索为辅助受力结构. 结构局部刚度较大,若单根斜拉索或吊索意外断裂,可在保持运营的状态下进行换索维修施工.
(2)在斜拉-悬索桥中,当单根斜拉索断索后,主梁失去支撑位置增加的重力与动力冲击作用会较为均匀地分散到剩余其他斜拉索中. 在单根吊索断索后,吊索断索位置的两侧第1根吊索在主梁动力作用下,应力增幅较大,断索冲击作用影响不会向远端吊索扩散. 越接近桥塔的断索引起的斜拉索或吊索应力增幅越小. 单根或多根拉索、吊索断索,动力放大系数DAF取2.0具有较为合理的工程应用价值.
(3)斜拉-悬索桥具有较高的结构安全冗余. 在跨中悬索结构区域,单侧吊索断索4根以上可能导致连续破坏. 斜拉索-吊索交替区域、斜拉索区域在极端作用下单侧断索达到8根时,由于冲击力能更均匀地扩散到斜拉索中,剩余斜拉索与吊索应力也不会超过设计强度,不会导致连续破坏. 本研究计算主要考虑桥梁结构缆索系统的安全性,多根吊索断索极限状态可能导致刚桁架主梁局部发生失稳与屈服,拟在后续研究中开展.
(4)在断索发生时,剩余斜拉索与吊索动应力的增加,主要来自于主梁作用. 在发生断索瞬间,若列车运行至断索位置,会造成列车竖向位移、加速度突变. 在断索发生时主梁局部会出现较大加速度响应,因此后续有必要使用多尺度分析思想,通过宏观模型获取桥梁动力响应,建立精细的轮对与轨道接触数值计算模型,详细研究断索脱离瞬间,高速列车通过时列车轮对与轨道接触的相互作用数据,为列车是否可能在断索作用下发生脱轨提供科学的判定依据.
参考文献
在役桥梁拉吊索腐蚀-疲劳损伤与破断机理分析
[J].
Analysis on corrosion-fatigue damage and fracture mechanism of cables/hangers in service bridges
[J].
大跨独塔斜拉桥拉索梁端锚固区抗疲劳性能
[J].
Fatigue performance of anchorage zone for long-span single pylon cable-stayed bridge
[J].
钢结构桥梁抗火研究综述
[J].
Review on fire resistance of steel structural bridge girders
[J].
近场爆炸时斜拉索抗爆性能分析
[J].
Anti-explosion performance of stay cable under near field blast load
[J].
船桥碰撞过程引发的冲击动力学论题
[J].
Impact dynamics topics motivated by ship-bridge collision process
[J].
Cable loss and progressive collapse in cable-stayed bridges
[J].DOI:10.1080/15732480902775615 [本文引用: 1]
Numerical and experi-mental study on the interaction cable structure during the failure of a stay in a cable stayed bridge
[J].DOI:10.1016/j.engstruct.2011.04.006 [本文引用: 1]
Numerical investigation of cable breakage events on long-span cable-stayed bridges under stochastic traffic and wind-ScienceDirect
[J].DOI:10.1016/j.engstruct.2015.07.009 [本文引用: 1]
Framework of nonlinear dynamic simulation of long-span cable-stayed bridge and traffic system subjected to cable-loss incidents
[J].DOI:10.1061/(ASCE)ST.1943-541X.0001440 [本文引用: 1]
Experimental and dynamic response analysis of cable-stayed bridge due to sudden cable loss
[J].
大跨混凝土斜拉桥施工过程中结构的断索动力响应
[J].
Broken cable-induced dynamic response of long-span concrete cable stayed bridge during construction
[J].
拉索损伤时V形双钢拱塔斜拉桥动力特性及抗震性能分析
[J].
Analysis of dynamic characteristics and seismic performance of V-shape double steel arch cable-stayed bridge with cable damage
[J].
拉索失效和主梁损伤斜拉桥静力性能退化模型试验
[J].
Model test on static performance degradation of cable-stayed bridge with cable rupture and main girder damage
[J].
单根吊索断裂时自锚式悬索桥强健性分析
[J].
Robustness analysis of self-anchored suspension bridge with loss of a single sling
[J].
悬索桥吊索断裂动力响应分析的有限元模拟方法研究
[J].
Research on simulation method of dynamic response analysis for suspension bridges subjected to hanger-breakage events
[J].
悬索桥断索动力响应有限元模型参数研究
[J].
Parameter study on finite element model of abrupt hanger-breakage event induced dynamic responses of suspension bridge
[J].
自锚式悬索桥断索动力冲击效应模型试验研究
[J].
Model testing research of impact effect on self-anchored suspension bridge subjected to hangers fracture
[J].
大跨悬索桥吊索抗火性能与新防护结构研究
[J].
Research on fire resistance performance and new structure idea for long-span suspension bridge slings
[J].
考虑突发断索事故的车桥系统动力行为分析方法
[J].
Dynamic behavior analysis method for vehicle-bridge system considering abrupt cable-breakage events
[J].
基于有限元-向量式有限元的斜拉桥非线性振动计算方法
[J].
Nonlinear vibration calculation method for cable-stayed bridge based on finite element and vector form finite element method
[J].
改进共旋坐标法的Timoshenko梁单元非线性分析
[J].DOI:10.6052/j.issn.1000-4750.2021.07.0508 [本文引用: 1]
Nonlinear analysis of timoshenko beam element based on improved corotational formulation
[J].DOI:10.6052/j.issn.1000-4750.2021.07.0508 [本文引用: 1]
基于流动坐标系的三维空间动力非线性有限元方法
[J].
A nonlinear dynamic finite element method in 3D space based on the co-rotational formulation
[J].
风、列车作用下大跨度斜拉桥索-梁相关振动研究
[J].
Investigation of cable-beam-related vibration in long-span cable-stayed bridge based on wind and train effects
[J].
悬索桥主缆系统设计及架设计算方法研究
[J].
Calculation methods for design and erection of cable curve of suspension bridge
[J].
基于遗传算法的斜拉桥成桥索力优化应用研究
[J].
Application of completed cable force optimization of cable-stayed bridge based on genetic algorithm
[J].