蜉蝣算法(mayfly algorithm, MA)是Zervoudakis等[1]根据自然界中蜉蝣的交配行为提出的群智能算法,结合了粒子群算法、遗传算法和萤火虫算法等经典群智能优化算法的优点,具有良好的全局寻优性能. 与其他群智能算法一样,MA的收敛速度慢且收敛精度低,为此研究者提出改进策略并应用于实际场景. 蒋宇飞等[2]引入Tent混沌映射和高斯变异进行种群调节,采用Sin混沌映射进行种群初始化,利用不完全伽马函数的自适应重力系数和随机反向学习策略优化MA,提高了算法的收敛精度和收敛速度. 王义等[3]提出基于黄金正弦与自适应融合的MA,提升了MA的寻优性能. Li等[4]提出采用混沌初始化、惯性权重和突变策略改进的MA,并将该算法用于解决平衡可再生能源运营成本和污染物排放混合动态经济环境调度模型,使运行成本降低,有效实现了经济与环境的平衡. 基于种群中值位置改进的MA将种群的中值位置引入蜉蝣的速度更新,以非线性重力系数来平衡探索阶段和开发阶段,水轮机调速器PID参数调节的应用结果表明,该算法不仅收敛速度和精度均得到提升,而且在解决实际应用问题时具有良好的性能[5].
综上所述,改进MA的方法集中在种群初始化的优化、参数的优化和与其他算法的结合等,考虑蜉蝣个体间的学习策略和信息交互的策略鲜见. 建设性的学习范例和有效的信息交互可以提高群智能算法的优化性能[6]. Liang等[7]提出交叉学习策略的混合粒子群优化(PSO-CL)算法,并设计基于交叉的综合学习策略来取代自学习策略和全局学习策略;PSO-CL算法基于搜索方向调整机制,将群体划分为2个子群体. Lynn等[8]提出加强探索和开发的综合学习粒子群优化算法,该算法将种群分为只专注勘探和只专注开发2个子种群. 在种群间信息共享的研究方向上,不同的拓扑结构(如全局耦合拓扑[9]、小世界拓扑[10]、金字塔拓扑[11]和环形拓扑[12]等)已被广泛采用.
现有学习策略和用于信息交流的拓扑结构存在不足之处. 一方面,这些学习策略虽然能够提高样本质量和优化性能,但是个体的位置更新策略变得复杂和繁琐;另一方面,固定拓扑结构虽然有助于丰富种群多样性,但是不利于算法后期的收敛. 基于优化粒子群算法的精英与普通粒子协同优化思路[6],本研究提出基于精英协同进化的蜉蝣算法(elite coevolutionary mayfly algorithm, ECMA),采用精英个体与普通个体协同进化策略,在为精英个体提供广泛的搜索空间的同时提升普通个体的集中开发能力;为了提高算法的收敛速度,引入新的自适应权重系数来平衡算法的探索和开发阶段;采用莱维飞行策略提升算法跳出局部最优的概率,丰富种群的多样性.
1. 蜉蝣算法
MA主要包括3个阶段:雄性蜉蝣的运动、雌性蜉蝣的运动以及蜉蝣的交配和变异.
1.1. 雄性蜉蝣的运动
雄性蜉蝣会聚集在一起,根据自身和邻居的经验来调整位置. 假设
式中:
式中:
式中:
式中:
1.2. 雌性蜉蝣的运动
与雄性蜉蝣不同,雌性蜉蝣不会聚集在一起,而是飞向雄性蜉蝣进行交配繁殖. 假设
式中:
式中:
式中:
1.3. 蜉蝣的交配与变异
蜉蝣的交配过程与吸引过程相同:最优的雌性与最优的雄性交配,次优的雌性与次优的雄性交配,依此类推产生2个后代:
式中:
式中:
2. 精英协同进化的蜉蝣算法
2.1. 精英与普通蜉蝣协同进化
在ECMA中,蜉蝣种群被分为精英种群和普通种群,即将性能较好的个体记为精英个体,其余的记为普通个体. ECMA的本质是通过精英个体与普通个体的协同作用实现探索和开发的良好平衡,从而提升算法的性能. 在这个协同作用中,精英个体探索具有巨大潜力的未知区域,普通个体在已经被探索到的潜力区域周围进行挖掘.采取单一复合样例
式中:
2.1.1. 雄性精英蜉蝣的学习范例
在MA中,所有的雄性个体会向蜉蝣群体最佳位置的方向飞去,容易失去种群多样性,算法极易陷入局部最优. 实际上,种群中的精英个体应该承担更多的探索责任,而不是在小区域聚集. 因此,精英个体应该增强抵抗被蜉蝣群体最佳位置吸引的能力,变得更自信,提升自我认知. 精英个体的历史最佳位置具有良好的特性,可能更接近全局最优,精英个体的学习范例为
精英雄性蜉蝣的位置更新为
2.1.2. 雄性普通蜉蝣的学习范例
普通个体的性能低于精英个体,因此不能仅依靠普通个体来探索解空间,可以将它们用于增强精英个体在已经探索到的有潜力区域的局部搜索. 本研究为普通个体设计的学习范例为精英个体历史最佳位置的加权中心. 这里的加权中心不是简单地取平均值,而是进行精英个体历史最佳位置的适应度加权,这种方式使得加权中心包含高质量的信息,能够为普通个体提供更好的优化方向. 加权中心的计算步骤如下. 1)根据适应度值计算精英个体的权重:
式中:
式中:
普通雄性蜉蝣的位置更新为
式中:
2.1.3. 精英蜉蝣数量的动态变化策略
精英蜉蝣的数量与普通蜉蝣数量直接决定ECMA的种群多样性和收敛速度. 在算法迭代的前期,注重维持种群的多样性,寻找有潜力的搜索区域,随着迭代次数的增加,重点转向局部的开发. 基于该原则,提出精英蜉蝣数量的动态变化策略
式中:
2.1.4. 雌性蜉蝣的位置更新
婚姻市场理论为社会学理论观点.该理论认为,在寻求配偶时,双方以交换方式获得所需资源. 市场可能出现供需不平衡,无法找到合适伴侣的情况. 在这种情况下,女性倾向于找更有社会地位或有其他资源优势的男性作为伴侣[13]. 对于雌性蜉蝣而言,如式(5)所示,MA中如果出现雌性蜉蝣的适应度比雄性蜉蝣更优时,雌性蜉蝣不会被雄性蜉蝣吸引,而是进行随机飞行,这不利于算法的收敛. 受婚姻市场理论启发,本研究提出新的雌性蜉蝣的位置更新规则:当雌性蜉蝣没有被雄性蜉蝣吸引时,即雌性蜉蝣的适应度值小于雄性蜉蝣的适应度值时,雌性蜉蝣会被由精英雄性蜉蝣个体的历史最佳位置组成的加权中心吸引,具体的实现方式为
式中:
2.2. 新的自适应重力系数
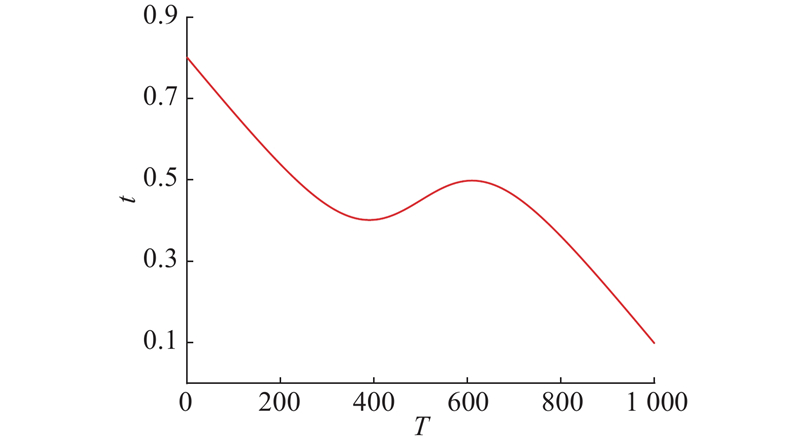
在MA中,重力系数对平衡搜索和开发能力起指导作用,展现了蜉蝣借鉴先验行为的能力. 重力系数的取值直接影响蜉蝣个体在迭代过程中的收敛速度和全局寻优能力. 参考文献[14],对logistic回归在[−6,6]的图像进行数学变换处理,引入用于改进MA的自适应非线性重力系数:
式中:
图 1
图 1 精英协同进化的蜉蝣算法的重力系数曲线
Fig.1 Gravity coefficient curve of elite coevolutionary mayfly algorithm
2.3. 引入莱维飞行的跳出策略
式中:
式中:
2.4. 基于精英协同进化的蜉蝣算法步骤
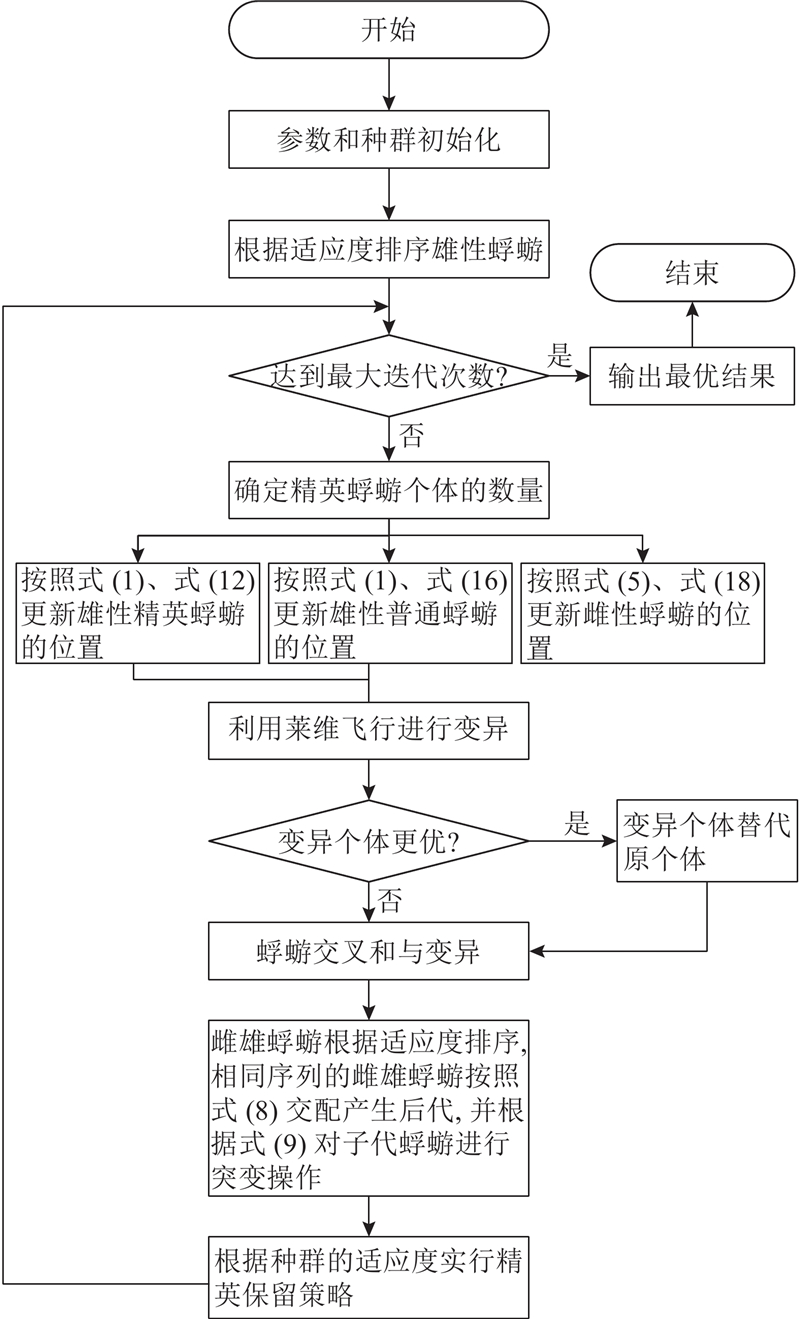
基于MA改进策略的ECMA流程图如图2所示.
图 2
2.5. 时间复杂度分析
假设种群大小为
假设雄性蜉蝣和雌性蜉蝣在每一维度上位置更新所需时间均为
子代种群变异所需的时间为
定义itermax为迭代次数,MA的时间复杂度为
在ECMA中,精英、普通蜉蝣协同进化的策略中增加了计算精英个体的权重时间
ECMA的时间复杂度为
可以看出,ECMA没有增加MA的时间复杂度.
3. 实验结果与仿真实验
仿真实验在Intel(R) Core(TM) i7-8550U CPU @ 1.80 GHz 2.00 GHz,8 GB 内存配置的平台进行,使用 Windows 10 操作系统,仿真软件为Matlab R2021a. 选取20个具有不同特征的基准测试函数进行ECMA的寻优性能验证,函数分为单峰和多峰2个类型,函数的详细信息如表1所示.
表 1 基准测试函数
Tab.1
| 类型 | 编号 | 名称 | 维度 | 取值范围 | 最优值 |
| 单峰函数 | F1 | sphere | 30 | [−100,100] | 0 |
| F2 | Schwefel’s problem 2.22 | 30 | [10,10] | 0 | |
| F3 | Schwefel’s problem 1.2 | 30 | [−100,100] | 0 | |
| F4 | Schwefel’s problem 2.21 | 30 | [−100,100] | 0 | |
| F5 | generalized Rosenbrock’s function | 30 | [−30,30] | 0 | |
| F6 | Step function | 30 | [−100,100] | 0 | |
| F7 | Quartic function | 30 | [−1.28,1.28] | 0 | |
| 多峰函数 | F8 | generalized Schwefel’s problem 2.26 | 30 | [−500,500] | −418.9829d |
| F9 | generalized Rastrigin’s function | 30 | [−5.12,5.12] | 0 | |
| F10 | Ackley’s function | 30 | [−32,32] | 0 | |
| F11 | generalized Griewank function | 30 | [−600,600] | 0 | |
| F12 | generalized penalized function | 30 | [−50,50] | 0 | |
| F13 | generalized penalized function | 30 | [−50,50] | 0 | |
| F14 | Shekel’s foxholes function | 2 | [−65,65] | 1 | |
| F15 | Kowalik’s function | 4 | [–5,5] | 0.00030 | |
| F16 | six-hump camel-back function | 2 | [−5,5] | −1.0316 | |
| F17 | Branin function | 2 | [−5,5] | 0.398 | |
| F18 | Goldstein-Price function | 2 | [−2,2] | 3 | |
| F19 | Hartman’s function | 3 | [1,3] | −3.86 | |
| F20 | Shekel’s family | 4 | [0,10] | −10.1532 |
3.1. 参数灵敏度分析
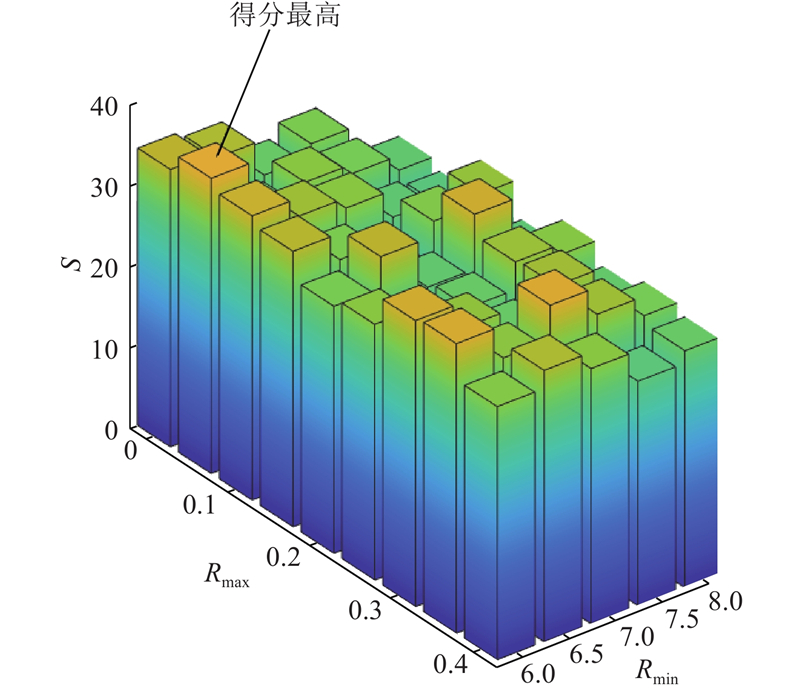
ECMA受
图 3
图 3 不同参数组合的性能呈现
Fig.3 Performance presentation of different parameter combinations
3.2. 消融实验分析
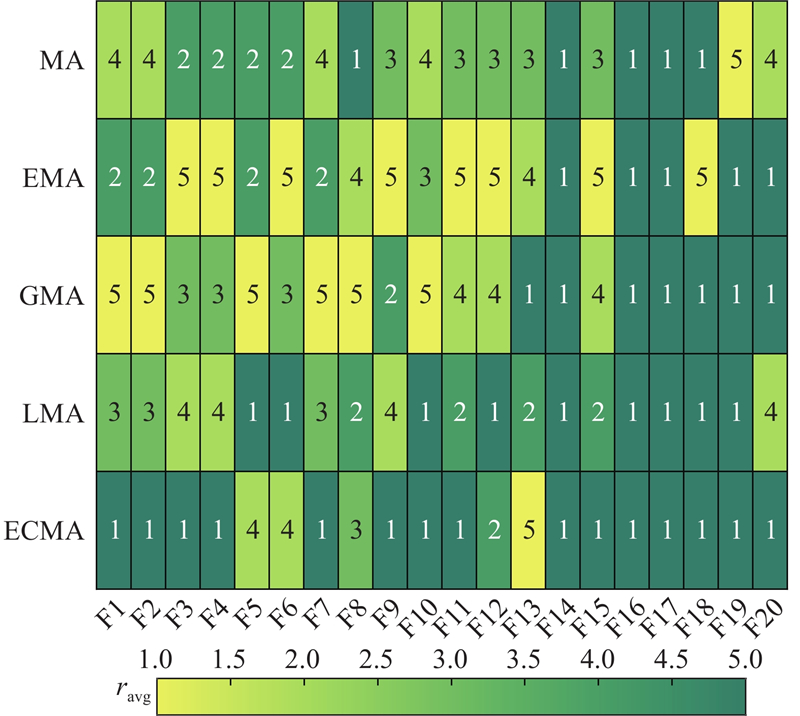
设计消融实验检验3个改进策略的算法提升效果. 引入精英协同进化策略的MA记为EMA,引入新的自适应重力系数对种群个体进行调节的MA记为GMA,引入莱维飞行策略的MA记为LMA. 在20个基准测试函数上进行MA、EMA、GMA、LMA和ECMA的对比实验,所有算法的最大迭代次数均为1 000,种群规模为40(雌雄蜉蝣各20),MA的其他初始参数取值分别为
5种算法在各测试函数独立运行30次的平均值排名
图 4
图 4 不同改进策略的蜉蝣算法在基准测试函数上的均值排名
Fig.4 Mean ranking of mayfly algorithms with different improvement in benchmark test function
3.3. 与典型的群智能算法对比
3.3.1. 寻优精度分析
参与对比的算法在20个测试函数独立运行30次的平均值avg和标准差std如表2所示. 在参与对比的算法中,ECMA有15个测试函数的结果排名第一,有17个测试函数的结果排名前三(除F6、F13和F18外),有7个测试函数的结果最佳,平均排名为1.75,优于其他算法.
表 2 不同群智能算法在基准测试函数上的优化结果
Tab.2
| 算法 | 函数 | avg | std | 函数 | avg | std | 函数 | avg | std | 函数 | avg | std | |||
| ECMA | F1 | 0 | 0 | F2 | 0 | 0 | F3 | 0 | 0 | F4 | 0 | 0 | |||
| MA | 7.02×10−19 | 2.33×10−18 | 1.24×10−9 | 2.41×10−9 | 2.49×10−6 | 2.56×10−6 | 5.21×10−1 | 1.89×10−1 | |||||||
| WOA | 8.76×10−148 | 4.79×10−147 | 2.97×10−104 | 1.07×10−103 | 2.27×104 | 1.01×104 | 3.69×101 | 2.94×101 | |||||||
| GWO | 1.53×10−58 | 5.75×10−58 | 1.32×10−34 | 1.69×10−34 | 2.34×10−14 | 1.13×10−13 | 1.29×10−14 | 1.88×10−14 | |||||||
| PSO | 1.18×10−8 | 5.87×10−8 | 9.27×10−2 | 1.41×10−1 | 4.97×101 | 2.47×102 | 5.92×10−1 | 3.59×10−1 | |||||||
| SCA | 1.48×10−2 | 3.46×10−2 | 1.78×10−5 | 3.54×10−5 | 3.77×103 | 2.98×103 | 1.91×101 | 1.19×101 | |||||||
| ECMA | F5 | 2.70×101 | 8.15×10−1 | F6 | 2.00×10−1 | 2.19×10−1 | F7 | 4.55×10−5 | 3.63×10−5 | F8 | −9.30×103 | 5.33×102 | |||
| MA | 2.92×101 | 2.15×101 | 3.26×10−19 | 8.91×10−19 | 1.26×10−2 | 4.86×10−3 | −9.55×103 | 5.45×102 | |||||||
| WOA | 2.72×101 | 5.32×10−1 | 8.79×10−2 | 1.08×10−1 | 2.34×10−3 | 2.79×10−3 | −1.15×104 | 1.46×103 | |||||||
| GWO | 2.70×101 | 8.14×10−1 | 7.25×10−1 | 4.22×10−1 | 8.04×10−4 | 4.37×10−4 | −5.89×103 | 9.99×102 | |||||||
| PSO | 4.55×101 | 3.99×101 | 7.95×10−7 | 3.62×10−6 | 1.86×10−2 | 8.72×10−3 | −6.33×103 | 8.90×102 | |||||||
| SCA | 8.95×102 | 1.64×103 | 4.71 | 6.51×10−1 | 4.75×10−2 | 6.90×10−2 | −3.93×103 | 2.86×102 | |||||||
| ECMA | F9 | 0 | 0 | F10 | 8.88×10−16 | 0 | F11 | 0 | 0 | F12 | 7.58×10−3 | 6.35×10−3 | |||
| MA | 8.69 | 4.32 | 1.97 | 3.77×10−1 | 1.19×10−2 | 1.06×10−2 | 4.15×10−2 | 5.84×10−2 | |||||||
| WOA | 0 | 0 | 3.02×10−15 | 2.40×10−15 | 1.65×10−3 | 9.03×10−3 | 8.25×10−3 | 1.16×10−2 | |||||||
| GWO | 5.46×10−1 | 1.82 | 1.60×10−14 | 3.22×10−15 | 3.50×10−3 | 6.81×10−3 | 3.95×10−2 | 2.44×10−2 | |||||||
| PSO | 5.38×101 | 1.48×101 | 1.25 | 8.51×10−1 | 4.37×10−2 | 3.78×10−2 | 1.56×10−1 | 2.53×10−1 | |||||||
| SCA | 1.56×101 | 2.12×101 | 1.24×101 | 9.59 | 2.32×10−1 | 2.23×10−1 | 3.55 | 5.65 | |||||||
| ECMA | F13 | 2.15 | 2.80×10−1 | F14 | 9.98×10−1 | 5.39×10−10 | F15 | 3.16×10−4 | 3.84×10−5 | F16 | −1.03 | 6.45×10−16 | |||
| MA | 2.54×10−2 | 5.74×10−2 | 9.98×10−1 | 4.12×10−17 | 9.76×10−4 | 3.66×10−3 | −1.03 | 6.58×10−16 | |||||||
| WOA | 2.11×10−1 | 1.64×10−1 | 1.82 | 1.89 | 6.26×10−4 | 3.07×10−4 | −1.03 | 6.29×10−11 | |||||||
| GWO | 4.93×10−1 | 1.77×10−1 | 4.91 | 4.57 | 3.06×10−3 | 6.91×10−3 | −1.03 | 5.61×10−9 | |||||||
| PSO | 1.22×10−1 | 3.10×10−1 | 4.63 | 3.50 | 1.07×10−3 | 3.66×10−3 | −1.03 | 6.78×10−16 | |||||||
| SCA | 2.47×103 | 8.76×103 | 1.53 | 8.92×10−1 | 9.50×10−4 | 3.46×10−4 | −1.03 | 2.56×10−5 | |||||||
| ECMA | F17 | 3.98×10−1 | 0 | F18 | 3.00 | 2.03×10−3 | F19 | −3.86 | 2.68×10−15 | F20 | −3.31 | 3.63×10−2 | |||
| MA | 3.98×10−1 | 0 | 3.00 | 1.14×10−15 | −3.86 | 2.71×10−15 | −3.29 | 5.35×10−2 | |||||||
| WOA | 3.98×10−1 | 2.20×10−6 | 3.00 | 1.97×10−5 | −3.86 | 2.77×10−3 | −3.24 | 1.18×10−1 | |||||||
| GWO | 3.98×10−1 | 9.06×10−7 | 3.00 | 1.23×10−5 | −3.86 | 2.40×10−3 | −3.24 | 9.24×10−2 | |||||||
| PSO | 3.98×10−1 | 0 | 3.00 | 1.08×10−15 | −3.86 | 2.71×10−15 | −3.27 | 5.99×10−2 | |||||||
| SCA | 3.98×10−1 | 1.31×10−3 | 3.00 | 2.62×10−5 | −3.85 | 1.40×10−3 | −3.04 | 1.02×10−1 |
从基准测试函数类型上进行具体分析. 1)在单峰函数方面,ECMA在F1~F4中均收敛到最优值0,WOA在F1和F2中也有较好的寻优精度,平均寻优精度超过10−100,其他算法的寻优精度较差. ECMA在F5和F7中的30次迭代平均值优于其他算法. ECMA在F6中的寻优效果比其他算法略差,原因是精英协同进化策略在一定程度上增加了MA的运算量,影响了算法的收敛速度. ECMA的均值和标准差与除MA以外的其他算法整体相差不大,且在部分指标中ECMA优于其他算法. 2)在多峰函数方面,ECMA在F8和F13中的寻优效果略差,原因是ECMA须进行适应度比较,增加了运算量,导致优化性能下降. ECMA在F9和F11中寻找到最优值0,WOA也在F9中寻找到最优值0,其他算法的寻优效果较差. ECMA在F10、F12、F15和F20中获得最佳性能,通过30次的迭代得到的平均值和标准差均优于其他算法. MA和PSO在F14和F18中获得最佳性能,但ECMA的平均寻优精度与这2个算法相同,只是稳定性略差. 所有算法在F16和F19中的平均寻优精度相似,但ECMA的标准差较小,这说明ECMA的鲁棒性更好;ECMA、MA和PSO在F17中的寻优效果相似.
3.3.2. 收敛曲线分析
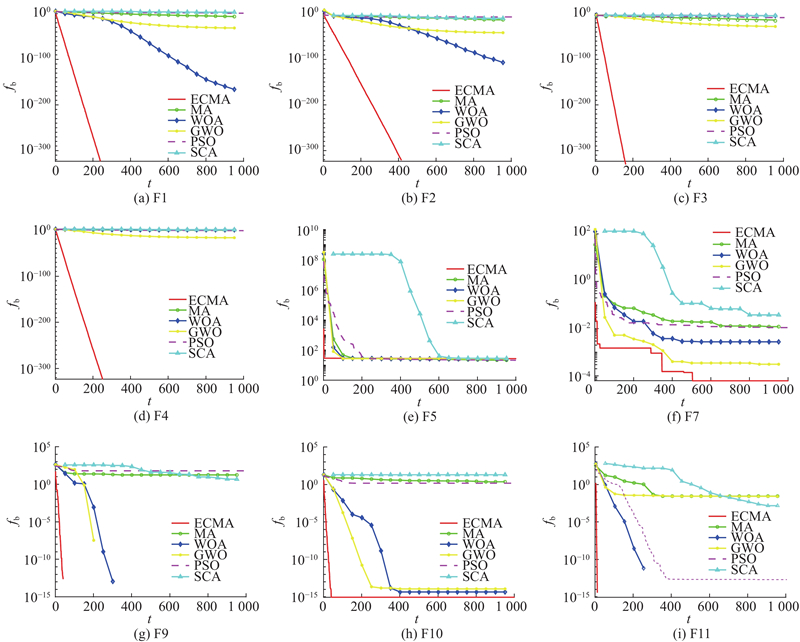
绘制不同群智能优化算法在各测试函数中的迭代收敛曲线,部分收敛曲线图如图5所示,其中
图 5
图 5 不同算法在基准测试中数上的收敛效果对比图
Fig.5 Convergence comparison effect of different algorithms in benchmark test function
3.4. 求解高维函数的实验分析
改进策略在处理较为复杂的现实问题时通常会陷入“维数灾难”,为了更好测试ECMA的高维适应性,在500维和1000维上进行MA和ECMA的对比实验,参数设置同前述实验. F3在高维上运行时间过长,ECMA在F6、F8和F13中的表现比MA差或相似,此外F14~F20为低维函数,因此选择9个基准测试函数作为实验函数,MA和ECMA在实验函数上独立运行30次后的平均值和标准差如表3所示,其中NaN表示算法在此维度上无法收敛. 可以看出,ECMA在各个维度上寻优精度均优于MA. 对于除F9和F11以外的函数,ECMA在高维上的寻优效果和在低维上的基本一致,说明ECMA处理高维函数问题的性能较好;对于F9和F11,ECMA 30次寻优中的平均值和标准差均优于MA,说明所提改进策略有利于提高MA的收敛精度. 实验结果表明,ECMA的高维度问题处理适用性和寻优性能较好,可以有效处理现实生活中复杂的高维问题.
表 3 2种蜉蝣算法在高维基准测试函数上的对比结果
Tab.3
| 函数 | 维度 | avg | std | ||
| MA | ECMA | MA | ECMA | ||
| F1 | 500 | 2.41×102 | 7.85×10−267 | 2.87×101 | 0 |
| F1 | 1000 | 7.95×103 | 1.20×10−248 | 9.83×102 | 0 |
| F2 | 500 | 9.36×101 | 1.17×10−174 | 8.15 | 0 |
| F2 | 1000 | NaN | 3.80×10−136 | NaN | 2.08×10−135 |
| F4 | 500 | 2.96×101 | 1.11×10−142 | 2.27 | 6.08×10−142 |
| F4 | 1000 | 3.36×101 | 5.35 | 1.72 | 1.25×101 |
| F5 | 500 | 2.69×104 | 4.98×102 | 3.34×103 | 3.16×10−1 |
| F5 | 1000 | 6.66×105 | 9.98×102 | 7.57×104 | 3.08×10−1 |
| F7 | 500 | 1.25×102 | 1.13×10−4 | 1.87×101 | 1.22×10−4 |
| F7 | 1000 | 1.21×102 | 8.66×10−5 | 1.30×101 | 8.15×10−5 |
| F9 | 500 | 4.88×102 | 1.65 | 3.32×101 | 3.05 |
| F9 | 1000 | 2.05×103 | 3.63 | 1.47×102 | 4.66 |
| F10 | 500 | 1.06×101 | 2.19×10−15 | 3.45×10−1 | 1.74×10−15 |
| F10 | 1000 | 1.19×101 | 3.49×10−15 | 3.23×10−1 | 1.60×10−15 |
| F11 | 500 | 2.31×102 | 1.04×10−1 | 3.88×101 | 3.23×10−1 |
| F11 | 1000 | 8.25×102 | 3.93 | 1.48×102 | 4.96 |
| F12 | 500 | 2.73×101 | 8.25×10−1 | 3.64 | 8.02×10−2 |
| F12 | 1000 | 2.71×101 | 8.30×10−1 | 4.72 | 7.58×10−2 |
3.5. 复杂问题处理能力验证
选取CEC2019测试函数[26]进行ECMA复杂问题处理能力验证实验. CEC2019测试函数集包括10个单目标测试函数F21~F30,具有复杂的空间特征,函数的理论最优值均为1. 依然选取MA、WOA、GWO、PSO和SCA作为对比算法,设置最大迭代次数为500,种群规模为30,其他参数设置同前述实验,独立运行30次并记录结果如表4所示. 可以看出,ECMA在F21、F22、F27和F30中的平均值和标准差均优于其他算法,体现了ECMA的优越性;ECMA在F26和F28中的平均值优于其他算法,说明ECMA寻优性能较好;ECMA在F23中的标准差不如其他算法,但平均值与其他算法相同;ECMA在F24、F25和F29中没有取得各个指标排名的首位,原因是ECMA引入的莱维飞行策略会在帮助算法跳出局部最优的同时降低了算法的局部搜索能力,导致优化性能下降,但是与MA相比,ECMA在F24和F25中的均值和方差仍有提升.
表 4 不同群智能算法在CEC2019函数上的优化结果
Tab.4
| 算法 | 函数 | avg | std | 函数 | avg | std | |
| ECMA | F21 | 5.11×104 | 6.92×103 | F22 | 1.72×101 | 6.60×10-2 | |
| MA | 2.32×1010 | 3.95×1010 | 2.08×101 | 1.10×101 | |||
| WOA | 5.74×1010 | 4.70×1010 | 1.74×101 | 6.19×10−3 | |||
| GWO | 1.07×108 | 1.51×108 | 1.73×101 | 1.40×10−4 | |||
| PSO | 8.04×1012 | 8.20×1011 | 1.23×104 | 3.02×103 | |||
| SCA | 4.61×109 | 4.22×109 | 1.75×101 | 4.61×10−2 | |||
| ECMA | F23 | 1.27×101 | 1.22×10-10 | F24 | 2.33×102 | 1.01×102 | |
| MA | 1.27×101 | 3.61×10-15 | 3.06×102 | 1.19×102 | |||
| WOA | 1.27×101 | 7.43×10−7 | 5.89×102 | 2.83×102 | |||
| GWO | 1.27×101 | 1.79×10−6 | 5.40×101 | 2.22×101 | |||
| PSO | 1.27×101 | 0 | 2.33×101 | 1.04×101 | |||
| SCA | 1.27×101 | 8.14×10−5 | 1.98×103 | 9.63×102 | |||
| ECMA | F25 | 1.66 | 4.35×10−1 | F26 | 8.06 | 1.56 | |
| MA | 1.69 | 4.44×10−1 | 8.71 | 2.40 | |||
| WOA | 1.76 | 2.43×10-1 | 9.64 | 1.15 | |||
| GWO | 2.39 | 1.97×10−1 | 1.16×101 | 2.40×10−1 | |||
| PSO | 1.48 | 1.59×10−1 | 9.98 | 9.32×10−1 | |||
| SCA | 2.34 | 1.87×10−1 | 1.11×101 | 7.51×10−1 | |||
| ECMA | F27 | 2.40×102 | 1.10×102 | F28 | 4.77 | 6.09×10−1 | |
| MA | 2.63×102 | 1.53×102 | 4.82 | 8.00×10−1 | |||
| WOA | 8.06×102 | 2.53×102 | 5.93 | 4.82×10-1 | |||
| GWO | 3.53×102 | 2.29×102 | 6.18 | 4.47×10-1 | |||
| PSO | 5.03×102 | 3.33×102 | 5.23 | 1.05 | |||
| SCA | 8.50×102 | 2.24×102 | 5.02 | 8.29×10-1 | |||
| ECMA | F29 | 4.04 | 5.49×10−1 | F30 | 1.96×101 | 2.59 | |
| MA | 2.40 | 2.30×10−1 | 1.98×101 | 2.62 | |||
| WOA | 4.83 | 9.21×10−1 | 2.03×101 | 1.02×10−1 | |||
| GWO | 1.12×102 | 9.35×101 | 2.05×101 | 4.52×10−2 | |||
| PSO | 4.40 | 7.46×10−1 | 2.04×101 | 2.02×10−1 | |||
| SCA | 2.39 | 3.16×10−2 | 2.05×101 | 5.89×10−2 |
4. 结 语
针对蜉蝣算法收敛精度低、收敛速度慢和易陷入局部最优无法逃逸等问题,本研究提出精英协同进化的蜉蝣算法. 所提算法根据适应度将雄性蜉蝣种群分为精英种群和普通种群,针对种群设置不同的学习样本.根据婚姻市场理论设计雌性蜉蝣的速度更新方式,在保持种群的多样性的同时,保证了算法的全局搜索能力和局部开发能力. 引入新的自适应重力系数,平衡算法的探索与开发;引入莱维飞行策略,帮助种群从局部最优区域逃逸并向其他方向扩散. 为了评估所提算法的有效性,采用20个基准测试函数和CEC2019测试函数进行多个群智能优化算法的对比实验. 实验结果表明,在参与对比的算法中,所提算法的整体表现优异. 后续将以多目标复杂问题的求解为研究重心,进一步完善算法机理,例如在精英种群和普通种群的划分机制方面,通过添加其他属性来综合评估个体的当前状态,使精英个体和普通个体在搜索过程中承担更为合理的角色.
参考文献
A mayfly optimization algorithm
[J].DOI:10.1016/j.cie.2020.106559 [本文引用: 1]
基于黄金正弦与自适应融合的蜉蝣优化算法
[J].
Mayfly optimization algorithm based on gold sine and adaptive merge
[J].
A hybrid dynamic economic environmental dispatch model for balancing operating costs and pollutant emissions in renewable energy: a novel improved mayfly algorithm
[J].DOI:10.1016/j.eswa.2022.117411 [本文引用: 1]
An improved mayfly optimization algorithm based on median position and its application in the optimization of PID parameters of hydro-turbine governor
[J].DOI:10.1109/ACCESS.2022.3160714 [本文引用: 1]
Elite-ordinary synergistic particle swarm optimization
[J].DOI:10.1016/j.ins.2022.07.131 [本文引用: 2]
A hybrid particle swarm optimization with crisscross learning strategy
[J].DOI:10.1016/j.engappai.2021.104418 [本文引用: 1]
Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation
[J].DOI:10.1016/j.swevo.2015.05.002 [本文引用: 1]
The fully informed particle swarm: simpler, maybe better
[J].DOI:10.1109/TEVC.2004.826074 [本文引用: 1]
Pyramid particle swarm optimization with novel strategies of competition and cooperation
[J].DOI:10.1016/j.asoc.2022.108731 [本文引用: 1]
Global genetic learning particle swarm optimization with diversity enhancement by ring topology
[J].DOI:10.1016/j.swevo.2018.07.002 [本文引用: 1]
A theory of marriage: part I
[J].
总结性自适应变异的粒子群算法
[J].
Self-conclusion and self-adaptive variation particle swarm optimization
[J].
自适应变异粒子群优化算法及在新冠肺炎疫情传播预测中的应用
[J].
Adaptive mutation particle swarm optimization and its application in predicting the COVID-19 epidemic transmission
[J].
粒子群优化算法的惯性权值递减策略研究
[J].
Study on the strategy of decreasing inertia weight in particle swarm optimization algorithm
[J].
一种自适应模拟退火粒子群优化算法
[J].
Adaptives simulated annealing particles swarm optimization algorithm
[J].
基于莱维飞行的改进简化粒子群算法
[J].
Improved and simplified particle swarm optimization algorithm based on Levy flight
[J].
结合莱维飞行和布朗运动的金鹰算法
[J].
Golden eagle optimizer algorithm combining Levy flight and brownian motion
[J].
双收敛因子策略下的改进灰狼优化算法
[J].
Improved grey wolf optimizer algorithm based on dual convergence factor strategy
[J].
The whale optimization algorithm
[J].DOI:10.1016/j.advengsoft.2016.01.008 [本文引用: 1]
Grey wolf optimizer
[J].DOI:10.1016/j.advengsoft.2013.12.007 [本文引用: 1]
SCA: a sine cosine algorithm for solving optimization problems
[J].DOI:10.1016/j.knosys.2015.12.022 [本文引用: 1]
A novel enhanced whale optimization algorithm for global optimization
[J].DOI:10.1016/j.cie.2020.107086 [本文引用: 1]