激光雷达和相机均是实现快速实景复刻的测量设备. 激光雷达基于脉冲或相位式原理测量周围环境到测站的距离,并结合角度码盘生成三维点云,优点是数据精度高、抗干扰性强,缺点是缺乏色彩和纹理信息,不利于解读复杂场景 [1]. 全景图像由多台相机同步采集的图像拼接而成,具有360°环境下丰富的视觉信息,被广泛应用于目标检测、场景理解、三维重建等领域,但缺乏空间三维信息[2]. 地面三维扫描仪惯以将激光雷达和相机同轴测量,并将点云与全景影像配准融合得到富有视觉特征的彩色点云,被应用于目标识别、三维建模、智能测绘等技术领域[3-4]. 全景图像与点云融合的关键是构建配准方法,即建立数据间的映射关系,主要分为以下4个类别.
3)基于无标靶. 利用自然场景的点线信息或灰度信息完成激光雷达与相机外参数标定,分为基于特征信息和基于互信息最大化2类标定方法. Bai等[15]利用激光点云与图像中平行线上的点求解旋转矩阵,根据点在线上的约束得到平移向量,该方法要求应用场景中有平行线特征. Pandey等[16]利用点云回波反射率与图像灰度值相关系数,使二者间联合直方图分散最小获得外参标定,在全景相机和激光系统中分别进行验证,该方法标定精度易受环境光照影响. 范光宇等[17]提出基于灰度相似性的配准方法,依据全景影像与深度图在水平、垂直方向细分区域的灰度相似性完成配准. 该方法配准精度与分割密度相关,且随着分割密度增加计算量剧增,冗余计算过多且数据配准有限. 将车道线、天际线、楼角等作为基元的方法[18-19]虽然灵活、简单,但标定精度普遍较低且稳定性差,依赖于特定环境,特征配对易出错.
上述4类配准方法均须建立相机与激光雷达的外参标定模型,利用点线或灰度特征解算模型参数,从而构建数据的映射关系,标定过程复杂,模型参数较多,不便于设备参数定期检校[22]. 本研究提出直接构建扫描仪三维点云与图像间像素级映射关系的方法;将具有旋转不变性的球形标靶作为特征基元,分别利用色彩信息和几何信息从全景图像和点云中高精度提取基元;在空间球坐标系下构建基元三角形,利用最小角距差法完成基元配对,并建立点云与全景影像的初始映射关系,基于改进Levenberg-Marquardt(L-M)算法和自由形变法(free-form deformation,FFD)的混合算法(iLM-FFD)优化映射关系.
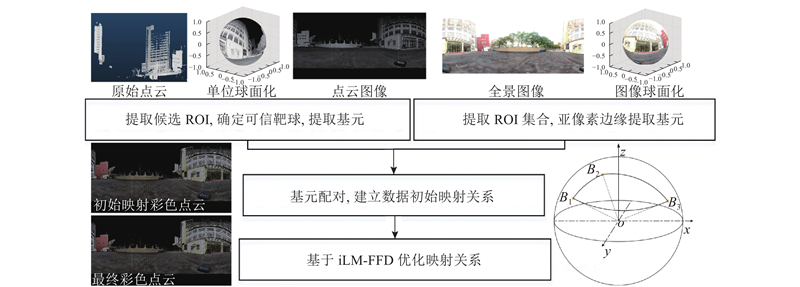
1. 点云与全景图像映射关系快速建立
如图1所示为点云与全景图像映射关系的算法框架,其中B1B2B3为基元三角形. 将三维点云与全景图像作为数据输入,通过1)在图像中提取特征基元,2)在点云中提取特征基元,3)基元配对与建立初始映射,4)混合算法优化映射关系4个主要步骤,实现在无需传感器外参数标定的情况下建立点云与全景图像间像素级的映射关系. 全景图像经预处理后,检测圆形特征感兴趣区域(region of interest,ROI),利用一维最大熵的改进Zernike矩亚像素边缘提取算法提取标靶中心,作为图像中的基元. 获取点云强度图,检测候选圆球ROI,利用球面点的三维信息从点云中提取可信靶球中心,作为点云中的基元. 利用最小角距差法将点云与图像的基元配对,并建立点云与全景图像的初始映射关系. 运用混合算法优化畸变导致的映射偏差,提升数据质量.
图 1
图 1 三维点云与全景图像映射关系的算法框架
Fig.1 Algorithm framework of mapping relationship between 3D point cloud and panoramic image
1.1. 提取全景图像特征基元
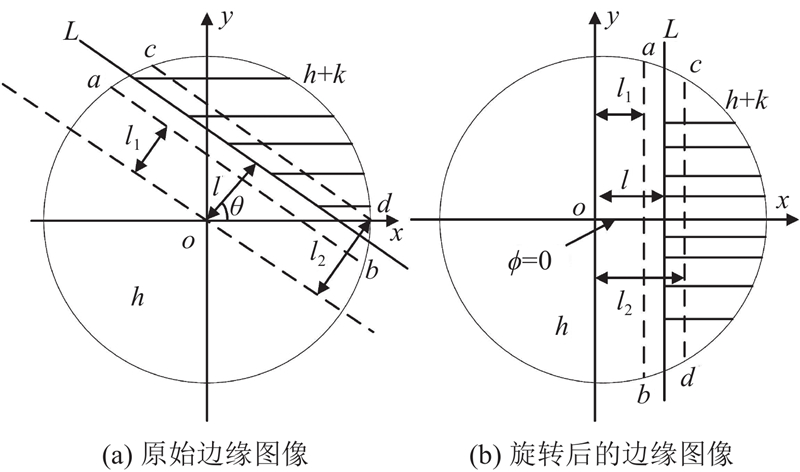
球形标靶具有旋转不变性,中心拟合精度高,颜色一般比周围环境反差大,为此通过检测圆形特征ROI和提取亚像素边缘来从全景图像中自动提取标靶中心. 全景图像信息单元较多全局处理效果欠佳,为此将图像分割成200张等尺寸子图,相邻图像间重叠100 pixel,检测每张子图的ROI. 每张子图像完成预处理、二值化、连通域处理等步骤,获得多个灰度区域;建立第
式中:
式中:
图 2
式中:
采用
利用边缘点拟合圆,剔除残差较大的点,得到最佳圆心坐标
1.2. 提取点云特征基元
利用球面点的三维信息从点云中高精度提取标靶中心. 以站心为原点将点云投影成强度图,将投影到同个像素的点云定义为点云群. 从强度图中获取候选ROI,利用ROI中的点云群拟合球面,得到拟合球半径
式中:
1.3. 基元配对与数据初始映射
准确配对点云与图像中的特征基元是建立数据映射关系的关键. 智能扫描仪的激光器中心与相机中心在结构上常同轴作业,杨必胜等[4]研究发现二者数据贴合度较高. 如图3(a)所示为全景图像,圆点为靶球的位置,直线段表示图像空间球坐标系中靶球之间的距离;图3(b)为点云强度图,圆点为靶球位置,直线段表示点云空间球坐标系中靶球之间的距离. 由图可知,靶球基元在点云和图像空间球坐标系中的几何结构相似. 本研究提出最小角距差法以完成基元配对. 从
图 3
图 3 点云和全景图像中基元的几何结构对比
Fig.3 Comparison of geometric structures for primitives in point cloud and panoramic image
式中:
式中:
1.4. 基于混合算法优化映射关系
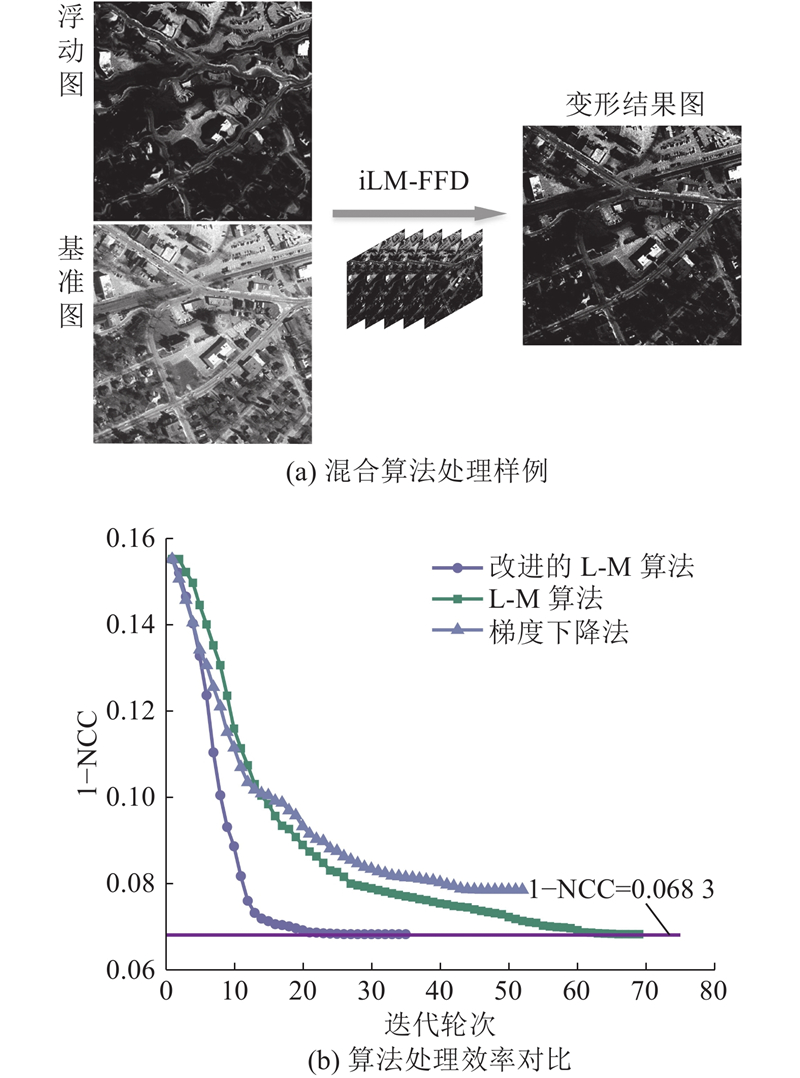
由于区域性图像畸变、错位造成部分区域的初映射关系存在一定偏差,达到像素级映射精度须进一步优化映射关系. 自由变形是局部特性变换模型,通过对变形图(
归一化互相关系数(normalized cross-correlation , NCC)不受灰度值线性变化影响,适用于纹理、模糊图像,将该参数作为对变形后
式中,
式中:floor为向下取整符号. 基于改进的L-M算法迭代优化控制参数. 差分法计算控制参数的梯度,
所有控制点的梯度组成一维梯度向量
合理更新控制步长
当结果远离解时,
式中:
图 4
图 4 所提混合算法的处理结果与效率
Fig.4 Processing results and efficiency of proposed hybrid algorithm
2. 算法验证与分析
实验于2023年7月在华中地区某高校进行,利用自研地面三维扫描仪采集不同场景的点云和全景图像数据,包括操场、楼间、室内、树林、广场等多个常见工作环境,每站至少采集2组不同分辨率的点云数据,共20组,部分数据样例如图5所示. 在Windows 10中基于Visual C++编程平台实现并验证所建立点云与全景图像间的映射关系. 点云的高、中、低分辨率为3 mm@10 m、6 mm@10 m、12 mm@10 m,激光器的发散角为0.5 mrad,点云的点位误差为3 mm@100 m,全景图像分辨率为7200 pixel×3 600 pixel,观测范围为360°×300°,实验选用半径为5 cm±1 mm的靶球作为特征基元.
图 5
从点云和全景图像中准确提取基元是算法实施的第一步. 如图6所示为10组数据经过本研究所提算法处理后的基元识别和配对结果, 其中NT为标靶数量. 实验结果表明:1)点云基元识别具有极高的准确率,标靶提取率达到96.7%. 点云中可信标靶均为真实靶球,原因是点云中信息丰富,可将强度、几何信息作为目标识别条件,大大增加了目标识别的准确性. 2)图像基元识别准确率高,但弱于点云识别,可以识别出76.7%的标靶. 由于标靶在图像识别中仅将RGB信息作为标靶判断依据,易受环境影响,有存在干扰目标的可能,影响了识别的准确性. 3)最小角距差法能够准确配对基元,被点云和图像同时识别的标靶均可以成功配对. 这是由于激光雷达与相机同轴测量,在空间球坐标中点云基元三角形与图像基元三角形稳定且具有较高的相似度,容易实现高成功率的基元配对.
图 6
图 6 点云与图像数据中标靶识别和配对结果
Fig.6 Recognition and pairing results of targets in point cloud and image data
为了定量分析映射结果的准确度,计算点云彩色图与点云强度图中对应标靶中心的像素偏移值,定义平均像素偏移为映射误差. 为了说明所建立的数据映射关系稳定性强,利用高分辨率数据建立点云与全景图像间的映射关系,改变测站位置并采集中、低分辨率数据验证映射关系,在3个场景中完成验证. 如图7所示为楼间场景下的映射实验结果,3个场景的高、中、低点云分辨率的映射误差分别为1.07、1.16、1.14 pixel,最大误差分别为1.48、1.62、1.86 pixel. 可以看出,1)高分辨率点云经初始映射得到的彩色点云质量良好,说明靶球中心提取精度高,映射算法合理,仅部分区域受图像畸变的影响出现较小偏移. 映射关系优化后得到的彩色点云无明显色彩偏移. 2)中、低分辨率点云依据映射关系能够直接得到高质量彩色点云,且不同点云分辨率的映射误差相差小于0.1 pixel. 结果说明所构建激光点云与全景图像间的映射关系稳定性强,不受测站和点云分辨率变化的干扰.
图 7
图 7 数据映射关系的建立与验证
Fig.7 Establishment and verification of data mapping relationship
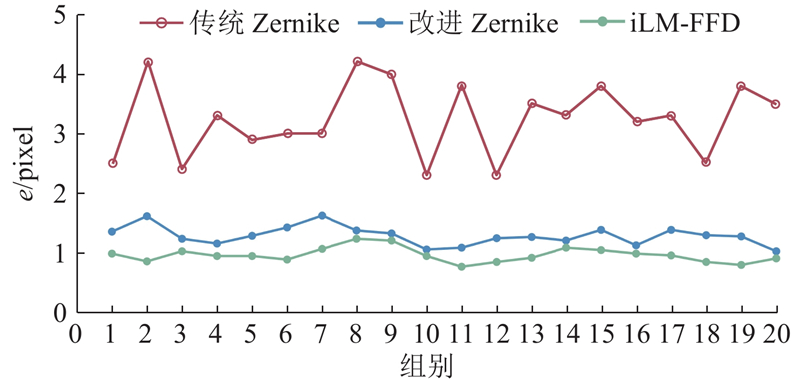
算法实现过程逐步提高点云与全景图像的映射精度. 如图8所示为不同算法处理下的映射误差对比. 20组对比数据相关误差(最大误差
图 8
图 8 不同算法处理下的映射误差对比
Fig.8 Comparison of mapping errors under different algorithms
表 1 不同算法处理下的映射误差统计
Tab.1
| 算法 | e1/pixel | e2/pixel | em/pixel | er/pixel |
| 传统Zernike | 12.62 | 1.73 | 3.24 | 0.62 |
| 改进Zernike | 2.87 | 0.46 | 1.26 | 0.20 |
| iLM-FFD | 1.62 | 0.28 | 0.96 | 0.12 |
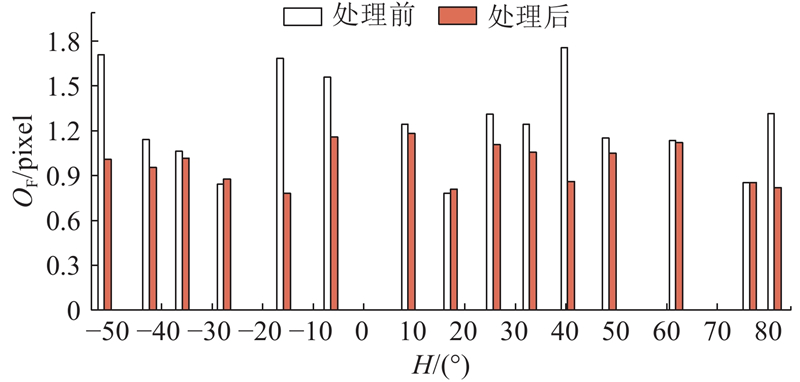
为了进一步说明iLM-FFD对点云映射关系的改善效果,在室内不同高度布设15个标靶,对比iLM-FFD处理前和处理后的标靶中心偏移OF,结果如图9所示. 图中,H为高度角. iLM-FFD对由图像区域性畸变造成的色彩偏移具有修正作用,映射误差最多降低了53.6%,该算法处理无畸变区域的效果不明显.
图 9
图 9 所提混合算法处理前、后不同高度角标靶的映射误差
Fig.9 Mapping errors of targets with different elevation angles before and after proposed hybrid algorithm processing
为了对比iLM-FFD与直接线性变换法、灰度相似法以及基于变种ICP的处理结果和效率,利用这4种方法处理10组不同场景下的测量数据,某场景的处理结果如图10所示. 图中,光斑打在靶球边缘形成的黑圈是靶球在点云中的实际边界,白色圆为依据各算法的映射关系赋靶球色彩的点云,黑圈与白色圆的贴合度能够直观地表现算法的映射效果. 可以看出,在4种算法中,iLM-FFD得到的黑圈与白色圆贴合度更高,建立的映射关系更准确. 4种算法处理10组数据的精度对比与评价如表2所示. 表中,Acc为映射精度,TT为耗时. 结果表明,1)传统标定方法多使用直接线性变换法解算模型参数,通过设定虚拟中心建立每张图像与点云之间的刚性配准数学模型,包括12个线性变换参数. 全景图像由多张不同位姿的图像拼接而成,标定过程烦琐,涉及的标定参数较多且不独立,模型未顾及如镜头畸变的非刚性误差的影响,映射精度为12.61 pixel. 2)灰度相似法无需建立传感器标定模型,依据全景影像与点云深度图在水平、垂直方向细分区域的灰度相似性完成数据配准. 配准精度与区域分割密度相关,理论上分割密度越大,数据配 准精度越高,但冗余计算量随分割密度而增加;此外,对于色彩重复度高的环境,灰度相似法出错的可能性较大. 实验中以2个像素为分割单元,映射精度为8.84 pixel. 3)变种ICP利用数据特征建立点云与图像的映射关系,将自序列全景影像虚拟生成多视立体密集匹配点云,继而使用变种ICP算法优化密集匹配点云与激光点云数据间3D-3D配准参数,间接优化全景图像与点云间的配准参数. 变种ICP的数据配准精度和自动化程度较高,映射精度为2.34 pixel,但由图像生成密集点云的过程较为复杂,数据密集匹配过程计算量较大,对数据处理终端的配置要求较高,数据映射关系受点云分辨率影响. 4) iLM-FFD实现在未标定传感器外参数的前提下建立点云与全景图像间像素级映射关系,先从点云和图像中自动提取和配对基元,再根据点云与全景图像在空间球坐标下相似性高的特点构建初始映射关系,最后逐像素优化映射关系. 相较于传统标定方法,iLM-FFD自动化程度和映射精度较高,初始映射参数仅2个,优化后得到稳定、准确的数据映射关系,点云与图像的映射精度为1.07 pixel,相比于灰度相似法提高了87.9%,相比于变种ICP算法提高了54.2%. 该结果能够用于生成真彩色点云,便于对地面三维扫描仪的数据质量进行定期检校.
图 10
图 10 点云与图像映射算法的数据映射结果
Fig.10 Data mapping results of algorithms for point cloud and image mapping
表 2 点云与图像映射算法的数据处理结果对比
Tab.2
| 算法 | Acc/pixel | 特点 | TT/s |
| 直接线性变换 | 12.61 | 算法简单,精度低 | 118 |
| 灰度信息相似性 | 8.84 | 算法适中,精度低 | 282 |
| 变种ICP | 2.34 | 算法复杂,精度高 | 494 |
| iLM-FFD | 1.07 | 算法适中,精度高 | 227 |
3. 结 论
(1)本研究从点云和全景图像中高精度提取靶球基元,利用最小角距差法将点云和全景图像中的基元准确配对. 该方法便于从数据中自动提取和配对基元,避免了出现错误基元对的问题. 相较于标准Zernike矩,基于一维最大熵的改进Zernike矩提取的基元中心的精度更高,初始映射精度提高了61.1%.
(2)混合优化算法对由于图像区域性畸变导致的初始映射偏移具有良好的修正作用. 相较于传统L-M算法,改进的L-M算法将优化效率提高约3倍,此外点云与全景图像的映射误差在初始映射关系的基础上最多降低了53.6%,有效提升了数据质量.
(3)本研究提出直接建立点云与图像映射关系的方法,无需对传感器外参数进行复杂标定即可建立点云与全景图像的映射关系. 相较于传统标定方法,所提方法自动化程度高,初始映射参数仅2个,优化后得到稳定且准确的数据映射关系,不受测站位置和点云分辨率变化的干扰. 在10组不同场景数据的处理结果中,所提方法数据映射精度为1.07 pixel,相比于灰度相似法提高了87.9%,相比于变种ICP算法提高了54.2%;所提方法的计算效率也较对比算法的高.
(4)相比于通过标定传感器间外参数建立数据转换模型,本研究实现了自动化提取和配对基元,建立和优化了映射关系,对设备数据质量的定期检校具有重要意义,对国产智能扫描仪的研发和传感器数据融合具有重要参考价值. 本研究所提算法对初始映射精度要求较高,同时须高精度提取标靶中心,标靶表面点云粗差数量会随着测量距离的增加而增加. 未来计划将抗差估计的方法引入标靶中心提取计算,致力于研究自适应的抗差估计算法拟合标靶,以保证特征点的提取精度.
参考文献
轻量型感知激光雷达关键技术发展综述
[J].DOI:10.3788/CJL202249.1910002 [本文引用: 1]
et al. Review on key technologies of lightweight type-aware LiDAR
[J].DOI:10.3788/CJL202249.1910002 [本文引用: 1]
面向智能化测绘的城市地物三维提取
[J].DOI:10.11947/j.issn.1001-1595.2022.7.chxb202207030 [本文引用: 1]
3D geospatial information extraction of urban objects for smart surveying and mapping
[J].DOI:10.11947/j.issn.1001-1595.2022.7.chxb202207030 [本文引用: 1]
激光点云与光学影像配准: 现状与趋势
[J].
Registration between laser scanning point cloud and optical images: status and trends
[J].
三维激光扫描点云数据处理研究进展、挑战与趋势
[J].
Progress, challenges and perspectives of 3D LiDAR point cloud processing
[J].
立体视觉和三维激光系统的联合标定方法
[J].
Joint calibration method for stereo vision system and 3D laser system
[J].
一种基于三维特征点集的激光雷达与相机配准方法
[J].
Calibration of LiDAR and camera based on 3D feature point sets
[J].
Automatic extrinsic calibration method for LiDAR and camera sensor setups
[J].DOI:10.1109/TITS.2022.3155228 [本文引用: 1]
A novel method for the extrinsic calibration of a 2D laser rangefinder and a camera
[J].DOI:10.1109/JSEN.2018.2819082 [本文引用: 1]
High-precision external parameter calibration method for camera and lidar based on a calibration device
[J].DOI:10.1109/ACCESS.2023.3247195 [本文引用: 1]
融合多种棋盘格约束的面阵相机和线激光外参标定
[J].
Extrinsic calibration of camera and 2D laser-rangefinder with various chessboard constrains
[J].
3D LIDAR-camera extrinsic calibration using an arbitrary trihedron
[J].
LiDAR-camera calibration using line correspondences
[J].DOI:10.3390/s20216319 [本文引用: 1]
Automatic extrinsic calibration of vision and lidar by maximizing mutual
[J].
基于灰度相似性的激光点云与全景影像配准
[J].
Registration of laser point cloud and panoramic image based on gray similarity
[J].
车载MMS激光点云与序列全景影像自动配准方法
[J].
Automatic registration of vehicle-borne mobile mapping laser point cloud and sequent panoramas
[J].
RGGNet: tolerance aware LiDAR-camera online calibration with geometric deep learning and generative model
[J].DOI:10.1109/LRA.2020.3026958 [本文引用: 1]
激光雷达与相机融合标定技术研究进展
[J].DOI:10.3788/IRLA20230427 [本文引用: 3]
Advancements in fusion calibration technology of lidar and camera
[J].DOI:10.3788/IRLA20230427 [本文引用: 3]
融入一维概率Hough变换与局部Zernike矩的双目视觉测量
[J].DOI:10.37188/OPE.20233112.1793 [本文引用: 1]
Binocular vision measurement method incorporating one-dimensional probabilistic Hough transform and local Zernike moment
[J].DOI:10.37188/OPE.20233112.1793 [本文引用: 1]
Automatic astronomical survey method based on video measurement robot
[J].DOI:10.1061/(ASCE)SU.1943-5428.0000300 [本文引用: 1]
Image-analysis via the general-theory of moments
[J].
Validation for 2D/3D registration II: the comparison of intensity- and gradient-based merit functions using a new gold standard data set
[J].DOI:10.1118/1.3553403 [本文引用: 1]
On the rate of convergence of the Levenberg-Marquardt method
[J].
A modified Levenberg-Marquardt algorithm for singular system of nonlinear equations
[J].
An efficient Levenberg–Marquardt method with a new LM parameter for systems of nonlinear equations
[J].DOI:10.1080/02331934.2018.1435655 [本文引用: 1]