偏态数据分布是指在数据集中存在不平衡的数据分布情况,其中某些属性的取值频率远高于其他属性. 该分布可能源于数据收集过程、自然数据特征或者是特定应用领域的限制等因素. 采用近似查询处理方法,往往无法有效处理这种偏态数据分布,导致查询结果的准确度下降. 分层抽样方法被认为是解决偏态数据分布的有效方法. 传统做法通常是依据概率进行抽样,但一次或几次抽样的随机性无法保证所抽样本的分布与原始偏态数据的分布相一致. 采用多次迭代的抽样方法可以减轻这一问题,但会带来显著的时间和空间成本.
本文提出结合分层分组抽样和变分自编码器生成模型的近似聚合查询新方法(group variational auto-encoder, GVAE),通过数据预处理、分层分组、模型优化等手段,训练优化的变分自编码器模型. 生成模型后设置采样比例,输入随机噪声到模型中,快速生成小批量样本并执行聚合查询. 实验表明,与基准方法相比,对偏态分布数据的近似聚合查询有更小的查询相对误差.
1. 相关工作
近似查询处理这一领域的研究历程总体上可以分为以下2个阶段. 1)Olken等[10]首次提出并实现了在关系型数据库上使用采样技术. 此后,在随机采样的基础上,分层抽样和各种离线构建数据概要的方法被广泛研究. 在分布式系统被提出后,研究者们关注于如何在分布式场景下离线或在线采样. 2)在深度学习技术推动的 AI 浪潮下,研究者逐渐意识到机器学习模型对数据的强大拟合能力,基于生成模型的AQP算法在这种背景下被提出. 现行的AQP算法主要包含在线算法、离线算法与机器学习算法3种[11-12]. 在线 AQP算法的主要目的是在查询执行期间设计合理的采样策略,基于在线采样计算OLAP的近似查询结果,并为该近似查询结果设计误差估计算法[13-14].
Thirumuruganathan等[21]提出使用变分自编码器模型(VAE-AQP)对原始数据分布进行建模,生成高效、交互式的总体估计. VAE-AQP存在处理偏态数据时相对误差不够精确的问题,难以拟合期望的数据分布,影响查询准确率.
GAN通过判别网络和生成网络相互对抗和学习的方法,降低生成样本和原始数据之间的聚合查询误差. Zhang 等[22]介绍了基于条件生成模型的近似查询处理方法 , 提出使用基于Wasserstein的条件生成对抗网络(conditional - Wasserstein generative adversarial network, CWGAN)来有效地处理Group-by查询,在节省计算资源的同时保持较高的结果精度. GAN在训练过程中没有明确的指标确定模型达到纳什均衡,容易出现模型坍塌的问题.
2. 基础定义
2.1. 聚合查询
讨论如下所示的查询语句:
其中,
2.2. 偏态系数
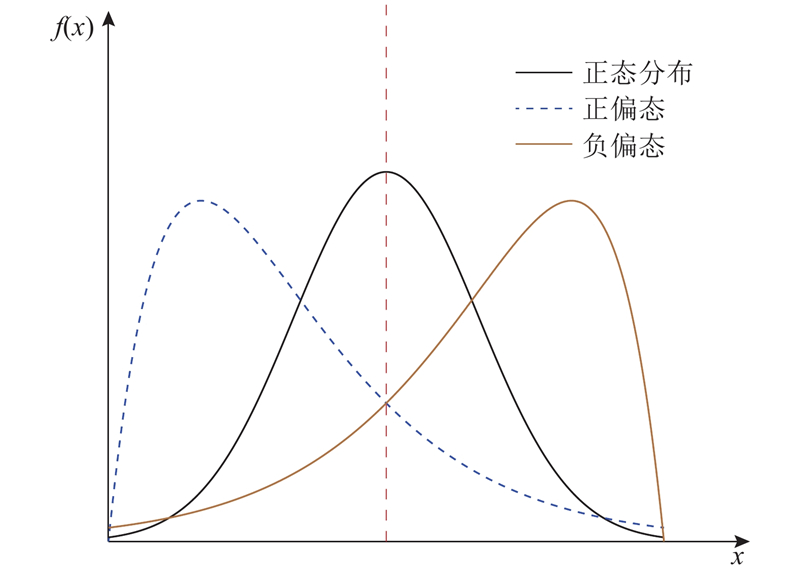
图 1
图 1 左偏分布、右偏分布与正态分布的比较
Fig.1 Comparison of left-skewed and right-skewed distribution with normal distribution
一般可以用偏态系数(coefficient of skewness, SK)刻画偏态程度,计算方法如下所示:
2.3. 聚合查询误差
聚合查询误差由相对误差(relative error difference)来计算,记为
设通过分组聚合查询语句
2.4. 不同偏态系数聚合查询的相对误差
以 PM2.5 数据集
表 1 PM2.5数据集的示例
Tab.1
| 年份 | 月份 | ρB/(μg·m−3) | CBWD | IWS/(m·s−1) |
| 2010 | 1 | 129 | NE | 1.79 |
| 2011 | 5 | 62 | CV | 0.89 |
| 2012 | 7 | 126 | SE | 20.57 |
利用CWGAN和VAE-AQP学习原数据分布生成的模型,对不同
表 2 不同模型下不同数据偏态系数的相对误差
Tab.2
| Field | SK | Rq/% | |
| VAE-AQP | CWGAN | ||
| Year | 0 | 2.90 | 3.38 |
| Month | −0.009 | 3.80 | 3.91 |
| CBWD | −0.114 | 4.01 | 5.27 |
| PM25 | 1.802 | 6.38 | 7.59 |
3. GVAE方法
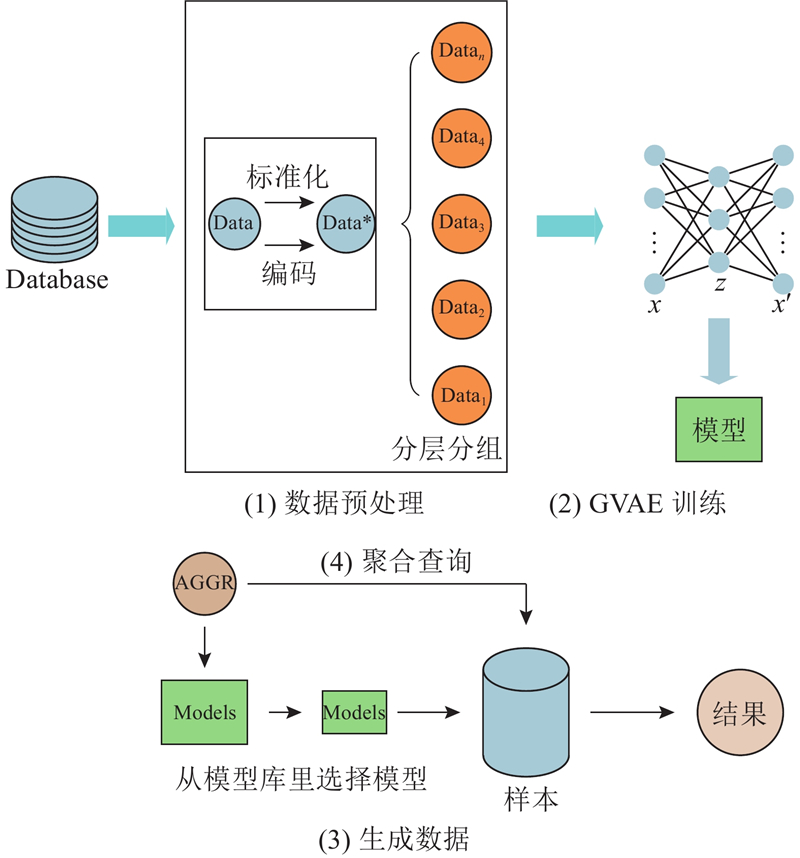
该GVAE方法的处理过程如图2所示,主要包括数据预处理、模型训练、数据生成、聚合查询4个步骤.
图 2
数据预处理是将数据集数据转换为可以被神经网络学习的数据,共分为数据编码、数据标准化和数据分层分组3部分. 其中数据编码将类别少的数据转换为数值,便于GVAE模型计算. 数据标准化可以在保留数据分布特征的前提下消除不同数据之间的量纲差异,便于神经网络梯度迅速下降,快速收敛.
数据分层分组是为了学习不同列的偏态分布并生成小样本数据,其中分组是为了使变分自编码器学习和生成小批量数据,而分层的目的是使每一组的数据分布都与原偏态数据的分布相似.
GVAE模型训练是将已经预处理好的数据输入到神经网络中学习,得到模型库后,根据不同的聚合查询语句从模型库中选取模型,根据一定的样本比例生成数据,对样本执行聚合查询. 3.2~3.4节将进一步描述上述内容.
3.1. 数据预处理
对数据进行预处理,包括数据的编码、标准化和分层分组3部分,如图2的数据预处理部分所示.
3.1.1. 数据编码
机器学习中常用的编码为二进制编码和独热编码(one-hot encoding),例如将数值
本文使用的是标签编码(label encoder)[24]. 标签编码是根据字符串形式的特征值在特征序列中的位置,为其指定一个数字标签. 针对有不同数据类型的数据,需要对其格式进行转换. 对每一列数据统计分类和类型个数. 分别对每一类标号,将真实值替换为标号值.
需要转换为编码的数据类型为类别和数值2类. 如表1所示,字段
3.1.2. 数据标准化
在机器学习算法中,数据标准化和归一化是2种常见的特征缩放(feature scaling)方法. 其中归一化指的是将数据的每一列的值缩放至0~1.0. 对于偏态分布数据,在缩放过程中会导致分布特征消失,因此不选择使用归一化.
通过数据标准化,可以缩小数据的取值范围,不会丢失原始数据分布的特征,也可以将数据转换为近似的标准高斯分布,便于GVAE模型学习数据分布. 标准化过程如下所示:
式中:
3.1.3. 分层分组
分层分组算法如算法1所示,为了便于GVAE一次性拟合每一组的分布,参考经典VAE学习图片数据的方法,将数据展开为一维向量,加速GVAE学习的速度,拟合更准确.
算法 1 分层分组算法 输入: 已编码和标准化的数据
根据算法1,对表1所示的数据集进行训练. 设置每一组样本的数据规模为1 000,记为基数. 将4 000条数据对应分为4组,聚合查询语句如式(1)所示,保持GVAE模型网络结构和采样比例不变,统计平均训练时间和查询准确率,如表3所示. 表中,
表 3 分组基数的比较
Tab.3
| Ng | Acc/% | |
| 100 | 13.26 | 96.20 |
| 1000 | 16.13 | 98.10 |
| 10000 | 124.02 | 98.24 |
不同分组方法对学习效率的影响,比较区间分组和分层分组方法,数据集分为样本大小相同的若干组. 任意重复选取2组数据,计算总体数据和单列数据(CBWD)的均值(mean)、方差(Std)和KL散度(KL)平均值,2种分组方法的比较结果如表4所示.
表 4 区间分组样本分布的比较
Tab.4
| 分组方式 | 数据取值 | mean | Std | KL |
| 区间分组 | 总体 | −0.006 5 | 0.961 4 | |
| 区间分组 | 总体 | −0.004 1 | 0.976 2 | |
| 区间分组 | 单列 | −0.021 2 | 1.002 5 | |
| 区间分组 | 单列 | 0.010 7 | 0.996 9 | |
| 分层分组 | 总体 | 0.003 6 | 0.993 0 | |
| 分层分组 | 总体 | 0.002 9 | 0.993 3 | |
| 分层分组 | 单列 | 0.001 1 | 0.999 8 | 0 |
| 分层分组 | 单列 | 0.001 1 | 0.999 8 | 0 |
分层分组算法是在对数据分组之前先对数据分层,根据不同的聚合查询语句
分层分组算法带来了更多的时间和空间开销. 假设总体大小为
每一组数据是从原始数据依据聚合查询语句的字段分层随机抽样得到,字段不同,分组分层抽样的方式不同,分组数据也不同. 不同的查询字段对应不同的模型. 有相同G的查询字段可以使用对应查询字段的查询语句训练得到的模型.
3.2. GVAE模型训练
针对本文关注的问题,GVAE与经典VAE模型相比,主要在神经网络结构和损失函数2个方面进行了改进.
3.2.1. 神经网络模型
变分自编码器是一类生成模型,它可以学习复杂的数据分布并生成样本. VAE的训练效率高,具有可解释的潜在空间.
生层模型中的潜在变量是捕获用于生成建模的数据特征的中间数据表示. 设
将
将式(5)代入式(6),式(6)也被称为变分目标(variational objective),此时可以将
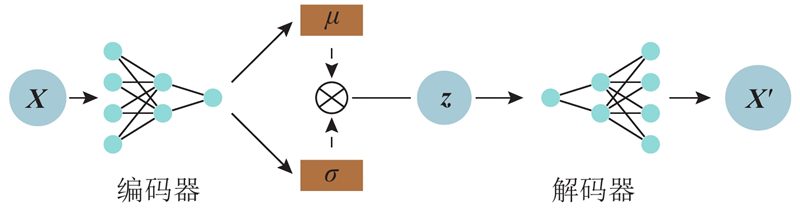
神经网络结构如图3所示,编码器将输入数据
图 3
经典VAE模型中,图片像素归一化后为
神经网络的其他部分设置如下:学习率为
3.2.2. 损失函数
经典VAE的损失函数由重构损失和KL损失2部分构成,如式(7)所示. 在模型训练的过程中,由于不同批数据分布相似但不完全相同,容易导致VAE后验崩塌(posterior collapse)的问题,即散度消失,重构部分过早达到ELBO上界.
针对该问题,参考文献[25],给KL项乘上权重系数
3.3. 数据生成
GVAE通过多个全连接层层学习数据的隐含变量得到模型,读取模型网络的变量. 将标准高斯分布变量
这是符合标准高斯分布的2×4的随机数字矩阵
3.4. 聚合查询
根据不同查询字段训练模型后,通过聚合查询语句的查询字段,从模型库中选取对应查询类的模型. 根据适当的采样比例,生成小批量数据,对数据进行逆变换,并保存到数据库中,最后查询数据,计算查询相对误差. 聚合查询过程如算法 2所示.
算法2 生成模型近似查询 输入: GVAE模型库
4. 实验与分析
4.1. 实验设置
实验环境为Intel(R) Core(TM) i7-7700HQ CPU;16 GB内存;500 GB硬盘;操作系统为Windows 10;采用Visual Studio Code 2019编辑器和Python3.10语言版本,使用Pytorch实现生成模型的搭建.
1) 实验数据集. 选用2个数据集进行实验,分别为 Beijing PM2.5 真实数据集和TPC-H合成数据集.
a) Beijing PM2.5 数据集. 该数据集包含了美国驻北京大使馆的PM2.5数据的信息和北京首都国际机场的气象数据. 数据集包括年月日、PM2.5、气温、压强和风向等字段,字段类型多样. 共43 824条数据. 控制不同列的偏态系数为0~1.0,间距为0.2,总共5份数据集.
b) TPC-H数据集. 获取TPC-H数据生成工具,通过调整参数和比例,设置偏态系数为0~1.0,间距为0.2,生成5份合成数据集. 每份数据集包括多个表,如订单(orders)和供应商(supplier). 每个表包含特定字段,模拟真实世界的企业数据仓库. 每一份合成数据集都是500万条,支持多种分组聚合查询.
2) 查询语句. 针对不同数据集的不同字段,执行分组聚合查询和条件查询语句,如下所示.
a) Beijing PM2.5数据集
1. SELECT YEAR, COUNT(*)
FROM PRSA_DATA
GROUP BY YEAR
2. SELECT CBWD, COUNT(*)
FROM PRSA_DATA
GROUP BY CBWD
3. SELECT AVG(PM25)
FROM PRSA_DATA
WHERE PM25 >
AND PM25 <
b) TPC-H数据集
4. SELECT P_MFGR, COUNT(*)
FROM PART
GROUP BY P_MFGR
5. SELECT O_ORDERPRIORITY, COUNT(*)
FROM ORDERS
GROUP BY O_ORDERPRIORITY
6. SELECT AVG(L_QUANLITY)
FROM LINEITEM
WHERE L_QUANLITY >
AND L_QUANLITY <
其中,
3) 评估指标. 对实验数据集进行测试,主要考虑训练时间和查询准确率. 查询准确率使用如式(3)所示的相对误差进行计算.
4) 实验过程.
a)数据分布拟合效果的实验.
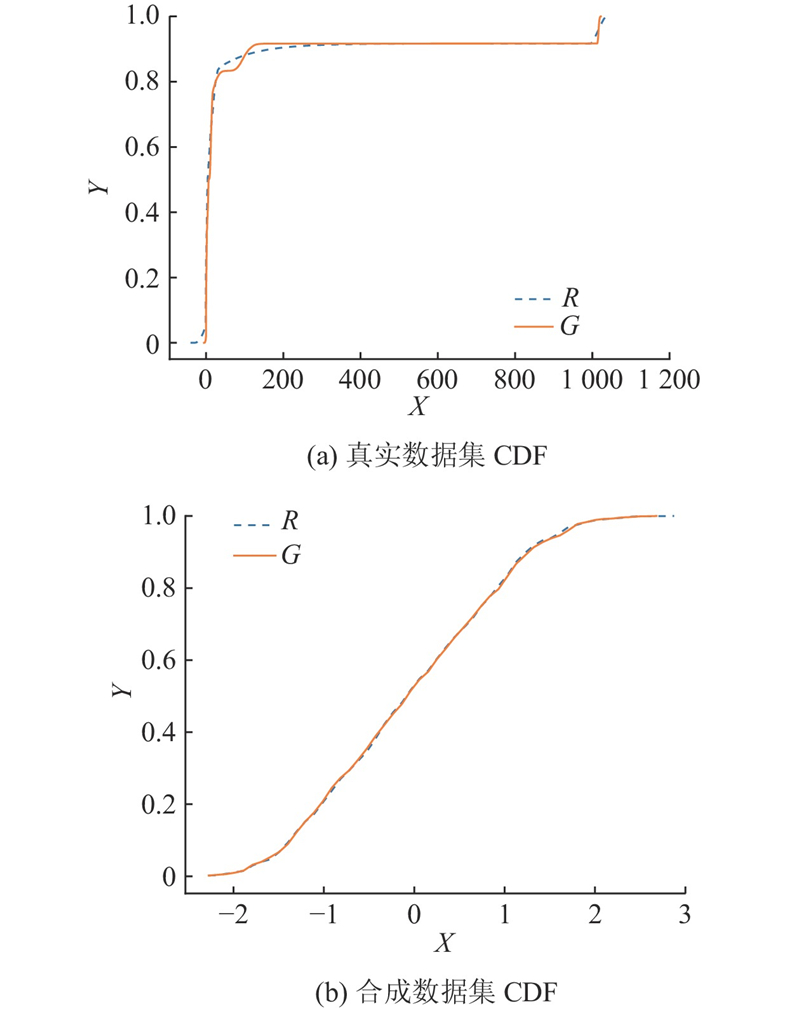
通过计算真实数据和生成数据的累积分布函数(CDF),观察模型拟合数据分布的效果.
b)不同模型方法的比较.
为了更好地体现GVAE对偏态数近似聚合查询的优越性,选择VAE-AQP和CWGAN模型方法与GVAE进行比较,对比不同模型方法在同偏态系数下的查询相对误差.
c)消融实验.
以GVAE模型方法为基础,将选择编码方式为标签编码还是独热编码、标准化或者归一化对聚合查询准确率的影响,分别记为GVAE(E)和GVAE(O)、GVAE(S)和GVAE(N).
将是否增加GVAE模型中改进的两部分,Sigmoid层和KL损失改进,分别记为GVAE(M)和GVAE(KL),开展消融实验,能够更好地体现该算法对偏态数据近似聚合查询的优越性.
d)其他实验.
测试其他变量,如不同维度或不同采样比例对聚合查询相对误差的影响.
4.2. 实验结果与分析
4.2.1. 数据分布拟合效果实验
为了度量原始数据分布和生成数据分布之间的相似性,选用连续列的kolmogorov-smirnov(
式中:
图 4
图4(a)、(b)的
4.2.2. 不同模型方法的比较
根据4.1节的查询语句,多次查询真实数据和生成数据,计算不同的评估指标.
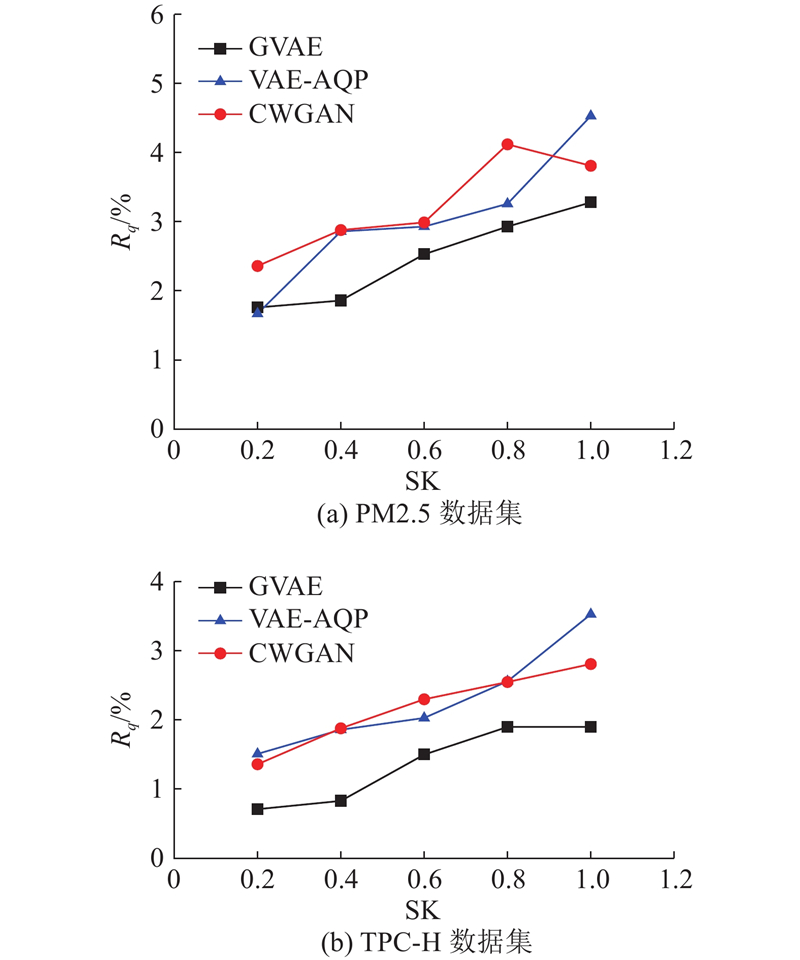
如图5(a)、(b)所示为PM2.5数据集和TPC-H数据集,分别统计在不同偏态系数的不同规模的数据集,近似聚合查询的相对误差平均值. 对比GVAE、VAE-AQP和CGWAN模型方法,针对不同偏态系数的数据,近似聚合查询有更小的查询相对误差,且随着偏态系数的提高,相对误差增大的幅度不超过2%,上升趋势更平缓,查询结果的相对误差偏移更小.
图 5
图 5 不同偏态系数查询的相对误差
Fig.5 Relative errors for queries with different bias coefficients
4.2.3. 消融实验
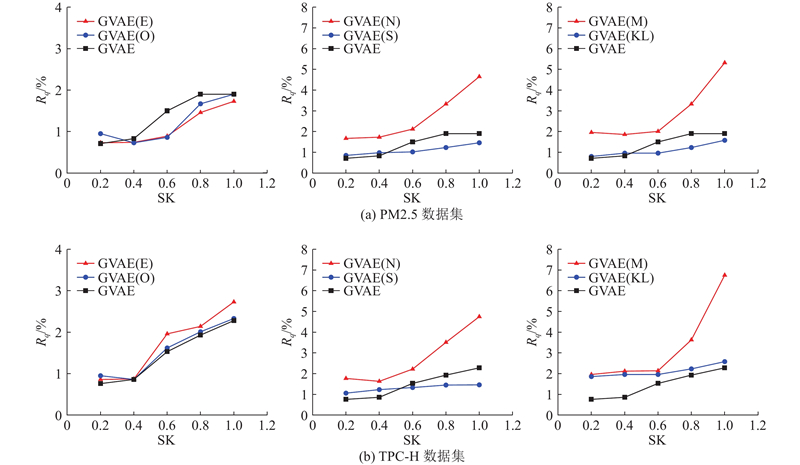
如图6(a)、(b)所示,分别测试PM2.5数据集和TPC-H数据集对不同条件下的GVAE模型计算不同偏态系数下的数据聚合查询误差,如4.1节的消融实验所示设置变量,可以看出不同变量对聚合查询相对误差的影响.
图 6
图 6 不同数据集和偏态系数的消融实验
Fig.6 Ablation experiment with different dataset and skewed coefficient
在相同消融条件下,GVAE(N)的查询相对误差比GVAE(S)高3%~5%,影响明显.
4.2.4. 其他实验
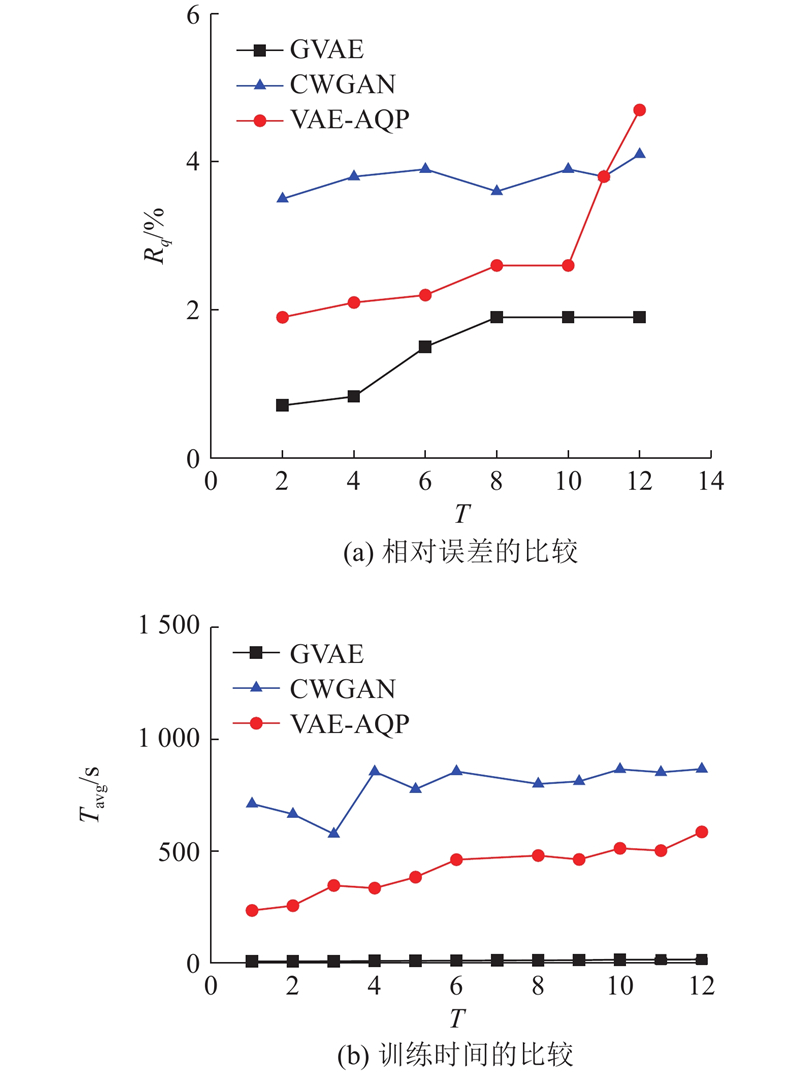
如图7(a)所示,在数据维度
图 7
如图8所示,对于不同规模的数据集PM2.5和TPC-H,
图 8
当模型生成数据时,只能生成分组基数的整数倍,提高抽样比例只会增加生成数据的组数,生成数据分布几乎不变,所以相对误差不会大幅波动.
5. 结 语
本文提出基于变分自编码器的数据近似查询处理优化方法,在数据预处理阶段通过数据编码和数据标准化,根据不同字段将偏态数据分层分组,便于GVAE方法更好地训练拟合的数据分布. 加入了对损失函数的优化,避免过拟合. 实验结果表明,与对比算法相比,该方法对偏态分布数据的聚合查询有更低的查询误差.
利用GVAE方法学习偏态数据分布迅速,损失函数很快就收敛到一个定值,难以衡量是否训练完成. 下一步将深入研究为何导致其快速收敛,寻找新的衡量指标判断训练是否结束.
参考文献
LAQP: learning-based approximate query processing
[J].DOI:10.1016/j.ins.2020.09.070 [本文引用: 1]
DeepDB: learn from data, not from queries!
[J].DOI:10.14778/3384345.3384349 [本文引用: 1]
Data warehousing and OLAP for decision support
[J].DOI:10.1145/253262.253373 [本文引用: 1]
Synopses for massive data: samples, histograms, wavelets, sketches
[J].
The skewness of science
[J].DOI:10.1002/(SICI)1097-4571(199210)43:9<628::AID-ASI5>3.0.CO;2-0 [本文引用: 1]
Multi-label classification: an overview
[J].DOI:10.4018/jdwm.2007070101 [本文引用: 1]
GAN-based tabular data generator for constructing synopsis in approximate query processing: challenges and solutions
[J].DOI:10.3390/make6010010 [本文引用: 1]