纳什均衡 (Nash equilibrium) [3] 是博弈论中的一个重要概念. 在均衡状态下, 任何玩家都不能仅通过更改自己的策略来获得更多的收益[4]. 现有研究中, 通常根据博弈特征与信息完备性的差异将两方零和博弈分为扩展式博弈(extensive-form game)和马尔科夫博弈(Markov game). 马尔科夫博弈(Markov games)被视为马尔科夫决策过程(Markov decision process, MDP)在博弈场景中的推广, 适用于描述完全信息、同时移动博弈. 其特点为在博弈过程中, 下一步的状态只依赖于当前状态, 而不依赖于之前的状态. 从原理上, 多智能体博弈强化学习方法可以分为2类: 基于值函数方法和基于策略方法. 对于两方零和马尔科夫博弈, 基于值函数方法旨在找到最优值函数, 并由其获取相应的平稳纳什均衡策略. 在状态转移概率未知的情况下, Littman[5]通过历史数据近似估计Bellman算子, 提出Minimax-Q学习, 将单智能体强化学习的Q学习算法[6]扩展到两方零和马尔科夫博弈. 对于大规模问题, 为了解决维度灾难, Fan等[7-9]将函数逼近思想引入Minimax-Q, 利用函数逼近对值函数进行近似, 但基于值函数的方法收敛速度较慢. 神经网络作为强大的非线性函数逼近器, 具有自动学习特征的能力, 使用神经网络对值函数和策略进行近似可以从原始数据中学习到适合问题的特征表示, 从而有效地解决大规模问题中维度灾难的问题.
基于策略的策略梯度方法在MDP中具有最先进的性能[10-11]. 在策略参数化的设定下, 寻找零和马尔科夫博弈的纳什均衡解通常表述为非凸非凹的极大极小优化问题[12-13]. Daskalakis等[14]探讨在多智能体竞争性环境中, 如何使用独立策略梯度方法(independent policy gradient, IPG)来训练多个智能体的策略, 以实现博弈最优解的学习. Nouiehed等[15]提出的嵌套梯度下降方法(nested gradient descent method)通过交替地对每个玩家的策略进行梯度下降来逐步逼近博弈的纳什均衡点, 与IPG(该方法中每个智能体的策略被看作是独立的)相类似, 两者本质都是单智能体强化学习方法. 在纳什均衡的基础上, Fiez等[16]提出双时间尺度算法(two-timescale algorithm), 其中追随者使用梯度博弈更新规则, 而不是精确的最佳响应策略, 该算法已被证明收敛于Stackelberg均衡. 然而, 该均衡只对应于零和博弈的单边均衡解, 并且无法分析同时移动博弈的收敛性. Perolat等[17]针对同时移动博弈, 将演员-评论家网络(Actor-Critic network)与虚拟博弈相结合, 提出基于样本平均策略的算法并解决了虚拟博弈算法中的收敛问题. 然而,在每轮迭代时都须求解一方的最佳响应策略, 因此对计算资源的消耗也是巨大的.
针对上述方法的不足, 本研究基于额外梯度法[18]提出双方玩家同时进行策略梯度更新的两方零和马尔科夫博弈策略优化算法. 1)基于参数化策略, 提出马尔科夫博弈策略梯度定理, 并进行了严格证明. 2)将回报作为状态动作价值函数的无偏估计, 基于额外梯度法提出马尔科夫博弈的策略梯度算法, 并证明该算法可以收敛到近似纳什均衡. 3)针对大规模的Oshi-Zumo游戏, 采用神经网络作为参数化策略, 验证了算法的有效性.
1. 两方零和马尔科夫博弈
1.1. 问题描述
两方零和马尔科夫博弈问题可以用一个五元组来描述[19], 定义如下:
式中:
式中:T为终止时刻.
给定联合策略
定义1 两方零和博弈最佳响应策略. 给定玩家2策略
相反地, 给定玩家1的策略
定义2 两方零和博弈纳什均衡策略. 如果2个玩家的策略
博弈双方处于纳什均衡中,意味着任何玩家都不能仅通过更改自己的策略来获得更多的奖励, 因此纳什均衡可以被视为“对最佳反应的最佳反应”. 对于整个博弈过程来说, 纳什均衡联合策略即为两方零和马尔科夫博弈的最优策略. 在两方零和博弈中, 始终存在着纳什均衡解, 其等价于一个最大最小问题的优化解[22], 即
因此, 将纳什均衡的求解过程转化为上述最大最小问题的优化过程.
1.2. 贝尔曼方程
为了描述不同时刻以及不同价值函数之间的关系, 为后续证明提供理论依据, 提出以下引理.
引理1 对于两方零和博弈, 给定联合策略
当前时刻状态动作价值函数与下一时刻状态价值函数之间关系的贝尔曼方程为
证明: 将式(3)所示的状态价值函数的定义展开, 结合式(4)可以得到
将回报
对式(12)中的第2项求期望就等于下一时刻的状态价值函数:
2. 马尔科夫博弈的策略梯度
为了实现纳什均衡策略的求解, 考虑参数化的策略
式中:
为了利用梯度法求解式(15), 须得到策略梯度, 即
定理1 对于两方零和马尔科夫博弈问题(式(1))和参数化的联合随机策略
式中:
证明: 首先考虑玩家1的策略参数
结合式(10), 式(18)中的第2项,可以得到
对于式(19)中
将
式(20)结尾处的
通过上述推导, 可以计算式(14)中指标函数的梯度:
式中:
由定理1可以得到两方零和马尔科夫博弈中2个玩家策略梯度, 从而可以利用梯度方法求解该最大最小优化问题(式(15)). 由状态动作价值函数的定义(式(4)), 可知回报
推论1 对于两方零和马尔科夫博弈问题(式(1))和参数化的联合随机策略
证明: 以玩家 1的梯度项为例,由式(4)、(16) 可知:
玩家2梯度项的证明同理, 推论1证毕.
3. 马尔科夫博弈策略梯度算法及收敛性
3.1. 求解最大最小优化问题的梯度方法
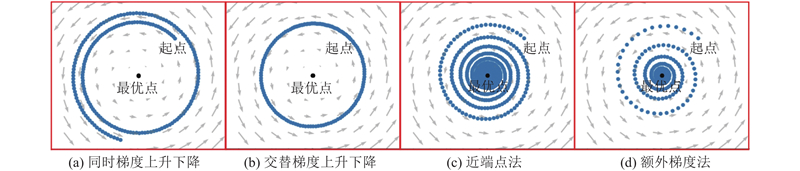
考虑凸凹函数
式中:
该问题中
图 1
第2种基于梯度的方法为交替梯度上升下降(alternating gradient ascent-descent), 参数
第3种改进的方法为近端点法(proximal point method), 更新形式为
显然式中
使用额外梯度法解决该优化问题, 相较于同时梯度上升下降、交替梯度上升下降具备良好的收敛性, 相较于近端点法具有良好的收敛速度, 如图1(d)所示. 额外梯度法的核心思想在于通过一个简单的梯度更新步骤逼近
相比梯度上升下降法, 每次迭代, 额外梯度法增加一步外推(extrapolation)点的计算, 使用外推点的梯度完成当前点的更新. 额外梯度法通过外推点的计算加大探索, 使得更新迭代时更容易找到逼近最优解的正确方向, 具备良好的收敛性.
3.2. 马尔科夫博弈策略梯度算法
基于额外梯度法提出适用于马尔科夫博弈的策略梯度算法. 该算法使用的策略梯度
基于此, 提出马尔科夫博弈策略梯度(Markov game policy gradient, MG-PG)算法, 如算法1所示.
算法1 MG-PG算法
输入可导的参数化联合策略
同时更新策略参数
1. for
2.根据联合策略
3. for
5.end for
6.根据联合策略
7. for
9.end for
9.end for
首先, 将输入的可导参数化联合策略
3.3. 马尔科夫博弈策略梯度算法的收敛性
当目标函数
假设1 两方零和马尔科夫博弈(式(1))和参数化的联合策略
1) 策略梯度
2) 存在
并且, 对任意
其中, 常数
3) 随机向量
的方差是有界的, 即
Pethick等 [18]给出了一类满足弱Minty变分不等式(weak Minty variational inequality, MVI)的非凸非凹minimax问题的额外梯度型算法. 本研究的问题设定中无约束项, 因此文献[18]的Assumption I(i)中的正则算子
是真实策略梯度
定理2 在假设1下, 令
即参数化联合策略
证明: 基于假设1, 根据文献[18]定理3.5可知, 当
接着令
在式(41)不等式两边同时除以
由式(42)可得, 若按照概率
令
存在
4. 仿真实验
4.1. 实验对象和评估指标
采用棋盘游戏Oshi-Zumo[23]来验证算法MG-PG的收敛性. 该游戏中有2个玩家, 是一种同时移动的零和博弈, 其难点在于每次决策时的不确定性和信息不对称性, 即每个玩家无法知道对手的决策, 需要更加复杂的策略来应对可能的动作. 一轮博弈往往须经过多步博弈才能分出胜负, 其游戏规则如下: 棋盘上有2N+1个格子一维排列, 编号1,···,2N+1, 在棋盘中心(第N+1个格子)有一面旗帜, 旗帜的移动方向取决于每一轮博弈中玩家1、2的每步博弈结果(移动格数始终为1). 如图2所示, 玩家1、2初始时各有X枚硬币, 每一步, 玩家1、2同时出硬币, 记为M1和M2, 然后比较M1和M2的大小, 旗帜始终往出币数少的一方移动, 即若M1>M2,旗帜向右移动一个格子; 若M1<M2,旗帜向左移动一个格子; 若M1=M2,旗帜不移动. 每一步博弈后2个玩家的总数减去出币数M1和M2,并开始下一步博弈. 比赛一直进行到双方的硬币都用完, 或者旗帜被推出棋盘外. 获胜者根据旗帜的位置确定−距离旗帜所在的位置近的玩家输掉比赛. 如果旗帜的最后位置是棋盘中心, 则比赛结果为平局.
图 2
图 2 Oshi-Zumo在不同设定下的状态变化示意图
Fig.2 Schematic diagrams of state of Oshi-Zumo in different settings
Oshi-Zumo的状态由3部分组成: 玩家1的剩余硬币数、玩家2的剩余硬币数和旗帜的位置. 旗帜位置由格子编号表示, 当旗帜从左移出第1个格子后, 旗帜位置为0; 当从右移出第2N+1个格子后, 旗帜位置为2N+2. 当游戏参数确定后, 初始状态也是确定的. 玩家的动作就是出币数, 仅当博弈结束后才获得奖励. 玩家1作为max玩家(期望收益为正), 获胜则奖励为1; 玩家2获胜则奖励为−1, 平局则奖励为0.
式中的最佳响应策略由单智能体强化学习算法训练获得. 由定义1、2可知, 当
4.2. 表格式softmax参数化策略
在第k迭代轮次, 将玩家在状态s下的策略参数
式中:
表 1 不同参数化策略设定下的算法超参数
Tab.1
| 参数 | |||||
| 表格式Softmax | 0.3 | 0.5 | 1.0 | 106 | 1 |
| 神经网络 | 0.1 | 0.3 | 1.0 | 8×106 | 1 |
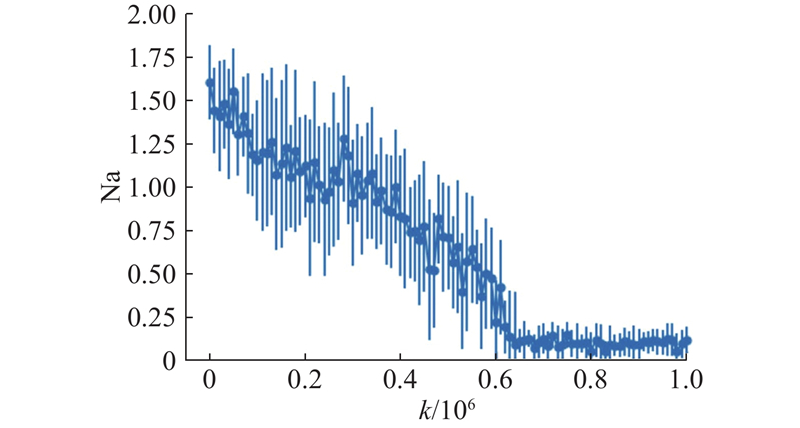
设置10组实验, 实验的评估数据如图3所示.图中, k表示策略参数更新的次数, Na表示纳什收敛指标的值, 圆点曲线表示10组实验纳什收敛指标的均值及变化趋势, 竖线表示10组实验纳什收敛指标的离散程度, 竖线的上下界分别由均值加减标准差得到.可以看出,实验中随着更新次数的增加, 纳什收敛指标虽然存在一定的方差, 但其均值整体呈减缓下降趋势, 当更新次数达到约60万次时, 纳什收敛指标的均值接近零, 此时联合策略达到近似纳什均衡.
图 3
图 3 策略参数化下MG-PG算法的纳什收敛指标
Fig.3 Nash convergence of MG-PG algorithm with policy parameterized
4.3. 神经网络参数化策略
在如图2(b)所示的游戏规模下, 状态动作空间大小急剧增长, 使用表格式softmax参数化策略容易导致实验过程中出现内存溢出的问题. 因此, 将神经网络作为参数化策略, 并通过MG-PG算法训练优化神经网络的参数, 最终达到近似纳什均衡.
在神经网络作为参数化策略的实验中, 2个玩家的初始币数都是50, 棋盘中共有
策略网络优化流程如下. 采用在线学习方式, 在第k轮次下, 将环境状态
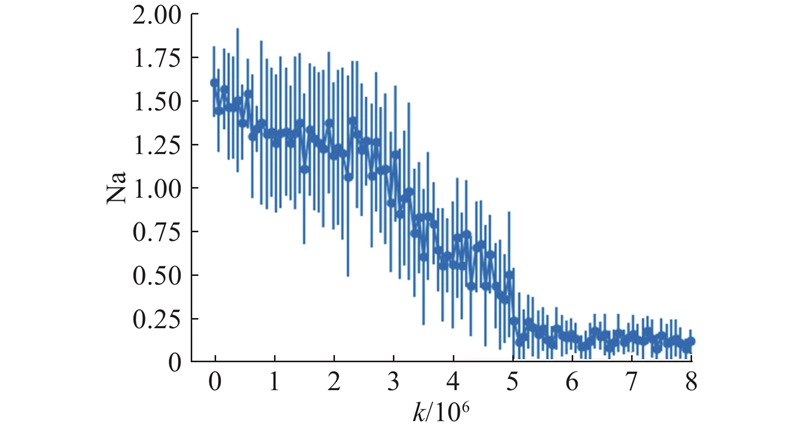
在神经网络设定下同样设置了10组实验,实验的评估数据如图4所示. 与策略参数化设定相类似,尽管纳什收敛指标存在一定的方差,但其均值整体呈减缓下降趋势. 当更新次数达到约500万次时,纳什收敛指标的均值接近零, 此时联合策略达到近似纳什均衡. 实验结果表明,MG-PG算法对于大规模博弈问题仍然适用.
图 4
图 4 神经网络下MG-PG算法的纳什收敛指标
Fig.4 Nash convergence of MG-PG algorithm with neural network setting
4.4. 对比实验
独立策略梯度方法本质上为单智能体强化学习,若2个玩家都使用常用的reinforce算法进行参数更新, 则更新式为
其中,
式中:ηd为学习率.
实验中玩家策略采用神经网络的形式, 参数
嵌套梯度下降方法则将最大最小优化问题(式(15))转化为如下最小优化问题:
其中,
进而有
因此, 嵌套梯度下降方法在每一轮迭代时, 先进行一次“嵌套内循环”, 近似计算出
将策略参数为
演员-评论家虚拟博弈算法通过Actor-Critic框架对虚拟博弈过程进行随机近似, 使得算法能够收敛到纳什均衡. 策略与价值函数的更新式如下.
Actor step:
Critic step:
式中:上标i表示玩家标号,
在实验中步长选择为
每种算法同样进行10组实验, 实验结果如图5所示. 每种算法都迭代更新了800万次. 可以看出, 独立策略梯度方法、嵌套梯度下降方法和双时间尺度算法3种方法在800万的更新次数内不收敛, 并且纳什收敛指标也没有明显下降的趋势. 3种方法都使用了reinforce算法, 因此在10组实验中都呈现出较大的方差. 演员-评论家虚拟博弈算法则在实验中表现良好, 纳什收敛指标呈现出较为平滑的下降趋势. 但该算法在800万次的更新中并未收敛到近似纳什均衡, 纳什收敛指标的均值在更新后约为0.50, 相较于MG-PG算法在500万次达到约0.15还存在一定的性能差距. 同时该算法在训练过程中由于要计算最佳响应策略,对于时间的消耗也是巨大的. 不过,得益于Actor-Critic框架值函数提供了对策略的评估, 策略改进更加稳定, 大大减小了不同实验组策略优化过程中的方差.
图 5
图 5 4种对比算法的纳什收敛指标图
Fig.5 Nash convergence index diagram of four comparison algorithms
综上,单智能体强化学习的思想及其方法在Oshi-Zumo这种同时移动博弈游戏中的表现欠佳. 演员-评论家虚拟博弈算法相较于本研究所提出的MG-PG算法收敛速度较慢, 但其Actor-Critic框架带来的小方差为本研究今后的工作提供了指导和启示.
5. 结 语
提出两方零和马尔科夫博弈的策略定理及其相关证明, 并基于随机策略梯度和额外梯度法提出适用于马尔科夫博弈的策略梯度算法. 该算法在外推点梯度计算阶段, 利用已知的博弈轨迹计算外推点的梯度, 改善探索方向, 使得算法更容易朝正确方向更新; 在策略参数更新阶段, 利用外推点的梯度更新策略参数. 最终在假设1的条件下分析得到该算法的收敛性.
在Oshi-Zumo上的大量实验表明, 本研究算法经过一定的迭代轮次可以有效地收敛到近似纳什均衡解. 应用神经网络拟合博弈策略, 解决了大规模博弈问题. 通过对比实验验证了MG-PG算法的优越性和有效性.
如何通过应用Actor-Critic Network减小MG-PG算法方差以及如何解决环境部分可观的马尔科夫博弈问题, 是未来可以继续研究的方向.
参考文献
Mastering the game of Go with deep neural networks and tree search
[J].DOI:10.1038/nature16961 [本文引用: 1]
Superhuman AI for multiplayer poker
[J].DOI:10.1126/science.aay2400 [本文引用: 1]
一种用于两人零和博弈对手适应的元策略演化学习算法
[J].
A meta-evolutionary learning algorithm for opponent adaptation in two-player zero-sum games
[J].
Equilibrium points in n-person games
[J].DOI:10.1073/pnas.36.1.48 [本文引用: 1]